Dynamics of a non-autonomous predator-prey system with Hassell-Varley-Holling Ⅱ function response and mutual interference

1.   Introduction

Since the functional response was proposed by Holling ^[1], many scholars have considered the dynamic behavior of systems with different functional response. The hybrid models combining Holling type and other functional response such as B-D and L-G type have received great attention (see e.g. ^{[2,3,4,5,6,7,8,9,10,11]}). Further, when several factors such as the growing process and gestation of population are taken into account, lots of models with time-delays and stage-structured have been investigated (see e.g. ^{[12,13,14,15,16,17,18,19]}). Some stochastic predator-prey systems have been studied due to the impact of environmental noise (see e.g. ^[20,21]).

Hassell ^[22] considered a predator-prey system between parasite and host. It was found either one or both of them would leave from the meeting place when two predators meet. This phenomenon is known as the mutual interference of predatory behavior in single-species population. Subsequently to this discovery, many authors began to pay close attention to the dynamic behavior of systems with mutual interference(see e.g. ^[23,24,25]). Fu and Chen ^[25] studied the autonomous model with mutual interference:

where $a-bx^\alpha-cx^{2\alpha}$ is the nonlinear average growth of the prey due to environmental changes in the habitat, $\frac{hx^\beta }{1+rx^\beta}$ is the nonlinear saturated function response and $m$ is interference parameter. It studied the persistence, the stability of the coexisting equilibrium point and the existence of limit cycles in ^[25].

Obviously, $\frac{hx^{\beta}}{1+rx^{\beta}}$ is monotone increasing function for any $x > 0$, that implies when the prey density increases, the predation rate increases. In other words, the predation rate is not affected by the number of predators. However, the predation rate can depend on its density in the real world. Hassell and Varley ^[26] found that the abundance of predators counteracts the predator rate by experiments, and obtained the functional response $\frac{{\alpha}x}{y^{\sigma}}$ which was named Hassell-Varley type functional response. The adaptive range of $\sigma$ is $(0, 1]$ and the value of $\sigma$ reflects the size of predator groups. Arditi ^[27] and Sutherland ^[28] combined Hassell-Varley type with Holling type functional response, and produced Hassell-Varley-Holling functional response $\frac{{\alpha}x}{y^{\sigma}+hx}$ (Ⅱ type) and $\frac{{\alpha}x^2}{y^{\sigma}+hx^2}$ (Ⅲ type) respectively. Subsequently, some Hassell-Varley-Holling type predator-prey systems had been discussed (see e.g. ^[29,30,31]).

In the paper, in order to better reflect the influence of predator groups on predation behavior, we choose Hassell-Varley-Holling Ⅱ functional response $\frac{hx}{y^{\sigma}+rx}$. According to the modeling mechanism of literature ^[25], we establish the following model:

However, the biological and environmental parameters are changing over time. When these factors are considered, the corresponding model should be non-autonomous. Many authors focused on the permanence, stability and positive periodic solution about the non-autonomous models (see e.g. ^{[2,5,7,12,13,14,15,18,23,24,29,32,33,34]}). To our knowledge, there is no literature considering the non-autonomous model with Hassell-Varley-Holling Ⅱ and mutual interference.

In the paper, let us discuss the model:

where $0\leq\alpha\leq1$, $0 < \sigma\leq1$, $0 < m\leq1$. $m$ is the mutual interference factor of predator. $a(t)$ represents the intrinsic growth rate, $b(t)$ measures the intra species competition rate, $c(t)$ denotes the removal coefficient of the prey. $f(t)$ and $d(t)$ are the increasing coefficient and the death rate of predator respectively. $h(t)$ and $r(t)$ denote the ability and the unit time number to search for prey. If ${\sigma} = m = 1$, the system (1.3) is well known as ratio-dependent predator-prey system. Especially, if ${\alpha} = {\sigma} = m = 1, c(t) = 0$, the system (1.3) has been studied by Fan ^[32].

One of our purpose is to obtain some conditions for the stability and periodic solutions of (1.3). The index $m$ and $\sigma$ of the term $\frac{h(t)xy^m}{r(t)x+y^\sigma}$ prevent us from directly using the methods in the literature (see e.g. ^{[5,18,23,24,29,32,33]}). Here, we employ different methods in Section 2 to prove the stability and find the priori bound.

The rest of this paper is organized as follow. Using the principle of comparison and constructing a suitable Liapunov function, we obtain the sufficient conditions for the permanence, non-permanence and globally asymptotic stability of system (1.3) in Section 2. In Section 3, the coincidence degree theorem is employed to find the conditions for the existence of positive periodic solutions. A sufficient and necessary condition is obtained when $m > {\sigma}$ and some sufficient conditions are obtained when $m = {\sigma}$. Finally, we give some examples to demonstrate the validity of results.

2.   Permanence and globally asymptotic stability

We suppose that all parameters are continuous and bounded functions in this section. Set

Clearly, (1.3) can be calculated by

Lemma 2.1 $R^2_+$ is positively invariant for system (1.3).

From the view of the biological significance, we consider the initial condition satisfies $x(t_0) > 0, y(t_0) > 0$ in the following discussion.

Theorem 2.2 If $f^l-r^ud^u > 0$ and $a^l-h^u(M_2^\varepsilon)^{m-\sigma} > 0$, then $\Gamma_\varepsilon$ is positively invariant for system (1.3), where

and $\varepsilon \geq0$ is small enough to satisfy $a^l-h^u(M_2^\varepsilon)^{m-\sigma} > 0$.

Proof. According to (1.3a), we have

Using the comparison theorem, if $0 < x(t_0)\leq M_1^\varepsilon$, then $x(t)\leq M_1^\varepsilon$ for any $t\geq t_0.$

Similarly, From (1.3b), we can write

Thus, we obtain $y(t)\leq M_2^\varepsilon$ for any $t\geq t_0$ when $0 < y(t_0)\leq M_2^\varepsilon.$

Meanwhile, (1.3a) yields

Hence, if $x(t_0)\leq m_1^\varepsilon,$ then $x(t)\geq m_1^\varepsilon$ for any $t\geq t_0.$

Similarly, (1.3b) reduces to

Thus, we obtain $y(t)\leq m_2^\varepsilon$ for any $t\geq t_0$ when $y(t_0)\geq m_2^\varepsilon.$ The proof is completed.

Theorem 2.3 If $f^l-r^ud^u > 0$ and $a^l-h^u(M_2^0)^{m-\sigma} > 0$ hold, system (1.3) is permanent.

Proof. From (1.3a), we have

By using the comparison theorem, it follows that

Meanwhile, for any $\varepsilon > 0$, there exists $T_1 > 0$ such that $x(t) < M_1^0+\varepsilon$ for all $t > T_0.$ Then, from (1.3b), we obtain

for $t > T_1$. Using the comparison theorem again, we show that

Since the arbitrariness of $\varepsilon$, we have

Using a similar argument, it is easy to obtain that

By the definition of persistence in ^[32], the conclusion is correct. The proof is completed.

From the proof of Theorem 2.3, we easily know two facts that system (1.3) is ultimately bounded and the ultimate bound is $\Gamma_\varepsilon$, which is asserted in the following theorem.

Theorem 2.4 If $f^l-r^ud^u > 0$ and $a^l-h^u(M_2^0)^{m-\sigma} > 0$, then system (1.3) is ultimately bounded, $\Gamma_\varepsilon$ in (2.1) is an ultimately bounded region.

Remark 2.5 If $m = \sigma = 1$, the above conclusions are refer to ^[32].

Theorem 2.6 If $f^u-r^ld^l < 0$, then system (1.3) is not permanent.

Proof. According to (1.3a), it is not difficult to have

Obviously, we have $\begin{aligned} \lim_{t\rightarrow +\infty}y(t) = 0. \end{aligned}$

Theorem 2.7 If $m = \sigma$ and $\frac{h^l}{r^u+1} > a^u+{\sigma}d^u$, then system (1.3) is not permanent.

Proof. If $m = \sigma$ and $\frac{h^l}{r^u+1} > a^u+{\sigma}d^u$, then we can obtain $\begin{aligned} \lim_{t\rightarrow +\infty}x(t) = 0 \end{aligned}$ under certain initial conditions by the following argument.

For $\frac{h^l}{r^u+1} > a^u+{\sigma}d^u$, there exists $\alpha > 1$, we have $\frac{e^l}{r^u \alpha+1} = a^u+{\sigma}d^u$. We can get $\begin{aligned} \lim_{t\rightarrow +\infty}x(t) = 0 \end{aligned}$ when the initial value satisfies $\frac{x(t_0)}{y^\sigma (t_0)} < \alpha$. Otherwise, there exists a first time $t_1$, for $t\in[t_0, t_1)$, we have $\frac{x(t_1)}{y^\sigma(t_1)} = \alpha$ and $\frac{x(t)}{y^\sigma(t)} < \alpha$.

For any $t\in[t_0, t_1]$, we have

which yields

However, for $t\geq t_0$, it leads to

then

Thus, for $t\in[t_0, t_1]$, it produces

Obviously, it contradicts the existence of $t_1$. Hence for $t\geq t_0$, it can be

namely,

The proof is completed.

In fact, the growth of predator is entirely dependent on the amount of available prey. That is to say, when the prey goes extinct, so does the predator. Thus, both the prey and predator go extinct eventually when $m = \sigma$ and $\frac{h^l}{r^u+1} > a^u+{\sigma}d^u$.

Theorem 2.8 If $(\hat{x}(t), \hat{y}(t))\in L_\varepsilon$ is a solution and parameters satisfy the following conditions:

Then system (1.3) is globally asymptotically stable.

Proof. Let $(x(t), y(t))$ be any solution, there exists $T_1 > t_0$, we have $(x(t), y(t))\in L_\varepsilon$ for any $t > T_1.$

Let us define the Liapunov function

The $D^+V(t)$ along the solution for $t > T_1$ is calculated as follows:

where $\xi(t)$ lies between $x(t)$ and $\hat{x}(t)$, $\eta_1(t)$ and $\eta_2(t)$ lie between $y(t)$ and $\hat{y}(t)$ respectively.

Let $G(t)\equiv|x(t)-\hat{x}(t))|+|y(t)-\hat{y}(t)|$ and $\lambda = \min\{E_1, E_2\}$, then for $t > T_1$, it follows that

We integrate both sides with (2.3) form $T_1$ to $t$, then

namely,

Obviously, we have

For $t > T_1$, we know that $x(t)$, $y(t)$, $\hat{x}(t)$ and $\hat{y}(t)$ are all bounded, it implies that their derivatives are bounded. Hence, ${G(t)}$ is uniformly continuous. We have

The proof is completed.

3.   Periodic solution

In this section, we suppose that all parameters are periodic functions with period $\omega$ and denote that $\bar{p} = \frac{1}{\omega}\int_0^\omega p(t)dt$.

Lemma 3.1 (see ^[35]) Let $L$ be a Fredholm operator of index zero and $N$ be $L-$ compact on $\mathop \Omega \limits^ -$. If

$(i)$ For each $\lambda \in \left({0, 1} \right)$, any $x \in \partial \Omega$ is such that $Lx \neq \lambda Nx$.

$(ii)$ $QNx \ne 0$ for each $x \in \partial \Omega \cap KerL$ and the Brouwer degree:

Then $Lx = Nx$ has at least one solution on $DomL \cap \mathop \Omega \limits^ -$.

Theorem 3.2 If $m > \sigma$, then the sufficient and necessary condition of system (1.3) which has at least one positive solution with period $\omega$ is $\overline{(\frac{f}{r})}-\bar{d} > 0$.

Proof. We prove the necessity first. Integrating (1.3b) over one period $\omega$, we obtain

Here, we assume that $(\tilde{x}(t), \tilde{y}(t))^T$ is a positive solution with period $\omega$.

Next, we proceed to prove the sufficiency via Lemma 3.1. The following notations can refer to (see ^[32,35]). Let

System (1.3) is rewritten as

Let

It can be seen that $X$ and $Z$ are Banach spaces.

Clearly, $KerL = \{v\in X\mid v\in R^2\},$ $ImL = \{ v\in Z\mid \int_0^\omega v(t)dt = 0 \}$ is closed in $Z$. Meanwhile, $\text{dim}KerL = \text{Co} \text{dim}ImL = 2$. So $L$ is a Freedom mapping of index zero.

On the other hand, $P$, $Q$ are continuous projectors and satisfy $P^2 = P$, $Q^2 = Q$, $Im P = Ker L$, $Im L = Ker Q = Im (I-Q)$. Hence, there is a mapping $K_p: Im L\rightarrow Dom L\cap Ker P$ and given by

Thus

Obviously, $QN$ and $K_p(I-Q)N$ are continuous mapping. Based on Arzela-Ascoli theorem, we have $K_p(I-Q)N(\bar{\Omega})$ is compact and $QN(\bar{\Omega})$ is bounded. Then $N$ is $L$ compact on $\bar{\Omega}$.

Next, we look for a set $\Omega$ which satisfies the coincidence degree theorem.

According to the above definition, the equation $Lx = \lambda Nx$ can be written as

For a certain $\lambda$, let $(\hat{x}(t), \hat{y}(t))^T\in X$ be a solution of (3.2). By integrating over $[0, \omega]$, we have

By (3.2) and (3.3), we have

Let

From (3.3a), we have

which yields

then

We transform (3.3a) again and obtain

If $\hat{x}(\eta_1)\geq \hat{y}(\eta_2)$, the inequality (3.6) reduces to

Using the function

then $g(0) = -\bar{a}$, $\begin{aligned} \lim_{u\rightarrow +\infty}g(u) = 0 \end{aligned}$, and $g(u)$ is strictly monotone increasing function over the interval $(0, +\infty)$. Therefore, there exists $\delta_1 > 0$ such that $\hat{x}(\eta_1)\geq \text{ln}\delta_1$.

If $x(\eta_1) < y(\eta_2)$, by the inequality (3.6) again, we have

Similarly, it exists $\delta_2 > 0$ such that $\hat{y}(\eta_2)\geq \text{ln} \delta_2$. Then

On the other hand, (3.3b) reduces to

thus

Taking $\delta = \text{max}\{ \delta_1, \frac{\bar{d}\sigma\delta_2 }{e^{2\bar{d}\omega}\bar{f}} \}$, then $\hat{x}(\eta_1)\geq \text{ln} \delta$. Therefore

(3.3b) can also produce

then

Therefore

Similarly, we also have

then

Hence

Obviously, $H_1, H_2, H_3$ and $H_4$ are independent of $\lambda$. Let

$QN v\neq (0, 0)^T$ for any $v\in\partial \Omega \cap Ker L$. Otherwise, there exists a constant vector $v = (v_1, v_2)\in\partial \Omega \cap R^2$ such that $QN v = (0, 0)^T$, that is

This contradicts the previous result which $H_1\leq v_1\leq H_2$ and $H_3\leq v_2\leq H_4$. We define the mapping as follows

for any $\theta\in [0, 1]$. Obviously, if $v = (v_1, v_2)\in Ker L \cap \partial\Omega$, then $\varphi(v_1, v_2, \theta) \neq 0$. We claim that $\varphi$ is a homotopic mapping. Taking $J = I$, then

However, $\varphi(v_1, v_2, 0) = 0$ implies

It is easy to know that (3.11) has a single solution $({v_1}^\ast, {v_2}^\ast)^T$.

We get a set $\Omega$ which satisfies the conditions in coincidence degree theorem. Therefore, (3.1) has at least a solution $(\hat{x}^*(t), \hat{y}^*(t))^T$ with period $\omega$, corresponding to (1.3) has a solution $(\exp\{\hat{x}^*(t)\}, \exp\{\hat{y}^*(t)\})^T$. The proof is completed.

Theorem 3.3 If the conditions $(i)$$m = \sigma$, $(ii)$ $\overline{(\frac{f}{r})}-\bar{d} > 0$, $(iii)$ $\bar{a} > \bar{h}$ hold, then system (1.3) has at least one positive periodic solution.

Proof. If $m = \sigma$, then (3.6) reduces to

Taking

Then $g(0) = \bar{h}-\bar{a} < 0$, $\begin{aligned} \lim_{u\rightarrow +\infty}g(u) = +\infty \end{aligned}$. Based on the analysis in Theorem 3.2, there exists $\delta > 0$ such that $\hat{x}(\eta_1)\geq \text{ln} \delta.$ Therefore,

The rest of the proof is completely the same as Theorem 3.2. The proof is completed.

Combine Theorem 2.8 and Theorem 3.2 (or Theorem 3.3), the following theorem is obvious.

Theorem 3.4 If the conditions in Theorem 2.8 and Theorem 3.2 (or Theorem 3.3) hold simultaneously, then the periodic solution of (1.3) is unique and globally asymptotically stable.

Remark 3.5 Theorem 3.3 admits that if $m > \sigma$, then the existence of positive periodic solution only depends on the relationship of the average intrinsic growth rate of prey, the average unit time number to search for prey and the average increasing coefficient of predator.

Remark 3.6 There is an interesting phenomenon: We derive the priori bounds for the solution of $Lx = {\lambda}Nx$ in the same way, however, we obtain sufficient and necessary conditions when $m > \sigma$ and only get sufficient conditions when $m = \sigma$. Especially, if $m = \sigma$ = 1, the result corresponds to results in ^[32].

The following theorem shows the properties of a boundary solution.

Theorem 3.7 System (1.3) has at least a boundary period solution, namely $(x^*(t), 0)$. Moreover, if $d(t)-\frac{f(t)}{r(t)}-h(t) > 0$, then $(x^*(t), 0)$ is globally asymptotically stable.

Proof. For the equation $\frac{dx}{dt} = x(a(t)-b(t)x^\alpha-c(t)x^{2\alpha})$, it is easy to obtain the first part of conclusion by using the proof method of Theorem 3.2. Since $d(t)-\frac{f(t)}{r(t)}-h(t) > 0$ implies $d(t)-\frac{f(t)}{r(t)} > 0$, it follows that $\begin{aligned} \lim_{t\rightarrow +\infty}y(t) = 0 \end{aligned}$ from system (1.3). Therefore, we just prove $\begin{aligned} \lim_{t\rightarrow +\infty}x(t) = x^*(t) \end{aligned}$. Define the following Liapunov function

The $D^+V(t)$ along the solution can be written as

The remaining proof details are similar as Theorem 2.7. This completes the proof.

4.   Numerical simulations

Several cases demonstrate the correctness of the previous conclusions in this section. We let $\rho = \overline{(\frac{f}{r})}-\bar{d}$, $x(0) = 1.5$, $y(0) = 1.4$. Choosing the parameters in (1.3) as follows:

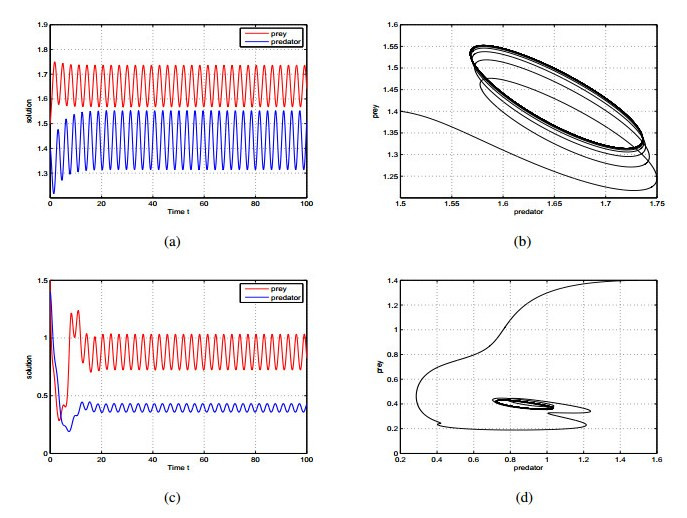
Example 4.1 Let $\sigma = 0.5, m = 0.75$, $h(t) = 1.1+0.1\text{sin}2t,$ others parameters are the same in (4.1). The solutions and phase portraits of (1.3) are shown in Figure 1.

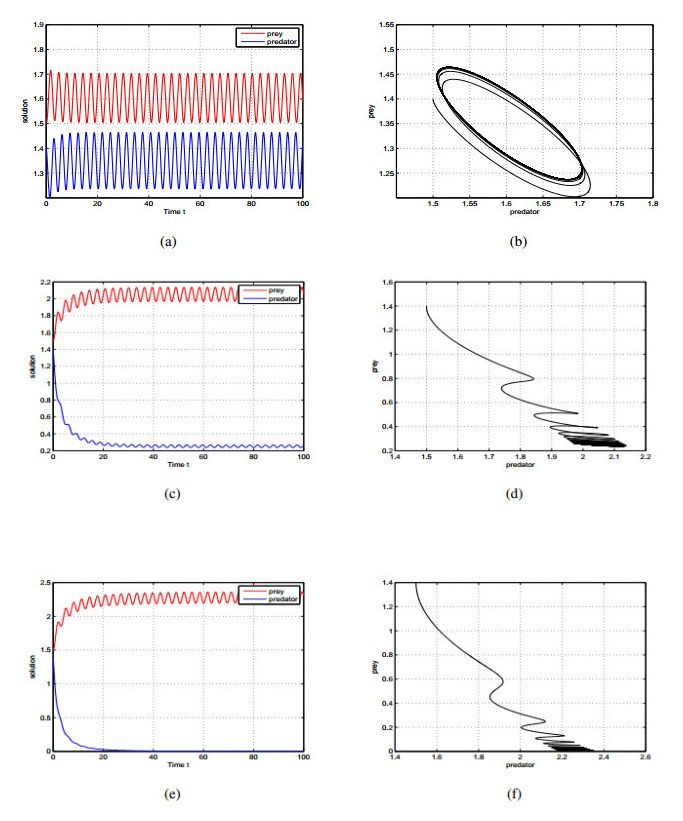
Example 4.2 Let $\sigma = m = 0.5$, $f(t) = 0.6+0.1\text{sin}2t, \rho = 0.4375$, others parameters are the same in (4.1). The solutions and phase portraits of (1.3) are shown in Figure 2.

The simulation results in Figure 1 shows that the following conclusions: If $\rho > 0$ and $\rho$ gets more and more small, the predator curve oscillates at a lower density and the prey curve oscillates at a higher density. If $\rho < 0$, then $\begin{aligned} \lim_{t\rightarrow +\infty}y(t) = 0 \end{aligned}$, namely, the positive periodic solution disappears. It also shows that $\rho = 0$ is the threshold, which confirms Theorem 3.2.

From (c, d) in Figure 2, we know $\bar{a} > \bar{h}$ is not necessary for positive periodic solution of system (1.3) but only sufficient when $\sigma = m$.

5.   Conclusions

In this paper, we discussed a non-autonomous Hassell-Varley-Holling type predator-prey system with mutual interference. Compared with that in ^[25], we believe our model reflects the influence of predator groups on predation behavior.

Firstly, we focused on permanence, extinction and globally asymptotic stability of the model by using the principle of comparison and a suitable Liapunov function and differential mean value theorem. The investigation showed that the shorter the time to search for prey is, the more favorable permanence is under the conditions of the Theorem 2.3. However, the conditions for globally asymptotic stability in Theorem 2.8 is too complex to be applied directly.

Secondly, we studied some conditions for the existence of a positive periodic solution by using the coincidence degree theorem and illustrate with some examples. When $m > \sigma$, we obtain a sufficient and necessary condition in Theorem 3.2, that is a perfect result. Figure 1 confirms this result. When $m = \sigma$, we only obtain some sufficient conditions in Theorem 3.3, but Figure 2 shows that the condition $\bar{a} > \bar{h}$ is not necessary. In addition, we give some sufficient conditions for the globally asymptotic stability of a boundary periodic solution.

This paper leaves a seemingly difficult problem that we can not solve: what are the conditions for the existence of a positive periodic solution when $m < \sigma$?

Acknowledgements

The authors thank the editor and referees for their valuable suggestions and comments, which improved the presentation of this manuscript. The research is supported by the Startup Foundation for Introducing Talent of Wuyi University (No. YJ201802).

Conflict of interest

For the publication of this article, no conflict of interest among the authors is disclosed.