The aim of this article is to introduce a new algorithm by integrating a viscosity-type method with the subgradient extragradient algorithm to solve the equilibrium problems involving pseudomonotone and Lipschitz-type continuous bifunction in a real Hilbert space. A strong convergence theorem is proved by the use of certain mild conditions on the bifunction as well as some restrictions on the iterative control parameters. Applications of the main results are also presented to address variational inequalities and fixed-point problems. The computational behaviour of the proposed algorithm on various test problems is described in comparison to other existing algorithms.
1.
Introduction and our main results
The classical rational Ramanujan-type series for π−1 (cf. [1,2,8,27] and a nice introduction by S. Cooper [10,Chapter 14]) have the form
where b,c,m are integers with bm≠0, d is a positive squarefree number, λ is a nonzero rational number, and a(k) is one of the products
In 1997 Van Hamme [47] conjectured that such a series (∗) has a p-adic analogue of the form
where p is any odd prime with p∤dm and λ∈Zp, ε1∈{±1} and εd=−1 if d>1. (As usual, Zp denotes the ring of all p-adic integers, and (⋅p) stands for the Legendre symbol.) W. Zudilin [53] followed Van Hamme's idea to provide more concrete examples. Sun [33] realized that many Ramanujan-type congruences are related to Bernoulli numbers or Euler numbers. In 2016 the author [44] thought that all classical Ramanujan-type congruences have their extensions like
where p is an odd prime, and n∈Z+={1,2,3,…}. See Sun [45,Conjectures 21-24] for more such examples and further refinements involving Bernoulli or Euler numbers.
During the period 2002–2010, some new Ramanujan-type series of the form (∗) with a(k) not a product of three nontrivial parts were found (cf. [3,4,9,29]). For example, H. H. Chan, S. H. Chan and Z. Liu [3] proved that
where Dn denotes the Domb number ∑nk=0(nk)2(2kk)(2(n−k)n−k); Zudilin [53] conjectured its p-adic analogue:
The author [45,Conjecture 77] conjectured further that
for each odd prime p and positive integer n.
Let b,c∈Z. For each n∈N={0,1,2,…}, we denote the coefficient of xn in the expansion of (x2+bx+c)n by Tn(b,c), and call it a generalized central trinomial coefficient. In view of the multinomial theorm, we have
Note also that
and
for all n∈Z+. Clearly, Tn(2,1)=(2nn) for all n∈N. Those Tn:=Tn(1,1) with n∈N are the usual central trinomial coefficients, and they play important roles in enumerative combinatorics. We view Tn(b,c) as a natural generalization of central binomial and central trinomial coefficients.
For n∈N the Legendre polynomial of degree n is defined by
It is well-known that if b,c∈Z and b2−4c≠0 then
Via the Laplace-Heine asymptotic formula for Legendre polynomials, for any positive real numbers b and c we have
(cf. [40]). For any real numbers b and c<0, S. Wagner [48] confirmed the author's conjecture that
In 2011, the author posed over 60 conjectural series for 1/π of the following new types with a,b,c,d,m integers and mbcd(b2−4c) nonzero (cf. Sun [34,40]).
Type Ⅰ. ∑∞k=0a+dkmk(2kk)2Tk(b,c).
Type Ⅱ. ∑∞k=0a+dkmk(2kk)(3kk)Tk(b,c).
Type Ⅲ. ∑∞k=0a+dkmk(4k2k)(2kk)Tk(b,c).
Type Ⅳ. ∑∞k=0a+dkmk(2kk)2T2k(b,c).
Type Ⅴ. ∑∞k=0a+dkmk(2kk)(3kk)T3k(b,c).
Type Ⅵ. ∑∞k=0a+dkmkTk(b,c)3,
Type Ⅶ. ∑∞k=0a+dkmk(2kk)Tk(b,c)2,
In general, the corresponding p-adic congruences of these seven-type series involve linear combinations of two Legendre symbols. The author's conjectural series of types Ⅰ-Ⅴ and Ⅶ were studied in [6,49,54]. The author's three conjectural series of type Ⅵ and two series of type Ⅶ remain open. For example, the author conjectured that
as well as its p-adic analogue
where p is any prime greater than 3.
In 1905, J. W. L. Glaisher [15] proved that
This actually follows from the following finite identity observed by the author [38]:
Motivated by Glaisher's identity and Ramanujan-type series for 1/π, we obtain the following theorem.
Theorem 1.1. We have the following identities:
and
where
Recall that the Catalan numbers are given by
For k∈N it is easy to see that
Thus, for any a,b,c,m∈Z with |m|≥64, we have
For example, (1.2) has the equivalent form
For any odd prime p, the congruence (1.4) of V.J.W. Guo and J.-C. Liu [19] has the equivalent form
(where E0,E1,… are the Euler numbers), and we note that this is also equivalent to the congruence
Recently, C. Wang [50] proved that for any prime p>3 we have
and
(Actually, Wang stated his results only in the language of hypergeometric series.) These two congruences extend a conjecture of Guo and M. J. Schlosser [21].
We are also able to prove some other variants of Ramanujan-type series such as
and
Now we state our second theorem.
Theorem 1.2. We have the identities
where
For k=j+1∈Z+, it is easy to see that
Thus, for any a,b,c,m∈Z with 0<|m|≤64, we have
For example, (1.77) has the following equivalent form
In contrast with the Domb numbers, we introduce a new kind of numbers
The values of Sn (n=0,…,10) are
respectively. We may extend the numbers Sn (n∈N) further. For b,c∈Z, we define
Note that Sn(1,1)=Sn and Sn(2,1)=Dn for all n∈N.
Now we state our third theorem.
Theorem 1.3. We have
Remark 1.1. The author found the 10 series in Theorem 1.3 in Nov. 2019.
We shall prove Theorems 1.1-1.3 in the next section. In Sections 3-10, we propose 117 new conjectural series for powers of π involving generalized central trinomial coefficients. In particular, we will present in Section 3 four conjectural series for 1/π of the following new type:
Type Ⅷ. ∑∞k=0a+dkmkTk(b,c)Tk(b∗,c∗)2,
where a,b,b∗,c,c∗,d,m are integers with mbb∗cc∗d(b2−4c)(b2∗−4c∗)(b2c∗−b2∗c)≠0.
Unlike Ramanujan-type series given by others, all our series for 1/π of types Ⅰ-Ⅷ have the general term involving a product of three generalized central trinomial coefficients.
Motivated by the author's effective way to find new series for 1/π (cf. Sun [35]), we formulate the following general characterization of rational Ramanujan-type series for 1/π via congruences.
Conjecture 1.1 (General Criterion for Rational Ramanujan-type Series for 1/π). Suppose that the series ∑∞k=0bk+cmkak converges, where (ak)k≥0 is an integer sequence and b,c,m are integers with bcm≠0. Suppose also that there are no a,x∈Z such that an=a(2nn)∑nk=0(2kk)2(2(n−k)n−k)xn−k for all n∈N. Let r∈{1,2,3} and let d1,…,dr∈Z+ with √di/dj irrational for all distinct i,j∈{1,…,r}. Then
for some nonzero rational numbers λ1,…,λr if and only if there are positive integers dj (r<j≤3) and rational numbers c1,c2,c3 with ∏ri=1ci≠0, such that for any prime p>3 with p∤m∏ri=1di and c1,c2,c3∈Zp we have
where εi∈{±1}, εi=−1 if di is not an integer square, and c2=c3=0 if r=1 and ε1=1.
For a Ramanujan-type series of the form (1.98), we call r its rank. We believe that there are some Ramanujan-type series of rank three but we have not yet found such a series.
Conjecture 1.2. Let (an)n≥0 be an integer sequence with no a,x∈Z such that an=a(2nn)∑nk=0(2kk)2(2(n−k)n−k)xn−k for all n∈N, and let b,c,m,d1,d2,d3∈Z with bcm≠0. Assume that limn→+∞n√|an|=r<|m|, and π∑∞k=0bk+cmkak is an algebraic number. Suppose that c1,c2,c3∈Q with c1+c2+c3=a0c , and
for all primes p>3 with p∤d1d2d3m and c1,c2,c3∈Zp. Then, for any prime p>3 with p∤m, c1,c2,c3∈Zp and (d1p)=(d2p)=(d3p)=δ∈{±1}, we have
Joint with the author's PhD student Chen Wang, we pose the following conjecture.
Conjecture 1.3 (Chen Wang and Z.-W. Sun). Let (ak)k≥0 be an integer sequence with a0=1. Let b,c,m,d1,d2,d3∈Z with bm≠0, and let c1,c2,c3 be rational numbers. If π∑∞k=0bk+cmkak is an algebraic number, and the congruence (1.100) holds for all primes p>3 with p∤d1d2d3m and c1,c2,c3∈Zp, then we must have c1+c2+c3=c.
Remark 1.2. The author [39,Conjecture 1.1(i)] conjectured that
for any prime p>3, which was confirmed by Y.-P. Mu and Z.-W. Sun [26]. This is not a counterexample to Conjecture 1.3 since ∑∞k=0(8k+5)T2k diverges.
All the new series and related congruences in Sections 3-9 support Conjectures 1.1-1.3. We discover the conjectural series for 1/π in Sections 3-9 based on the author's previous PhilosophyaboutSeriesfor 1/π} stated in [35], the PSLQ algorithm to discover integer relations (cf. [13]), and the following DualityPrinciple based on the author's experience and intuition.
Conjecture 1.4 (Duality Principle). Let (ak)k≥0 be an integer sequence such that
for any prime p∤6dD and k∈{0,…,p−1}, where d and D are fixed nonzero integers. If a0,a1,… are not all zero and m is a nonzero integer such that
for some b,d1,d2,d3∈Z+, c∈Z and λ1,λ2,λ3∈Q, then m divides D, and
for any prime p>3 with p∤dD.
Remark 1.3 (ⅰ) For any prime p>3 with p∤dDm, the congruence (1.102) holds modulo p by (1.101) and Fermat's little theorem. We call ∑p−1k=0ak/(Dm)k the dual of the sum ∑p−1k=0ak/mk.
(ⅱ) For any b,c∈Z and odd prime p∤b2−4c, it is known (see, e.g., [39,Lemma 2.2]) that
for all k=0,1,…,p−1.
For a series ∑∞k=0ak with a0,a1,… real numbers, if limk→+∞ak+1/ak=r∈(−1,1) then we say that the series converge at a geometric rate with ratio r. Except for (7.1), all other conjectural series in Sections 3-9 converge at geometric rates and thus one can easily check them numerically via a computer.
In Section 10, we pose two curious conjectural series for π involving the central trinomial coefficients.
2.
Proofs of Theorems 1.1-1.3
Lemma 2.1. Let m≠0 and n≥0 be integers. Then
Remark 2.1. The eight identities in Lemma 2.1 can be easily proved by induction on n. In light of Stirling's formula, n!∼√2πn(n/e)n as n→+∞, we have
Proof of Theorem 1.1. Just apply Lemma 2.1 and the 36 known rational Ramanujan-type series listed in [16]. Let us illustrate the proofs by showing (1.1), (1.2), (1.71) and (1.72) in details.
By (2.1) with m=−64, we have
Note that
and recall Bauer's series
So, we get
This proves (1.1). By (2.2) with m=−64, we have
and hence
Combining this with (1.1) we immediately get (1.2).
In view of (2.7) with m=−6403203, we have
and hence
In 1987, D. V. Chudnovsky and G. V. Chudnovsky [8] got the formula
which enabled them to hold the world record for the calculation of π during 1989–1994. Note that
and hence
This proves (1.71).
By (2.8) with m=−6403203, we have
and hence
Note that
Therefore, with the help of (1.71) we get
This proves (1.72).
The identities (1.3)–(1.70) can be proved similarly.
Lemma 2.2. Let m and n>0 be integers. Then
Remark 2.2. This can be easily proved by induction on n.
Proof of Theorem 1.2. We just apply Lemma 2.2 and use the known identities:
Here, the first identity was found and proved by D. Zeilberger [52] in 1993. The second, third and fourth identities were obtained by J. Guillera [17] in 2008. The fifth identity on K was conjectured by Sun [33] and later confirmed by K. Hessami Pilehrood and T. Hessami Pilehrood [22] in 2012. The last four identities were also conjectured by Sun [33], and they were later proved in the paper [18,Theorem 3] by Guillera and M. Rogers.
Let us illustrate our proofs by proving (1.77)-(1.79) and (1.82)-(1.83) in details.
In view of (2.11) with m=16, we have
for all n∈Z+, and hence
Notice that
So we have
and hence (1.77) holds.
By (2.11) with m=−64, we have
for all n∈Z+, and hence
Since 16k3+4k2−2k−1=(4k−1)(2k+1)2−2k(4k+1) and
we see that
and hence (1.78) holds. In light of (2.12) with m=−64, we have
for all n∈Z+, and hence
Since 16k3+12k2+6k+1=2k(2k+1)(4k+1)+(4k+1), with the aid of (1.78) we obtain
This proves (1.79).
By (2.13) with m=−27, we have
As
and
we see that (1.82) follows. By (2.14) with m=−27, we have
and hence
As
with the aid of (1.82) we get
and hence (1.83) follows.
Other identities in Theorem 1.2 can be proved similarly.
For integers n≥k≥0, we define
For n∈N we set
Lemma 2.3. For any n∈N, we have
and
where fn denotes the Franel number ∑nk=0(nk)3.
Proof. For n,i,k∈N with i≤k, we set
By the telescoping method for double summation [7], for
with 0≤i≤k, we find that
where
and
with (−1)!,(−2)!,… regarded as +∞, and p(n,i,k) and q(n,i,k) given by
and
respectively. Therefore
and hence
satisfies the recurrence relation
As pointed out by J. Franel [14], the Franel numbers satisfy the same recurrence. Note also that u(0)=f0=1 and u(1)=f1=2. So we always have u(n)=fn. This proves (2.19).
The identity (2.20) can be proved similarly. In fact, if we use v(n) denote the left-hand side or the right-hand side of (2.20), then we have the recurrence
In view of the above, we have completed the proof of Lemma 2.3.
Lemma 2.4. For any c∈Z and n∈N, we have
Proof. For each k=0,…,n, we have
If i,j∈N and i+j=r≤n/2, then
with the aid of the Chu-Vandermonde identity. Therefore
This proves (2.21).
Lemma 2.5. For k∈N and l∈Z+, we have
Proof. Let n=k+l. Then
and
Hence
This proves (2.22).
To prove Theorem 1.3, we need an auxiliary theorem.
Theorem 2.6. Let a and b be real numbers. For any integer m with |m|≥94, we have
Proof. Let N∈N. In view of (2.21),
and similarly
where we consider (x−1) as 0.
If l is an integer in the interval (N/2,N], then by Lemma 2.5 we have
where Pl(x) is the Legendre polynomial of degree l. Thus
and
Recall that
As |m|≥94, we have |m|>16(3+2√2)≈93.255 and hence
converges. Thus
and hence by the above we have
and
Therefore, with the aid of (2.19), we obtain
and
In view of (2.25) and (2.20),
Combining this with (2.24), we immediately obtain the desired (2.23).
Proof of Theorem 1.3. Let a,b,m∈Z with |m|≥6. Since
for any n∈N, we have 4nSn(1,m)=Sn(4,16m) for all n∈N. Thus, in light of Theorem 2.6,
Therefore
It is known (cf. [5,4]) that
So we get the identities (1.88)-(1.97) finally.
3.
New series involving Tn(b,c) for 1/π related to types Ⅰ-Ⅷ
Now we pose a conjecture related to the series (Ⅰ1)-(Ⅰ4) of Sun [34,40].
Conjecture 3.1. We have the following identities:
Remark 3.1. For each k\in{\Bbb N} , we have
since \binom{2k}k = (k+1)C_k and \binom{2k}{k+1} = kC_k . Thus, for example, [40,(I1)] and (I1 ' ) together imply that
and (I5) and (I5 ' ) imply that
For the conjectural identities in Conjecture 3.1, we have conjectures for the corresponding p -adic congruences. For example, in contrast with (I2 ' ), we conjecture that for any prime p>3 we have the congruences
and
Concerning (I5) and (I5 '' ), we conjecture that
and
for each n = 2,3,\ldots , and that for any prime p{\equiv}1\ ({\rm{mod}}\ 4) with p = x^2+4y^2\ (x,y\in{\Bbb Z}) we have
and
By [40,Theorem 5.1], we have
for any prime p{\equiv}3\ ({\rm{mod}}\ 4) . The identities (I5), (I5 ' ) and (I5 '' ) were formulated by the author on Dec. 9, 2019.
Next we pose a conjecture related to the series (Ⅱ1)-(Ⅱ7) and (Ⅱ10)-(Ⅱ12) of Sun [34,40].
Conjecture 3.2. We have the following identities:
Remark 3.2. We also have conjectures on related congruences. For example, concerning (Ⅱ), for any prime p>3 we conjecture that
and that
where x and y are integers. The identities (Ⅱ13), (Ⅱ13 ' ), (Ⅱ14) and (Ⅱ14 ' ) were found by the author on Dec. 11, 2019.
The following conjecture is related to the series (Ⅲ1)-(Ⅲ10) and (Ⅲ12) of Sun [34,40].
Conjecture 3.3. We have the following identities:
and
The following conjecture is related to the series (Ⅳ1)-(Ⅳ21) of Sun [34,40].
Conjecture 3.4. We have the following identities:
For the five open conjectural series (Ⅵ1), (Ⅵ2), (Ⅵ3), (ⅥI2) and (ⅥI7) of Sun [34,40], we make the following conjecture on related supercongruences.
Conjecture 3.5. Let p be an odd prime and let n\in{\Bbb Z}^+ . If ( \frac 3p) = 1 , then
divided by (pn)^2 is a p -adic integer. If p\not = 5 , then
divided by (pn)^2 is a p -adic integer. If ( \frac 7p) = 1 but p\not = 3 , then
divided by (pn)^2 is a p -adic integer. If p{\equiv}\pm1\ ({\rm{mod}}\ 8) but p\not = 7 , then
divided by (pn)^2 is a p -adic integer. If ( \frac{-6}p) = 1 but p\not = 7,31 , then
divided by (pn)^2 is a p -adic integer.
Now we pose four conjectural series for 1/\pi of type Ⅷ.
Conjecture 3.6. We have
Remark 3.3. The author found the identity (Ⅷ1) on Nov. 3, 2019. The identities (Ⅷ2), (Ⅷ3) and (Ⅷ4) were formulated on Nov. 4, 2019.
Below we present some conjectures on congruences related to Conjecture 3.6.
Conjecture 3.7. (ⅰ) For each n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two ( i.e., n\in\{2^a:\ a\in{\Bbb N}\}) .
(ⅱ) Let p\not = 2,5 be a prime. Then
If ( \frac 3p) = ( \frac{-5}p) = 1 , then
for all n\in{\Bbb Z}^+ .
(ⅲ) Let p\not = 2,5 be a prime. Then
Remark 3.4. The imaginary quadratic field {\Bbb Q}(\sqrt{-5}) has class number two.
Conjecture 3.8. (ⅰ) For any n\in{\Bbb Z}^+ , we have
and the number is odd if and only if n is a power of two.
(ⅱ) Let p>3 be a prime. Then
If ( \frac 3p) = ( \frac{-5}p) = 1 , then
for all n\in{\Bbb Z}^+ .
(ⅲ) Let p>5 be a prime. Then
Remark 3.5. This conjecture can be viewed as the dual of Conjecture 3.7. Note that the series \sum_{k = 0}^\infty \frac{(40k+27}{(-6)^k}T_k(4,1)T_k(1,-1)^2 diverges.
Conjecture 3.9. (ⅰ) For each n\in{\Bbb Z}^+ , we have
(ⅱ) Let p>3 be a prime. Then
If p{\equiv}1,9\ ({\rm{mod}}\ {20}) , then
divided by (pn)^2 is a p -adic integer for each n\in{\Bbb Z}^+ .
(ⅲ) Let p>5 be a prime. Then
Remark 3.6. The imaginary quadratic field {\Bbb Q}(\sqrt{-15}) has class number two.
Conjecture 3.10. (ⅰ) For each n\in{\Bbb Z}^+ , we have
(ⅱ) Let p>5 be a prime. Then
If p{\equiv}1,9\ ({\rm{mod}}\ {20}) , then
divided by (pn)^2 is a p -adic integer for each n\in{\Bbb Z}^+ .
(ⅲ) Let p>5 be a prime. Then
Remark 3.7. This conjecture can be viewed as the dual of Conjecture 3.9. Note that the series
diverges.
Conjecture 3.11. (ⅰ) For each n\in{\Bbb Z}^+ , we have
(ⅱ) Let p>3 be a prime. Then
If ( \frac {-1}p) = ( \frac {15}p) = 1 , then
divided by (pn)^2 is an p -adic integer for any n\in{\Bbb Z}^+ .
(ⅲ Let p>7 be a prime. Then
where x and y are integers.
Remark 3.8. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-105}) has class number 8 .
Conjecture 3.12. (ⅰ) For each n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
(ⅱ) Let p>5 be a prime. Then
If ( \frac 3p) = ( \frac{-5}p) = 1 , then
divided by (pn)^2 is a p -adic integer for each n\in{\Bbb Z}^+ .
(ⅲ) Let p>5 be a prime with p\not = 11 . Then
where x and y are integers.
Remark 3.9. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-165}) has class number 8 .
4.
Congruences related to Theorem 1.3
Conjectures 4.1–4.14 below provide congruences related to (1.88)–(1.97).
Conjecture 4.1. (ⅰ) For any n\in{\Bbb Z}^+ , we have
(ⅱ) Let p>3 be a prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 3) , then
for all n\in{\Bbb Z}^+ .
(ⅲ) For any prime p>3 , we have
Conjecture 4.2. (ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
(ⅱ) Let p\not = 7 be an odd prime. Then
and moreover
for all n\in{\Bbb Z}^+ .
(ⅲ) For any prime p\not = 2,7 , we have
where x and y are integers.
Conjecture 4.3. (ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
(ⅱ) Let p be an odd prime with p\not = 5 . Then
If p{\equiv}1\ ({\rm{mod}}\ 3) , then
for all n\in{\Bbb Z}^+ .
(ⅲ) For any prime p\not = 2,5 , we have
where x and y are integers.
Conjecture 4.4. (ⅰ) For any n\in{\Bbb Z}^+ , we have
(ⅱ) Let p\not = 5 be an odd prime. Then
for all n\in{\Bbb Z}^+ .
(ⅲ) For any prime p>3 with p\not = 11 , we have
where x and y are integers.
Conjecture 4.5. (ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
(ⅱ) Let p be an odd prime with p\not = 7 . Then
If p{\equiv}1,3\ ({\rm{mod}}\ 8) , then
for all n\in{\Bbb Z}^+ .
(ⅲ) For any prime p\not = 2,7 , we have
where x and y are integers.
Conjecture 4.6. (ⅰ) For any n\in{\Bbb Z}^+ , we have
(ⅱ) Let p\not = 13 be an odd prime. Then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
(ⅲ) For any prime p>3 with p\not = 19 , we have
where x and y are integers.
Conjecture 4.7. (ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
(ⅱ) Let p be an odd prime with p\not = 5,13 . Then
If ( \frac{-6}p) = 1 , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
(ⅲ)For any odd prime p\not = 5,13 , we have
where x and y are integers.
Conjecture 4.8. (ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
(ⅱ) Let p\not = 7,31 be an odd prime. Then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
(ⅲ) For any prime p>3 with p\not = 7,31 , we have
where x and y are integers.
Conjecture 4.9. (ⅰ) For any n\in{\Bbb Z}^+ , we have
(ⅱ) Let p\not = 5,7 be an odd prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 3) , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
(ⅲ) For any prime p>7 with p\not = 17 , we have
where x and y are integers.
Conjecture 4.10. (ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm(ⅱ) Let p\not = 5,53 be an odd prime. Then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>5 with p\not = 59 , we have
where x and y are integers.
Conjecture 4.11. For any odd prime p ,
Also, for any prime p{\equiv}1\ ({\rm{mod}}\ 4) we have
Conjecture 4.12. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
\rm(ⅱ) For any odd prime p and positive integer n , we have
\rm(ⅲ) Let p be an odd prime. Then
Conjecture 4.13. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
\rm(ⅱ) Let p>3 be a prime. Then
If p{\equiv}\pm1\ ({\rm{mod}}\ {12}) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>3 , we have
Conjecture 4.14. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm(ⅱ) Let p be an odd prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 3) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>3 , we have
where x and y are integers.
Conjecture 4.15. Let p be an odd prime with p\not = 5 . Then
where x and y are integers. If ( \frac{-5}p) = 1 , then
Remark 4.1. We also have some similar conjectures involving
modulo p^2 , where p is a prime greater than 3 .
Motivated by Theorem 2.6, we pose the following general conjecture.
Conjecture 4.16. For any odd prime p and integer m\not{\equiv}0\ ({\rm{mod}}\ p) , we have
and
Remark 4.2 We have checked this conjecture via \mathsf{Mathematica}. In view of the proof of Theorem 2.6, both (4.51) and (4.52) hold modulo p .
5.
Series for 1/\pi involving T_n(b,c) and Z_n=\sum_{k=0}^n \binom nk \binom{2k}k \binom{2(n-k)}{n-k}
The numbers
were first introduced by D. Zagier in his paper [51] the preprint of which was released in 2002. Thus we name such numbers as Zagier numbers. As pointed out by the author [41,Remark 4.3], for any n\in{\Bbb N} the number 2^nZ_n coincides with the so-called CLF (Catalan-Larcombe-French) number
Let p be an odd prime. For any k = 0,\ldots,p-1 , we have
by F. Jarvis and H.A. Verrill [24,Corollary 2.2], and hence
Combining this with Remark 1.3(ⅱ), we see that
for any b,c,m\in{\Bbb Z} with p\nmid (b^2-4c)m .
J. Wan and Zudilin [49] obtained the following irrational series for 1/\pi involving the Legendre polynomials and the Zagier numbers:
Via our congruence approach (including Conjecture 1.4), we find 24 rational series for 1/\pi involving T_n(b,c) and the Zagier numbers. Theorem 1 of [49] might be helpful to solve some of them.
Conjecture 5.1. We have the following identities for 1/\pi .
Below we present some conjectures on congruences related to (5.1) , (5.2) , (5.4) and (5.9) .
Conjecture 5.2. (ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p be an odd prime with p\not = 5 . Then
If p{\equiv}\pm1\ ({\rm{mod}}\ {5}) , then
for all n\in{\Bbb Z}^+ .
\rm (ⅲ) For any prime p>5 , we have
Conjecture 5.3. (ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p>3 be a prime with p\not = 7 . Then
If ( \frac 7p) = 1 , then
for all n\in{\Bbb Z}^+ .
\rm (ⅲ) For any prime p>3 with p\not = 7 , we have
Conjecture 5.4. \rm(i) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p>3 be a prime. Then
If p{\equiv}1,3\ ({\rm{mod}}\ 8) , then
for all n\in{\Bbb Z}^+ .
\rm (ⅲ) For any prime p>3 , we have
Conjecture 5.5. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p be an odd prime with p\not = 5 . Then
If ( \frac{-15}p) = 1 , then
for all n\in{\Bbb Z}^+ .
\rm (ⅲ) For any prime p>5 , we have
where x and y are integers.
6.
Series for 1/\pi involving T_k(b,c) and the Franel numbers
Sun [36,37] obtained some supercongruences involving the Franel numbers f_n = \sum_{k = 0}^n \binom nk^3\ (n\in{\Bbb N}) . M. Rogers and A. Straub [30] confirmed the 520 -series for 1/\pi involving Franel polynomials conjectured by Sun [34].
Let p be an odd prime. By [24,Lemma 2.6], we have f_k{\equiv}(-8)^kf_{p-1-k}\ ({\rm{mod}}\ p) for each k = 0,\ldots,p-1 . Combining this with Remark 1.3(ⅱ), we see that
for any b,c,m\in{\Bbb Z} with p\nmid (b^2-4c)m .
Wan and Zudilin [49] deduced the following irrational series for 1/\pi involving the Legendre polynomials and the Franel numbers:
Via our congruence approach (including Conjecture 1.4), we find 12 rational series for 1/\pi involving T_n(b,c) and the Franel numbers; Theorem 1 of [49] might be helpful to solve some of them.
Conjecture 6.1. We have
We now present a conjecture on congruence related to (6.3) .
Conjecture 6.2. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p>5 be a prime. Then
If ( \frac{-5}p) = 1 , then
for all n\in{\Bbb Z}^+ .
\rm (ⅲ) For any prime p>5 , we have
Remark 6.1 This conjecture was formulated by the author on Oct. 25, 2019.
Conjecture 6.3. For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p be an odd prime. Then
If ( \frac{-5}p) = 1 , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm (ⅲ) Let p>5 be a prime. Then
Remark 6.2. This conjecture is the dual of Conjecture 6.2.
The following conjecture is related to the identity (6.8) .
Conjecture 6.4. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p>2 be a prime with p\not = 7,11 . Then
If ( \frac {-39}p) = 1 , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm (ⅲ) Let p>3 be a prime with p\not = 7,11,13 . Then
where x and y are integers.
Remark 6.3. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-273}) has class number 8 .
The following conjecture is related to the identity (6.10) .
Conjecture 6.5. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p>3 be a prime with p\not = 23 . Then
If ( \frac p{23}) = 1 , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm (ⅲ) Let p>3 be a prime with p\not = 23 . Then
where x and y are integers.
Remark 6.4. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-345}) has class number 8 .
The following conjecture is related to the identity (6.12) .
Conjecture 6.6. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm (ⅱ) Let p be an odd prime with p\not = 11,13 . Then
If ( \frac {-14}p) = 1 , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm (ⅲ) Let p>3 be a prime with p\not = 7,11,13 . Then
where x and y are integers.
Remark 6.5. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-462}) has class number 8 .
The identities (6.5),\, (6.6),\,(6.7),\,(6.9),\,(6.11) are related to the quadratic fields
(with class number 8 ) respectively. We also have conjectures on related congruences similar to Conjectures 6.4, 6.5 and 6.6.
7.
Series for 1/\pi involving T_n(b,c) and g_n=\sum_{k=0}^n \binom nk^2 \binom{2k}k
For n\in{\Bbb N} let
It is known that g_n = \sum_{k = 0}^n \binom nk f_k for all n\in{\Bbb N} . See [43,20,26] for some congruences on polynomials related to these numbers.
Let p>3 be a prime. For any k = 0,\ldots,p-1 , we have
by [24,Lemma 2.7(ⅱ)]. Combining this with Remark 1.3(ⅱ), we see that
for any b,c,m\in{\Bbb Z} with p\nmid (b^2-4c)m .
Wan and Zudilin [49] obtained the following irrational series for 1/\pi involving the Legendre polynomials and the sequence (g_n)_{n{\geq}0} :
Using our congruence approach (including Conjecture 1.4), we find 12 rational series for 1/\pi involving T_n(b,c) and g_n ; Theorem 1 of [49] might be helpful to solve some of them.
Conjecture 7.1. We have the following identities.
Now we present a conjecture on congruences related to (7.6) .
Conjecture 7.2. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
\rm(ⅱ) Let p>7 be a prime. Then
If p{\equiv}1,3\ ({\rm{mod}}\ 8) , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p>7 be a prime. Then
where x and y are integers.
Remark 7.1. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-210}) has class number 8 .
The following conjecture is related to the identity (7.8) .
Conjecture 7.3. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
\rm(ⅱ) Let p>7 be a prime. Then
If ( \frac p3) = ( \frac p{5}) , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p>11 be a prime. Then
where x and y are integers.
Remark 7.2. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-330}) has class number 8 .
Now we pose a conjecture related to the identity (7.10) .
Conjecture 7.4. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm(ⅱ) Let p>7 be a prime with p\not = 17 . Then
If ( \frac p7) = ( \frac p{17}) , then
is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p>7 be a prime with p\not = 17 . Then
where x and y are integers.
Remark 7.3. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-357}) has class number 8 .
Now we pose a conjecture related to the identity (7.12) .
Conjecture 7.5. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
\rm(ⅱ) Let p>7 be a prime. Then
If ( \frac {-14}p) = 1 , then
divided by (pn)^2 is a p -adic integer for each n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p>11 be a prime. Then
where x and y are integers.
Remark 7.4. Note that the imaginary quadratic field {\Bbb Q}(\sqrt{-462}) has class number 8 . We believe that 462 is the largest positive squarefree number d for which the imaginary quadratic field {\Bbb Q}(\sqrt{-d}) can be used to construct a Ramanujan-type series for 1/\pi .
The identities (7.5),\,(7.7),\,(7.9),\,(7.11) are related to the imaginary quadratic fields {\Bbb Q}(\sqrt{-165}) , {\Bbb Q}(\sqrt{-210}) , {\Bbb Q}(\sqrt{-345}) , {\Bbb Q}(\sqrt{-330}) (with class number 8 ) respectively. We also have conjectures on related congruences similar to Conjectures 7.2, 7.3, 7.4 and 7.5.
To conclude this section, we confirm an open series for 1/\pi conjectured by the author (cf. [34,(3.28)] and [35,Conjecture 7.9]) in 2011.
Theorem 7.1. We have
where
Proof. The Franel numbers of order 4 are given by f_n^{(4)} = \sum_{k = 0}^n \binom nk^4\ (n\in{\Bbb N}) . Note that
By [11,(8.1)], for |x|<1/16 and a,b\in{\Bbb Z} , we have
Since
putting a = 16 , b = 5 and x = -1/20 in (7.30) we obtain
As
by Cooper [9], we finally get
This concludes the proof of (7.29).
8.
Series and congruences involving T_n(b,c) and \beta_n=\sum_{k=0}^n \binom nk^2 \binom{n+k}k
Recall that the numbers
are a kind of Apéry numbers. Let p be an odd prime. For any k = 0,1,\ldots,p-1 , we have
by [24,Lemma 2.7(ⅰ)]. Combining this with Remark 1.3(ⅱ), we see that
for any b,c,m\in{\Bbb Z} with p\nmid (b^2-4c)m .
Wan and Zudilin [49] obtained the following irrational series for 1/\pi involving the Legendre polynomials and the numbers \beta_n :
Using our congruence approach (including Conjecture 1.4), we find one rational series for 1/\pi involving T_n(b,c) and the Apéry numbers \beta_n (see (8.1) below); Theorem 1 of [49] might be helpful to solve it.
Conjecture 8.1. (ⅰ) We have
Also, for any n\in{\Bbb Z}^+ we have
\rm(ⅱ) Let p>5 be a prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 4) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p>5 be a prime. Then
Remark 8.1. This conjecture was formulated by the author on Oct. 27, 2019.
Conjecture 8.2. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb Z}^+\} .
\rm(ⅱ) Let p be a prime. Then
If ( \frac {-15}p) = 1\ ( i.e., p{\equiv}1,2,4,8\ ({\rm{mod}}\ {15})) , then
divided by (pn)^2 is a p -adic integer for any n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>5 , we have
Remark 8.2. This conjecture was formulated by the author on Nov. 13, 2019.
Conjecture 8.3. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
\rm(ⅱ) Let p>3 be a prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 4) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any odd prime p , we have
Remark 8.3. This conjecture was formulated by the author on Nov. 13, 2019.
Conjecture 8.4. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a = 0,2,3,4,\ldots\} .
\rm(ⅱ) Let p be any odd prime. Then
If p{\equiv}\pm1\ ({\rm{mod}}\ 8) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any odd prime p , we have
Conjecture 8.5. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
\rm(ⅱ) Let p>3 be a prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 4) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p\not = 2,5 be a prime. Then
Conjecture 8.6. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
\rm(ⅱ) Let p be an odd prime. Then
If ( \frac{33}p) = 1 , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) Let p>3 be a prime. Then
Conjecture 8.7. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n is a power of two.
\rm(ⅱ) Let p>5 be a prime. Then
If ( \frac{-15}p) = 1 , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>7 , we have
9.
Series and congruences involving w_n=\sum_{k=0}^{\lfloor n/3\rfloor}(-1)^k3^{n-3k} \binom n{3k} \binom{3k}k \binom{2k}k and T_n(b,c)
The numbers
were first introduced by Zagier [51] during his study of Apéry-like integer sequences, who noted the recurrence
Lemma 9.1. Let p>3 be a prime. Then
Proof. Note that
with the help of the known congruence \sum_{k = 0}^{p-1} \binom{2k}k \binom{3k}k/27^k{\equiv}( \frac p3)\ ({\rm{mod}}\ {p^2}) conjectured by F. Rodriguez-Villegas [28] and proved by E. Mortenson [25]. Similarly,
By induction,
for all n\in{\Bbb N} . In particular,
So we have w_k{\equiv}( \frac{-3}p)27^kw_{p-1-k}\ ({\rm{mod}}\ p) for k = 0,1 . (Note that w_0 = 1 and w_1 = 3 .)
Now let k\in\{1,\ldots,p-2\} and assume that
Then
and hence
In view of the above, we have proved the desired result by induction.
For Lemma 9.1 one may also consult [31,Corollary 3.1]. Let p>3 be a prime. In view of Lemma 9.1 and Remark 1.3(ⅱ), we have
for any b,c,m\in{\Bbb Z} with p\nmid (b^2-4c)m .
Wan and Zudilin [49] obtained the following irrational series for 1/\pi involving the Legendre polynomials and the numbers w_n :
Using our congruence approach (including Conjecture 1.4), we find five rational series for 1/\pi involving T_n(b,c) and the numbers w_n ; Theorem 1 of [49] might be helpful to solve them.
Conjecture 9.1. We have
Below we present our conjectures on congruences related to the identities (9.2) and (9.5).
Conjecture 9.2. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
\rm(ⅱ) Let p>3 be a prime. Then
If ( \frac p7) = 1\ ( i.e., p{\equiv}1,2,4\ ({\rm{mod}}\ 7)) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>7 , we have
Conjecture 9.3. \rm(ⅰ) For any n\in{\Bbb Z}^+ , we have
and this number is odd if and only if n\in\{2^a:\ a\in{\Bbb N}\} .
\rm(ⅱ) Let p>3 be a prime with p\not = 7 . Then
If ( \frac p7) = 1\ ( i.e., p{\equiv}1,2,4\ ({\rm{mod}}\ 7)) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>3 with p\not = 7,13 , we have
Now we give one more conjecture in this section.
Conjecture 9.4. \rm(ⅰ) For any integer n>1 , we have
\rm(ⅱ) Let p>3 be a prime. Then
If p{\equiv}1\ ({\rm{mod}}\ 4) , then
for all n\in{\Bbb Z}^+ .
\rm(ⅲ) For any prime p>3 , we have
Remark 9.1. For primes p>3 with p{\equiv}3\ ({\rm{mod}}\ 4) , in general the congruence (9.16) is not always valid for all n\in{\Bbb Z}^+ . This does not violate Conjecture 1.2 since \lim_{k\to+\infty}|w_kT_k(10,-2)|^{1/k} = \sqrt{27}\times\sqrt{10^2-4(-2)} = 54 . If the series \sum_{k = 0}^\infty \frac{2k+1}{54^k}w_kT_k(10,-2) converges, its value times \pi/\sqrt3 should be a rational number.
10.
Series for \pi involving T_n and related congruences
Let p be an odd prime and let a,b,c,d,m\in{\Bbb Z} with m(b^2-4c)\not{\equiv}0\ ({\rm{mod}}\ p) . Then
with the aid of [33,Lemma 2.1]. Thus
in view of Remark 1.3(ⅱ).
Let p>3 be a prime. By the above, the author's conjectural congruence (cf. [35,Conjecture 1.3])
implies that
Motivated by this, we pose the following curious conjecture.
Conjecture 10.1. We have the following identities:
Remark 10.1. The two identities were conjectured by the author on Dec. 7, 2019. One can easily check them numerically via \mathsf{Mathematica} as the two series converge fast.
Now we state our related conjectures on congruences.
Conjecture 10.2. For any prime p>3 , we have
and
Conjecture 10.3. (ⅰ) We have
for all n\in{\Bbb Z}^+ , and also
for each prime p>3 .
\rm(ⅱ) For any prime p{\equiv}1\ ({\rm{mod}}\ 3) and n\in{\Bbb Z}^+ , we have
Remark 10.2. See also [45,Conjecture 67] for a similar conjecture.
Let p be an odd prime. We conjecture that
and
Though (10.6) implies the congruence
and (10.7) with p>3 implies the congruence
we are unable to find the exact values of the two converging series
Acknowledgment
The author would like to thank Prof. Qing-Hu Hou at Tianjin Univ. for his helpful comments on the proof of Lemma 2.3.











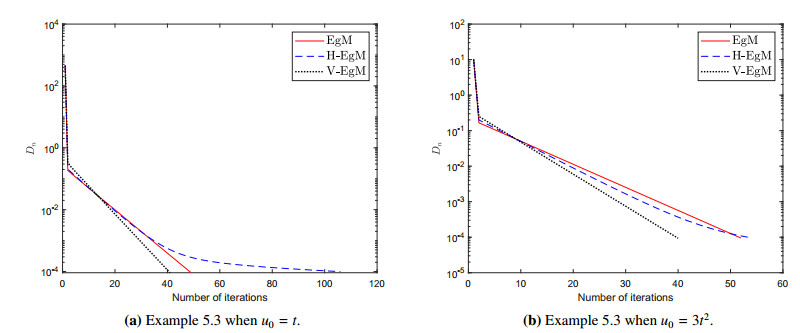
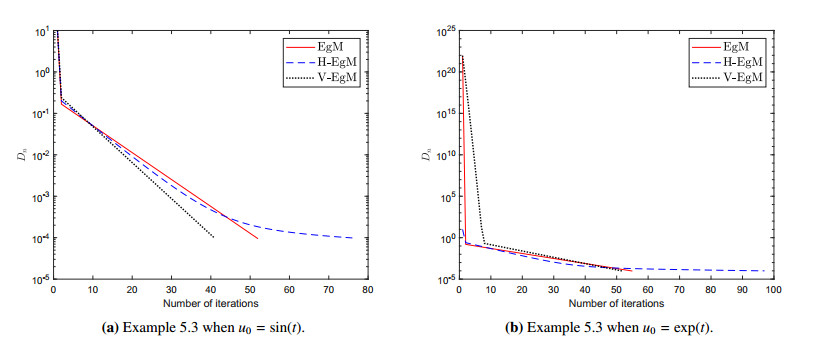
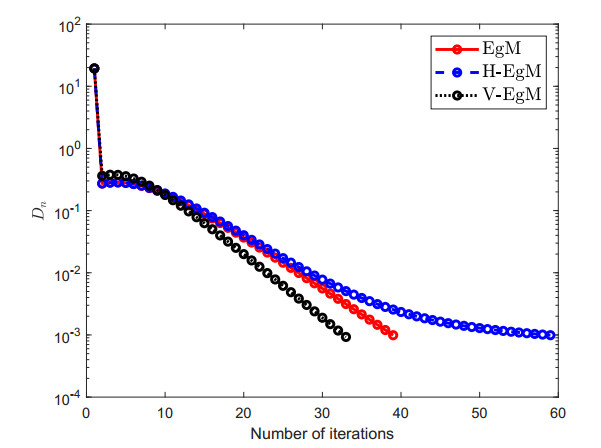
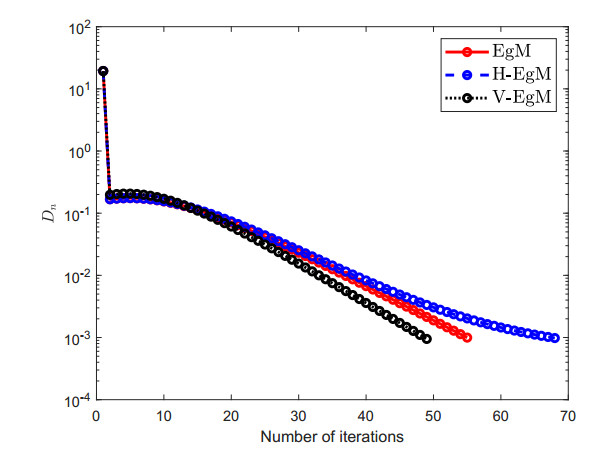


 DownLoad:
DownLoad: