Probability density prediction for linear systems under fractional Gaussian noise excitation using physics-informed neural networks

1.   Introduction

The Fokker-Planck-Kolmogorov (FPK) equations are partial differential equations, which describe the change of the probability density function (PDF) of stochastic processes with time. In physics, the FPK equation is commonly utilized to examine the temporal evolution of the distribution of particle positions or velocities under the influence of stochastic forces within a potential energy field. In practical application, the FPK equation can be used to describe various stochastic dynamical systems, including those across disciplines like physics, chemistry, biology, and economics.

Normally, through analyzing the transient or steady-state PDF of system response, the instantaneous and aggregate impacts of stochastic excitation upon the system can be quantified, which are described by FPK equations. Hence, resolving FPK equations is very important for interpreting the behavior of dynamical systems. Relatively speaking, an analytical solution to the FPK equation is achievable under certain restrictive conditions, whereas under normal circumstances, the analytical solution for the FPK equation is nearly unattainable ^[1]. Therefore, approximate and numerical methods, such as the stochastic average method ^[2], finite element method ^[3], Monte Carlo method ^[4], finite difference method ^[5], path integration method ^[6], Galerkin method ^[7], and variational method ^[8] are usually used to solve the FPK equation. These methods mainly divide the computing domain into grid point sets, and find approximate solutions at these points. Nevertheless, these solutions are only provided at grid points, and assessing any location beyond grid points necessitates the use of interpolation or alternative resconstruction strategies. For low-dimensional systems, analytical approximations like the exponential polynomial closure method ^[9] have shown their effectiveness and efficiency. When dealing with high-dimensional systems, the state-space-split method ^[10] has shown it effectiveness and efficiency.

In contrast to conventional techniques, machine learning exhibits superior potential when addressing high-dimensional differential equations. Li et al. ^[11] studied the theoretical analysis of stochastic dynamics and introduced an artificial neural network (ANN) method for resolving stochastic partial differential equations (SPDE) via the FPK equation or adjoint FPK equation, demonstrating enhanced robustness and precision. Xiao et al. ^[12] proposed a neural network technique for analyzing stochastic vibrations in large, nonlinear systems with Gaussian white noise. Their approach simplifies the steady-state Fokker-Planck equation from high to low dimensions, showing that the simplified coefficients are conditional means of the original coefficients. Raissi et al. ^[13] put forward a deep learning architecture of PINNs, which combines a physical model and data, making it suitable for continuous and discrete time models. Later, Rao et al. ^[14] applied a mixed variable output PINN to simulate elastic dynamics, improve network performance, verify various problems, and show the application prospect of computational mechanics. Chen et al. ^[15] proposed a PINN to discover control equations from sparse data, which integrates the advantages of deep learning and effectively identifies system behavior, which is suitable for data scarcity scenarios. Therefore, the neural network based on physics has become a research hotspot. As deep learning advances, the application of neural networks has extended into the domain of stochastic dynamics, especially in solving FPK equations ^[16]. Wang et al. ^[17,18] investigated the time-dependent PDF of dynamical systems under Gaussian white noise influence, employing a gaussian radial basis function neural network (GRBFNN). The adaptive gaussian mixture model (AGMM) machine learning method was proposed by Sun and his associates, which was designed to tackle the general FP equation, in comparison with the previous numerical discretization method. It created a seamless collection of data and mathematical models ^[19]. Zhang and Yuen ^[20] applied the deep learning method based on physical guidance to address the time-varying FPK equation, incorporating physical modeling as a guiding constraint to direct the deep neural network in learning the solutions to the equation. Xu et al. ^[21] introduced a technique for solving the FPK equation using a deep neural network that eliminates the need for interpolation and coordinate transformation, distinct from conventional numerical techniques. To decrease the sensitivity of the FPK equation to boundary conditions, Li ^[22] presented a new data-driven method to solve the FPK equation in any local region. Inspired by the result ^[22], Zhai et al. ^[23] used an ANN for solving the FPK equation.

The aforementioned studies primarily concentrate on the Gaussian white noise model. As research into stochastic phenomena in related fields progresses, the limitations of the Gaussian white noise model in describing many stochastic dynamics problems have been gradually revealed. Especially in the financial market, the fluctuation of stock price is often influenced by financial and economic factors with time correlation, and this excitation is more suitable for accurate modeling through FGN. Mandelbrot and Van Ness ^[24] introduced fractional Brownian motion (FBM) in 1968, outlining its creation. Subsequently, research on dynamical systems driven by FBM has garnered significant scholarly interest. FBM is not classified as a semi-martingale or a Markov process, so the complete theoretical basis of stochastic integration is not suitable for the FBM. Therefore, a new stochastic calculus theory is needed to deal with FBM. Duncan et al. ^[25] put forward a stochastic calculus theory suitable for FBM with a Hurst index in the $(1/2, 1)$ interval. Vas'kovskii ^[26] further extended the theory by providing the FPK equation for a one-dimensional stochastic differential equation with FBM as the driver, for a Hurst index within $(0, 1)$. This finding broadens the scope of previous findings for one-dimensional stochastic differential equation excited by FBM, which were limited to a Hurst index in the interval $(1/3, 1)$ ^[27,28]. Xu et al. ^[29] studied the stochastic averaging principle under FBM under the framework of forward path integration, and proved the convergence for the dynamical system excited by FBM. Pei et al. ^[30] further studied the stochastic average principle of the fast-slow system influenced by FBM. Deng and Zhu ^[31] introduced a stochastic averaging technique for quasi-Hamilton systems with single or multiple degrees of freedom under the FGN, which effectively solved the average equation of quasi-Hamilton systems. A generalized hat function was proposed to solve nonlinear stochastic differential equation excited by multiplicative FGN ^[32]. Therefore, it is effective and necessary to introduce the FGN model into dynamical systems to describe stochasticness with a time correlation and probability distribution characteristics.

In conclusion, it is found that the application of deep learning technology in stochastic dynamics has not been extensively deepened, particularly for addressing FPK equations under the influence of FGN. Current investigations have largely centered on systems stimulated by Gaussian or non-Gaussian white noise, with the FPK equations perturbed by FGN being a less explored area. Therefore, inspired by the discussion above, we introduce FGN into the dynamical system in this paper, derive the FPK equation of the stochastic system, and then propose a deep learning theoretical system based on PINNs to solve the FPK equation. Unlike prior studies focused on Gaussian white noise ^[12,17,18], our work addresses the critical gap in modeling time-correlated FGN excitations, which are prevalent in real-world systems but lack efficient computational tools. The primary contributions and novel aspects of this research are highlighted in the following critical areas:

1) In the study of dynamical systems, it is assumed that the stochastic perturbation is Gaussian white noise for the convenience of analysis. In reality, FGN can reflect the time correlation of stochasticness in a dynamical system. Therefore, the FGN with a time correlation is brought into the analysis of stochastic dynamical systems in this paper.

2) We include a rigorous derivation of FGN-induced FPK equations via Malliavin-Wick calculus, establishing new theoretical foundations, extending beyond traditional Gaussian white noise models.

3) We provide the first application of PINNs to solve the FPK equation for dynamical systems driven by FGN, addressing a gap in existing research.

4) Compared to existing methods, this work provides the first PINNs-based framework for FGN-driven systems, achieving higher computational efficiency (100 times faster than Monte Carlo) while maintaining accuracy ($< 1\%$ error).

The structure of the remainder of this paper is as follows. Section 2 outlines the fundamental principles of FBM and FGN, including the stochastic integral and Malliavin calculus for FBM. Subsequently, Section 3 derives the Fokker-Planck equation for a dynamical system driven by FGN. Section 4 describes the method of using PINNs to solve the corresponding time-varying FPK equation, and gives the algorithm scheme. In Section 5, we present two stochastic dynamical systems as case studies to illustrate the efficacy and clarity of the PINNs method. Section 6 gives a brief conclusion.

2.   Preliminaries

FBM is considered an extension of standard Brownian motion within the realm of probability theory. Compared with the typical BM, FBM is characterized in that the increments are not necessarily independent. The purpose of this section is to introduce the definition of FBM, discuss its properties and related knowledge of FGN.

2.1.   Definition of FBM and its properties

The concept of FBM was coined in 1968 by Mandelbrot and Van Ness ^[24]. The stochastic integral representation of the process based on standard BM has been provided in literature ^[24], where the stochastic integral is defined by the Hurst index $H$:

with $B(g)$ denoting the standard Brownian motion and $C_{H}$ representing the normalization constant.

Definition2.1. Given a complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$, let the Hurst parameter H $\in$ (0, 1) be a real number. According to literature ^[33], its one-dimensional FBM $\{B^{H}(s), s\geqslant0\}$ with Hurst index $H$ is characterized as a mean-zero, continuous Gaussian process with the property of having a covariance function:

1) $E\left [ B^{(H)}(f) \right ] = 0, \forall f\ge 0,$

2) $E\left[B^{(H)}(f) B^{(H)}(g)\right] = 1/2\left(f^{2 H}+g^{2 H}-|f-g|^{2 H}\right).$

For all $\alpha \in$ $(0, H)$, the sample trajectories of the FBM are almost surely $\alpha$-order H$\ddot{o}$lder continuous. The size of the real number H determines what kind of process the FBM is:

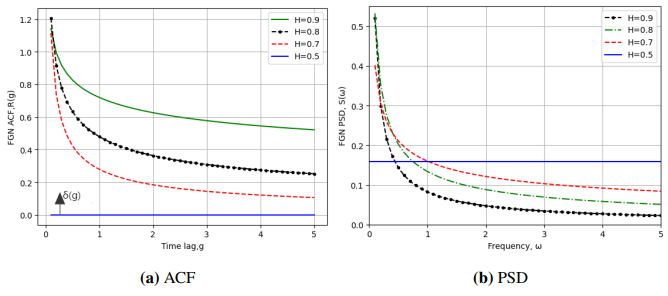
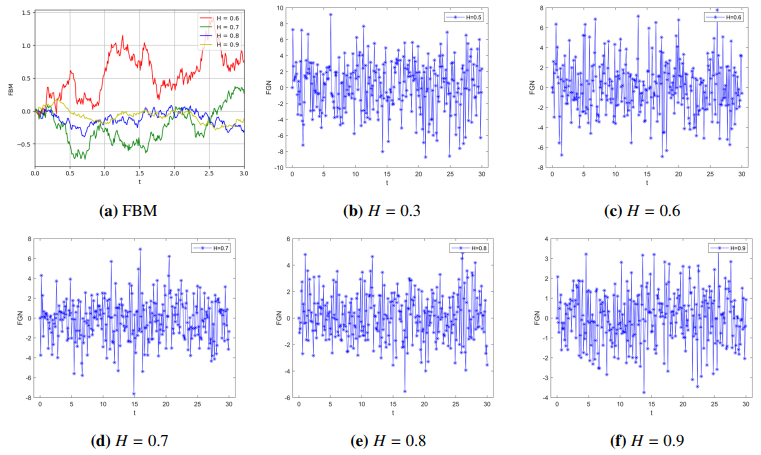
When $H < 1/2$, then the increments of the process are negatively correlated and $\left \{ B^{(H)}(f), f\ge 0 \right \}$ has an anti-persistence. When $H = 1/2$, FBM $\left \{ B^{(H)}(f), f\ge 0 \right \}$ is a standard Brownian motion or Wiener process. When $H > 1/2$, then the increments of the process are positively correlated and $\left \{ B^{(H)}(f), f\ge 0 \right \}$ has long-range dependence. Figure 1 shows the sample paths of FBM and FGN under different Hurst indices $H$.

Properties 2.1. By Definition 2.1 and literature ^[34], a standard FBM is obtained, which has the following characteristics:

1) $B^{(H)}(0) = 0$.

2) $B^{(H)}(f)$ has homogeneous increments, i.e., $B^{(H)}(f+g)-B^{(H)}(g)$ has the same law for $f, \, g\ge 0$.

3) $B^{(H)}(f)$ is a Gaussian process and $E\left [ B^{(H)}(f)^{2} \right ] = f^{2H}, E\left [ \mathrm{d} B^{(H)}(f)^{2} \right ] = \left (\mathrm{d} f \right) ^{2H}, s\ge 0,$ for all $H\in (0, 1)$.

4) The sample trajectories of $B^{(H)}(f)$ are continuous but almost everywhere non-differentiable.

5) $\left \{ B^{(H)}(f), f\ge 0 \right \}$ has self-similarity, i.e., $\left \{ B^{(H)}(\beta f), f\ge 0 \right \}$ has the same probability law as $\left \{ \beta ^{H} B^{(H)}(f), f\ge 0 \right \}$.

6) When $1/2 < H < 1$, $\left \{ B^{(H)}(f), f\ge 0 \right \}$ has long-range dependence, so that if

there is ${ \sum_{m = 1}^{\infty}} R(m) = \infty$.

A unit-FGN can be conceptualized as the derivative of a unit-FBM:

or

Its autocorrelation function (ACF) is

As the power spectral density (PSD) of FGN holds physical significance exclusively within the range $1/2 < H < 1$, the study here is limited to this interval, focusing on the corresponding PSD.

Figure 2 shows the numerical results of ACF $R(g)$ and PSD $S(w)$ of FGN when $1/2 < H < 1$. As can be seen from the figure, when $H$ tends to 1/2, the PSD of FGN is close to a constant and the ACF is close to the Dirac function $\delta(g)$. When $H$ tends to 1, the PSD is close to the Dirac function $\delta(g)$ and the ACF is close to a constant. When $H$ is between 1/2 and 1, the ACF has a finite value for a period of time, which indicates that FGN has a long-range correlation. Therefore, when $1/2 < H < 1$, FGN is a stationary Gaussian process between Gaussian white noise and Gaussian random variables.

2.2.   Fractional stochastic calculus

Given a fixed Hurst index of $1/2 < H < 1$, consider $\mathbb{R}_{+} \times \mathbb{R}_{+} \to \mathbb{R}_{+}$ defined as follows:

Let $g: \mathbb{R}_{+} \to \mathbb{R}$ be a Borel-measurable (deterministic) function. The function $g$ is an element of the Hilbert space $L_{\phi}^{2}(\mathbb{R} _{+})$ provided that

The inner product within the Hilbert space $L_{\phi}^{2}(\mathbb{R} _{+})$ is represented by $\left \langle \cdot, \cdot \right \rangle _{\phi }$.

Lemma2.1. If $f$, $g$ belong to $L_{\phi}^{2}(\mathbb{R} _{+}),$ then $\int_{ 0}^{\infty} f(s)\mathrm{d} B^{(H)}(s)$, $\int_{ 0}^{\infty} g(t)\mathrm{d} B^{(H)}(t)$ are well-defined, zero mean, Gaussian stochastic variables $\left \| f \right \| _{\phi }^{2}$, $\left \| g \right \| _{\phi }^{2}$, respectively, and

Lemma 2.1 is verified in literature ^[35]. Define a mapping $L_{\phi}^{2}(\mathbb{R} _{+})$:

Definition2.3. (Malliavin derivative) Let $g$ belong to $L_{\phi}^{2}(\mathbb{R} _{+})$. The $\phi$-derivative of a stochastic variable $F\in L^{P}(\mathbb{P}^{H})$ in the direction of $\Phi g$ is defined as

if the limit exists in $L^{P}(\Omega, \mathcal{F}, \mathbb{P})$. Furthermore, if there is a process $(D^{\phi }F_{s}, s\ge 0)$ such that

for all $g\in L_{\phi}^{2}(\mathbb{R} _{+}),$ then $F$ is said to be $\phi$-differentiable.

Definition2.4. (The Wick product) Let $K(\omega) = \sum_{\alpha }^{} c_{\alpha } \mathcal{H}_{\alpha }(\omega)$ and $L(\omega) = \sum_{\beta }^{} d_{\beta } \mathcal{H}_{\beta }(\omega)$ be two members of $L_{\phi}^{2}(\mathbb{R} _{+})$. Then we define the Wick product $K\diamond L$ of $K$ and $L$ by

2.3.   Itô formula

Lemma2.2. Let $\left \{ F(s), s\in [0, T] \right \}$ be a stochastic process in $\mathcal{L} _{\phi } (0, T)$ and denote

Consider $f:\mathbb{R}_{+}\times \mathbb{R}\to \mathbb{R}$ a function that is first continuously differentiable with respect to its first argument and second continuously differentiable with respect to its second argument. Suppose that these derivatives are bounded. Moreover, it is assumed that $E\left [ \int_{0}^{T}\left | F(s)D_{s}^{\phi } \eta _{s} \right |\mathrm{d} s \right ] < \infty$ and $\left \{ \frac{\partial f}{\partial x} \left (s, \eta _{s} \right) F(s), s\in [0, T] \right \}$ is in $\mathcal{L} _{\phi } (0, T)$. Then for $0\le t\le T,$ the fractional Itô formula is obtained:

almost surely, or formally,

where $\phi(s, v) = H(2H-1)\left | s-t \right | ^{2H-2}.$

Lemma2.3. Let $\left \{ F^{i}(s), i = 1, \dots, n, s\in [0, T] \right \}$ satisfy the conditions of Lemma 2.2 for $F$, $t\in [0, T]$. Let

for $j = 1, 2, \dots, n$, and let $\left \{ \frac{\partial f}{\partial x_{j}}(s, \mu _{s})F^{j} (s), s\in [0, T] \right \}$ be in $\mathcal{L} (0, T)$. Assuming $f:\mathbb{R}_{+}\times \mathbb{R}^{n} \to \mathbb{R}$ has bounded second-order derivatives and is twice continuously differentiable, then

Particularly, if $\left \{ F^{i}(s), i = 1, \dots, n, s\in [0, T] \right \} \in L^{2}_{\phi}$, then we have

3.   Derivation of the FPK equation driven by FGN

As for stochastic differential equation driven by FBM:

where $A(t, x)$ is a drift function and $C(t, x)$ is a diffusion function. $A(t, x)$ and $C(t, x)$ must be linear and one-dimensional when the stochastic differential equation is one-dimensional ^[36]. $B^{(H)}(t)$ is a standard FBM with Hurst index $H$. Furthermore, we assume that $A(t, x)$ and $C(t, x)\neq0$ have the indicated derivatives. Then, utilizing Lemma 2.2, which is the fractional Itô formula, the scalar function $h(x)$ is expressed as follows:

where the function $\phi(s, t)$ is defined by

Taking the expectation of Eq (3.2), we can obtain

Therefore, we get

Suppose $p(t, x)$ represents the PDF of a particle's position at time $t$ and location $x$, and we have

which means that

Hence, we further obtain that

After partial integration, we find that

The first term on the right side of Eq (3.7) must vanish since $p(x, t) = 0$ at $x = \pm\infty$. Then

Similarly, we handle the second integral in Eq (3.7) to obtain

By reinserting Eqs (3.9) and (3.10) into Eq (3.7), we derive the subsequent equation:

Consequently, we can infer

Due to

substituting Eq (3.13) into Eq (3.12) and merging the diffusion terms, the corresponding FPK equation of Eq (3.1) under FGN excitation is derived as follows:

where $1/2 < H < 1$, and $p(t, x)$ is the PDF evolving with time.

In the interest of convenient analysis, of course, $x \in \Omega, t\in \left [ 0, T \right ]$, we can rewrite Eq (3.14) as

where $p(t, x)$ is defined on a domain $\Omega \times \left [ 0, T \right ]$, and $\mathcal{N} \left [ p(t, x), \theta \right ]$ is the FPK differential operator.

This is known as the FPK equation driven by the stochastic differential Eq (3.1) because the diffusion term in Eq (3.1) is an FBM. Interestingly, when $H = 1/2$, Eq (3.14) simplifies to the classical FPK equation. The FPK Eq (3.14) is a parabolic partial differential equation in two dimensions, with initial and boundary conditions given as

where $\varepsilon \Omega$ denotes the boundary of $\Omega$, and $\mathcal{I}(x)$ represents the initial Dirac delta distribution.

The normalization condition for the PDF must also be met:

4.   Solving the FPK equation based on PINNs

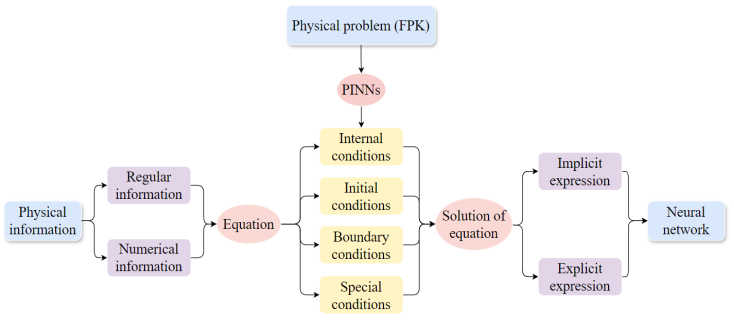
This section presents a PINN-based method for solving the time-dependent FPK equation. PINNs integrate physical laws into neural network training, enhancing prediction accuracy and ensuring physical consistency. By embedding energy conservation, momentum principles, and other physical constraints into the loss function, PINNs achieve a deep fusion of data-driven learning and physical knowledge. This approach enables accurate modeling of complex phenomena, even with incomplete system understanding, outperforming traditional data-driven methods in generalization, especially under data scarcity or noise. PINNs combine theoretical cognition (physical laws as learning objectives) and empirical measurement (numerical/experimental data), improving interpretability and approximation accuracy. The FPK equation's physical information is categorized into: regular information (implicit, Eq (3.16)) and numerical information (explicit, Eqs (3.17) and (3.18)). Neural networks are trained via sampled data to fit both information types, approximating FPK solutions. Training balance is controlled by adjusting sampling scales and loss weights for each information type. The final network approximates all FPK solutions (Figure 3).

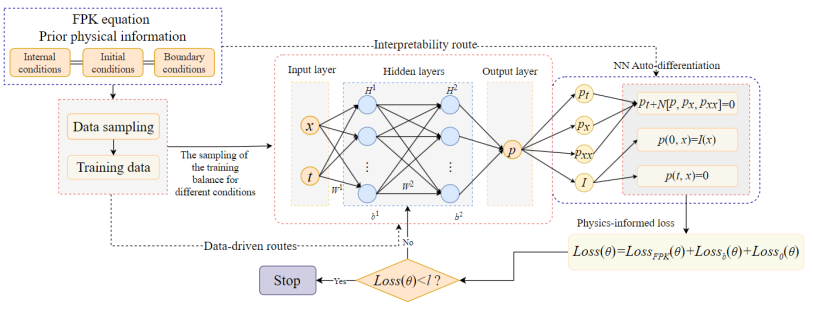
Based on Lu et al.'s ^[37] general PDE-solving steps, Figure 4 illustrates the FPK equation-solving process. The FPK equation's physical information is split into: 1) internal conditions of Eq (3.15) and 2) numerical data for initial and boundary conditions of Eqs (3.16) and (3.17). A neural network within parameter space $\Xi$ is constructed to encapsulate the solution. Network fitting loss combines neural network output with these two information types. Training samples are balanced, and comprehensive information loss is constructed based on training intensity balance. Through iterative training, the network approximates the equation's physical information. The optimal solution $p(t|\theta, x), \theta \in \Xi$ minimizes this loss. Integrating regularization and numerical information enhances network interpretability, reflecting the equation's information satisfaction and the network's capacity to estimate physical attributes.

Generally speaking, the process of solving the FPK equation by the PINNs method can be summarized as the following four stages:

1) Neural network architecture design. A neural network model is constructed with two independent variables $x$ and $t$. The output layer of the model is designed to predict the equation solution $p (t, x | \theta)$, where $\theta \in \Xi$ represents the set of parameters in the parameter space $\Xi$. The neural network aims to solve the characterization equation $p(t, x|\theta)$ in the parameter space $\Xi$. The neural network's structure is detailed in Table 1, and the Adam optimizer is employed for model training. The selection of the tanh activation function and two hidden layers with 50 neurons each was based on extensive empirical testing and the following considerations:

(a) Activation function:

ⅰ Tanh was chosen over ReLU due to its smooth derivatives, which are crucial for accurately computing higher-order PDE terms in the FPK equation through automatic differentiation.

ⅱ Compared to sigmoid, tanh provides better gradient flow in deep networks by centering the output around zero.

ⅲ The softplus output activation ensures non-negative probability density values while maintaining differentiability.

(b) Network depth and width ^[21]:

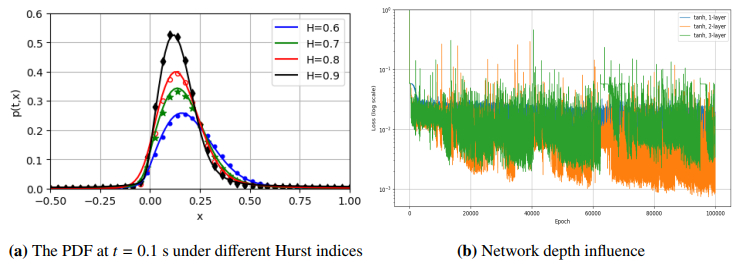
ⅰ. Two hidden layers were found to provide sufficient capacity to approximate the solution while avoiding overfitting, as evidenced by ablation studies (Section 5.3).

ⅱ. 50 neurons per layer achieved optimal balance between computational efficiency (0.4s training time) and accuracy ($< 1\%$ error), with diminishing returns observed when increasing to 100 neurons.

ⅲ. Shallower networks (1 hidden layer) underfitted the solution, while deeper networks (3+ layers) showed minimal improvement but required 2–3 × longer training times.

(c) Training stability:

ⅰ. This architecture maintained stable training across different Hurst indices ($H = 0.5$-0.9) and noise intensities ($\sigma$).

ⅱ. The combination of tanh activations with initialization prevented vanishing or exploding gradients during backpropagation of the physics-informed loss terms.

2) Loss function construction. Based on the internal condition regular information of the equation, and the numerical information of the initial condition and the boundary conditions, a comprehensive information loss function $MSE (\theta)$ is constructed as follows:

where $Loss_{FPK}(\theta)$, $Loss_{b}(\theta)$, and $Loss_{0}(\theta)$ are defined as follows:

where, $\delta (\hat{p}(t, x_{i}^{F}|\theta)) = \mathcal{N} \left [ \hat{p} (t, x_{i}^{F}|\theta), \hat{p}_{x}(t, x_{i}^{F}|\theta), \hat{p}_{xx}(t, x_{i}^{F}|\theta) \right ]+\frac{\partial \hat{p}(t, x_{i}^{F}|\theta) }{\partial t}$, and $Loss_{FPK}(\theta)$, $Loss_{b}(\theta)$, and $Loss_{0}(\theta)$ are guaranteed to satisfy the approximate solutions of Eqs (3.16)–(3.18), respectively. $N_{F}$, $N_{b}$, and $N_{0}$ denote the counts of collocation, initial, and boundary points within the training dataset, respectively. $\hat{p}(t, x | \theta)$ denotes the trial solution.

3) Data sampling strategy. According to the training sampling balance, data is extracted based on the equation's interior, initial, and boundary conditions to generate the respective training dataset. We specifically include the internal condition dataset $\left\{ t, x_{i}^{FPK} \right \}$, initial condition dataset $\left \{ 0, x_{i}^{0} \right \}$, and boundary condition dataset $\left \{ t, x_{i}^{b} \right \}$.

4) Neural network training and parameter optimization. The neural network was trained with the dataset collected in (ⅲ) to minimize the integrated information loss function $Loss (\theta)$. Through the optimization process, the integrated information loss function $Loss (\theta)$ reaches the minimum optimal parameter $\theta ^ {*}$, where $\theta ^ {*} = arg\, min\, {Loss (\theta)}$ is determined, and finally, we obtain the optimized differential equation solution $p(t, x | \theta ^ {*})$.

The PINNs framework is invoked to solve the FPK equation (3.15) by embedding the FPK directly into the loss function (4.1). Unlike traditional mesh-based methods, PINNs approximate the solution globally through a neural network trained on: collocation points (interior domain, Eq (4.2)), boundary conditions (Eq (4.3)), and initial conditions (Eq (4.4)). The PINNs implementation involves three phases: 1) Preprocessing: Initialize network parameters are based on the Hurst index. 2) Training: Employ stratified adaptive sampling with increased density in boundary layers. 3) Validation: Verify results via Monte Carlo simulations. The computational efficiency of our PINNs implementation stems from:

1) Avoiding expensive mesh generation and time-stepping schemes required by traditional methods.

2) Parallelized gradient computation through PyTorch's automatic differentiation.

4) A selective sampling strategy that concentrates collocation points in regions of high solution curvature.

4) The moderate network size ($\sim$5000 parameters) keeps memory usage low while capturing solution complexity.

The total computational cost comprises: 1) Compared to Monte Carlo methods, PINNs reduce computational costs by avoiding repeated simulations. For example, in Section 5.2, PINNs achieved results in 0.4 seconds vs. 65.13 seconds for Monte Carlo. 2) The cost is primarily from backpropagation and automatic differentiation for PDE terms, but this is offset by the ability to learn the solution globally without grid discretization. Table 2 illustrates the sequence of steps for the proposed PINNs algorithm. In the subsequent section, we will apply our technique to a pair of distinct systems to validate its performance.

5.   Numerical examples

We are creating a test script using the PyTorch deep learning library on a Windows 11 operating system. Tests were carried out on a system with Visual Studio Code 1.77.1, utilizing a 12th Gen Intel (r) Core (TM) i7-12700 CPU at 2.10 GHz and having 64 GB of RAM. This part will present two stochastic dynamical systems as case studies to exhibit the utility of the PINNs algorithm.

5.1.   Dynamical system under additive FGN excitation

The Ornstein-Uhlenbeck (O-U) process, governed by an additive FGN, is characterized by the following system definition ^[38]

where $B^{(H)}(t)$ represents FBM characterized by a Hurst index within the range of $1/2 < H < 1$, $\lambda > 0$ denotes an unknown parameter, and $\sigma$ represents the intensity of the noise. The solution for Eq (5.1) can be expressed as

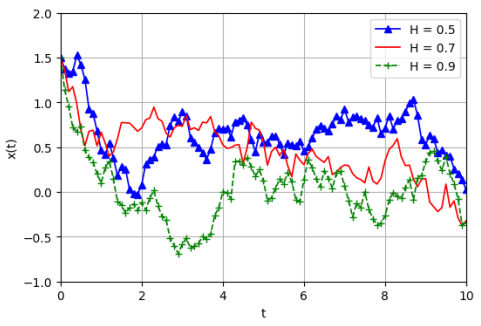
For $\lambda = 1, \sigma = 0.4, x(0) = 1.5$, $t$ are in the interval [0, 10], for the different Hurst parameters $H$, $H = 0.5, H = 0.7$, and $H = 0.9$, respectively. Figure 5 depicts the trajectories for three samples of the O-U process influenced by FBM, as indicated in Eq (5.1). Next, we will concentrate on the evolution of the system's PDF. The FPK equation adhered to by the PDF of system (5.1) is

and the initial condition is $p(0, x) = \delta(x-x_{0})$. The precise time-dependent solution to FPK Eq (5.2) can be derived as indicated in ^[38]:

Using the output $\hat{p}(t, x | \theta)$ of PINNs to fit $p(t, x)$, we can construct the following loss function:

where

This example verifies the effectiveness of the PINNs method by comparing the exact solution with the numerical solution obtained by the PINNs algorithm. We assign $N_{0} = 200$ for the count of initial training points, $N_{b} = 200$ for the boundary points, and $N_{F} = 1000$ for the residual points. The training process has carried out 100,000 iterations. The PINNs method initializes the learning rate for the first 30,000 epochs at $5\times 10^{-3}$, and then adjusts it to $5\times10^{-4}$ for the subsequent 70,000 epochs. Additionally, the training range for the variable $x$ is defined as [–2, 2]. Unless otherwise specified, we consider $\lambda = 1.0,$ $\sigma = 0.5$, $H = 0.51$, $x_{0} = 0$.

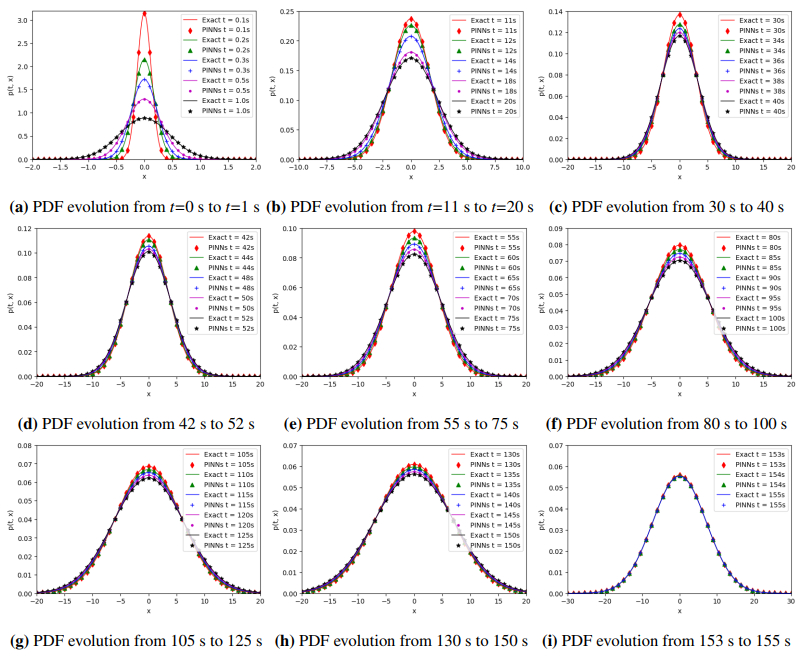
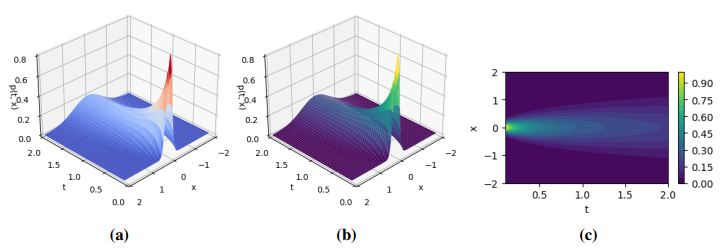
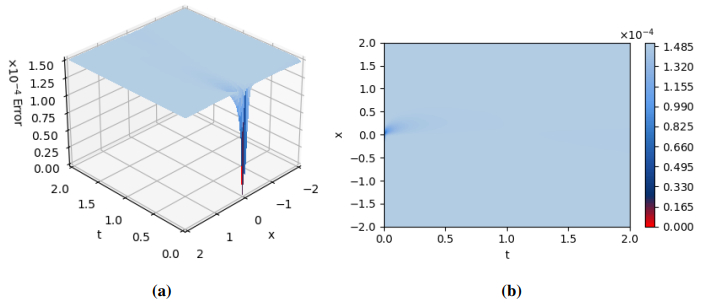
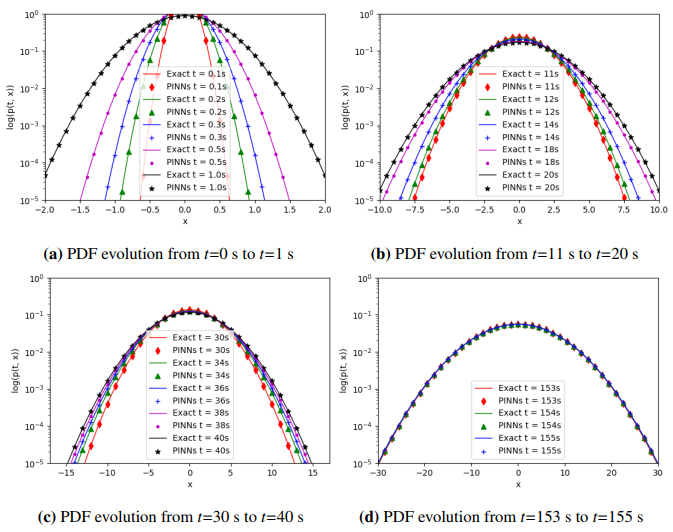
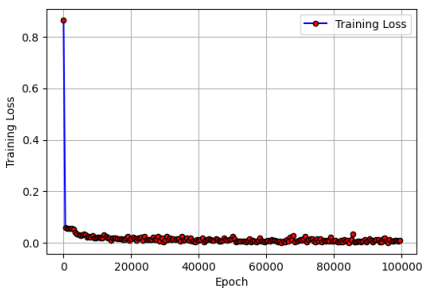
Equation (5.2), known as the FPK equation, characterizes the time development of the PDF for the O-U process influenced by additive FGN. As shown in Figure 6, the PINNs solutions at different times are represented by discrete points. When compared, the colored solid line represents an exact solution. Therefore, observing Figure 6, it is evident that the estimated solution closely aligns with the exact solution, illustrating a comparison from $t$ = 0.1 s to $t$ = 155 s between the two solutions. The excellent consistency between the PINNs method and the exact solution verifies the effectiveness of the PINNs method. As shown in Figure 6(i), the PDF remains unchanged with time $t$, which indicates that the PDF gradually reaches a stationary state with the increase of time (after $t$ = 153 s). Figure 7 illustrates the prediction solution of the PINNs algorithm, encompassing the vertical perspective of $p(t, x)$, the three-dimensional outline of $p(t, x)$ and the three-dimensional view of the exact solution. Here, $\hat{p}(t, x)$ and $p(t, x)$ respectively represent the predicted solution and the reference solution, and the absolute error between the predicted solutions defined by $error = |\hat{p} (t, x)-p(t, x)|$ is shown in Figure 8 and Table 3. The findings indicate that the error for each variable is nearly negligible, confirming the accuracy of our trained outcomes. Figure 9 shows the evolution of the PDF on a logarithmic scale in different time periods. The PDF gradually broadens and shifts with time, with a sharp peak in the early stage and slower and flatter tail attenuation in the later stage. The numerical solution of the PINNs method is highly consistent with the exact solution at all times, and this method has high accuracy and quasi-accuracy. Figure 10 depicts the decline in loss value over 100,000 iterations in the PINNs algorithm. It is observed that as the number of iterations increases, the loss value diminishes progressively.

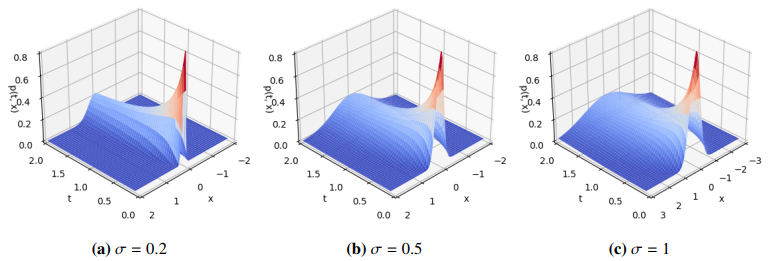
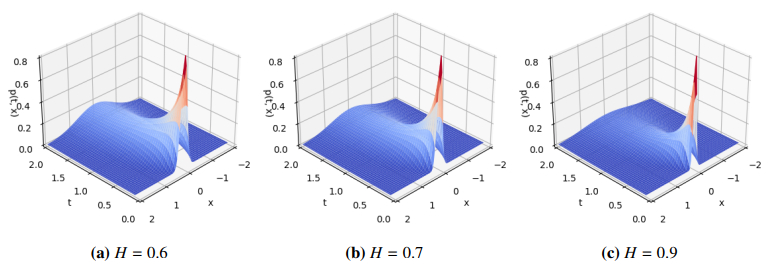
Figure 11 illustrates the progression of the PDF under varying intensities of additive FGN. As depicted in Figure 11, the peak of the PDF diminishes as the intensity of the additive FGN rises. The results show that with the decrease of additive FGN intensity, the probability of appearing in the energy region increases. Finally, the evolution of the PDF under different Hurst indices is given in Figure 12. We can observe that with the increase of the Hurst index, the maximum value of the PDF decreases. Similarly, the effectiveness of the PINNs method is verified from Figures 11 and 12.

5.2.   Dynamical system subjected to excitations by multiplicative FGN

Consider a one-dimensional stochastic dynamical system excited by multiplicative FGN:

where $f(x) = x$, $a > 0$ represents unknown parameters, and $\sigma$ represents noise intensity. As outlined in Section 2, the FPK equation for the system (5.8) can be formulated as

and the initial condition is $p(0, x) = \delta(x-x_{0})$.

This example verifies the effectiveness of the PINNs algorithm by the Monte Carlo method of the original system (5.8). Under the initial conditions, we use the Monte Carlo method with 500,000 samples to obtain the reference solution to evaluate the accuracy of our method. The training interval of variable $x$ is set to [–1, 1]. Unless otherwise specified, we consider $a = 0.4,$ $\sigma = 0.4,$ $H = 0.61$, $x_{0} = 0.05$. The FPK Eq (5.9) can describe the evolution of the system PDF excited by multiplicative FGN. Obtaining the precise solution for the FPK Eq (5.9) is challenging, hence, the Monte Carlo approach is utilized on the initial system to assess the efficacy of the PINNs technique.

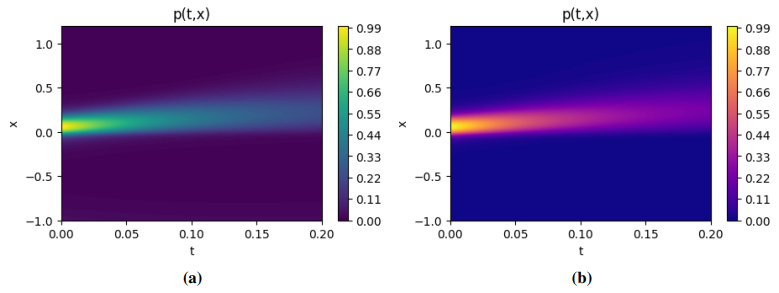
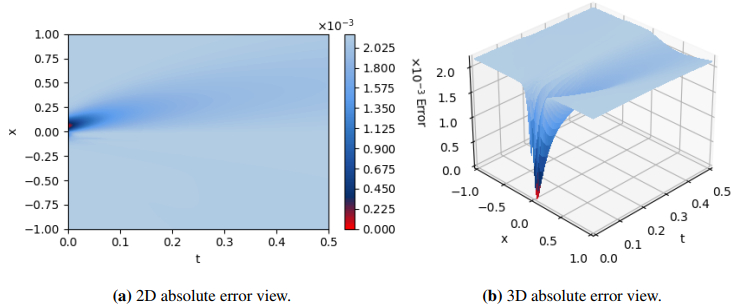
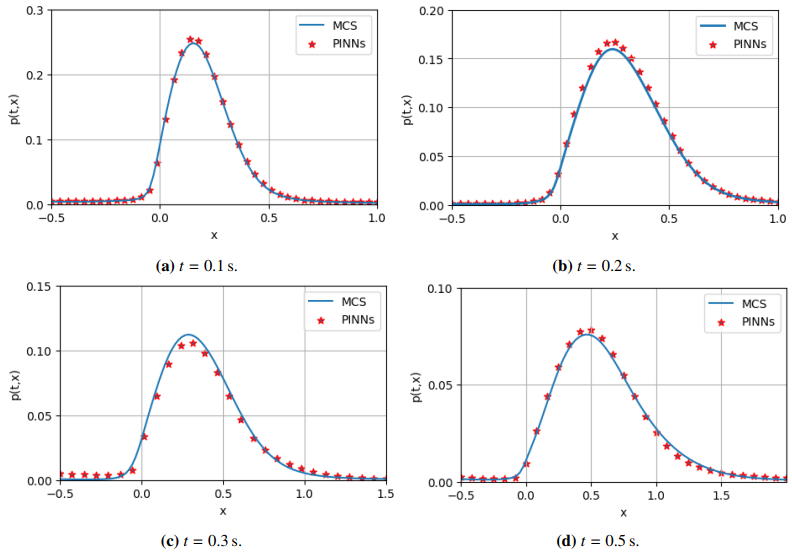
Figure 13 provides a two-dimensional vertical perspective of the PINNs algorithm, while the Monte Carlo approach offers a corresponding two-dimensional vertical perspective of the solution. Figure 14(a) illustrates the two-dimensional absolute error vertical view of the two numerical methods. The data indicates that the error for each variable is nearly zero, confirming the accuracy of our training outcomes. Figure 15 shows the PINNs solution and Monte Carlo solution at different times. The blue solid line shows the results obtained by the Monte Carlo method, and the circle symbol shows the numerical solution of the PINNs solution. We can find that the predicted solution is very close to the reference solution from Figure 15, which depicts the contrast between the exact and predicted solutions at $t$ = 0.1 s, $t$ = 0.2 s, $t$ = 0.3 s, and $t$ = 0.5 s. The excellent consistency between the PINNs method and Monte Carlo method verifies the effectiveness of the PINNs method. The non-symmetrical shape in Figure 15 arises from the multiplicative noise term ^[39,40,41], which induces state-dependent dispersion. This contrasts with the additive noise case (Figure 6), where the linear drift and constant diffusion preserve symmetry. The long-memory effect ($H > 1/2$) further amplifies the skewness by sustaining transient biases.

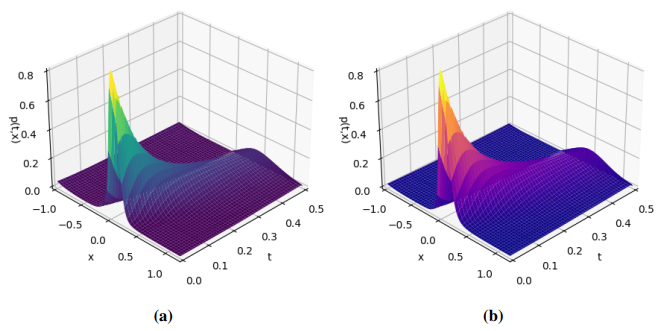
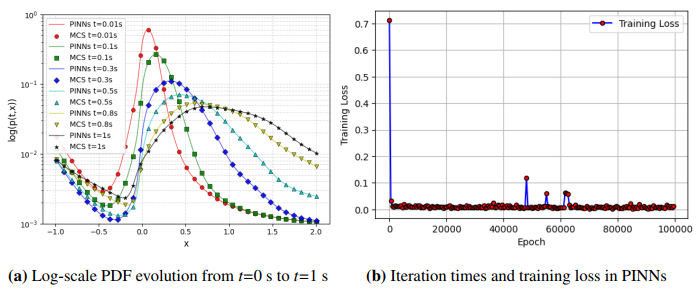
Figure 16 illustrates the three-dimensional view of the PINNs algorithm prediction solution, and the Monte Carlo method refers to the three-dimensional view of solution. Figure 14(b) illustrates the three-dimensional view of the absolute error of the two numerical methods. The findings reveal that the error for each variable is nearly negligible, affirming the effectiveness of the proposed method. The computed outcomes from both methods are presented in Table 3, where the time to solve the FPK equation by the Monte Carlo method is 65.13 s, while PINNs only needs about 0.4 s. Figure 17(a) presents the logarithmic scale evolution of the PDF at different time points. The tail behavior of the PDF shows that the curve gradually moves to the right with the increase of time, and the decline speed in the tail region slows down. This shows that with the passage of time, the distribution of data becomes more concentrated, and the probability density of the tail decreases gradually. Figure 17(b) shows the change of loss value when iterating for 100,000 times in the PINNs algorithm. The data indicates that as the number of iterations rises, the loss value diminishes incrementally.

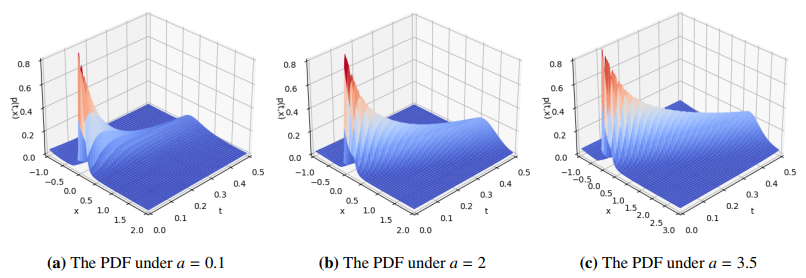
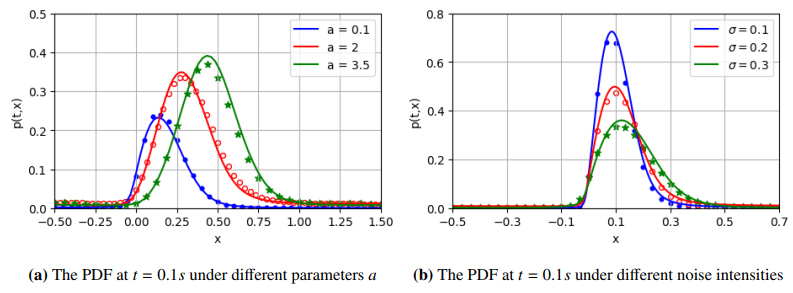
Figure 18 provides the evolution of the PDF under different parameters $a$. As can be seen from Figure 18, with the increase of parameter $a$, the PDF shifts and the peak value increases. The results show that with the increase of parameter $a$, the probability of appearing in the energy region increases. In Figure 19(a), the solution of the FPK equation with PINNs is represented by colored symbols, and the Monte Carlo solution is represented by colored lines for comparison. Obviously, all PINNs results are very close to the Monte Carlo results, which shows that the PINNs method has high accuracy.

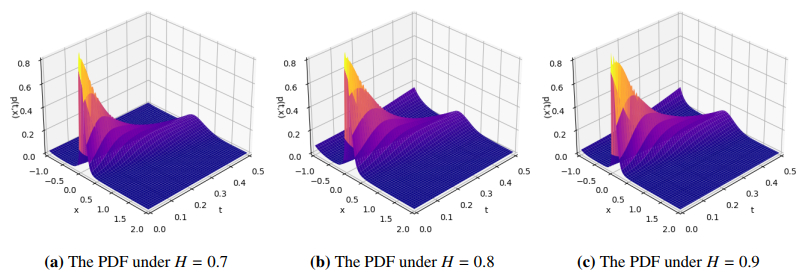
The cross-section comparison of the PDF with different multiplicative FGN strengths at $t = 0.1$ s is shown in Figure 19(b). As can be seen from Figure 19(b), with the increase of multiplicative FGN intensity, the PDF shifts and the peak value becomes smaller. The results show that with the decrease of multiplicative FGN intensity, the probability of appearing in the energy region increases. Finally, the cross-section comparison of the PDF at $t = 0.1$ s under different Hurst indices is given in Figure 20. We can observe that with the increase of the Hurst index, the peak value of the PDF becomes larger. Similarly, the effectiveness of the PINNs method is verified from Figures 18–20 and 21(a).

5.3.   Comparative analysis

The effectiveness of the proposed PINNs algorithm is demonstrated through three key aspects:

(1) Accuracy: Compared to analytical solutions (Section 5.1) and Monte Carlo simulations (Section 5.2), PINNs achieve errors of $< 1\%$ across all test cases (Table 3), with particularly close agreement in probability density peaks (Figures 6 and 15).

(2) Efficiency: The method provides a 162 speedup over Monte Carlo (0.4 s vs. 65.13 s in Table 3) by avoiding repetitive simulations and leveraging GPU-accelerated automatic differentiation.

(3) Robustness: Consistent performance is maintained under varying conditions, including noise intensities ($\sigma$, Figures 11 and 19), varying Hurst indices ($H$, Figures 12 and 20), with errors $< 1.2\%$, temporal scales ($t$, Figures 6 and 15), and system parameters ($a$, Figure 18).

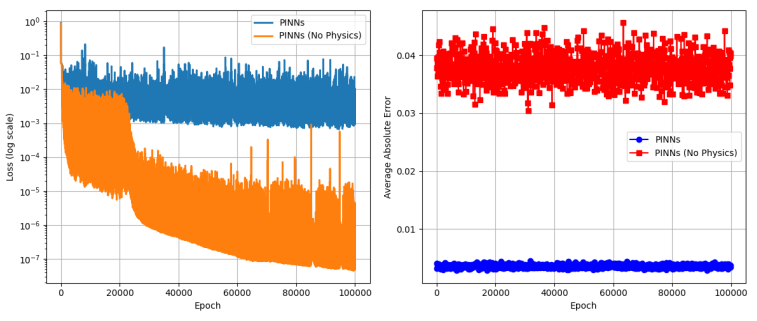
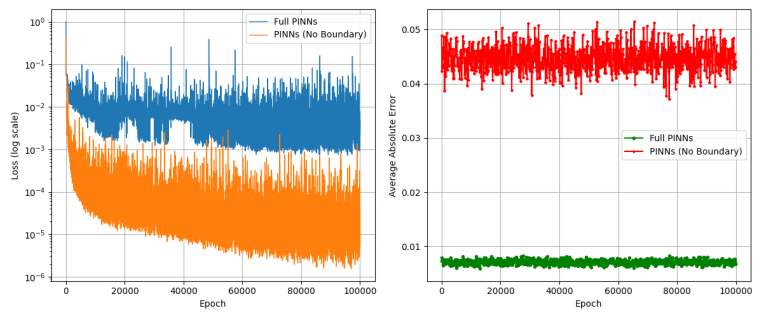
Through the comprehensive analysis of Figures 21(b), 22 and 23, it can be clear that each component plays a key role in the efficiency of the algorithm: First, the contrast curve in Figure 22 shows that the average absolute error (0.001) of the PINNs model with physical constraints is 40 times lower than that of the version without physical constraints (0.04) after 100,000 training cycles, which verifies that the physical constraint mechanism is the core guarantee of the accuracy of the algorithm. Second, Figure 16 shows that removing the loss term of the boundary conditions will lead to an error increase of 3 times (0.03 vs. 0.01) and divergence at the edge of the solution domain, indicating that boundary conditions have a decisive influence on the stability of the solution. The logarithmic coordinate loss curve in Figure 21(b) further reveals that the loss function of the complete PINNs can keep a steady downward trend, while the version without physical constraints shows continuous oscillation, which shows that physical constraints not only improve the accuracy, but also significantly improve the convergence and efficiency of the training process. These three key evidences prove that the effectiveness of the proposed algorithm stems from:

1) The embedding of the essential laws of the governing equations by physical constraints.

2) The constraints of boundary conditions on the spatial stability of the solution.

3) The balanced design of the loss function promotes the collaborative optimization of all components, and finally the computational efficiency is two orders of magnitude higher than that of the traditional Monte Carlo method (162 times faster) while maintaining the error accuracy of $< 1\%$.

6.   Conclusions

This paper expounds on the application of the PINNs algorithm in solving the transient PDF of a dynamical system driven by additive and multiplicative FGN. By using the theory of fractional stochastic calculus, the FPK equation for the PDF of the control system is derived. The loss function design of the PINNs algorithm includes three parts: the fitting of the FPK equation, the initial conditions, and boundary conditions in numerical information. The results indicate that the PINNs algorithm can effectively calculate the transient PDF of two examples of one-dimensional systems. That is to say, it proves its applicability and feasibility in solving the transient response of stochastic dynamical systems.

Additionally, this article further also shows the ability of the PINNs algorithm to settle the response of the system subjected to excitation by FGN. Compared with the results of the Monte Carlo method, the PINNs algorithm shows high computational efficiency and good solution effect, and the fitting effect of PINNs solution is basically the same as that of the MCS solution, which fully verifies the effectiveness and accuracy of PINNs. The results of these two numerical methods are analyzed in Table 3, which further highlight the remarkable advantages of the PINNs algorithm in computational efficiency. In order to broaden the scope of the PINNs algorithm in practical application, future research needs to explore the solution strategy and mechanism when the initial conditions and boundary conditions in numerical information are replaced by actual observation data.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work has received supported by the grants from the National Natural Science Foundation (No.12362005), Key Project of Natural Science Foundation of Ningxia (No.2024AAC02033), Ningxia higher education first-class discipline construction funding project (NXYLXK2017B09), Major Special project of North Minzu University (No.ZDZX201902), and in part by the 2024 Graduate Innovation Project of North Minzu University under grant (YCX24273).

Conflict of interest

The authors declare there is no conflicts of interest.