Figure 1.
Study flowchart.
In this paper, we consider an initial-Neumann boundary value problem for a two-species chemotaxis system
{∂u∂t=Δu−χ∇⋅(u∇w)+u(a1−b1um−1+c1v), (x,t)∈Ω×(0,Tmax),∂v∂t=Δv−ξ∇⋅(v∇w)+v(a2−b2vl−1−c2u), (x,t)∈Ω×(0,Tmax),∂w∂t=Δw−(uα+vβ)w, (x,t)∈Ω×(0,Tmax),
where the domain Ω⊂Rn(n≥2) is bounded and smooth, Tmax∈(0,∞], and parameters ai,bi,ci,m,l,α, β,χ,ξ>0 with m,l>1,i=1,2. In the current work, we provide a sufficient condition of global classical solvability to the above system. More precisely, for some suitable initial data, if m>max{α(n+2)2,1} and l>max{β(n+2)2,1}, then the system has a global classical solution. Compared to previous work, the existence result established here is more generalized, depending only on the nonlinear power exponents and spatial dimensions.
Citation: Chang-Jian Wang, Yuan-Hao Zang. Boundedness of solutions in a two-species chemotaxis system[J]. Electronic Research Archive, 2025, 33(5): 2862-2880. doi: 10.3934/era.2025126
| [1] | Sujit Nair . Current insights into the molecular systems pharmacology of lncRNA-miRNA regulatory interactions and implications in cancer translational medicine. AIMS Molecular Science, 2016, 3(2): 104-124. doi: 10.3934/molsci.2016.2.104 |
| [2] | Radwa El-Sayed Mahmoud Marie, Aya Mohamed kamal Lasheen, Hebat-Allah Hassan Nashaat, Mona A. Atwa . Assessment of serum interleukin 19 level in patients with warts. AIMS Molecular Science, 2023, 10(1): 1-10. doi: 10.3934/molsci.2023001 |
| [3] | Amrit Krishna Mitra . Familiar fixes for a modern malady: a discussion on the possible cures of COVID-19. AIMS Molecular Science, 2020, 7(3): 269-280. doi: 10.3934/molsci.2020012 |
| [4] | Mairembam Stelin Singh, PV Parvati Sai Arun, Mairaj Ahmed Ansari . Unveiling common markers in COVID-19: ADAMTS2, PCSK9, and OLAH emerged as key differential gene expression profiles in PBMCs across diverse disease conditions. AIMS Molecular Science, 2024, 11(2): 189-205. doi: 10.3934/molsci.2024011 |
| [5] | Irene Mwongeli Waita, Atunga Nyachieo, Daniel Chai, Samson Muuo, Naomi Maina, Daniel Kariuki, Cleophas M. Kyama . Differential expression and functional analysis of micro RNAs in Papio anubis induced with endometriosis for early detection of the disease. AIMS Molecular Science, 2020, 7(4): 305-327. doi: 10.3934/molsci.2020015 |
| [6] | Mohd Shukri Abd Shukor, Mohd Yunus Abd Shukor . Molecular docking and dynamics studies show: Phytochemicals from Papaya leaves extracts as potential inhibitors of SARS–CoV–2 proteins targets and TNF–alpha and alpha thrombin human targets for combating COVID-19. AIMS Molecular Science, 2023, 10(3): 213-262. doi: 10.3934/molsci.2023015 |
| [7] | Ahmed Yaqinuddin, Abdul Hakim Almakadma, Junaid Kashir . Kawasaki like disease in SARS-CoV-2 infected children – a key role for neutrophil and macrophage extracellular traps. AIMS Molecular Science, 2021, 8(3): 174-183. doi: 10.3934/molsci.2021013 |
| [8] | Amir Khodavirdipour, Fariba Keramat, Seyed Hamid Hashemi, Mohammad Yousef Alikhani . SARS-CoV-2; from vaccine development to drug discovery and prevention guidelines. AIMS Molecular Science, 2020, 7(3): 281-291. doi: 10.3934/molsci.2020013 |
| [9] | Archana M Navale, Vanila Devangan, Arpit Goswami, Vikas Sahu, Lavanya S, Devanshu Patel . Effects of pre-existing metformin therapy on platelet count, serum creatinine, and hospitalization in COVID-19 patients with diabetes mellitus. AIMS Molecular Science, 2023, 10(4): 311-321. doi: 10.3934/molsci.2023018 |
| [10] | Amal Feiroze Farouk, Areez Shafqat, Shameel Shafqat, Junaid Kashir, Khaled Alkattan, Ahmed Yaqinuddin . COVID-19 associated cardiac disease: Is there a role of neutrophil extracellular traps in pathogenesis?. AIMS Molecular Science, 2021, 8(4): 275-290. doi: 10.3934/molsci.2021021 |
In this paper, we consider an initial-Neumann boundary value problem for a two-species chemotaxis system
{∂u∂t=Δu−χ∇⋅(u∇w)+u(a1−b1um−1+c1v), (x,t)∈Ω×(0,Tmax),∂v∂t=Δv−ξ∇⋅(v∇w)+v(a2−b2vl−1−c2u), (x,t)∈Ω×(0,Tmax),∂w∂t=Δw−(uα+vβ)w, (x,t)∈Ω×(0,Tmax),
where the domain Ω⊂Rn(n≥2) is bounded and smooth, Tmax∈(0,∞], and parameters ai,bi,ci,m,l,α, β,χ,ξ>0 with m,l>1,i=1,2. In the current work, we provide a sufficient condition of global classical solvability to the above system. More precisely, for some suitable initial data, if m>max{α(n+2)2,1} and l>max{β(n+2)2,1}, then the system has a global classical solution. Compared to previous work, the existence result established here is more generalized, depending only on the nonlinear power exponents and spatial dimensions.
Coronavirus disease 2019 (COVID-19) was announced in December 2019, then pandemic condition was declared [1]. The clinical features of COVID-19 are wide-ranging, from asymptomatic and mild cases to severely affected ones. Severe patients may develop acute respiratory distress syndrome and multi-organ failure. Old age and the presence of comorbidities are the main risk factors of COVID-19 severity and mortality [2]. However, mild patients may dramatically worsen in a brief time and have severe respiratory failure [3]. Therefore, it might be essential to develop biomarkers that can early predict the COVID-19 severity and prognosis of those patients [4].
Long noncoding RNA (lncRNA) highly upregulated in liver cancer (HULC) detected at human chromosome 6 in the q24.3 band. LncRNA HULC was identified in 2007 as an overexpressed LncRNA in liver cancer [5]. Also, many cancer types show overexpression of lncRNA HULC [6]. lncRNA HULC regulates inflammation in vascular endothelial cells resulting in their dysfunction [7],[8]. Endothelial dysfunction contributes to severe COVID-19 that causes increased endothelial factors [9].
Also, lncRNA HULC causes interleukin (IL)-6 to release in human endothelial cells [10]. In COVID-19, high levels of IL-6 are linked with adverse clinical outcomes [11]. The lncRNA HULC regulates microRNA (miRNA)-9 expression. The inhibition of miRNA-9 by lncRNA HULC is achieved by methylation of the miRNA-9 promoter [12]. The downregulation of miRNA-9 plays roles in the pathogenesis and progression of COVID-19 through the acute inflammatory response mediated by IL-6 [13].
Based on the previous information, this study hypothesized that lncRNA HULC might be a potential biomarker for COIVD-19. This study aimed to evaluate the role of lncRNA HULC, miRNA-9, and IL-6 in estimating the severity and predicting the prognosis of COVID-19.
A case-control study of patients from Zagazig University Hospitals was conducted in December 2021. The subjects' participation was confirmed by the patient or first-degree relatives by signing the written participation consent. The Zagazig University Faculty of Human Medicine's Institutional Review Board approved the study's procedure (No.: 9393). The patients were assessed using a comprehensive history and clinical examination includes the assessment of disease severity. The markers were evaluated at the time of diagnosis. The 28-day mortality rate was the primary outcome.
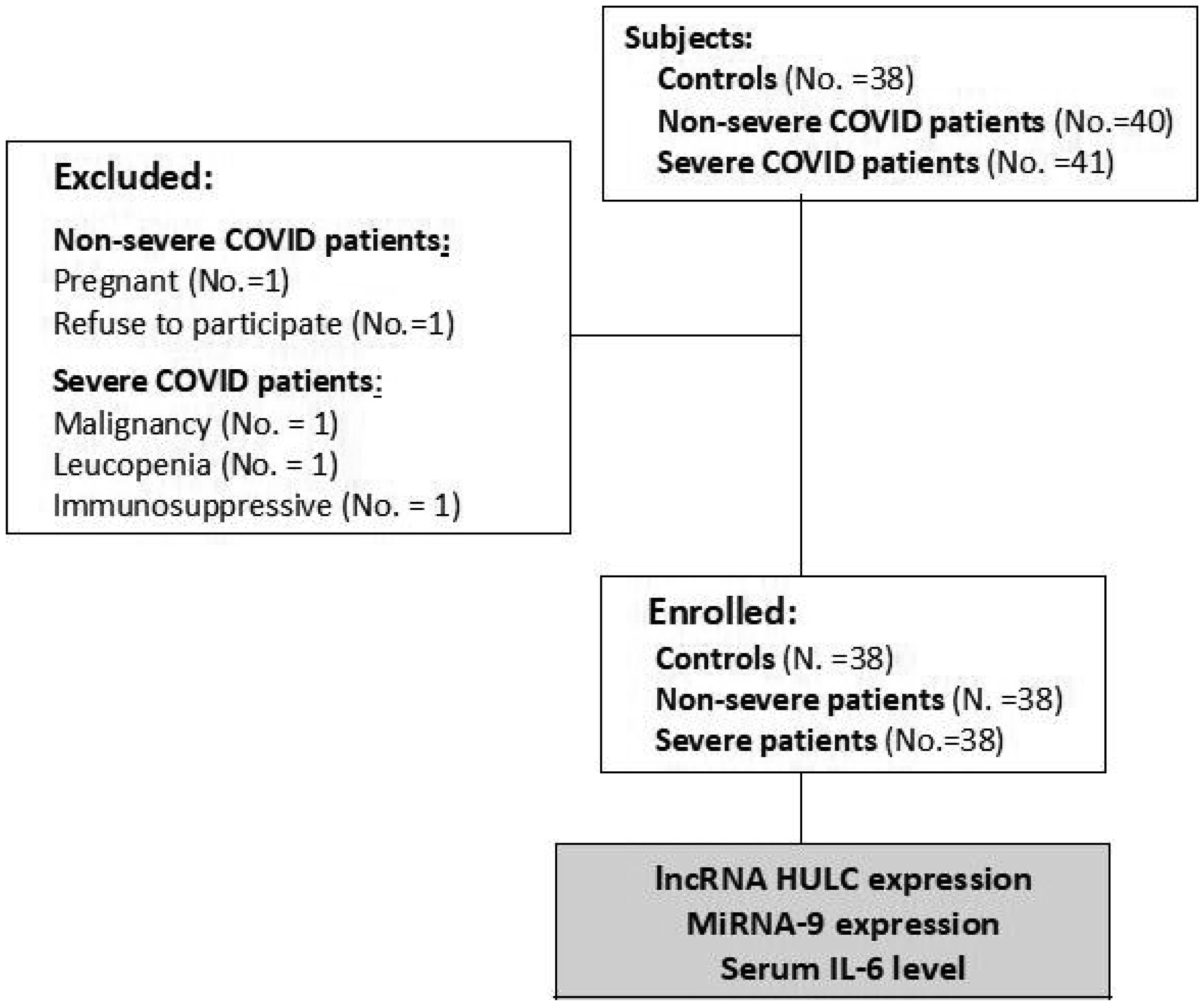
The sample size was estimated using Epi Info program 6 (Atlanta, Ga, USA) using the mean and standard deviation of IL-6 levels from previous study of Rostamian et al. [14] with 95% statistical power and 95% confidence limit. There were 38 non-severe COVID-19 patients, 38 severe COVID-19 patients, and 38 healthy controls consecutively enrolled in this study. Based on detection of viral nucleic acid in the nasopharyngeal swab, all the patients were diagnosed as COVID-19 positive. The patients who suffered from malignancies, leucopenia, and pregnant females were excluded. Patients treated with immunosuppressive drugs in the past month were excluded. The severity grading criteria were carried out in accordance with the Egyptian Ministry of Health and Population's COVID-19 management protocol (2021). Mild cases had only mild symptoms and normal imaging. Moderate cases showed positive imaging findings but their oxygen saturation equal to or more than 92%. The patients were classified as severe if the following criteria are meet (decreased oxygen saturation less than 92%, low partial pressure of oxygen to the fraction of inspired oxygen ratio below 300 mmHg, high respiration rate above 30 breath per minute, or presence of more than 50% lung infiltrates). The critical illness was considered if the patients have respiratory failure, septic shock, and/or multiorgan dysfunction. Both severe and critically ill cases were included in the severe group while mild and moderate patients were assigned in the non-severe group (Figure 1).
In a BD Vacutainer ® plastic EDTA tube and plain tube (Becton, Dickinson and Company, Franklin Lakes, NJ), whole blood was collected. At room temperature, the EDTA tube was centrifuged at 1200 x g for 3 minutes. The plasma was transferred into a 1.5 mL RNase-free microcentrifuge tube and recentrifuged for 10 minutes at 4 °C at 12000 x g. The miRNA-9 and lncRNA-HULC analyses were performed from this separated plasma. After 30 minutes of blood collection in the plain tube, the tube was centrifuged for 10 minutes at 1200 x g. Serum was aliquoted in 1.5 mL sterile microcentrifuge tubes and kept at -80 °C until IL-6 measurement.
RNA extraction: extraction of RNAs from the plasma was carried out according to the manufacturer's instructions using the miRNeasy Serum/Plasma Kit (QIAGEN, GmbH, Hilden, Germany). A NanoDrop-2000 spectrophotometer (Thermo Scientific, USA) was used to assess the quantity and quality of the extracted RNA.
Reverse transcription (RT): all RNA species were converted into complementary DNA (cDNA) by the miScript RT II kit (QIAGEN GmbH, Hilden, Germany) using 1 µg of extracted RNA and miScript HiFlex Buffer. The mixture was incubated at 37 °C for 60 min and 95 °C for 5 min. The Gene Amp PCR System 9700 thermocycler (Perkin Elmer, Singapore) was used for the RT. The cDNA was kept at a temperature of -80 °C until analysis.
Quantitative real-time polymerase chain reaction (RT-qPCR): the RT-qPCR reaction was performed using a StepOne™ System (Applied Biosystems, USA) using miScript SYBR Green PCR Kit and target-specific miScript primers assay for lncRNA HULC and miRNA-9 (QIAGEN, GmbH, Hilden, Germany). cDNA was diluted by mixing 20 µL with 100 µL of RNase-free water. In a final volume of 25 µL, the PCR reaction was carried out. The thermal profile for this PCR reaction was an initial incubation for 15 minutes at 95 °C followed by 40 subsequent cycles of (15 sec at 94 °C, 30 sec at 55 °C, and 30 sec at 7°C). Fluorescence measurement was expressed as cycle threshold (CT). At the end of all cycles, the melting curve was generated to ensure the reaction specificity. The expression of lncRNA HULC and miRNA-9 were normalized by the expression level of glyceraldehyde 3-phosphate dehydrogenase (GAPDH) and small nucleolar RNA, C/D box 68 (SNORD 68), respectively. The fold change formula of 2− ΔΔCT was utilized to calculate the relative expression levels [15].
Human IL-6 enzyme-linked immunosorbent assay (ELISA) Kit (Bioassay Technology Laboratory, Shanghai, China) was utilized to measure serum IL-6. Based on the manufacturer's procedure, the assay steps were performed. The Sunrise™ absorbance reader (Tecan Trading AG, Männedorf, Switzerland) was used for reading the plates. Serum IL-6 values were presented in pg/mL. This Kit showed intra-assay and inter-assay precision coefficients of < 10% and < 12%, respectively.
The Shapiro–Wilk test was used to check the data, and a non-parametric distribution was detected. To compare parameters, the Kruskal-Wallis H test and the chi-squared test were utilized. The post-hoc test (Dunn's test with Bonferroni adjustment) was used for multiple comparisons. The Spearman's correlation test was utilized to assess the degree of association. Receiver Operator Characteristic (ROC) curve was used to assess the laboratory test's performance. The area under the ROC curve (AUC) and its 95% confidence interval (CI) were estimated. The highest Youden's index was used to determine the best cutoff point. The odds ratio was calculated using Logistic Regression Analysis to clarify the association. Kaplan-Meier survival analysis, log-rank testing, and Cox regression analysis were used to assess the outcome. A p-value of less than 0.05 was considered as statistically significant. The software used was SPSS 20.0 (SPSS Inc., Chicago, IL, USA).
| Parameters | Controls (No.: 38) | Non-severe (No.: 38) | Severe (No.: 38) | p-value |
| Age, years | 54 [27-77] | 50 [30-65] | 60.5 [27-78] b | 0.03*# |
| Sex, male | 20 (52.6) | 21 (55.3) | 23 (60.5) | 0.78 |
| Smoking | 9 (23.7) | 7 (18.4) | 8 (21.1) | 0.85 |
| Symptoms | ||||
| Fever | 11 (28.9) | 13 (34.2) | 0.62 | |
| Fatigue | 13 (34.2) | 14 (36.8) | 0.81 | |
| Bone &muscles ache | 8 (21.1) | 9 (23.7) | 0.78 | |
| Headache | 16 (42.1) | 14 (36.8) | 0.64 | |
| Sore throat | 24 (63.2) | 22 (57.9) | 0.63 | |
| Cough | 19 (50) | 22 (57.9) | 0.49 | |
| Dyspnea | 2 (5.3) | 19 (50) | <0.001* | |
| Gastrointestinal tract symptoms | 3 (7.9) | 2 (5.3) | 0.64 | |
| Ocular symptoms | 4 (10.5) | 2 (5.3) | 0.39 | |
| Co-morbidities | ||||
| Diabetes | 7 (18.4) | 10 (26.3) | 0.41 | |
| Hypertension | 7 (18.4) | 15 (39.5) | 0.04* | |
| Coronary heart disease | 2 (5.3) | 6 (15.8) | 0.14 | |
| Chest diseases | 6 (15.8) | 5 (13.2) | 0.74 | |
| Outcome | ||||
| Mortality | 0 (0) | 7 (18.4) | 0.005* | |
| Laboratory parameters | ||||
| LncRNA HULC, fold change | 1 [0.81-1.3] | 2.19 [1-4.4]a,c | 4.23 [1.3-6.5]a,b | <0.001* # |
| MiRNA-9, fold change | 1.02 [0.76-1.22] | 0.71 [0.27-0.97]a,c | 0.37 [0.21-1]a,b | <0.001*# |
| Serum IL-6, pg/mL | 2.7 [2-7.9] | 18.4 [3.6-77.1]a,c | 71.7 [25.9-220]a,b | <0.001*# |
DownLoad:
CSV
The demographic and clinical characteristics of controls and patients were presented in Table 1. Regards subjects' age, there was a non-significant difference between controls and both patient groups (p = 0.48, and 0.07, for non-severe and severe respectively). The severe group had significantly higher patients' age than the non-severe group (p = 0.011). The most prevalent symptoms were sore throat, cough, fatigue, and headache. Dyspnea percentage was higher in severe patients than that of non-severe patients. Regarding comorbidities, hypertension was more prevalent in severe patients. No mortality was detected among non-severe patients; seven patients from the severe group (18.4%) died in the hospital. LncRNA HULC expression and IL-6 level were increased in severe patients compared to non-severe patients and controls (p < 0.001). On the other hand, miRNA-9 showed the lowest expression levels in the severe patients in comparison with non-severe patients and controls (p < 0.001) (Table 1).
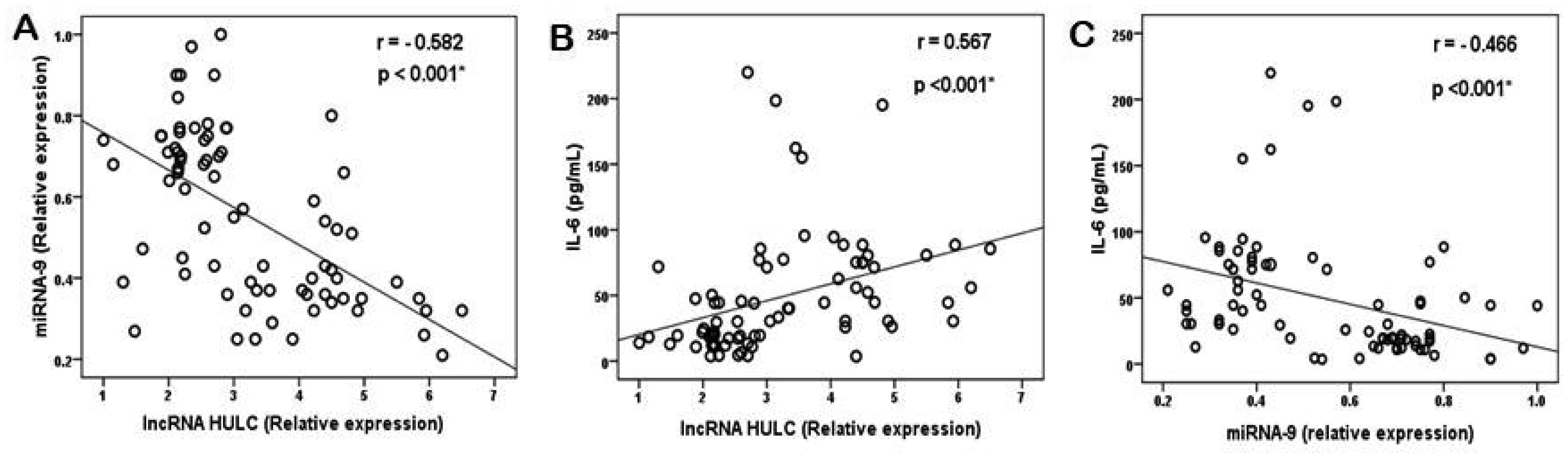
The role of markers in detecting the COVID-19 infection was assessed by ROC curve analysis. The lncRNA HULC, miRNA-9, and IL-6 showed ROC-AUC values of 0.993 (95% CI: 0.980–1.006), 0.984 (95% CI: 0.967–1.00), and 0.984 (95% CI: 0.968–1.00) respectively. So, lncRNA HULC had higher performance characteristics in differentiate healthy individuals from COVID-19 patients. In COVID-19 patients, the correlation analysis of LncRNA HULC was performed. As presented in Figure 2, lncRNA HULC was negatively correlated with miRNA-9 (p < 0.001, r = −0.582) (Figure 2A) and positively correlated with IL-6 (p < 0.001, r = 0.567) (Figure 2B). Furthermore, miRNA-9 showed a negative correlation with IL-6 (p <0.001, r = −0.0466) (Figure 2C).
| Parameters | Cutoff | Youden's index | Sensitivity | Specificity | PPV | NPP | Accuracy |
| lncRNA HULC, fold-change | > 2.89 | 0.89 | 94.7% | 97.4% | 97.3% | 94.9% | 96.1% |
| miRNA-9, fold-change | < 0.61 | 0.76 | 92.1% | 84.2% | 95.4% | 91.4% | 88.2% |
| IL-6, pg/mL | > 30.3 | 0.79 | 94.7% | 84.2% | 85.7% | 94.1% | 89.5% |
DownLoad:
CSV
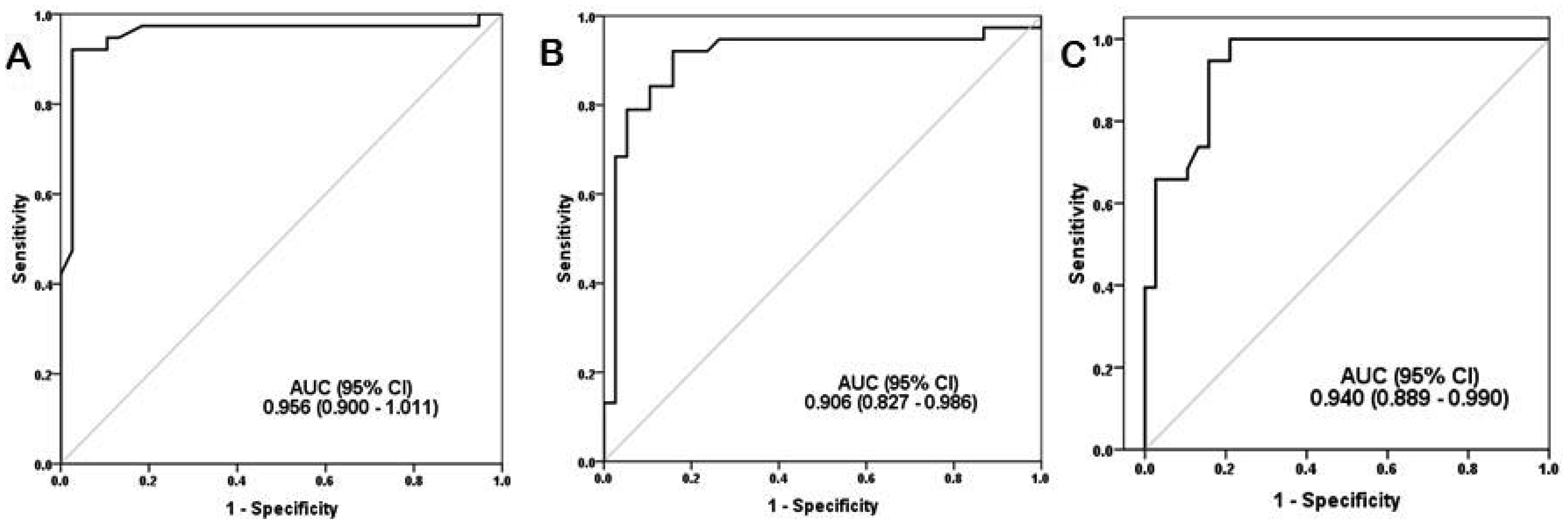
ROC curve analysis was performed on COVID-19 patients, to evaluate markers as predictors of disease severity. ROC curves were performed, and ROC-AUC was assessed (Figure 3). The lncRNA HULC was the most accurate predictor of COVID-19 severity. Table 2 presents the performance criteria of the markers. Further assessment of the association between lncRNA HULC and COVID-19 severity was performed by Multivariate Logistic Regression Analysis. The lncRNA HULC expression was adjusted to age, dyspnea, hypertension, miRNA-9, and IL-6. The lncRNA HULC expression had an adjusted odds ratio of 52.5 (95% CI: 1.43−192.2, p = 0.031). So, lncRNA HULC expression seems to be an independent predictor of COVID-19 severity.
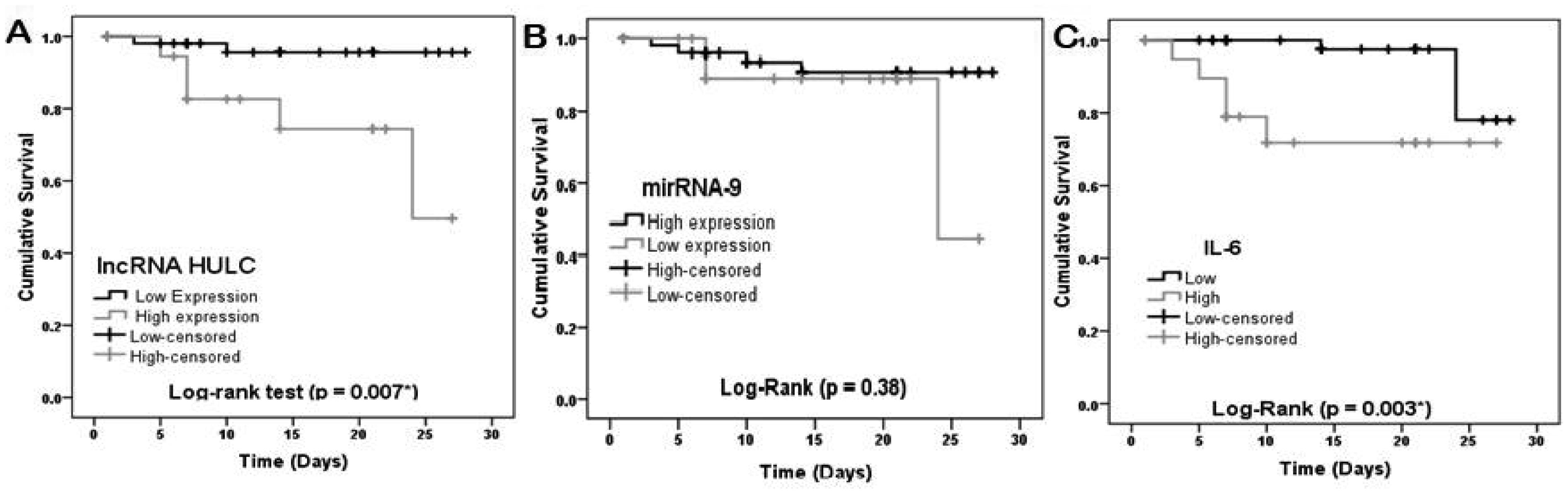
During the follow-up period of all COVID-19 patients, seven of 76 patients died (9.2%); all of them from the severe group. The role of markers in prediction of COVID-19 mortality was evaluated by ROC curve analysis. The lncRNA HULC, miRNA-9, and IL-6 showed ROC-AUC values of 0.744 (95% CI: 0.487−1.002), 0.756 (95% CI: 0.619−0.892), and 0.752 (95% CI: 0.605−0.898), respectively. The cutoff values for predicting mortality of lncRNA HULC (4.2-fold-change), miRNA-9 (0.39-fold-change), and IL-6 (54.1 pg/mL). The overall survival was assessed by the Kaplan–Meier curve (Figure 4), which showed lower survival in patients with elevated lncRNA HULC and IL-6 (log-rank test: p = 0.007 and 0.003, respectively). The Cox Regression Analysis showed that a high lncRNA HULC expression > 4.2 fold-change was associated with COVID-19 mortality (hazard ratio = 2.2, 95% CI: 1.3–3.7, and p = 0.007). The lncRNA HULC had an adjusted hazard ratio of 1.9 (95% CI: 1.02–3.56, p = 0.043) after the adjustment of IL-6. So, the lncRNA HULC could be a significant independent prognostic factor for COVID-19 mortality.
The role of lncRNAs in regulating COVID-19-mediated infection and subsequent disease outcomes has become evident [16]. In vascular endothelial cells, TNF-induced apoptosis was regulated by lncRNA HULC contributes to vascular endothelial dysfunction [17]. COVID-19 is an endotheliopathy that causes the associated inflammation and cytokine storm [18]. Endothelial dysfunction could be a common factor in both adults and children with severe COVID-19 [19]. Endothelial activation and dysregulated cytokine networks promote severe COVID-19, recovery reliant on endothelial integrity renewal [9]. So, LncRNA HULC could have a regulatory role in the pathogenesis and progression of COVID-19.
The host's miRNAs could influence COVID-19 pathogenesis. MiRNAs as an epigenetic modulator may contribute to COVID-19 patients' overcomplications [20]. The lncRNA HULC acts as a sponge for many miRNAs that have anti-inflammatory properties. The lncRNA HULC can influence miRNA-9 expression by regulating DNA methyltransferase [12],[17],[21]. In endothelial cells, miRNA-9 suppresses apoptosis and inflammation [22]. Furthermore, miRNA-9 is an inflammatory regulator can indirectly inhibit JAK-STAT signaling cascade through targeting the pathway regulators [13]. The miRNA-9 specifically targets JAK1 and JAK3 [23],[24]. Zhang et al. [23] demonstrated that overexpression of miRNA9 inhibited STAT3 activity. Shen et al. [25] reported that overexpression of miRNA 9 suppressed the inflammatory response by lowering the production of IL-1, IL-6, and TNF-α. In COVID-19 patients, the IL-6/JAK/STAT pathway is significantly active, exacerbating the host's inflammatory reactions. Surprisingly, activation of this route in a positive feedback loop resulted in more production of IL-6 [26]. IL-6 is the main mediator of inflammation and cytokine storm [27] seems to be due to the downregulation of miRNA-9 activates the IL6/Jak/STAT3 pathway.
LncRNA and miRNA molecules meet most of the requirements for an optimal biomarker, including specificity and sensitivity [28]. As a result, the current study was conducted to determine the relevance of these markers in COVID-19. Also, we assess their ability to determine COVID-19 severity and prognosis at the initial diagnosis. To the authors' knowledge, the predictive role of lncRNA HULC and miRNA-9 in COVID-19 is not previously assessed.
The lncRNA HULC was found to be up-regulated in COVID-19 patients compared to controls. More up-regulation was detected in severe patients in comparison with non-severe ones. Although lncRNA HULC is required for the pro-inflammatory response that mediated by increased levels of IL-6 [29],[30], some experimental reports showed that overexpression of lncRNA HULC inhibits inflammation and injury [31]–[33]. LncRNA HULC inhibits the expressions of inflammatory factors (IL-1, IL-6, and IL-8), protects cells from hypoxia-induced inflammation damage, and promote angiogenesis [31]. Also, lncRNA HULC had a protective effect against myocardial injury [33] and TNF-α-induced cells injury [32]. IL-6 levels showed the same pattern as lncRNA HULC, confirming Grifoni et al. [34] and Tang et al. [35] findings.
MiRNA-9, on the other hand, had the lowest expression levels in severe patients as compared to non-severe patients and controls. Changed microRNAs expression can identify COVID-19 infection, according to Li et al. [36] and Farr et al. [37]. Furthermore, COVID-19 severity is predicted by circulating microRNA patterns [38] The lncRNA HULC had a negative correlation with miRNA-9 and a positive association with IL-6. Morenikeji et al. [39] revealed several lncRNAs that were correlated to cytokine storm during COVID-19. Furthermore, there was a negative correlation between miRNA-9 and IL-6.
The role of the investigated markers in determining the severity of COVID-19 was evaluated in this study. All the markers were found to be significant predictors of COVID-19 severity. In agreement with Fernández-Pato et al. [40], who reported that COVID-19 alters plasma miRNAs at an initial stage, suggesting miRNAs are extremely useful as indicators of disease severity. In patients infected with COVID-19, IL-6 is a predictor of severe illness [41],[42]. In the current study, the most accurate marker was the lncRNA HULC. lncRNA HULC expression appears to be an independent predictor of COVID-19 severity after adjustment of other significant factors. The findings of this study may help in the detection of COVID-19 patients who are possibly severe early in the disease course.
This study investigated the prognostic value of the studied markers in COVID-19 patients. Patients with higher lncRNA HULC and IL-6 had a lower survival rate, but only lncRNA HULC could be a significant independent predictive factor for COVID-19 mortality. In agreement with Talwar et al. [43], who reported that IL-6 is not a reliable predictor of COVID-19 clinical outcomes. The results of this study revealed the clinical efficacy of lncRNA HULC in COVID-19. The generation of lncRNA HULC targeted therapies may be beneficial.
This study design showed some limitations. First, this is a single-center study. Second, lack of serial measurements of the markers that may define the COVID-19 course. Third, changes in the levels of the markers in response to treatment were not evaluated. Finally, this study did not assess the exact molecular mechanism of lncRNA HULC in COVID-19. Further experimental studies of molecular pathway are recommended.
In COVID-19 patients, the lncRNA HULC had a positive correlation with IL-6 and a negative correlation with miRNA-9. These preliminary data need further studies to be confirmed. The lncRNA HULC was the most accurate predictor of COVID-19 severity and mortality. The COVID-19 severity and mortality appear to be predicted independently by the lncRNA HULC.
| [1] |
E. Keller, L. Segel, Initiation of slime mold aggregation viewed as an instability, J. Theor. Biol., 26 (1970), 399–415. https://doi.org/10.1016/0022-5193(70)90092-5 doi: 10.1016/0022-5193(70)90092-5
|
| [2] |
C. Wang, P. Wang, X. Zhu, Global dynamics in a chemotaxis system involving nonlinear indirect signal secretion and logistic source, Z. Angew. Math. Phys., 74 (2023), 237. https://doi.org/10.1007/s00033-023-02126-2 doi: 10.1007/s00033-023-02126-2
|
| [3] |
M. Winkler, Boundedness in the higher-dimensional parabolic-parabolic chemotaxis system with logistic source, Commun. Partial Differ. Equations, 35 (2010), 1516–1537. https://doi.org/10.1080/03605300903473426 doi: 10.1080/03605300903473426
|
| [4] |
C. Lo, J. Rodrigues, Global existence for nonlocal quasilinear diffusion systems in nonisotropic nondivergence form, Math. Nachr., 297 (2024), 2122–2147. https://doi.org/10.1002/mana.202200250 doi: 10.1002/mana.202200250
|
| [5] |
M. Winkler, Does a "volume-filling effect" always prevent chemotactic collapse?, Math. Methods Appl. Sci., 33 (2010), 12–24. https://doi.org/10.1002/mma.1146 doi: 10.1002/mma.1146
|
| [6] |
C. Wang, J. Zhu, Blow-up analysis to a quasilinear chemotaxis system with nonlocal logistic effect, Bull. Malays. Math. Sci. Soc., 47 (2024), 60. https://doi.org/10.1007/s40840-024-01659-7 doi: 10.1007/s40840-024-01659-7
|
| [7] |
M. Winkler, How far do chemotaxis-driven forces influence regularity in the Navier-Stokes system?, Trans. Am. Math. Soc., 369 (2017), 3067–3125. https://doi.org/10.1090/tran/6733 doi: 10.1090/tran/6733
|
| [8] |
J. Zheng, An optimal result for global existence and boundedness in a three-dimensional Keller-Segel-Stokes, J. Differ. Equations, 267 (2019), 2385–2415. https://doi.org/10.1016/j.jde.2019.03.013 doi: 10.1016/j.jde.2019.03.013
|
| [9] |
W. Zhang, Global solutions in a chemotaxis consumption model with singular sensitivity, Z. Angew. Math. Phys., 74 (2023), 165. https://doi.org/10.1007/s00033-023-02049-y doi: 10.1007/s00033-023-02049-y
|
| [10] |
H. Liu, C. Lo, Determining a parabolic system by boundary observation of its non-negative solutions with biological applications, Inverse Probl., 40 (2024), 025009. https://doi.org/10.1088/1361-6420/ad149f doi: 10.1088/1361-6420/ad149f
|
| [11] |
N. Bellomo, A. Bellouquid, Y. Tao, M. Winkler, Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues, Math. Models Methods Appl. Sci., 25 (2015), 1663–1763. https://doi.org/10.1142/S021820251550044X doi: 10.1142/S021820251550044X
|
| [12] |
P. Liu, J. Shi, Z. Wang, Pattern formation of the attraction-repulsion Keller-Segel system, Discrete Contin. Dyn. Syst. Ser. B, 18 (2013), 2597–2625. https://doi.org/10.3934/dcdsb.2013.18.2597 doi: 10.3934/dcdsb.2013.18.2597
|
| [13] |
G. Fragnelli, Positive periodic solutions for a system of anisotropic parabolic equations, J. Math. Anal. Appl., 367 (2010), 204–228. https://doi.org/10.1016/j.jmaa.2009.12.039 doi: 10.1016/j.jmaa.2009.12.039
|
| [14] |
H. Alaa, N. Alaa, A. Bouchriti, A. Charkaoui, An improved nonlinear anisotropic model with p(x)-growth conditions applied to image restoration and enhancement, Math. Meth. Appl. Sci., 47 (2024), 7546–7575. https://doi.org/10.1002/mma.9989 doi: 10.1002/mma.9989
|
| [15] |
A. Charkaoui, A. Ben-Loghfyry, S. Zeng, A novel parabolic model driven by double phase flux operator with variable exponents: Application to image decomposition and denoising, Comput. Math. Appl., 174 (2024), 97–141. https://doi.org/10.1016/j.camwa.2024.08.021 doi: 10.1016/j.camwa.2024.08.021
|
| [16] |
A. Charkaoui, A. Ben-Loghfyry, S. Zeng, Nonlinear parabolic double phase variable exponent systems with applications in image noise removal, Appl. Math. Modell., 132 (2024), 495–530. https://doi.org/10.1016/j.apm.2024.04.059 doi: 10.1016/j.apm.2024.04.059
|
| [17] |
J. Ahn, M. Winkler, A critical exponent for blow-up in a two-dimensional chemotaxis-consumption system, Calc. Var. Partial Differ. Equations, 62 (2023), 6. https://doi.org/10.1007/s00526-023-02523-5 doi: 10.1007/s00526-023-02523-5
|
| [18] |
W. Lyu, Asymptotic stabilization for a class of chemotaxis-consumption systems with generalized logistic source, Nonlinear Anal., 217 (2022), 112737. https://doi.org/10.1016/j.na.2021.112737 doi: 10.1016/j.na.2021.112737
|
| [19] |
Y. Wang, M. Winkler, Finite-time blow-up in a repulsive chemotaxis-consumption system, Proc. Roy. Soc. Edinburgh Sect. A, 153 (2023), 1150–1166. https://doi.org/10.1017/prm.2022.39 doi: 10.1017/prm.2022.39
|
| [20] |
Y. Tao, Boundedness in a chemotaxis model with oxygen consumption by bacteria, J. Math. Anal. Appl., 381 (2011), 521–529. https://doi.org/10.1016/j.jmaa.2011.02.041 doi: 10.1016/j.jmaa.2011.02.041
|
| [21] |
K. Baghaei, A. Khelghati, Boundedness of classical solutions for a chemotaxis model with consumption of chemoattractant, C. R. Math. Acad. Sci. Paris, 355 (2017), 633–639. https://doi.org/10.1002/mma.4264 doi: 10.1002/mma.4264
|
| [22] |
M. Fuest, Analysis of a chemotaxis model with indirect signal absorption, J. Differ. Equations, 267 (2019), 4778–4806. https://doi.org/10.1016/j.jde.2019.05.015 doi: 10.1016/j.jde.2019.05.015
|
| [23] |
J. Lankeit, Y. Wang, Global existence, boundedness and stabilization in a high-dimensional chemotaxis system with consumption, Discrete Contin. Dyn. Syst., 37 (2017), 6099–6121. https://doi.org/10.3934/dcds.2017262 doi: 10.3934/dcds.2017262
|
| [24] |
C. Wang, Z. Zheng, X. Zhu, Dynamic behavior analysis to a generalized chemotaxis-consumption system, J. Math. Phys., 65 (2024), 011503. https://doi.org/10.1063/5.0176530 doi: 10.1063/5.0176530
|
| [25] |
Y. Chiyo, S. Frassu, G. Viglialoro, A nonlinear attraction-repulsion Keller-Segel model with double sublinear absorptions: Criteria toward boundedness, Commun. Pure Appl. Anal., 22 (2023), 1783–1809. https://doi.org/10.3934/cpaa.2023047 doi: 10.3934/cpaa.2023047
|
| [26] |
C. Wang, Z. Zheng, Global boundedness for a chemotaxis system involving nonlinear indirect consumption mechanism, Discrete Contin. Dyn. Syst. B, 29 (2024), 2141–2157. https://doi.org/10.3934/dcdsb.2023171 doi: 10.3934/dcdsb.2023171
|
| [27] |
X. Bai, M. Winkler, Equilibration in a fully parabolic two-species chemotaxis system with competitive kinetics, Indiana Univ. Math. J., 65 (2016), 553–583. https://doi.org/10.1512/iumj.2016.65.5776 doi: 10.1512/iumj.2016.65.5776
|
| [28] |
M. Mizukami, Boundedness and asymptotic stability in a two-species chemotaxis-competition model with signal-dependent sensitivity, Discrete Contin. Dyn. Syst. Ser. B, 22 (2017), 2301–2319. https://doi.org/10.3934/dcdsb.2017097 doi: 10.3934/dcdsb.2017097
|
| [29] |
M. Mizukami, Improvement of conditions for asymptotic stability in a two-species chemotaxiscompetition model with signal-dependent sensitivity, Discrete Contin. Dyn. Syst. Ser. B, 13 (2020), 269–278. https://doi.org/10.3934/dcdss.2020015 doi: 10.3934/dcdss.2020015
|
| [30] |
K. Lin, C. Mu, Convergence of global and bounded solutions of a two-species chemotaxis model with a logistic source, Discrete Contin. Dyn. Syst. Ser. B, 22 (2017), 2233–2260. https://doi.org/10.3934/dcdsb.2017094 doi: 10.3934/dcdsb.2017094
|
| [31] |
K. Lin, C. Mu, L. Wang, Boundedness in a two-species chemotaxis system, Math. Methods Appl. Sci., 38 (2015), 5085–5096. https://doi.org/10.1002/mma.3429 doi: 10.1002/mma.3429
|
| [32] |
L. Miao, H. Yang, S. Fu, Global boundedness in a two-species predator-prey chemotaxis model, Appl. Math. Lett., 111 (2021), 106–639. https://doi.org/10.1016/j.aml.2020.106639 doi: 10.1016/j.aml.2020.106639
|
| [33] |
L. Wang, C. Mu, X. Hu, P. Zheng, Boundedness and asymptotic stability of solutions to a two-species chemotaxis system with consumption of chemoattractant, J. Differ. Equations, 264 (2018), 3369–3401. https://doi.org/10.1016/j.jde.2017.11.019 doi: 10.1016/j.jde.2017.11.019
|
| [34] |
J. Zhang, X. Hu, L. Wang, L. Qu, Boundedness in a quasilinear two-species chemotaxis system with consumption of chemoattractant, Electron. J. Qual. Theory Differ. Equations, 31 (2019), 1–12. https://doi.org/10.14232/ejqtde.2019.1.31 doi: 10.14232/ejqtde.2019.1.31
|
| [35] |
Q. Zhang, W. Tao, Boundedness and stabilization in a two-species chemotaxis system with signal absorption, Comput. Math. Appl., 78 (2019), 2672–2681. https://doi.org/10.1016/j.camwa.2019.04.008 doi: 10.1016/j.camwa.2019.04.008
|
| [36] |
G. Ren, B. Liu, Global existence and asymptotic behavior in a two-species chemotaxis system with logistic source, J. Differ. Equations, 269 (2020), 1484–1520. https://doi.org/10.1016/j.jde.2020.01.008 doi: 10.1016/j.jde.2020.01.008
|
| [37] |
G. Ren, B. Liu, Global solvability and asymptotic behavior in a two-species chemotaxis system with Lotka-Volterra competitive kinetics, Math. Models Methods Appl. Sci., 31 (2021), 941–978. https://doi.org/10.1142/S0218202521500238 doi: 10.1142/S0218202521500238
|
| [38] |
M. Winkler, Global generalized solutions to a multi-dimensional doubly tactic resource consumption model accounting for social interactions, Math. Models Methods Appl. Sci., 29 (2019), 373–418. https://doi.org/10.1142/S021820251950012X doi: 10.1142/S021820251950012X
|
| [39] |
Y. Tao, M. Winkler, Large time behavior in a forager-exploiter model with different taxis strategies for two groups in search of food, Math. Models Methods Appl. Sci., 29 (2019), 2151–2182. https://doi.org/10.1142/S021820251950043X doi: 10.1142/S021820251950043X
|
| [40] |
J. Wang, M. Wang, Global bounded solution of the higher-dimensional forager-exploiter model with/without growth sources, Math. Models Methods Appl. Sci., 30 (2020), 1297–1323. https://doi.org/10.1142/S0218202520500232 doi: 10.1142/S0218202520500232
|
| [41] |
D. Wu, S. Shen, Global boundedness and stabilization in a forager-exploiter model with logistic growth and nonlinear resource consumption, Nonlinear Anal. Real World Appl., 72 (2023), 103–854. https://doi.org/10.1016/j.nonrwa.2023.103854 doi: 10.1016/j.nonrwa.2023.103854
|
| [42] |
H. Ou, L. Wang, Boundedness in a two-species chemotaxis system with nonlinear resource consumption, Qual. Theory Dyn. Syst., 23 (2024), 14. https://doi.org/10.1007/s12346-023-00873-1 doi: 10.1007/s12346-023-00873-1
|
| [43] |
Y. Choi, Z. Wang, Prevention of blow-up by fast diffusion in chemotaxis, J. Math. Anal. Appl., 362 (2010), 553–564. https://doi.org/10.1016/j.jmaa.2009.08.012 doi: 10.1016/j.jmaa.2009.08.012
|
| [44] |
M. Delgado, I. Gayte, C. Morales-Rodrigo, A. Suárez, An angiogenesis model with nonlinear chemotactic response and flux at the tumor boundary, Nonlinear Anal., 72 (2010), 330–347. https://doi.org/10.1016/j.na.2009.06.057 doi: 10.1016/j.na.2009.06.057
|
| [45] | H. Schmeisser, H. Triebel, Function spaces, differential operators and nonlinear analysis, in Teubner-Texte zur Mathematik, 133 (1993), 9–126. https://doi.org/10.1007/978-3-663-11336-2 |
| [46] |
J. Wang, Global existence and boundedness of a forager-exploiter system with nonlinear diffusions, J. Differ. Equations, 276 (2021), 460–492. https://doi.org/10.1016/j.jde.2020.12.028 doi: 10.1016/j.jde.2020.12.028
|
| [47] |
C. Stinner, C. Surulescu, M. Winkler, Global weak solutions in a PDE-ODE system modeling multiscale cancer cell invasion, SIAM J. Math. Anal., 46 (2014), 1969–2007. https://doi.org/10.1137/13094058X doi: 10.1137/13094058X
|
| [48] |
M. Winkler, Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segal model, J. Differ. Equations, 248 (2010), 2889–2905. https://doi.org/10.1016/j.jde.2010.02.008 doi: 10.1016/j.jde.2010.02.008
|
| [49] |
J. Wang, Global existence and stabilization in a forager-exploiter model with general logistic sources, Nonlinear Anal., 222 (2022), 112–985. https://doi.org/10.1016/j.na.2022.112985 doi: 10.1016/j.na.2022.112985
|
| [50] | A. Friedman, Partial Different Equations, Holt Rinehart and Winston, New York, 1969. |
| [51] | L. Nirenberg, On elliptic partial differential equations, Ann. Sc. Norm. Super. Pisa Sci. Fis. Mat., III. Ser., 13 (1959), 115–162. |
| 1. | Iulia Virginia Iancu, Carmen Cristina Diaconu, Adriana Plesa, Alina Fudulu, Adrian Albulescu, Ana Iulia Neagu, Ioana Madalina Pitica, Laura Denisa Dragu, Coralia Bleotu, Mihaela Chivu‐Economescu, Lilia Matei, Cristina Mambet, Saviana Nedeianu, Corneliu Petru Popescu, Camelia Sultana, Simona Maria Ruta, Anca Botezatu, LncRNAs expression profile in a family household cluster of COVID‐19 patients, 2024, 28, 1582-1838, 10.1111/jcmm.18226 |
Chang-Jian Wang, Yuan-Hao Zang. Boundedness of solutions in a two-species chemotaxis system[J]. Electronic Research Archive, 2025, 33(5): 2862-2880. doi: 10.3934/era.2025126
| Parameters | Controls (No.: 38) | Non-severe (No.: 38) | Severe (No.: 38) | p-value |
| Age, years | 54 [27-77] | 50 [30-65] | 60.5 [27-78] b | 0.03*# |
| Sex, male | 20 (52.6) | 21 (55.3) | 23 (60.5) | 0.78 |
| Smoking | 9 (23.7) | 7 (18.4) | 8 (21.1) | 0.85 |
| Symptoms | ||||
| Fever | 11 (28.9) | 13 (34.2) | 0.62 | |
| Fatigue | 13 (34.2) | 14 (36.8) | 0.81 | |
| Bone &muscles ache | 8 (21.1) | 9 (23.7) | 0.78 | |
| Headache | 16 (42.1) | 14 (36.8) | 0.64 | |
| Sore throat | 24 (63.2) | 22 (57.9) | 0.63 | |
| Cough | 19 (50) | 22 (57.9) | 0.49 | |
| Dyspnea | 2 (5.3) | 19 (50) | <0.001* | |
| Gastrointestinal tract symptoms | 3 (7.9) | 2 (5.3) | 0.64 | |
| Ocular symptoms | 4 (10.5) | 2 (5.3) | 0.39 | |
| Co-morbidities | ||||
| Diabetes | 7 (18.4) | 10 (26.3) | 0.41 | |
| Hypertension | 7 (18.4) | 15 (39.5) | 0.04* | |
| Coronary heart disease | 2 (5.3) | 6 (15.8) | 0.14 | |
| Chest diseases | 6 (15.8) | 5 (13.2) | 0.74 | |
| Outcome | ||||
| Mortality | 0 (0) | 7 (18.4) | 0.005* | |
| Laboratory parameters | ||||
| LncRNA HULC, fold change | 1 [0.81-1.3] | 2.19 [1-4.4]a,c | 4.23 [1.3-6.5]a,b | <0.001* # |
| MiRNA-9, fold change | 1.02 [0.76-1.22] | 0.71 [0.27-0.97]a,c | 0.37 [0.21-1]a,b | <0.001*# |
| Serum IL-6, pg/mL | 2.7 [2-7.9] | 18.4 [3.6-77.1]a,c | 71.7 [25.9-220]a,b | <0.001*# |
DownLoad:
CSV
| Parameters | Cutoff | Youden's index | Sensitivity | Specificity | PPV | NPP | Accuracy |
| lncRNA HULC, fold-change | > 2.89 | 0.89 | 94.7% | 97.4% | 97.3% | 94.9% | 96.1% |
| miRNA-9, fold-change | < 0.61 | 0.76 | 92.1% | 84.2% | 95.4% | 91.4% | 88.2% |
| IL-6, pg/mL | > 30.3 | 0.79 | 94.7% | 84.2% | 85.7% | 94.1% | 89.5% |
DownLoad:
CSV
| Parameters | Controls (No.: 38) | Non-severe (No.: 38) | Severe (No.: 38) | p-value |
| Age, years | 54 [27-77] | 50 [30-65] | 60.5 [27-78] b | 0.03*# |
| Sex, male | 20 (52.6) | 21 (55.3) | 23 (60.5) | 0.78 |
| Smoking | 9 (23.7) | 7 (18.4) | 8 (21.1) | 0.85 |
| Symptoms | ||||
| Fever | 11 (28.9) | 13 (34.2) | 0.62 | |
| Fatigue | 13 (34.2) | 14 (36.8) | 0.81 | |
| Bone &muscles ache | 8 (21.1) | 9 (23.7) | 0.78 | |
| Headache | 16 (42.1) | 14 (36.8) | 0.64 | |
| Sore throat | 24 (63.2) | 22 (57.9) | 0.63 | |
| Cough | 19 (50) | 22 (57.9) | 0.49 | |
| Dyspnea | 2 (5.3) | 19 (50) | <0.001* | |
| Gastrointestinal tract symptoms | 3 (7.9) | 2 (5.3) | 0.64 | |
| Ocular symptoms | 4 (10.5) | 2 (5.3) | 0.39 | |
| Co-morbidities | ||||
| Diabetes | 7 (18.4) | 10 (26.3) | 0.41 | |
| Hypertension | 7 (18.4) | 15 (39.5) | 0.04* | |
| Coronary heart disease | 2 (5.3) | 6 (15.8) | 0.14 | |
| Chest diseases | 6 (15.8) | 5 (13.2) | 0.74 | |
| Outcome | ||||
| Mortality | 0 (0) | 7 (18.4) | 0.005* | |
| Laboratory parameters | ||||
| LncRNA HULC, fold change | 1 [0.81-1.3] | 2.19 [1-4.4]a,c | 4.23 [1.3-6.5]a,b | <0.001* # |
| MiRNA-9, fold change | 1.02 [0.76-1.22] | 0.71 [0.27-0.97]a,c | 0.37 [0.21-1]a,b | <0.001*# |
| Serum IL-6, pg/mL | 2.7 [2-7.9] | 18.4 [3.6-77.1]a,c | 71.7 [25.9-220]a,b | <0.001*# |
| Parameters | Cutoff | Youden's index | Sensitivity | Specificity | PPV | NPP | Accuracy |
| lncRNA HULC, fold-change | > 2.89 | 0.89 | 94.7% | 97.4% | 97.3% | 94.9% | 96.1% |
| miRNA-9, fold-change | < 0.61 | 0.76 | 92.1% | 84.2% | 95.4% | 91.4% | 88.2% |
| IL-6, pg/mL | > 30.3 | 0.79 | 94.7% | 84.2% | 85.7% | 94.1% | 89.5% |
