Numerical investigation of a new cut finite element method for Stokes interface equations

1.   Introduction

The Stokes equations describe the motion of viscous, incompressible fluids at low Reynolds numbers. They are fundamental in fluid mechanics and serve as a simplification of the Navier–Stokes equations, where inertial forces are negligible compared to viscous forces. Stokes equations are widely used in various applications, including microfluidics, porous media flow, and biomedical modeling. In many practical scenarios, the fluid domain consists of multiple subdomains with different material properties, such as fluids with varying viscosities. These problems are referred to as Stokes interface problems, where the governing equations remain the same in each subdomain, but the physical properties, such as the viscosity, may change discontinuously across an interface. The interface conditions impose jump conditions on the stress and velocity due to the difference in the material properties.

In this paper, we consider the Stokes interface problem in a bounded, contractible, and open domain $\Omega\subset\mathbb{R}^d$ ($d = 2$ or $3$ is the dimension) which is divided into two subdomains, $\Omega^-$ and $\Omega^+$, by a smooth interface $\Gamma$, with a polygonal boundary $\partial\Omega$. The governing equations solve the velocity field ${\bf{u}}$ and pressure $p$ in each subdomain,

The interface conditions on $\Gamma$ are to enforce jump conditions on the velocity and stress tensor

Here, $\epsilon({\bf{u}}) = \frac{1}{2}(\nabla{\bf{u}}+\nabla{\bf{u}}^\top)$ represents the strain tensor, $\mu$ is the viscosity, and ${\bf{f}}$ is the external force function. We denote the difference in the trace value from two subdomains by $\left[w\right]_\Gamma = w|_{\Omega^-}-w|_{\Omega^+}$. The functions ${\bf g}$ and ${ \mathit{\boldsymbol{\sigma}}}$ specify the interface conditions. In our problem, the viscosity $\mu$ is a piecewise constant, denoted as $\mu^\pm$, taking different values in the subdomains $\Omega^\pm$. Additionally, we assume ${\bf{u}}^+$ satisfies the homogeneous Dirichlet boundary condition ${\bf{u}}^+|_{\partial\Omega} = 0$ and the pressure unknown satisfies $\int_\Omega pd\mathbf{x} = 0.$ The Stokes interface problem (1.1)–(1.4) is an active area of research in computational fluid dynamics, with ongoing developments aimed at improving accuracy, stability, and efficiency in solving interface problems.

However, because of the discontinuities between the interfaces in (1.1)–(1.4), advanced strategies are needed to handle the computational difficulties. The major numerical challenge is to design a stable numerical scheme to resolve the potential geometric and solution singularities. Another critical challenge is to ensure the preservation of mass conservation within the discretization. Therefore, the traditional finite element methods (FEMs) may struggle with resolving this problem, leading to loss of accuracy and stability. In the past decades, several kinds of numerical methods have been developed to address these challenges, including fitted and unfitted FEMs. The fitted mesh approaches ^[1,2] align the computational mesh with the interface to capture discontinuities accurately but require complex mesh generations. A frequently encountered problem in practical applications of fitted FEMs is the generation of a high-quality mesh that conforms to the computational domain. If the domain is complex, the mesh generation problem is highly non-trivial. For instance, the simulation of flow around an object embedded in a channel typically requires a mesh discretization of the domain surrounding the object. Furthermore, the mesh must be modified or regenerated each time when the object is translated, scaled, or rotated, which introduces extra challenges in the practical non-stationary problems. On the other hand, for unfitted FEMs, these methods allow the interface to cut through a fixed background mesh, avoiding the need for mesh conforming to the interface and handling deforming geometries without the need for expensive and complicated remeshing procedures. Techniques such as the cut finite element method (CutFEM) ^[3,4,5,6], the extended finite element method ^[7,8,9], and the immersed interface methods ^{[10,11,12,13,14,15]} fall into this category. In our previous work ^[6], we extended the CutFEM idea to an enriched Galerkin scheme, which approximated the velocity by a continuous linear Galerkin basis enriched by a special designed piecewise $L^2$ basis function. However, that scheme only reduced the pressure effects but was not completely independent of pressure and viscosity values. Besides, some machine learning-based schemes have also been developed, such as the schemes based on the physics-informed neural networks (PINNs) in ^[16,17].

In this paper, we follow the CutFEM to develop a new stable finite element scheme for solving the interface problem (1.1)–(1.4), in which the fluid surface can cut elements in the computational mesh in an arbitrary manner. Such CutFEM is especially beneficial for realistic applications, especially when employing interface tracking techniques, such as arbitrary Lagrangian Eulerian methods. The new scheme for the Stokes interface problem on an unfitted mesh is constructed as follows: the interface condition on a surface cutting through a background mesh is imposed using the Nitsche method, while the stability with respect to small and anisotropic cuts of the bulk elements is ensured by adding local ghost penalty stabilization terms. This newly developed algorithm is based on the inf-sup stable Stokes pair CG$\mathbb{P}_1$-RT$_0$/DG$\mathbb{P}_0$ proposed in ^[18], where velocity unknowns are approximated by a continuous piecewise linear continuous element space enriched by the lowest-order Raviart–Thomas (RT) element, and pressure unknowns are approximated by the piecewise constant function. For the regular Stokes equation, the algorithm is proved to satisfy the inf-sup stability and is able to provide the optimal rate in convergence. Furthermore, this stable pair is a parameter-free scheme that ensures pressure robustness and divergence-free constraints. Building on the advantages of the method described above, we extend this stable Stokes element pair to investigate the Stokes interface problem.

In our scheme, the CG$\mathbb{P}_1$ basis functions for the velocity and the DG$\mathbb{P}_0$ basis functions for the pressure are used in both subdomains $\Omega^\pm$, while the RT$_0$ basis functions for velocity are used globally in $\Omega$. That is, we have doubly defined functions in the interface elements for both the CG$\mathbb{P}_0$ and DG$\mathbb{P}_0$ basis functions, while the RT$_0$ basis functions are defined with single values. A similar idea had been used in ^[15], where a Petrov–Galerkin immersed finite element scheme was used for the Stokes interface problem. In that work, the immersed spaces $\mathbb{P}_1$ and $\mathbb{P}_0$ for velocity and pressure are constructed based on the jump conditions. The velocity space is then enriched with the lowest-order RT$_0$ element to ensure the inf-sup stability. These immersed functions are used as the trial function spaces, while the test function spaces are the same as the standard finite element spaces. However, this scheme does not provide the viscosity robustness. That means that velocity errors are dependent on viscosity. Thus, numerical pollutions may be produced when simulating the problem with a small viscosity. Moreover, in previous research ^[5], it is a challenge to preserve the divergence-free constraint, even though finite element pairs are divergence-free for the standard Stokes equation. In contrast, in this paper, instead of modifying the basis functions or using the Petrov–Galerkin scheme, we incorporate the ghost penalty terms ^[19] as shown in the CutFEM ^[6] for the Darcy problem. The authors in ^[20] extended a similar idea to investigate the Stokes equation in the fictitious domain. Moreover, in order to derive a stable inf-sup condition with a well-conditioned system, one may need to tune the parameters with appropriate values for the Stokes interface problem. Following the idea in ^[19], we design an appropriate ghost penalty term for the pressure, which can preserve the desired robustness and mass conservation properties.

In summary, the advantages of our proposed scheme include: 1) it is a second-order stable numerical method based on an unfitted mesh, making it well-suited for problems with complex geometries; 2) it utilizes a symmetric Galerkin formulation, which is advantageous for designing fast and efficient linear solvers; 3) it is pressure-robust and viscosity-robust, enabling superior performance in practical computations, especially in cases coupled with varying viscosity values exhibiting high contrast; and 4) it is able to provide an efficient method with the lowest computational cost and is preferred for practical applications with low regularities.

The remainder of the paper is organized as follows: In Section 2, after collecting the necessary preliminaries on meshing and finite element space definitions, we propose the formulation to approximate the Stokes interface problem. Next, we investigate the corresponding linear system of the new scheme and check its inf-sup constant and condition number for the corresponding linear system in Section 3. Then, several benchmark interface problems are reported in Section 4 to validate the proposed numerical scheme. Finally, we discuss the concluding remarks and potential future work in Section 5.

2.   Preliminaries and numerical scheme

In this paper, we focus on the smooth interface defined by a level-set function $\phi({\bf{x}}) = 0$ such that $\Omega^+: = \{{\bf{x}}:\phi({\bf{x}}) > 0\}$ and $\Omega^-: = \{{\bf{x}}:\phi({\bf{x}}) < 0\}$. Let ${\bf{n}}$ be the unit outward normal of $\partial\Omega^-$. The jump operator and average operator across the interface $\Gamma$ are defined as

where $w$ can be either a scalar or vector-valued function.

2.1.   Weak formulation

Define the following two function spaces:

We will use the standard notations for Sobolev space. For example, the notation $(\cdot, \cdot)_\omega$ for the $L^2(\omega)$ inner product on $\omega$ and $\langle\cdot, \cdot\rangle_e$ for the $L^2(e)$ inner product on edge/face $e$. The weak formulation is of the Stokes equations (1.1)–(1.4) to find $({\bf{u}}, p)\in{\bf{V}}\times Q$ such that

where

with $\lambda$ being a stabilization parameter and

Here, we adopt Nitsche's technique to enforce the interface jump conditions into the variation form.

2.2.   Finite element mesh and spaces

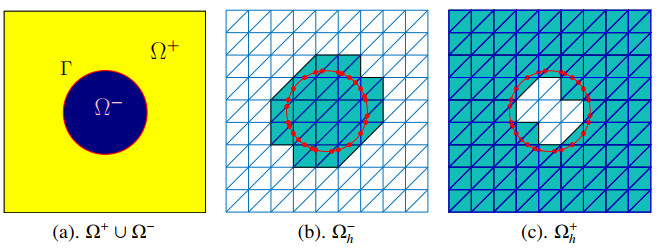
This section introduces the computational mesh and the finite element spaces that we need in order to develop our numerical method. Let $\mathcal{T}_h$ be a uniform triangular mesh ($d = 2$) or tetrahedral mesh ($d = 3$) of the domain $\Omega$, where $h > 0$ denotes the mesh size. This mesh is assumed to be an unfitted mesh to the interface $\Gamma$. Furthermore, we assume that the interface $\Gamma$ is a closed, smooth, and simply connected surface that does not intersect the boundary $\partial\Omega$. Corresponding to the subdomain $\Omega^\pm$, we define the active meshes $\mathcal{T}_h^\pm$ as following:

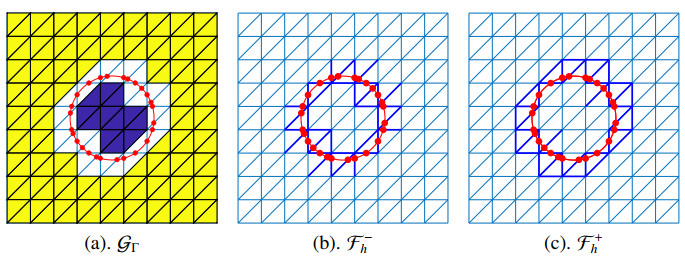
The subdomains that the active mesh $\mathcal{T}_h^\pm$ covers are denoted by $\Omega_h^\pm$. We define the sets of elements that have an intersection with $\Gamma$ by $\mathcal{G}_\Gamma$ and denote the subdomain covered by $\mathcal{G}_\Gamma$ by $\Omega_h^\Gamma$. The interior edges/faces of the interface elements $T\cap\Gamma\neq\emptyset, \forall T\in\mathcal{T}_h^\pm$ are denoted as $\mathcal{F}_h^\pm$. For the two-dimensional interface problem, Figure 1 illustrates the subdomains and active meshes (shown in green color); Figure 2 illustrates the interface element $\mathcal{G}_\Gamma$ (shown in white color) and the edges in $\mathcal{F}_h^\pm$ (shown in blue color).

We make the following assumptions for the CutFEM as in ^[21]:

● Assumption 1: The triangulation $\mathcal{T}_h$ is quasi-uniform.

● Assumption 2: The interface $\Gamma$ either cuts an element $T\in\mathcal{T}_h$ exactly twice and each edge at most once, or ${\Gamma}\cap \bar{T}$ coincides with an edge of $T$.

● Assumption 3: For all elements $T\in\mathcal{G}_\Gamma$, there exist elements $T$ such that $T^-\subset\Omega^-$ and $T^+\subset\Omega^+$ and $\bar{T}^-\cap \bar{T}\neq\emptyset$ and $\bar{T}^+\cap \bar{T}\neq\emptyset$.

● Assumption 4: The mesh coincides with the outer boundary $\partial\Omega$.

For any integer $k \ge 0$, $\mathbb{P}_k({\mathcal{D}})$ denotes the set of polynomials defined on ${\mathcal{D}} \subset \mathbb{R}^{d}$ whose total degree is less than or equal to $k$. Let $\widehat{{\bf{C}}_{h}} = {\bf{C}}_{h}^-\oplus{\bf{C}}_{h}^+$ with

and

As above, the active finite element space ${\bf{C}}_{h}^\pm$ is restricted to the active domain $\Omega_h^\pm$. According to the homogeneous Dirichlet boundary condition, let

Denote ${\bf{V}}_h = {\bf{C}}_{h} \oplus {\bf{R}}_{\bf h}$ the discrete velocity space. On the other hand, we employ the piecewise constant space for the pressure. That is, the pressure space is defined by $\widehat{Q}_h = Q_h^-\oplus Q_h^+$ with

Furthermore, after enforcing the mean zero condition, we denote $Q_h = \{q = (q^-, q^+)\in\widehat{Q}_h\vert\; \int_{\Omega^-} q^-d\mathbf{x} + \int_{\Omega^+} q^+d\mathbf{x} = 0, \text{ where }q^-\in Q_h^-, q^+\in Q_h^+\}$.

Remark 2.1. Note that $\Omega_h^-\cap\Omega_h^+ = \Omega_h^\Gamma$ and therefore the functions in ${\bf{C}}_{h}$ and $Q_h$ are double-valued functions on the cells in $\mathcal{G}_\Gamma$. However, the functions in ${\bf{R}}_{\bf h}$ are single-valued functions in all cells in $\mathcal{T}_h$. Without the functions in ${\bf{R}}_{\bf h}$, the CG$\mathbb{P}_1$-RT$_0$/DG$\mathbb{P}_0$ pair is not inf-sup stable for the regular Stokes equation, which is also true for the Stokes interface problem. As the enrichment/stabilization trick in solving the Stokes equations, we also use the function in ${\bf{R}}_{\bf h}$ to stabilize our simulation.

Remark 2.2. For any function ${\bf{v}}_h\in{\bf{V}}_h$, there is a unique decomposition such that ${\bf{v}}_h = {\bf{v}}_h^C+{\bf{v}}_h^R$, where ${\bf{v}}_h^C = ({\bf{v}}_h^{C, -}, {\bf{v}}_h^{C, +})\in{\bf{C}}_{h}$, ${\bf{v}}_h^{C, \pm}\in{\bf{C}}_{h}^\pm$, and ${\bf{v}}_h^R\in{\bf{R}}_{\bf h}$. We view ${\bf{v}}_h^C$ as the "continuous" component (though there may be discontinuity across the interface $\Gamma$) of the function ${\bf{v}}_h$ and ${\bf{v}}_h^R$ as the RT component of the solution. It is noted that ${\bf{v}}_h^R$ belongs to the global $H(div; \Omega)$ space.

Next, we define the jump operator, which is used in the ghost penalty terms. Assume that two adjacent elements $T_1, T_2\in\mathcal{T}_h^+$ share the interior edge / face $e\in\mathcal{F}_h^+$ with a fixed normal direction pointing from $T_1$ to $T_2$. Then the jump operator on edge/face $e$ is defined as

The definition can be extended to $e\in\mathcal{F}_h^-$ and scalar-valued functions.

2.3.   Finite element scheme

Now, we consider the new CutFEM in this paper, in which the velocity is approximated using a piecewise linear continuous Galerkin element enriched by the lowest-order Raviart–Thomas element, while the pressure is approximated using a piecewise constant element. The detail is:} find ${\bf{u}}_h = { {\bf{u}}_h^C+{\bf{u}}_h^R} \in{\bf{V}}_h, p_h \in Q_h$ such that the following equations hold for $\forall ({\bf{v}}_h, q_h)\in{\bf{V}}_h\times Q_h,$

where

with $\rho$ being a stabilization parameter. In fact, in the practical computation, we do not need to tune the value in $\rho$ and will take $\rho = 20$ across all the numerical experiments. Here we employ the ghost penalty terms to control the condition number in the linear system and choose

where $\lambda_\Gamma$ is a penalty parameter.

Remark 2.3. The comparison of three different $a^R(\cdot, \cdot)$ terms was discussed in ^[18]. In this paper, we focus on one choice of $a^R(\cdot, \cdot)$, although the other two terms also work in our CutFEM scheme. It is well known that CG$\mathbb{P}_1$/DG$\mathbb{P}_0$ is not an inf-sup stable pair for the incompressible fluid. The enriched element ${\bf{u}}_h^R\in$RT$_0$ can be viewed as the stabilization technique in the scheme. As discussed in the reference ^[18], there are several advantages to this scheme, including preserving the conservation of mass, the optimal convergence rate, the small size in the linear system, and the ease of implementation in the static condensation technique. By extending the scheme to the Stokes interface problem, some of the advantages can be inherited here.

Remark 2.4. We also remark that, for the classical ghost penalty term, the widely used stabilization term for the pressure is as below

However, by using the above pressure ghost penalty, the scheme may violate the mass conservation property and the viscosity robustness, which are the preferred features. In the numerical examples, we will compare our algorithm with the one with the above stabilization term to highlight the advantage in our scheme.

2.4.   Divergence-free property

Theorem 2.5. Let $({\bf{u}}_h, p_h)\in{\bf{V}}_h\times \hat{Q}_h$ be a solution of the CutFEM (2.1) and (2.2). Then the following holds:

Proof. This result can be established as follows: First, $\nabla\cdot{\bf{u}}_h\in \hat{Q}_h$. Then by choosing $q = \nabla\cdot{\bf{u}}_h$, it implies,

Thus, we see that $\nabla\cdot{\bf{u}}_h = 0.$ □

Remark 2.6. However, due to the pressure constraint ${ \int_{\Omega^-} p_h^-d\mathbf{x}+\int_{\Omega^+} p_h^+d\mathbf{x} = 0}$, our numerical experiments do not achieve the divergence-free property. Nevertheless, the numerical divergence values remain globally constant, and the constant decreases as the penalty parameter increases. Some studies have explored modifying this constraint by imposing an alternative condition on the velocity component ^[19,20]. We also demonstrate that by tuning the parameter $\lambda$, the global constant value for $\nabla\cdot{\bf{u}}_h$ in (2.1) and (2.2) is approaching 0. However, how to choose the parameter values to obtain the desired mass conservation is still unknown. We leave such an investigation for future work.

3.   Stability test

In this section, we test the properties of the linear system generated by our proposed algorithm. We report the number of degrees of freedom (DoF), condition number, and inf-sup constant for the following two sets of Stokes interface problems:

where $r$ is in the polar coordinate. The parameters in our simulations are chosen as $\lambda = 1E1/h$, $\lambda_\Gamma = 10$, and $\rho = 20$.

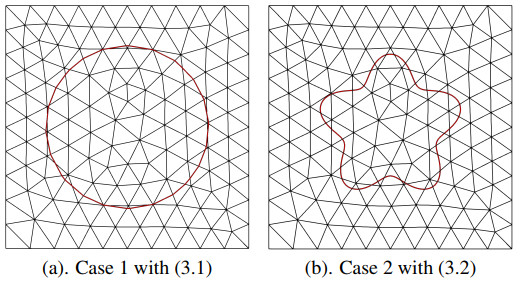
We generate a triangular mesh by dividing each dimension into equally spaced $N$ segments. The coarsest level of meshes is illustrated in Figure 3. As noted in this figure, the background mesh is not aligned with the interface (red curve). The next level of mesh is generated by uniformly refining the mesh from the previous level. As can be observed from Figure 3(a), a small cut may be contained in our numerical test.

First, in Table 1, we compare the degrees of freedom for our scheme (2.1) and (2.2) (denoted as DoF) with the scheme proposed in ^[20] (denoted as DoF in ^[20]). In the previous work ^[20], only the lowest-order RT$_0$ was used, but the edge-based basis functions in the interface elements were doubled. In our numerical scheme, we enrich the global, single-defined RT$_0$ basis functions but double the continuous Galerkin linear basis function in the interface elements to approximate the velocity. However, these RT$_0$ basis functions can be eliminated through static condensation (denoted as DoF with SC), and the resulting linear system is of size related to the continuous Galerkin basis function ${\bf{v}}^C_h$. It is noted that after static condensation, the DoF in the linear system is the fewest. In addition, compared to the use of pure RT$_0$ functions in the velocity, our proposed scheme provides a natural way to handle the Dirichlet boundary condition on $\partial\Omega$.

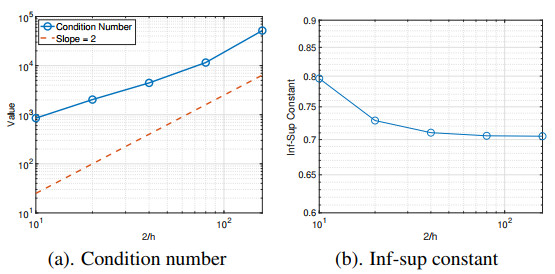
Next, we test the condition number and the inf-sup constant for the linear system for Case 1 with (3.1) on a mesh sequence. We set $\mu^- = \mu^+ = 1$, and the numerical results are illustrated in Figure 4. As shown in Figure 4(a), the condition number increases at the order $\mathcal{O}(h^{-2})$, which is in agreement with our expectation. In addition, the inf-sup constant shows a constant behavior and validates the inf-sup stability for our numerical algorithm.

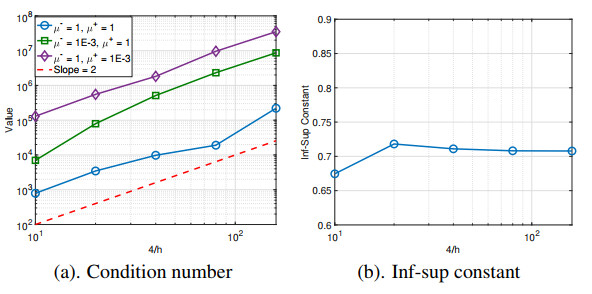
Last, we test the case with the setting in (3.2). Again, as shown in Figure 5, the condition number increases at the order $\mathcal{O}(h^{-2})$ for varying values in $\mu^-$ and $\mu^+$. Similarly, as above, the inf-sup constant is stable with respect to the mesh size $h$.

4.   Convergence order and efficiency tests

In this section, we shall test the algorithm and check the errors measured in the following norms:

In all the following tests, we shall take $\lambda = 1E1/h$, $\lambda_\Gamma = 10$, and $\rho = 20$ without specification. The mean zero condition is enforced by adding another equation corresponding to $\int_\Omega p_h d{\bf{x}} = 0$ to the derived linear system and then this non-square linear matrix is solved via the least-squares method.

4.1.   2D: Static drop test

First, we test the algorithm with varying viscosity values. Set the domain to be $\Omega = (-1, 1)^2$, the interface to be a circle centered at the origin with the radius $R = 2/3$, and the exact solution to be

As the linear polynomial for the velocity and the constant approximation for the pressure are employed in this scheme, the constant velocity and pressure can be resolved. The error profiles and the convergence results are reported in Table 2, from which we can observe that all numerical simulations agree well with the exact solutions up to the machine accuracy. This verifies the effectiveness of the proposed scheme.

4.2.   2D test: Discontinuous vortex

Then, with the same domain and interface as that in the previous test, choosing the exact solution as

we shall demonstrate our algorithm by a test with a continuous velocity and discontinuous pressure in this subsection. We will see that although the exact velocity is a linear polynomial, the linear FEM may not resolve the velocity due to the interface conditions. However, such a mismatch can be improved by increasing the value of the penalty parameter $\lambda$.

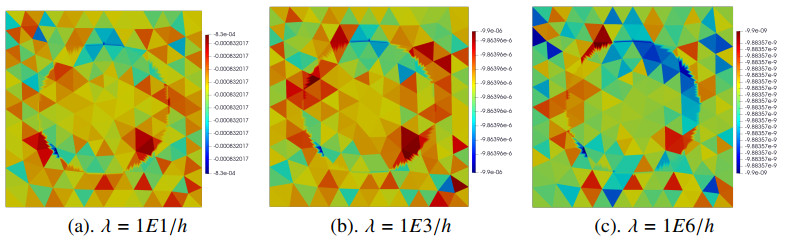
Letting $\mu^+$ and $\mu^-$ be 1, we first test the divergence $\nabla\cdot{\bf{u}}_h$ on a coarse mesh ($h = 2/N = 2/20$) for different penalty parameters $\lambda = 1E1/h, \; 1E3/h, \; 1E6/h.$ From the results in Figure 6, we can find that the values of $\nabla\cdot{\bf{u}}_h$ are nearly a global constant. For example, the divergence values corresponding to $\lambda = 1E1/h$ are nearly $-8.3E-4$ globally (see Figure 6(a)). As $\lambda$ increases, the divergence values will decrease, which will become $-9.9E-6$ (see Figure 6(b)) and $-9.9E-9$ (see Figure 6(c)) for $\lambda = 1E3/h$ and $\lambda = 1E6/h$, respectively. These suggest that divergence values are highly dependent on the penalty parameter $\lambda.$

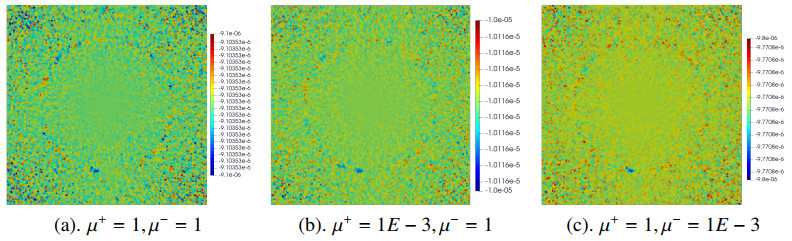
Next, setting the penalty parameter $\lambda = 10/h$ and the mesh size $h = 2/N = 2/100$, we study the divergence values for varying values in $\mu^+$ and $\mu^-$. Figure 7(a)–(c) show that the divergence values are $-9.1E-6$, $-1.0E-5$, and $-9.8E-6$ in the tested cases, which are barely affected by viscosity values. Then we collect the detailed error profiles and convergence results for different parameter values and viscosity values in Tables 3 and 4. It is obvious that the optimal convergence orders are observed in all tests. It is second-order convergent for the velocity in the $L^2$-norm, while it is first-order convergent for both the velocity in the $H^1$-norm and the pressure in the $L^2$-norm. In addition, as the values of $\lambda$ increase, the errors are significantly reduced with the same factor. However, large values in $\lambda$ may introduce challenges in the linear solver. Moreover, from the simulations we can see that the errors are independent of viscosity values, which validates the viscosity robustness of the proposed scheme.

In contrast, we also investigate the error profiles for employing ${S(p_h, q_h)}$ given in Remark 2.4 instead of $G_2(\cdot, \cdot)$. With the same parameter values used in Table 3, the errors reported in Table 5 show that the scheme with the penalty term ${S(p_h, q_h)}$ produces around 100 times higher errors in all tested norms, although the optimal convergence rates can be observed in the numerical experiment.

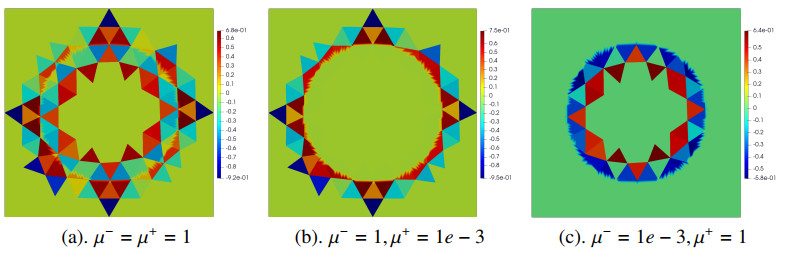
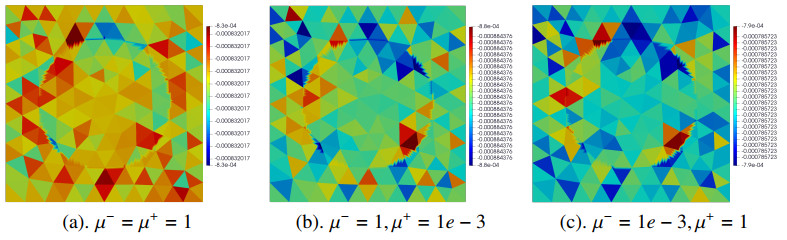
Finally, we further compare the divergence values $\nabla\cdot{\bf{u}}_h$ for these two penalty terms. With the same parameters, the piecewise divergence for each cell is plotted in Figures 8 and 9, from which we can clearly observe the differences between two schemes. Using the classical penalty term, the divergence is far away from zero for elements around the interface (see Figure 8). In addition, the divergence values show the dominance in the regions with a smaller viscosity. However, for the proposed scheme, three constant patterns are observed in the tests (see Figure 9), which show the value $-8E-4$ in all tests. These validate the divergence-preserving feature in our scheme.

4.3.   2D test: Flower interface

In this subsection, with $\Omega = (-2, 2)^2$ and the level set function as

we test our algorithm with the following exact solutions, which have discontinuities in both the velocity and pressure

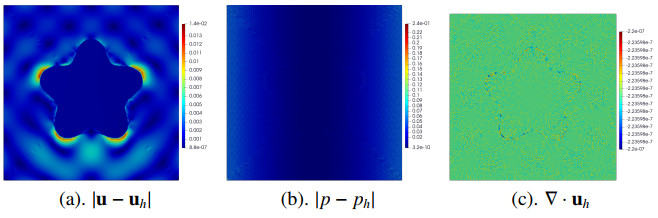
The error profiles and the convergence results are reported in Table 6, where the desired convergence orders for the velocity and pressure are achieved and a slight discrepancy for the errors corresponding to different viscosity values is observed. These are similar to that in Subsection 4.2, which again validates the correctness and the viscosity robustness of the proposed scheme.

Furthermore, we plot the numerical solutions, errors, and $\nabla\cdot{\bf{u}}_h$ in Figure 10. One can observe that the larger velocity errors are around the interface; however, the divergence $\nabla\cdot{\bf{u}}_h$ is nearly a constant with a value of $-6.7E-7$ globally. Similar results are obtained when increasing the viscosity values (see Figure 11). The divergence remains a constant pattern in this case as well.

4.4.   2D test: Gear interface

Let $\Omega = (-2, 2)^2$ and the exact solution be

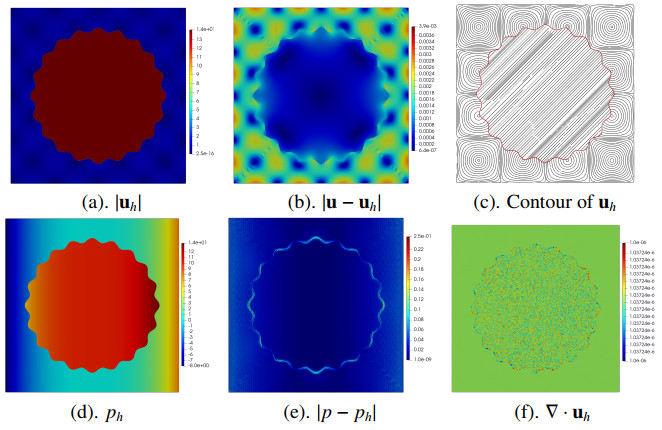
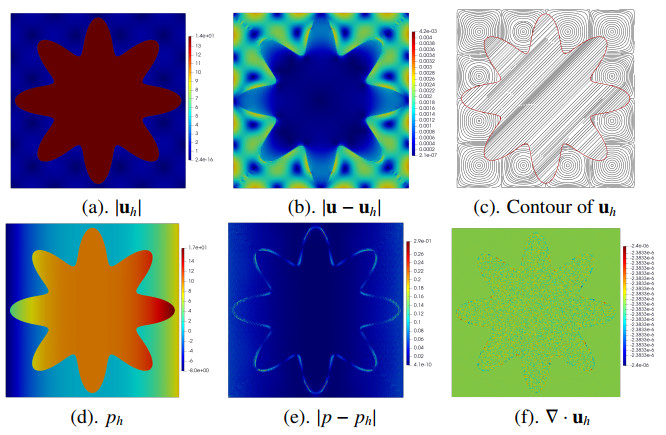
In this subsection, we will test the proposed scheme on the problem with a gear interface. Setting the interface to $\phi({\bf{x}}) = r-0.05\cos(20\theta)-1.5$ with $(r, \theta)$ denoting the polar coordinate, we list the convergence profiles in Table 7. Obviously, optimal convergence rates can be observed in this case. In addition, we present the numerical solutions in Figure 12 with $h = 1/40$, which agree well with the exact solutions. All of these confirm that our scheme can perform very well on this kind of irregular interface problem, too.

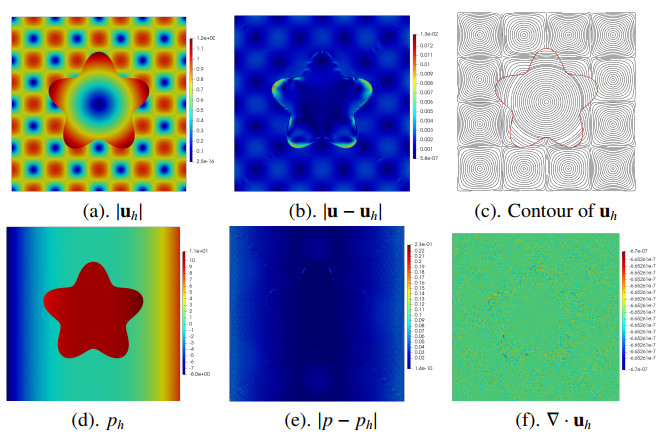
4.5.   2D test: Star interface

With the same domain and exact solutions as that in Subsection 4.4, we further test the proposed scheme on the problem with a star interface defined as $\phi({\bf{x}}) = r - 0.4\cos(8\theta)-1.5.$ Table 8 reports the error profiles with this irregular interface. The velocity errors in the $L^2$- and $H^1$-norm converge at the order $\mathcal{O}(h^2)$ and $\mathcal{O}(h)$, respectively. And the pressure error in the $L^2$-norm converges at the order $\mathcal{O}(h)$. Moreover, the numerical solutions, errors, and numerical divergence are plotted in Figure 13 ($h = 1/40$), which confirms the well-performed numerical solutions for the velocity and pressure. Again, the numerical divergence shows the global constant behavior with a value around ${-2.4E-6}$.

4.6.   3D problem

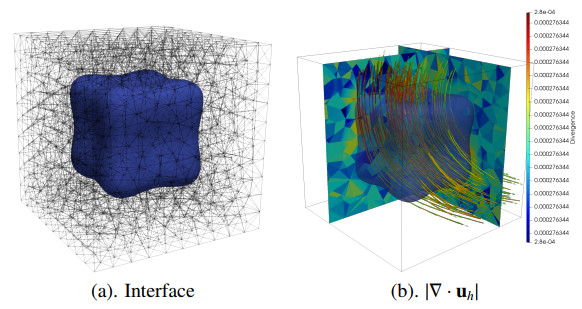
We consider a 3D interface problem in this subsection. Let $\Omega = (0, 1)^3$ and the level set function $\phi({\bf{x}}) = \hat{x}^4+\hat{y}^4+\hat{z}^4 - (\hat{x}^2+\hat{y}^2+\hat{z}^2)$ (see Figure 14(a)), where $\hat{x} = 4(x-0.5), \ \hat{y} = 4(y-0.5), \ \hat{z} = 4(z-0.5)$. The exact solution is chosen as

In this test, the velocity is a continuous function with homogeneous interface condition $[{\bf{u}}]_\Gamma = 0$, while the pressure is a piecewise discontinuous linear function. With a tetrahedral partition, we plot two slices of $\nabla\cdot{\bf{u}}_h$ and streamlines of ${\bf{u}}_h$ in Figure 14(b). The color bar shows the global constant behavior in $\nabla\cdot{\bf{u}}_h$ and thus validates conservation in our proposed scheme. In addition, the error profiles corresponding to various viscosity values are reported in Table 9. For all contrast values in $\mu^-$ and $\mu^+$, we can observe the optimal convergence rate. All of these confirm that the proposed scheme works well for the Stokes interface problem in 3D, too.

5.   Concluding remarks

In this paper, we propose a new CutFEM solver for the Stokes interface problem. The velocity variable is approximated using a piecewise continuous Galerkin linear finite element enriched with the lowest-order Raviart–Thomas element, while the pressure variable is approximated using a piecewise constant finite element. The developed scheme provides a stable and accurate approximation of the problem with an optimal convergence rate. Furthermore, by tuning the parameter values, one can achieve a good approximation that preserves the mass conservation. We demonstrate the effectiveness of the proposed scheme through several numerical tests. In future work, we will extend our scheme to the stochastic problem ^[22], the time-dependent Stokes problem with a moving interface ^[14,23], and the coupled problems ^[24,25].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work of K. Wang is partially supported by the Natural Science Foundation of Chongqing (No. CSTB2024NSCQ-MSX0221). The work of L. Mu is partially supported by the National Science Foundation under the grant DMS-2309557.

Conflict of interest

The authors declare that there are no conflicts of interest.