Figure 1.
Study site (Dodiongan Waterfalls) in Bonbonon, Iligan City, Philippines.
In this paper, we considered a partitioned epidemic model with reaction-diffusion behavior, analyzed the dynamics of populations in various compartments, and explored the significance of spreading parameters. Unlike traditional approaches, we proposed a novel paradigm for addressing the dynamics of epidemic models: Inferring model dynamics and, more importantly, parameter inversion to analyze disease spread using Reaction-Diffusion Disease Information Neural Networks (RD-DINN). This method leverages the principles of hidden disease spread to overcome the black-box mechanism of neural networks relying on large datasets. Through an embedded deep neural network incorporating disease information, the RD-DINN approximates the dynamics of the model while predicting unknown parameters. To demonstrate the robustness of the RD-DINN method, we conducted an analysis based on two disease models with reaction-diffusion terms. Additionally, we systematically investigated the impact of the number of training points and noise data on the performance of the RD-DINN method. Our results indicated that the RD-DINN method exhibits relative errors less than 1% in parameter inversion with 10% noise data. In terms of dynamic predictions, the absolute error at any spatiotemporal point does not exceed 5%. In summary, we present a novel deep learning framework RD-DINN, which has been shown to be effective for reaction-diffusion disease modeling, providing an advanced computational tool for dynamic and parametric prediction of epidemic spread. The data and code used can be found at https://github.com/yuanfanglila/RD-DINN.
Citation: Xiao Chen, Fuxiang Li, Hairong Lian, Peiguang Wang. A deep learning framework for predicting the spread of diffusion diseases[J]. Electronic Research Archive, 2025, 33(4): 2475-2502. doi: 10.3934/era.2025110
| [1] | Fırat Evirgen, Fatma Özköse, Mehmet Yavuz, Necati Özdemir . Real data-based optimal control strategies for assessing the impact of the Omicron variant on heart attacks. AIMS Bioengineering, 2023, 10(3): 218-239. doi: 10.3934/bioeng.2023015 |
| [2] | Sarbaz H. A. Khoshnaw, Kawther Y. Abdulrahman, Arkan N. Mustafa . Identifying key critical model parameters in spreading of COVID-19 pandemic. AIMS Bioengineering, 2022, 9(2): 163-177. doi: 10.3934/bioeng.2022012 |
| [3] | Honar J. Hamad, Sarbaz H. A. Khoshnaw, Muhammad Shahzad . Model analysis for an HIV infectious disease using elasticity and sensitivity techniques. AIMS Bioengineering, 2024, 11(3): 281-300. doi: 10.3934/bioeng.2024015 |
| [4] | Mehmet Yavuz, Waled Yavız Ahmed Haydar . A new mathematical modelling and parameter estimation of COVID-19: a case study in Iraq. AIMS Bioengineering, 2022, 9(4): 420-446. doi: 10.3934/bioeng.2022030 |
| [5] | Daniel Borchert, Diego A. Suarez-Zuluaga, Yvonne E. Thomassen, Christoph Herwig . Risk assessment and integrated process modeling–an improved QbD approach for the development of the bioprocess control strategy. AIMS Bioengineering, 2020, 7(4): 254-271. doi: 10.3934/bioeng.2020022 |
| [6] | Bashdar A. Salam, Sarbaz H. A. Khoshnaw, Abubakr M. Adarbar, Hedayat M. Sharifi, Azhi S. Mohammed . Model predictions and data fitting can effectively work in spreading COVID-19 pandemic. AIMS Bioengineering, 2022, 9(2): 197-212. doi: 10.3934/bioeng.2022014 |
| [7] | Sarbaz H. A. Khoshnaw, Azhi Sabir Mohammed . Computational simulations of the effects of social distancing interventions on the COVID-19 pandemic. AIMS Bioengineering, 2022, 9(3): 239-251. doi: 10.3934/bioeng.2022016 |
| [8] | Prasantha Bharathi Dhandapani, Dumitru Baleanu, Jayakumar Thippan, Vinoth Sivakumar . On stiff, fuzzy IRD-14 day average transmission model of COVID-19 pandemic disease. AIMS Bioengineering, 2020, 7(4): 208-223. doi: 10.3934/bioeng.2020018 |
| [9] | Norliyana Nor Hisham Shah, Rashid Jan, Hassan Ahmad, Normy Norfiza Abdul Razak, Imtiaz Ahmad, Hijaz Ahmad . Enhancing public health strategies for tungiasis: A mathematical approach with fractional derivative. AIMS Bioengineering, 2023, 10(4): 384-405. doi: 10.3934/bioeng.2023023 |
| [10] | Lakshmi N Sridhar . Integration of bifurcation analysis and optimal control of a molecular network. AIMS Bioengineering, 2024, 11(2): 266-280. doi: 10.3934/bioeng.2024014 |
In this paper, we considered a partitioned epidemic model with reaction-diffusion behavior, analyzed the dynamics of populations in various compartments, and explored the significance of spreading parameters. Unlike traditional approaches, we proposed a novel paradigm for addressing the dynamics of epidemic models: Inferring model dynamics and, more importantly, parameter inversion to analyze disease spread using Reaction-Diffusion Disease Information Neural Networks (RD-DINN). This method leverages the principles of hidden disease spread to overcome the black-box mechanism of neural networks relying on large datasets. Through an embedded deep neural network incorporating disease information, the RD-DINN approximates the dynamics of the model while predicting unknown parameters. To demonstrate the robustness of the RD-DINN method, we conducted an analysis based on two disease models with reaction-diffusion terms. Additionally, we systematically investigated the impact of the number of training points and noise data on the performance of the RD-DINN method. Our results indicated that the RD-DINN method exhibits relative errors less than 1% in parameter inversion with 10% noise data. In terms of dynamic predictions, the absolute error at any spatiotemporal point does not exceed 5%. In summary, we present a novel deep learning framework RD-DINN, which has been shown to be effective for reaction-diffusion disease modeling, providing an advanced computational tool for dynamic and parametric prediction of epidemic spread. The data and code used can be found at https://github.com/yuanfanglila/RD-DINN.
Water plays a vital role in maintaining life [1]. Its importance is underscored by the fact that many great civilizations in the past sprang up along or near water bodies. Humans have relied very much on water as a water resource for domestic and commercial purposes [2]. One of the bodies of water that should be considered a water resource is the waterfall. Most studies tend to focus more on the water quality assessment of the rivers and lakes but there is no study that assesses the water quality of a waterfall [3].
Waterfalls, most of which are formed from different tributaries that cascade [4] from a high elevation over a cliff or rock, have received very little attention from researchers all over the world [5]. In Africa, the researchers abstain from studying the waterfalls because waterfalls for them are sacred. They even named these after the deities and gods associated with these waterfalls and treated them as their venue for worshiping and contemplating [6]. Knowledge of the waterfall systems in Africa is therefore limited in terms of the study of water [7] and its geological features because the natural monuments can serve as revenue generation which boosts the nation's ecotourism [8]
Improving and developing water resources promotes the socioeconomic of different nations around the globe. Because of human activities, the water resource is threatened by pollution and irresponsible actions by humans [9]. In developing countries, clean water is scarce because of environmental pollution and degradation. In California, different studies have been conducted to obtain information on the occurrence of emerging contaminants in the water environment [10]. The numerous emerging contaminants propagated in an aquatic environment continue to grow rapidly in an uncontrolled manner [11]. This is perilous mainly because of the potential risks [12] to human health and the environment [13].
The proliferation of water pollution around the globe is a prevalent issue that gained the attention of public health administrations [14]. Drinking water is especially polluted in underdeveloped countries. According to Echoing Sustainability in Mena (EcoMENA) (2020), around 3.2 million children die annually because of poor quality water, poor sanitation and polluted drinking water while there is also a limited number of wastewater treatment facilities. Contaminated water due to industrial waste is the cause of numerous diseases such as diarrhea, intestinal worms and even cholera. The industrial waste that contaminated the water threatened the perception of risk [15]. The acceptability and judgment of the community's environmental health risk perception, especially if the water resource is near a garbage dumpsite play an integral role in understanding the possible repercussions and consequences [16,17]. Thus, this will pave the way for people to not trust the drinking water as potable and safe.
The residents of Barangay Bonbonon and Digkilaan feel that their livelihood and food security [7,18] are threatened by landfill leachate that has contaminated Dodiongan Falls. A documentary film and empirical evidence vividly showed and explicitly explained the critical condition of Dodiongan Falls due to the garbage dumpsite releasing an overflowing dark-colored secretion from the treatment box to the water resource (waterfall) down to every resident in the neighboring places where the lives are susceptible to any kind of diseases.
This study was designed to assess the water quality of Dodiongan Falls in Barangay Bonbonon, Iligan City, Philippines. Investigating and determining the physicochemical and microbiological parameters of this waterfall is crucial for interpreting its water quality. The findings of this study could serve as baseline data that could help the Department of Education (DepEd), city tourism's office, city health office (CHO), local governmental units (LGUs) and other related agencies to create management plans for the site to avoid serious health hazards.
The study area was Dodiongan Waterfalls in Kabacsanan-Bonbonon, Iligan City, which is a province of Lanao del Norte, Philippines with coordinates of +8° 16' 20.53", +124° 18' 48.77". Dodiongan Falls is a 20-meter (65.5 ft) high waterfall. The climate is a tropical hinterland type, with wet (June–October) and dry (November–May) seasons. The average annual temperature in the area is 27.0 ℃. The precipitation averages reach 3180 mm. The driest month is April with 80 mm of precipitation. The greatest amount of precipitation occurs in October, with an average of 780 mm. With an average of 27.8 ℃, May is the warmest month of the year. The lowest average temperature in the year occurs in January when it is around 26.1 ℃. Unlike other waterfalls in Iligan City that are bedded in different rivers, the water source of Dodiongan Falls is a product of several underground springs that flows to the top via various tributaries [19].
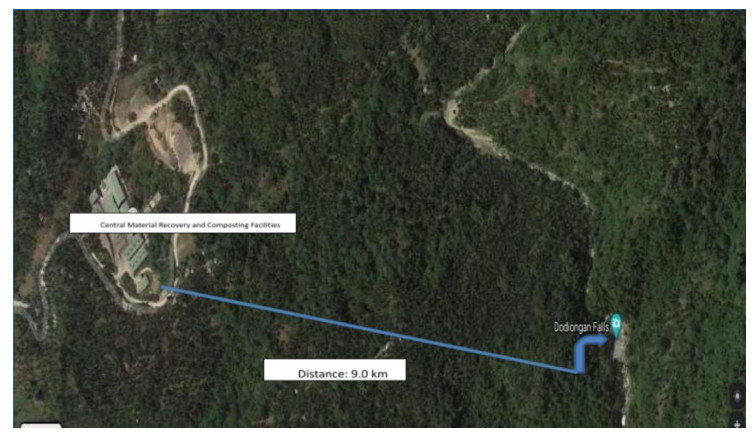
The Philippines is a developing country with abundant water resources, yet, it is coupled with different environmental issues. One of the cities in the Philippines is known as the City of Waterfalls in Iligan City because of its numerous waterfalls with distinct beauty and an exquisite scenery. There are 44 known waterfalls in this city and one of those is identified as a chute waterfall named the Dodiongan Falls of Bonbonon. However, the location of this waterfall is a neighborhood of a city garbage dumpsite [20] called the Central Material Recovery and Composting Facilities (CMRCF). It was observed by the residents in Bonbonon that the waterfalls had turned sour and smell stinky. It was also observed by the teachers of Sultan Mamarinta Panandigan Integrated School -a neighboring school- that the learners living in Dodoiongan were having absenteeism issues. This observation urged the researcher to probe the reasons behind the pollution of the water [21] and the learners' habitual absences.
The study area was divided into three distinct stations. The three sampling sites were designated as D1 (upstream), D2 (midstream) and D3 (downstream). The first station was located where the various tributaries sprung over. At that site, a little nipa house was installed on one of the rock formations where residents observed that there were people living in that area who were mining for gold. The second station was like a man-made pool. Visitors usually have a hard time reaching this area because though this is above the waterfalls, the path to get there is very dangerous. One would have to use mountain climbing gear such as climbing ropes, carabiner and a climbing harness for your safety. The third station was at the waterfalls where most of the visitors engage in recreational activities.
Water samples were collected in triplicates last February 2018 by using the standard operating procedure (SOP) in collecting the water sample indicated in the World Health Organization (WHO) [22]. The samples were stored in sterile 250 ml polyethylene bottles, sealed, labeled, stored in a cooler container and then, transported to the laboratory for analyses. The physicochemical and heavy metal parameters such as the pH, alkalinity, turbidity, mercury, and lead concentrations were determined in the FAST Laboratory in Cagayan De Oro City.
The physicochemical parameters such as the pH, total alkalinity and turbidity were determined in situ or in the laboratory. A EUTECH Instruments pH 510 model was used to measure the pH through [22] 4500+ B electrometric method. Alkalinity was determined using the 2320 B titration method. An acid of known strength (the titrant) added to a volume of a treated sample of water. The amount of acid required to change the water sample to a specific pH level shows the alkalinity of the sample. The pH endpoint is indicated by a color change.
Alkalinity was gauged in units of milligrams per liter (mg/L) of CaCO3.Turbidity was assayed by applying the nephelometric method using a Fast Tracker Turbidimeter HI98703 model.
Schardinger [28] introduced E. coli as an indicator of fecal contamination. This was based on the idea that E. coli is found in the human gastrointestinal tract and that animal feces and is not typically found in other niches. In addition, since E. coli can be simply identified by its capacity to ferment glucose it was easier to isolate them. Thus, the presence of E. coli in water or food became an indicator of recent fecal contamination and the potential presence of any pathogens.
E. Coli examination was done following the standard methods of the Bacteriological Analytical Manual [28]. The 5-tube Most Probable Number (MPN) [28] test was used to determine the presence of fecal coliforms in the water samples. This method is a multi-step, statistical assay consisting of presumptive, confirmed and completed phases. For the fecal assessment, serial dilutions of each sample were placed in broth media.
For the presumptive test, serial dilutions (10 ml; 1 ml; 0.1 ml) of a water sample were inoculated into five large lactose broth tubes and inverted Durham tubes. The tubes were incubated at 370 ℃ for 48 hours. The presence of gas bubbles in the Durham tube is an indicator of positive coliforms. For the confirmatory test, all tubes that tested positive for coliforms were inoculated in brilliant green lactose bile broth inverted in Durham tubes. Following incubation, the samples that displayed positive results for the confirmatory test were streaked in agar plates containing eosin methylene blue (EMB) for the completion test. The plates were incubated at 370 ℃ for 48 hours. To determine the MPN of fecal coliforms, an MPN table was utilized based on the number of positive tubes.
To assess the levels of the heavy metals, water samples, each amounting to 6.0 liters from each of the three sites of the waterfalls were collected and placed in sterile polythene containers that have been pre-washed and sterilized. The samples were chilled and brought to the laboratory at a temperature of 4 C. It was then directly analyzed to within ±1.0 nm accuracy using an atomic absorption spectrophotometer (AAS) 7000 model. For each heavy metal, a specific concentration standard was applied to prepare a calibration curve that allowed the concentration of the heavy metal to be read directly from the AAS visual display unit (VDU) system. The lead was tested in accordance with 3030 E nitric acid digestion and 3111 B direct air-acetylene flame AAS while mercury was tested through 3112 B standard method.
Summary of the results for the level of pH, alkalinity and turbidity of Dodiongan Falls was presented in Table 1. These values had been placed alongside natural background levels for tropical surface waters that are in accordance with the guidelines and the standards of the World Health Organization (WHO) [22] and the Philippine national water quality standards (PNWQS).
| No. of Stations | Measured Parameter | Results | WHO Standards (PNWQS)/ Highest Desirable Maximum/ Permissible |
| D1 | pH | 7.6 | 6.5–8.5 6.5–9.5 |
| D2 | 7.4 | 6.5–8.5 6.5–9.5 | |
| D3 | 7.2 | 6.5–8.5 6.5–9.5 | |
| D1 | Total Alkalinity as CaCO3 (mg/L) | 257 | 20–200 20–200 |
| D2 | 257 | 20–200 20–200 | |
| D3 | 257 | 20–200 20–200 | |
| D1 | Turbidity (mg/L) | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU |
| D2 | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU | |
| D3 | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU |
DownLoad:
CSV
The results obtained by counting the number of E. coli is summarized in Table 2 for the category and color-code scheme for fecal coliforms in water supplies, Table 3 presumptive test result, Table 4 confirmatory test result and Table 5 completed test result. The three sampling sites were distinctly gauged according to the number of positive tubes with an MPN index per 100 ml, category and color-code scheme. The remarks are based on the WHO (1997) guidelines presented in Table 2. Further, the table shows to which category the three sampling sites in the study belong in terms of counts per 100 ml.
| Count per 100 ml | Category and Color-Code Scheme | Remark |
| 0 | A (blue) | Within WHO recommendation |
| 1–10 | B (green) | Low risk |
| 10–100 | C (yellow) | Intermediate risk |
| 100–1000 | D (orange) | High risk |
| > 1000 | E (red) | Very high risk |
DownLoad:
CSV
| Sampling Site | Number of Tubes | MPN Index per Tubes 100 ml | Category and Color, Code Scheme | Remark | ||
| 10 ml | 1 ml | 0.1 ml | ||||
| D1 | 5 | 4 | 2 | 220 | D (orange) | High risk |
| D2 | 5 | 4 | 3 | 280 | D (orange) | High risk |
| D3 | 5 | 5 | 4 | 920 | E (red) | Very high risk |
DownLoad:
CSV
| Sampling Site | Number of Tubes | MPN Index per Tubes 100 ml | Category and Color, Code Scheme | Remark | ||
| 10 ml | 1 ml | 0.1 ml | ||||
| D1 | 5 | 4 | 2 | 220 | D (orange) | High risk |
| D2 | 5 | 4 | 3 | 280 | D (orange) | High risk |
| D3 | 5 | 5 | 4 | 1600 | E (red) | Very high risk |
DownLoad:
CSV
| Sampling Site | Number of Positive Tubes | ||
| 10 ml | 1 ml | 0.1 ml | |
| D1 | ++++ | ++ | + |
| D2 | ++++ | ++ | ++ |
| D3 | +++++ | +++ | +++ |
| Note: +: number of tubes which show indicating of coliform bacteria. | |||
DownLoad:
CSV
As shown in Table 6, there was less than 0.01 mg/L of lead and less than 0.001 mg/L of mercury which is a good indication that the water has no high concentration of these heavy metals. Further, the results were in conformity within the recommended limits of the WHO standards and PNWQS. This means that, though it was less than what is considered a threat to human health, it does not mean that there is an absence of it; it showed a trace of these heavy metals which can gradually become a source of water contamination. Assessing the water quality of the Payatas Open dumpsite in Quezon City Metropolitan Manila, Philippines showed that there was no significant amount of lead in the two sets from the study area, but, since there was a presence of the total coliform, the water quality is still poor and there is pollution.
| Sampling Site | Measured Parameter | Results | WHO Standards/PNWQS | |
| Highest Desirable | Maximum Desirable | |||
| D1 | Lead (mg/L) | Less than 0.01b | 0.01 | 0.01 |
| D2 | Less than 0.01b | 0.01 | 0.01 | |
| D3 | Less than 0.01b | 0.01 | 0.01 | |
| D1 | Mercury (mg/L) | Less than 0.01b | 0.001 | 0.001 |
| D2 | Less than 0.01b | 0.001 | 0.001 | |
| D3 | Less than 0.01b | 0.001 | 0.001 | |
| Note: b: method detection limit. | ||||
DownLoad:
CSV
The pH values at the three stations (7.2 to 7.6) were within the standard for recreational waters Class B based on guidelines of the World Health Organization (WHO) [22] and the Philippine national water quality standards (PNWQS) [21], the pH of the waterfalls would not adversely affect their domestic use, their recreational activities, or the aquatic ecosystem [23]. The well-buffered nature of the water from the waterfalls can be attributed to the fact that, naturally, running waters or surface waters are influenced by the nature of deposits over which they flow this was taken into consideration with the fact that the waterfall is a product of numerous springs that flow to the top via different tributaries [24].
The results for the alkalinity of the waterfalls were not alarming. The total alkalinity contributed by CaCO3 reached 257 mg/L. This result is not within the highest desirable or maximum permissible range (alkalinity range 20–200) indicated in the guidelines of the WHO standards and PNWQS. However, since geology can considerably affect the alkalinity, there are no general standards for this parameter. Waters with high alkalinity are able to resist major shifts in pH because alkalinity is the ability of water to neutralize an acid.
Turbidity has no human or animal health effects but it can inhibit decontamination and disinfection of the water which provides a medium for microbial growth. The results show that the three stations have the same turbidity of 4.95 NTU. Ideally, according to the WHO and PNWQS guidelines, the highest desirable turbidity of water should not be in excess of 1 NTU. Though the result is less than 5 NTU which means that the turbidity of the water is within the maximum permissible range, it is highly recommended that it should not be in excess of 1 NTU. The turbidity of water higher than 1 NTU can cause problems in water purification processes such as flocculation and filtration [25]. Highly turbid water is often associated with the probability of microbiological contamination [26] as excessive turbidity makes it difficult to disinfect water to make it suitable for domestic and recreational use; this can later become the main cause of recreational waterborne illness as discussed in [27].
The MPN of the total coliform revealed that there was an increasing count of E. coli from the upstream to downstream stations (220 < 280 < 1,600 MPN/100 ml). The Upstream and midstream stations were associated with a high risk while the downstream station associated with a very high risk. These results have indicated fecal pollution of the water sources [28], and they imply that these water sources pose a very serious health risk to their consumers [29]. The poor microbiological quality might be a result of fecal contamination in the water by human beings and animals or they could have been deposited in sediment and infiltrated the meteoric water [30]. The highest E. coli (1,600 MPN/100 ml) recorded downstream could be attributed to the landfill leachate from the neighborhood garbage dumping site in the area [31]. The presence of these bacteria in the water can result in different diseases such as typhoid, diarrhea, infections, hepatitis, giardiasis, dracunculiasis, cholera and amoebiasis [32]. This might be the reason behind the increasing rate of absenteeism among all the learners in the nearby schools.
The implication of maintaining and sustaining water quality standards on health is very essential. Every constituent of water has a safety implication because the consumption of poor-quality water can lead to serious health hazards. Water standards concerning the monitoring, control and surveillance of the water bodies remain the top priority from the perspective of ensuring optimal public health. Ultimately, this study can be a baseline study to give insight into the current situation of the residents in the nearby waterfalls which is in perilous condition, especially for the learners. It is highly recommended that there will be the creation of a management plan. This management plan should be crafted and supported by the baseline data from the findings and results of the physicochemical, heavy metal, and E. coli analyses. The different agencies such as the DepEd, Department of Environment and Natural Resources, the city tourism's office, CHO, and the local governmental unit (LGU) have to be convened to craft this management plan purposely to resolve the problem arising from the landfill leachate and thus, be able to protect Dodiongan Falls, the people and their livelihoods that sustain their basic needs.
The corresponding author is grateful to have the incessant support of his family, especially his mother who inspired him to always make a difference with his existence by taking actions that are tantamount to nation-building and environmental protection and preservation, and to his sister, Lovely Joy Cabello-Snow, who supported him financially throughout this endeavor and served as a listening ear when the author was about to give up. Also, to his professor, Prof. Nelfa D. Canini, for the knowledge, guidance regarding the technical aspect of the paper, and encouragement extended to him while pursuing and completing this study.
The authors confirm that there is no conflict of interest regarding this manuscript.
| [1] |
W. O. Kermack, A. G. McKendrick, A contribution to the mathematical theory of epidemics, Proc. R. Soc. Lond. A, 115 (1927), 700–721. http://doi.org/10.1098/rspa.1927.0118 doi: 10.1098/rspa.1927.0118
|
| [2] |
T. Sigler, S. Mahmuda, A. Kimpton, J. Loginova, P. Wohland, E. Charles-Edwards, et al., The socio-spatial determinants of COVID-19 diffusion: The impact of globalisation, settlement characteristics and population, Global. Health, 17 (2021), 56. https://doi.org/10.1186/s12992-021-00707-2 doi: 10.1186/s12992-021-00707-2
|
| [3] |
N. Sene, SIR epidemic model with Mittag–Leffler fractional derivative, Chaos, Solitons Fractals, 137 (2020), 109833. https://doi.org/10.1016/j.chaos.2020.109833 doi: 10.1016/j.chaos.2020.109833
|
| [4] |
J. A. Backer, A. Berto, C. McCreary, F. Martelli, W. H. M. van der Poel, Transmission dynamics of hepatitis E virus in pigs: Estimation from field data and effect of vaccination, Epidemics, 4 (2012), 86–92. https://doi.org/10.1016/j.epidem.2012.02.002 doi: 10.1016/j.epidem.2012.02.002
|
| [5] | R. Anderson, R. May, Infectious Diseases of Humans: Dynamics and Control, Oxford Academic, 1991. https://doi.org/10.1093/oso/9780198545996.001.0001 |
| [6] | A. Nauman, M. Rafiq, M. A. Rehman, M. Ali, M. O. Ahmad, Numerical modeling of SEIR measles dynamics with diffusion, Commun. Math. Appl., 9 (2018), 315–326. |
| [7] |
T. N. Sindhu, A. Shafiq, Z. Huassian, Generalized exponentiated unit Gompertz distribution for modeling arthritic pain relief times data: Classical approach to statistical inference, J. Biopharm. Stat., 34 (2024), 323–348. https://doi.org/10.1080/10543406.2023.2210681 doi: 10.1080/10543406.2023.2210681
|
| [8] |
T. N. Sindhu, A. Shafiq, M. B. Riaz, T. A. Abushal, H. Ahmad, E. M. Almetwally, et al., Introducing the new arcsine-generator distribution family: An in-depth exploration with an illustrative example of the inverse weibull distribution for analyzing healthcare industry data, J. Radiat. Res. Appl. Sci., 17 (2024), 100879. https://doi.org/10.1016/j.jrras.2024.100879 doi: 10.1016/j.jrras.2024.100879
|
| [9] |
T. N. Sindhu, A. Shafiq, Q. M. Al-Mdallal, Exponentiated transformation of Gumbel Type-Ⅱ distribution for modeling COVID-19 data, Alexandria Eng. J., 60 (2021), 671–689. https://doi.org/10.1016/j.aej.2020.09.060 doi: 10.1016/j.aej.2020.09.060
|
| [10] |
A. Shafiq, A. B. Çolak, T. N. Sindhu, S. A. Lone, A. Alsubie, F. Jarad, Comparative study of artificial neural network versus parametric method in COVID-19 data analysis, Results Phys., 38 (2022), 105613. https://doi.org/10.1016/j.rinp.2022.105613 doi: 10.1016/j.rinp.2022.105613
|
| [11] |
A. Shafiq, A. B. Çolak, T. N. Sindhu, S. A. Lone, T. A. Abushal, Modeling and survival exploration of breast carcinoma: A statistical, maximum likelihood estimation, and artificial neural network perspective, Artif. Intell. Life Sci., 4 (2023), 100082. https://doi.org/10.1016/j.ailsci.2023.100082 doi: 10.1016/j.ailsci.2023.100082
|
| [12] |
G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, L. Yang, Physics-informed machine learning, Nat. Rev. Phys., 3 (2021), 422–440. https://doi.org/10.1038/s42254-021-00314-5 doi: 10.1038/s42254-021-00314-5
|
| [13] |
M. Raissi, P. Perdikaris, G. E. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, J. Comput. Phys., 378 (2019), 686–707. https://doi.org/10.1016/j.jcp.2018.10.045 doi: 10.1016/j.jcp.2018.10.045
|
| [14] |
S. Cai, Z. Mao, Z. Wang, M. Yin, G. E. Karniadakis, Physics-informed neural networks (PINNs) for fluid mechanics: A review, Acta Mech. Sin., 37 (2021), 1727–1738. https://doi.org/10.1007/s10409-021-01148-1 doi: 10.1007/s10409-021-01148-1
|
| [15] |
A. Yazdani, L. Lu, M. Raissi, G. E. Karniadakis, Systems biology informed deep learning for inferring parameters and hidden dynamics, PLOS Comput. Biol., 16 (2020), e1007575. https://doi.org/10.1371/journal.pcbi.1007575 doi: 10.1371/journal.pcbi.1007575
|
| [16] | M. Raissi, N. Ramezani, P. N. Seshaiyer, On parameter estimation approaches for predicting disease transmission through optimization, deep learning and statistical inference methods, Lett. Biomath., 6 (2019), 1–26. |
| [17] | S. Shaier, M. Raissi, P. Seshaiyer, Data-driven approaches for predicting spread of infectious diseases through DINNs: Disease informed neural networks, Lett. Biomath., 9 (2022), 71–105. |
| [18] |
S. Yin, J. Wu, P. Song, Optimal control by deep learning techniques and its applications on epidemic models, J. Math. Biol., 86 (2023), 36. https://doi.org/10.1007/s00285-023-01873-0 doi: 10.1007/s00285-023-01873-0
|
| [19] |
F. V. Difonzo, L. Lopez, S. F. Pellegrino, Physics informed neural networks for learning the horizon size in bond-based peridynamic models, Comput. Methods Appl. Mech. Eng., 436 (2025), 117727. https://doi.org/10.1016/j.cma.2024.117727 doi: 10.1016/j.cma.2024.117727
|
| [20] | F. V. Difonzo, L. Lopez, S. F. Pellegrino, Physics informed neural networks for an inverse problem in peridynamic models, Eng. Comput., 2024 (2024). https://doi.org/10.1007/s00366-024-01957-5 |
| [21] |
D. Ouedraogo, I. Ibrango, A. Guiro, Global stability for reaction-diffusion SIR model with general incidence function, Malaya J. Mat., 10 (2022), 139–150. https://doi.org/10.26637/mjm1002/004 doi: 10.26637/mjm1002/004
|
| [22] |
J. P. C. Santos, E. Monteiro, J. C. Ferreira, N. H. T. Lemes, D. S. Rodrigues, Well-posedness and qualitative analysis of a SEIR model with spatial diffusion for COVID-19 spreading, Biomath, 12 (2023), 2307207. https://doi.org/10.55630/j.biomath.2023.07.207 doi: 10.55630/j.biomath.2023.07.207
|
| [23] |
S. Chinviriyasit, W. Chinviriyasit, Numerical modelling of an SIR epidemic model with diffusion, Appl. Math. Comput., 216 (2010), 395–409. https://doi.org/10.1016/j.amc.2010.01.028 doi: 10.1016/j.amc.2010.01.028
|
| [24] |
P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6 doi: 10.1016/S0025-5564(02)00108-6
|
| [25] | Y. LeCun, Y. Bengio, G. Hinton, Deep learning, Nature, 521 (2015), 436–444. https://doi.org/10.1038/nature14539 |
| [26] | A. G. Baydin, B. A. Pearlmutter, A. A. Radul, J. M. Siskind, Automatic differentiation in machine learning: A survey, J. Mach. Learn. Res., 18 (2018), 1–43. |
| [27] |
M. Raissi, G. E. Karniadakis, Hidden physics models: Machine learning of nonlinear partial differential equations, J. Comput. Phys., 357 (2018), 125–141. https://doi.org/10.1016/j.jcp.2017.11.039 doi: 10.1016/j.jcp.2017.11.039
|
| [28] | K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, (2016), 770–778. https://doi.org/10.1109/CVPR.2016.90 |
| [29] | A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, et al., Attention is all you need, preprint, arXiv: 1706.03762. |
| [30] |
M. D. McKay, R. J. Beckman, W. J. Conover, A comparison of three methods for selecting values of input variables in the analysis of output from a computer code, Technometrics, 21 (1979), 239–245. https://doi.org/10.2307/1268522 doi: 10.2307/1268522
|
| [31] |
E. Massad, M. N. Burattini, F. B. A. Coutinho, L. F. Lopez, The 1918 influenza A epidemic in the city of São Paulo Brazil, Med. Hypotheses, 68 (2007), 442–445. https://doi.org/10.1016/j.mehy.2006.07.041 doi: 10.1016/j.mehy.2006.07.041
|
| [32] |
N. Sene, 2-Numerical methods applied to a class of SEIR epidemic models described by the Caputo derivative, Methods Math. Model., 2022 (2022), 23–40. https://doi.org/10.1016/B978-0-323-99888-8.00003-6 doi: 10.1016/B978-0-323-99888-8.00003-6
|
| [33] |
S. L. Brunton, J. L. Proctor, J. N. Kutz, Discovering governing equations from data by sparse identification of nonlinear dynamical systems, Proc. Natl. Acad. Sci. U.S.A., 113 (2016), 3932–3937. https://doi.org/10.1073/pnas.1517384113 doi: 10.1073/pnas.1517384113
|
| 1. | Atta Ullah, Hamzah Sakidin, Shehza Gul, Kamal Shah, Yaman Hamed, Thabet Abdeljawad, Mathematical model with sensitivity analysis and control strategies for marijuana consumption, 2024, 10, 26668181, 100657, 10.1016/j.padiff.2024.100657 | |
| 2. | Mudassar Iqbal, Nooraini Zainuddin, Hanita Daud, Ramani Kanan, Hira Soomro, Rahimah Jusoh, Atta Ullah, Iliyas Karim Khan, A modified basis of cubic B-spline with free parameter for linear second order boundary value problems: Application to engineering problems, 2024, 36, 10183647, 103397, 10.1016/j.jksus.2024.103397 | |
| 3. | Atta Ullah, Hamzah Sakidin, Kamal Shah, Yaman Hamed, Thabet Abdeljawad, A mathematical model with control strategies for marijuana smoking prevention, 2024, 32, 2688-1594, 2342, 10.3934/era.2024107 | |
| 4. | Jalal Al Hallak, Mohammed Alshbool, Ishak Hashim, Amar Nath Chatterjee, Implementing Bernstein Operational Matrices to Solve a Fractional‐Order Smoking Epidemic Model, 2024, 2024, 1687-9643, 10.1155/2024/9141971 |
Xiao Chen, Fuxiang Li, Hairong Lian, Peiguang Wang. A deep learning framework for predicting the spread of diffusion diseases[J]. Electronic Research Archive, 2025, 33(4): 2475-2502. doi: 10.3934/era.2025110
| No. of Stations | Measured Parameter | Results | WHO Standards (PNWQS)/ Highest Desirable Maximum/ Permissible |
| D1 | pH | 7.6 | 6.5–8.5 6.5–9.5 |
| D2 | 7.4 | 6.5–8.5 6.5–9.5 | |
| D3 | 7.2 | 6.5–8.5 6.5–9.5 | |
| D1 | Total Alkalinity as CaCO3 (mg/L) | 257 | 20–200 20–200 |
| D2 | 257 | 20–200 20–200 | |
| D3 | 257 | 20–200 20–200 | |
| D1 | Turbidity (mg/L) | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU |
| D2 | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU | |
| D3 | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU |
DownLoad:
CSV
| Count per 100 ml | Category and Color-Code Scheme | Remark |
| 0 | A (blue) | Within WHO recommendation |
| 1–10 | B (green) | Low risk |
| 10–100 | C (yellow) | Intermediate risk |
| 100–1000 | D (orange) | High risk |
| > 1000 | E (red) | Very high risk |
DownLoad:
CSV
| Sampling Site | Number of Tubes | MPN Index per Tubes 100 ml | Category and Color, Code Scheme | Remark | ||
| 10 ml | 1 ml | 0.1 ml | ||||
| D1 | 5 | 4 | 2 | 220 | D (orange) | High risk |
| D2 | 5 | 4 | 3 | 280 | D (orange) | High risk |
| D3 | 5 | 5 | 4 | 920 | E (red) | Very high risk |
DownLoad:
CSV
| Sampling Site | Number of Tubes | MPN Index per Tubes 100 ml | Category and Color, Code Scheme | Remark | ||
| 10 ml | 1 ml | 0.1 ml | ||||
| D1 | 5 | 4 | 2 | 220 | D (orange) | High risk |
| D2 | 5 | 4 | 3 | 280 | D (orange) | High risk |
| D3 | 5 | 5 | 4 | 1600 | E (red) | Very high risk |
DownLoad:
CSV
| Sampling Site | Number of Positive Tubes | ||
| 10 ml | 1 ml | 0.1 ml | |
| D1 | ++++ | ++ | + |
| D2 | ++++ | ++ | ++ |
| D3 | +++++ | +++ | +++ |
| Note: +: number of tubes which show indicating of coliform bacteria. | |||
DownLoad:
CSV
| Sampling Site | Measured Parameter | Results | WHO Standards/PNWQS | |
| Highest Desirable | Maximum Desirable | |||
| D1 | Lead (mg/L) | Less than 0.01b | 0.01 | 0.01 |
| D2 | Less than 0.01b | 0.01 | 0.01 | |
| D3 | Less than 0.01b | 0.01 | 0.01 | |
| D1 | Mercury (mg/L) | Less than 0.01b | 0.001 | 0.001 |
| D2 | Less than 0.01b | 0.001 | 0.001 | |
| D3 | Less than 0.01b | 0.001 | 0.001 | |
| Note: b: method detection limit. | ||||
DownLoad:
CSV
| No. of Stations | Measured Parameter | Results | WHO Standards (PNWQS)/ Highest Desirable Maximum/ Permissible |
| D1 | pH | 7.6 | 6.5–8.5 6.5–9.5 |
| D2 | 7.4 | 6.5–8.5 6.5–9.5 | |
| D3 | 7.2 | 6.5–8.5 6.5–9.5 | |
| D1 | Total Alkalinity as CaCO3 (mg/L) | 257 | 20–200 20–200 |
| D2 | 257 | 20–200 20–200 | |
| D3 | 257 | 20–200 20–200 | |
| D1 | Turbidity (mg/L) | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU |
| D2 | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU | |
| D3 | 4.95 | Ideally below 1.0 NTU Less than 5.0 NTU |
| Count per 100 ml | Category and Color-Code Scheme | Remark |
| 0 | A (blue) | Within WHO recommendation |
| 1–10 | B (green) | Low risk |
| 10–100 | C (yellow) | Intermediate risk |
| 100–1000 | D (orange) | High risk |
| > 1000 | E (red) | Very high risk |
| Sampling Site | Number of Tubes | MPN Index per Tubes 100 ml | Category and Color, Code Scheme | Remark | ||
| 10 ml | 1 ml | 0.1 ml | ||||
| D1 | 5 | 4 | 2 | 220 | D (orange) | High risk |
| D2 | 5 | 4 | 3 | 280 | D (orange) | High risk |
| D3 | 5 | 5 | 4 | 920 | E (red) | Very high risk |
| Sampling Site | Number of Tubes | MPN Index per Tubes 100 ml | Category and Color, Code Scheme | Remark | ||
| 10 ml | 1 ml | 0.1 ml | ||||
| D1 | 5 | 4 | 2 | 220 | D (orange) | High risk |
| D2 | 5 | 4 | 3 | 280 | D (orange) | High risk |
| D3 | 5 | 5 | 4 | 1600 | E (red) | Very high risk |
| Sampling Site | Number of Positive Tubes | ||
| 10 ml | 1 ml | 0.1 ml | |
| D1 | ++++ | ++ | + |
| D2 | ++++ | ++ | ++ |
| D3 | +++++ | +++ | +++ |
| Note: +: number of tubes which show indicating of coliform bacteria. | |||
| Sampling Site | Measured Parameter | Results | WHO Standards/PNWQS | |
| Highest Desirable | Maximum Desirable | |||
| D1 | Lead (mg/L) | Less than 0.01b | 0.01 | 0.01 |
| D2 | Less than 0.01b | 0.01 | 0.01 | |
| D3 | Less than 0.01b | 0.01 | 0.01 | |
| D1 | Mercury (mg/L) | Less than 0.01b | 0.001 | 0.001 |
| D2 | Less than 0.01b | 0.001 | 0.001 | |
| D3 | Less than 0.01b | 0.001 | 0.001 | |
| Note: b: method detection limit. | ||||
