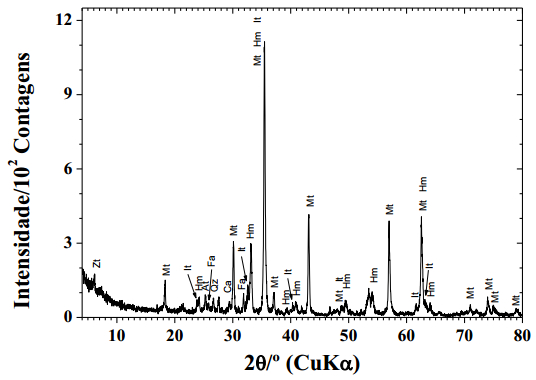
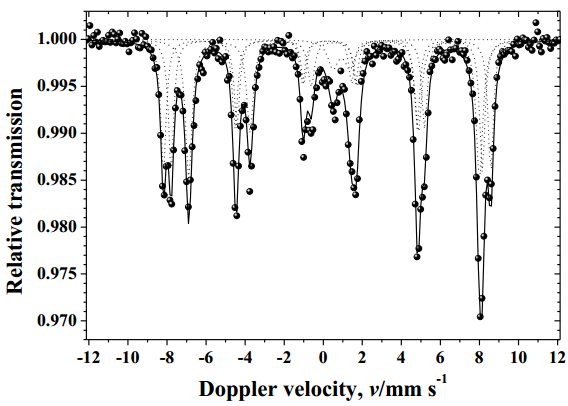
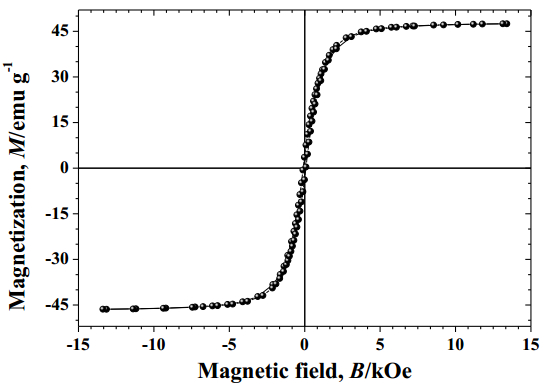
Biodiesel is an interesting alternative fuel for complementing or even completely replacing the mineral diesel. It is industrially obtained through the transesterification reaction of triacylglycerol in bio-oils with alcohol of short molecular chain, to produce the corresponding mixture of esters of fatty acids (biodiesel). Mineral rejects from mining usually constitute a major environmental and economic problem. Herein, it is described the study devoted to evaluate the chemical efficiency of the transesterification reaction of triacylglycerols in soybean oil with methanol, catalyzed by a material based on the magnetic fraction from rejects of a phosphate ore being commercially exploited in Tapira, Minas Gerais, Brazil. The magnetite-containing material from those mining tailings was used to form a new heterogeneous catalyst, by first mixing it with a commercial synthetic calcium oxide. The mixture was then heated at 200 ℃ for 4 h. The magnetic, crystallographic and 57Fe hyperfine structures of the resulting catalyst were assessed by VSM magnetometer, X-ray diffraction and 57Fe Mössbauer spectroscopy, respectively. The transesterification reaction was performed at 65 ℃, at a molar ratio methanol:oil 30:1. The chemical yields in esters for this heterogeneously catalyzed transesterification was 99 ± 1 mass%, through a reaction completed in 135 ± 30 min. The reaction catalyzed by the sole magnetic fraction, without CaO, did not produce any esters even after 24 h reaction; the pure CaO catalyst yielded 84 ± 10 mass% esters, after reaction completion, which took 128 ± 16 min. The magnetic fraction with CaO was found to act synergically on the transesterification reaction. From the technological, economic and environmental points of view, these results strongly evidence the real viability of using this magnetic fraction-CaO catalyst, to produce biodiesel.
1.
Introduction
DFC has captivated a lot of consideration across various analysis and engineering disciplines, particularly in modelling [1], neural networks [2] and image encryption [3]. The developing approach portraying real-world problems have been exhibited to be helpful in numerical devices to analyze, comprehend and predict the nature within humankind live [4,5,6,7,8,9,10]. In 1974, Daiz et al. [11] introduced the idea of DFC and composed it with an infinite sum. Later on, in 1988, Gray et al. [12] extended this concept and implemented it on the finite sum. This concept is known as the nabla difference operator in the literature. Atici and Eloe [13] proposed the theory of fractional difference equations, although the practical implementation is presented in [14]. Yilmazer [15] proposed discrete fractional solution of a nonhomogeneous non-Fuchsian differential equations. Yilmazer and Ali [16] derived the discrete fractional solutions of the Hydrogen atom type equations. Many researchers' focus is directed towards modeling and analysis of various problems in bio-mathematical sciences. This field demonstrates several distinguished kernels depending on discrete power law, discrete exponential-law and discrete Mittag-Leffler law kernels which correspond to the Liouville-Caputo, Caputo-Fabrizio and the Atangana-Baleanu nabla(delta) difference operators generalized ℏZ time scale [17,18,19].
Numerous utilities have been developed via DFC such as the solution of fractional difference equations and discrete boundary value problems are proposed in terms of new mathematical techniques [20,21,22,23]. Therefore, the conventional methodology of DFC have some intriguing and less-acknowledged opportunities for modelling. DFC is proposed to depict the customary practice of time scale analysis, with discussing its numerical approximations in ˇℏZ. Furthermore, we observe that ˇℏ-discrete fractional calculus is tremendously momentous in applied sciences and can also address the requirements of synchronous operation of various mechanisms, see [24,25,26].
Among the computational models formulated in fractional calculus, discrete AB-fractional operators, which is a universal operator of fractional calculus that has been traditionally employed to develop modern operators and their characterizations have been proposed in research article [27,28]. Moreover, DFC has been theoretically presented more by introducing and analyzing discrete forms of these fractional operators [13]. Here, we intend to find the discrete fractional inequalities analogous to fractional operators having ℏ-discrete Mittag-Leffler kernels, encompassing and simplifying these operators in such a manner as to recuperate certain appropriate traits such as discrete inequalities for AB-fractional sums.
Mathematical inequalities [29,30,31,32,33,34,35,36,37,38] initially alluded to adjust, harmony, and coordination. Until modern times, refinements of inequalities were characterized as invariance to change [39,40,41,42,43]. Physics comprehends fractional inequalities as predictability, while Psychology accentuates that inequality is the trait of magnificence and art [44].
Numerous investigations have been directed on fractional inequalities in the natural science [45], engineering sciences, see [41,46,47,48] and the references cited therein. Landscapes, structures, and mechanical equipment all demonstrate inequalities attributes. Therefore, we intend to find the discrete version of the Grüss type and some further connected modifications by the ℏ-discrete AB-fractional sums depending on ℏ-discrete generalized Mittag-Leffler kernel. This stands as an inspiration for the current paper. The intensively investigated Grüss inequality can be presented as follows:
Theorem 1.1. (See [49]) Let F,G:[c,d]→R be two positive functions such that α≤F(x)≤A and β≤G(x)≤B for all x∈[c,d] and α,β,A,B∈R. Then
where the constant 1/4 can not be improved.
The Grüss inequality Eq (1.1) has been broadly and intensely investigated in engineering and applied analysis, and various developed consequences have been acquired so far. Nevertheless, the prevalent existence of Grüss inequality in scientific fields is not in direct proportion to the consideration it has acknowledged. In application viewpoint, practically all mechanical structures are found to have inequality Eq (1.1), and the vast majority of them have the qualities of discrete and continuous fractional operators [50,51,52,53,54,55,56,57,58,59,60,61,62,63].
Inspired by the excellent dynamical properties of ℏ-discrete AB-fractional sums differences formulation [64], the limitations of fractional calculus can be ameliorated via discrete and continuous state-of-the-art techniques for effective information chaotic map applications, that can be inferred as a generalization of nonlocal/nonsingular type kernels. These investigations promote further sum/difference operators and related inequalities. It is our aim in this investigation to explore the discrete version of the Grüss type and certain other associated variants with some traditional and forthright inequalities in the frame of ℏ-discrete AB-fractional sums. We also would like to mention that besides these variants, several other intriguing generalizations are derived. The comparison of Grüss type with other discrete fractional calculus frameworks is currently under investigation. Finally, two examples are presented that correlate with some well-known inequalities in the relative literature and with the proposed strategy.
2.
Preliminaries on discrete fractional calculus
In this section, we evoke some basic ideas related to fractional operator, discrete generalized Mittag Leffler functions and the time scale calculus, see the detailed information in [13]. For the sake of simplicity, we use the notation, for c,d∈R and ℏ>0, Nc,ℏ={c,c+ℏ,c+2ℏ,...} and Nd,ℏ={d,d+ℏ,d+2ℏ,...}.
2.1. Basics on delta and nabla ℏ-factorials
Definition 2.1. ([65])The backward difference operator of a function F on ℏZ is stated as
where ρℏ(t)=t−ℏ denotes the backward jump operator. Also, the forward difference operator of a function F on ℏZ is stated as
where σℏ(t)=t+ℏ denotes the forward jump operator.
Definition 2.2. ([65]) (ⅰ) For any t,α∈R and ℏ>0, the delta ℏ-factorial function is stated as
where Γ denotes the Euler gamma function. For ℏ=1, then t(α)=Γ(t+1)Γ(t+1−α). Also, the division by a pole leads to zero.
(ⅱ) For any t,α∈R and ℏ>0, the nabla ℏ-factorial function is stated as
For ℏ=1, we observe that t(α)=Γ(t+α)Γ(t).
Lemma 2.3. ([64]) Let t∈T=Nc,ℏ, then for all t∈Tι, we obtain
Lemma 2.4. ([66]) For the time scale T=Nc,ℏ then the nabla Taylor polynomial
2.2. Nabla ℏ-discrete Mittag-Leffler function
Now we present the concept of nabla ℏ-discrete Mittag-Leffler function which is introduced by [6].
Definition 2.5. ([6]) Let α,ϱ,Ω∈C having ℜ(α)>0 such that λ∈R with |λℏα|<1, then the nabla discrete Mittag-leffler function is defined
For ϱ=1, we have
The following remark illustrates the strengthening properties why ℏZ is important.
Remark 1. In view of ℏZ:
Ⅰ. letting ℏ=1, we attain the nabla discrete Mittag-Leffler function stated in [67,68].
Ⅱ. letting 0<ℏ<1, the interval of convergence to which λ lies. Observe that, when ℏ↦0, then α∈(0,1). Moreover, when ℏ↦1 guarantee convergence for λ=−α1−α,α∈(0,12).
For further investigation of the discrete Mittag-Leffler function we refer the reader to [4].
2.3. Left and right delta fractional sums on ℏZ
Definition 2.6. ([26]) For some ι∈N,α>0 and let d=c+ιℏ. Assume that a function F be defined on T=Nc,ℏ∩Nd,ℏ. Then the delta ℏ-fractional sums in the left and right case are defined as follows
and
respectively.
2.4. Left and right nabla fractional sums on ℏZ
Definition 2.7. ([6,66]) Assume that ℏ>0 and the backward jump operator is ρ(x)=x−ℏ. A function F:Nc,ℏ↦R is said to be nabla ℏ-fractional sum of order α, if
Also, the nabla right ℏ-fractional sum of order α>0(ending at d) for F:Nd,ℏ↦R is described as follows
2.5. Nabla ℏ-fractional differences with ℏ-discrete Mittag Leffler kernels
Now, we demonstrate the some new concepts which we will be utilized for proving coming results of this paper, see [4]. Also, we use the notation, λ=−α1−α and ρ(x)=x−ℏ.
Definition 2.8. ([64]) For α∈[0,1],ℏ>0 with |λℏα|<1 and let F be a function defined on Nc,ℏ∩d,ℏN with c<d such that c≡d(modℏ), then the left nabla ABC-fractional difference (in the sense of Atangana and Baleanu) is described as
and in the left Riemann sense by
Definition 2.9. ([64]) For 0<α<1 and let the left ℏ-fractional sum concern to (ABRcˆ∇αℏF)(x) defined on Nc,ℏ is stated as follows
The right ℏ-fractional sum is defined on d,ℏN by
3.
Discrete Grüss type inequalities
In this section, we present a different concept of Grüss type inequalities, which consolidates the ideas of ℏ-discrete AB-fractional sums.
Theorem 3.1. Let α∈(0,1) and let F be a positive function on Nc,ℏ. Suppose that there exist two positive functions ϕ1,ϕ2 on Nc,ℏ such that
Then, for x∈{c,c+ℏ,c+2ℏ,...}, one has
Proof. From Eq (3.1), for θ,λ∈Nc,ℏ, we have
Therefore,
Taking product both sides of Eq (3.4) by 1−αB(α,ℏ)(1−α+αℏ), we get
Replacing λ by t in Eq (3.5) and conducting product both sides by α(x−ρ(t))α−1ℏB(α,ℏ)Γ(α), we have
Summing both sides for t∈{c,c+ℏ,c+2ℏ,...}, we get
Adding Eqs (3.5) and (3.6), we have
arrives at
Taking product both sides of Eq (3.7) by 1−βB(β,ℏ)(1−β+βℏ), we have
Also, replacing θ by ˉt in Eq (3.8) and conducting product both sides by β(x−ρ(ˉt))β−1ℏB(β,ℏ)Γ(β), we have
Summing both sides for ˉt∈{c,c+ℏ,c+2ℏ,...}, we get
Adding Eqs (3.8) and (3.9), then in view of Definition 2.9, yields the inequality Eq (3.2). This completes the proof.
Some special cases which can be derived immediately from Theorem 3.1.
Choosing ℏ=1, then we attain a new result for discrete AB-fractional sum.
Corollary 1. Let α∈(0,1) and let F be a positive function on Nc. Suppose that there exist two positive functions ϕ1,ϕ2 on Nc such that
Then, for x∈{c,c+1,c+2,...}, one has
Theorem 3.2. Let α,β∈(0,1) and let F and G be two positive functions on Nc,ℏ. Suppose that Eq (3.1) satisfies and also one assumes that there exist two positive functions Ω1,Ω2 on Nc,ℏ such that
Then, for x∈{c,c+ℏ,c+2ℏ,...}, one has
Proof. To prove Eq (M1), from Eqs (3.1) and (3.12), we have for λ,θ∈Nc,ℏ that
Therefore,
Taking product both sides of Eq (3.17) by 1−αB(α,ℏ)(1−α+αℏ), we get
Moreover, replacing λ by t in Eq (3.17) and conducting product both sides by α(x−ρ(t))α−1ℏB(α,ℏ)Γ(α), we have
Summing both sides for t∈{c,c+ℏ,c+2ℏ,...}, we get
Then, we have
Taking product both sides of Eq (3.16) by 1−βB(β,ℏ)(1−β+βℏ), we have
Further, replacing θ by ˉt in Eq (3.19) and conducting product both sides by β(x−ρ(ˉt))β−1ℏB(β,ℏ)Γ(β), we have
Summing both sides for ˉt∈{c,c+ℏ,c+2ℏ,...}, we get
Adding Eqs (3.19) and (3.21), we conclude the desired inequality Eq (M1).
To prove Eqs (M2)–(M4), we utilize the following inequalities:
Some special cases which can be derived immediately from Theorem 3.2.
Choosing ℏ=1, then we attain a new result for discrete AB-fractional sums.
Corollary 2. Let α,β∈(0,1) and let F and G be two positive functions on Nc. Suppose that Eq (3.1) satisfies and also one assumes that there exist two positive functions Ω1,Ω2 on Nc such that
Then, for x∈{c,c+1,c+2,...}, one has
Theorem 3.3. Let α,β∈(0,1) and let F and G be two positive functions on Nc,ℏ with p,q>0 satisfying 1p+1q=1. Then, for x∈{c,c+ℏ,c+2ℏ,...}, one has
Proof. According to the well-known Young's inequality:
setting a=F(θ)G(λ) and b=F(λ)G(θ),θ,λ>0, we have
Taking product both sides of Eq (3.24) by 1−αB(α,ℏ)(1−α+αℏ), we have
Moreover, replacing λ by t in Eq (3.25) and conducting product both sides by α(x−ρ(t))α−1ℏB(α,ℏ)Γ(α), we have
Summing both sides for t∈{c,c+ℏ,c+2ℏ,...}, we get
Adding Eqs (3.24) and (3.27), we get
In view of Definition 2.9, yields
Again, taking product both sides of Eq (3.29) by 1−βB(β,ℏ)(1−β+βℏ), we have
Further, replacing θ by ˉt in Eq (3.29) and conducting product both sides by β(x−ρ(ˉt))β−1ℏB(β,ℏ)Γ(β), we have
After summing the above inequality Eq (3.31) both sides for ˉt∈{c,c+ℏ,c+2ℏ,...}, yields the desired assertion Eq (M9).
The remaining variants can be derived by adopting the same technique and accompanying the selection of parameters in Young inequality.
Repeating the foregoing argument, we obtain Eqs (M10)–(M12).
(I) Letting ℏ=1, then we attain a result for discrete AB-fractional sums.
Corollary 3. Let α,β∈(0,1) and let F and G be two positive functions on Nc with p,q>0 satisfying 1p+1q=1. Then, for x∈{c,c+1,c+2,...}, one has
Example 3.4. Let α,β∈(0,1) and let F and G be two positive functions on Nc,ℏ with p,q>0 satisfying p+q=1. Then, for x∈{c,c+ℏ,c+2ℏ,...}, one has
Proof. The example can be proved with the aid of the weighted AM–GM inequality with the same technique as we did in Theorem 3.3 and utilizing the following assumptions:
Example 3.5. Let α∈(0,1) and let F and G be two positive functions on Nc,ℏ with p,q>1 satisfying 1p+1q=1. Let
Then, for x∈{c,c+ℏ,c+2ℏ,...}, one has
Proof. From Eq (3.34) and the inequality
then we can write as,
Taking product both sides of Eq (3.36) by 1−αB(α,ℏ)(1−α+αℏ), we have
Replacing θ by t in Eq (3.36) and conducting product both sides by α(x−ρ(t))α−1ℏB(α,ℏ)Γ(α), we have
Summing both sides for t∈{c,c+ℏ,c+2ℏ,...}, we get
Adding Eqs (3.37) and (3.39), yields
on the other hand, it follows from γΥ>0 and
that
then from Eqs (3.40) and (3.42), we obtain,
Which implies (i). By some change of (i), analogously, we get (ii) and (iii).
4.
Conclusions
Unlike some known and established inequalities in the literature, the Grüss type inequalities have been presented via the ℏ-discrete AB-fractional sums with different values of parameters on the domain ℏZ that can be implemented to solve the qualitative properties of difference equations. Our consequences can be applied to overcome the obstacle of obtaining estimation on the explicit bounds of unknown functions and also to extend and unify continuous inequalities by using the simple technique. Several novel consequences have been derived by the use of discrete ℏ-fractional sums. The noted consequences can also be extended to the weighted function case. Certainly, the case ℏ↦1 recaptures the outcomes of the discrete AB-fractional sums. For indicating the strength of the offered fallouts, we employ them to investigate numerous initial value problems of fractional difference equations.
Acknowledgments
Authors are grateful to the referees for their valuable suggestions and comments.
Conflict of interest
The authors declare no conflict of interest.













 DownLoad:
DownLoad: