Citation: Shota Tobaru, Ryuto Shigenobu, Foday Conteh, Naomitsu Urasaki, Abdul Motin Howlader, Tomonobu Senjyu, Toshihisa Funabashi. Optimal operation method coping with uncertainty in multi-area small power systems[J]. AIMS Energy, 2017, 5(4): 718-734. doi: 10.3934/energy.2017.4.718
| [1] | Bitian Wu . Day ahead scheduling model of wind power system based on fuzzy stochastic chance constraints—considering source-load dual-side uncertainty case. AIMS Energy, 2025, 13(3): 471-492. doi: 10.3934/energy.2025018 |
| [2] | Sameer Thakare, Neeraj Dhanraj Bokde, Andrés E. Feijóo-Lorenzo . Forecasting different dimensions of liquidity in the intraday electricity markets: A review. AIMS Energy, 2023, 11(5): 918-959. doi: 10.3934/energy.2023044 |
| [3] | Gerardo Guerra, Juan A. Martinez Velasco . A virtual power plant model for time-driven power flow calculations. AIMS Energy, 2017, 5(6): 887-911. doi: 10.3934/energy.2017.6.887 |
| [4] | Vishal Chaudhary, Hari Mohan Dubey, Manjaree Pandit, Surender Reddy Salkuti . A chaotic Jaya algorithm for environmental economic dispatch incorporating wind and solar power. AIMS Energy, 2024, 12(1): 1-30. doi: 10.3934/energy.2024001 |
| [5] | Yan Li, Yaheng Su, Qixin Zhao, Bala Wuda, Kaibo Qu, Lei Tang . An electricity price optimization model considering time-of-use and active distribution network efficiency improvements. AIMS Energy, 2025, 13(1): 13-34. doi: 10.3934/energy.2025002 |
| [6] | Andrew A. Chien, Fan Yang, Chaojie Zhang . Characterizing curtailed and uneconomic renewable power in the mid-continent independent system operator. AIMS Energy, 2018, 6(2): 376-401. doi: 10.3934/energy.2018.2.376 |
| [7] | Gerardo Guerra, Juan A. Martinez-Velasco . Optimal sizing and operation of energy storage systems considering long term assessment. AIMS Energy, 2018, 6(1): 70-96. doi: 10.3934/energy.2018.1.70 |
| [8] | V. V. Thang, Thanhtung Ha . Optimal siting and sizing of renewable sources in distribution system planning based on life cycle cost and considering uncertainties. AIMS Energy, 2019, 7(2): 211-226. doi: 10.3934/energy.2019.2.211 |
| [9] | Chiara D’Alpaos, Michele Moretto . Do smart grid innovations affect real estate market values?. AIMS Energy, 2019, 7(2): 141-150. doi: 10.3934/energy.2019.2.141 |
| [10] | Dalong Guo, Chi Zhou . Potential performance analysis and future trend prediction of electric vehicle with V2G/V2H/V2B capability. AIMS Energy, 2016, 4(2): 331-346. doi: 10.3934/energy.2016.2.331 |
There are many isolated islands in Japan which are not connected to the main grid. The power systems in these islands mainly depend on diesel generators (DGs), which is not economically viable. However, these remote islands are rich in natural resources and have good geographical locations that make them suitable for renewable energy generation. Therefore, renewable energy systems (RESs) such as photovoltaic (PV) and wind generator (WG) systems have been introduced [1,2,3,4,5,6,7,8]. However, generated power by RESs varies according to the time and season as well as the weather conditions such as solar radiatoin and wind speed [9,10,11]. In case where PV and WG are introduced into small power systems, the power systems are affected because the rate of RESs to load demand is relatively large. Also, there are cases wherein the operational plan created on day-ahead cannot work because of forecasting error. In such scenario, the operational plan should be revisited based on new weather information. As a measure against the generated power fluctuation of RESs, battery energy storage system (BESSs) are often utilized. BESSs are very effective system because they allow the generated power fluctuation to be suppressed by charging and discharging [12,13,14,15,16].
Moreover, demand response (DR) programs are attracting much attention these days [17,18,19,20,21,22,23,24,25]. DR programs enable Power Companies to control the load consumption of customers, and they are divided into time-based and incentive-based programs. Several literatures have developed DR models [19,20,21,22]. Furthermore, the effectiveness of DR has been investigated and the benefit it makes to the supply-side by using demand-side resources [22,23,24,25]. However, this paper utilizes real-time pricing (RTP) as a time-based programs to correspond to the fluctuation of powers generated by RESs. RTP encourages customer to increase or reduce the load consumption by varying electricity prices.
With the power system reform in Japan, the power markets transactions are also increasing. In particular, spot (day-ahead) market, intraday hour-ahead market and forward market have been established by the Japan electric power exchange (JEPX). Day-ahead market is wherein power transaction is conducted based on the power generation and demand plan of next day, and hour-ahead market is wherein you adjusts the plan in intraday. In the forward market, the power transaction is performed on fixed price for the relatively far future [26]. These markets make it possible to deal with uncertainty related to the generated power fluctuation [27,28,29,30,31].
This paper presents the optimal operation method coping with the forecasting errors caused by the generated power of the RESs considering the reforecasting and re-planning, the RTP, and two kinds of power markets in multi-area small power systems. The purpose of this research is to indicate the cooperative optimal opration method for a group of isolated small power systems which have RESs and BESS to relieve a economical burden. Furthermore, the process of scheduling the plan that contains RTP and two kinds of power markets is presented, as a measure to cope with uncertainty of renewable energies. The ultimate goal of this study is to reduce the total operational cost for a group of the power systems.Two kinds of power markets are considered for power transactions in three small power systems. The power transactions for the next day are performed in the day-ahead market, and the power transactions in the hour-ahead market are conducted every 3 hours in focused day. However, reforecasing and re-planning are carried out at the same time to reduce forecasting error. Furthermore, the RTP is applied to level the load profiles by varying the electricity prices every hour. The proposed method has achieved to reduce the total operational cost of the multi-area small power systems by using the surplus power obtained through two kinds of power markets effectively even if the forecasting errors of the power generated by RESs and the load demand occur.
The rest of the paper is organized as follows. Section 2 describes the multi-area small power systems model and scenario-based method. The transactions in two mentioned markets and the RTP are discussed in Sections 3 and 4, respectively. In Section 5, the proposed operation method is explained in detail. Section 6 indicates the simulation results and discussion. Finally, conclusion and future work are given in Section 7.
The multi-area small power systems model assumed in this paper is illustrated in Fig. 1. It can be seen that each power system performs a power trading via power markets. Table 1 shows the installed capacity in each power system (PS). Furthermore, Fig. 2 shows the configuration of resources in the power system 1 (PS1) which includes two types of DG, PV, and BESS. The power generated by PV and load profile in PS1 are indicated by solid lines in Figs. 3(b) and 3(c). It is assumed that the hourly prediction data of demand, wind, and irradiance are obtained, and updated every 3 hours. However, uncertainties are considered by using scenario-based method. Fig. 3 shows normal distributions and the load demand and the power generated by PV. The forecasting error increases in proportion to time, and thus, the normal distributions for making scenario are assumed as shown in Fig. 3(a). In Figs. 3(b) and 3(c), the dotted lines represent the scenario examples of the load demand and the power generated by PV.
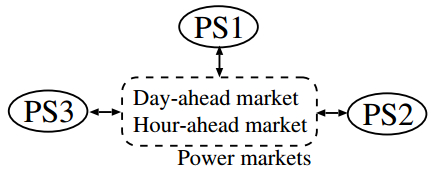 Figure 1. Multi-area small power systems model.
Figure 1. Multi-area small power systems model.| PS1 | PS2 | PS3 | |
| Max Load(MW) | 1.0 | 0.85 | 0.85 |
| DG1(0.5MW/unit) | 1 | 1 | 1 |
| DG2(0.35MW/unit) | 2 | 1 | 1 |
| PV(MW) | 0.5 | 0.5 | 0.5 |
| WG(MW) | – | 0.5 | 0.75 |
| BESS((0.5MW/5.0MWh)/unit) | 1 | 1 | 1 |
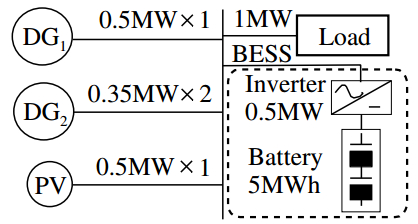 Figure 2. Configuration of Power System 1 (PS1).
Figure 2. Configuration of Power System 1 (PS1).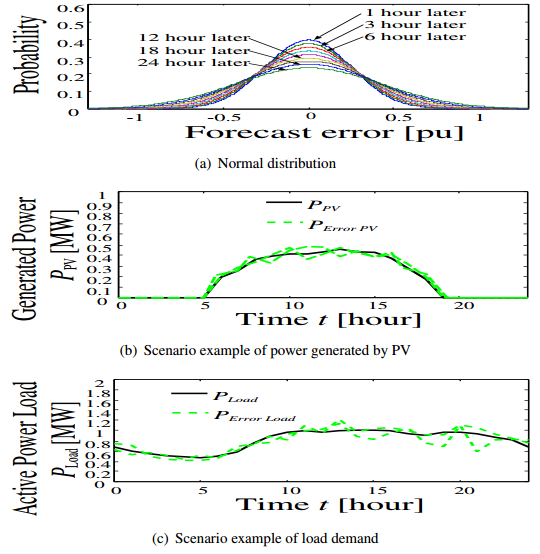 Figure 3. Making scenario.
Figure 3. Making scenario.As mentioned earlier, the day-ahead and hour-ahead markets are considered. This paper determines the bidding price and bidding power by using fuzzy inference. Furthermore, the membership function used in bidding is shown on the following equations.
| SFse=ksePdl (Pdl≤0) | (3.1) |
| CRhse=CRhse+SFse | (3.2) |
| CRlse=CRlse+SFse | (3.3) |
| MSse=(PRma−CRlse)CRhse−CRlse (CRlse<PRma≤CRhse) | (3.4) |
where, SFse is shift function for selling; kse is coefficient; Pdl is the difference between load demand and generation output (expected surplus power); CRhse is maximum criterion price; CRlse is minimum criterion price; MSse is membership function; PRma is the trading price. First, the validities obtained from membership function are evaluated as shown in Figs. 4(a) and 4(b) and then, the bidding price and bidding power are determined in Fig. 4(c) by using center-of-gravity method. As a decision criterion for the bidding price and bidding power, the minimum difference between the bidding powers in each PS is employed. Moreover, these equations are:
| min:3∑PS=1PPSbid(t) | (3.5) |
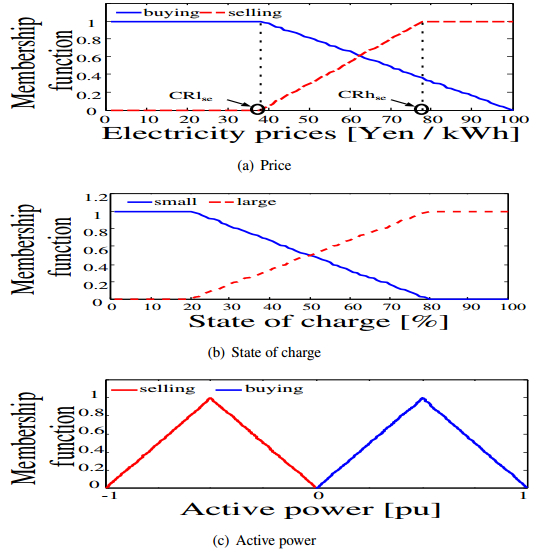 Figure 4. Membership functions.
Figure 4. Membership functions.| PPSdl(t)=kl×(P′PSload(t)−N∑i=1PPSDGi(t))+kBE×MS′PSBE×PPSBE | (3.6) |
| PPSbid(t)=MS′PSse×PPSdl(t) | (3.7) |
where PPSbid(t) is the bidding power in PS th power system at time t; PPSdl(t) is the difference between load demand and generation output (expected surplus power) in PS th power system at time t; kl is the weight for load demand; P′PSload is the difference between load demand and RES output in PS th power system at time t; N is the number of DG introduced into power systems; PPSDGi(t) is the output power of the i th DG in PS th power system at time t; kBE is the weight for the state of charge (SOC); MS′PSBE is the validity of SOC in PS th power system; PPSBE is the charging and discharging power of BESS in PS th power system at time t; MS′PSse is the validity of the expected surplus power.
The sigmoid function is utilized as a demand response model of customer to the electricity price. The load demands are levelized by the RTP shown in Fig. 5 and Eq. (4.1). The equation of demand amount to electricity price is:
| hrtp(t)=11+exp(PRrtp(t)−SF1)+SF2 | (4.1) |
| ΔPLoad(t)=hrtp(t)×(P′Load(t)−T∑t=1P′Load(t)T) | (4.2) |
| PRTPLoad(t)=PLoad(t)+ΔPLoad(t) | (4.3) |
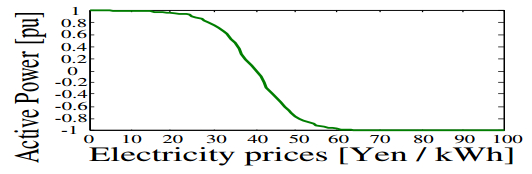 Figure 5. Sigmoid function.
Figure 5. Sigmoid function.where, hrtp(t) is the variation rate of load demand at time t; PRrtp(t) is the set price at time t; SF1 is the left-right shift coefficient; SF2 is the top-bottom shift coefficient; ΔPLoad(t) is the response amount at time t; P′Load(t) is the difference between load demand and RES output at time t; PRTPLoad(t) is the difference between load demand and RES output at time t after RTP. The response amounts are determined based on this sigmoid function.
The flow of operational method proposed in this paper is shown in Fig. 6. Planning the operational plan and bidding to the day-ahead market are performed by using the forecasting load in the preceding day. In the forecast day, the reforecasting and re-planning, RTP, and transactions in the hour-ahead market are performed every 3 hour by calculating the shortage and surplus power caused by the forecasting errors.
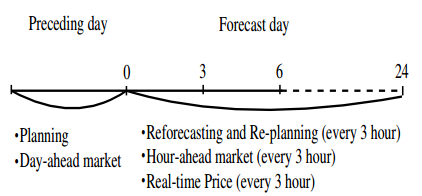 Figure 6. Operation scheduling flow.
Figure 6. Operation scheduling flow.This section describes the objective function, constraints and optimization method to reduce the total operational cost of multi-power systems.
The objective function is to minimize the total operational cost of multi-power systems in this paper. The start/stop and output plan for the DG, the charging and discharging plan for the BESS, the demand response plan, and interchanging power are determined such that the objective function is minimized. Furthermore, the objective function and the total cost of multi-power systems are given by
| min : TC=100∑s=1ps(TCPS1+TCPS2+TCPS3) | (5.1) |
| TCPS=24∑t=1[N∑i=1(Fi(t)(PDGi(t))+SUi(t)+SDi(t))+CBESS+Cday(t)+Chour(t)] | (5.2) |
where, ps is the probability of error; s is the scinario number; TC is the total cost; Fi(t)(PDGi(t)) is the fuel cost [Yen] of the i th DG at time t; PDGi(t) is the output power [kW] of the i th DG at time t; SUi(t) and SDi(t) are the starting and stopping cost [Yen] of the i th DG at time t; CBESS is the energy cost [Yen] of BESS used in one day; Cday and Chour are trading prices in the day-ahead and hour-ahead markets, respectively.
Furthermore, fuel cost is decided by:
| Fi(PDGi)=Q×PDGi×PRcQc×ηi | (5.3) |
where, Q is the heat value, it has been considered in this paper by 9 970 [kJ/kW]; PRc is the fossil fuel cost which is considered as 90 000 [Yen/kL]; Qc is the heat value of fossil fuel (heat value of fossil fuel has taken by 41.9×106 [kJ/kL]); ηi(t) is the generating efficiency of the i th DG at time t.
The total amount of outputs of each DG, the charging and discharging power of BESS and the interchanging power should be equal to load demand at every time as follows:
| N∑i=1PDGi(t)+PBESS(t)+PRe(t)+Pday(t)+Phour(t)=PRTPLoad(t) | (5.4) |
where, PRe(t) is the output [kW] of RESs at time t; PBESS(t) is the charging and discharging power [kW] of the BESS at time t; Pday(t) and Phour(t) are the trading power [kW] in the day-ahead and hour-ahead markets, respectively. PLoad(t) is the load demand [kW] at time t.
The controllable load PRTPLoad after RTP must be within the limit of P′minLoad and P′maxLoad every time as follows:
| P′minLoad(t)≤PRTPLoad(t)≤P′maxLoad(t) | (5.5) |
where, PRTPLoad is the modified load demand by RTP [kW]. In addition, P′maxLoad and P′minLoad represent the maximum and minimum load demand [kW], respectively. P′minLoad and P′maxLoad are:
| P′maxLoad(t)=P′Load(t)+PrtpPRTPLoad(t) | (5.6) |
| P′minLoad(t)=P′Load(t)−PrtpPRTPLoad(t) | (5.7) |
where, Prtp is the response power [kW]; P′Load is the load demand before RTP [kW]. Furthermore, the load consumption after RTP should be equal to the load consumption before RTP as follows:
| Wre(T)=|∫T0Pin(t)dt−∫T0Pde(t)dt|=0 | (5.8) |
where, Wre(T) is the controlled load consumption [kW]; Pin(t) is the increased load power [kWh]; Pde(t) is the decreased load power [kW] as follows:
| Pin(t)=PRTPLoad(t)−P′Load, (PRTPLoad≥P′Load) | (5.9) |
| Pde(t)=P′Load(t)−PRTPLoad, (P′Load≥PRTPLoad) | (5.10) |
The generation output of each DG must be limited within a specified range as follows:
| PDGi(t)≤PmaxDGi | (5.11) |
where, PmaxDGi and the maximum output power [MW] of DGi. Furthermore, the spinning reserve must be installed in each DG to cope with load demand fluctuation as follows:
| PDGi(t)+Prei≤PmaxDGi | (5.12) |
where, Prei is the spinning resereve [kW] of the i th DG which is considered as 10[%].
The charging and discharging power of BESS need to be within PminBESS and PmaxBESS as follows:
| PminBESS≤PBESS(t)≤PmaxBESS | (5.13) |
where, PminBESS and PmaxBESS are the maximum charging power [kW] and maximum discharging power of the BESS. Furthermore, the BESSs can be charged and discharged within the limit ranges of SOCmin and SOCmax as follows:
| SOCmin≤SOC(t)≤SOCmax | (5.14) |
where, SOCmin and SOCmax are the minimum and maximum SOC [%] for BESS at time t, it is considered by 20% and 80% to cope with the output fluctuated of RESs.
In this paper, the unit commitment for the DG, the charging and discharging plan for the BESS, and the trading power are determined by using this optimization method, Tabu-search. The optimization flowchart is shown in Fig. 7.
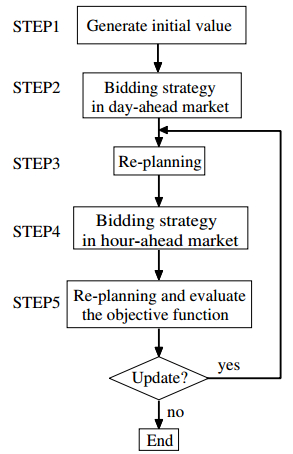 Figure 7. Flow chart of proposed method.
Figure 7. Flow chart of proposed method.STEP1: The forecasting data of the load demand and the power generated by PV and WG are inputted.
STEP2: The unit commitment plans of DGs are determined by the forecasting data in each power system, and then determine the bidding power to the bidding price in day-ahead market by calculating the shortage and surplus power from the determined plan.
STEP3: The contract processing is conducted from the bidding price and power in day-ahead market, and the electricity is traded by determining the contract price and power. In addition, the operational plan is created considering the day-ahead market.
STEP4: The reforecasting and re-planning are conducted, and calculate the shortage and surplus power caused by the forecasting error of the power supply and demand. Furthermore, the bidding power to the bidding price in hour-ahead market is determined by calculating the shortage and surplus power from the determined plan.
STEP5: The operational plan is determined considering the hour-ahead market. Furthermore, if forecasting data is updated, the algorithm proceeds to STEP3, or it ends.
To confirm the effectiveness of the proposed method, this Section makes a comparison between three cases: the operational plan is determined without considering two kinds of power markets and the RTP in Case 1. Case 2 adresses the day-ahead market and RTP, and Case 3 looked at proposed method, the operational plan is determined by considering the reforecasting and re-planning, the day-ahead and hour-ahead markets, and the RTP. In this paper, the operational plan of one day is determined, and it is assumed that forecasting data is updated every 3 hour. Furthermore, the uncertainty regarding the power supply-demand is considered by applying scenario-based method and using 100 kinds of scenarios with respect to the load demand and the output of RESs. Three cases are operated in each scenario, and the method for confirming the effectiveness is to calculate the expectation value of the operational cost.
The simulation results of three cases are illustrated in Figs. 8, 9 and 10, respectively. It can be seen from Fig. 8 that the number of starts and stops of the DGs in PS2 are many at morning, while that of in PS3 are many at night. This is because the DGs are required to start and stop to cope with forecasting error of the load demand and power generated by RESs. In particular, the SOC reaches 80% after 16:00 in the PS3 because the surplus power occurred in large amount caused by the forecasting error. Therefore, the DGs start and stop frequently because the BESS cannot charge. From Figs. 9 and 11(a), PS1 is obtained profit by selling electricity in day-ahead market. In PS2 and PS3, they meet the load demands in the forenoon by buying electricity in day-ahead market and charging and discharging of the BESSs. The results show that day-ahead market brings about reduction in the number of starts and stops of the DGs. At night, DG in PS3 unavoidably stopped because BESS cannot charge. Furthermore, in PS2 and PS3 in case 3, the forecasting errors of the load demand and the renewable energies are compensated by interchanging electricity through two kinds of power markets and RTP as shown in Figs. 9 and 11(b). It is clear from Figs. 8, 9 and 10 that the number of starts and stops of the DGs in proposed method is less than that of the DGs in Case 1 and Case 2. Fig. 12 shows the simulation results of RTP. The load demand is decreased when the electricity price is expensive, while it is increased when the electricity price is low as shown in Fig. 12. Thereby, it is accomplished to level the load demands in each PS. The expected values of the Fuel and operational costs in each case are listed in Table 2. It can be seen that the value of the proposed method has the lowest cost of three cases. Thus, the high-efficiency operation has been achieved, even when the forecasting error occur.
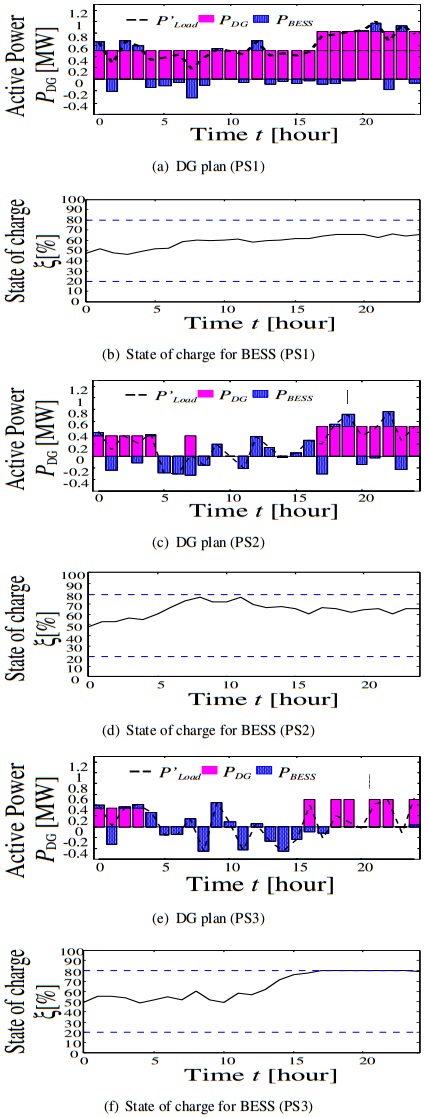 Figure 8. Simulation results of Case 1.
Figure 8. Simulation results of Case 1. Figure 9. Simulation results of Case 2.
Figure 9. Simulation results of Case 2.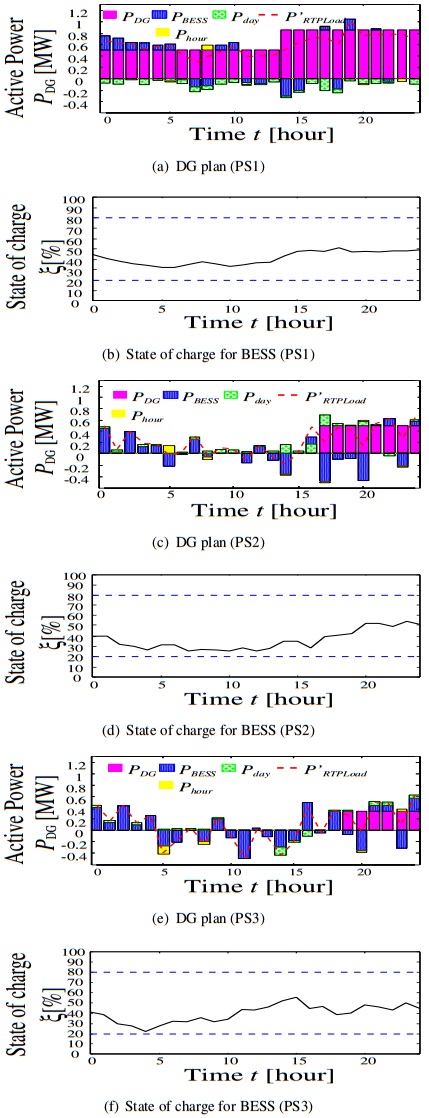 Figure 10. Simulation results of Case 3.
Figure 10. Simulation results of Case 3.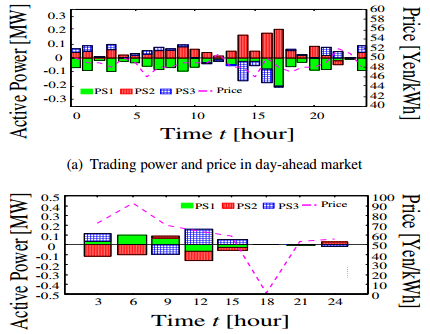 Figure 11. Simulation results for power markets.
Figure 11. Simulation results for power markets.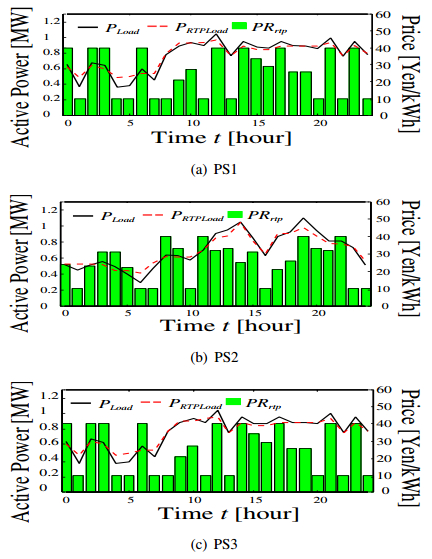 Figure 12. Simulation results of RTP.
Figure 12. Simulation results of RTP.| Case 1 | Case 2 | Case 3 | |
| RTP | without | with | with |
| Day-ahead market | without | with | with |
| Hour-ahead market | without | without | with |
| Fuel cost [Yen] | 2,810,100 | 2,168,100 | 1,738,900 |
| (100%) | (77.2%) | (61.9%) | |
| Operational cost [Yen] | 2,937,047 | 2,294,047 | 1,865,847 |
| (100%) | (78.1%) | (63.5%) |
In recent year, RES and BESS have been introducing into the power systems in isolated small islands in Japan because of its low economic cost as compared to DGs. However, the problem of uncertainty of renewable energies has a bad effect on the power systems, especially in the case of the small systems. therefore, as countermeasures towards the above problem, the process of creating the effective operational plan for RTP, power trading at the markets, and the unit commitment of DGs has been explained in this paper. Furthermore, the uncertainty of renewable energies is faithfully modeled in simulation by taking into account that forecast errors are increased in proportion to the time.
This paper focuses on determining the optimal operation plan capable of coping with uncertainty regarding the power supply-demand by considering the reforecasting and re-planning, the day-ahead and hour-ahead markets, and RTP. By applying RTP, it was able to create the operational plan which can cope with the output variation of RESs by using the DR ability of customers, and to effectively use energies. The power markets enable to transact the shortage and surplus power caused by the output variations of RESs with neighborhood islands. Furthermore, the optimal amount of trading power were determined by fuzzy inference in this paper. The proposed method utilized renewable energies effectively by suppressing the surplus and shortage powers caused by a forecasting error. Fortunately the proposed method was able to reduce the total operational cost of the multi-area small power systems even if the forecasting errors relating the power supply-demand occurred.
In this work, the optimum installed capacity of DGs, RESs and BESSs are not considered. However, optimum installed capacity is required to be considered for coping with uncertainty regarding the power supply-demand with increase in RESs. Thus, this study can be extended into the optimal operation method considering the optimum installed capacity of each system for the future research.
All authors declare on conflicts of interst in this paper.
| [1] |
Amenedo JLR, Arnalte S, Burgos JC, et al. (2002) Automatic generation control of a wind farm with variable speed wind turbines. IEEE T Energy Conver 17: 279–284. doi: 10.1109/TEC.2002.1009481

|
| [2] | Senjyu T, Hayashi D, Sakamoto Y, et al. (2005) Generating power leveling of renewable energy for small power system in isolated island. IEE Japan 125: 1209–1215. |
| [3] | Senjyu T, Tokudome M, Yona A, et al. (2009) A Frequency Control Approach by Decentralized Controllable Loads in Small Power Systems. IEE Japan 129: 1074–1080. |
| [4] | Senjyu T, Kikunaga T, Tokudome M, et al. (2009) Coordinate Control ofWind Turbine and Battery in Wind Turbine Generator System. IEE Japan 129: 653–660. |
| [5] | Kurohane K, Senjyu T, Yona A, et al. (2010) A High Quality Power Supply System with DC Smart Grid. 2010 IEEE PES Transmission and Distribution Conference and Exposition. |
| [6] | Ogimi K, Kamiyama S, Palmer M, et al. (2013) Optimal OperationPlanning ofWind Farm Installed BESS Using Wind Power Forecast Data of Wind Turbine Generators Considering Forecast Error. Int J Emerg Electric Power Syst 14: 207–218. |
| [7] | Bracale A, Carpinelli G, Fazio AD, et al. (2015) Advanced, Cost-Based Indices for Forecasting the Generation of Photovoltaic Power. Int J Emerg Electric Power Syst 16: 195–206. |
| [8] | Shimoji T, Tahara H, Matayoshi H, et al. (2015) Comparison and Validation of Operational Cost in Smart Houses with the Introduction of a Heat Pump or a Gas Engine. Int J Emerg Electric Power Syst 16: 59–74. |
| [9] | MengyanW, HigaW, Yona A, et al. (2012) Optimal Operation of Power Systems with Power Players. 2012 International Conference on Renewable Energy Research and Applications (ICRERA). |
| [10] | Higa S, Mengyan W, Yona A, et al. (2013) Optimal Operation Method Considering Uncertainly of Renewable Energy and Load Demand in Micro-grids. The 5th International Conference on Advanced Power System Automation and Protection. |
| [11] | Higa S, Howlader AM, Shiroma Y, et al. (2014) Optimal Operation Method Considering Replanning and Uncertainly in Power Systems. The International Conference on Electrical Engineering 2014. |
| [12] |
Zheng Y, Dong ZY, Luo FJ, et al. (2014) Optimal Allocation of Energy Storage System for Risk Mitigation of DISCOs With High Renewable Penetrations. IEEE T Power Syst 29: 212–220. doi: 10.1109/TPWRS.2013.2278850

|
| [13] |
Zhang L, Li Y (2013) Optimal Energy Management of Wind-Battery Hybrid Power System With Two-Scale Dynamic Programming. IEEE T Sust Energy 4: 765–773. doi: 10.1109/TSTE.2013.2246875

|
| [14] |
Ahn SJ, Nam SR, Choi JH, et al. (2013) Power Scheduling of Distributed Generators Economic and Stable Operation of a Microtrid. IEEE T Smart Grid 4: 398–405. doi: 10.1109/TSG.2012.2233773

|
| [15] |
Zhao B, Zhang X, Chen J, et al. (2013) Operation Optimization of Standalone Microgrids Considering Lifetime Characteristics of Battery Energy StorageSystem. IEEE T Sust Energy 4: 934–943. doi: 10.1109/TSTE.2013.2248400

|
| [16] | He D, Tan Z, Harley RG, et al. (2012) Chance Constrained Unit Commitment With Wind Generation and Superconducting Magnetic Energy Storages. 2012 IEEE Power and Energy Society General Meeting. |
| [17] | Reddy SS, Abhyankar AR, Bijwe PR, et al. (2014) Co-optimization of Energy and Demand-Side Reserves in Day-Ahead Electricity Markets. Int J Emerg Electric Power Syst 15: 77–91. |
| [18] | Nguyen MY, Nguyen DM (2015) A Generalized Formulation of Demand Response under Market Environments. Int J Emerg Electric Power Syst 16: 217–224. |
| [19] |
Aalami HA, Moghaddam MP, Yousefi GR, et al. (2010) Demand response modeling considering Interruptible/Curtailable loads and capacity market programs. Appl Energy 87: 243–250. doi: 10.1016/j.apenergy.2009.05.041

|
| [20] | Andebili MR, Shen H (2017) Energy Management of End Users Modeling their Reaction from a GENCOs Point of View. 2017 International Conference on Computing, Networking and Communications (ICNC). |
| [21] |
Andebili MR (2016) Modeling nonlinear incentive-based and price-based demand response programs and implementing on real power markets. Electr Pow Syst Res 132: 115–124. doi: 10.1016/j.epsr.2015.11.006

|
| [22] | Andebili MR, Shen H (2017) Price-Controlled Energy Management of Smart Homes for Maximizing Profit of a GENCO. IEEE T Syst Man Cy A. |
| [23] |
Andebili MR (2015) Risk-Cost Based Generation Scheduling Smartly Mixed with Reliability and Market-Driven Demand Response Measures. Int T Electr Energy Syst 25: 994–1007. doi: 10.1002/etep.1884

|
| [24] | AndebiliMR(2016) Nonlinear demand response programs for residential customers with nonlinear behavioral models. Energ Buildings 119: 352–362. |
| [25] |
Andebili MR (2013) Investigating effects of responsive loads models on unit commitment collaborated with demand-side resources. IET Gener Transm D 7: 420–430. doi: 10.1049/iet-gtd.2012.0552

|
| [26] | Japan Electric Power Exchange, JEPX, 2017. Available from: http://www.jepx.org/index.html. |
| [27] |
Nguyen MY, Yoon YT (2014) Optimal Scheduling and Operation of Battery/Wind Generation System in Response to Real-time Market Prices. IEE T Electr Electr Eng 9: 129–135. doi: 10.1002/tee.21947

|
| [28] |
Havel P (2014) Utilization of Real-Time Balancing Market for Transmission System Control Under Uncertainty. IEEE T Power Syst 29: 450–457. doi: 10.1109/TPWRS.2012.2228676

|
| [29] | Kiviluoma J, O'Malley M, Tuohy A, et al. (2011) Impact ofWind Power on the Unit Commitment, Operating Reserves, and Market Design. 2011 IEEE Power and Energy Society General Meeting. |
| [30] | Vlachos AG, Biskas PN, et al. (2011) Balancing Supply and Demand Under Mixed Pricing Rules in Multi-Area Electricity Markets. IEEE T Power Syst 26: 1444–1453. |
| [31] | Ma J, Silva V, Belhomme R, et al. (2013) Evaluating and Planning Flexibility in Sustainable Power Systems. 2013 IEEE Power and Energy Society General Meeting (PES). |
| PS1 | PS2 | PS3 | |
| Max Load(MW) | 1.0 | 0.85 | 0.85 |
| DG1(0.5MW/unit) | 1 | 1 | 1 |
| DG2(0.35MW/unit) | 2 | 1 | 1 |
| PV(MW) | 0.5 | 0.5 | 0.5 |
| WG(MW) | – | 0.5 | 0.75 |
| BESS((0.5MW/5.0MWh)/unit) | 1 | 1 | 1 |
| Case 1 | Case 2 | Case 3 | |
| RTP | without | with | with |
| Day-ahead market | without | with | with |
| Hour-ahead market | without | without | with |
| Fuel cost [Yen] | 2,810,100 | 2,168,100 | 1,738,900 |
| (100%) | (77.2%) | (61.9%) | |
| Operational cost [Yen] | 2,937,047 | 2,294,047 | 1,865,847 |
| (100%) | (78.1%) | (63.5%) |
| PS1 | PS2 | PS3 | |
| Max Load(MW) | 1.0 | 0.85 | 0.85 |
| DG1(0.5MW/unit) | 1 | 1 | 1 |
| DG2(0.35MW/unit) | 2 | 1 | 1 |
| PV(MW) | 0.5 | 0.5 | 0.5 |
| WG(MW) | – | 0.5 | 0.75 |
| BESS((0.5MW/5.0MWh)/unit) | 1 | 1 | 1 |
| Case 1 | Case 2 | Case 3 | |
| RTP | without | with | with |
| Day-ahead market | without | with | with |
| Hour-ahead market | without | without | with |
| Fuel cost [Yen] | 2,810,100 | 2,168,100 | 1,738,900 |
| (100%) | (77.2%) | (61.9%) | |
| Operational cost [Yen] | 2,937,047 | 2,294,047 | 1,865,847 |
| (100%) | (78.1%) | (63.5%) |