Designing an energy management system for household consumptions with an off-grid hybrid power system

Mohamed Elweddad; Muhammet Güneşer; Ziyodulla Yusupov; Mohamed Elweddad; Muhammet Güneşer; Ziyodulla Yusupov

doi:10.3934/energy.2022036

AIMS Energy

2022, Volume 10, Issue 4: 801-830. doi: 10.3934/energy.2022036

Previous Article Next Article

Research article Topical Sections

Designing an energy management system for household consumptions with an off-grid hybrid power system

Department of Electrical and Electronic Engineering, Karabuk University, Karabuk, Turkey

Received: 06 March 2022 Revised: 13 June 2022 Accepted: 23 June 2022 Published: 15 July 2022

This paper analyzes the effect of meteorological variables such as solar irradiance and ambient temperature in addition to cultural factors such as consumer behavior levels on energy consumption in buildings. Reducing demand peaks to achieve a stable daily load and hence lowering electricity bills is the goal of this work. Renewable generation sources, including wind and Photovoltaics systems (PV) as well as battery storage are integrated to supply the managed home load. The simulation model was conducted using Matlab R2019b on a personal laptop with an Intel Core i7 with 16 GB memory. The model considered two seasonal scenarios (summer and winter) to account for the variable available energy sources and end-user electric demand which is classified into three demand periods, peak-demand, mid-demand, and low-demand, to evaluate the modeled supply-demand management strategy. The obtained results showed that the surrounding temperature and the number of family members significantly impact the rate of electricity consumption. The study was designed to optimize and manage electricity consumption in a building fed by a standalone hybrid energy system.

Keywords:

Citation: Mohamed Elweddad, Muhammet Güneşer, Ziyodulla Yusupov. Designing an energy management system for household consumptions with an off-grid hybrid power system[J]. AIMS Energy, 2022, 10(4): 801-830. doi: 10.3934/energy.2022036

Related Papers:

[1]	Abshir Ashour, Taib Iskandar Mohamad, Kamaruzzaman Sopian, Norasikin Ahmad Ludin, Khaled Alzahrani, Adnan Ibrahim . Performance optimization of a photovoltaic-diesel hybrid power system for Yanbu, Saudi Arabia. AIMS Energy, 2021, 9(6): 1260-1273. doi: 10.3934/energy.2021058
[2]	Zijian Hu, Hong Zhu, Chen Deng . Distribution network reconfiguration optimization method based on undirected-graph isolation group detection and the whale optimization algorithm. AIMS Energy, 2024, 12(2): 484-504. doi: 10.3934/energy.2024023
[3]	Mulualem T. Yeshalem, Baseem Khan . Design of an off-grid hybrid PV/wind power system for remote mobile base station: A case study. AIMS Energy, 2017, 5(1): 96-112. doi: 10.3934/energy.2017.1.96
[4]	Aoshuang Ye, Yichao Li, Dong Xu, Zhiwei Wu, Guohua Chen, Junjie Tang, Zhiyuan Zhu . A hybrid algorithm based on improved sine cosine algorithm and population incremental learning and its application to economic load dispatch in power systems. AIMS Energy, 2024, 12(6): 1294-1333. doi: 10.3934/energy.2024059
[5]	S. Vinoth John Prakash, P.K. Dhal . Cost optimization and optimal sizing of standalone biomass/diesel generator/wind turbine/solar microgrid system. AIMS Energy, 2022, 10(4): 665-694. doi: 10.3934/energy.2022032
[6]	Gerardo Guerra, Juan A. Martinez-Velasco . Optimal sizing and operation of energy storage systems considering long term assessment. AIMS Energy, 2018, 6(1): 70-96. doi: 10.3934/energy.2018.1.70
[7]	Yanting Liu, Zhe Xu, Yongjia Yu, Xingzhi Chang . A novel binary genetic differential evolution optimization algorithm for wind layout problems. AIMS Energy, 2024, 12(1): 321-349. doi: 10.3934/energy.2024016
[8]	Kokou Aménuvéla Toka, Yawovi Nougbléga, Komi Apélété Amou . Optimization of hybrid photovoltaic-thermal systems integrated into buildings: Impact of bi-fluid exchangers and filling gases on the thermal and electrical performances of solar cells. AIMS Energy, 2024, 12(5): 1075-1095. doi: 10.3934/energy.2024051
[9]	Kaovinath Appalasamy, R Mamat, Sudhakar Kumarasamy . Smart thermal management of photovoltaic systems: Innovative strategies. AIMS Energy, 2025, 13(2): 309-353. doi: 10.3934/energy.2025013
[10]	V. V. Thang, Thanhtung Ha . Optimal siting and sizing of renewable sources in distribution system planning based on life cycle cost and considering uncertainties. AIMS Energy, 2019, 7(2): 211-226. doi: 10.3934/energy.2019.2.211

Abstract

1. Introduction

In consideration of the increasingly severe energy crisis and environmental pollution, renewable energy has garnered significant attention and recognition ^[1]. The renewable and emission-free characteristics of solar energy have garnered extensive attention, rendering it a subject of great significance in the academic community ^[2,3]. The photovoltaic system, serving as a solar energy-to-electricity conversion system, assumes a pivotal role within the power grid ^[4]. For the PV models ^[5], the single-diode and double-diode models are the most frequently employed in practice. The design and evaluation of photovoltaic systems rely heavily on the precision of parameters such as current and resistance, which play a pivotal role ^[6]. The photovoltaic parameter extraction is performed within a simulated operational environment of an authentic photovoltaic system, where the current-voltage data is measured under all operational conditions of the actual photovoltaic system ^[7,8]. Therefore, it is extremely significant to extract PV model parameters accurately, quickly, and reliably.

In recent years, photovoltaic parameter extraction has emerged as a prominent research area, with numerous optimization methods proposed to address this issue ^[9]. These methods are analytical methods ^[10] and numerical approaches ^[11]. The implementation of analytical methods is straightforward, involving the analysis of mathematical equations to address problems. However, analytical methods heavily rely on selected values and inaccurate choices can result in flawed models. The field of numerical methods can be categorized into deterministic approaches and metaheuristic algorithms. Deterministic methods, such as the Newton-Raphson method ^[12], Lambert W function ^[13], Gauss-Seidel method ^[14], and iterative curve fitting ^[15], are commonly employed. Deterministic methods exhibit excessive reliance on initial values and are prone to falling into local optima. Metaheuristic algorithms are a general class of heuristic algorithms that do not rely on domain-specific knowledge but provide a general framework for searching the solution space of a problem to find an approximately optimal solution. Metaheuristic algorithms often meet some requirements of the search process, and then the heuristic algorithm implemented according to these requirements is called a metaheuristic algorithm. Many metaheuristic algorithms are inspired by some random phenomena in nature. Metaheuristic methods exhibit flexibility in the objective function and initial values, making them easily implementable. The inspiration for the mutation, crossover, and selection strategies of differential evolution comes from the theory of evolution in nature. Chaotic local search based differential evolution algorithms use the chaotic local search (CLS) mechanism to avoid premature convergence of evolutionary algorithms ^[16]. The non-dominated evolutionary optimization strategy based on covariance matrix adaptation (CMA-ES) is an evolutionary optimization strategy aimed at reducing the number of iterations required to converge to the optimal solution ^[17]. The Bayesian optimization framework is an excellent algorithm that considers heteroscedastic noise to adjust hyperparameters in control problems ^[18]. Consequently, metaheuristic algorithms find extensive applications in optimization problems across diverse domains. Numerous scholars have employed meta-heuristic techniques for addressing the challenge of parameter extraction in photovoltaic modeling, such as genetic algorithm (GA) ^[19], differential evolution (DE) ^[20], particle swarm optimization (PSO) ^[21], simulated annealing algorithm (SA) ^[22], moth-flame optimization ^[23], artificial bee colony algorithm (ABC) ^[24], teaching-based optimization algorithm (TLBO) ^[25], JAYA ^[26], etc. Many scholars have proposed improved algorithms to solve this problem, as reviewed below.

In ^[27], an improved PSO incorporating a cross-sorting and dynamic population reduction strategy is proposed for extracting photovoltaic parameters. In ^[28], an improved PSO based on an adaptive mutation strategy is proposed, which can avoid premature phenomena and accurately extract photovoltaic parameters. In ^[29], an improved DE to identify photovoltaic parameters under all conditions. In ^[30], a hybrid algorithm of DE/WOA is proposed, which combines exploration of DE and exploitation of WOA and can accurately extract photovoltaic parameters. In ^[31], a novel formulation is proposed for the computation of the scale factor and crossover rate, thereby enhancing the performance of adaptive differential evolution through its implementation. In ^[32], the present study proposes a novel teaching-learning-based artificial bee colony algorithm, which combines the advantages of the teaching-learning-based optimization algorithm and the artificial bee colony algorithm, aiming to effectively extract photovoltaic parameters. In ^[33], an enhanced and simplified teach-learn optimization algorithm (STLBO) is proposed for parameter identification in proton exchange membrane (PEM) fuel cells and photovoltaic models. In ^[34], introduces a novel approach, namely the generalized oppositional teaching-learning-based optimization, for parameter extraction of photovoltaic models. In ^[35], an improved JAYA algorithm is proposed to effectively identify the parameters of a PV mode. In ^[36], the individual is quantified by probability, and then the evolutionary strategy is selected adaptively based on probability. A performance-guided JAYA is proposed to identify PV parameters. In ^[37], for accurate extract photovoltaic parameters, a multiple learning backtracking search algorithm is proposed. In ^[38], a memory-based improved gorilla troop optimizer is proposed, incorporating the exploration gorilla adaptive mutation mechanism (EGAMM) and gorilla memory saving technology. This algorithm effectively parameters the identification of photovoltaic models. In ^[39], introduces an enhanced whale optimization algorithm that incorporates two prey search strategies for precise extraction of photovoltaic parameters. In ^[40], introduces a novel chaotic whale optimization algorithm, which primarily employs chaotic mapping techniques to automatically compute and adapt internal parameters. This algorithm is effective in the precise extraction of photovoltaic parameters. In ^[41], proposes an improved pigeon-inspired optimization (PIO) algorithm based on the Taguchi method for the extraction of photovoltaic parameters. Simulation results show that the proposed algorithm is superior to the comparison algorithm. In ^[42], a two-phase quasi-affine transformation evolution with feedback (tfQUATRE) algorithm was proposed to extract PV parameters. This algorithm improves the ability of exploration and development by adjusting the search trend in different stages. Using historical populations as a form of feedback to guide the search for promising areas, maintain population diversity, and improve exploration ability. The experimental results show that the algorithm has strong competitiveness. In ^[43], propose a scale-free network-based differential evolution method. This method is based on the scale-free network-based population structure and a mutation operator that utilizes the neighborhood information provided by the scale-free structure. The experimental results indicate that this method can efficiently and reliably extract photovoltaic parameters. In ^[44], propose a differential evolution variant (PDcDE) to tackle the parameter estimation of solar PV models. This method uses an auto-controlled population strategy to adjust the population size during a search process, setting the diversity control parameters for determining the scaling factor and avoiding local optima through reverse search. In ^[45], a directional permutation differential evolution algorithm (DPDE) is proposed to tackle the parameter estimation of several kinds of solar PV models. DPDE utilizes the information generated by the search population and differential vector direction and has a strong global search ability to jump out of local optima.

These methods play a crucial role in PV model parameter extraction. However, owing to the multimodal characteristics inherent in the PV model, numerous existing methodologies are susceptible to encountering local optima during the parameter extraction process. There is still significant potential for enhancing the convergence speed and accuracy, particularly in the double diode model (DDM). Therefore, additional exploration of alternative methods is necessary for effective PV model parameter extraction.

The term "hybrid technology" refers to the amalgamation of two or more algorithms, harnessing their respective strengths to yield a novel algorithm that outperforms any single algorithm ^[46]. According to hybrid technology, the present study proposes a hybrid algorithm integrating dwarf mongoose optimization algorithm (DMO) and WOA. Dwarf mongoose optimization algorithm ^[47] is a swarm intelligence based metaheuristic algorithm, proposed in 2022 by Jeffrey et al. The algorithm models the foraging behavior of a population of dwarf mongooses, incorporating three social groups: the alpha group, the babysitter group, and the scout group. This algorithm considers the entire family as a unit for foraging activities, with the female chief leading the initiation of foraging tasks and making decisions regarding path selection, distance covered, and choice of sleeping mounds. Whale optimization algorithm ^[48] is a population-based metaheuristic algorithm, which was proposed by Mirjalili in 2016 and has been widely applied to solve various optimization problems. The algorithm mainly simulates the collective behavior of humpback whales, providing a novel method for problem-solving. In this paper, a hybrid algorithm of dwarf mongoose optimization algorithm and whale optimization algorithm is proposed. The primary improvement lies in synergizing the strengths of DMO and WOA to enhance the algorithm's capability to escape local optima and expedite convergence speed. The algorithm incorporates adaptive weights to effectively balance the trade-off between exploration and exploitation abilities. DMOWOA has a strong ability to jump out of local optimal and fast convergence. The novelty of DMOWOA is that the search phase of the algorithm is divided into two stages, which make full use of the exploration ability of DMO and the exploitation ability of WOA. The proposed algorithm is employed to solve various photovoltaic models to validate its performance. Experimental results show that the proposed algorithm has excellent performance and competitiveness for the extraction of photovoltaic parameters.

The main contributions of this paper are:

(1) A hybrid metaheuristic DMOWOA optimization algorithm is proposed for extracting photovoltaic model parameters.

(2) The DMOWOA used a mixture of DMO's Alpha group search stage, scout group search stage, and WOA's Bubble-net attacking method to look for optimal fitness. Chaotic adaptive weights are introduced to balance exploration and exploitation.

(3) The DMOWOA algorithm is employed to solve five PV models, and the obtained results are compared with those achieved by DMO, WOA, and those reported in the existing literature.

The rest of the paper is organized as follows: Section 2 explains the mathematical formula of the photovoltaic model. Section 3 introduces basic DMO and WOA. Section 4 explains the hybrid algorithm DMOWOA. Section 5 presents the experimental analysis and results of different PV models. Finally, Section 6 gives the conclusion.

2. Problem model

This section presents the prevalent models utilized in photovoltaic systems, including the single diode model (SDM), double diode model (DDM), and photovoltaic module based on SDM. Additionally, the objective function is introduced.

2.1. Single diode model

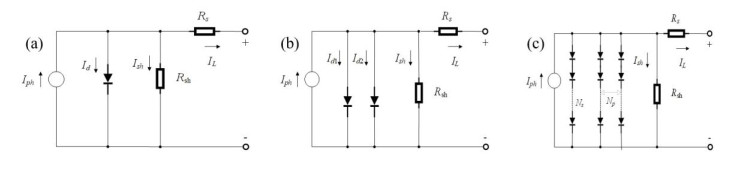
Figure 1(a) shows the equivalent circuit diagram of the single diode model. The figure shows that SDM consists of a diode, a photocurrent source, and two resistors. The mathematical model is as follows ^[49]:

$I_o = I_{ph} - I_d - I_{sh}$

(1)

where I_ph, I_d, and I_sh are the photocurrent, diode current, and shunt resistance current, respectively.

Figure 1. Equivalent circuit: (a) SDM, (b) DDM, and (c) PV module.

DownLoad: Full-Size Img PowerPoint

The mathematical model of I_d and I_sh is as follows:

$I_d = I_{sd}(\exp (\frac{{V + IR_s}}{{aV_t}}) - 1)$

(2)

$I_{sh} = \frac{{V + IR_s}}{{R_{sh}}}$

(3)

where I_sd, V, R_s, and R_sh are the diode reverse saturation current, battery output voltage, series resistance, and shunt resistance, respectively.

The mathematical model of V_t is as follows:

$V_t = \frac{{k \cdot T}}{q}$

(4)

where k ( = 1.3806503 × 10^–23 J/K), T, and q ( = 1.60217646 × 10^–19 C) are Boltzmann's constant, the temperature in Kelvin, and the charge of the electron, respectively.

In summary, Eq (1) can be expressed as follows:

$I_o = I_{ph} - I_{sd}(\exp (\frac{{V + I_{Rs}}}{{aV_t}}) - 1) - \frac{{V + I_{Rs}}}{{R_{sh}}}$

(5)

In Eq (5), there are five unknown photovoltaic parameters (I_ph, I_sd, R_s, R_sh, and a) that need to be extracted. The effective operation of photovoltaic systems depends on these parameters.

2.2. Double diode model

The double diode model is one of the most commonly used PV models due to its simplicity and accuracy. It consists of a photocurrent source, two diodes, and two resistors, among which the two diodes are in a parallel state. Figure 1(b) shows its equivalent circuit diagram. The mathematical model of DDM is as follows ^[50]:

$I_o = I_{ph} - I_{d1} - I_{d2} - I_{sh}$

(6)

where I_d1 and I_d2 are the currents of two diodes in parallel. Their mathematical models are as follows:

$I_{d1} = I_{sd1}(\exp (\frac{{V + IR_s}}{{a_1V_t}}) - 1)$

(7)

$I_{d2} = I_{sd2}(\exp (\frac{{V + IR_s}}{{a_2V_t}}) - 1)$

(8)

where I_sd1 and I_sd2 are the saturation current at the two diodes, respectively, and a₁ and a₂ are ideal factors for both diodes.

In summary, Eq (6) can be expressed as follows:

$I_o = I_{ph} - I_{sd1}(\exp (\frac{{V + IR_s}}{{a_1V_t}}) - 1) - I_{sd2}(\exp (\frac{{V + IR_s}}{{a_2V_t}}) - 1) - \frac{{V + IR_s}}{{R_{sh}}}$

(9)

The formula reveals the presence of seven unknown parameters(I_ph, I_sd1, I_sd2, R_s, R_sh, a₁, and a₂)within the DDM model that necessitate extraction.

2.3. Photovoltaic module

The PV module is composed of multiple SDMs in series or parallel ^[51]. The mathematical model of the PV module is as follows:

${I_o} = {I_{ph}}{N_p} - {I_{sd}}{N_p}(\exp (\frac{{V + I{R_s}{N_s}}}{{{a_1}{N_s}{V_t}}}) - 1) - \frac{{V + I{R_s}{N_s}/{N_p}}}{{{R_{sh}}{N_s}/{N_p}}}$

(10)

where N_s and N_p are the number of cells in series and parallel, respectively. In this paper, the value of N_p is set to 1. In summary, Eq (10) can be expressed as follows:

${I_o} = {I_{ph}}{N_p} - {I_{sd}}(\exp (\frac{{V + I{R_s}{N_s}}}{{{a_1}{N_s}{V_t}}}) - 1) - \frac{{V + I{R_s}{N_s}}}{{{R_{sh}}{N_s}}}$

(11)

According to Eq (11), there are five unknown parameters (I_ph, I_sd, R_s, R_sh, and a) in the PV model module that need to be extracted.

2.4. Objective function

The optimal solution to the parameter extraction problem is to minimize the difference between the simulated current data and the measured current data. The root means square error (RMSE) is used for measurement error ^[52,53]. Therefore, the mathematical modeling of the PV model is as follows:

$RMSE(X) = \sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {f{{(V_k, I_k, X)}^2}} }$

(12)

where N represents the number of experimental data. The objective function of the single diode model is as follows:

$\left\{ {\begin{array}{*{20}{l}} {f(V,I,X) = {I_{ph}} - {I_{sd}}(\exp (\frac{{V + I{R_s}}}{{a{V_t}}}) - 1) - \frac{{V + I{R_s}}}{{{R_{sh}}}} - Io}\\ {X = \left\{ {{I_{ph}},{I_{sd}},{R_s},{R_{sh}},a} \right\}} \end{array}} \right.$

(13)

The objective function of the double diode model is as follows:

$\left\{ {\begin{array}{*{20}{l}} {f(V,I,X) = {I_{ph}} - {I_{sd1}}(\exp (\frac{{V + I{R_s}}}{{{a_1}{V_t}}}) - 1) - {I_{sd2}}(\exp (\frac{{V + I{R_s}}}{{{a_2}{V_t}}}) - 1) - \frac{{V + I{R_s}}}{{{R_{sh}}}} - {I_o}}\\ {X = \left\{ {{I_{ph}},{I_{sd1}},{I_{sd2}},{R_s},{R_{sh}},{a_1},{a_2}} \right\}} \end{array}} \right.$

(14)

The objective function of the PV module is as follows:

$\left\{ {\begin{array}{*{20}{l}} {f(V,I,X) = {I_{ph}}{N_p} - {I_{sd}}(\exp (\frac{{V + I{R_s}{N_s}}}{{{a_1}{N_s}{V_t}}}) - 1) - \frac{{V + I{R_s}{N_s}}}{{{R_{sh}}{N_s}}} - {I_o}}\\ {X = \left\{ {{I_{ph}},{I_{sd}},{R_s},{R_{sh}},a} \right\}} \end{array}} \right.$

(15)

3. Proposed hybrid DMO and WOA (DMOWOA)

3.1. DMO

The DMO ^[47] algorithm is a population-based metaheuristic algorithm proposed by Jeffrey O. Agushaka et al. The algorithm splits the mongoose population into three different groups: the alpha group, the scout group, and the babysitter group. Under the guidance of a female leader, the entire population collaboratively forages as a cohesive unit. In case the alpha group fails to locate food, an exchange occurs between members of the alpha and the babysitter group. Consequently, members of the alpha group simultaneously engage in foraging activities while searching for a sleeping mound. DMO requires only one manually controlled parameter to reduce the complexity of the algorithm application. When the members of the Alpha group have insufficient abilities, they will exchange members of the alpha group and the babysitter group, which gives DMO the ability to maintain population diversity. The sleep mound mechanism can prevent algorithms from entering local optima.

3.1.1. Initialization

Initializes the DMO's mathematical model, as shown in Eq (16).

$X = \left[ {\begin{array}{*{20}{c}} X_{1, 1}&X_{1, 2}& \cdots &X_{1, d - 1}&{X1, d} \\ X_{2, 1}&X_{2, 1}& \cdots &X_{2, d - 1}&X_{2, d} \\ \vdots & \vdots &X_{i, j}& \vdots & \vdots \\ X_{N, 1}&X_{N, 2}& \cdots &X_{N, d - 1}&X_{N, d} \end{array}} \right]$

(16)

where X represents the candidate solution; X_{i, j} represents the position of the ith mongoose in the jth dimension, and its mathematical model is shown in Eq (17); and N and d represent the population count and the dimension size for the problem, respectively.

$X_{i, j} = unifrnd(lb, ub, d)$

(17)

where unifrnd is used to generate uniformly distributed random numbers, ub and lb represent the upper and lower bounds for the given problem respectively, and d represents the dimension size of the problem.

3.1.2. Alpha group

The foraging route of the dwarf mongoose is determined by the female leader, who is generated in the alpha group. The probability of each female individual in the alpha group becoming a leader is determined by Eq (18).

$\alpha = \frac{{fit(i)}}{{\sum\nolimits_{i = 1}^n {fit(i)} }}$

(18)

where fit(i) represents the fitness value of the ith individual; n represents the number of individuals in the alpha group, n = N − bs; and bs represents the number of individuals in the babysitters group.

Foraging paths are chosen by the alpha females, and its mathematical model is as follows:

$X_{{\text{i}} + 1} = X_i + p \times peep \times (X_i - X_k)$

(19)

where X_i+1 represents the new food source location, X_i is the location of the ith individual, p represents the random number between [−1, 1], peep is set to 2, and X_k is a random individual in the alpha group. The sleeping mound (sm_i) is the resting place of dwarf mongooses, and its mathematical model is as follows:

$sm_i = \frac{{fit(i + 1) - fit(i)}}{{\max \left\{ {\left| {fit(i + 1), } \right.\left. {fit(i)} \right|} \right\}}}$

(20)

The mathematical model of the mean sleeping mound is as follows:

$\varphi = \frac{{\sum\nolimits_{i = 1}^n {sm_i} }}{n}$

(21)

3.1.3. Scout group

The individual members of the scout group will not return to their previous sleeping mound. This guarantees the algorithm's exploration ability. The mathematical model of the sleeping mound is as follows:

$X_{i + 1} = \left\{ \begin{array}{l} X_i - C \times p \times r \times \left| {X_i - \overrightarrow M } \right|{\text{ }}\;if\;{\text{ }}\varphi i + 1{\text{ }} \gt \varphi i{\text{ }} \\ X_i + C \times p \times r \times \left| {X_i - \overrightarrow M } \right|{\text{ }}else \end{array} \right.$

(22)

where X_i+1 is the position of the next sleeping mound; C represents the parameter controlling the mobility of the mongoose population, which will linearly decrease with the number of iteration, as shown in Eq (23); p is a random number between [−1, 1]; r represents a random number between [0, 1]; M is the vector that determines the direction in which the mongoose moves to the new sleeping mound, expressed by Eq (24); and φ is represented by Eq (21).

$C = {(1 - \frac{t}{{Max\_t}})^{(2\frac{t}{{Max\_t}})}}$

(23)

where t represents the iteration number and Max_t represents the maximum iteration count.

$\overrightarrow M = \sum\nolimits_{i = 1}^n {\frac{{Xi - sm_i}}{{X_i}}}$

(24)

where n represents the number of members in the scout group, X_i represents the position of the ith individual, and sm_i is the value of the sleeping mound.

3.1.4. Babysitter group

The size of the babysitter group, typically consisting of subordinate individuals caring for their offspring, is determined based on the population size. This influences the algorithm by proportionally decreasing the alpha group's foraging potential over time. Parameter L resets the information about foraging locations for other members. The fitness weight of the babysitter is set to zero, which ensures the average weight of the alpha group in the next iteration is reduced, which means the group movement is hindered thereby, emphasizing exploitation.

3.2. WOA

WOA ^[48] is a population-based metaheuristic algorithm proposed by Mirjalili and Lewis in 2016. WOA encompasses three distinct mathematical models: encircling prey, bubble-net attacking method, and search for prey. The three population updating mechanisms of WOA are independent of each other, and the global exploration and local development processes in the optimization stage can be operated and controlled separately. WOA does not require parameter adjustment, which improves the efficiency of algorithm usage and reduces application difficulty.

3.2.1. Encircling prey

Whales can recognize prey and use cooperative strategies to encircle their targets. The mathematical model is as follows:

$\overrightarrow V = \left| {\overrightarrow S \times \overrightarrow {{X^*}_t} - \overrightarrow {X_t} } \right|$

(25)

$\overrightarrow X _{t + 1} = \overrightarrow {{X^*}_t} - \overrightarrow A \times \overrightarrow V$

(26)

where X* and X represent the current optimal solution and the position of individual whales respectively. The mathematical models of A and S are shown as follows:

$\overrightarrow A = 2 \times \overrightarrow a \times \overrightarrow r - \overrightarrow a$

(27)

$\overrightarrow S = 2 \times \overrightarrow r$

(28)

where a decreases from 2 to 0 during iteration and r represents the vector between [0, 1].

3.2.2. Bubble-net attacking method

Spiral update position: the whales make a spiral motion, and the mathematical model is as follows:

$\overrightarrow X _{t + 1} = \overrightarrow {{V^{'}}} \cdot {e^{bl}} \cdot \cos (2\pi l) + \overrightarrow {{X^*}_t}$

(29)

where $\overrightarrow {{V^{'}}} = \left| {\overrightarrow {{X^*}_t} - \overrightarrow X_ t} \right|$ represents the distance between the ith whale and its prey, b is the constant that defines the shape of the logarithmic spiral, and l represents the random number between [−1, 1].

The whale follows a spiral trajectory, gradually encircling its prey within a confined circumference. To simulate these concurrent actions effectively, assign equal probabilities to both the updates of the narrow circle and spiral models governing the whale's position. The mathematical representation is as follows:

$\overrightarrow X _{t + 1} = \left\{ \begin{array}{l} \overrightarrow {{X^*}_t} - \overrightarrow A \times \overrightarrow V {\text{ }}if{\text{ }}\;p < 0.5 \\ \overrightarrow {{V^{'}}} \cdot {e^{bl}} \cdot \cos (2\pi l) + \overrightarrow {{X^*}_t} {\text{ }}if\;{\text{ }}p \geqslant 0.5{\text{ }} \end{array} \right.$

(30)

where p represents a random number between [0, 1].

3.2.3. Search for prey

Whales hunt at random based on the location of their peers. When an individual hunts, it moves away from the reference whale in the population. The mathematical model of the random hunt phase is as follows:

$\overrightarrow X _{t + 1} = \overrightarrow {X_{rand}} - \overrightarrow A \cdot \overrightarrow V$

(31)

$\overrightarrow V = \left| {\overrightarrow S \cdot \overrightarrow {X_{rand}} - \overrightarrow X } \right|$

(32)

where X_rand represents a random individual whale and |A| ≥ 1 or |A| < 1.

4. Adaptive weighted DMO hybrid WOA

4.1. Adaptive weight

Inertial weight is used to balance global and local search ^[54]. During the early stage, global search can enhance the algorithm's efficacy in identifying the optimal solution. During the later stage, local search can enhance the exploitability of the algorithm and improve the accuracy of the solution. In this paper, the chaotic inertia weight is adopted ^[55,56], and the mathematical model is as follows:

$w = (w_{\max} - w_{\min} ) \times \frac{{T - t}}{T} + w_{\min} \times z$

(33)

where w_max and w_min are 0.9 and 0.4 respectively, z = 4z(1 − z), and the value range of z is [0, 1].

Equation (19) will be substituted by Eq (34), and Eq (22) will be replaced by Eq (35).

$X_{{\text{i}} + 1 }= X_i + w \times p \times peep \times (X_i - X_k)$

(34)

$X_{i + 1} = \left\{ \begin{array}{l} X_i - w \times C \times p \times r \times \left| {Xi - \overrightarrow M } \right|{\text{ }}\;if{\text{ }}\;\varphi _{i + 1}{\text{ }} \gt \varphi _i{\text{ }} \\ X_i + w \times C \times p \times r \times \left| {X_i - \overrightarrow M } \right|{\text{ }}else \end{array} \right.$

(35)

Chaos inertial weight exhibits the characteristics of general inertial weight and chaos, which can better balance the global search and local search of the algorithm.

4.2. Hybrid DMOWOA method

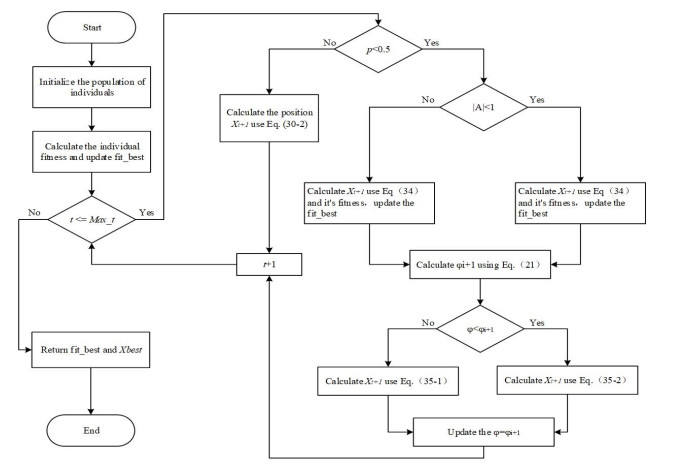
Whale optimization algorithm ^[36] is a highly efficient algorithm that demonstrates exceptional capabilities in solving various optimization problems. It is worth noting that WOA's ability to exploit in the late stages of the algorithm is excellent. The proposed algorithm removes the babysitter mechanism from the DMO and lets the alpha group and the scout group run simultaneously. Make sure they are foraging and looking for a sleeping mound at the same time. During the p < 0.5 stage of WOA, if |A| < 1, the alpha group performs both foraging and sleep mound search, that is, Eq (26) of WOA will be replaced by the Eqs (34) and (35) of DMO. If |A| ≥ 1, the scout group engages in foraging and sleep mound search, that is, Eq (26) of WOA will be replaced by Eqs (34) and (35) of the scout group. Mining for bubble network attack of WOA, namely the position of spiral update, when WOA is at p ≥ 0.5 stage. The pseudo-code and flow chart of DMOWOA are shown in Algorithm 1 and Figure 2 respectively.

Table Algorithm 1. DMOWOA's pseudo-code.

1.	Step 1. Initialization
2.	Set the values of Max_t, t, N, d, peep, w_max, w_min, A, fit_best, Xbest, $\varphi$
4.	Step 2. Main loop
5.	while t $\leqslant$ Max_t
6.	Calculate the value of C using Eq (23) and w using Eq (33)
7.	for i = 1:N
8.	Calculate the value of A using Eq (27)
9.	for j = 1:d
10.	if p < 0.5
11.	if \|A\| $\geqslant$ 1
12.	Calculate the position X_i+1 using Eq (34) and $\varphi$ _i+1 using Eq (21)
13.	Calculate the X_i+1'fitness and update the fit_best
14.	if $\varphi$ _i+1 > $\varphi$
15.	Calculate the position X_i+1 using Eq (35-1)
16.	else
17.	Calculate the position X_i+1 using Eq (35-2)
18.	end
19.	Update the $\varphi$ = $\varphi$ _i+1
20.	end
21.	if \|A\| < 1
22. 23. 24.	Calculate the position X_i+1 using Eq (34) Calculate the X_i+1'fitness and update the fit_best Calculate the $\varphi$ _i+1 using Eq (21)
25.	if $\varphi$ _i+1 > $\varphi$
26	Calculate the position X_i+1 using Eq (35-1)
27	else
28.	Calculate the position X_i+1 using Eq (35-2)
29.	end
30.	Update the $\varphi$ = $\varphi$ _i+1
31.	end
32.	if p $\geqslant$ 0.5
33.	Calculate the position X_i+1 using Eq (30-2)
34.	end
35.	end
36.	end
37.	end while
38.	Step 3. Return fit_best and Xbest

| Show Table

DownLoad: CSV

Figure 2. The flow diagram of DMOWOA.

DownLoad: Full-Size Img PowerPoint

4.3. Exploration and exploitation

Exploration and exploitation are the cornerstones of metaheuristic algorithms ^[57]. When achieving a balance between exploration and exploitation, algorithms can quickly converge during optimization. Effectively controlling the balance between exploration and exploitation is a challenging task. Representing the changing process of exploration and development is also important. According to ^[57], the current proportion of exploration and development can be determined based on the position between individuals. Its mathematical model is as follows:

$Expa = (\frac{{Dv}}{{Dv_{\max} }}) \times 100\%$

(36)

$Expi = (\frac{{\left| {Dv - Dv_{\max} } \right|}}{{Dv_{\max} }}) \times 100\%$

(37)

where Expa is the level of exploration, Expi is the level of exploitation, Dv is the dimension-wise diversity, and Dv_max is the maximum diversity value in the entire optimization process. The mathematical models of Dv and Dv_max are shown below:

$Dv = \frac{1}{d}\sum\limits_1^d {Dv_j}$

(38)

$Dv_j = \frac{1}{N}\sum\limits_1^N {\left| {X_{i, j} - median(X_j)} \right|}$

(39)

where X_{i, j} represents the jth dimension of the ith individual, N is the population size, d is the dimension of the given problem, and median(X_j) is the median value of the jth dimension in the whole population.

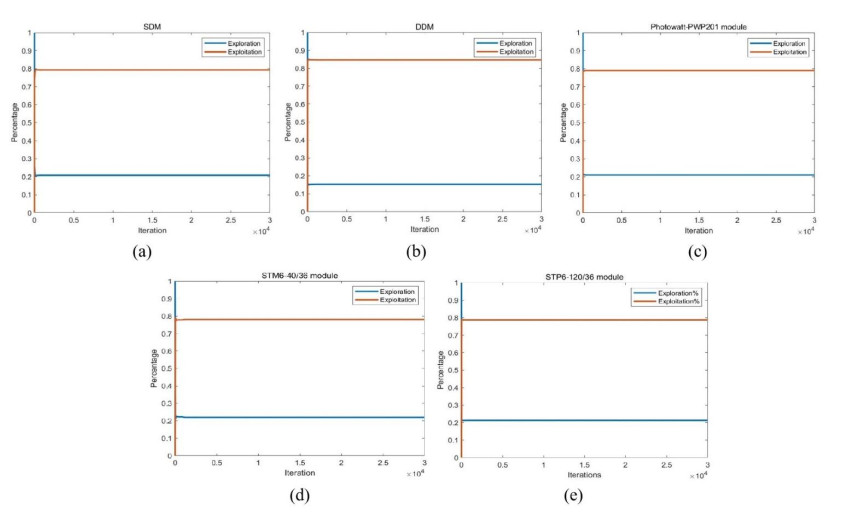
Figure 3 shows the variation process of exploration and development proportion when DMOWOA solves different photovoltaic models. As shown in the graph, DMOWOA has a fast convergence speed and stable changes in exploration and exploitation.

Figure 3. The percentage of exploration and exploitation: (a) single diode model, (b) double diode model, (c) Photowatt-PWP201 module, (d) STM6-40/36 module, and (e) STP6-120/36 module.

DownLoad: Full-Size Img PowerPoint

4.4. Computational complexity

The computational complexity of DMOWOA depends on the population size, the problem size, the number of iterations, the computation of the sleep mound search, and the computation of the fitness function. The computational complexity of the solution update process is O(Max_t × d × sm) + O(CFE), including finding the best location, evaluating the next sleep hill, and updating the solution location for all solutions. The total number of iterations is Max_t, the dimension size of the given problem is d, CFE is the cost of function evaluation, and the population size is N. Therefore, the computational complexity of the proposed DMOWOA is O(Max_t × d × sm × N + CFE × N).

The detailed process of DMOWOA is shown in Algorithm 1 and Figure 2. At the beginning of optimization, individuals set out to search for food, and when |A| ≥ 1, individuals will extensively search for food to determine its range. During subsequent foraging phases, individuals will search for food near the previous sleep mound to avoid reducing the efficiency of searching for food. When |A| < 1, individuals will locate food within the determined range of food sources. To utilize the DMOWOA algorithm, it just needs to determine the population size and the maximum number of iterations.

5. Results and analysis

In this chapter, the DMOWOA is applied to extract three different PV models to verify the performance of the algorithm, including single diode, double diode, and PV modules. Current and voltage data of SDM and DDM ^[12] were measured on a commercial silicon R.T.C France solar cell with a diameter of 57 mm at 1000 W/m² at 33 ℃. PV modules include Photowatt-PWP201 ^[12], mono-crystalline STM6-40/36 ^[58], and poly-crystalline STP6-120/36 ^[58], and their respective current and voltage data can be found in their respective literature. Table 1 shows the value range of parameters of the PV model, which is consistent with the previous literature. The upper and lower bounds of the parameter values of the PV models are shown in Table 1.

Table 1. Upper and lower bounds for PV model parameters.

Parameter	SDM/DDM		Photowatt-PWP201		STM6-40/36		STP6-120/36
Parameter	lb	ub	lb	ub	lb	ub	lb	ub
I_ph(A)	0	1	0	2	0	2	0	8
I_sd, I_sd1, I_sd2(μA)	0	1	0	50	0	50	0	50
R_s(Ω)	0	0.5	0	2	0	0.36	0	0.36
R_sh(Ω)	1	100	0	2000	0	1000	0	1500
a, a₁, a₂	1	2	1	50	1	60	1	50

| Show Table

DownLoad: CSV

To evaluate the performance of DMOWOA, compared DMOWOA with several established optimization algorithms including SA ^[22], DMO ^[47], WOA ^[48], DE ^[59], PSO ^[60], and GWO ^[64]. At the same time, it is compared with the algorithms proposed in other literature, including TLABC ^[32], GOTLBO ^[34], IJAYA ^[35], MLBSA ^[37], and IGBO ^[61], whose data is from their respective literature. The experimental conditions of all algorithms are run independently for 30 times, with the upper limit of 30000 for each iteration. Parameter configurations of the compared algorithms are provided in Table 2. In addition, this experiment uses MATLAB2021b for simulation experiments, and a Windows 10 64-bit operating system PC with Intel Core i7-9700 processor @3.00GHz and 16.0 GB RAM serves as the experimental platform.

Table 2. Parameter setting of compared algorithms.

Algorithms	Parameter setting
DMOWOA	N = 50
DMO	N = 50, bs = 3
PSO	N = 50, w = 0.729, c1 = 1.49445, c2 = 1.49445
GWO	N = 50, a = 2~0
SA	N = 50
DE	N = 50
WOA	N = 50, a = 2~0

| Show Table

DownLoad: CSV

5.1. Results on the SDM

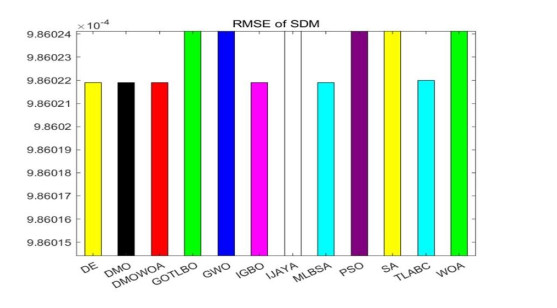
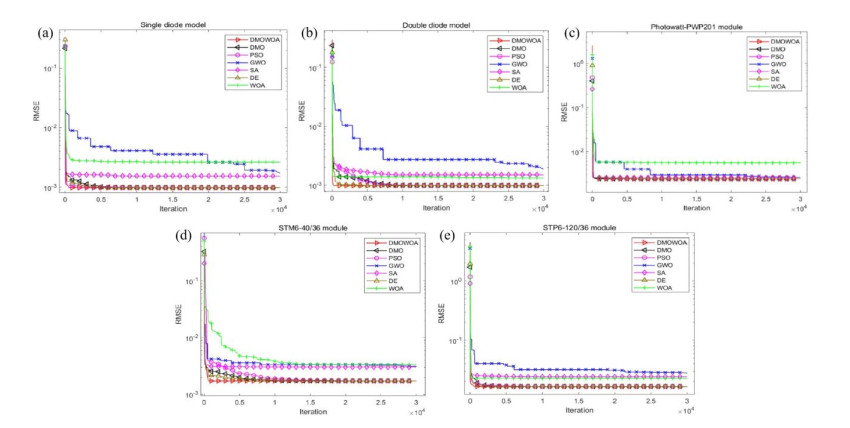
Table 3 shows the parameters of SDM extracted by each algorithm. The minimum RMSE values in the table are shown in boldface type. Table 3 reveals that the DOMWOA, DMO, DE, MLBSA, and TLABC exhibit the optimal RMSE. WOA has the maximum RMSE. The accuracy of the extracted parameters increases as the RMSE decreases, as stated by ^[62]. The bar chart of SDM is shown in Figure 4. Therefore, the results of DMOWOA are more accurate than those of WOA, SA, PSO, GWO, GOTLBO, and IJAYA.

Table 3. SDM parameters are extracted from each algorithm.

Method	I_ph (A)	I_sd (μA)	R_s (Ω)	R_sh (Ω)	a	RMSE	Runtime (s)
DMOWOA	0.76077	0.32301	0.03637	53.71840	1.48118	9.860219E-04	483.44
DMO	0.76077	0.32306	0.03637	53.72317	1.48119	9.860219E-04	501.54
WOA	0.76147	0.29578	0.03658	44.37821	1.47253	1.107616E-03	532.68
DE	0.76077	0.32302	0.03637	53.71899	1.48118	9.860219E-04	531.65
SA	0.76069	0.38973	0.03562	59.42678	1.50032	1.049349E-03	1049.39
PSO	0.76077	0.32350	0.03637	53.75926	1.48133	9.860259E-04	513.35
GWO	0.76102	0.33113	0.03622	50.98459	1.48375	1.005399E-03	561.26
IGBO ^[61]	0.760776	0.323021	0.036377	53.718531	1.481184	9.860219E-04	NA
GOTLBO ^[34]	0.760780	0.331552	0.036265	54.115426	1.483820	9.87442E-04	NA
MLBSA ^[37]	0.760776	0.32302	0.036377	53.71852	1.481184	9.8602E-04	NA
TLABC ^[32]	0.76078	0.32302	0.03638	53.71636	1.48118	9.86022E-04	NA
IJAYA ^[35]	0.7608	0.3228	0.0364	53.7595	1.4811	9.8603E-04	NA

| Show Table

DownLoad: CSV

Figure 4. RMSE bar chart of SDM.

DownLoad: Full-Size Img PowerPoint

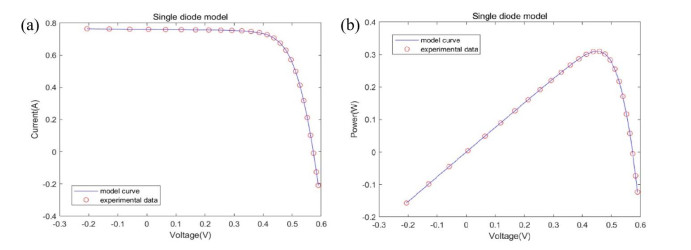
To further validate the accuracy of DMOWOA, Figure 5 plots the Ⅰ-Ⅴ and P-V curves of DMOWOA. Table 4 shows the integral absolute error (IAE) values. Figure 4 shows that the simulation results obtained using DMOWOA exhibit excellent agreement with the experimental measurements. In addition, according to Table 4, the IAE values of current are less than 2.51E-03, and the IAE values of voltage are less than 1.46E-02, thereby confirming the high precision of the parameters extracted by DMOWOA.

Figure 5. Comparison of experimental data and model data on SDM: (a) Ⅰ-Ⅴ curve, (b) P-V curve.

DownLoad: Full-Size Img PowerPoint

Table 4. SDM: IAE of DMOWOA.

Item	Model data		Experiment current data		Experiment power data
Item	V_M (V)	I_M (A)	I_E (A)	IAE_I (A)	P_E (W)	IAE_P (W)
1	−0.2057	0.7640	0.764087182	0.00008718	−0.15717120	0.00001640
2	−0.1291	0.7620	0.762662561	0.00066256	−0.09845974	0.00008550
3	−0.0588	0.7605	0.761354779	0.00085478	−0.04476766	0.00005030
4	0.0057	0.7605	0.760153460	0.00034650	0.00433287	0.00000198
5	0.0646	0.7600	0.759054675	0.00094530	0.04903493	0.00006110
6	0.1185	0.7590	0.758041810	0.00095820	0.08982795	0.00011400
7	0.1678	0.7570	0.757091116	0.00009112	0.12703989	0.00001500
8	0.2132	0.7570	0.756140826	0.00085920	0.16120922	0.00018300
9	0.2545	0.7555	0.755086333	0.00041370	0.19216947	0.00010500
10	0.2924	0.7540	0.753663340	0.00033670	0.22037116	0.00009840
11	0.3269	0.7505	0.751390433	0.00089043	0.24562953	0.00029000
12	0.3585	0.7465	0.747353327	0.00085333	0.26792617	0.00031000
13	0.3873	0.7385	0.740116716	0.00161672	0.28664720	0.00063000
14	0.4137	0.7280	0.727381749	0.00061830	0.30091783	0.00025600
15	0.4373	0.7065	0.706972218	0.00047222	0.30915895	0.00021000
16	0.4590	0.6755	0.675279776	0.00022020	0.30995342	0.00010100
17	0.4784	0.6320	0.630757962	0.00124200	0.30175461	0.00059400
18	0.4960	0.5730	0.571928111	0.00107190	0.28367634	0.00053200
19	0.5119	0.4990	0.499606814	0.00060681	0.25574873	0.00031000
20	0.5265	0.4130	0.413648598	0.00064860	0.21778599	0.00034000
21	0.5398	0.3165	0.317509874	0.00100987	0.17139183	0.00055000
22	0.5521	0.2120	0.212154600	0.00015460	0.11713055	0.00008500
23	0.5633	0.1035	0.102250802	0.00124920	0.05759788	0.00070400
24	0.5736	−0.0100	−0.008718296	0.00128170	−0.00500081	0.00074000
25	0.5833	−0.1230	−0.125508482	0.00250850	−0.07320910	0.00146300
26	0.5900	−0.2100	−0.208473677	0.00152632	−0.12299947	0.00090053
SIAE				0.02152594		0.00874621
Note: SIAE: Sum of IAE.

| Show Table

DownLoad: CSV

5.2. Results on the DDM

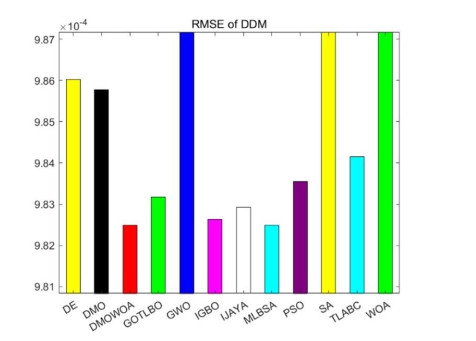
This section presents and analyzes the experimental data of DDM. Table 5 shows the parameters of DDM extracted by each algorithm. The minimum RMSE value is indicated in boldface. Figure 6 shows the bar chart of DDM. As shown in Table 5, the RMSE of DMOWOA and MLBSA are the lowest, followed by IJAYA, GOTLBO, PSO, TLABC, DMO, DE, SA, and GWO. WOA has the highest RMSE.

Table 5. DDM parameters are extracted from each algorithm.

Method	I_ph (A)	I_sd1 (μA)	I_sd2 (μA)	R_s (Ω)	R_sh (Ω)	a₁	a₂	RMSE	Runtime (s)
DMOWOA	0.760784	0.223112	0.774202	0.03675	55.55108	1.44995	2	9.824894E-04	501.87
DMO	0.760745	0.268287	0.288613	0.03645	54.61122	1.47161	2	9.857786E-04	511.14
WOA	0.760737	0.681735	0.30963	0.03670	60.94388	1.331801	1.6412	1.11496E-03	542.06
DE	0.7607742	0.322691	0.598969	0.03637	53.72476	1.63652	1.4811	9.86023E-04	544.85
SA	0.7608018	0.162530	1	0.03714	55.35953	1.94119	1.4241	9.88079E-04	1135.89
PSO	0.760775	0.357170	0.274889	0.03653	54.57654	1.46751	2	9.835519E-04	538.62
GWO	0.7606555	0.204797	0.807745	0.03640	60.71382	1.90417	1.4460	1.01086E-03	521.41
IGBO ^[61]	0.76077	0.21969	0.11923	0.03643	53.86796	1.517865	1.4468	9.826373E-04	NA
GOTLBO ^[34]	0.76075	0.80019	0.22046	0.0368	56.07530	1.99997	1.44897	9.83177E-04	NA
MLBSA ^[37]	0.7608	0.22728	0.73835	0.0367	55.4612	1.4515	2	9.8249E-04	NA
TLABC ^[32]	0.76081	0.42394	0.24011	0.03667	54.66797	1.9075	1.4567	9.84145E-04	NA
IJAYA ^[35]	0.7601	0.00504	0.75094	0.0376	77.8519	1.2186	1.6247	9.8293E-04	NA

| Show Table

DownLoad: CSV

Figure 6. RMSE bar chart of DDM.

DownLoad: Full-Size Img PowerPoint

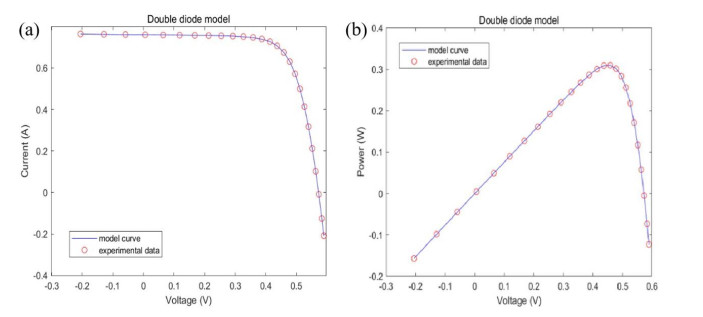
To validate the accuracy of DMOWOA, Figure 6 shows the Ⅰ-Ⅴ and P-V curves of DDM. Table 6 shows the IAE values for DDM. It can be observed from Figure 6 that the simulation results obtained using DMOWOA exhibit excellent agreement with the experimental measurements. Figure 7 further confirms the close match between DMOWOA's simulations and the model data. Furthermore, according to Table 6, the current-related IAE values are all less than 2.51E-03, and the power-related IAE values are all less than 1.46E-01, thereby confirming the high precision of the parameters extracted by DMOWOA.

Table 6. DDM: IAE of DMOWOA.

Item	Model data		Experiment current data		Experiment power data
Item	V_M (V)	I_M (A)	I_E (A)	IAE_I (A)	P_E (W)	IAE_P (W)
1	−0.2057	0.7640	0.763979398	0.00002060	−0.15715048	0.00000432
2	−0.1291	0.7620	0.762601709	0.00060170	−0.09845188	0.00007768
3	−0.0588	0.7605	0.761336799	0.00083679	−0.04476660	0.00004920
4	0.0057	0.7605	0.760174234	0.00032577	0.00433299	0.00000186
5	0.0646	0.7600	0.759109304	0.00089070	0.04903846	0.00005754
6	0.1185	0.7590	0.758124007	0.00087599	0.08983769	0.00010381
7	0.1678	0.7570	0.757191858	0.00019185	0.12705679	0.00003219
8	0.2132	0.7570	0.756247066	0.00075293	0.16123187	0.00016053
9	0.2545	0.7555	0.755180370	0.00031963	0.19219340	0.00008135
10	0.2924	0.7540	0.753724314	0.00027569	0.22038899	0.00008061
11	0.3269	0.7505	0.751399328	0.00089932	0.24563244	0.00029399
12	0.3585	0.7465	0.747299496	0.00079949	0.26790687	0.00028662
13	0.3873	0.7385	0.740006804	0.00150680	0.28660464	0.00058359
14	0.4137	0.7280	0.727242128	0.00075787	0.30086007	0.00031353
15	0.4373	0.7065	0.706846066	0.00034606	0.30910378	0.00015133
16	0.4590	0.6755	0.675208453	0.00029155	0.30992068	0.00013382
17	0.4784	0.6320	0.630761645	0.00123836	0.30175637	0.00059243
18	0.4960	0.5730	0.571998419	0.00100158	0.28371122	0.00049678
19	0.5119	0.4990	0.499711545	0.00071154	0.25580234	0.00036424
20	0.5265	0.4130	0.413739086	0.00073908	0.21783363	0.00038913
21	0.5398	0.3165	0.317550239	0.00105023	0.17141362	0.00056692
22	0.5521	0.2120	0.212124746	0.00012474	0.11711407	0.00006887
23	0.5633	0.1035	0.102162901	0.00133710	0.05754836	0.00075319
24	0.5736	−0.0100	−0.008792057	0.00120794	−0.00504312	0.00069288
25	0.5833	−0.1230	−0.125543076	0.00254308	−0.07322928	0.00148338
26	0.5900	−0.2100	−0.208367065	0.00163293	−0.12293657	0.00096343
SIAE				0.02127933		0.00878322

| Show Table

DownLoad: CSV

Figure 7. Comparison of experimental data and model data on DDM: (a) Ⅰ-Ⅴ curve, (b) P-V curve.

DownLoad: Full-Size Img PowerPoint

5.3. Results on photovoltaic modules

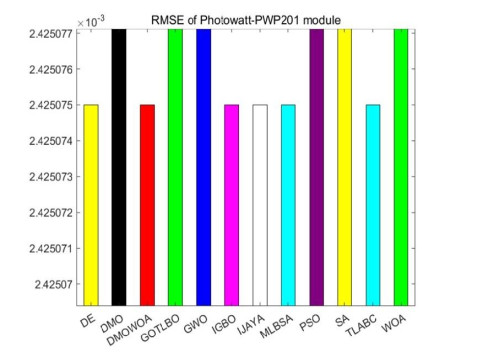
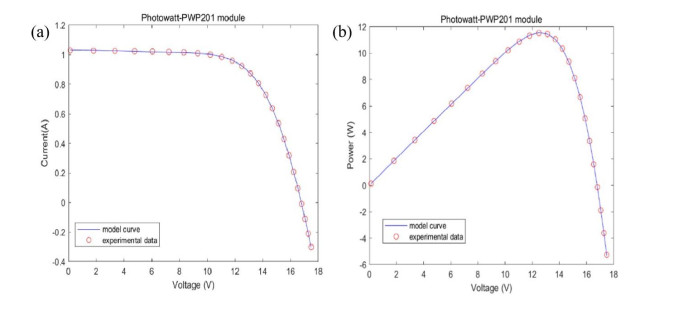
This section presents and analyzes the experimental results of three photovoltaic modules extracted by DMOWOA. Table 7 summarizes the experimental results of each algorithm for the Photowatt-PWP201 module, and Figure 8 is a bar chart of the results. As shown in Table 7, DMOWOA, MLBSA, TLABC, and IJAYA had the lowest RMSE values, followed by DMO, PSO, GOTLBO, and GWO. WOA had the highest RMSE value.

Table 7. Photowatt-PWP201 module parameters are extracted from each algorithm.

Method	I_ph (A)	I_sd (μA)	R_s (Ω)	R_sh (Ω)	a	RMSE	Runtime (s)
DMOWOA	1.030514	3.482239	1.201272	981.971946	48.642809	2.425075E-03	488.08
DMO	1.663914	1.735726	0.154112	573.027822	54.724284	2.425081E-03	507.10
WOA	1.026966	4.124698	1.189613	1953.97648	49.287535	2.604337E-03	529.81
DE	1.0305156	3.481452	1.201295	981.730091	48.641944	2.425075E-03	537.03
SA	1.0297633	3.985231	1.1871969	1153.36510	49.164517	2.453717E-03	1037.09
PSO	1.0305369	3.471742	1.2015711	978.090865	48.631283	2.425089E-03	520.57
GWO	1.0299345	4.035756	1.1853753	1136.06045	49.214774	2.460404E-03	557.67
IGBO ^[61]	1.030514	3.482264	1.201271	981.982332	48.642836	2.425075E-03	NA
GOTLBO ^[34]	1.030439	3.4573	1.201258	982.1211	48.61538	2.427130E-03	NA
MLBSA ^[37]	1.0305	3.4823	1.2013	981.9823	48.6428	2.425075E-03	NA
TLABC ^[32]	1.03056	3.4715	1.20165	972.93567	48.63131	2.42507E-03	NA
IJAYA ^[35]	1.030514	3.4822	1.201272	981.9763	48.64281	2.425075E-03	NA

| Show Table

DownLoad: CSV

Figure 8. RMSE bar chart of Photowatt-PWP201 module.

DownLoad: Full-Size Img PowerPoint

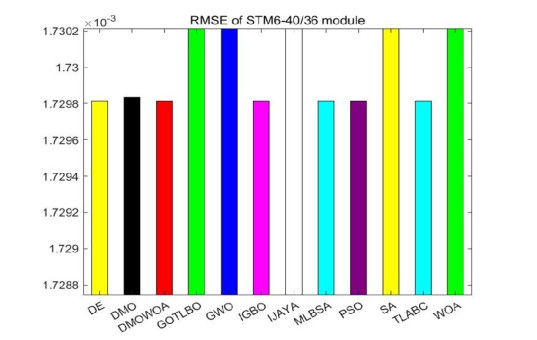
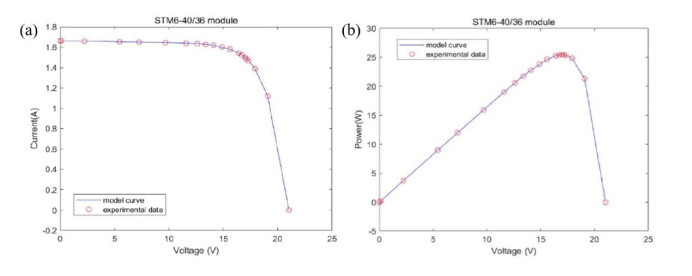
For the STM6-40/36 module, Table 8 shows the parameters extracted by each algorithm, and Figure 9 is the bar chart of RMSE. As shown in Table 8, only DMOWOA, MLBSA, and TLABC achieved the lowest RMSE values. SA had the highest RMSE value.

Table 8. STM6-40/36 module parameters are extracted from each algorithm.

Method	I_ph (A)	I_sd (μA)	R_s (Ω)	R_sh (Ω)	a	RMSE	Runtime (s)
DMOWOA	1.6639047	1.7386536	0.1538559	573.417952	54.730897	1.729814E-03	493.08
DMO	1.6639143	1.7357265	0.1541121	573.027824	54.724282	1.729834E-03	509.05
WOA	1.6620926	2.0608957	0.1378843	663.11838	55.408003	1.884297E-03	524.98
DE	1.6639003	1.7416859	0.1536555	573.732383	54.737794	1.729815E-03	533.03
SA	1.6619204	3.8724258	0.0565242	775.104134	58.093992	2.572752E-03	991.59
PSO	1.6639057	1.7379582	0.1539021	573.347891	54.729314	1.729814E-03	510.36
GWO	1.6603481	3.3048336	0.0850471	860.127103	57.389381	2.494334E-03	570.67
IGBO^[61]	1.663905	1.738653	0.153856	573.418117	54.730896	1.729814E-03	NA
GOTLBO^[63]	1.663236	2.9641	0.002246	17.90892	1.581384	2.233818E-03	NA
MLBSA^[27]	1.663905	1.7387	0.004274	15.92829	1.520303	1.729814E-03	NA
TLABC^[27]	1.6639	1.7387	0.0043	15.9283	1.5203	1.7298E-03	NA
IJAYA^[63]	1.6637	1.8353	0.0040	15.9449	1.5263	1.7548E-03	NA

| Show Table

DownLoad: CSV

Figure 9. RMSE bar chart of STM6-40/36 module.

DownLoad: Full-Size Img PowerPoint

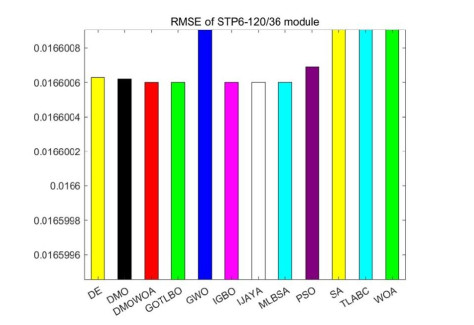
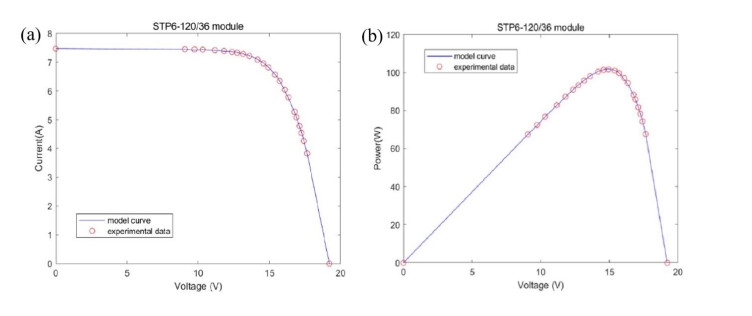
Table 9 summarizes the results of each algorithm for the STP6-120/36 module. Figure 10 presents the RMSE values of each algorithm for the STP6-120/36 module, indicating that DMOWOA, GOTLBO, MLBSA, TLABC, and IJAYA achieved the lowest RMSE values, followed by DMO, DE, PSO, and SA. GWO achieved the maximum RMSE.

Table 9. STP6-120/36 module parameters are extracted from each algorithm.

Method	I_ph (A)	I_sd (μA)	R_s (Ω)	R_sh (Ω)	a	RMSE	Runtime(s)
DMOWOA	7.4725388	2.3348795	0.1654074	799.416456	45.363577	1.660060E-02	488.63
DMO	7.4724523	2.3379871	0.1653883	805.843419	45.367562	1.660062E-02	502.95
WOA	7.4701126	2.5580463	0.1639131	1134.88340	45.639551	1.664355E-02	528.12
DE	7.4724591	2.3406457	0.1653676	806.593423	45.370987	1.660063E-02	529.53
SA	7.4713237	2.3449073	0.1653393	938.835347	45.501526	1.661138E-02	1002.39
PSO	7.4724061	1.7379582	0.1539021	811.83797	45.376454	1.660069E-02	518.40
GWO	7.4982327	7.5755745	0.1424305	934.576494	49.212400	1.925649E-02	566.35
IGBO ^[61]	7.472530	2.334995	0.165407	799.916580	45.363725	1.660060E-02	NA
GOTLBO ^[63]	7.472529	2.334887	0.004595	22.220503	1.260100	1.660060E-02	NA
MLBSA ^[27]	7.47253	2.3350	0.00459	22.21991	1.260103	1.660060E-02	NA
TLABC ^[27]	7.4725	2.3349	0.0046	22.2117	1.2601	1.6601E-02	NA
IJAYA ^[63]	7.47253	2.3350	0.00459	22.21809	1.260102	1.660060E-02	NA

| Show Table

DownLoad: CSV

Figure 10. RMSE bar chart of STP6-120/36 module.

DownLoad: Full-Size Img PowerPoint

The Ⅰ-Ⅴ and P-V curves of the Photowatt-PWP201 module are shown in Figure 11, and its IAE values are shown in Table 10. Table 10 reveals that the current-related IAE values remain below 4.83E-03, while power-related IAE values stay below 7.98E-02. Table 11 shows the IAE of the STM6-40/36 module calculated by DMOWOA, and Figure 12 shows the Ⅰ-Ⅴ and P-V curves. In Table 11, the current-related IAE values are all below 2.80E-03, and the power-related IAE values are all below 4.69E-02. Table 12 shows the IAE value of DMOWOA for the STP6-120/36 module, and Figure 13 shows the Ⅰ-Ⅴ and P-V curves of the STP6-120/36 module solved by DMOWOA. In Table 12, the current-related IAE values are all below 3.26E-02, and the power-related IAE values are all below 5.32E-01. The precision of the extracted parameters of DMOWOA be validated based on the data presented in both the table and figure.

Figure 11. Comparison of experimental data and model data on Photowatt-PWP201 module: (a) Ⅰ-Ⅴ curve, (b) P-V curve.

DownLoad: Full-Size Img PowerPoint

Table 10. Photowatt-PWP201 module: IAE of DMOWOA.

Item	Model data		Experiment current data		Experiment power data
Item	V_M (V)	I_M (A)	I_E (A)	IAE_I (A)	P_E (W)	IAE_P (W)
1	0.1248	1.0315	1.029118847	0.00238115	0.12843403	0.00029717
2	1.8093	1.0300	1.027380741	0.00261926	1.85883997	0.00473903
3	3.3511	1.0260	1.025741449	0.00025855	3.43736217	0.00086643
4	4.7622	1.0220	1.024106793	0.00210679	4.87700137	0.01003297
5	6.0538	1.0180	1.022291430	0.00429143	6.18874786	0.02597946
6	7.2364	1.0155	1.019930298	0.00443030	7.38062361	0.03205941
7	8.3189	1.0140	1.016362718	0.00236272	8.45501981	0.01965521
8	9.3097	1.0100	1.010495764	0.00049576	9.40741241	0.00461541
9	10.2163	1.0035	1.000628591	0.00287141	10.22272187	0.02933518
10	11.0449	0.9880	0.984548016	0.00345198	10.87423438	0.03812682
11	11.8018	0.9630	0.959521338	0.00347866	11.32407893	0.04105447
12	12.4929	0.9255	0.922838511	0.00266149	11.52892923	0.03324972
13	13.1231	0.8725	0.872599390	0.00009939	11.45120905	0.00130430
14	13.6983	0.8075	0.807274025	0.00022597	11.05828178	0.00309547
15	14.2221	0.7265	0.728336268	0.00183627	10.35847124	0.02611559
16	14.6995	0.6345	0.637137811	0.00263781	9.36560725	0.03877450
17	15.1346	0.5345	0.536212884	0.00171288	8.11536751	0.02592381
18	15.5311	0.4275	0.429511145	0.00201115	6.67078054	0.03123529
19	15.8929	0.3185	0.318774291	0.00027429	5.06624793	0.00435928
20	16.2229	0.2085	0.207389294	0.00111071	3.36445578	0.01801887
21	16.5241	0.1010	0.096166930	0.00483307	1.58907197	0.07986213
22	16.7987	−0.0080	−0.008325661	0.00032566	−0.13986028	0.00547068
23	17.0499	−0.1110	−0.110936796	0.00006320	−1.89146128	0.00107762
24	17.2793	−0.2090	−0.209247621	0.00024762	−3.61565242	0.00427872
25	17.4885	−0.3030	−0.300863984	0.00213602	−5.26165978	0.03735572
SIAE				0.04892354		0.51688326

| Show Table

DownLoad: CSV

Table 11. STM6-40/36 module: IAE of DMOWOA.

Item	Model data		Experiment current data		Experiment power data
Item	V_M (V)	I_M (A)	I_E (A)	IAE_I (A)	P_E (W)	IAE_P (W)
1	0.0000	1.6630	1.663458477	0.00045848	0.00000000	0.00000000
2	0.118	1.663	1.663252528	0.00025253	0.19626380	0.00002980
3	2.237	1.661	1.659551023	0.00144898	3.71241564	0.00324136
4	5.434	1.653	1.653914907	0.00091491	8.98737360	0.00497160
5	7.260	1.650	1.650566119	0.00056612	11.98311002	0.00411002
6	9.680	1.645	1.645430806	0.00043081	15.92777020	0.00417020
7	11.59	1.640	1.639233735	0.00076626	18.99871899	0.00888101
8	12.60	1.636	1.633712893	0.00228711	20.58478245	0.02881755
9	13.37	1.629	1.627286004	0.00171400	21.75681387	0.02291613
10	14.09	1.619	1.618313771	0.00068623	22.80204103	0.00966897
11	14.88	1.597	1.603090239	0.00609024	23.85398276	0.09062276
12	15.59	1.581	1.581588568	0.00058857	24.65696578	0.00917578
13	16.40	1.542	1.542330778	0.00033078	25.29422476	0.00542476
14	16.71	1.524	1.521192818	0.00280718	25.41913199	0.04690801
15	16.98	1.500	1.499194924	0.00080508	25.45632981	0.01367019
16	17.13	1.485	1.485275448	0.00027545	25.44276842	0.00471842
17	17.32	1.465	1.465654417	0.00065442	25.38513450	0.01133450
18	17.91	1.388	1.387589528	0.00041047	24.85172845	0.00735155
19	19.08	1.118	1.118391479	0.00039148	21.33890942	0.00746942
20	21.0200	0.0000	−0.000024852	0.00002485	−0.00052239	0.00052239
SIAE				0.02190395		0.28400442

| Show Table

DownLoad: CSV

Figure 12. Comparison of experimental data and model data on STM6-40/36 module: (a) Ⅰ-Ⅴ curve, (b) P-V curve.

DownLoad: Full-Size Img PowerPoint

Table 12. STP6-120/36 module: IAE of DMOWOA.

Item	Model data		Experiment current data		Experiment power data
Item	V_M (V)	I_M (A)	I_E (A)	IAE_I (A)	P_E (W)	IAE_P (W)
1	19.2100	0.0000	0.002281450	0.00228145	0.04382665	0.04382665
2	17.65	3.83	3.833350655	0.00335065	67.65863906	0.05913906
3	17.41	4.29	4.267341161	0.02265884	74.29440961	0.39449039
4	17.25	4.56	4.541152144	0.01884786	78.33487448	0.32512552
5	17.10	4.79	4.784403781	0.00559622	81.81330466	0.09569534
6	16.90	5.07	5.085581533	0.01558153	85.94632791	0.26332791
7	16.76	5.27	5.274825808	0.00482581	88.40608054	0.08088054
8	16.34	5.75	5.782600330	0.03260033	94.48768939	0.53268939
9	16.08	6.00	6.044320443	0.04432044	97.19267272	0.71267272
10	15.71	6.36	6.347122775	0.01287723	99.71329880	0.20230120
11	15.39	6.58	6.566551247	0.01344875	101.05922369	0.20697631
12	14.93	6.83	6.813611664	0.01638834	101.72722214	0.24467786
13	14.58	6.97	6.957709845	0.01229015	101.44340954	0.17919046
14	14.17	7.10	7.087575446	0.01242455	100.43094407	0.17605593
15	13.59	7.23	7.217384025	0.01261598	98.08424890	0.17145110
16	13.16	7.29	7.283998507	0.00600149	95.85742035	0.07897965
17	12.74	7.34	7.331344298	0.00865570	93.40132636	0.11027364
18	12.36	7.37	7.363181985	0.00681802	91.00892933	0.08427067
19	11.81	7.38	7.395998685	0.01599869	87.34674447	0.18894447
20	11.17	7.41	7.420314779	0.01031478	82.88491608	0.11521608
21	10.32	7.44	7.439089236	0.00091076	76.77140092	0.00939908
22	9.740	7.42	7.446761859	0.02676186	72.53146051	0.26066051
23	9.060	7.45	7.452540600	0.00254060	67.52001784	0.02301784
24	0.0000	7.4800	7.470986525	0.00901348	0.00000000	0.00000000
SIAE				0.31712351		4.55926232

| Show Table

DownLoad: CSV

5.4. Statistical results and convergence curves

In this section, the experimental results and convergence curves of different algorithms for solving the parameters of the photovoltaic model are presented and analyzed. Table 13 shows the minimum, maximum, average, and standard deviation of RMSE for PV models solved by different algorithms. All of the algorithms were run independently 30 times. In Table 13, Min represents the lowest RMSE value, Max represents the highest RMSE value, Mean represents the average RMSE value, and SD represents the algorithm's stability. The lowest RMSE values for each module are in bold. Due to the lack of specific experimental data in the literature, comparisons are limited to four basic statistical indicators, consistent with the methods of comparison in the literature. The statistical analysis of the proposed methodology is limited.

Table 13. Statistical results of different algorithms for solving photovoltaic models.

PV model	Method	RMSE
		Min	Max	Mean	SD
SDM	DMOWOA	9.860219E-04	9.964806E-04	9.870776E-04	3.188117E-06
	DMO	9.860219E-04	9.860226E-04	9.860221E-04	1.807731E-10
	WOA	1.107616E-03	4.578496E-02	7.102568E-03	1.236875E-02
	DE	9.860219E-04	1.438509E-03	1.001135E-03	8.260681E-05
	SA	1.049349E-03	2.246603E-03	1.881534E-03	3.583774E-04
	PSO	9.860259E-04	9.861631E-04	9.860669E-04	3.742250E-08
	GWO	1.005399E-03	3.815095E-02	6.366746E-03	1.267456E-02
	IGBO ^[61]	9.860219E-04	9.864489E-04	9.860444E-04	8.838088E-08
	GOTLBO ^[34]	9.87442E-04	1.98244E-03	1.33488E-03	2.99407E-04
	MLBSA ^[37]	9.8602E-04	9.8602E-04	9.8602E-04	9.1461E-12
	TLABC ^[32]	9.86022E-04	1.03970E-03	9.98523E-04	1.86022E-05
	IJAYA ^[35]	9.8603E-04	1.0622E-03	9.9204E-04	1.4033E-05
DDM	DMOWOA	9.824894E-04	1.409552E-03	9.990270E-04	7.755141E-05
	DMO	9.857786E-04	9.881073E-04	9.863471E-04	5.804664E-07
	WOA	1.114960E-03	4.118252E-02	8.491764E-03	1.326261E-02
	DE	9.860225E-04	1.106283E-03	1.011058E-03	2.937064E-05
	SA	9.880796E-04	2.206404E-03	1.335049E-03	2.916275E-04
	PSO	9.835519E-04	9.892810E-04	9.860059E-04	1.062786E-06
	GWO	1.010862E-03	3.808132E-02	2.65525E-03	6.70687E-03
	IGBO ^[61]	9.826373E-04	1.370334E-03	1.026447E-03	1.131003E-03
	GOTLBO ^[34]	9.83177E-04	1.78774E-03	1.24360E-03	2.09115E-04
	MLBSA ^[37]	9.8249E-04	9.8798E-04	9.8518E-04	1.3482E-06
	TLABC ^[32]	9.84145E-04	1.50482E-03	1.05553E-03	1.55034E-04
	IJAYA ^[35]	9.8293E-04	1.0622E-03	9.9204E-04	1.4033E-05
Photowatt-PWP201	DMOWOA	2.425075E-03	2.608133E-03	2.528525E-03	9.102414E-05
	DMO	2.425081E-03	2.425201E-03	2.425115E-03	2.670061E-08
	WOA	2.604337E-03	2.742507E-01	5.317646E-02	1.020819E-01
	DE	2.425075E-03	2.425715E-03	2.425124E-03	1.212543E-07
	SA	2.453717E-03	4.271164E-03	2.647786E-03	3.345887E-04
	PSO	2.425089E-03	2.478674E-03	2.428055E-03	9.703640E-06
	GWO	2.460404E-03	2.888445E-03	2.647212E-03	1.062403E-04
	IGBO ^[61]	2.425075E-03	2.430055E-03	2.425573E-03	1.574886E-06
	GOTLBO ^[63]	2.427130E-03	2.574944E-03	2.469844E-03	3.1248E-05
	MLBSA ^[37]	2.425075E-03	2.425312E-03	2.425084E-03	4.336794E-08
	TLABC ^[63]	2.42507E-03	2.44584E-03	2.42647E-03	3.99568E-06
	IJAYA ^[35]	2.4251E-03	2.4393E-03	2.4289E-03	3.7755E-06
STM6-40/36	DMOWOA	1.729814E-03	3.585698E-02	3.419714E-03	6.185169E-03
	DMO	1.729834E-03	1.729963E-03	1.729883E-03	3.131366E-08
	WOA	1.884297E-03	7.355741E-03	3.726836E-03	1.181472E-03
	DE	1.729815E-03	1.733418E-03	1.730283E-03	6.743370E-07
	SA	2.572751E-03	3.197710E-03	3.025829E-03	1.597912E-04
	PSO	1.729814E-03	1.734963E-03	1.730976E-03	1.294072E-06
	GWO	2.494334E-03	3.376361E-03	3.291131E-03	1.616028E-04
	IGBO ^[61]	1.729814E-03	1.729840E-03	1.729816E-03	8.152893E-09
	GOTLBO ^[63]	2.0281E-03	3.3307E-03	2.5944E-03	3.696259E-04
	MLBSA ^[27]	1.7298E-03	2.7932E-03	1.7788E-03	1.968672E-04
	TLABC ^[27]	1.7298E-03	6.5053E-03	2.1827E-03	9.22E-04
	IJAYA ^[63]	1.7298E-03	3.3248E-02	2.7814E-03	5.754224E-03
STP6-120/36	DMOWOA	1.660060E-02	2.846505E-02	1.784015E-02	3.673024E-03
	DMO	1.660062E-02	1.660071E-02	1.660066E-02	2.601586E-08
	WOA	1.664356E-02	3.558664E-02	2.582329E-02	5.148497E-03
	DE	1.660063E-02	1.664268E-02	1.664078E-02	7.583427E-06
	SA	1.661138E-02	2.593994E-02	2.380168E-02	1.903130E-03
	PSO	1.660069E-02	1.664214E-02	1.662816E-02	1.878813E-05
	GWO	1.925649E-02	1.413122E-02	7.216812E-02	2.532743E-01
	IGBO ^[61]	1.660060E-02	1.664210E-02	1.661328E-02	1.980840E-05
	GOTLBO ^[63]	1.7987E-02	3.6968E-02	2.5473E-02	5.612662E-03
	MLBSA ^[27]	1.6601E-02	1.8269E-02	1.6731E-02	3.01E-04
	TLABC ^[27]	1.6601E-02	2.1497E-02	1.6963E-02	9.47E-04
	IJAYA ^[63]	1.66006E-02	1.7155E + 00	1.3486E-01	4.298527E-01

| Show Table

DownLoad: CSV

Figure 13. Comparison of experimental data and model data on STP6-120/36 module: (a) Ⅰ-Ⅴ curve, (b) P-V curve.

DownLoad: Full-Size Img PowerPoint

For the single diode model, according to Table 13, DMOWOA achieves the lowest RMSE value, while DMO excels across minimum, maximum, and average RMSE. Furthermore, MLBSA exhibits the lowest standard deviation, indicating consistent performance.

In the double diode model analysis, Table 13 reveals that DMOWOA and MLBSA share the lowest minimum RMSE. Notably, DMO achieves the lowest mean and standard deviation, demonstrating overall stability and accuracy. Finally, MLBSA has the lowest maximum RMSE, suggesting its potential for robust performance across diverse scenarios.

For the Photowatt-PWP201 module, according to Table 13, DMOWOA achieves the lowest minimum RMSE. Interestingly, DMO dominates in all three categories, boasting the lowest maximum mean square error, root mean square error, and standard deviation.

Table 13 shows that DMOWOA obtains the lowest value in the 'Min' category for both the STM6-40/36 and STP6-120/36 modules. For the STM6-40/36 module, IGBO also achieves the lowest values in the 'Max' and 'SD' categories, while DMO achieves the lowest value in the 'Mean' category. For the STP6-120/36 module, DMOWOA performs well in all categories, demonstrating its strong competitiveness. DMO achieves the lowest values in the 'Max', 'Mean', and 'SD' categories for this module.

A visual inspection of Figure 14 suggests that DMOWOA achieves the fastest convergence speed. DMOWOA's performance is particularly noteworthy for the DDM and STM6-40/36 modules, where it converges to the optimal solution in the fewest iterations. Based on the results, DMOWOA is a promising candidate for the robust, efficient, and accurate extraction of photovoltaic model parameters.

Figure 14. Convergence curves: (a) single diode model, (b) double diode model, (c) Photowatt-PWP201 module, (d) STM6-40/36 module, (e) STP6-120/36 module.

DownLoad: Full-Size Img PowerPoint

5.5. Comparison with literature

This section compares the experimental results of DMOWOA for various PV models with those reported in the literature. Table 3 compares the performance of DMOWOA, IGBO ^[61], GOTLBO ^[34], MLBSA ^[37], TLABC ^[35], and IJAYA ^[35] in solving the SDM. DMOWOA achieves the lowest RMSE value among all algorithms in Table 3. In Table 5, DMOWOA and MLBSA achieve the lowest RMSE values, followed by IGBO ^[61], IJAYA ^[35], GOTLBO ^[34], and TLABC ^[35].

The analysis findings for various photovoltaic models are proposed as follows. For the Photowatt-PWP201 module, in Table 7, DMOWOA and IGBO ^[61], GOTLBO ^[63], MLBSA ^[37], TLABC ^[63] all got the minimum RMSE, and the worst was IJAYA. In Table 8, the results of extracting parameters of the STM6-40/36 module are shown. DMOWOA and IGBO ^[61], MLBSA ^[27], TLABC ^[27], IJAYA ^[63] all obtained the minimum RMSE, and GOTLBO ^[63] got the maximum. For the STP6-120/36 module, in Table 9, DMOWOA and IGBO ^[61], MLBSA ^[27], TLABC ^[27], IJAYA ^[63] all obtained the minimum RMSE, and GOTLBO ^[63] obtained the maximum RMSE.

Overall, DMOWOA achieved the lowest RMSE value in all models. This is consistent with the results of previous studies and even outperforms other methods in some models. Therefore, DMOWOA is a promising candidate for efficient, accurate, and alternative PV model parameter extraction.

6. Conclusions and future work

The accurate extraction of photovoltaic parameters plays a key role in the design and efficient operation of photovoltaic systems. In this study, combining the DMO and the WOA, an adaptive dwarf mongoose optimization algorithm of the hybrid whale algorithm is proposed. In this method, the integration of the search phase of dwarf mongoose and the bubble net attack mode of the whale optimization algorithm was employed to enhance its capability to escape local optima. Reconcile exploration and exploitation by incorporating inertia weights. The proposed algorithm is employed to solve various photovoltaic models to validate its performance. The experimental results are compared with other established algorithms. The test data demonstrates that DMOWOA can quickly and accurately obtain results and has strong competitiveness in accuracy and reliability. The proposed DMOWOA can serve as an efficient alternative approach for addressing the parameter estimation of photovoltaic models. However, the proposed DMOWOA cannot solve multi-objective optimization problems. In future work, the proposed algorithm can be enhanced by incorporating other methodologies, thereby addressing various optimization problems within the energy domain.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (U21A20464), the Innovation Project of Guangxi Graduate Education (YCSW2023259).

Conflict of interest

The authors declare no conflict of interest.

Author contributions

Shijian Chen carried out the DMOWOA algorithm studies, participated in the drafted the manuscript. Yongquan Zhou carried out the review & editing; Qifang Luo carried out the DMOWOA test. All authors read and approved the final manuscript.

References

[1]	Du P, Lu N (2011) Appliance commitment for household load scheduling. IEEE Trans Smart Grid 2: 411–419. https://doi.org/10.1109/TSG.2011.2140344 doi: 10.1109/TSG.2011.2140344
[2]	Mishra A, Irwin D, Shenoy P, et al. (2013) Greencharge: Managing renewable energy in smart buildings. IEEE J Selected Areas Commun 31: 1281–1293. https://doi.org/10.1109/JSAC.2013.130711 doi: 10.1109/JSAC.2013.130711
[3]	Li W, Logenthiran T, Woo WL (2015) Intelligent multi agent system for smart home energy management. IEEE Innovative Smart Grid Technologies Asia (ISGT ASIA), Bangkok, Thailand. https://doi.org/10.1109/ISGT-Asia.2015.7386985 doi: 10.1109/ISGT-Asia.2015.7386985
[4]	Corno F, Razzak F (2012) Intelligent energy optimization for user intelligible goals in smart home environments. IEEE Trans Smart Grid 3: 2128–2135. https://doi.org/10.1109/TSG.2012.2214407 doi: 10.1109/TSG.2012.2214407
[5]	Khan ZA, Ahmed S, Nawaz R, et al. (2015) Optimization based individual and cooperative DSM in smart grids: A review. Power Generation System and Renewable Energy Technologies (PGSRET), IEEE. https://doi.org/10.1109/PGSRET.2015.7312239 doi: 10.1109/PGSRET.2015.7312239
[6]	Boynuegri AR, Yagcitekin B, Baysal M, et al. (2013) Energy management algorithm for smart home with renewable energy sources. 4th International Conference on Power Engineering, Energy and Electrical Drives, IEEE, 1753–1758. https://doi.org/10.1109/PowerEng.2013.6635883
[7]	Saha A, Kuzlu M, Khamphanchai W, et al. (2014) A home energy management algorithm in a smart house integrated with renewable energy. IEEE PES Innovative Smart Grid Technologies, Europe, IEEE, 1–6. https://doi.org/10.1109/ISGTEurope.2014.7028970 doi: 10.1109/ISGTEurope.2014.7028970
[8]	Et-Tolba El H, Ouassaid, M, Maaroufi M (2016) Smart home appliances modeling and simulation for energy consumption profile development: Application to Moroccan real environment case study. In 2016 International Renewable and Sustainable Energy Conference (IRSEC), 1050–1055. https://ieeexplore.ieee.org/abstract/document/7983908
[9]	Schné T, Jaskó S, Simon G (2015) Dynamic models of a home refrigerator. MACRo 1: 103–112. https://doi.org/10.1515/macro-2015-0010 doi: 10.1515/macro-2015-0010
[10]	Shareef H, Ahmed MS, Mohamed A, et al. (2018) Review on home energy management system considering demand responses, smart technologies, and intelligent controllers. IEEE Access 6: 24498–24509. https://doi.org/10.1109/ACCESS.2018.2831917 doi: 10.1109/ACCESS.2018.2831917
[11]	Boodi A, Beddiar K, Benamour M, et al. (2018) Intelligent systems for building energy and occupant comfort optimization: A state of the art review and recommendations. Energies 11: 2604. https://doi.org/10.3390/en11102604 doi: 10.3390/en11102604
[12]	Zhang D, Evangelisti S, Lettieri P, et al. (2016) Economic and environmental scheduling of smart homes with microgrid: DER operation and electrical tasks. Energy Convers Manag 110: 113–124. https://doi.org/10.1016/j.enconman.2015.11.056 doi: 10.1016/j.enconman.2015.11.056
[13]	Naz M, Iqbal Z, Javaid N, et al. (2018) Efficient power scheduling in smart homes using hybrid grey wolf differential evolution optimization technique with real time and critical peak pricing schemes. Energies 11: 384. https://doi.org/10.3390/en11020384 doi: 10.3390/en11020384
[14]	Xiong G, Chen C, Kishore S, et al. (2011) Smart (in home) power scheduling for demand response on the smart grid. ISGT 2011, IEEE, 1–7. Available from: https://ieeexplore.ieee.org/abstract/document/5759154.
[15]	Radhakrishnan A, Selvan MP (2014) Load scheduling for smart energy management in residential buildings with renewable sources. In 2014 Eighteenth National Power Systems Conference (NPSC), 1–6. https://doi.org/10.1109/NPSC.2014.7103825 doi: 10.1109/NPSC.2014.7103825
[16]	Zhang Y, Zeng P, Li S, et al. (2015) A novel multiobjective optimization algorithm for home energy management system in smart grid. Math Probl Eng, 2015. https://doi.org/10.1155/2015/807527 doi: 10.1155/2015/807527
[17]	Fanti MP, Mangini AM, Roccotelli M (2018) A simulation and control model for building energy management. Control Eng Pract 72: 192–205. https://doi.org/10.1016/j.conengprac.2017.11.010 doi: 10.1016/j.conengprac.2017.11.010
[18]	dos Reis FB, Tonkoski R, Hansen TM (2020) Synthetic residential load models for smart city energy management simulations. IET Smart Grid 3: 342–354. https://doi.org/10.1049/iet-stg.2019.0296 doi: 10.1049/iet-stg.2019.0296
[19]	Hosseini A, Safari MM, Nazari heris M, et al. (2021) Application of Internet of Things (IoT) to demand side management in smart grids. In: Introduction to Internet of Things in Management Science and Operations Research, 169–183. Springer, Cham. https://doi.org/10.1007/978-3-030-74644-5_8
[20]	Tostado-Véliz M, Gurung S, Jurado F (2022) Efficient solution of many objective home energy management systems. Int J Electr Power Energy Syst 136: 107666. https://doi.org/10.1016/j.ijepes.2021.107666 doi: 10.1016/j.ijepes.2021.107666
[21]	Tostado-Véliz M, Mouassa S, Jurado F (2021) A MILP framework for electricity tariff choosing decision process in smart homes considering 'Happy Hours' tariffs. Int J Electr Power Energy Syst 131: 107139. https://doi.org/10.1016/j.ijepes.2021.107139 doi: 10.1016/j.ijepes.2021.107139
[22]	Tostado-Véliz M, Bayat M, Ghadimi A, et al. (2021) Home energy management in off grid dwellings: Exploiting flexibility of thermostatically controlled appliances. J Cleane Prod 310: 127507. https://doi.org/10.1016/j.jclepro.2021.127507 doi: 10.1016/j.jclepro.2021.127507
[23]	Tostado-Véliz M, Icaza-Alvarez D, Jurado F (2021) A novel methodology for optimal sizing photovoltaic-battery systems in smart homes considering grid outages and demand response. Renewable Energy 170: 884–896. https://doi.org/10.1016/j.renene.2021.02.006 doi: 10.1016/j.renene.2021.02.006
[24]	Molla T, Khan B, Moges B, et al. (2019) Integrated optimization of smart home appliances with cost-effective energy management system. CSEE J Power Energy Syst 5: 249–258. https://doi.org/10.17775/CSEEJPES.2019.00340 doi: 10.17775/CSEEJPES.2019.00340
[25]	Lee S, Choi DH (2020) Energy management of smart home with home appliances, energy storage system and electric vehicle: A hierarchical deep reinforcement learning approach. Sensors 20: 2157. https://doi.org/10.3390/s20072157 doi: 10.3390/s20072157
[26]	Waseem M, Lin Z, Liu S, et al. (2020) Optimal GWCSO-based home appliances scheduling for demand response considering end users comfort. Electr Power Syst Res 187: 106477. https://doi.org/10.1016/j.epsr.2020.106477 doi: 10.1016/j.epsr.2020.106477
[27]	Alimi OA, Ouahada K (2018) Smart home appliances scheduling to manage energy usage. 2018 IEEE 7th International Conference on Adaptive Science & Technology (ICAST), IEEE. https://doi.org/10.1109/ICASTECH.2018.8507138 doi: 10.1109/ICASTECH.2018.8507138
[28]	Mahmood A, Javaid N, Khan NA, et al. (2016) An optimized approach for home appliances scheduling in smart grid. In 2016 19th International Multi Topic Conference (INMIC), 1–5. https://doi.org/10.1109/INMIC.2016.7840158 doi: 10.1109/INMIC.2016.7840158
[29]	Amer A, Shaban K, Gaouda, et al. (2021) Home energy management system embedded with a multi-objective demand response optimization model to benefit customers and operators. Energies 14: 257. https://doi.org/10.3390/en14020257 doi: 10.3390/en14020257
[30]	Minhas DM, Frey G (2019) Modeling and optimizing energy supply and demand in home area power network (HAPN). IEEE Access 8: 2052–2072. https://doi.org/10.1109/ACCESS.2019.2962660 doi: 10.1109/ACCESS.2019.2962660
[31]	Soleimani H, Chhetri P, Fathollahi-Fard A, et al. (2022) Sustainable closed-loop supply chain with energy efficiency: Lagrangian relaxation, reformulations and heuristics. Ann Oper Res: 1–26. https://doi.org/10.1007/s10479-022-04661-z doi: 10.1007/s10479-022-04661-z
[32]	Ghadami N, Gheibi M, Kian Z, et al. (2021) Implementation of solar energy in smart cities using an integration of artificial neural network, photovoltaic system and classical Delphi methods. Sustain. Cities Soc 74: 103149. https://doi.org/10.1016/j.scs.2021.103149 doi: 10.1016/j.scs.2021.103149
[33]	Shahsavar M, Akrami M, Gheibi M, et al. (2021) Constructing a smart framework for supplying the biogas energy in green buildings using an integration of response surface methodology, artificial intelligence and petri net modelling. Energy Convers Manag 248: 114794. https://doi.org/10.1016/j.enconman.2021.114794 doi: 10.1016/j.enconman.2021.114794
[34]	Arturo Soriano L, Yu W, Rubio JDJ (2013) Modeling and control of wind turbine. Math Probl Eng, 2013. https://doi.org/10.1155/2013/982597 doi: 10.1155/2013/982597
[35]	Vinod, Kumar R, Singh SK (2018) Solar photovoltaic modeling and simulation: As a renewable energy solution. Energy Rep 4: 701–712. https://doi.org/10.1016/j.egyr.2018.09.008 doi: 10.1016/j.egyr.2018.09.008
[36]	Dubarry M, Baure G, Pastor-Fernández C, et al. (2019) Battery energy storage system modeling: A combined comprehensive approach. J Energy Storage 21: 172185. https://doi.org/10.1016/j.est.2018.11.012 doi: 10.1016/j.est.2018.11.012
[37]	Tecchio P, Ardente F, Mathieux F, et al. (2019) Understanding lifetimes and failure modes of defective washing machines and dishwashers. J Cleane Prod 215: 1112–1122. https://doi.org/10.1016/j.jclepro.2019.01.044 doi: 10.1016/j.jclepro.2019.01.044
[38]	Bengtsson P, Berghel J, Renström R, et al. (2015) A household dishwasher heated by a heat pump system using an energy storage unit with water as the heat source. J Int Acad Refrig 49: 19–27. https://doi.org/10.1016/j.ijrefrig.2014.10.012 doi: 10.1016/j.ijrefrig.2014.10.012
[39]	Lopez J, Pouresmaeil E, Canizares C, et al. (2018) Smart residential load simulator for energy management in smart grids. IEEE Trans Ind Electron 66: 14431452. https://doi.org/10.1109/TIE.2018.2818666 doi: 10.1109/TIE.2018.2818666
[40]	Zhang W, Lian J, Chang CY, et al. (2013) Aggregated modeling and control of air conditioning loads for demand response. IEEE Trans Power Syst 28: 4655–4664. https://doi.org/10.1109/TPWRS.2013.2266121 doi: 10.1109/TPWRS.2013.2266121
[41]	Elamari K, Lopes LAC, Tonkoski R, et al. (2011) Using electric water heaters (EWHs) for power balancing and frequency control in PV-Diesel Hybrid mini-grids. Doctoral dissertation, Concordia University. https://doi.org/10.3384/ecp11057842

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)