Citation: Pedro J. B. F. N. Beirão, Cândida M. S. P. Malça, Raimundo P. Felismina. Influence of design parameters on the structural and fatigue behaviors of a floating point wave energy converter[J]. AIMS Energy, 2017, 5(2): 209-223. doi: 10.3934/energy.2017.2.209
| [1] | Cândida M. S. P. Malça, Pedro J. B. F. N. Beirão, Raimundo P. Felismina . Influence of material selection on the structural behavior of a wave energy converter. AIMS Energy, 2014, 2(4): 359-372. doi: 10.3934/energy.2014.4.359 |
| [2] | Pedro Beirão, Duarte Valério . Numerical comparison between deep water and intermediate water depth expressions applied to a wave energy converter. AIMS Energy, 2015, 3(4): 525-546. doi: 10.3934/energy.2015.4.525 |
| [3] | Navid Majdi Nasab, Jeff Kilby, Leila Bakhtiaryfard . Integration of wind and tidal turbines using spar buoy floating foundations. AIMS Energy, 2022, 10(6): 1165-1189. doi: 10.3934/energy.2022055 |
| [4] | Frederick N.-F. Chou, Chia-Ying Chang, Yang-Yih Chen, Yi-Chern Hsieh, Chia-Tzu Chang . Experiment of a new style oscillating water column device of wave energy converter. AIMS Energy, 2015, 3(3): 421-427. doi: 10.3934/energy.2015.3.421 |
| [5] | Angelo Minotti . Hybrid energy converter based on swirling combustion chambers: the hydrocarbon feeding analysis. AIMS Energy, 2017, 5(3): 506-516. doi: 10.3934/energy.2017.3.506 |
| [6] | Wan Nabila Mohd Fairuz, Illani Mohd Nawi, Mohamad Radzi Ahmad, Ramani Kannan . Design analysis and simulation of serpentine-shaped piezoelectric cantilever beam for pipeline vibration-based energy harvester. AIMS Energy, 2024, 12(3): 561-599. doi: 10.3934/energy.2024027 |
| [7] | Carla Viveiros, Rui Melicio, Victor Mendes, Jose Igreja . Adaptive and predictive controllers applied to onshore wind energy conversion system. AIMS Energy, 2018, 6(4): 615-631. doi: 10.3934/energy.2018.4.615 |
| [8] | Chris Knight, Scott McGarry, Jennifer Hayward, Peter Osman, Sam Behrens . A review of ocean energy converters, with an Australian focus. AIMS Energy, 2014, 2(3): 295-320. doi: 10.3934/energy.2014.3.295 |
| [9] | Lin Dong, Michael Grissom, Frank T. Fisher . Resonant frequency of mass-loaded membranes for vibration energy harvesting applications. AIMS Energy, 2015, 3(3): 344-359. doi: 10.3934/energy.2015.3.344 |
| [10] | Chi Van Nguyen, Thuy Nguyen Vinh . Design of energy balancing circuit for battery cells connected in series based on modifying the bidirectional CuK converter. AIMS Energy, 2022, 10(2): 219-235. doi: 10.3934/energy.2022012 |
The demand for energy production, specifically for electricity, has been consistently raising since the last century. More recently, in the last decades the world energy consumption increased considerably and in the future the tendency is to grow even further. Renewable energy sources will soon play an important role. Among them, ocean wave energy is one of the most promising alternatives to fossil fuels regarding the production of electricity [1]. The energy that can be extracted from sea waves offers a high-power density when compared with more developed technologies like solar and wind energies. Although suffering from strong inter-annual and inter-seasonal variabilities [2,3], wave energy supplies a more stable source of renewable energy, when compared with those renewable energies. This allows the utilization of wave energy converters (WEC) over the year. Moreover, their customization through engineering solutions will permit to match those devices to different ocean climates [4].
Although at an early stage of development, wave energy must be considered as a promising source of energy supply. However, suitable devices to deal with this kind of energy source and convert it into electricity are not yet technically feasible and commercially available. It is expected that they will be in the medium and long term, as they are currently under development. Some of the several WEC concepts being tested have already reached full scale [5]. However, they are not yet competitive and require a great deal of investigation in several areas, namely from structural, dynamics and aerodynamics standpoints. Finite element analysis (FEA) has been extensively used in several engineering domains. In the renewable energy field, the structural and fatigue analysis is mainly dedicated to wind systems [6,7,8]. Still, its application to the wave energy field is not so much exploited, being primarily devoted to mooring systems [9] and inspired by the knowledge gathered from offshore floating structures, like oil platforms and shipbuilding [10,11,12].
This numerical study is focused on structural and fatigue analysis of a floating point WEC through numerical results obtained by FEA. The objective is to avoid plastic deformation and short fatigue life. It is divided in several parts, described as follows: a) The first purpose comprises the analysis of several WEC design parameters, such as the type of materials and dimensions employed in the WEC components. It will be shown if there is any relation between different materials and dimensions, and stress concentrations and displacement fields, to avoid plastic deformation. b) The second goal includes the analysis of the influence of several buoy characteristics, such as dimensions, geometries and submerged conditions. It will be shown if there is any relation between buoy dimensions or components’ dimensions or the selection of different materials and stress concentrations and displacement fields, to avoid plastic deformation. In what concerns the buoy geometries, it will be determined which is the one leading to the best WEC structural behavior. Concerning the buoy submerged conditions, it will be determined the buoy critical position. c) The final aim comprises the analysis between fatigue and materials and dimensions selected for the WEC components.
It is expected that numerical results, obtained by means of simulations, could give some guidance to improve the structural components, to enhance their mechanical performance on the structural and fatigue behaviors of the entire WEC. Specifically, it is intended to show if there is any relation between applied forces (simulating several sea conditions) and the selection of dimensions and materials of the WEC components. WEC components can, thus, be optimized to reach the best structural performance, according with several specific characteristics [13,14,15,16].
Finally, this paper does not aim to show any kind of correlation between structural problems and energy production. Moreover, this paper is not focused on any structural problems observed in a specific WEC.
Based on a well proven conventional design of a near shore floating point absorber WEC defined by a very small characteristic dimension when compared with the typical wave length [17] this study analyzes, from a structural standpoint, several design parameters. The main components of the WEC used in this study include a floating buoy (assumed to have different characteristics) connected by supporting cables to a double effect hydraulic cylinder. An electric linear generator, connected to the piston rod of the double effect hydraulic cylinder acts as power take-off (PTO) responsible by the conversion of the wave energy into electrical energy. A cardan joint connects the double effect hydraulic cylinder to the mooring system. The cardan joint allows six modes of motion, however and due to simplicity reasons the buoy is assumed to oscillate only in heave mode. Figure 1 schematizes the WEC used in this study.
Figure 1. 3D CAD model of the WECIts working principle is quite simple: when submitted to the sea waves the buoy heaves upwards under the influence of a wave crest and heaves downwards under the effect of a wave trough. Therefore, the piston rod of the hydraulic cylinder can travel between a fully advanced position and a fully retracted position, respectively.
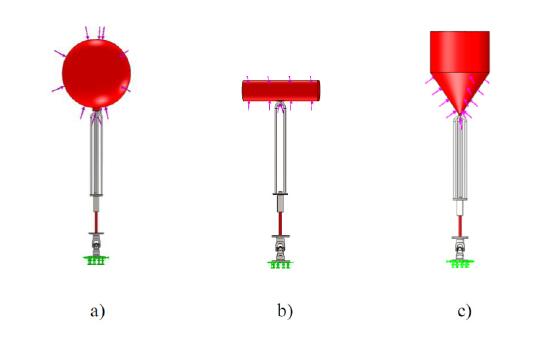
The objective of this study is to analyze the influence of several design parameters, such as buoy characteristics-dimensions, geometries and submerged conditions-on the WEC structural behavior, when a resultant force is applied to the external surface of the buoy. Therefore, three different geometries were considered for the buoy-spherical, cylindrical and tulip (tulip geometry results from a combination between a cone and a cylinder). Additionally, for the spherical buoy geometry, three different radiuses were assumed. Three different submerged conditions were also considered for the buoy-totally submerged, partially submerged and buoy at the surface.
To perform the study, a tridimensional computer aided design (3D CAD) numerical model was initially built and several FEA were performed through the Simulation tool of SolidWorks® software [18]. This commercial finite element code needs, among other inputs, the pressure value related with the resultant force that acts upon the buoy. That value was obtained, by means of simulations, by a time domain simulator obtained from the dynamic model of the WEC [19]. Figure 2 shows the boundary and load conditions applied to the developed 3D CAD models [20].
Figure 2. 3D CAD models with boundary and load conditionsConcerning the boundary conditions, it can be observed that the inferior half of the cardan joint is rigidly fixed. This means that constraints of no displacements and rotations are applied to simulate the WEC mooring system at the sea bottom [20].
The finite element model for the three buoy geometries is shown in Figure 3. For a better accuracy, a relatively fine mesh of triangular elements was applied. The selected solid mesh resulted from the meshing sensitivity study previously performed [20].
Figure 3. Mesh geometry for the three buoy geometriesRegarding the elastic material properties of the buoy, most of the buoys commercially available employ different materials for the core and shell. However, due to simplicity reasons, it was assumed that both the buoy core and shell are made of polyethylene. Additionally, it is assumed that all remaining components of the WEC are made of stainless steel AISI 316 (SS) and/or high strength steel (HSS). Table 1 summarizes the relevant elastic material properties considered for both the buoy and the remaining components of the WEC [20].
| Material | Young’s modulus [MPa] | Poisson coefficient | Yield strength [MPa] | Density [kgm-3] |
| Polyethylene | 1860 x 10-6 | 0.39 | 30 | 940 |
| AISI 316 SS | 193000 | 0.27 | 172 | 8000 |
| HSS | 21000 | 0.28 | 620 | 7700 |
DownLoad: CSVThe resultant external force assumed to act upon the buoy was computed by means of simulations obtained from a dynamic simulator based on the dynamic model of the WEC. Due to the dynamic model nonlinearities, the simulator was built in the time domain using Matlab/Simulink software.
The dynamic model of the WEC assumes that the floating buoy is excited by sea waves. Linear wave theory is used since it is also assumed that wave amplitudes and oscillations are sufficiently small when compared with the wavelength [5,17]. The external force acting on the buoy results from the influence of two forces: i) hydrostatic force resulting from the combination of PTO force, buoyancy force exerted on the buoy due to the instantaneous buoy position with respect to the seawater free surface and drag force; ii) hydrodynamic force decomposed into two components acting upon the wetted buoy surface, known as heave excitation force due to the incident waves acting upon the assumed stationary buoy and radiation force due to the energy transfer from the heaving buoy to the waves that are being radiated away from the buoy [17]. The derived equations were grouped into a dynamic model block, under individual subsystems. Another block simulates the sea waves. Several inputs such as buoy and wave data, among others are needed to run the simulation. A more detailed description about the dynamic model and simulator can be found in [19].
Pressure values, needed as inputs in the commercial finite element code, were obtained from the relation between the resultant external force acting upon the buoy [it was assumed a maximum resultant hydrodynamic force of 50 × 103 N (peak to peak amplitude)] and the projected area of the buoy. Those values can change due to variations, for instance, in the buoy geometry or radius and/or in wave parameters. If the wave input parameters are modified different results will be obtained.
To analyze the influence of several buoy characteristics-dimensions, geometries and submerged conditions-on the structural behavior of the WEC, several simulations were done using the Simulation tool of SolidWorks® software [18]. FEA provides an insight into the magnitude of the displacement (deformation) and stress concentrations, as well as their location. In the following figures areas where maximum values occur are displayed in red. Notice that when considering the wave crest, the hydraulic cylinder piston rod is assumed to be at fully advanced position. This position of the hydraulic cylinder piston rod leads to a higher magnitude of stresses in the piston rod than those achieved for the retracted position of the hydraulic cylinder piston rod, as shown in [20]. Therefore, results presented hereafter correspond to the full advanced hydraulic cylinder piston rod.
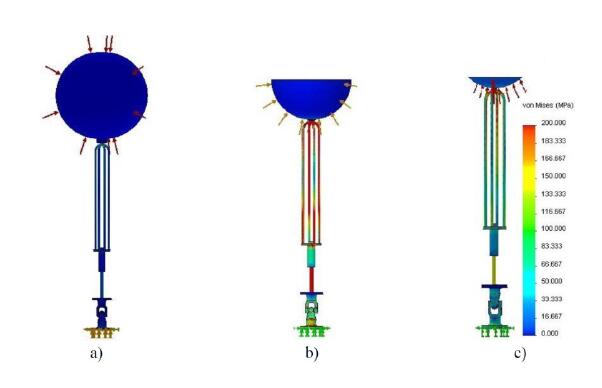
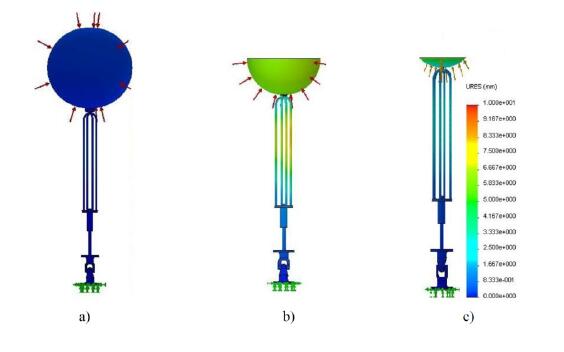
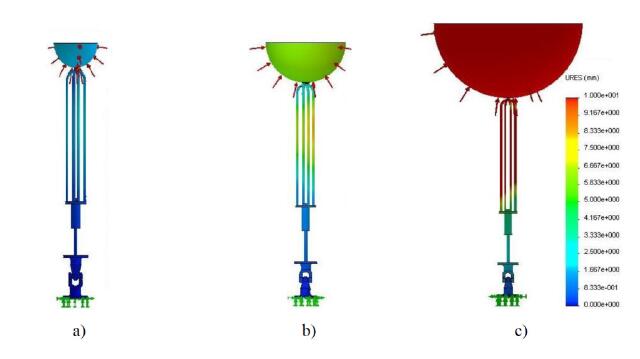
The influence of the three different submerged buoy conditions-buoy at the surface, partially and totally submerged buoy-on the structural behavior of the WEC is shown in Figure 4 and 5, respectively. Stress and displacement fields are displayed for the spherical buoy geometry.
Figure 4. Von Mises stress field for 200 mm radius spherical buoy for different buoy submerged conditions: a) totally submerged, b) partially submerged and c) at the surface
Figure 5. Displacement field for 200 mm radius spherical buoy for different buoy submerged conditions: a) totally submerged, b) partially submerged and c) at the surfaceFor the buoy at the surface, a considerable decrease on both maximum stresses and displacements was obtained. This is remarkable for the totally submerged buoy, where stresses and displacements reached values around six and eight times, respectively, lower than those verified for the partially submerged condition of the buoy. Among the three positions considered, the partially submerged buoy position corresponds to the critical buoy position. Moreover, this is the most expected position of the buoy when it heaves due to the action of the sea waves. Therefore, only the submerged condition corresponding to the buoy partially submerged was considered in the following analysis.
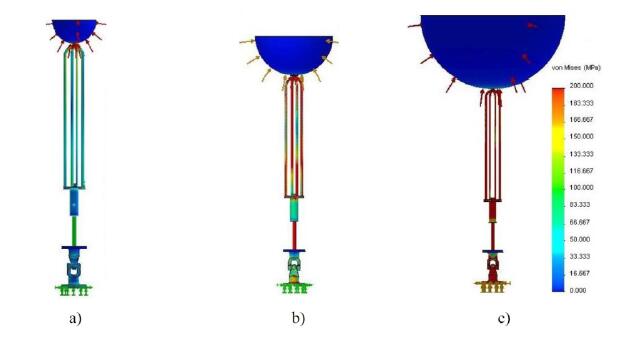
Figure 6 shows the Von Mises stress gradient determined by FEM for partially submerged polyethylene spherical buoys with radius of 100 mm, 200 mm and 400 mm, respectively. Corresponding displacement fields are shown in Figure 7.
Figure 6. Von Mises stress field for a) 100 mm, b) 200 mm and c) 400 mm radius spherical
Figure 7. Displacement field for a) 100 mm, b) 200 mm and c) 400 mm radius sphericalIt can be seen from Figure 6 and7 that the spherical buoy with radius of 100 mm leads to the lowest values of stresses and displacements and, consequently, to the best mechanical structural behavior because the yield strength of the materials is never attained and plastic deformation is not reached.
For the radius of 200 mm and 400 mm the scenario is substantially different. Plastic deformation is reached for most of the components (excluding the buoy) since maximum stress values largely exceed the yield strength of AISI 316 SS. The collapse of the structure is, therefore, predictable. This conclusion is supported by the displacement field values shown in Figure 7. The increase of the buoy dimensions lead to a significantly increase of the displacements, reaching unacceptable values for the two highest radii simulated. As expected, maximum displacements take place at the buoy and at the supporting cables, whereas areas of highest stress concentration occur in the piston rod and in the supporting cables.
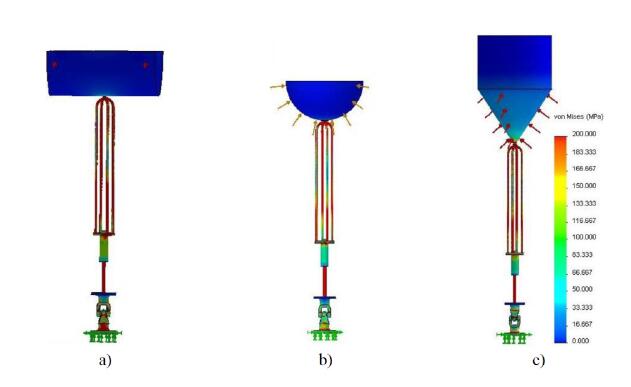
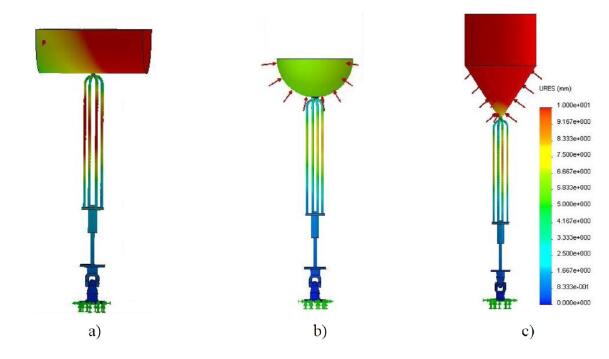
The influence of the buoy geometry on the structural behavior was also studied. Figure 8 and 9 illustrate the resulting Von Mises stress and displacement fields for the three different buoy geometries under study.
Figure 8. Von Mises stress field for a) cylindrical, b) 200 mm radius spherical and c) tulip
Figure 9. Displacement field for a) cylindrical, b) 200 mm radius spherical and c) tulipResults reveal that for maximum stress values, no significant differences were observed between geometries. However, for the cylindrical buoy geometry, a greater number of WEC components are submitted to maximum stress values. Additionally, since maximum stresses are greater than the yield stress of the AISI 316 SS used for the supporting cables, piston rod and cardan joint, plastic deformation is reached. The greatest magnitude of stresses and displacements founded in the cylindrical geometry is justified by its higher projected area (where the corresponding pressure is applied).
If the comparison between buoy geometries is made in terms of the displacement field values, the superior mechanical behavior achieved by the spherical geometry is unquestionable, which is confirmed by the lower displacements obtained, as shown in Figure 9. For cylindrical and tulip buoy geometries and for the design parameters considered-applied load, dimensions of the components and materials-the displacements have the same magnitude of the component dimensions, which means that greater deformations take place and that the collapse of the structure is reached.
This situation can be avoided by adjusting (function of the magnitude of the applied resultant force) the dimensions and/or through a suitable selection of the elastic material properties of the WEC components, as shown in the following section.
The WEC numerical model that was developed allows the single simulation of each one of the following design parameters-material and dimensions selected for the WEC components or their combination.
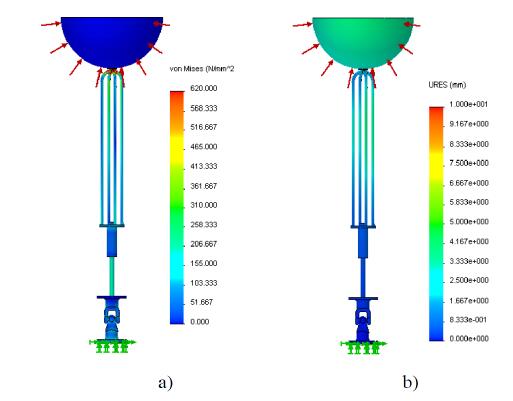
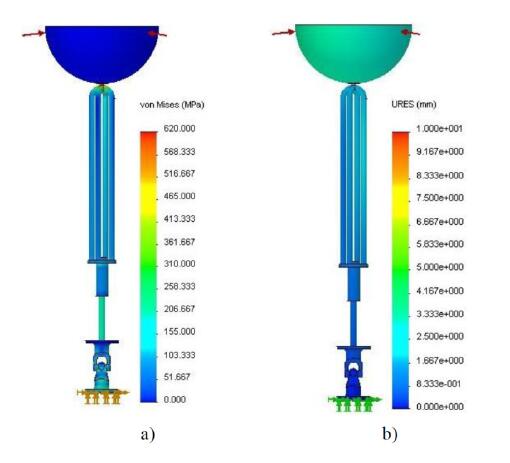
As an example, Figure 10 shows, for the 200 mm radius spherical buoy, the influence on maximum stress and displacement values if HSS with yield strength of 620 MPa is selected for the components, instead of the original SS with yield strength of 172 MPa (values from Table 1). Although a slight increase on the buoy deformation, maximum stresses decrease substantially.
Figure 10. a) Von Mises stress and b) displacement fields for 200 mm radius spherical buoy, HSS components, 15 mm supporting cables and 20 mm piston rod diametersConcerning the resizing of the WEC, an increase of 5 mm on both the supporting cables and piston rod diameters was considered. Additionally, a different selection of materials was also assumed for the components, which are now assumed to be made of HSS instead of SS.
Figure 11 shows the results obtained in terms of maximum stress and displacements. A significant reduction of maximum stress and displacement values was obtained.
Figure 11. a) Von Mises stress and b) displacement fields for 200 mm radius spherical buoy, HSS components, 20 mm supporting cables and 25 mm piston rod diametersTable 2 summarizes all cases and combinations previously studied.
| Von Mises stress field [MPa] | Displacement field [mm] | |
| Cylindrical | Figure 8 | Figure 9 |
| Spherical | Figures 4,6,8 | Figures 5,7,9 |
| Tulip | Figure 8 | Figure 9 |
| Buoy totally submerged | Figure 4 | Figure 5 |
| Buoy partially submerged | Figure 4 | Figure 5 |
| Buoy at the surface | Figure 4 | Figure 5 |
| 100 mm | Figure 6 | Figure 7 |
| 200 mm | Figures 4,6,8,10,11 | Figures 5,7,9,10,11 |
| 400 mm | Figure 6 | Figure 7 |
DownLoad: CSVTable 3 compiles the maximum Von Mises stress field and displacement field values, numerically obtained by means simulations.
| Figure | Von Mises stress field [MPa] | Figure | Displacement field [mm] |
| Figure 4a | 33 | Figure 5a | 0.9 |
| Figure 4b | 194 | Figure 5b | 7.6 |
| Figure 4c | 176 | Figure 5c | 3.4 |
| Figure 6a | 137 | Figure 7a | 2.7 |
| Figure 6b | 194 | Figure 7b | 7.6 |
| Figure 6c | 198 | Figure 7c | 9.7 |
| Figure 8a | 198 | Figure 9a | 9.5 |
| Figure 8b | 194 | Figure 9b | 7.6 |
| Figure 8c | 197 | Figure 9c | 9.7 |
| Figure 10a | 370 | Figure 10b | 5.1 |
| Figure 11a | 230 | Figure 11b | 3.4 |
DownLoad: CSVFrom the obtained FEA results, simulated load magnitude, dimensions of the components and selected material, it is shown that: i) increasing the buoy dimensions leads to a significant increase of both maximum values of stresses and displacements, which means that an increase of plastic deformation can be expected for the highest radius tested; ii) spherical buoy geometry leads to the lowest values of stresses and displacements, when compared with the tulip, but mainly with cylindrical buoy geometries and iii) partially submerged condition corresponds to the critical buoy position since highest maximum stresses and displacements are reached.
The influence of the materials selected for the components and corresponding dimensions, as well as the increase of stress concentration on the WEC fatigue lifetime estimation is briefly presented in this section.
The fatigue lifetime of the WEC components is predicted by the number of cycles to failure N. The Soderberg failure criterion was chosen to perform FEA [21]. A load cycle with a stress ratio R of −1 was chosen to simulate the external resultant force acting upon the buoy due to the sea waves.
The simultaneous action of fatigue and corrosion causes pitting at the surface of the components. Pitting corrosion acts as stress concentrations points, where fatigue cracking will start and grow rapidly. Since steels do not exhibit a definite endurance limit when tested in a corrosive environment, the surface finish factor, KA, which represents the surface condition modification factor, could be taken as a fatigue strength reduction factor ranging from 0.1 to 1 [22,23]. This factor was used to simulate numerically the action of the corrosion since it is equivalent to the reduction of the number of cycles that cause failure at a certain alternating stress [24]. Values of KA equal to 0.1, which simulates an accelerated corrosion process and 0.5, corresponding to an acceptable surface finish value for a considerable number of cycles in the long-term fatigue, were chosen to simulate the fatigue phenomenon with and without corrosion, respectively [23].
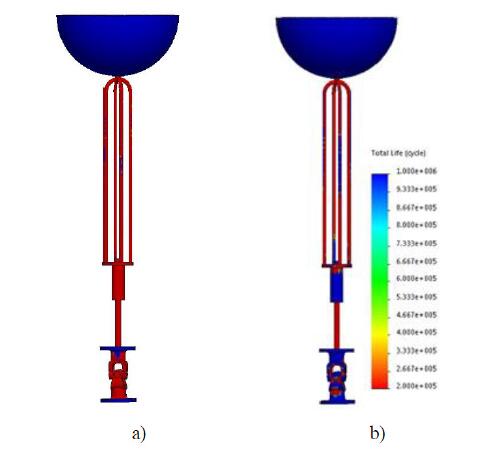
The influence of two different fatigue strength reduction factor KA on the fatigue life prediction is shown in Figure 12.
Figure 12. Number of cycles to failure for 200 mm radius spherical buoy, 15 mm supporting cables, 20 mm piston rod diameter, HSS components: a) KA = 0.1 and b) KA = 0.5An effective reduction in fatigue life occurs with the decreasing of KA due to the increase of the induced stress concentration, as shown in Figure 12a. In fact, as better surface finish is, lower is the stress surface concentration. This means that the component fatigue strength is greater because the probability of fatigue nucleation cracks is reduced.
Nevertheless, for a number of cycles greater than 106, surface parameters such as surface finish, type of coating, surface material metallurgical state, surface residual stresses, among others, must be improved.
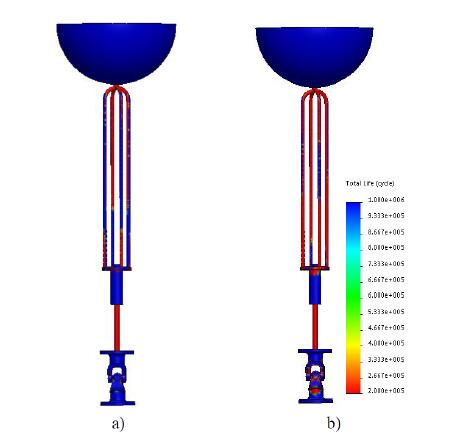
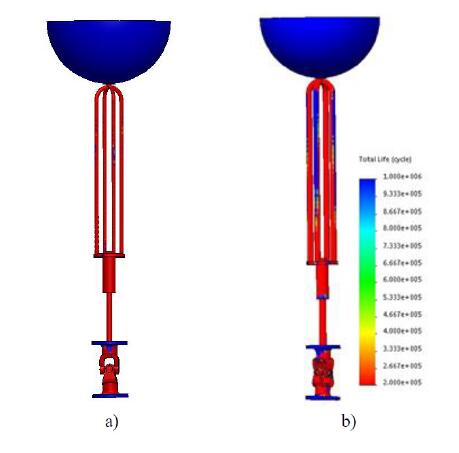
Alternatively, other kind of materials or components dimensions can be tested, as shown through Figure 13 and 14.
Figure 13. Number of cycles to failure for 200 mm radius spherical buoy, 15 mm supporting cables, 20 mm piston rod diameter, KA= 0.5 for a) SS and b) HSS components
Figure 14. Number of cycles to failure for 200 mm radius spherical buoy, HSS components, KA= 0.1 and for a) 15 mm supporting cables and 20 mm piston rod diameter, and b) 20 mm supporting cables and 25 mm piston rod diameterThe influence of two different materials on the fatigue life prediction is shown in Figure 13. As expected, SS presents a better fatigue strength when compared with HSS. However, both materials lead to a reduced number of cycles before failure namely at the supporting cables and piston rod.
Concerning the influence of the dimension of the components on the fatigue strength, as expected and shown in Figure 14, no effective reduction in fatigue life is observed. Figure 14b shows a very slight increase of fatigue strength mainly for the supporting cables. When corrosion and fatigue happen simultaneously it can be expected that the increase on the dimensions of the components affect positively the fatigue strength. In fact, in fatigue with corrosion the crack initiation phase is very small, becoming the duration of the propagation phase dominant in the component life. Thus, it can be expected that greater component dimensions lead to greater fatigue strength. This is due to the longest path the crack must travel through until the occurrence of the final break of the component.
From these results, it can be concluded that the developed numerical model can also be used to predict and optimize the fatigue lifetime of the WEC components.
A brief characterization of the WEC used in this study is initially given. A numerical model of the WEC was developed and its performance evaluated using a finite element commercial code. The influence of several design parameters, such as buoy dimensions, geometries and submerged conditions on the structural behavior of the WEC, was analyzed and numerical results were obtained. Supporting cables were assumed as rigid bodies, thus neglecting their flexibility. For the magnitude of the simulated applied force, dimensions of the components and materials selected, FEA results, obtained by means of simulations, demonstrate that the increase in buoy dimensions leads to the increase on both maximum stress concentrations and displacement fields. The increase in buoy dimensions requires the resizing of the components or the selection of materials with greater yield strength, to avoid plastic deformation. It was also shown that the spherical buoy geometry leads to the best WEC structural behavior since it induces lower stresses and displacements. Furthermore, it was also demonstrated that the cylindrical buoy geometry leads to a chaotic scenario due to a high level of stresses and displacements when compared with spherical and tulip geometries. In what concerns the three buoys submerged conditions, it was verified that the partially submerged buoy corresponds to the critical buoy position, since highest maximum stresses and displacements are reached when compared with the other conditions. Results obtained from fatigue life analysis demonstrate the capacity of the developed WEC numerical model to predict the maximum number of load cycles before failure.
All authors declare no conflicts of interest in this paper.
| [1] |
Valério D, Beirão P, Sá da Costa J (2007) Optimization of wave energy extraction with the archimedes wave swing. Ocean Eng 34: 2330–2344. doi: 10.1016/j.oceaneng.2007.05.009
|
| [2] |
Guillou N, Chapalain G (2015) Numerical modelling of nearshore wave energy resource in the sea of Iroise. Renew Energ 83: 942–953. doi: 10.1016/j.renene.2015.05.021
|
| [3] |
Neill S, Hashemi M (2013) Wave power variability over the northwest European shelf seas. Appl Energ 106: 31–46. doi: 10.1016/j.apenergy.2013.01.026
|
| [4] |
Leijon M, Danielsson O, Eriksson M, et al. (2006) An electrical approach to wave energy conversion. Renew Energ 31: 1309–1319. doi: 10.1016/j.renene.2005.07.009
|
| [5] |
Falcão A (2010) Wave energy utilization: a review of the technologies. Renew Sust Energ Rev 14: 899–918. doi: 10.1016/j.rser.2009.11.003
|
| [6] | Shoele K, Prowell I, Zhu Q, et al. (2011) Dynamic and structural modelling of a floating wind turbine. Int J Offshore Polar 21: 155–160. |
| [7] | Robertson A, Jonkman J (2011) Loads analysis of several offshore floating wind turbine concepts, Proceedings of the 21th International Offshore and Polar Engineering Conference (ISOPE), Maui, Hawaii, USA. |
| [8] | Aubault A, Cermelli C, Roddier D (2009) WindFloat: a floating foundation for offshore wind turbines–Part III: Structural analysis, Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, Hawaii, USA. |
| [9] | Kim B, Sung H, Kim J, et al. (2013) Comparison of linear spring and nonlinear FEM methods in dynamic coupled analysis of floating structure and mooring system. J Fluid Struct 42: 205–227. |
| [10] |
Fujikubo M (2005) Structural analysis for the design of VLFS. Mar Struct 18: 201–226. doi: 10.1016/j.marstruc.2005.07.005
|
| [11] |
Dong P (2005) A robust structural stress method for fatigue analysis of offshore/marine structures. J Offshore Mech Arct 127: 68–74. doi: 10.1115/1.1854698
|
| [12] | Hansen V, Wang L, Sodahl N, et al. (2004) Guidelines on coupled analyses of deepwater floating systems, Offshore Technology Conference, Houston, USA. |
| [13] |
Thorburn K, Karlsson KE, Wolfbrandt A, et al. (2006) Time stepping finite element analysis of a variable speed synchronous generator with rectifier. Appl Energ 83: 371–386. doi: 10.1016/j.apenergy.2004.10.016
|
| [14] |
Yueh CY, Chuang SH (2012) A boundary element model for a partially piston-type porous wave energy converter in gravity waves. Eng Anal Bound Elem 36: 658–664. doi: 10.1016/j.enganabound.2011.11.011
|
| [15] |
Nader JR, Zhu SP, Cooper P (2012) A finite-element study of the efficiency of arrays of oscillating water column wave energy converters. Ocean Eng 43: 72–81. doi: 10.1016/j.oceaneng.2012.01.022
|
| [16] |
Wang S, Soares C (2014) Numerical study on the water impact of 3D bodies by an explicit finite element method. Ocean Eng 78: 73–88. doi: 10.1016/j.oceaneng.2013.12.008
|
| [17] | Falnes J (2004) Ocean waves and oscillating systems: linear interactions including wave-energy extraction, 1st Ed., Cambridge, Cambridge University Press. |
| [18] | Planchard D, Planchard M (2013) SolidWorks 2013 tutorial with video instruction, Schroff Development Corporation. |
| [19] |
Beirão P, Valério D (2015) Numerical comparison between deep water and intermediate water depth expressions applied to a wave energy converter. AIMS Energ 3: 525–546. doi: 10.3934/energy.2015.4.525
|
| [20] |
Malça C, Beirão P, Felismina R (2014) Influence of material selection on the structural behavior of a wave energy converter. AIMS Energ 2: 359–372. doi: 10.3934/energy.2014.4.359
|
| [21] | Shigley J, Mischke C (1988) Mechanical engineering design, 5th Ed., McGraw-Hill Inc. Available from https://www.amazon.com/Mechanical-Engineering-Design-McGraw-Hill/dp/0070568995. |
| [22] | Spotts M (1998) Design of machine elements, 7th Ed., Prentice Hall. |
| [23] | Campbell F (2008) Elements of metallurgy and engineering alloys, ASM International. |
| [24] | CATI Tech Notes: Fatigue Strength Reduction Factor, 2014. Available from: https://www.cati.com/blog/2014/11/fatigue-strength-reduction-factor/. |
| 1. | Shuai Shi, Fuchun Yang, Shulong Fan, Zhuang Xu, Design and analysis of a microminiature omnidirectional wave energy-harvesting device based on a spatial slider–crank mechanism, 2023, 13, 2158-3226, 10.1063/5.0175835 | |
| 2. | Giovanni Aiello, Salvatore Alfonzetti, Santi Agatino Rizzo, Nunzio Salerno, Thin Conductor Modelling Combined with a Hybrid Numerical Method to Evaluate the Transferred Potential from Isolated Grounding System, 2019, 12, 1996-1073, 1210, 10.3390/en12071210 |
Figures(14) / Tables(3)
Pedro J. B. F. N. Beirão, Cândida M. S. P. Malça, Raimundo P. Felismina. Influence of design parameters on the structural and fatigue behaviors of a floating point wave energy converter[J]. AIMS Energy, 2017, 5(2): 209-223. doi: 10.3934/energy.2017.2.209
| Material | Young’s modulus [MPa] | Poisson coefficient | Yield strength [MPa] | Density [kgm-3] |
| Polyethylene | 1860 x 10-6 | 0.39 | 30 | 940 |
| AISI 316 SS | 193000 | 0.27 | 172 | 8000 |
| HSS | 21000 | 0.28 | 620 | 7700 |
DownLoad: CSV| Von Mises stress field [MPa] | Displacement field [mm] | |
| Cylindrical | Figure 8 | Figure 9 |
| Spherical | Figures 4,6,8 | Figures 5,7,9 |
| Tulip | Figure 8 | Figure 9 |
| Buoy totally submerged | Figure 4 | Figure 5 |
| Buoy partially submerged | Figure 4 | Figure 5 |
| Buoy at the surface | Figure 4 | Figure 5 |
| 100 mm | Figure 6 | Figure 7 |
| 200 mm | Figures 4,6,8,10,11 | Figures 5,7,9,10,11 |
| 400 mm | Figure 6 | Figure 7 |
DownLoad: CSV| Figure | Von Mises stress field [MPa] | Figure | Displacement field [mm] |
| Figure 4a | 33 | Figure 5a | 0.9 |
| Figure 4b | 194 | Figure 5b | 7.6 |
| Figure 4c | 176 | Figure 5c | 3.4 |
| Figure 6a | 137 | Figure 7a | 2.7 |
| Figure 6b | 194 | Figure 7b | 7.6 |
| Figure 6c | 198 | Figure 7c | 9.7 |
| Figure 8a | 198 | Figure 9a | 9.5 |
| Figure 8b | 194 | Figure 9b | 7.6 |
| Figure 8c | 197 | Figure 9c | 9.7 |
| Figure 10a | 370 | Figure 10b | 5.1 |
| Figure 11a | 230 | Figure 11b | 3.4 |
DownLoad: CSV| Material | Young’s modulus [MPa] | Poisson coefficient | Yield strength [MPa] | Density [kgm-3] |
| Polyethylene | 1860 x 10-6 | 0.39 | 30 | 940 |
| AISI 316 SS | 193000 | 0.27 | 172 | 8000 |
| HSS | 21000 | 0.28 | 620 | 7700 |
| Von Mises stress field [MPa] | Displacement field [mm] | |
| Cylindrical | Figure 8 | Figure 9 |
| Spherical | Figures 4,6,8 | Figures 5,7,9 |
| Tulip | Figure 8 | Figure 9 |
| Buoy totally submerged | Figure 4 | Figure 5 |
| Buoy partially submerged | Figure 4 | Figure 5 |
| Buoy at the surface | Figure 4 | Figure 5 |
| 100 mm | Figure 6 | Figure 7 |
| 200 mm | Figures 4,6,8,10,11 | Figures 5,7,9,10,11 |
| 400 mm | Figure 6 | Figure 7 |
| Figure | Von Mises stress field [MPa] | Figure | Displacement field [mm] |
| Figure 4a | 33 | Figure 5a | 0.9 |
| Figure 4b | 194 | Figure 5b | 7.6 |
| Figure 4c | 176 | Figure 5c | 3.4 |
| Figure 6a | 137 | Figure 7a | 2.7 |
| Figure 6b | 194 | Figure 7b | 7.6 |
| Figure 6c | 198 | Figure 7c | 9.7 |
| Figure 8a | 198 | Figure 9a | 9.5 |
| Figure 8b | 194 | Figure 9b | 7.6 |
| Figure 8c | 197 | Figure 9c | 9.7 |
| Figure 10a | 370 | Figure 10b | 5.1 |
| Figure 11a | 230 | Figure 11b | 3.4 |
