1. Introduction
The increase in the use of renewable energy sources combined with energy efficiency measures has reduced consumption and imports of fossil fuels and has consequently contributed to increase the representativeness of renewable energies in final energy consumption. The overall capacity of all wind turbines installed worldwide by the end of 2017 reached 539 GW [1]. The annual onshore and offshore wind installations achieved, respectively, 12.5 GW and 3.1 GW in EU. There are differences between onshore and offshore exploitation of wind energy, mostly due to the: the wind speed is relatively more stable at offshore than at onshore; the wind speed at offshore is about 20% higher than at onshore. Both these differences imply that the utilization rate is higher at offshore than at onshore. Economically wind energy conversion systems at offshore tend to have larger capacity and benefit from lager areas than the limited and mostly occupied areas at onshore. But, some issues must be regarded with caution, for instance, regarding preservation of fishing, boat navigation, ocean habitat and species, marine conservation zone, landscape view from land to sea and vice versa. Higher reliability, resistant to corrosion due to the difficulties and costs of maintenance or repairing at offshore and consideration of action of sea waves on wind energy conversion systems are needed. Turbines need to be designed to take advantage of the higher level of the wind speed, i.e., the design must consider a higher value for the cut-out wind speed: the wind speed at which the wind turbine shuts down to prevent mechanical damage of the structure. Foundations work at offshore are more expensive, than on onshore where the process uses either rods drilled into the ground or a reinforced concrete pad set in the ground. Turbines need to be designed to take advantage of the higher level of the wind speed at offshore, i.e., the design must consider a higher value for the cut-out wind speed: The wind speed at which the wind turbine shuts down to prevent mechanical damage of the structure. Foundations work at offshore are more expensive, than on onshore where the process uses either rods drilled into the ground or a reinforced concrete pad set in the ground.
The technology applied on wind energy conversion systems having variable-speed and variable-pitch (VSVP) has been reported in literature due to advantageous energy capturing [2,3]. Also, amongst the electrical generators available for equipping wind turbines having VSVP, doubly-fed induction generator (DFIG) stands out in industry and became the mainstream choice [4,5].
Control system architectures are necessary to improve the quality of electrical energy delivered into the electric grid. Pitch control is widely used to ensure the best performance during the capture of energy under all operational wind scenarios [6,7,8]. Control strategies have to deal with unforeseen variables such as wind speed variability and intermittence, to achieve the goal of an overall acceptable performance. Various control techniques are used by researchers in the architecture of control strategies, amongst a wide variety of control types, some are mentioned here: Robust multivariable gain-scheduled control [9], fuzzy proportional integral [10], adaptive linear quadratic control [11], data-driven and adaptive PI control [12], sliding-mode control [13].
A suitable design for control and supervision under the unpredictable character of the wind energy is challenge in order to maximize power output. Thus, the controller needs to have access to the variables generator speed and pitch angle. The performance during the capture of wind energy is a prominent issue and has been dealt not only by research on turbine design and advanced control strategy, but also by condition monitoring using a supervisor. Some works addressed this issue, such as: Classification of wind turbine condition monitoring methods and techniques with a focus on trends and future challenges [14], supervisory control and data acquisition system [15]. The supervisory control theory is behind the architecture proposed in this paper and is suitable for control application with event-based operations as can be seen in previous works [16,17].
This paper presents the following contributions: A two-level control architecture, consisting in a supervisory level (event-based supervisor) and an execution level (LQG and MPC controllers); a study and implementation of adaptive controllers and predictive controllers; a study of an event-based supervisor, having the objective of determining the most suitable operational state among the possible states; a simulation of the system with the distinct types of controllers with and without the presence of an event-based supervisor; and an evaluation of the system performance driven from the assessment of the results obtained with the action of each controller. In the overview of this paper, Section 2 presents the onshore energy conversion system modelling, Section 3 presents the control and supervision strategy applied to the system, namely the LQG, MPC in the execution level, an event-based supervisor in the supervision level and is also defined the operating regions according to the wind speed. Section 4 presents the simulation results as well the performance of the system without and with supervisor. Conclusions remarks are given in Section 5.
2. Onshore energy conversion system modelling
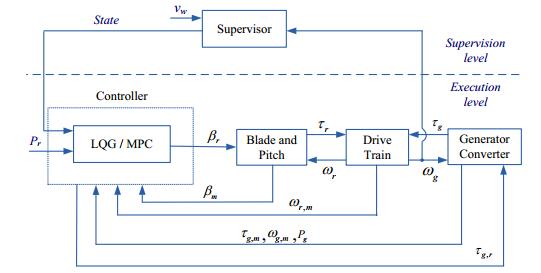
A mathematical model representing an appropriate and thorough dynamic of an onshore energy conversion system is developed in this section. The development of the mathematical model is based on the benchmark model developed in [19], whose electric power output is 4.8 MW. The proposed control and supervision hierarchical structure is represented by a block diagram model composed by the following functional systems: Mechanical system (blade-pitch angle and two-mass drive train), controllers (LQG and MPC), electrical system (generator and two-level converter) and event-based supervisor. The block diagram model shown in Figure 1, is composed by the following variables: vw is the wind speed in m/s, τg and τr are the generator and turbine rotor torques in Nm, ωg and ωr are the generator and turbine rotor speed in rad/s, βr is the pitch angle in degrees, Pg and Pr are the generator and reference power in MW. The r and m subscripts designate respectively reference and measurements values.
2.1. Blade and pitch modelling
This model combines the aerodynamic with blade and pitch models. The aerodynamic torque is given by:
|
τr(t)=ρπR3Cp(λ(t),β(t))vw(t)22
|
(1)
|
Where R is the radius of the blades, ρ is the air density, Cp(λ(t),β(t)) is the power coefficient, which is a function of the tip speed ratio λ(t) and the pitch angle β(t). The tip speed ratio is given by:
From Eq 2, variations of the wind speed can lead to two consequences:
a) If the turbine rotor speed is held constant, then λ(t) will change, leading to a consequent change in the power coefficient;
b) If the turbine rotor speed is suitably adjusted, then λ(t) can be held at a reference point and as a result power coefficient can be kept at a desired value.
The power coefficient of a wind turbine using pitch control [20,21,22,23] is given by:
|
{Cp(λ,β)=0.73(151λi−0.58β−0.002β2.14−13.2)e−18.4λiλi=11(λ−0.02β)−0.003(β3+1)
|
(3)
|
The pitch angle can be modelled as a second order differential equation given by:
|
¨β(t)=−2ξωn(t)˙β(t)−ω2nβ(t)+ω2nβr(t)
|
(4)
|
2.2. Drive-train modelling
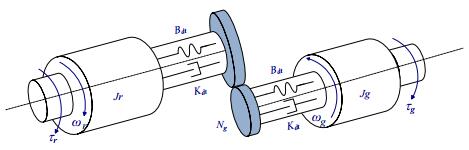
The mechanical drive train is composed by two shafts, a low-speed shaft from the rotor side, a high-speed shaft from the generator side, connected by a transmission equipped with a gear box. The two-mass drive train is shown in Figure 2.
The mathematical model to describe the dynamic of the drive train is a two-mass model. On the rotor side, the mass Jr concentrates the inertia of the hub, turbine blades and low-speed shaft inertia. On the generator side, Jg concentrates the generator inertia and high-speed shaft. The low-speed shaft and high-speed shaft are connected by a gear box with a ratio Ng. The torsion shaft stiffness is Kdt and torsion shaft damping is Bdt. The angular deviation due to the damping and stiffness coefficients between the turbine and the generator is θΔ(t). The linear model for the drive train model is given by:
|
Jr˙ωr(t)=τr(t)+BdtNgωg(t)−KdtθΔ(t)−(Bdt+Br)ωr(t)
|
(5)
|
|
Jg˙ωg(t)=KdtNgθΔ(t)+BdtNgωr(t)−(BdtN2g+Bg)ωg(t)−τg(t)
|
(6)
|
|
˙θΔ(t)=ωr(t)−1Ngωg(t)
|
(7)
|
2.3. Generator and converter modelling
The model for the generator and the power converter is described by the state equation given by:
|
˙τg(t)=−αgcτg(t)+αgcτg,r(t)
|
(8)
|
Where αgc is a first order constant and τg,r is the reference torque of the generator. The power of electric generator is given by:
Where ηg is the efficiency of the generator.
3. Control and supervision strategy
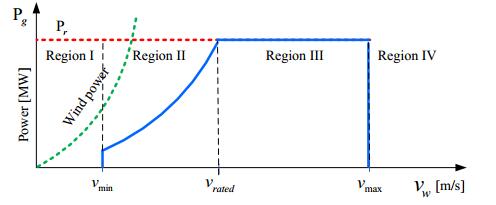
The onshore energy conversion system components, the wind speed and the wind turbulence, the tip speed ratio and the pitch angle are some of the variables considered in the control design to achieve the rated power with an acceptable overall performance. In this paper two distinct controller are considered, adaptive and predictive. The control and supervision strategy are based on the switching from Region Ⅱ (constant-pitch, generator torque control) to Region Ⅲ (variable-pitch control, constant torque). Region Ⅱ (wind speed is between 5 m/s and 13 m/s) and Region Ⅲ (wind speed is between 14 m/s and 22.5 m/s) can be seen at the regions of power operation as shown in Figure 3.
Figure 3 shows that in Region Ⅱ, the control objective is to extract optimal power reducing oscillation on the drive train, thus torque control is applied. The pitch angle and tip speed ratio are set to their optimal value to achieve this control objective and the rotor speed must be adjusted to the reference rotor speed given by:
|
ωref(t)=λopt(t)vw(t)R
|
(10)
|
The optimal electric generator torque is given by:
|
{τg,r(k)=Kopt(ωref(k)Ng)2Kopt=12ρAR3Cpmaxλ3opt
|
(11)
|
Where λopt is the optimal point for achieving maximum CP and A is the area swept by the blades.
Figure 3 shows that in Region Ⅲ, the control objective is to control the output generator power through pitch control. To achieve this control objective, the pitch angle varies according the error between nominal speed and the output generator speed. The pitch reference and generator torque reference should be adjusted at the same time and the latter is given by:
|
τg,r(k)=Pr(k)ηgωg(k)
|
(12)
|
Switching between Region Ⅱ and Region Ⅲ is determined by the electric generator power,
Pg, and the generator speed, ωg, the control mode switching is performed according to the following conditions: Switching from Region Ⅱ to Region Ⅲ is enabled if Pg>Prandωg>ωnom and switching back from Region Ⅲ to Region Ⅱ is enable if ωg<ωnom−ωΔ. The non-null threshold ωΔ is required to enable preventing sudden switches from Region Ⅲ and Region Ⅱ.
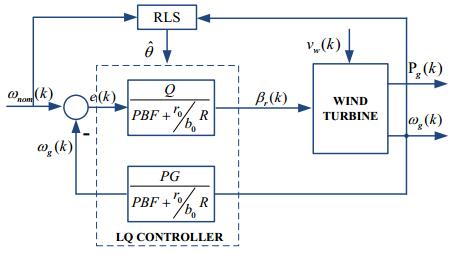
3.1. Adaptive linear quadratic gaussian controller
Discrete adaptive linear quadratic gaussian control (LQG) deals with unpredicted variables and the adaptation depends on estimation of parameter ˆθ(k). Using recursive least squares algorithm, polynomials parameters from A1(z−1) and B1(z−1) can be estimated, obtaining parameters ˆθ(k)=[ˆa11ˆa12ˆb11ˆb12]. The dynamic development of this controller is presented in [24]. The dynamical system of the onshore wind turbine benchmark around a nominal set-point r(k) is represented by an ARX model, thus the linear quadratic control transfer function is given by:
|
Y(z)U(z)=(b11z−1+b12z−2)(1+a11z−1+a12z−2)
|
(13)
|
Where the Z-transform of the system output and control input are respectively Y(z) and U(z). The performance index H is given by:
|
H(k)=(Py(k+d)−Qr(k))2+(χu(k))2
|
(14)
|
Where P and Q assume a unit value, the scalar χ=0.4 is chosen to achieve an acceptable closed-loop performance and optimal control u(k) minimizes performance index.
The LQG pitch control structure is shown in Figure 4.
The polynomials F(z−1) and G(z−1) can be determined by solving the Diophantine equation. The optimal control that minimizes the performance index is given by:
|
u(k)=∧b11∧b112+χ2[(ρ2−∧b12∧b11∧b11)u(k−1)+∧a11y(k)+∧a12y(k−1)+r(k)]
|
(15)
|
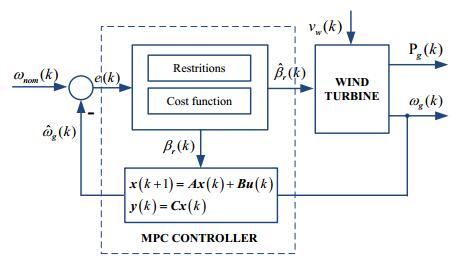
3.2. Model predictive controller
Model predictive controller [25] use the states of the blades and pitch model, drive train and nonlinear aerodynamics as input. By optimizing the best output according to the operating region and control objective, the model predictive controller generates reference values for β(k) and τg, r (k). From Eq 1 to Eq 9 a linear state space model representing the onshore energy conversion system dynamics at certain operating wind speed is given by:
|
{x(k+1)=Ax(k)+Bu(k)y(k)=Cx(k)
|
(16)
|
Where x=[ωrωgθΔτgβ]T∈R5 is the state vector, u=[τg,rβr]T∈R2 is the control input and y=[ωgPg]T∈R2 is the measured output. One important purpose in this region is to maintain the generator speed very close to the nominal speed with the least stress on the generator and pitch control system. To accomplish this objective, one must follow the mathematical formulation for the objective function, i.e., the cost function is given by:
|
minu(k)⋯u(k+Np−1)J(k)=∑Npj=1[r(k+j)−ˆy(k+j|k)]TQ(j)[r(k+j)−ˆy(k+j|k)]⏟QuadraticError+∑Np−1j=0[u(k+j|k)]TR(j)[u(k+j|k)]⏟ControlEffort
|
(17)
|
In Eq 17 the cost function is associated with the prediction horizon, given by the periods j with j = 1, …, Np. The first term is a quadratic functional, weighted by matrix Q, of the difference between reference r(k+j) and predicted output ˆy(k+j|k) and is used for penalization of the error. Also, the second term is a quadratic functional, weighted by matrix R, measuring the control effort u(k+j|k).
The MPC pitch control structure is shown in Figure 5.
The optimization problem consists in the minimization of the cost function subjected to the following constraints: βmin⩽βr⩽βmax, (ωnom−ωΔ)⩽ωg⩽(ωnom+ωΔ) and also νmin⩽νw⩽νmax. Where ωnom is the nominal generator speed and ωΔ is a small offset that introduce some hysteresis in the switching scheme avoiding frequent switching from control modes.
3.3. Supervisor
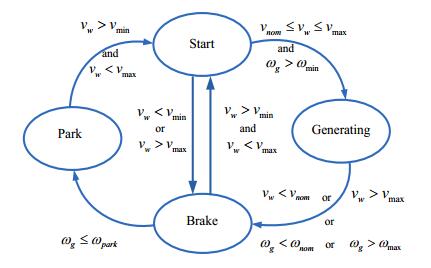
The onshore energy conversion system event-based supervisor is based on finite state machine (FSM) also known by finite-state automaton or state machine. This machine is a mathematical model of computation to conveniently schedule the operational states of a process. The states are such as: start, production and stop. The machine is in only one state at a time and can change from one state to another when initiated by a triggering event or condition called a transition. The machine is a set of: behavior states, transitions that define the transit between states and rules or conditions to be fulfilled in order to enable a transition. The specification of a machine is given by the list of states and the triggering condition for transitions. The FSM is described by a quintuple model [26] given by:
In Eq 18 the Σ is the input alphabet, Qf is the finite set of states, ∂=∑×Q is the transition function, q0 is the initial state and Qm is the set of final states. The event-based supervisor deterministic version of an FSM used in this paper has the state transition diagram shown by Figure 6.
In Figure 6, the operational states are park, start, generating and brake, typifying the regions of power operation as follow:
a) In the Park state, the wind turbine is in shutdown mode and the generator is disconnected from the electric grid. This state corresponds to Region I.
b) In the Start state, the wind speed must be above the cut-in speed (vmin). The wind turbine should be started to capture energy from the wind power. The generator is connected to the electric grid, but not necessarily at rated power in the majority of the operation in Region Ⅱ. From this state and depending on the accuracy of the transitions (wind speed and generator speed), one can enter into the generating state or into the brake state. This state corresponds to Region Ⅱ.
c) In the Generating state, also known as power production, the wind speed must be within the rated wind speed (vrated) and the cut-out speed (vmax). The generator is connected to the electric grid at rated power, by conveniently curtailment of the capture of kinetic energy from the wind. This state corresponds to Region Ⅲ.
d) In the Brake state, also known as slow down state, the pitch angle is adjusted in order to decrease the rotation of the wind turbine. From this state and according to the value of the conditions, one can enter into the start state or into the park state.
4. Results
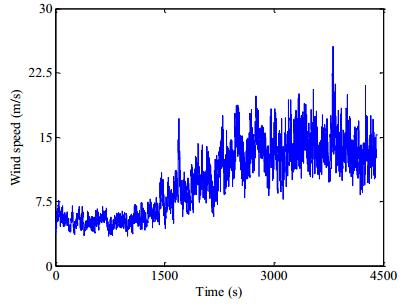
The mathematical model of the WECS equipped with a two-level power converter topology is used in the simulations. The simulations in order to compare the performance without or with the supervisor are carried out in Matlab/Simulink. The time horizon considered in the simulations is of 4500 s, and the sampling time Ts is of 0.01 s. The WECS has a rated electric power of 4.8 MW for a wind speed vw of 13 m/s, where ωnom is 162 rad/s, ωΔ is 15 rad/s and ωmax is 200 rad/s [19,27,28,29]. The series for the wind speed used in the simulations are the ones given in [19], having amplitudes in the range of 7.5 m/s to 22.5 m/s between Region Ⅱ and Region Ⅲ, but an addition of white noise to the wind speed is considered in order to have an augment effect of intermittence of wind energy. The wind speed with the addition of white noise is shown in Figure 7.
4.1. Without supervisor
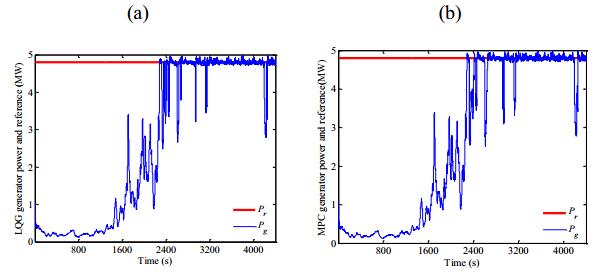
The following figures represent the simulations of the controllers, LQG and MPC, without the presence of the event-based supervisor. The electric output and reference power of the LQG and the MPC controllers are shown in Figures 8a, b.
In Figure 8 both controllers, the electric output power follows the reference power with some oscillations around the reference power having some decreases in the output power. Major strengths of MPC are abilities to handle multivariable interactions and operating constraints in systematic manner. MPC is formulated as a constrained optimization problem, which is solved on-line repeatedly by carrying out model-based forecasting over a moving window of time. More importantly, MPC facilitates optimal control systems with unequal number of manipulated inputs and measured outputs. LQG provides a systematic approach to designing a control law for linear multi-variable systems. However, some difficulties associated with the classical LQG formulation is inability to handle operating constraints explicitly. Operating constraints, such as limits on manipulated inputs or on their rates of change, limits on controlled outputs arising out of product quality or safety considerations, are commonly encountered in any control application.
MPC can be viewed as modified versions of LQ (or LQG) formulation, which can deal with the operating constraints in a systematic manner. Origins of MPC can be traced to the classical linear quadratic optimal control (LQOC) formulation. These techniques, although have different mechanisms, are similar, thus, giving similar outputs.
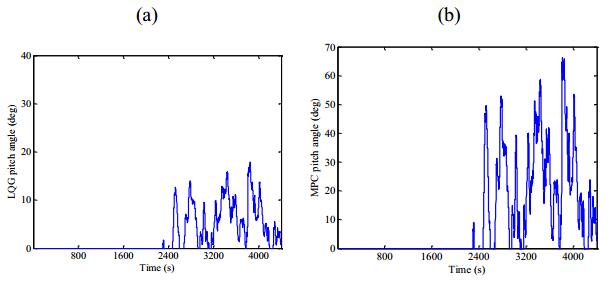
The LQG controller and the MPC controller pitch angles are shown in Figures 9a, b.
In Figure 9 LQG controller provides pitch angle variations between 7 degrees and 18 degrees. MPC controller provides pitch angle variations between 10 degrees and 65 degrees.
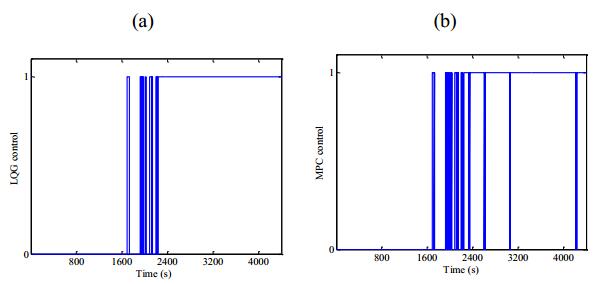
The switching between Region Ⅱ and Region Ⅲ is shown in Figures 10a, b.
In Figure 10 Region Ⅱ (0) corresponds to startup operational mode and Region Ⅲ (1) corresponds to generation operational mode. Both controllers present, with some frequency, switching between Region Ⅱ and Region Ⅲ.
4.2. With supervisor
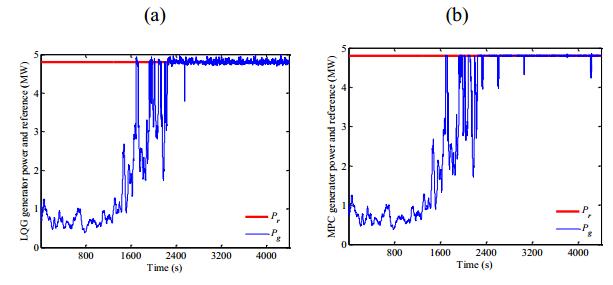
The following figures represent the simulations of the controllers, LQG and MPC, with the presence of the event-based supervisor. The electric output and reference power of LQG and the MPC controllers are shown in Figures 11a, b.
In Figure 11 MPC controller allows a smoother response around reference power, when compared to the one obtained with the LQG controller, however presents several peaks.
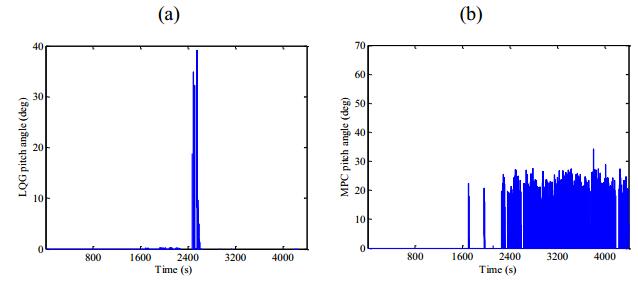
The LQG controller and the MPC controller pitch angles are shown in Figures 12a, b.
In Figure 12 LQG controller pitch angle variation only occurs in a small interval of time reaching the maximum of 40 degrees. LQG controller contributes to less variation on the pitch angle. MPC controller provides pitch angle variations between 15 degrees and 25 degrees having one peak above 30 degrees.
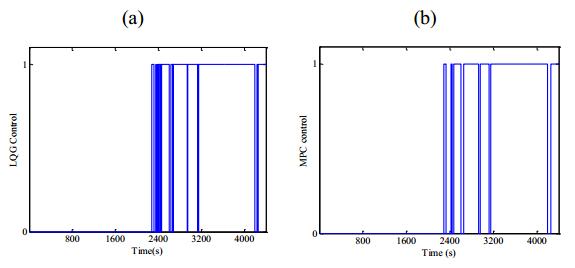
The switching between Region Ⅱ and Region Ⅲ is shown in Figures 13a, b.
In Figure 13 the transition between the two operational states is due to the need of sustaining the electric output at the rated power. The LQG controller allows a less frequent switching between Region Ⅱ and Region Ⅲ, with permanence in Region Ⅲ while MPC controller presents few switching between Region Ⅱ and Region Ⅲ.
4.3. Performance assessment
The metrics used in the evaluation of the performance of the controller are the integral of time multiplied by the absolute value of the error (ITAE) and the integral of the square value (ISV). The ITAE is given by:
And the ISV is given by:
The control performances for the WECS without or with supervisor control are summarized in Table 1.
Table 1. Performance assessment results.
| Controller |
LQG |
MPC |
| Without Supervisor |
| ITAE |
1.0792 × 1015 |
1.0886 × 1015 |
| ISV |
1.0770 × 107 |
1.4791 × 107 |
| With Supervisor |
| ITAE |
7.0328 × 1014 |
7.0250 × 1014 |
| ISV |
2.7171 × 105 |
1.7276 × 107 |
In Table 1 considering the values obtained without the event-based supervisor, the error between the electrical output and the reference power is smaller with the LQG controller, although with the MPC the error is close to that presented by the LQG controller. As far as the control effort is concerned, the LQG controller has a smaller error when compared to the MPC controller, consuming less energy. Considering the values obtained under the event-based supervisor, both controllers accomplish equivalent performance with respect to the error between electric output and reference power. Regarding the control action effort, it is observed that the lowest effort is obtained with the LQG controller while the MPC requires more energy to maintain the output power around reference power.
5. Conclusion
An onshore energy conversion system connected to the electric grid and under an event-based supervisor control is presented. The control and supervision strategy proposed for the onshore energy conversion system is based on a hierarchical structure with two levels. LQG and MPC controllers are in the execution level whereas the event-based supervisor is placed in the supervision level.
The closed loop response between LQG and MPC without supervisor is quite similar, with abrupt variations around reference power. The pitch angle variations achieve lower amplitude values with the LQG controller. In terms of performance, LQG controller outperforms the latter at expense of lower control effort.
The closed loop response with supervisor remains similar as the above one, with smoother variations around reference power. The pitch angle variations with LQG only occurs in a small interval of time reaching the maximum of 40 degrees. In terms of performance, LQG controller maintains superiority over MPC.
Acknowledgments
This work is funded by: European Union through the European Regional Development Fund, included in the COMPETE 2020 (Operational Program Competitiveness and Internationalization) through the ICT project (UID/GEO/04683/2013) with the reference POCI010145FEDER007690; Portuguese Funds through the Foundation for Science and Technology-FCT under the project LAETA, reference UID/EMS/50022/2013; Portuguese Foundation for Science and Technology (FCT) under Project UID/EEA/04131/2013.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: