Abbreviations: PV: Photovoltaic; SSDG: Small Scale Distributed Generation; MSDG: Medium Scale Distributed Generation; LCOE: Levelised Cost of Electricity; I-V: Current-Voltage Curve; P-V: Power-Voltage Curve; Isc: Short-Circuit Current; Voc: Open circuit voltage; mono-Si: Monocystalline Silicon PV Cell; poly-Si: Polycrystalline Silicon PV Cell
1. Introduction
The photovoltaics sector has seen huge improvements during the last decade, with the addition of at least 98 GWp in 2017 which is equivalent to total global installed capacity in 2012 to reach 402 GW [1]. Such progress is driven by decreasing cost of the PV modules as well as the balance of system costs. A variety of renewable technology promotion mechanisms as well as subsidies have been making PV power systems more affordable. Promotion mechanisms include feed in tariffs, net metering, tendering and energy auctions. In Mauritius, initially feed in tariff was introduced in 2011. With the tariff being almost five times more than the marginal cost of electricity at that time, it was not a sustainable mechanism. Therefore, recently the Central Electricity Board (CEB) introduced net metering mechanism for both small scale and medium scale distributed generators. For such mechanisms, the system must be designed in such a way that total annual renewable electricity production is equal to consumption for SSDG and thirty percent of annual consumption for MSDG [2,3,4].
In order to obtain a reliable LCOE, it is crucial that the system engineer guarantees the PV system as a reliable power source. For the purpose, as a minimum, the performance of PV modules in outdoor conditions must be adequately known. All PV modules are rated at standard test conditions (STC). Therefore, it is very important to know how outdoor environmental factors such as intensity and temperature affect the performance of PV cells and modules. Outdoor experimentation of solar cells is essential to maximize their performance and to assess utilization requirements and limits. More generally, tests with direct exposure to the sun are useful to understand the behavior of components and new materials for solar applications in real working conditions. Ambient factors are uncontrollable, but can be monitored to know the environmental situation of the solar exposure. Fontani et al. [5] proposed a methodology to execute solar exposure tests which was practically applied on photovoltaic cells for a solar cogeneration system. Their main result was the continuous I-V curves for the cells in different conditions of solar concentration and temperature. Mageed et al. [6] investigated the effect of temperature on the electrical performance of multi-crystalline Si panels using the shunt current measurement techniques. It was concluded that temperature dependence of shunt current is negligible. Khan et al. [7] investigated the effect of light intensity on solar cell parameters such as parallel resistance (Rpa), series resistance (Rse), diode ideality factor (a) and reverse saturation current (Io). They observed that an increase in intensity resulted in a decrease in Rse, a and Io whereas Rpa initially increased and then became nearly constant. Chegaar et al. [8] experimentally investigated the effect of light intensity on different solar cell parameters for polycrystalline solar cells with all measurement done at room temperature. They observed that the short-circuit current, the photocurrent and the ideality factor increased linearly with the light intensity whereas the open-circuit voltage and efficiency of the cell increased logarithmically. Chander et al. [9,10] investigated the effect of cell temperature on open-circuit voltage, maximum power point, fill factor and cell efficiency of mono-crystalline silicon solar cell and concluded that open-circuit voltage increases with decrease in temperature.
When we refer to the performance of a PV cell or module, the most important parameter is, of course, the maximum power point, which is usually determined by varying the forward bias voltage across the device under test while illuminated. Some of the I-V, irradiance and temperature measurement techniques are as follows [11]: Use a variable resistor (varying load), voltmeter and ammeter to easily obtain the I-V and P-V curves of a given solar cell experimentally; for high power modules or arrays, a popular load for I-V measurements is a capacitor. As experiments can help assess performance of PV modules under prevailing conditions, only a mathematical model which uses outdoor condition parameters of modules can accurately simulate operation of a PV technology for forecasted weather conditions. Two main models for PV cells are the one diode and two diode model. Rustemli and Dincer [12] modelled a typical Lorentz LA30-12S photovoltaic panel using the one-diode model in MATLAB/Simulink and tested it for various temperatures successfully. Said et al. [13] presented a PV array model using Matlab/Simulink with the assistance of SimPowerSystem toolbox, which made the simulation of the dynamic performance of PV-based power systems easier. Kessaissia et al. [14] modelled and simulated the mono-Si and poly-Si based solar modules using the one-diode model in Matlab. They analysed the behaviour of the solar cells for various light intensities and cell temperatures. The simulated results were found to be in good agreement with experimental results (environmental conditions). Krismadinata et al. [15] used the same technique as Kessaissia et al. to model and simulate a typical 125 W solar panel. The proposed model was tested for different irradiance levels and temperatures whereby the results matched the solar panel's datasheet. Bellia et al. [16] presented a detailed modeling of a PV module using MATLAB/SIMULINK. The one-diode model with both series and parallel resistors was chosen for greater accuracy. The effect of irradiance and temperature on the output of the PV module was successfully analyzed. PV cells and modules were modelled by Bouraiou et al. and Bana and Saini [17,18] using the one-diode and two-diode models in MATLAB/Simulink in order to compare the accuracy of the two models. The simulated results of both models were compared with the respective manufacturer's datasheet. The two-diode model was observed to be more accurate under low light intensity while the one-diode model confirmed its effectiveness at high irradiance level. Various techniques and equations have been prosed for quantifying the cell temperature with respect to site specific weather conditions [19,20,21,22].
Generally, temperature coefficients of solar panels are provided in datasheets, but the latter are provided for STC whereas for outdoor conditions, the temperature coefficients may be different. While measuring I-V characteristics of PV cells, it is very difficult to obtain the short-circuit current and open-circuit voltage points. Secondly, temperature coefficients of the open-circuit voltage and intensity variation of short-circuit current are very important for system design and modelling. Knowledge of temperature dependence of fundamental electrical parameters and the temperature coefficients under outdoor conditions is critical. During this research, a methodology is proposed for estimation of the fundamental parameters through a combination of experimental measurements and technology dependent mathematical models of PV cells. Experiments are performed on three technologies, namely mono, poly and multi junction amorphous silicon cell technology in the tropical conditions of Mauritius. The research provides a simple and effective method of deriving short-circuit current and open-circuit voltage as well as their temperature coefficients.
2. Methodology
The research was conducted in several phases. During first phase, I-V measurements were performed for three Si based PV cell technologies under outdoor conditions. All measurements were performed in Mauritius in the eastern part during the month of October. Temperature and solar irradiance were also recorded during each set of experiment. During the second phase a mathematical model was developed for simulating the IV characteristic of the cells and it was validated using statistical indices. In the third phase results were assessed and performance of the cells was assessed.
2.1. Measurement of electrical characteristics of PV cells
The PV technologies which were investigated are: ⅰ) Mono-Si; ⅱ) poly-Si; and ⅲ) multi-junction amorphous-Si. They represent the standard cells which are used in manufacturing solar panels and their main technical characteristics as well as brand/supplier, model and country of origin of the cells are provided in Table 1.
Table 1. Characteristics of Cells.
| Cell Technology |
Monocrystalline |
Pollycrystalline |
Thin-Film |
| Average Power (W) |
3.2–3.4 |
2.4 |
0.5 |
| Average Voltage (V) |
0.58 |
0.5 |
1.5 |
| Average Current (A) |
5.93 |
4.8 |
0.35 |
| Efficiency (%) |
22.5 |
15.3 |
8.2 |
| Dimensions |
5 × 5 inch |
5 × 5 inch |
200 × 60 × 1 mm |
| Brand/Supplier |
Eco-Worthy |
Sunpower |
Uni-Solar |
| Model |
Mono-5 × 5-cell-for-DIY |
5 × 5 inch Sharp Solar Cell |
Flexible DIY 0.5W2V/330mA |
| Originating Country |
United States |
Japan |
China |
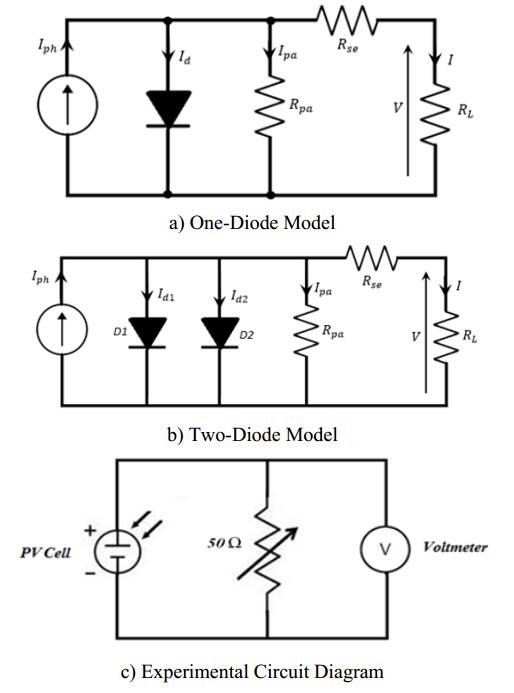
In order to obtain the current (I) and voltage (V) values of PV cells at varying intensity of light, a potentiometer was used as load to the PV cells. Figure 1 shows the circuit diagram of the experiment designed with respect to the one-diode and two-diode models. The potentiometer was calibrated before performing the experiments such that the angle of rotation of the shaft gives the values of the resistance. Voltage readings were taken for different resistance values at different light intensities and temperatures. Care was taken to ensure that during each set of measurement there were no fluctuations in the intensity of sunlight and temperature was constant. The current and power values were then calculated for each resistance and voltage readings. The experiments were performed for a period of 12 days with 10 experiments performed for each technology per day. The experiments were performed to obtain the I-V and P-V characteristic curves of each technology with varying intensity and temperature. The results obtained were sorted according to cell temperature and thereafter with respect to light intensity to investigate the effect of those environmental factors independently.
2.2. Measurement of environmental parameters
Global horizontal solar irradiance was measured using a SolData reference cell which was mounted on an adjustable tilt and orientation structure. It was adjusted at the same inclination as the PV cells, that is, horizontally, so that the measured values of solar irradiance corresponded to the solar irradiance incident on the PV modules. The device has a calibration factor of 160 mV/kWm−2, that is, it outputs a voltage of 160 mV for every 1 kW/m2 of light intensity. Diffuse component of radiation was measured using the reference cell when it was covered by a card board placed at a distance of 30 cm above the surface of the cell. The accuracy of the equipment is 3%. The SolData reference cell together with a temperature sensor was connected to a HOBO U12 data logger. The temperature sensor measured ambient temperature. The environmental parameters were measured at intervals corresponding to I and V measurement times. This approach was crucial since the actual light intensity and temperature (real-life readings) are stochastic and unpredictable variables. The method adopted ensured the minimization of errors regarding the measurements of the solar irradiance and temperature.
2.3. Modeling of PV cells
The monocrystalline and polycrystalline technologies were modelled using the one-diode model whereas the multi junction thin-film technology was modelled using the Two-Diode Model developed in C-Language using Dev C++. The model takes cell temperature, light intensity and resistance values together with fundamental electrical characteristic of the cells which include diode ideality factor, series resistance, shunt resistance, current temperature coefficient, voltage temperature coefficient, reverse diode saturation current as inputs and then outputs the corresponding current, voltage and power. The latter were obtained by solving the five parameter diode model of a solar cell. The IV curves were hence obtained by feeding the essential cell parameters to the models. The wafer technology were simulated using one diode Eq 1, while the multi-junction thin film amorphous silicon technology was simulated using the two diode current Eq 2. For the purpose, essential electrical parameters of modules, such as photo current, Iph, open circuit voltage, Voc, shunt resistance, Rp, series resistance, Rse and ideality factor, a, as defined for the cell are fed in the mathematical model.
|
I={Iph−Ios[exp(V+IRseVTa)−−1]−V+IRseRp}
|
(1)
|
|
I={Iph−Ios1[exp(V+IRseVTa1)−−1]−Ios2[exp(V+IRseVTa2)−−1]−V+IRseRp}
|
(2)
|
In the equations above, VT is the thermal energy, Iph is the photo current, Ios is the saturation current and T is the cell temperature. According to Duffie [19], the temperature of a PV cell is determined by an energy balance equation, as solar energy which is absorbed is partly converted into thermal energy and partly into electrical energy. The cell temperature, Tc, at any ambient temperature, Ta, is found from:
|
Tc−TaTNOCT−Ta,NOCT=STSNOCTUL,NOCTUL[1−ηc(τα)]
|
(3)
|
where TNOCT is the Nominal Operating Cell Temperature (NOCT), Ta, NOCT is the NOCT condition (20 ℃), ST is irradiance at given temperature, SNOCT is irradiance at NOCT condition, UL is the loss coefficient and UL, NOCT is the loss coefficient at NOCT, ηc is the efficiency of the module and τα is the effective transmittance-absorbance product which can be considered to be 0.9 [19]. The ratio of the loss coefficients can be assumed to be unity.
The mean absolute bias error (MABE) was hence calculated for each set of results in order to evaluate the model. MABE was computed using Eq 4.
where, m is the number of number of samples, E if the measured value and M is the value obtained through modeling. Ideally, MABE should be zero or close to zero.
3. Data analysis and discussions
3.1. Effect of environmental parameters on PV cells
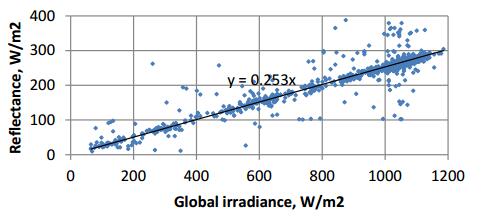
While performing the experiments, it was seen that the intensity and temperature were unpredictable due to a fluctuating nature. Moreover, an increase in light intensity should have resulted in an increase of temperature. However, another important element was wind which had a cooling effect and the same fluctuating characteristic as intensity and temperature that was beyond the control of the experimenters. Consequently, in a way, the cooling effect of wind compensated for the expected rise in temperature cell due to increasing irradiance. An additional analysis was made to investigate the effect of diffused component of radiation on the performance of the cells. The latter is the non-direct rays of light which are incident on the cells due to surrounding environment. Furthermore, the relationship between global intensity and diffuse component was also analysed. It was seen that diffuse component constituted around 25% of the global intensity as shown in Figure 2.
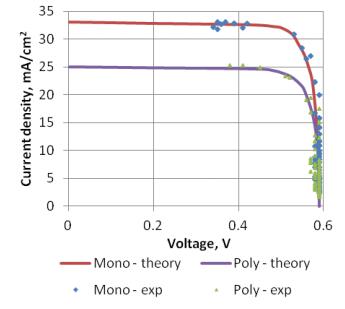
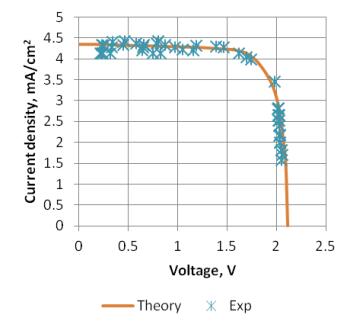
From the experimental results, it was observed that due to resistance limits, the short circuit current (Isc) and open circuit voltage (Voc) could not be obtained. Therefore, in order to quantify effect of environment on Isc and Voc, it was critical to perform modelling and extract the latter parameters. The wafer technologies, being uni-junction, were modelled using the one-diode model and the multi-junction amorphous Si Technology was modelled using the two-diode model. The initial conditions were set as: irradiance of 1000 W/m2 and temperature representing the conditions of experiment. Essential parameters as obtained from the five parameter model were used and they were hence adjusted such that the MABE was near to zero. It was observed that maximum MABE for mono-Si cell was 0.64 mA/cm2 A, 0.53 mA/cm2 for poly-Si and 0.25 mA/cm2 for thin film cell, which are less than 1.8%, 1.7% and 6% respectively. Based on the results obtained and the I-V curves as shown in Figures 3 and 4, it can be concluded that the simulation results were close to the experimental results. Thus, the developed models were in good agreement with the experimental readings and can be used to extract Isc and Voc values for further evaluation of effect of environment of cells.
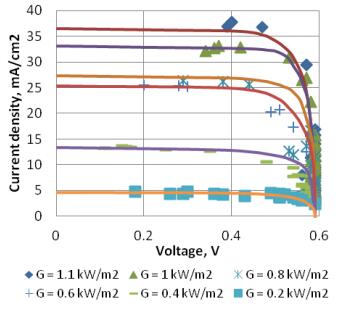
For a better comparison of effects of environment on each technology, the current obtained was divided by surface area of each cell to obtain current density. The sorted data of each cell technology was investigated for light intensity values of 200,400,600,800, 1000, 1100 W/m2. As shown in Figure 5, as intensity of light increased, the I-V curves of the monocrystalline cell technology shifted upwards with significant increase in short-circuit currents with slight changes in open-circuit voltages. Similar observations were made for all three cell technologies. However, the increase rates of the open-circuit voltages were different for the different cell technologies. This is because the cells are manufactured with different materials each with their own physical characteristics (such as diode ideality factor, diode saturation current or temperature coefficients). However the behavior of the monocrystalline and the polycrystalline cells were close enough.
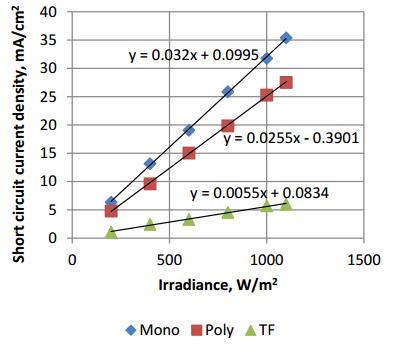
As shown in Figure 6, it was seen that the increase rate of the current density of the cells with respect to intensity was different. For mono-Si current increases by 32 μA/cm2 per unit change in irradiance, for poly-Si current increases by 25.5 μA/cm2 per unit change in irradiance and for thin film current increases by 5.5 μA/cm2 per unit increase in solar power. An increase in light intensity meant an increase in the number of incident photons which in turn resulted in an increase in generated electron hole pairs (EHP). Silicon solar cells are categorized by their lattice structure and the way single crystal grains grow in the bulk of the semiconductor. Mono crystals are one crystal structures, while poly crystals are structures with large number of grain boundaries which act as traps to EHPs. Amorphous structures contain a high density of dangling bonds with highest number of EHP traps. Therefore, mono crystals exhibit a better performance in terms of photo current density.
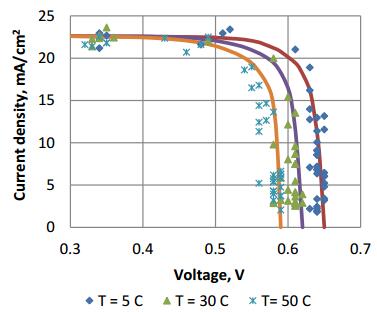
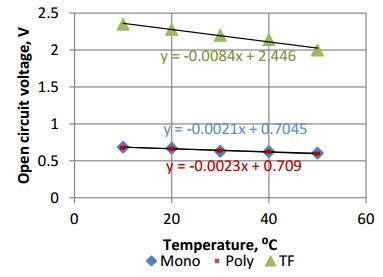
The sorted data were analyzed for temperature values of 5, 30 and 50 ℃. It was observed that an increase in temperature made the I-V curves shift to the left (consequent decrease in open-circuit voltages with almost unaffected short-circuit currents). An increase in temperature meant an increase in intrinsic carrier concentration which in turn resulted in a decrease in the in-built potential of the cell. The latter reflected as explained the decrease noted in the open-circuit voltages. Figure 7 shows the I-V curves for the polycrystalline cell technology for varying temperatures. Similar observations were made for all three cell technologies except that the rate of decrease of the open-circuit voltages being different for each cell technology. As shown in Figure 8, the thin film technology exhibited a higher rate of decrease of open circuit voltage with temperature (8.4 mV/℃) compared to the wafer technologies: 2.3 mV/℃ for poly-Si and 2.1 mV/℃ for mono-Si. Therefore, the wafer technology is more appropriate for sites with high variations in temperature as performance of wafer technology cells are stable in such conditions compared to thin film technology.
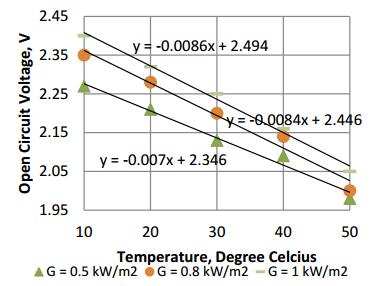
Another interesting observation was that, increase in the intensity of light resulted in a change in open-circuit voltage temperature coefficient. As shown in Figure 9 and Table 2, the most notable changes occurred for amorphous type thin film cell, where at 500 W/m2 the temperature coefficient was −7 mV/℃ and increases to −8.6 mV/℃ when the intensity of light is 1 kW/m2. While for the wafer based technologies, the change in open circuit voltage temperature coefficient is not considerable.
Table 2. Temperature coefficient of open-circuit voltage for mono, poly and Thin Film (a-Si) cell technology.
| Irradiance, W/m2 |
Open-circuit voltage temperature coefficient TkVoc, mV/℃ |
| mono |
poly |
Thin film |
| 1000 |
2.2 |
2.3 |
8.6 |
| 800 |
2.1 |
2.3 |
8.4 |
| 500 |
2 |
2.1 |
7 |
Based on the above, it can be concluded that wafer technologies have a better performance in terms of increase in current with respect to increase in irradiance and also lower decrease in voltage with increase in temperature. Therefore, they are more appropriate for regions with considerable changes in temperature over the year.
4. Conclusion
An effective and simple way of obtaining the intensity dependence of short-circuit current and temperature dependence of open-circuit voltage has been proposed. A combination of resistive load based I-V curve measurement and mathematical model was used for the purpose. As the MABE was nearly zero, the one diode model and two diode model can be reliably be used to simulate wafer based and multi junction a-Si cells respectively. Short-circuit current and open-circuit voltage could be extracted using a combination if experimental and simulation I-V curves. It was observed that light intensity highly affected the current parameters while having little effect on the voltage. Wafer based technologies have better response to intensity of light than a-Si technology. It also noted that cell temperature affected the voltage parameters while having no effect on the current parameters. Temperature coefficient of open-circuit voltage for wafer technologies was lower than a-Si technology. Hence, wafer technologies are more appropriate for locations with greater variations in temperature. Furthermore, it was also noted that reflectance was directly proportional to global intensity. It was inferred that reflectance depends on the surrounding environment which defines how much light will be reflected.
Acknowledgements
The authors would like to thank the University of Mauritius for provision of equipment and facilitating the research.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: