In the recent years microfluidic technology has affirmed itself as a powerful tool in medical and biological research. Among the different applications, cell manipulation has been widely investigated. Micro-flowcytometers, micromixers, cell sorters and analyzers are only few examples of the developed devices. Various methods for cell manipulation have been proposed, such as hydrodynamic, magnetic, optical, mechanical, and electrical, in this way categorized according to the manipulating force employed. In particular, when cells are manipulated by hydrodynamic effects, there is no needing of applying external forces. This brings to a simplification in the design and fabrication phase, and at the same time undesired effects on the biological sample are limited. In this paper, we will discuss the physics of the relevant hydrodynamic effects in microfluidics, and how they are exploited for cell manipulation.
1.
Introduction
This paper focuses on the constrained multi-objective optimization problems (CMOPs), which exist widely in the real world [1,2,3,4,5,6,7] and are generally formulated as follows [8,9,10]:
where f1(x),f2(x),⋯,fm(x) are m real-valued objective functions, gi(x)⩽0 and hj(x)=0 are inequality and equality constraints, respectively, and Ω is the search space. In order to facilitate the analysis, the constraint violation value of an individual x is usually calculated as:
where ε (e.g., ε=10−4) is a sufficiently small positive number to relax equality constraints hj(x)=0,j=r+1,⋯,q. Obviously, if and only if c(x)=0, the individual x satisfies all the constraints and is called the feasible solution. When c(x)>0, x is recorded as an infeasible solution. For any two solution x1,x2∈Ω, if F(x1)≠F(x2) and ∀i=1,..,m, fi(x1)⩽fi(x2), then it is said that x1 dominates x2, denoted as x1≺x2. A solution that is not dominated by other solutions in Ω is called the unconstrained Pareto optimal solution, and the geometry formed by all unconstrained Pareto optimal solutions in the objective space is defined as the unconstrained Pareto front (UPF). Similarly, the constrained Pareto front (CPF) is formed by all the feasible solutions that are not dominated by other feasible ones in Ω. Therefore, the essence of dealing with CMOP is to find a set of feasible solutions which are uniformly distributed on its CPF.
In the research community, a variety of constrained multi-objective evolutionary algorithms (CMEAs) have been proposed to deal with CMOPs [11,12,13,14,15,16]. Therein, many different constraint handling techniques (CHTs) have been used to balance objectives and constraints statically or dynamically. In penalty-based CHTs [17,18,19], the constraint violation value of an individual is transformed into the punishment for its objectives by the dynamic and adaptive penalty functions. Feasibility-led CHTs, such as constraint dominance principle (CDP) [20,21,22,23,24] and epsilon constraint-handling method (EC) [25,26,27], prefer individuals with smaller constraint violation values. Considering that the working populations guided by these two types of CHTs are easy to get stuck in the local areas and then fail to find the CPFs [24,28], several new CHTs tend to use the method of ignoring the feasibility and only optimizing the objectives to improve their global search ability. For example, the push and pull search (PPS) [29,30] first pushes the working populations toward UPFs without considering constraints in its push stage, and then pulls them back to CPFs by an improved EC in the pull stage. In C-TAEA [31] and CCMO [32], one population that prefers feasible solutions is used to provide search pressure to CPFs, while another population that ignores feasibility to optimize the objectives is used to force the working population to jump out of the local regions. Many numerical experiments show that these new CHTs do improve the ability of the working population to cross the complex feasible regions in front of the CPFs. Nevertheless, as overly emphasize the importance of optimizing constraints and objectives, these CHTs may mislead the population to jump over the feasible regions containing constrained Pareto optimal solutions. This would lead to missing some or even all of the fragments of CPF. So, it is still a valuable research topic to design the effective CHTs to deal with CMOPs.
To deal with the CMOPs effectively, this paper proposes a compound distance-based CHT, which aims to guide the population to explore the valuable areas that are not dominated by feasible solutions and avoid the insufficient search for some areas. Specifically, according to the angle and ℓp-norm, we first introduce a compound distance into the objective space to measure individual's search diameter. Then, the individuals with large search diameters in the valuable areas are given priority to be preserved. This effectively guides the working population to distribute evenly in the valuable areas and avoid missing the feasible regions containing constrained Pareto optimal solutions. In other words, the compound distance-based CHT is effective in guiding the working population to find CPFs. Accordingly, we propose a CMEA with the compound distance-based CHT, which is denoted as CD-CMEA, for solving CMOPs. Similar to the existing CMEAs, the proposed CD-CMEA also use a feasibility-oriented archive to record the best solutions for CMOPs. Besides, to balance the local search and global search in the evolutionary process, we use a dynamic mixing strategy to select individuals from the archive and the current population evenly scattered in the valuable areas to generate offspring. A series of numerical experiments on several benchmark problems are carried out to test the performance of the proposed CD-CMEA. And the experimental results show that CD-CMEA performs better than the state-of-the-art CEMAs in dealing with different CMOPs.
The main contributions of this paper can be summarized as follows:
1.We propose a novel compound distance-based CHT that guides the population to explore the valuable areas evenly. It can effectively prevent the population from being stuck in local areas.
2.We introduce a dynamic mixing strategy to guide the generation of offspring in each generation. This helps to make full use of the information of the current population and the archive to balance the local search and global search in the evolution process.
3.We carry out a series of numerical experiments to verify the effectiveness of the proposed algorithm.
The rest of this paper is organized as follows. Section 2 describes the compound distance-based CHT in detail. In Section 3, we embed the compound distance-based CHT into evolutionary algorithm for dealing with CMOPs. Section 4 organizes a series of numerical experiments to compare the performances of the proposed algorithm and the existing CMEAs. Section 5 concludes this paper.
2.
Compound distance-based constraint handling technique
In this section, we describe in detail the proposed compound distance-based CHT, which aims to guide the population to explore the valuable areas that are not dominated by feasible solutions and is quite different from the existing CHTs. Let the objective vector of any individual xq in Ω be Fq=(f1(xq),...,fm(xq))T, and fmini (i=1,...,m) be the minimum value that has been found on the i-th objective. To facilitate the analysis, we shift the objective space to Rm+ according to the following transformations:
and introduce two symbols as follows:
Besides, before introducing the proposed compound distance-based CHT, we first give a lemma, which is helpful to prove the properties of the compound distance involved.
Lemma 1. ∀fi(x1),fi(x2),fi(x3)>0,
Proof. (i) If fi(x1)⩾max(fi(x2),fi(x3))>0, then the right side of inequality (2.3) can be simplified as
(ii) If 0<fi(x1)⩽min(fi(x2),fi(x3)), then we can get that
(iii) If 0<f(x2,x3)i,min⩽fi(x1)⩽f(x2,x3)i,max, then it follows 1f(x2,x3)i,min⩾1fi(x1)⩾1f(x2,x3)i,max>0. The right side of inequality (2.3) is calculated as
According to the Sequence Inequality,
By substituting Eq (2.8) into Eq (9), we have
Thus, we have from (i), (ii) and (iii) that ∀fi(x1),fi(x2),fi(x3)>0,
2.1. Compound distance
When dealing with unconstrained multi-objective optimization problems, the angle is widely used as a diversity measure and has shown its effectiveness of guiding the population to evenly search for different segments of PF [33,34,35,36]. However, it can not accurately reflect the relative distance between different individuals. For example, point A=(1,1) is close to point B=(2,2) and far from point C=(100,100), but it is easy to get that the angular distance between A,B is equal to that between A,C. This is not conducive to guiding the population to search different regions evenly when dealing with CMOPs. In order to take the advantage of angle in guiding the population to search for the different segments of CPF and overcome its deficiency in measuring the relative distance between different individuals, we introduce a new compound distance in the objective space Rm+ of CMOPs, which takes into account both the angular distance and the relative position between considered individuals and defines the distance between any two points F1,F2∈Rm+ as:
where ⟨∗,∗⟩ represents the angle between the two vectors, and k is a constant greater than 0. For the three points A,B,C mentioned above, we can easily calculate that
This shows that the compound distance dp(∗,∗) can effectively evaluate the crowding degree of individuals. As a distance function in the objective space, dp(∗,∗) needs to satisfy four necessary properties, which are proved as below.
Property 1 (Non-negativity). dp(F1,F2)⩾0, for all F1,F2∈Rm+.
Proof. For all F1,F2∈Rm+, it is the fact that
Thus, according to the definition of dp(∗,∗) (see Eq (2.11)), we can easily get that dp(F1,F2)⩾0.
Property 2 (Identity). dp(F1,F2)=0, if and only if F1=F2.
Proof. According to the definition of dp(∗,∗),
Property 3 (Symmetry). ∀F1,F2∈Rm+, dp(F1,F2)=dp(F2,F1).
Proof. It is obvious.
Property 4 (Triangle inequality). ∀F1,F2,F3∈Rm+, dp(F1,F2)+dp(F1,F3)⩾dp(F2,F3).
Proof. For any F1,F2,F3∈Rm+, it is obvious that
Besides, according to the Minkowski Inequality,
By using Lemma 1, we can further transform Eq (2.16) as follows
So, it can inferred from Eq (2.15) and Eq (2.17) that
2.2. Compound distance-based CHT
Using the compound distance dp(∗,∗), we define the search diameter of a point Fi in F⊂Rm+ as:
Since Properties 1 to 4 have shown that dp(∗,∗) is a measure in the space Rm+, the larger the value of dp(Fi,Fj) obviously means that the distance between two individuals Fi,Fj is larger. So, a point Fi with a large search diameter Rp(Fi|F) means that it has a great contribution for F to searching different areas. Consider the point set F={A,B,C}⊂R2+ mentioned in Subsection 2.1 as an example. It is easy to get that Rp(A|F)=dp(A,B), Rp(B|F)=dp(B,A), Rp(C|F)=dp(C,B). As dp(A,B)=dp(B,A)=2p√2<dp(C,B)=50p√2, it follows that Rp(A|F)=Rp(B|F)<Rp(C|F), which is consistent with the distribution of points A,B,C in space R2+. Therefore, in the process of reducing the size of the considered population, the proposed compound distance-based CHT preferentially removes the individuals with the smallest search diameters and retains the individuals with larger search diameters.
Suppose that the size of the considered population is N∗, which exceeds its limited size N. Then the pseudo codes of pruning it using the proposed compound distance-based CHT is shown in Algorithm 1. Specifically, it first calculates the search diameter of each solution by the use of Eq (2.12) and determines the number of deleted solutions according to DN=N∗−N. After that, the DN worst solutions with the smallest search diameters are removed from the considered population one by one (Lines 3 to 7 in Algorithm 1). Considering that the removal of the worst individual may affect the search diameters of some remaining individuals and then results in the inaccurate of determining the next worst solutions, we update the search diameters of all remaining individuals in Line 7. Finally, the N retained individuals in the considered population are output as the results.
It is easy to get that in the process of determining the best individuals in the considered population, the proposed compound distance-based CHT do not take into account their performance in optimizing constraints and objectives. This is the main difference between the proposed compound distance-based CHT and the existing CHTs. In this way, the proposed compound distance-based CHT can avoid being lured to the local areas by deceptive constraints and guide the working population search for CPFs more effectively.
3.
Proposed algorithm framework
In this section, we embed the compound distance-based CHT into evolutionary algorithm and propose a new CMEA with the compound distance-based CHT (denoted as CD-CMEA) to solve the CMOPs. The details of the proposed CD-CMEA are described below.
3.1. Update mechanism of the current population
Due to the emergence of new individuals, the size N∗ of the working population Xt in the t-generation will exceed the preset size N. In order to effectively guide the Xt to search for CPFs, we use the compound distance-based CHT to select the N individuals of Xt who perform best in uniformly searching valuable areas to form the current population Xt+1 of the next generation. Specifically, we first identify the set of individuals located in the valuable areas as:
If the size of VXt is small than N, i.e., |VXt|<N, we initialize the current population of the next generation Xt+1 as VXt and then select (N−|VXt|) individuals closest to the valuable areas from the remaining individuals to fill Xt+1, where the distance from an individual to the valuable areas determined by VXt is calculated as:
Otherwise, we use Algorithm 1 to select the best N individuals of VXt who perform best in uniformly searching valuable areas to form Xt+1. We simplify the above steps to the pseudo-code form in Algorithm 2.
3.2. Archive
In the proposed CD-CMEA, the best solutions for solving CMOPs are recorded in an archive, which prefers feasible solutions. The pseudo codes of forming the archive are shown in Algorithm 3. First, the feasible solutions of the working population are used to initialize the archive. Then, if the number of individuals in archive is smaller than the preset size N, the infeasible solutions with the smallest constraint violation values are selected to fill the archive; otherwise, we use environmental selection of PREA [37,38], which has showed its excellent performance in dealing with different unconstrained MOPs and won the championship in IEEE WCCI 2018 Competition of Many-Objective Optimization, to prune the archive. The specific steps of environmental selection of PREA is as follows:
1.Shift the archive Λ to R+m as:
where fFmini is the minimum value found by feasible solutions on the objective fi.
2.Calculate the fitness value of each individual xi∈Λ by the following equation:
3.Determine the nondominated solutions in Λ:
If |Λ′|⩽N, terminate the calculation and let Λ retain only the N individuals with the best value of Fitness(x|Λ). Otherwise, let Λ=Λ′ and mark N solutions with the best fitness values:
These solutions are then used to form a promising region and to identify valuable candidates ΛC as follows:
After that, the individuals with the minimum crowding distance in Λ are eliminated one by one until the size of Λ is reduced to N. In each iteration, the one with the smaller fitness value of the two nearest individuals is removed from Λ. Therein, a parallel distance is used to measure the distance between any two solutions in Λ and is calculated as follows:
where ˆfil=f′l(xi)/fmax∗l.
3.3. Offspring production
To balance the local search and global search in the evolutionary process, we introduce a dynamic mixing strategy to randomly select individuals from the current population and the archive to form the mating pool of size N. Therein, the number of individuals selected from the current population of the t-th generation is calculated as:
where T is the maximum number of evolutionary generation, and function ⌊∗⌋ returns the largest integer not exceed the argument. The individuals of mating pool selected from the archive is (N−Nt). According to Eq (3.9), it is easy to get that with the deepening of the optimization process, that is, the increase of t value, the number Nt of individuals from the current population in mating pool gradually decreased from the initial N to 0. This helps the CMEA to make full use of the information of individuals evenly scattered in the valuable areas for global search in the early evolutionary stage, and to focus on local search using the archive in the late evolutionary stage. For each individual x in the mating pool, its two spouses have a 0.7 probability of being the individuals with the smallest angles with x in the objective space, and a 0.3 probability of being randomly selected from the mating pool. After that, we implement the differential evolution operator (DE) [39] and polynomial mutation (PM) [40] for these matched individuals to produce offspring. The specific steps for generating offspring are shown in Algorithm 4.
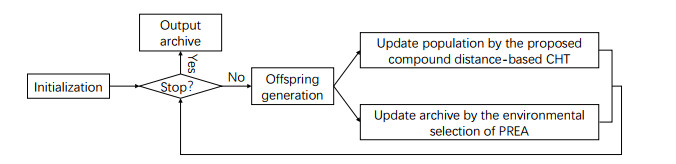
3.4. Framework of the proposed CD-CMEA
The flow chart of the proposed CD-CMEA is given in Figure 1, and its pseudo-code is shown in Algorithm 5. Specifically, N individuals are randomly generated to initialize the current population X0 and the archive Λ. After that, the following steps are repeated many times until the stopping criteria are met, which include using Algorithm 4 to produce offspring Y, updating the archive Λ by Algorithm 3, and using Algorithm 2 to select the best N solutions from Xt, Λ and Y to form the next generation population Xt+1. Finally, archive Λ is output as the result. For simplicity, in the proposed CD-CMEA, we set the parameters k and p of the compound distance (see Eq (2.4)) as π2p√m and 1, respectively. According to the framework of the proposed CD-CMEA, it can be easily found that the complexity of CD-CMEA mainly lies in two the processes: 1) calculating the search diameter of each individual by Eq (2.12); and 2) updating the archive set by the environmental selection of PREA. As the complexity of calculating the search diameter of an individual is O(mNlogN), the complexity of calculating all individuals in the current population is O(mN2logN). Also, the number of objectives m is generally smaller than the population size N and the complexity of PREA is O(N3) [37]. Therefore, the complexity of the proposed CD-CMEA is O(N3).
4.
Numerical experiments and analysis
In this section, we have carried out a series of numerical experiments to investigate the performance of the proposed algorithm CD-CMEA, which is compared with that of other state-of-the-art CMEAs.
4.1. Experimental design
In our simulation experiments, several benchmark suites, including CTP1-8 [41], DASCMOP1-9 [42], MW1-14 [43], C-DTLZ-series [20] and DC1-3-DTLZ1 [31], are regarded as the test problems. To vividly show the performance difference between the proposed CD-CMEA and the existing CMEAs, six state-of-the-art algorithms, that is, CMOEA/D-DE-CDP [22], CMOEA/D-DE-SR [22], C-TAEA [31], PPS [29], ToP [44] and AnD [23], are selected for comparison. The core ideas of these comparison algorithms are given below.
1.CMOEA/D-DE-CDP [22] is a decomposition-based differential evolution algorithm. It uses the CDP to determine the best solutions in the current population. Specifically, in the process of evaluating the quality of candidate solutions, the solutions with smaller constraint violation values are considered to be better. And when the constraint violation values of the candidate solutions are all the same, the solutions with the best fitness values under the evaluation of Tchebycheff method are regarded as the optimal solutions.
2.CMOEA/D-DE-SR [22] is an improved version of CMOEA/D-DE-CDP and uses a stochastic ranking approach (SR) to balance the constraints and objectives. Specifically, when the candidate solutions are both infeasible and the randomly generated number is smaller than the preset small probability value pf, it ignores the constraint and determines the optimal solutions according to the performances of these candidate individuals on optimizing objectives; Otherwise, it also uses the CDP to selects the best solutions.
3.C-TAEA [31] is a two-archive CMEA that simultaneously maintains two collaborative archives, i.e., the convergence oriented archive CA and diversity oriented archive DA. Therein, CA prefers feasible individuals and provides pressure to push the population to search for CPF, while DA evaluated by only optimizing the objectives focuses on exploring the areas that have not been exploited by CA.
4.PPS [29] is such a CMEA that divides the search process into two different stages: the push stage and the pull stage. In the push stage, constraints are ignored, and the population is evolved by optimizing only the objectives. In the pull stage, it uses an improved ϵ-CDP to pull the population to search for the CPF.
5.ToP [44] is a two-phase based CMEA for CMOPs. In the first phase, it transforms the original CMOP into a constrained single-objective optimization problem, which is then solved by a constrained single-objective evolutionary algorithm. In the second phase, it focuses on the promising area discovered in the first phase and uses the NSGA-II with CDP to find the CPF.
6.AnD [23] is a CMEA that uses angle-based selection strategy, shift-based density estimation strategy, and CDP. In the process of comparing individual quality, those with smaller violations of constraints will be selected for the next generation.
Considering that the released version of these compared algorithms may be their best form, we set their private parameters to be consistent with those in their published papers. For the sake of fairness, in terms of public parameters, the population size and the maximum function evaluation of all algorithms on each test problem are set to 100 and 2×105, respectively. And the number of independent runs of the algorithms on each test problem is set to 20.
Two widely used metrics, i.e., inverted generational distance (IGD) [45] and hypervolume (HV) [46], are adopted in this paper to evaluate the performance of the seven considered algorithms on each test problem. These two metrics are defined as follows:
IGD-metric: Let P be a set of uniformly distributed points on the CPF, and S is the final feasible results of an algorithm in the objective space, then the IGD of S to P is calculated as:
Obviously, the smaller the IGD(\mathbf{S}|\mathbf{P}) is, the better it is to approximate the CPF with \mathbf{S} . For each test instance in this paper, we use the method of Das and Dennis [47] to generate the uniformly distributed point set \mathbf{P} with the size of 10, 000.
HV-metric: Let \mathbf{z}^* = (z_1, ..., z_m)^T = 1.1\times (f^{\max}_1, ..., f^{\max}_m)^T be a reference point determined by the maximum value of each objective, i.e., f^{\max}_i, i = 1, ..., m, in the CPF. Then the HV value of the feasible solution set \mathbf{S} obtained by a CMEA is calculated as:
where VOL(\ast) is the Lebesgue measure. It is easy to get that a large value of HV(\mathbf{S}|\mathbf{z}) means good quality of \mathbf{S} in the objective space.
To hear the voice from statistics, we use the Wilcoxon Rank Sum Test with a significance level of 0.05 to analyze the performance differences between the proposed CD-CMEA and the other six existing CMEAs on each test problem. Therein, three symbols "+", "=" and "-" are introduced, which represent that the final results obtained by the compared algorithms are significantly better than, equal to, and worse than the proposed CD-CMEA, respectively.
4.2. Experimental results and analysis
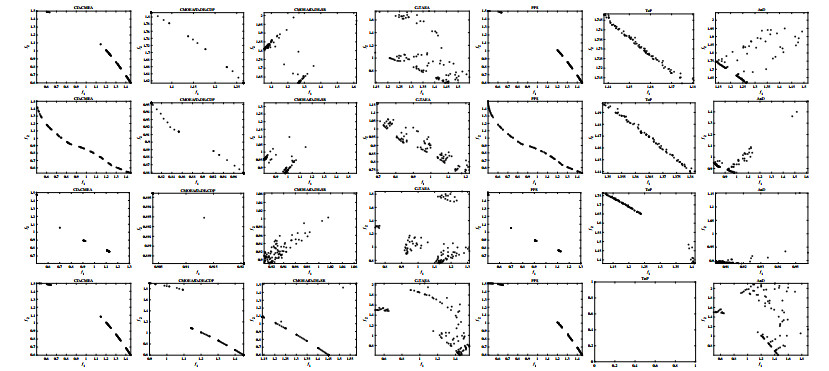
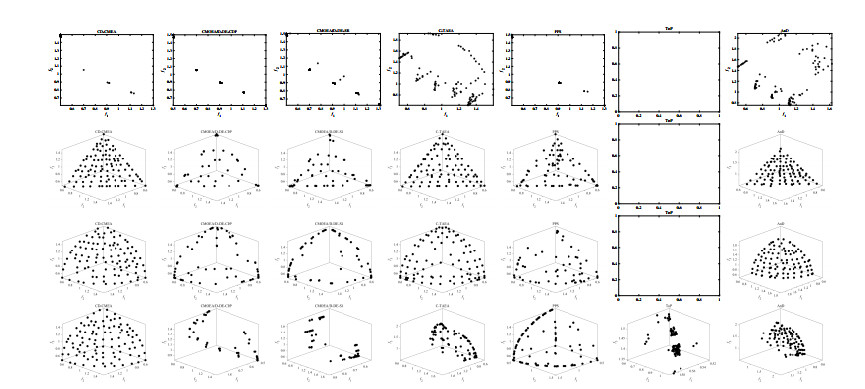
The comparison results among the seven considering CMEAs on each test instance under IGD and HV metrics are listed in Tables 1 and 2. In these tables, we highlight the best algorithm for each test problem with a gray background and a bold way. Besides, in order to visually show the excellent performance of the proposed CD-CMEA, we take DASCMOP series as the examples to draw the feasible solutions obtained by these seven comparing algorithms in Figures 2 and 3. As can be seen from these Tables 1 and 2, compared with the other six CMEAs, the proposed CD-CMEA performs better in the test instances, and it has better robustness in dealing with different CMOPs. This is to be expected. Next, we will analyze the reasons for this in detail.
When dealing with CTP1-5, 7, C2-DTLZ2, C3-DTLZ4 and DC1-DTLZ1, we can see that there is little difference in the performance of the seven algorithms. The main reason for this is that the constraints of these instances are very simple and they actually do not pose any challenge for the seven algorithms to find the CPFs. So, the proposed CD-CMEA and the other six algorithms can easily find the CPFs of these test instances, and the slight difference in performance among them is caused by their diversity maintenance mechanism. Since these problems have irregular PFs, which are captured more accurately by the PREA adopted in CD-CMEA than by the reference point-based and angle-based diversity maintenance mechanism of other algorithms [37], it is not surprising that the proposed CD-CMEA outperforms CMOEA/D-DE-CDP, CMOEA/D-DE-SR, C-TAEA, PPS, and AnD on them. Besides, Tables 1 and 2 also show that ToP performs better than the proposed CD-CMEA in solving CTP1-5, 7. That is not surprising. Because the update mechanism of ToP is NSGA-II, which has excellent performance in capturing irregular CPF in two-dimensional objective space. As NSGA-II performs poorly in selecting the individuals with good diversity in the space with the dimension number larger than 2, we can see that the performance of ToP on the three-objective instances C2-DTLZ2, C3-DTLZ4 and DC1-DTLZ1 is poor. When it comes to CTP6, 8, whose CPFs below the infeasible regions in the objective space, the feasibility-led CMEAs, i.e., CMOEA/D-DE-CDP, CMOEA/D-DE-SR, ToP and AnD, are easily trap into the local areas and than fail to find the entire CPFs. As the individuals of the working population in the proposed CD-CMEA are forced to distribute evenly in the valuable areas according to their search diameters, they can easily cross the infeasible regions of the CTP6, 8 and find the CPFs. So, it is natural that the performance of CD-CMEA is better than that of CMOEA/D-DE-CDP, CMOEA/D-DE-SR, ToP and AnD on CTP6, 8. Due to the objective-led CHT that ignores the constraints to only optimize the objectives, C-TAEA and PPS can also effectively force the working population to cross the infeasible region in front of CPFs and find CPFs of CTP6, 8. Nevertheless, because the diversity maintenance mechanism of CD-CMEA performs better than that of C-TAEA and PPS in capturing the irregular CPFs of CTP6, 8, CD-CMEA is better than C-TAEA and PPS in dealing with CTP6, 8.
For dealing with DASCMOP1-9, MW1-14, DC2-DTLZ1 and DC3-DTLZ1, it can see from Tables 1 and 2 that the proposed CD-CMEA is superior to CMOEA/D-DE-CDP, CMOEA/D-DE-SR, ToP and AnD. The reason for this is easy to get. As there are complex infeasible regions in front of the CPFs of DASCMOP1-9, MW1-14, DC2-DTLZ1 and DC3-DTLZ1 in the objective space, the feasibility-led CHT in CMOEA/D-DE-CDP, CMOEA/D-DE-SR, ToP and AnD fails to guide the working population to cross these infeasible regions, and this leads to the poor performances of CMOEA/D-DE-CDP, CMOEA/D-DE-SR, ToP and AnD on DASCMOP1-9, MW1-14, DC2-DTLZ1 and DC3-DTLZ1. For the three algorithms CD-CMEA, C-TAEA and PPS, they can effectively cross the complex infeasible regions of these instances and find the CPFs. However, because some instance of DASCMOP-series is the unbalanced problem, that is, the probability of populations appearing in different regions of the objective space is very different, the objective-led CHT in C-TAEA and PPS is easy to mislead the working population to the local feasible regions and miss some other feasible regions containing CPF fragments. So, C-TAEA and PPS fail to find the entire CPFs of some instance of DASCMOP1-9. As the individuals of the working population in the proposed CD-CMEA are forced to distribute evenly in the valuable areas according to their search diameters, they can easily find the entire CPFs of DASCMOP1-9. In addition, the CPFs of DASCMOP1-9, MW1-14, DC2-DTLZ1 and DC3-DTLZ1 are irregular, and CD-CMEA performs better than C-TAEA and PPS in capturing them. Therefore, it is not surprising that CD-CMEA is superior to C-TAEA and PPS on DASCMOP1-9, MW1-14, DC2-DTLZ1 and DC3-DTLZ1.
In summary, compared with the six state-of-the-art CMEAs, i.e., CMOEA/D-DE-CDP, CMOEA/D-DE-SR, C-TAEA, PPS, ToP and AnD, the proposed CD-CMEA performs better and has better robustness in dealing with different CMOPs. In other words, the proposed CD-CMEA is a promising algorithm for CMOPs.
4.3. Further investigation
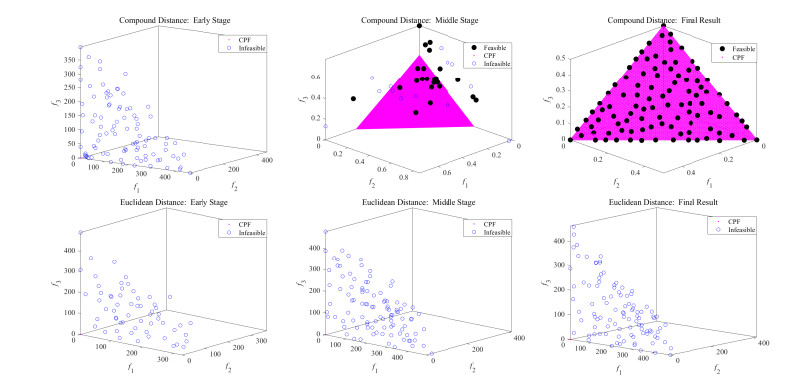
In order to investigate the effective of the proposed compound distance, we take the DC2-DTLZ1 as an example to compare the differences of archives obtained by the proposed algorithm using the compound distance and the Euclidean distance, respectively. The comparison results are shown in Figure 4. It can be seen from Figure 4 that Euclidean distance prefers the solutions far from the origin in the objective space and fails to guide the population to cross the infeasible regions in front of CPF. On the contrary, the proposed compound distance can effectively guide the population to search the different areas of the objective space evenly, whether they are close to or far from the origin. This makes the population guided by the proposed compound distance easily cross the infeasible regions in front of CPF and then find CPF of DC2-DTLZ1. Therefore, compared with Euclidean distance, the proposed compound distance is more beneficial to guide the population to explore the objective space evenly when solving the CMOPs.
5.
Conclusions and future work
In this paper, we introduce a compound distance into the objective space to measure individual's search diameter according to the angle and \ell_p -norm. After that, a compound distance-based CHT, in which the individuals with larger search diameter in the valuable areas are given priority to be preserved, is proposed to force the working population to fully explore the valuable areas that are not dominated by feasible solutions. Embedding the compound distance-based CHT in the evolutionary algorithm, we proposed a new method named CD-CMEA to deal with CMOPs. Numerical experimental results show that the proposed CD-CMEA performs better than the other six existing state-of-the-art CMEAs in dealing with different CMOPs. So, CD-CMEA is a promising method for solving CMOPs. Considering that the main characteristic of the proposed CD-CMEA is to force the working population to explore the valuable areas uniformly, we believe that the CHTs with similar properties should also perform well in dealing with CMOPs. Thus, in the future, we will further study the other forms of CHTs that can force the working population to explore the valuable areas evenly.
Conflict of interest
The authors declared that they have no conflicts of interest to this work.
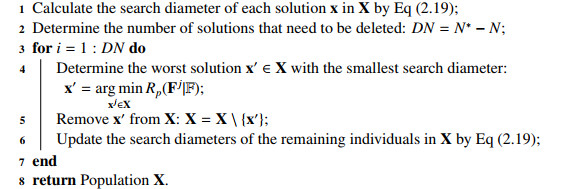









 DownLoad:
DownLoad: