1. Introduction
Lignocellulosic biomass has attracted considerable attention as potential feedstocks for production of fuel ethanol mainly because they are renewable and available in very large quantities. The biochemical conversion route for ethanol production from lignocellulosic biomass consists of two key consecutive steps, namely production of fermentable sugars and bioconversion of those sugars to ethanol by suitable microorganisms. Fermentable sugars can be produced from the carbohydrate fractions by hydrolysis with concentrated sulfuric acid or by enzymatic hydrolysis. Typically a pretreatment step is required prior to enzymatic hydrolysis. The purpose of pretreatment is to chemically or physically alter the structure of the matrix, thus allowing enzymatic hydrolysis to proceed at high rates and achieve high sugar yields [1]. Normally, pretreatment/enzymatic hydrolysis is more favorable than direct hydrolysis by concentrated sulfuric acid.
The key enzyme in hydrolysis of cellulose is cellulase. Cellulase is a complex system consisting of an endo-β-(1→4)-glucanase and an exo-β-(1→4)-glucanase. The products of the combined actions of the two enzymes are glucose oligomers such as cellobiose and cellotriose. Fungi and some aerobic cellulolytic bacteria also produce a cellobiase [β-(1→4)-glucosidase], which produces glucose from cellobiose and cellotriose [2]. Cellulase has been known to be strongly inhibited by its own products, i.e. glucose and cellobiose [3]. To alleviate this problem in cellulosic ethanol production, a process called simultaneous saccharification and fermentation (SSF) was developed. In this process, enzymatic hydrolysis and fermentation are carried out simultaneously in a single reactor. Thus, the sugars that are released in the enzymatic hydrolysis step are quickly fermented to ethanol and hence their inhibition on the cellulase system is significantly reduced or almost completely eliminated [1]. In the SSF process, however, there arises another problem as a result of the accumulation of ethanol. It has been observed that ethanol inhibited both partially purified cellulases and early commercial cellulase enzyme products [3,4,5,6,7,8,9,10,11,12]. The inhibition of Trichoderma reesei cellulase by ethanol was found to be non-competitive in two separate studies [3,7]. In another study, the inhibitory effect of ethanol on cellulase from Trichoderma viride was found to be more significant in the later stages of the hydrolysis than in the initial stages of this process. It was also suggested that ethanol inhibited cellulase by depressing the adsorption of exoglucanase on cellulose [11].
The early commercial cellulase enzyme products such as Spezyme CP and GC220 (Genencor International, Rochester, NY, USA) were developed mainly for viscosity reduction instead of production of fermentable sugars from lignocellulosic materials. These products, therefore, did not have sufficient cellobiase activity and normally a cellobiase such as Novo 188 (Novozymes, Franklinton, NC, USA) was added to allow high glucose yields. To lower the costs and improve the economics of cellulosic ethanol production, new products, e.g. Accellerase® 1000 and 1500 (DuPont Industrial Biosciences, Palo Alto, CA, USA), were developed. These new enzyme products contain high levels of cellobiase activity and hence addition of cellobiase such as Novo 188 is no longer needed. For cellulosic ethanol to be economically feasible all the available carbohydrates must be converted to ethanol [1]. Although the recently developed commercial cellulase enzyme products contain hemicellulase activities, special products were developed for hydrolysis of the hemicellulosic fractions to fermentable sugars, e.g. Accellerase® XY (DuPont Industrial Biosciences, Palo Alto, CA, USA).
Distillation is one of the most energy-intensive unit operations in commercial fuel ethanol process. Since the energy demand and thus operating cost of distillation decrease with increase in ethanol concentration in the feed stream, it is highly desirable to obtain final ethanol concentrations in the fermentor as high as possible. Typically the minimum ethanol concentration that should be achieved in the fermentation to ensure an economically feasible process is about 50 g/L [13]. Since cellulosic materials tend to absorb water quickly and increase their bulk volume, high final ethanol concentrations could not be obtained in a simple batch SSF process. To bring final ethanol concentrations to 50 g/L or higher, a fed-batch SSF process was needed. In such a process, both substrate and fresh enzyme had to be added at intervals during the course of the fermentation [14]. Thus, some of the enzyme would be in short contact with the ethanol produced and some would be exposed to ethanol for extended periods. Therefore, it is of interest to study the effect of ethanol on the activities of cellulolytic enzyme products at various contact times.
In the present investigation, the effect of ethanol on the hydrolytic activities of some of the commercial enzyme products recently developed for fermentable sugar production from lignocellulosic feedstocks was studied. In this report, we present and discuss the results of our study on the effect of ethanol on the initial rates and the final glucose concentrations obtained after an extended period. The initial rates were calculated as the average rates of glucose production during the first 2 h of hydrolysis.
2. Materials and Methods
2.1. Materials
Accellerase® 1500 and Accellerase® XY were kindly provided by DuPont Industrial Biosciences. Accellerase® 1500 is a cellulase complex reported by the manufacturer to contain endoglucanase activity of 2200-2800 CMC units/g and β-glucosidase activity of 525-775 pNPG units/g. One CMC unit liberates 1 mmol of reducing sugars (expressed as glucose equivalents) in one minute at 50 °C and pH 4.8. One pNPG unit liberates 1 mmol of nitrophenol from p-nitrophenyl-β-D-glucopyranoside per minute at 50 °C and pH 4.8. In filter paper units (FPU), the specific activity of Accellerase® 1500 was reported as 76.5 FPU/mL [14]. Accellerase® XY is a hemicellulase enzyme complex reported by the manufacturer to contain xylanase activity of 20,000-30,000 units/g. One xylanase unit liberates 1 mmol of reducing sugars (expressed as xylose equivalents) from a xylan substrate in one minute. Straw of the Thoroughbred barley variety was obtained from the Foundation Seed Farm of the Virginia Crop Improvement Association (Mt. Holly, VA, USA) in September 2010. The straw was pretreated using the soaking in aqueous ammonia (SAA) procedure as described in a previous study [15]. The pretreated barley straw was used in the present study.
Beechwood xylan (catalog number X4252), cellobiose (catalog number C7252) and a-cellulose (catalog number C8002) were purchased from Sigma-Aldrich (St. Louis, MO, USA). All other chemicals were purchased from various suppliers and were of reagent grade.
2.2. Methods
The experiments performed in the present study are summarized in Table 1.
Table 1. Details of the experiments performed to study the effect of ethanol on selected commercial cellulolytic enzyme products.
| Commercial enzyme products | Accellerase® 1500 | Accellerase® XY |
| Components of experimental mixtures in 50 mM citric acid buffer (pH 4.8) | 1. a-Cellulose 50 g/L
2. Enzyme 0.25 mL/g cellulose
3. Ethanol at 0, 2.5, 5, 7.5, 10 and 15% (v/v) | |
| 1. Cellobiose 50 g/L
2. Enzyme 0.25 mL/g cellulose
3. Ethanol at 0, 2.5, 5 and 10% (v/v) | 1. Xylan 50 g/L
2. Enzyme 0.25 mL/g cellulose
3. Ethanol at 0, 2.5, 5 and 10% (v/v) |
| 1. Pretreated barley straw 50 g/L
2. Enzyme 0.25 mL/g cellulose
3. Ethanol at 0, 2.5, 5, 7.5, 10 and 15% (v/v) | 1. Pretreated barley straw 50 g/L
2. Enzyme 0.25 mL/g cellulose
3. Ethanol at 0, 2.5, 5, 7.5, 10 and 15% (v/v) |
The selection of 50 g/L (i.e. 5 wt%) for initial barley straw and xylan concentration was based on our past experience in which it was observed that pretreated barley straw and other lignocellulosic materials at that concentration after absorbing liquid and expanding would still leave sufficient free liquid to allow good mixing. This initial concentration also was used for a-cellulose and cellobiose to keep the initial substrate concentrations the same throughout the investigation. All experiments were performed in duplicate and the average results are reported. The effect of ethanol on α-cellulose hydrolysis was studied with Accellerase® 1500. In the base-line experiment, i.e. with no ethanol present, 6.50 g a-cellulose was suspended in 123.5 mL of 50 mM citric acid buffer at pH 4.8 in a 250-mL beaker containing a small stir bar. The slurry was thoroughly mixed on a magnetic stir plate. A volume of 1.625 mL enzyme then was added. Portions of 10.0 mL then were removed and transferred into 20-mL glass scintillation vials. The polypropylene caps with polyethylene liner then were tightly screwed in place. A total number of 10 vials were prepared as described. The vials were securely taped onto the platform in an incubator shaker (New Brunswick Scientific, Edison, NJ, USA) preset at 50 °C. The platform then was set in circular motion at a speed of 250 rpm. At 2, 4, 6, 24 and 48 h two vials were removed. Samples were taken from the removed vials and placed in microcentrifuge tubes. The tubes were securely capped and immediately immersed in a boiling water bath for 5 min to deactivate the enzyme. These tubes then were centrifuged on an Eppendorf microcentrifuge (Hauppauge, NY, USA) at 13, 000 rpm for 3 min. The supernatants were syringe-filtered through a 0.2-micron filter and stored in a freezer until use for sugar analysis. To study the effect of 2.5, 5, 7.5, 10 and 15% v/v ethanol on cellulose hydrolysis, 3.25, 6.50, 9.75, 13.0, and 19.5 mL buffer, respectively, were replaced by equal volumes of ethanol and the same procedure was repeated.
In the experiments performed to study the effect of ethanol on the cellobiase activity of Accellerase® 1500, α-cellulose was replaced with the same quantity of cellobiose, i.e. 6.50 g, and the enzyme dosage was kept at 0.25 mL/g substrate.
The effect of ethanol on enzymatic hydrolysis of pretreated barley straw was studied using Accellerase® 1500 and Accellerase® XY. In these experiments, because it was difficult to reproducibly distribute the slurries having exactly the same solid contents, the vials were set up individually. The moisture content of the barley straw was pre-determined on a moisture balance (model MB45, Ohaus Corporation, Pine Brook, NJ, USA) and the quantity equivalent of 0.50 g dry mass was weighed and placed in each vial. The volumes of buffer, ethanol and enzyme were added accordingly as described previously. The enzyme loading in these experiments was 0.25 mL/g glucan in the pretreated barley straw, which was determined as 49.2 wt% dry-basis by the standard NREL procedure [16].
The samples were analyzed for sugars (glucose and xylose) by HPLC using a series 1200 Agilent Technologies system equipped with a refractive index detector (Santa Clara, CA, USA). The sugar concentrations were determined using a Bio-Rad Aminex HPX-87H column (Hercules, CA, USA) maintained at 65 °C with 5 mM H2SO4 as the mobile phase at a flow rate of 0.6 mL/min.
3. Results and Discussion
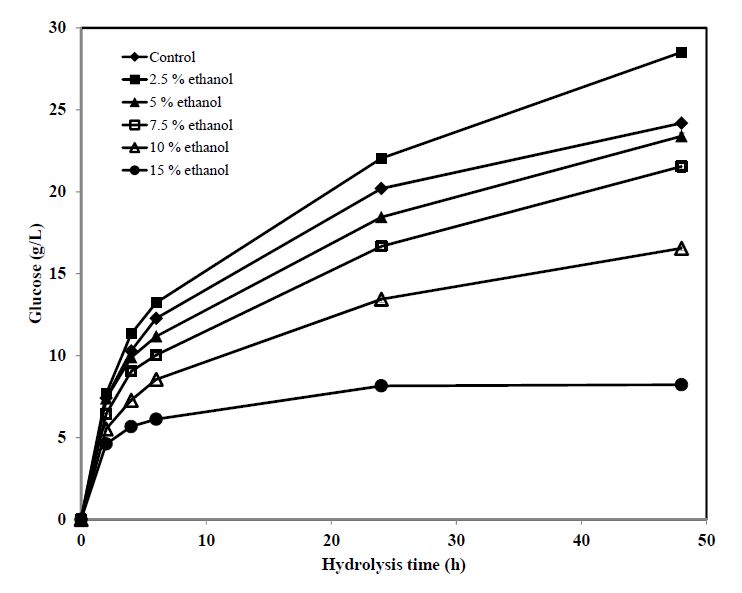
The time courses of glucose production during the hydrolysis of a-cellulose by Accellerase® 1500 at various ethanol levels are shown in Figure 1. The initial rates of glucose production and its final concentrations together with their corresponding increases or decreases with respect to the base-line results are summarized in Table 2. It was assumed that since the glucose concentrations at 2 h were still low (less than 8 g/L in all cases), the feedback inhibition due to glucose accumulation was negligible and the observed increases or decreases in glucose production were mainly due to the effect of ethanol. The results indicated that at 2.5% ethanol acted as an activator. At this ethanol level, the initial glucose production rate was improved by 3.4% and the final glucose concentration was improved by 17.9%. The reason for ethanol to act as an activator at 2.5% was not clear. It could be that ethanol at this low level changed the enzyme configuration into a more favorable one, which was similar to the reason for acetone activation of cellulase proposed in a previous study [3]. At 5% and higher levels, ethanol became an inhibitor. At the highest ethanol level tested, i.e. 15%, the initial glucose production rate was decreased by 38% and the final glucose concentration by 66%. Ethanol at 15% is the typical final concentration in a commercial starch-based process. In a commercial cellulosic ethanol process, the final concentration is more likely to be about 10%. At this level, the enzyme was inhibited but still retained significant activity. The decreases of the initial glucose production rate and final glucose concentration with respect to the base-line results were only 26% and 32%, respectively. These were significantly lower than the corresponding decreases compared to the base-line results observed at 15% ethanol. Comparison of the glucose concentration profiles obtained in the base-line experiment and in the experiments with ethanol present at 5% and higher levels revealed interesting observation. For example, the concentrations of glucose obtained at 6 h in the base-line experiment and in the presence of 15% ethanol were 12.3 g/L and 6.1 g/L, respectively. Although the glucose concentration in the base-line experiment was twice of that obtained in the presence of 15% ethanol, glucose production in the former case continued at a high rate whereas glucose production in the latter was greatly decreased and, in fact, almost completely stopped. Similar observation could be made on the results obtained with ethanol at 5%, 7.5% and 10%. These observations indicated that when ethanol acted as an inhibitor, its inhibition was much stronger than the feedback inhibition exerted by glucose.
Table 2. Initial rates and final glucose production from hydrolysis of a-cellulose by Accellerase® 1500 at 0.25 mL/g cellulose and at ethanol levels of 0, 2.5, 5, 7.5, 10 and 15%.
| Ethanol (% v/v) | Initial rate (g glucose/L-h) | Relative increase/decrease (%) | Final glucose concentration (g/L) | Relative increase/decrease (%) |
| 0 | 3.71 | 0 | 24.19 | 0 |
| 2.5 | 3.83 | 3.4 | 28.52 | 17.9 |
| 5 | 3.69 | –0.4 | 23.39 | –3.3 |
| 7.5 | 3.22 | –13.1 | 21.55 | –10.9 |
| 10 | 2.76 | –25.5 | 16.56 | –31.5 |
| 15 | 2.31 | –37.8 | 8.22 | –66.0 |
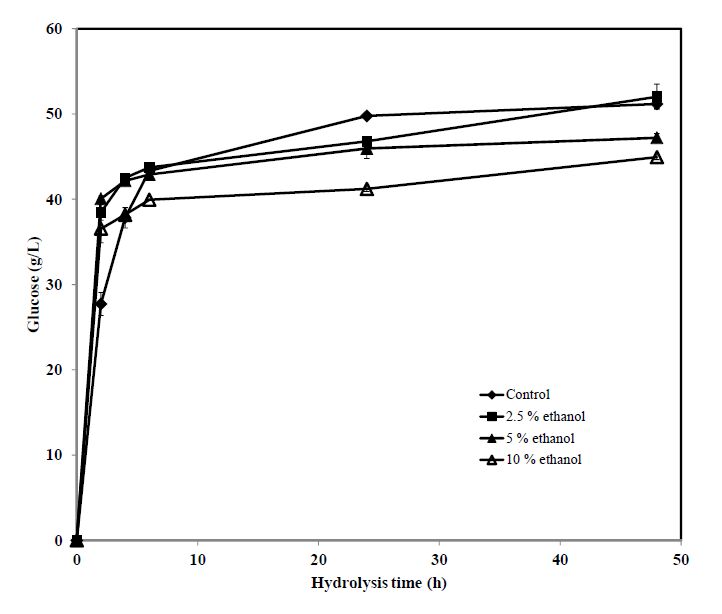
The effect of ethanol at 2.5, 5 and 10% on the cellobiase activity in Accellerase® 1500 was studied using cellobiose as substrate at the same initial concentration as a-cellulose in the previous experiments, i.e. 50 g/L. The results are shown in Figure 2 and Table 3. Ethanol at all three levels increased the initial rates of glucose production. The largest increase, which was 45% compared to the base-line, occurred at 5% ethanol. Final glucose concentrations were slightly increased at 2.5% ethanol but were decreased by ethanol at 5% and 10%. Compared to the base-line result, the final glucose concentrations at 5% and 10% ethanol were reduced by 8% and 12%, respectively. The results indicated that at 5% the inhibitory effects of ethanol on the cellobiase activity and glucanase activities were approximately equal but at 10%, and likely at higher levels, those effects were stronger on the latter.
Table 3. Initial rates and final glucose production from hydrolysis of cellobiose by Accellerase® 1500 at 0.25 mL/g cellobiose and at ethanol levels of 0, 2.5, 5 and 10%.
| Ethanol (% v/v) | Initial rate (g glucose/L-h) | Relative increase/decrease (%) | Final glucose concentration (g/L) | Relative increase/decrease (%) |
| 0 | 13.86 | 0 | 51.17 | 0 |
| 2.5 | 19.24 | 38.8 | 52.02 | 1.7 |
| 5 | 20.03 | 44.5 | 47.20 | –7.8 |
| 10 | 18.27 | 31.8 | 44.94 | –12.2 |
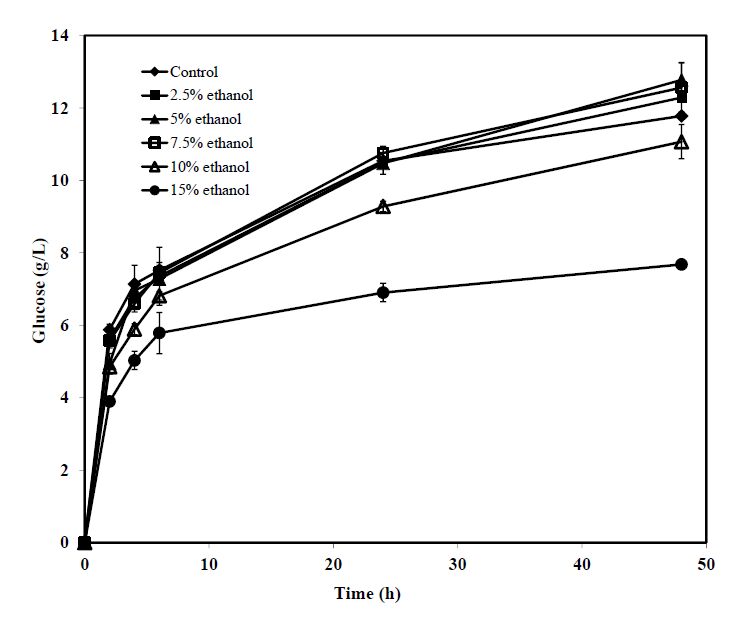
Barley straw pretreated by the SAA method was used to investigate the effect of ethanol on the activities of Accellerase® 1500 toward an actual lignocellulosic substrate. The time courses of glucose production are shown in Figure 3 and the increases/decreases of the initial glucose production rates and final glucose concentrations with respect to the base-line results are given in Table 4. The results in Table 4 indicated that ethanol at all levels had an inhibitory effect on the initial rates of glucose production. However, as the hydrolysis progressed, the inhibition was reversed for ethanol at 7.5% and lower levels. The final glucose concentrations in these experiments were all higher than that obtained in the base-line experiment. The inhibitory effect continued during the entire hydrolysis process with ethanol at 10% and 15%. In both cases, the final glucose concentrations were significantly lower than those in the base-line experiment. It was probable that, since barley straw had a much more complex structure than pure a-cellulose, the switch from initial inhibition to activation by ethanol at 7.5% and lower levels when the hydrolysis progressed could be a combined effect of enzyme adsorption on the substrate and the reaction with ethanol at these low levels, which caused the enzymes to assume more favorable structures. Further studies are needed to confirm this hypothesis.
Table 4. Initial rates and final glucose production from hydrolysis of SAA-pretreated barley straw by Accellerase® 1500 at 0.25 mL/g cellulose and at ethanol levels of 0, 2.5, 5, 7.5, 10 and 15%.
| Ethanol (% v/v) | Initial rate (g glucose/L-h) | Relative increase/decrease (%) | Final glucose concentration (g/L) | Relative increase/decrease (%) |
| 0 | 2.94 | 0 | 11.78 | 0 |
| 2.5 | 2.81 | –4.4 | 12.29 | 4.3 |
| 5 | 2.47 | –16.0 | 12.77 | 8.4 |
| 7.5 | 2.79 | –5.3 | 12.56 | 6.6 |
| 10 | 2.43 | –17.5 | 11.07 | –6.0 |
| 15 | 1.95 | –33.8 | 7.68 | –34.8 |
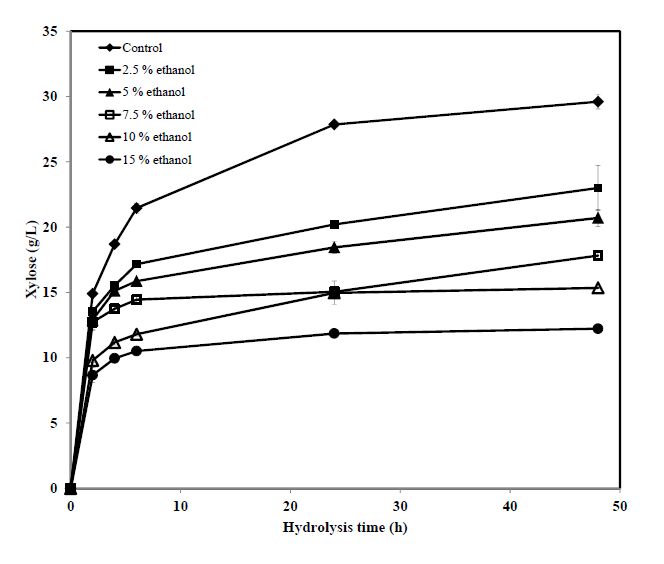
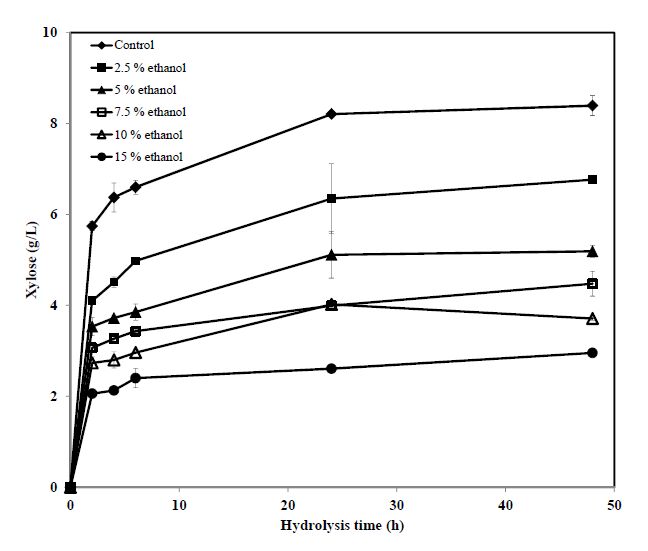
In order to produce ethanol from lignocellulosic feedstocks economically, it is very important that all the available carbohydrates can be utilized efficiently. Most of the commercial cellulolytic enzyme products focused on the hydrolysis of cellulose. Accellerase® XY is one of the few enzyme products that were developed specifically for hydrolysis of hemicellulose in lignocellulosic biomass to produce xylose as the major fermentable sugar. Thus, the effect of ethanol on the activities of the enzymes in this commercial product would be of particular interest. The effect of ethanol on Accellerase® XY was studied with beechwood xylan and SAA-pretreated barley straw as substrates. The time courses of xylose production are shown in Figure 4, and the initial xylose production rates together with final xylose concentrations obtained with beechwood xylan are summarized in Table 5. It can be seen that ethanol at all levels tested acted as an inhibitor. With ethanol at 10%, which likely is the final concentration in a commercial cellulosic ethanol process as discussed previously, the initial production rate and final concentration of xylose were reduced by 34% and 48% compared to the base-line, respectively. The results obtained with SAA-pretreated barley straw as substrate are plotted in Figure 5 and summarized in Table 6. Similar to the case of xylan, ethanol at all levels acted as an inhibitor. The inhibition of ethanol on xylose production from SAA-pretreated barley straw was significantly higher than the inhibition observed with xylan substrate. For example, at 10% ethanol, the decreases in initial xylose production rate and final xylose concentration obtained with SAA-pretreated barley straw compared to the base-line results were 52% and 56%, respectively.
Table 5. Initial rates and final xylose production from hydrolysis of beechwood xylan by Accellerase® XY at 0.25 mL/g xylan and at ethanol levels of 0, 2.5, 5, 7.5, 10 and 15%.
| Ethanol (% v/v) | Initial rate (g xylose/L-h) | Relative increase/decrease (%) | Final xylose concentration(g/L) | Relative increase/decrease (%) |
| 0 | 7.45 | 0 | 29.59 | 0 |
| 2.5 | 6.77 | –9.1 | 22.99 | –22.3 |
| 5 | 6.46 | –13.4 | 20.71 | –30.0 |
| 7.5 | 6.37 | –14.6 | 17.82 | –39.8 |
| 10 | 4.90 | –34.2 | 15.35 | –48.1 |
| 15 | 4.34 | –41.8 | 12.22 | –58.7 |
Table 6. Initial rates and final xylose production from hydrolysis of SAA-pretreated barley straw by Accellerase® XY at 0.25 mL/g cellulose and at ethanol levels of 0, 2.5, 5, 7.5, 10 and 15%.
| Ethanol (% v/v) | Initial rate (g xylose/L-h) | Relative increase/decrease (%) | Final xylose concentration (g/L) | Relative increase/decrease (%) |
| 0 | 2.87 | 0 | 8.39 | 0 |
| 2.5 | 2.05 | –28.6 | 6.76 | –19.4 |
| 5 | 1.77 | –38.5 | 5.19 | –38.1 |
| 7.5 | 1.53 | –46.7 | 4.48 | –46.6 |
| 10 | 1.37 | –52.4 | 3.71 | –55.8 |
| 15 | 1.03 | –64.1 | 2.95 | –64.8 |
4. Conclusion
The effect of ethanol at various levels, from 2.5% to 15%, on the activities of two recently developed commercial lignocellulosic biomass hydrolytic enzyme products was investigated. Depending on the substrate and the concentration, ethanol acted as either activator or inhibitor. In all cases, inhibition was observed when ethanol was at 10% or higher. Even at this level, which is the expected final concentration in a commercial biomass-based ethanol process, the enzymes still retained significant activities. The results obtained in this study could be used to determine approximately the enzyme dosages that are required in a fed-batch SSF process for ethanol production from a lignocellulosic feedstock.
Conflict of Interest
Mention of trade names or commercial products in this article is solely for the purpose of providing specific information and does not imply recommendation or endorsement by the U.S. Department of Agriculture (USDA). USDA is an equal employment provider and employer.









 DownLoad:
DownLoad: