1. Introduction
Mosquitoes are small biting insects comprising of the family Culicidae. There are about 3,500 mosquito species in the world (grouped into 41 genera) [4,30,43]. Mosquito species, such as Anopheles, Aedes aegypti, Aedes albopictus and Culex, play significant roles as vectors of some major infectious diseases of humans, such as malaria, yellow fever, Chikungunya, west Nile virus, dengue fever, Zika virus and other arboviruses [4,48]. These diseases are transmitted from human-to-human via an effective bite from an infected female adult mosquito [4,51]. While adult male mosquitoes feed on plant liquids such as nectar, honeydew, fruit juices and other sources of sugar for energy, female mosquitoes, in addition to feeding on sugar sources (for energy), feed on the blood of human and other animals solely to acquire the proteins needed for eggs development [4,30,49,51].
Mosquitoes are the best known disease vector for vector-borne diseases (VBDs) of humans (VBDs account for 17% of the estimated global burden of all infectious diseases) [76,78]. Mosquito is the world's deadliest animal (accounting for more human deaths annually than any other animal), spreading human diseases such as malaria, dengue and yellow fever, which together are responsible for several million deaths and hundreds of millions of cases annually [13,49]. For example, malaria, transmitted by female Anopheles mosquitoes, is endemic in 91 countries, with about 40% of the world's population at risk, causing up to 500 million cases and over 1 million deaths annually [48,49,77]. Similarly, dengue, transmitted by female Aedes mosquitoes, causes over 20 million cases a year in more than 100 countries [48,77].
The life-cycle of the mosquito is completed via four distinct stages, namely: eggs, larva, pupa and adult stages, with the first three largely aquatic [48]. A female mosquito can lay about 100-300 eggs per oviposition [4,48], and this process is temperature dependent [4]. The eggs are laid at a convenient breeding site, usually a swamp or humid area in the aquatic environment (the Anopheles species typically lays their eggs on the surface of the water) and after about 2-3 days, they hatch into larva. Larvae develop through four instar stages [48,4]. At the end of each larval stage, the larvae molt, shedding their skins to allow for further growth (the larvae feed on microorganisms and organic matter in the water) [4]. During the fourth molt, the larvae mature into pupae (the whole process of maturation from larvae to pupae takes 4-10 days [51]). The pupae then develop into adult mosquitoes in about 2-4 days [4,51].
The duration of the entire life-cycle of the mosquito, from egg laying to the emergence of an adult mosquito, varies between 7 and 20 days [51], depending on the ambient temperature of the breeding site (typically a swamp or humid area) and the mosquito species involved [28] (for instance, Culex tarsalis, a common mosquito in California (USA), might go through its life cycle in 14 days at 700F and take only 10 days at 800F [48]). Adult mosquitoes usually mate within a few days after emerging from the pupal stage, after which they go questing for blood meal (required to produce eggs) [4]. Once a blood meal is taken, the female mosquito moves to a convenient breeding site where it lays its eggs [52]. The chances of survival of the female adult mosquitoes depend on temperature and humidity, as well as their ability to successfully obtain a blood meal while avoiding host defenses [4].
The introduction, abundance and distribution of mosquitoes worldwide have been affected by various environmental (climatic) factors such as temperature, humidity, rainfall and wind [2,15,47,54,55,57,58,60,67,79]. These factors have direct effect on different ecological aspects of the mosquito species which includes the oviposition process, development during aquatic stages and the biting rate of mosquitoes [2,47,60]. Furthermore, the oviposition process, development at aquatic stages, emergence of the adult and other developmental processes in the larval habitats of mosquitoes, play a key role in the determination of abundance and distribution of mosquitoes [3,56].
Understanding mosquito population dynamics is crucial for gaining insight into the abundance and dispersal of mosquitoes, and for the design of effective vector control strategies (that is, understanding mosquito population dynamics has important implications for the prediction and assessment of the effects of many vector control strategies [51,52]). The purpose of the current study is to qualitatively assess the impact of temperature and rainfall on the population dynamics of female mosquitoes in a certain region, and taking into consideration the dynamics of the human-vector interaction. This study extends earlier mosquito population biology in literature such as the model in [1], by designing a new temperature-and rainfall-dependent mechanistic mosquito population model that incorporates some more notable features of mosquitoes population ecology such as four stages for larval development and three different dispersal (questing for blood meal, fertilized and resting at breeding site) states of female adult mosquitoes. The non-autonomous model is formulated in Section 2 and its autonomous version is analyzed in Section 3. The full non-autonomous model is analyzed and simulated in Section 4. Since malaria is the world's most important parasitic infectious disease [34], numerical simulations of the model will be carried out using parameters relevant to the population biology of adult female Anopheles mosquitoes in Section 5 (it is worth stating that there are approximately 430 species of the Anopheles mosquitoes, of which 30-40 transmit malaria in humans (i.e., they are vectors) [4,43]).
2. Model formulation
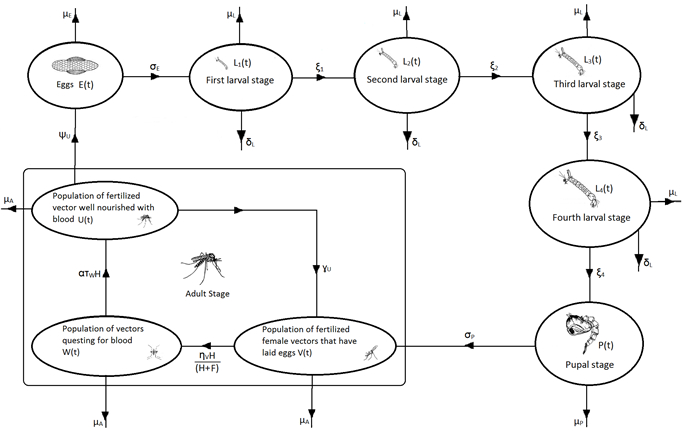
This study is based on the formulation and rigorous analysis of a mechanistic model for the dynamics of female Anopheles mosquitoes in a population. The model splits the total immature mosquito population at time t (denoted by IM(t)) into compartments for eggs (E(t)), four larval stages (Li(t); i=1,2,3,4) and pupae (P(t)), so that IM(t)=E(t)+4∑i=1Li(t)+P(t). Similarly, to account for the mosquito gonotrophic cycle, the population of adult female Anopheles mosquitoes at time t (AM(t)) is sub-divided into compartments for the class of unfertilized female vectors not questing for blood meal and fertilized female mosquitoes that have laid eggs at the mosquitoes breeding site (V(t)), the class of fertilized, but not producing, female mosquitoes questing for blood meal (W(t)), and the class of fertilized, well-nourished with blood, and reproducing female mosquitoes (U(t)), so that AM(t)=U(t)+V(t)+W(t). Let N represents the amount of nutrients for the larvae (assumed to be constant or uniformly available at the breeding sites). The model is given by the following deterministic system of nonlinear differential equations.
|
dEdt = ψU(T)(1−UKU)U−[σE(R,ˆT)+μE(ˆT)]E,dL1dt = σE(R,ˆT)E−[ξ1(N,R,ˆT)+μL(ˆT)+δLL]L1,dLidt = ξ(i−1)(N,R,ˆT)L(i−1)−[ξi(N,R,ˆT)+μL(ˆT)+δLL]Li;i=2,3,4,dPdt = ξ4(N,R,ˆT)L4−[σP(R,ˆT)+μP(ˆT)]P,dVdt = σP(R,ˆT)P+γUU−ηVHH+FV−μA(T)V,dWdt = ηVHH+FV−[τWH+μA(T)]W,dUdt = ατWHW−[γU+μA(T)]U,L = 4∑i=1Li.
|
(1)
|
In (1), R=R(t), T=T(t), and ˆT=ˆT(t) denote rainfall, air temperature and water temperature at time t, respectively. Typically, a sinusoidal function, such as
|
T(t)=T0[1+T1 cos(2π365(ωt+θ))],
|
(where T0 is the mean annual temperature, T1 captures variation about the mean, and ω and θ represent, respectively, the periodicity and phase shift of the function) is used to model local temperature fluctuations [2,24] (and similar appropriate time-dependent functions are used to account for rainfall and water temperature variability [1,55]). Thus, the functions T(t),ˆT and R(t) are assumed to be continuous, bounded, positive and ω-periodic. Furthermore, the parameters ψU(T),σE(R,ˆT), σP(R,ˆT), ξi(N,R,ˆT) (for i=1,2,3,4), μE(ˆT), μL(ˆT), μP(ˆT) and μA(T) are non-negative, ω-periodic, continuous and bounded functions defined on [0,∞). The term ψU(T)(1−UKU) represents the density-dependent eggs oviposition rate (where KU>U(t) for all t≥0 is the environmental carrying capacity of female adult mosquitoes and ψU(T) is the temperature-dependent egg deposition rate). Eggs hatch into the first larval stage at a rainfall-and temperature-dependent rate σE(R,T). Larvae in Stage i mature into Stage i+1 at a rate ξi(N,R,T)(i=1,2,3), which is assumed to depend on temperature, rainfall and amount of nutrients. Larvae in Stage 4 (L4 class) mature into pupae at a nutrient-, rainfall-and temperature-dependent rate ξ4(N,R,T). It should be emphasized that the maturation rates for the larval stages (ξi; i=1,2,3,4) are dependent on nutrient, temperature and rainfall because, while nutrients are needed for the growth and development of the larvae, rainfall is required for availability of breeding sites and habitats and favorable temperature values improve development of the larvae [12,33,55,57,58,74]. However, extreme climate conditions such as excessive rainfall washes out the larval breeding sites, such as small stagnant water on yards or lawn, and also too hot or too cold are not favorable for the survival and maturation of the larvae [2,33,55,57,58].
Pupae mature into the female adult mosquitoes of type V at a rainfall-and temperature-dependent rate σP(R,ˆT). These female adult mosquitoes quest for blood meal at the human habitat at a rate ηV (and become female adult mosquitoes of type W) [51]. The term HH+F accounts for the preference of human blood, as opposed to that of other animals [28,32,52] (where H is the population density of humans that are accessible to the mosquitoes (local to the breeding sites of the mosquitoes) and F is a positive constant representing a constant alternative food source for the female adult mosquitoes) [51]. At the human habitat, female adult mosquitoes of type W interact with humans according to standard mass action law, at a constant rate τW [51,52]. This interaction can be successful with probability α∈[0,1], so that questing mosquitoes successfully obtain blood meals and become vectors of type U (at the rate ατW) which, in turn, return to become female adult mosquitoes of type V at a rate γU after laying eggs (see [51,52] for further details on the derivation of the U−V−W component of the model). Furthermore, the parameters μE(ˆT),μL(ˆT),μP(ˆT),μA(T) represent, respectively, the temperature-dependent natural death rate for female eggs, female larvae, female pupae and female adult mosquitoes, and δLL is the density-dependent mortality rate for larvae, accounting for intra and inter-species larval competition for resources (nutrients) and space (Abdelrazec and Gumel [1] and Lutambi et. al. [41] also incorporated density-dependent larval mortality in their models). A flow diagram of the model (1) is depicted in Figure 1, and the model variables and parameters are described in Table 1.
Table 1. Description of state variables and parameters of the model (1).
| Variables |
Description |
|
E
|
Population of female eggs |
|
Li
|
Population of female larvae at Stage
i
(with
i=1,2,3,4
) |
|
P
|
Population of female pupae |
|
V
|
Population of fertilized female mosquitoes that have laid eggs at the breeding site |
|
(including unfertilized female mosquitoes not questing for blood meal) |
|
W
|
Population of fertilized, but non-reproducing, female mosquitoes questing for blood meal |
|
U
|
Population of fertilized, well-nourished with blood, and reproducing female mosquitoes |
| Parameters |
Description |
|
ψU
|
Deposition rate of female eggs |
|
σE
|
Maturation rate of female eggs |
|
ξi
|
Maturation rate of female larvae from larval stage
i
to stage
i+1
(with
i=1,2,3
) |
|
σP
|
Maturation rate of female pupae |
|
μE
|
Natural mortality rate of female eggs |
|
μL
|
Natural mortality rate of female larvae |
|
μP
|
Natural mortality rate of female pupae |
|
μA
|
Natural mortality rate of female adult mosquitoes |
|
δL
|
Density-dependent mortality rate of female larvae |
|
τW
|
Constant mass action contact rate between female adult mosquitoes of type
W
and humans |
|
α
|
Probability of successfully taking a blood meal |
|
γU
|
Rate of return of female adult mosquitoes of type
U
to the mosquitoes breeding site |
|
ηV
|
Rate at which female adult mosquitoes of type
V
visit human habitat sites |
|
H
|
Constant population density of humans at human habitat sites |
|
F
|
Constant alternative source of blood meal for female adult mosquitoes |
|
KU
|
Environmental carrying capacity of female adult mosquitoes |
|
pi
|
The daily survival probability of Stage
i
(with
i=E,1,2,3,4,P
) |
|
di
|
The average duration spent in Stage
i
(with
i=E,1,2,3,4,P
) |
|
ei
|
Rate of nutrients intake for female larvae in Stage
j
(with
j=1,2,3,4
) |
|
N
|
Total available nutrient for female larvae |
|
R
|
Cumulative daily rainfall |
|
T
|
Daily mean ambient temperature |
|
ˆT
|
Daily mean water temperature in the breeding site |
|
pMi
|
Maximum daily survival probability of aquatic Stage
i
(with
i=E,1,2,3,4,P
) |
|
RIM
|
Rainfall threshold |
2.1. Time-dependent parameters
The functional forms of the nutrient-, rainfall- and temperature-dependent parameters of the model (1) are formulated as follows. This functional forms derived from [2,47,59,60], characterizes the female Anopheles mosquitoes (which transmits malaria in humans). The per-capita rate of deposition of female eggs (ψU(T)) defined using the quadratic function used in [47], is given by
|
ψU(T)=−0.153T2+8.61T−97.7.
|
Similarly, following [47], the per-capita death rate of the female adult mosquitoes (μA(T)) is defined as
|
μA(T)=−ln(−0.000828T2+0.0367T+0.522).
|
Furthermore, following [60], the per-capita death rate of female eggs (μE(ˆT)), female larvae (μL(ˆT)) and female pupae (μP(ˆT)) are defined, respectively, as
|
μE(ˆT)=11.011+20.212[1+(ˆT12.096)4.839]−1,μL(ˆT)=18.130+13.794[1+(ˆT12.096)4.839]−1,μP(ˆT)=18.560+20.654[1+(ˆT19.759)6.827]−1.
|
Similarly, following [60], the per-capita maturation rate of eggs (into larvae) and pupae (into female adult mosquitoes) are given by
|
σi(R,ˆT)=(1−pi)pdii1−pdii; i={E,P},
|
where di=di(ˆT)>1(i={E,P}) is the average duration spent in Stage i, given by
and pi=pi(R,ˆT), (where 0≤pi(R,ˆT)<1) is the daily survival probability of immature mosquitoes in Stage i (assumed to be determined by the mean daily water temperature (ˆT (∘C)) and cumulative daily rainfall (R (mm))), so that
|
pi(R,ˆT)=pi(R)pi(ˆT),
|
(2)
|
with pi(ˆT)=exp(−μi(ˆT)) (it should be stated that, in line with [60], the definition of pi(R,ˆT)=pi(R)pi(ˆT) emphasizes the assumed independence of temperature and rainfall with each other). Following [59] (Supplemental Material), the rainfall-dependent daily probability of survival of immature mosquitoes, pi(R) (with i={E,L1,L2,L3,L4,P}) is given by
|
pi(R)=R(RIM−R)(4pMi/R2IM),i={E,L1,L2,L3,L4,P},
|
(3)
|
where pMi is the peak daily survival probability of immature mosquito stage i (i=E=eggs;i=Lj=larvae in Stagej;j={1,2,3,4};i=P=pupae) and RIM>R(t)>0, for all t, is the maximum rainfall threshold in the community. The per capita maturation rate of larvae (ξj; j=1,2,3,4), assumed to depend on amount of available nutrients (N), rainfall (R) and water temperature (ˆT), is given by
|
ξj(N,R,ˆT)=ξj(N)ξj(R,ˆT); j=1,2,3,4,
|
where ξj(N)=ejN, with ej representing the rate of nutrients intake for female larvae in stage j. Furthermore, ξj(R,ˆT) is given by
|
ξj(R,ˆT)=(1−pj)pdjj1−pdjj; j=1,2,3,4,
|
with pj having similar definition as above, dj=dL(ˆT)=1/μL(ˆT), for j=1,2,3,4. It is assumed that water and air temperature obey the linear relation (see, for instance, [2,35,57,62,64]), given by ˆT=T+θT, where θT>0 is a small increment in temperature.
Furthermore, since almost all communities within tropical and sub-tropical regions of the world record temperatures in the range [16,40]0C [11], it is plausible to assume that 160C ≤T(t),ˆT(t)≤400C for this study. Using this assumption, the minimum and maximum values of the temperature-dependent parameters of the model (i.e., the per capita rate of deposition of eggs (ψU(T)), per capita death rate of female eggs (μE(T)), per capita death rate of female larvae (μL(T)), per capita death rate of female pupae (μP(T)) and per capita death rate of female adult mosquitoes (μA(T))) are tabulated in Table 2.
Table 2. Range of values of temperature-dependent parameters in the temperature range [16,40]0C.
| Temperature (0C) |
ψU(T)
|
μE(ˆT)
|
μL(ˆT)
|
μP(ˆT)
|
μA(T)
|
| 16-40 |
0.892-23.431 |
0.194-0.932 |
0.091-0.122 |
0.040-0.115 |
0.074-0.408 |
The non-autonomous model (1) is an extension of the autonomous model for the population biology of the mosquito developed in [51,52], by including:
(ⅰ) aquatic stages of the mosquito (i.e., adding the E,L1,L2,L3,L4 and P classes);
(ⅱ) the effect of climate variables (i.e., adding the dependency on temperature and rainfall).
It also extends the model by Lutambi et. al. [41] by, inter alia:
(ⅰ) incorporating the effect of climate variable (temperature and rainfall);
(ⅱ) using logistic growth rate for egg oviposition rate (a constant rate was used in [41]);
(ⅲ) incorporating four larval stages (only one larval class was used in [41]).
Furthermore, the model (1) extends the non-autonomous climate-driven mosquito population biology model developed by Abdelrazec and Gumel [1] by
(ⅰ) including the dynamics of adult female mosquitoes (i.e., including compartments U, V and W);
(ⅱ) including four larval classes (a single larval class is considered in [1]);
(ⅲ) including dependence on (constant and uniform availability of) nutrients for the four larval stages.
2.2. Basic properties
Since, as stated in Section 2, R=R(t), T=T(t) and ˆT=ˆT(t), the temperature-and rainfall-dependent parameters of the model will, from now on, be expressed as functions of t only. The basic properties of the non-autonomous model (1) will now be explored. Let, from now on, μM(t)=min{μE(t),μL(t),μA(t)}. It is convenient to define M(t)=IM(t)+AM(t), the total number of immature and matured mosquitoes at time t. It then follows from (1) that the rate of change of M(t) is given by (where a dot represents differentiation with respect to time t)
|
˙M ≤ ψU(t)(1−UKU)U−δLL2−μM(t)M−(1−α)τWHW,≤ ψU(t)(1−UKU)U−μM(t)M, t>0.
|
(4)
|
In order to study the asymptotic dynamics of the mosquito population, subject to fluctuations in temperature and rainfall, we assume that the mosquito population stabilizes at a periodic steady-state. Furthermore, following [40,55], it is assumed that for the time ω-periodic function, ψU(t)∈C1(0,R+), there exists a positive number, h0, such that
|
ψU(t)(1−UKU)U−μM(t)A<0 for all A≥h0.
|
Lemma 2.1. For any ϕ∈Ω=C([0,R9+]), the model (1) has a unique non-negative solution through ϕ, and all solutions are uniformly-bounded.
Proof. Let ϕ:[0,∞]→R9+ be the vector-valued functions such that ϕ(0)=(E(0),L1(0),L2(0),L3(0),L4(0), P(0),V(0),W(0),U(0)). The system (1) can then be re-written as:
|
dϕdt=f(t,ϕ(t)),t≥0ϕ(0)=ϕ0,
|
where,
|
f(t,ϕ(t))=[ψU(t)[1−ϕ9(0)KU]ϕ9(0)−[σE(t)+μE(t)]ϕ1(0)σE(t)ϕ1(0)−[ξ1(t)+μL(t)+δLϕL(0)]ϕ2(0)ξ(i−2)(t)ϕ(i−1)(0)−[ξ(i−1)(t)+μL(t)+δLϕL(0)]ϕi(0);i=3,4,5ξ4(t)ϕ5(0)−[σP(t)+μP(t)]ϕ6(0)σP(t)ϕ6(0)+γUϕ9(0)−ηVHH+Fϕ7(0)−μA(t)ϕ7(0)ηVHH+Fϕ7(0)−[τWH+μA(t)]ϕ8(0)ατWHϕ8(0)−[γU+μA(t)]ϕ9(0)],
|
ϕL(0)=5∑i=2ϕi(0), with ϕ9(0)<KU. Thus, for all ϕ∈Ω, the function f(t,ϕ(t)) is continuous and Lipschitzian (with respect to ϕ in each compact set in R×Ω) [40]. Hence, there is a unique solution of system (1) through (0,ϕ). It should be noted that fi(t,π)≥0 whenever π≥0 and πi(0)=0 [40]. Hence, it follows (from Remark 5.2.1 in [69]) that Ω is positively-invariant with respect to the model (1).
For the total mosquito population M(t), the rate of change of M(t) satisfies Equation (5). Thus, it follows from the comparison principle [37], that the solution exists for all t≥0. Moreover,
|
lim supt→∞(E(t)+L(t)+P(t)+V(t)+W(t)+W(t))≤M∗(t),
|
where M∗(t) is the unique periodic solution of
|
˙M∗=ψU(t)(1−UKU)U−μM(t)M∗, t>0,
|
(5)
|
given by,
|
M∗(t) = e−∫t0μM(s)ds×{∫t0[ψU(s)(1−U(s)KU)U(s)e∫s0μM(τ)dτ]ds+ ∫ω0ψU(s)(1−U(s)KU)U(s)exp[∫s0μM(ζ)dζ]exp[∫ω0μM(s)ds]−1}.
|
Thus, all solutions of the model (1) are ultimately-bounded [40]. Moreover, it follows from (5) that ˙M∗<0 whenever M∗>h0. Hence, all solutions of the model (1) are uniformly-bounded [40,55].
3. Analysis of autonomous model
It is instructive to, first of all, analyze the dynamics of the autonomous equivalent of the non-autonomous model (1) to determine whether or not it has some qualitative features that do not exist in the model (1). Consider, now, the non-autonomous model (1) with all rainfall-and temperature-dependent parameters set to a constant (i.e., σE(t)=σE,σP(t)=σP,ξi(t)=ξi,μE(t)=μE,μL(t)=μL,μA(t)=μA), given by:
|
dEdt = ψU(1−UKU)U−(σE+μE)E,dL1dt = σEE−[ξ1+μL+δLL]L1,dLidt = ξ(i−1)L(i−1)−[ξi+μL+δLL]Li;i=2,3,4,dPdt = ξ4L4−(σP+μP)P,dVdt = σPP+γUU−ηVHH+FV−μAV,dWdt = ηVHH+FV−(τWH+μA)W,dUdt = ατWHW−(γU+μA)U,L = 4∑i=1Li,
|
(6)
|
where, now, ξi=ξi(N)=eiN.
3.1. Asymptotic stability of trivial equilibrium point
In this section, some results for the existence and linear asymptotic stability of the trivial equilibrium point of the autonomous model (6) will be provided. It is convenient to introduce the following parameter groupings (noting that α<1):
|
{τ∗W=τWH, η∗V=ηVHH+F, CE=σE+μE, CP=σP+μP,Ci=ξi+μL (for i=1,2,3,4), C5=η∗V+μA, C6=τ∗W+μA, C7=γU+μA,B=σEσPξ1ξ2ξ3ξ4, C=C1C2C3C4CECP, D=C5C6C7−ατ∗Wη∗VγU>0.
|
(7)
|
The autonomous model (6) has a trivial equilibrium solution, denoted by T0, given by
|
T0=(E∗,L∗1,L∗2,L∗3,L∗4,P∗,V∗,W∗,U∗)=(0,0,0,0,0,0,0,0,0).
|
The linear stability of T0 (in Ω) is obtained by using the next generation matrix [23,73] for the system (1). Using the notation in [73], the non-negative matrix F and the non-singular matrix V, for the new egg deposition terms and the remaining transfer terms, are, respectively, given (at the trivial equilibrium, T0) by
|
F=[00F1000000]andV=[V100V2V300V4V5],
|
where 0 denotes a zero matrix of order 3, and
|
F1=[00ψU000000],V1=[CE00−σEC100−ξ1C2],V2=[00−ξ2000000],V3=[C300−ξ3C400−ξ4CP],V4=[00−σP000000],V5=[C50−γU−η∗VC600−ατ∗WC7].
|
It follows from [73] that the associated vectorial reproduction number of the autonomous model (6) [63], denoted by R0=ρ(FV−1), is given by (where ρ is the spectral radius of the next generation matrix FV−1)
where τ∗W,η∗V,B,C,Ci (i=E,P,1,…,7) and D are as defined in (7). The threshold quantity, R0, measures the average number of new adult mosquitoes (offspring) produced by one reproductive mosquito during its entire reproductive period [52]. The result below follows from Theorem 2 in [73].
Theorem 3.1. The trivial equilibrium (T0) is locally-asymptotically stable (LAS) whenever R0<1, and unstable whenever R0>1.
Theorem 3.2. The trivial equilibrium point (T0) of the autonomous model (6) is GAS whenever R0≤1.
Proof. Consider the Lyapunov function
|
K1= ατ∗Wη∗Vξ4σP[σEξ1ξ2ξ3E+CEξ1ξ2ξ3L1+C1CEξ2ξ3L2+C1C2CEξ3L3+C1C2C3CEL4]+C1C2C3C4CE[σPη∗Vατ∗WP+CPη∗Vατ∗WV+CPC5ατ∗WW+CPC5C6U].
|
It is convenient to define
|
S=ατ∗Wη∗Vξ4σP[CEξ1ξ2ξ3L1+C1CEξ2ξ3L2+C1C2CEξ3L3+C1C2C3CEL4].
|
Thus, the Lyapunov derivative is given by
|
˙K1= ατ∗Wη∗Vξ4σP[σEξ1ξ2ξ3˙E+CEξ1ξ2ξ3˙L1+C1CEξ2ξ3˙L2+C1C2CEξ3˙L3+C1C2C3CE˙L4]+C1C2C3C4CE[σPη∗Vατ∗W˙P+CPη∗Vατ∗W˙V+CPC5ατ∗W˙W+CPC5C6˙U],= ατ∗Wη∗VB[ψU(1−UKU)U]+C1C2C3C4CE(CPη∗Vατ∗WγUU−CPC5C6C7U)−δLLS,= ατ∗Wη∗VBψUU−CDU−ατ∗Wη∗VBψUUKUU−δLLS,= [CD(R0−1)−ατ∗Wη∗VBψUUKU]U−δLLS,
|
where τ∗W,η∗V,B,C,Ci (i=E,P,1,…,7) and D are as defined in (7). Thus, it follows that, for R0≤1 in Ω, the Lyapunov derivative ˙K1<0. Furthermore, it follows from the LaSalle's Invariance Principle (Theorem 6.4 of [39]) that the maximal invariant set contained in {(E(t),L1(t),L2(t),L3(t),L4(t),P(t),V(t),W(t), U(t))∈Ω:˙K1=0} is the singleton {T0}. Hence, T0 is GAS in Ω whenever R0≤1.
Theorem 3.2 shows that the mosquito population (both immature and mature) will be effectively controlled (or eliminated) if the associated vectorial reproduction threshold, R0, can be brought to (and maintained at) a value less than or equal to unity.
3.2. Existence of non-trivial equilibrium point
The existence of a non-trivial equilibrium of the model (6) will now be explored. Let T∗∗1=(E∗∗,L∗∗1,L∗∗2, L∗∗3,L∗∗4,P∗∗,V∗∗,W∗∗,U∗∗) represents an arbitrary non-trivial equilibrium of the model (6). Solving for the state variables of the model (6) at T∗∗1 gives
|
E∗∗=ψUCE(1−U∗∗KU)U∗∗,E∗∗=1σE(C1+δLL∗∗)L∗∗1,L∗∗1=1ξ1(C2+δLL∗∗)L∗∗2,L∗∗2=1ξ2(C3+δLL∗∗)L∗∗3,L∗∗3=1ξ3(C4+δLL∗∗)L∗∗4, L∗∗4=CPDU∗∗ατ∗Wη∗VσPξ4,P∗∗=DU∗∗ατ∗Wη∗VσP,V∗∗(U∗∗)=C6C7U∗∗ατ∗Wη∗V, W∗∗=C7U∗∗ατ∗W, U∗∗=ατ∗Wη∗VσPξ4L∗∗4CPD.
|
(9)
|
It follows from (9) that
|
L∗∗i=(Ci+1+δLL∗∗)L∗∗i+1ξi;i=1,2,3.
|
(10)
|
Multiplying the second, third, fourth and fifth equations of (9), and substituting the expressions for E∗∗ and L∗∗4 into the resulting equation (and simplifying), gives
|
Bατ∗Wη∗VψU(1−U∗∗KU)=CECPD4∏i=1(Ci+ˉL∗∗).
|
(11)
|
Substituting the expression for U∗∗ in (9) into (11), and simplifying, gives (it can be shown that L∗∗4>0)
|
L∗∗4=KUCPDατ∗Wη∗VσPξ4[1−CECPD4∏i=1(Ci+δLL∗∗)Bατ∗Wη∗VψU].
|
(12)
|
Furthermore, substituting the expressions for Li (i=1,2,3), given in (10), into L∗∗=4∑i=1L∗∗i gives,
|
L∗∗=1ξ1ξ2ξ3[ξ1ξ2ξ3+ξ1ξ2(C4+δLL∗∗)+ξ14∏i=3(Ci+δLL∗∗)+4∏i=2(Ci+δLL∗∗)]L∗∗4.
|
(13)
|
Finally, substituting (12) into (13), and simplifying, shows that the non-trivial equilibria of the model (6) satisfy the following polynomial:
|
b7(L∗∗)7+b6(L∗∗)6+b5(L∗∗)5+b4(L∗∗)4+b3(L∗∗)3+b2(L∗∗)2+b1(L∗∗)+b0=0,
|
(14)
|
where the coefficients bi (i=0,…,7) are constants, and are given in Appendix A1. It follows from the expressions of bi (i=0,…,7) in Appendix A1 that:
(ⅰ) the coefficients bi (i=0,…,7)>0 whenever R0<1. Thus, no positive solution exists whenever R0<1. Furthermore, when R0=1, the coefficients bi (i=1,…,7)>0 and b0=0 (thus, the polynomial has no positive roots for the case when R0=1).
(ⅱ) the polynomial (14) has at least one positive root whenever R0>1 (using the Descartes' Rule of Signs).
These results are summarized below.
Theorem 3.3. The model (6) has at least one non-trivial equilibrium whenever R0>1, and no non-trivial equilibrium whenever R0≤1.
Furthermore, it is worth stating that, for the special case of the autonomous model (6) with no density-dependent larval mortality (i.e., δL=0), the coefficients bi (i=2,…,7)=0 and b1=1. Thus, in this case, the polynomial (14) reduces to L∗∗+b0=0, so that (where Q1 and X6 are defined in Appendix A)
Thus, in the absence of density-dependent larval mortality (i.e., δL=0), the model (6) has a unique non-trivial equilibrium (denoted by T1=(E∗∗,L∗∗1,L∗∗2,L∗∗3,L∗∗4, P∗∗,V∗∗,W∗∗,U∗∗)) when R0>1 (the components of this equilibrium can be obtained by substituting (15) into (9)).
Theorem 3.4. The model (6) with δL=0 has a unique non-trivial equilibrium whenever R0>1, and no non-trivial equilibrium otherwise.
3.2.1. Asymptotic Stability of Non-Trivial Equilibrium Point: Special Case
Consider the special case of the autonomous model (6) in the absence of density-dependent mortality rate for larvae (i.e., δL=0) so that the autonomous model (6) has a unique non-trivial equilibrium (T1) when R0>1. Linearizing the autonomous model (6), with δL=0, at T1 gives:
|
J(T1)=[−CE0000000ψU(2R0−1)σE−C100000000ξ1−C200000000ξ2−C300000000ξ3−C400000000ξ4−CP00000000σP−C50γU000000η∗V−C600000000ατ∗W−C7].
|
The eigenvalues of the matrix J(T1) satisfy the following polynomial:
|
P9(λ)= λ9+A8λ8+A7λ7+A6λ6+A5λ5+A4λ4+A3λ3+A2λ2+A1λ+CD(R0−1),
|
(16)
|
where τ∗W,η∗V and Ci (i=E,P,1,…,7) are as defined in (7) and Ai (i=1,…,8) are positive constants given in Appendix A2. It is convenient to re-write the polynomial (16) as
|
P9(λ)=F(λ)G(λ)+CD(R0−2),
|
(17)
|
where,
|
F(λ)=(λ+CE)(λ+CP)(λ+C1)(λ+C2)(λ+C3)(λ+C4),
|
(18)
|
and,
|
G(λ)=λ3+(C5+C6+C7)λ2+(C5C6+C5C7+C6C7)λ+D,
|
(19)
|
so that,
|
F(λ)G(λ)= λ9+A8λ8+A7λ7+A6λ6+A5λ5+A4λ4+A3λ3+A2λ2+A1λ+CD.
|
(20)
|
The asymptotic stability of T1 will be explored using the properties of Bézout matrices [31]. Consequently, it is convenient to recall the following four results:
Theorem 3.5.(Routh-Hurwitz)[31]. Let A be an n×n complex matrix, and let Ek be the sum of all principal minors of A of order k, k∈<n>. Let Ω(A) be the n×n Hurwitz matrix of A and assume that Ω(A) is real. Then A is stable if and only if all leading principal minors of Ω(A) are positive.
Definition 3.6.(Bézout Matrix)[31]. Let a(x) and b(x) be two polynomials with real coefficients of degree n and m respectively, n≥m. The Bézoutiant defined by a(x) and b(x) is the bilinear form
|
a(x)b(y)−a(y)b(x)x−y=n−1∑i,k=0bikxiyk.
|
The symmetric matrix (bik)n−10 associated with this bilinear form is called the Bézout matrix and is denoted by Ba,b. Each entry bi,j of Ba,b can be computed separately by the entry formula
|
bi,j=min(i,n−1−j)∑k=max(0,i−j)(bi−kaj+1+k−ai−kbj+1+k) for all i,j≤n.
|
Theorem 3.7.(Liénard-Chipart)[31] Let f(x)=xn−anxn−1−…−a1 be a polynomial with real coefficients, and let an−1=−1. Define the polynomials
|
h(u)=−a1−a3u−⋯,g(u)=−a2−a4u−⋯.
|
The polynomial f(x) is negative stable if and only if the Bézout matrix Bh,g is positive definite and ai<0 for all i∈<n>.
Theorem 3.8. (Sylvester's Criterion)[27] A real, symmetric matrix is positive definite if and only if all its principal minors are positive.
We claim the following result.
Lemma 3.9. The polynomial F(λ)G(λ), defined by Equations (18), (19) and (20), is Hurwitz stable (i.e., all its roots have negative real part).
Proof. It follows from the equation for F(λ) in (18) that all roots of F(λ) are negative. Furthermore, consider G(λ)=0 from (19). That is,
|
G(λ)=λ3+(C5+C6+C7)λ2+(C5C6+C5C7+C6C7)λ+D=0.
|
Using the Routh-Hurwitz Criterion (Theorem 3.5), the principal minors, Δk (k=1,2,3), of the associated Hurwitz matrix for G(λ) are
|
Δ1= C5+C6+C7>0,Δ2= (C5+C6+C7)(C5C6+C5C7)+C6C7(C6+C7)+ατ∗Wη∗VγU>0,Δ3= DΔ2>0.
|
Thus, all the roots of G(λ) have negative real part. Hence, all nine roots of F(λ)G(λ) have negative real part.
Remark 1. It follows from Lemma 3.9 and Theorem 3.7 that the corresponding Bézout matrix of F(λ)G(λ) is positive-definite [31].
Remark 2. Consider P9(λ)=F(λ)G(λ)+CD(R0−2). Then, P9(λ)≤F(λ)G(λ) whenever 1<R0≤2. Thus, it follows from Lemma 3.9 that all nine roots of P9(λ) have negative real part whenever 1<R0≤2 (hence, T1 is LAS whenever 1<R0≤2).
Furthermore, consider the characteristic polynomial P9(λ) given in (16). Let A0=CD(R0−1), with C and D as defined in (7), so that
|
P9(λ)=λ9+A8λ8+A7λ7+A6λ6+A5λ5+A4λ4+A3λ3+A2λ2+A1λ+A0.
|
To apply Theorem 3.7, let
|
h(u)=A0+A2u+A4u2+A6u3+A8u4,
|
and,
|
g(u)=A1+A3u+A5u2+A7u3+u4.
|
Thus, it follows from Definition 3.6 that the corresponding Bézout matrix of P9(λ), denoted by Bh,g(P9), is given by
|
Bh,g(P9)=[A1A2−A0A3A1A4−A0A5A1A6−A0A7A1A8−A0A1A4−A0A5A3A4−A2A5+A1A6−A0A7A3A6−A2A7+A1A8−A0A3A8−A2A1A6−A0A7A3A6−A2A7+A1A8−A0A5A6−A4A7+A1A8−A2A5A8−A4A1A8−A0A3A8−A2A5A8−A4A7A8−A6].
|
Sylvester's Criterion (Theorem 3.8) can be used to obtain the necessary and sufficient conditions for Bh,g(P9) to be positive-definite. First of all, it is evident that Bh,g(P9) is symmetric. It then suffices to show that the kth leading principal minor of Bh,g(P9) is positive (i.e., to show that the determinant of the upper-left k×k sub-matrix of Bh,g(P9) is positive). It is convenient to introduce the following notations:
(ⅰ) b(J)i,j:0≤i,j≤3,J∈{FG,P9} are the entries of the corresponding Bézout matrix of the polynomial F(λ)G(λ) (denoted by Bh,g(FG)) and P9(λ) (clearly, Bh,g(FG)=Bh,g(P9) when A0=CD).
(ⅱ) Δ(P9)k is the kth leading principal minor of Bézout matrix Bh,g(P9).
Therefore, Bh,g(P9) can be re-written (in terms of the entries of the positive-definite Bézout matrix, Bh,g(FG). That is, in terms of b(FG)i,j) as
|
Bh,g(P9)=[b(FG)0,0−CDKA3b(FG)0,1−CDKA5b(FG)0,2−CDKA7b(FG)0,3−CDKb(FG)1,0−CDKA5b(FG)1,1−CDKA7b(FG)1,2−CDKb(FG)1,3b(FG)2,0−CDKA7b(FG)2,1−CDKb(FG)2,2b(FG)2,3b(FG)3,0−CDKb(FG)3,1b(FG)3,2b(FG)3,3].
|
where C and D are as defined in (7) and K=(R0−2). It follows from Remark 2 that the Bézout matrix, Bh,g(P9), is a positive definite matrix for 1<R0≤2. Furthermore, the Bézout matrix, Bh,g(P9), can be re-written as (after row-column operations)
|
Bh,g(P9)=[Δ(P9)1b(P9)0,1b(P9)0,2b(P9)0,30Δ(P9)2Δ(P9)1b(P9)1,2−b(P9)0,1b(P9)0,3b(P9)0,0b(P9)1,3−b(P9)0,1b(P9)0,4b(P9)0,000Δ(P9)3Δ(P9)2B1000Δ(P9)4Δ(P9)3],
|
(21)
|
where B1=B1(b(P9)i,j) 0≤i,j≤3. However, since the kth leading principal minor of a triangular matrix is the product of its diagonal elements up to row k, Sylvester's Criterion is equivalent to finding conditions for which all the diagonal elements of Bézout matrix, Bh,g(P9), in (21) are all positive (i.e., finding the conditions for which Δ(P9)k are positive for all k=1,2,3,4) [63]. For example, it can be verified that the first leading principal minor of the matrix Bh,g(P9), given by
|
Δ(P9)1= A1A2−CD(R0−1)A3=A1A2−CDA3−CD(R0−2)A3= b(FG)0,0−CD(R0−2)A3,
|
is positive whenever the following inequality holds:
where, b(FG)0,0=A1A2−CDA3>0 is the first leading principal minor of Bh,g(FG) and Z1 is the positive constant such that Δ(P9)1 is positive whenever R0<2+Z1. Similarly, we obtain constants Zk=Zk(b(FG)i,j(0≤i,j≤3),Ai(1≤i≤9),C,D) such that the kth principal minor Δ(P9)k is positive whenever R0<2+Zk, for each k=2,3,4 (i.e., Zi (i=1,2,3,4), is the constant such that R0<2+Zi makes the determinant of the associated matrix of minors of matrix (21) to be positive). Therefore, the result below follows (from the above derivations and Remark 2).
Theorem 3.10 Consider the model (6) with δL=0. The unique non-trivial equilibrium (T1) is LAS in Ω∖{T0} whenever
|
1<R0<RC0=2+min{Zk:Δ(P9)k>0 for all k=1,2,3,4},
|
and unstable whenever R0>RC0.
The results above (Theorem 3.4 and Theorem 3.10) show that the condition R0>1 defines the existence of a unique non-trivial equilibrium (T1) of the model (6) with δL=0 (which is LAS if 1<R0<RC0). Thus, it can be deduced that, to maintain a non-trivial mosquito population, each reproducing female mosquito (of type U) must produce at least one egg during its entire reproductive life period (see also [51]). In other words, an increase in female mosquitoes of type U(t) leads to a corresponding increase in the number of female eggs laid in the population (E(t). We claim the following result.
Theorem 3.11. Consider a special case of the model (6) with sgn(E∗∗−E(t))=sgn(U∗∗−U(t)) for all t≥0 and δL=0. Then, the non-trivial equilibrium (T1) of the model (6) with δL=0 is GAS in Ω∖{T0} whenever 1<R0<RC0.
Proof. The proof of Theorem 3.11, based on using a non-linear Lyapunov function of Goh-Voltera type, is given in Appendix B.
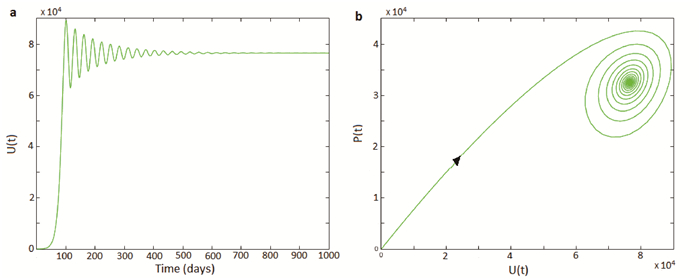
The ecological implication of Theorem 3.11 is that mosquitoes will persist in the community whenever the associated conditions for the global asymptotic stability of the non-trivial equilibrium (T1) are satisfied. The results of Theorem 3.11 are illustrated numerically, by simulating the compartment of adult mosquitoes of type U in autonomous model (6) with δL=0 using appropriate parameter values (Figure 2). These simulation results show convergence of the solution of U(t) to U∗∗ (in line with Theorem 3.11). It is worth mentioning that, for the fixed values of the parameters used in Figure 2, the associated bifurcation point of the model (6) with δL=0 is ψU=ψ∗U=107.889493160695073 (so that, Δ4=0). This is equivalent to R0=RC0=4.5573. Therefore, for this particular set of parameter values, the non-trivial equilibrium (T1) is LAS for 1<R0<4.5573, and unstable whenever R0>4.5573.
3.3. Hopf Bifurcation analysis: Special case
Consider the model (6) with δL=0 and R0>1 (so that T1 exists, by Theorem 3.4). Hopf bifurcation can occur (at a fixed value of a chosen bifurcation parameter) when the Jacobian of the system (6) with δL=0, evaluated at T1, has a pair of purely imaginary eigenvalues. That is, when P9(λ) given in (16), has a pair of purely imaginary roots.
The rank and signature of the Bézout matrix, Bh,g(P9), can be used to evaluate the number of roots with negative real parts [61]. The direct effect of the characteristic polynomial P9 having a pair of purely imaginary eigenvalues is that the rank of the Bézout matrix, Bh,g(P9), is reduced by exactly one [61]. From the stability point of view, this possibility represent the existence of a boundary (Hopf bifurcation) [61]. To prove the existence of Hopf bifurcation, it also suffices to verify the transversality condition [20].
Theorem 3.12. Consider the autonomous model (6) with δL=0. A Hopf bifurcation occurs whenever R0=RC0=2+Z4 or, equivalently, whenever
|
ψU=ψ∗U=CD(2+Z4)ατ∗Wη∗VB=CDRC0ατ∗Wη∗VB,
|
where Z4 is as defined in Theorem 3.10.
Proof. To prove Theorem 3.12, it is sufficient to establish the transversality condition [20]. Let ψU=ψ∗U be a bifurcation parameter (and all other parameters of the model (6) are fixed). Then R0=RC0=2+Z4. Since Z4<Zi (i=1,2,3), it follows from Theorem 3.10 that Δ(P9)i>0 for all i=1,2,3. Furthermore, Δ(P9)4 can be re-written as
|
Δ(P9)4=|b(FG)0,0−(ατ∗Wη∗VψUB−2CD)A3b(FG)0,1−(ατ∗Wη∗VψUB−2CD)A5b(P9)0,2b(P9)0,3b(FG)1,0−(ατ∗Wη∗VψUB−2CD)A5b(FG)1,1−(ατ∗Wη∗VψUB−2CD)A7b(P9)1,2b(P9)1,3b(FG)2,0−(ατ∗Wη∗VψUB−2CD)A7b(FG)2,1−(ατ∗Wη∗VψUB−2CD)b(P9)2,2b(P9)2,3b(FG)3,0−(ατ∗Wη∗VψUB−2CD)b(P9)3,1b(P9)3,2b(P9)3,3|.
|
Hence, Δ(P9)4(ψU)=0 if and only if ψU=ψ∗U. Furthermore, it can be verified that
|
dΔ(P9)4(ψU)dψU|ψU=ψ∗U= Tr(Adj(Bh,g(P9)(ψU))|ψU=ψ∗UdBh,g(P9)(ψU)dψ|ψU=ψ∗U)≠0,
|
where 'Tr' and 'Adj' denote, respectively, the trace and adjoint of a matrix. Similarly, let μA be a bifurcation parameter (and all other parameters of the model (6) are fixed). Thus,
|
dΔ(P9)4(μA)dψ|μA=μ∗A= Tr(Adj(Bh,g(P9)(μA))|μA=μ∗AdBh,g(P9)(μA)dμA|μA=μ∗A),
|
for all Δ(P9)4(μ∗A)=0. It can be verified that dΔ(P9)4(μA)dψ|μA=μ∗A≠0.
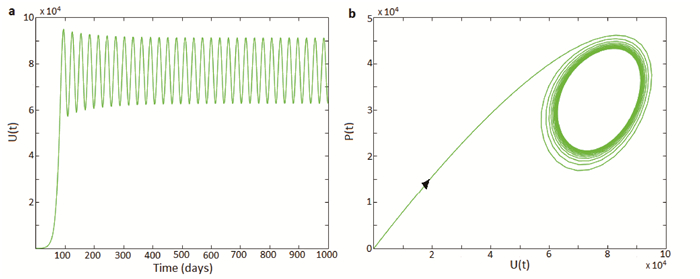
Theorem 3.12 shows that sustained oscillations are possible, with respect to the autonomous model (6) with δL=0, whenever R0=RC0. This result, which is numerically illustrated in Figure 3(a), is in line with that reported in [1] (where both logistic and Maynard-Smith-Slatkin eggs-laying functions are used). It is worth mentioning that, in the proof of Theorem 3.12, two bifurcation parameters (ψU and μA) were considered. The reason is, as noted in [1], that the transversality condition may fail at some points if only one parameter is used (see also [20]). The nature of the Hopf bifurcation property of the model (6) is investigated numerically. The results obtained, depicted in Figure 3(b), show convergence of the solutions to a stable limit cycle. It should be mentioned that the presence of bifurcation was not shown in the dynamics of mosquito population biology model developed in [41].
3.3.1. Numerical illustrations
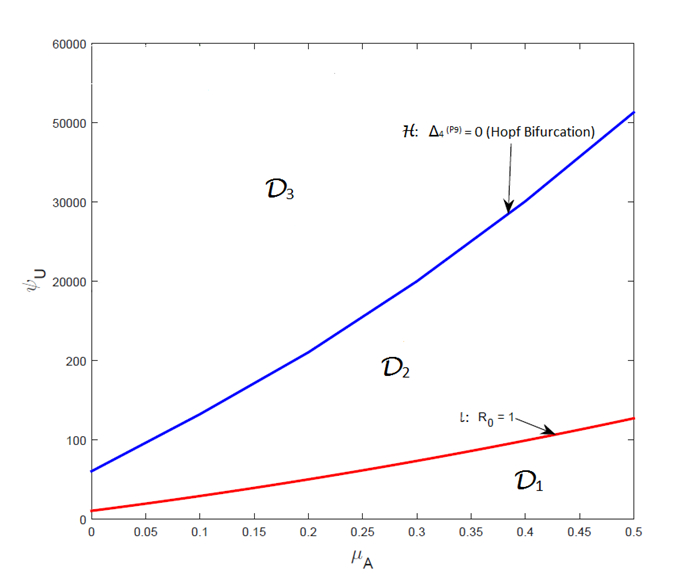
In this section, a bifurcation diagram for the autonomous model (6) with δL=0, which summarizes the main results obtain in Section 3, will be generated in the μA−ψU plane as follows:
(ⅰ) Solving for ψU from R0=1 gives the following equation for ψlU (depicted in Figure 4):
|
l: ψU=ψlU=CD(μA)ατ∗Wη∗VB.
|
(ⅱ) Solving for ψU from Δ(P9)4=0 (and fixing all parameters of the models (using their values as in Figure 4), except the parameters, μA and ψU) give the following curve Δ(P9)4=0:
|
H: ψU=ψ∗U=CD(μA)[2+Z4(μA)]ατ∗Wη∗VB,
|
where B,C and D are as defined in (7) and Z. The curves l and H (depicted in Figure 4) divide the μA−ψU plane into three distinct regions, namely D1, D2 and D3, given by:
|
D1 ={(μA,ψU):0<ψU≤ψlU;μA>0},D2 ={(μA,ψU):ψlU<ψU<ψ∗U;μA>0},D3 ={(μA,ψU):ψU>ψ∗U;μA>0}.
|
The regions can be described as follows (see also Table 3):
Table 3. Stability properties of the solutions of the autonomous model (6).
| Threshold Condition |
T0
|
T1
|
Existence of Stable Limit Cycle |
|
R0≤1
|
GAS |
No |
No |
|
1<R0<RC0
|
Unstable |
LAS |
No |
|
R0>RC0
|
Unstable |
Unstable |
Yes |
(ⅰ) Region D1: In this region, R0≤1. Hence, in this region (note that δL=0), the trivial equilibrium (T0) is globally-asymptotically stable (in line with Theorem 3.2).
(ⅱ) Region D2: Here, 1<R0<RC0. Thus, the model has two equilibria, namely the unstable trivial equilibrium (T0) and the locally-asymptotically stable non-trivial equilibrium (T1). The model undergoes a Hopf bifurcation whenever R0=RC0.
(ⅲ) Region D3: In this region, R0>RC0. Thus, the model has the unstable trivial equilibrium (T1), unstable non-trivial equilibrium and a stable limit cycle.
3.4. Uncertainty and sensitivity analysis for autonomous model
Sensitivity analysis determines the effects of parameters on the model outcomes [16]. The effect of these uncertainties, as well as the determination of the parameters that have the greatest influence on the mosquitoes dispersal dynamics (with respect to a given response function), are carried out using an uncertainty and sensitivity analysis [2,14,44,45,46,55]. In particular, following [14], the Latin Hypercube Sampling (LHS) and Partial Rank Correlation Coefficients (PRCC) will be used for the autonomous model (6). The range and baseline values of the parameters, tabulated in Table 4, will be used. Appropriate response functions are chosen for these analyses.
Table 4. Values and ranges of the parameters of the autonomous model (6).
| Parameters |
Baseline Value |
Range |
Reference |
|
ψU
|
50/day |
(10 -100)/day |
[2,
22,
38,
40,
65] |
|
KU
|
40000 |
(50−3×106)
|
[2,
38,
65] |
|
σE
|
0.84/day |
(0.7 -0.99)/day |
[22] |
|
μE
|
0.05/day |
(0.01−0.07)/day |
[22] |
|
ξ1
|
0.095/day |
(0.05−0.15)/day |
|
|
ξ2
|
0.11/day |
(0.06−0.17)/day |
|
|
ξ3
|
0.13/day |
(0.08−0.19)/day |
|
|
ξ4
|
0.16/day |
(0.08−0.23)/day |
|
|
μL
|
0.34/day |
(0.15−0.48)/day |
[22] |
|
δL
|
0.04/ml |
(0.02−0.06)/ml |
[29] |
|
σP
|
0.8/day |
(0.5−0.89)/day |
[22] |
|
μP
|
0.17/day |
(0.12−0.21)/day |
|
|
γU
|
0.89/day |
(0.30−1)/day |
[51,
52] |
|
η∗V
|
0.8/day |
(0.46−0.92)/day |
[51,
52] |
|
τ∗W
|
16 |
(12−20)
|
[51] |
|
α
|
0.86 |
(0.75−0.95)
|
[51] |
|
μA
|
0.05/day |
(0.041−0.203)/day |
[2,
19,
38,
53,
65] |
|
pME
|
0.9
|
|
[60] |
|
pML1
|
0.15
|
|
|
|
pML2
|
0.20
|
|
|
|
pML3
|
0.25
|
|
|
|
pML4
|
0.35
|
|
|
|
pMP
|
0.75
|
|
[60] |
Using the population of female adult mosquitoes of type U as the response function, it is shown in Table 5 that the top three PRCC-ranked parameters of the autonomous version of the model are the probability of female adult mosquito of type W successfully taking a blood meal (α), the natural mortality rate of female adult mosquitoes (μA) and the natural mortality rate of female larvae (μL). Similarly, using the population of female adult mosquitoes of type V as the response function, the top three PRCC-ranked parameters are the natural mortality rate of female larvae (μL), the deposition rate of female eggs (ψU) and the maturation rate of female larvae from Stage 1 to Stage 2 (ξ1). Furthermore, using the population of female larvae in stage 4 (L4) and population of female pupae (P) as the response functions, it is shown that the same top three PRCC-ranked parameters appeared as in the case when the population of female adult mosquitoes of type V is chosen as the response function for both cases. However, using the vectorial reproduction number of the autonomous version of the model (R0) as the response function, the top three PRCC-ranked parameters are the natural mortality rate of female larvae (μL), the deposition rate of female eggs (ψU) and the natural mortality rate of female adult mosquitoes (μA).
Table 5. PRCC values for the parameters of the autonomous model (6) using total number of adult mosquitoes of type U, adult mosquitoes of type V, fourth instar larvae (L4), pupae (P), and R0 as output. The top (most dominant) parameters that affect the dynamics of the model with respect to each of the six response function are highlighted in bold font. "Notation: a line (−) indicates the parameter is not in the expression for R0".
| Parameters |
U
Class |
V
Class |
L4
Class |
P
Class |
R0
|
|
ψU
|
+0.6863
|
+0.8509
|
+0.9083
|
+0.8958
|
+0.88
|
|
KU
|
+0.1174
|
+0.1783
|
+0.1952
|
+0.2218
|
−
|
|
σE
|
+0.0066
|
+0.1099
|
−0.0959
|
+0.0046
|
+0.031
|
|
μE
|
−0.1118
|
+0.0045
|
−0.0326
|
−0.0291
|
−0.082
|
|
ξ1
|
+0.4598
|
+0.6525
|
+0.6896
|
+0.7019
|
+0.63
|
|
ξ2
|
+0.4366
|
+0.6337
|
+0.6817
|
+0.6543
|
+0.60
|
|
ξ3
|
+0.3224
|
+0.5714
|
+0.2781
|
+0.5779
|
+0.49
|
|
ξ4
|
+0.4213
|
+0.6473
|
+0.0914
|
+0.2447
|
+0.55
|
|
μL
|
-0.7842
|
-0.9103
|
-0.9193
|
-0.9427
|
-0.96
|
|
δL
|
−0.1121
|
−0.0679
|
−0.0807
|
−0.0699
|
−
|
|
σP
|
+0.0621
|
−0.3878
|
+0.1045
|
+0.0088
|
+0.093
|
|
μP
|
−0.1031
|
−0.1578
|
−0.0648
|
+0.0171
|
−0.051
|
|
γU
|
−0.0948
|
−0.2255
|
−0.2908
|
−0.2934
|
−0.25
|
|
η∗V
|
+0.2278
|
+0.1773
|
+0.2047
|
+0.2521
|
+0.16
|
|
τ∗W
|
-0.6390
|
+0.0956
|
−0.0123
|
+0.0523
|
−0.026
|
|
α
|
+0.9284
|
+0.5431
|
+0.6106
|
+0.6224
|
+0.55
|
|
μA
|
-0.8597
|
−0.2584
|
−0.5379
|
−0.3373
|
-0.69
|
In summary, this study identifies five parameters that dominate the population dynamics and dispersal of the mosquito, namely the probability of female adult mosquito of type W successfully taking a blood meal (α), the natural mortality rate of female adult mosquitoes (μA), the natural mortality rate of female larvae (μL), the deposition rate of female eggs (ψU) and the maturation rate of female larvae (ξi). The effect of the aforementioned most dominant parameters (α,ψU,ξi,μL and μA) on the population dynamics of the mosquito and the reproduction threshold (R0) is tabulated in Table 6.
Table 6. Control measures obtained from the sensitivity analysis of the model (6).
| Control measure by model (1) |
Effect on population dynamics of mosquitoes |
Effect on vectorial reproduction number R0 |
Environmental interpretation |
| Significant reduction in the value of
α
: (probability of successfully taking a blood meal) |
Significant decrease in the population size of adult mosquitoes of type
U
|
Significant decrease in the value of
R0
|
Personal protection against mosquito bite plays an important role in minimizing the size of mosquito population in the community. |
| Significant reduction in the value of
ψU
: (deposition rate of female eggs) |
Significant decrease in the population size of all three adult mosquito compartments |
Significant decrease in the value
R0
|
The removal of mosquito breeding (egg laying) sites, such as removal of stagnant waters, is an effective control measure against the mosquito population. |
| Significant reduction in the value of
ξi
(maturation rate of female larvae) and significant increase of
μL
(natural mortality rate of female larvae) |
Significant decrease in the population size of all three adult mosquito compartments |
Significant decrease in the value
R0
|
The removal of mosquito breeding sites and use of larvicides are effective control measures against the mosquito population. |
| Significant increase in the value of
μA
: (natural mortality rate of female adult mosquitoes) |
Significant decrease in the population size of adult mosquitoes of type
U
|
Significant decrease in the value of
R0
|
The use of insecticides and insecticides treated bednets (ITNs) are important control measures against the mosquito population. |
4. Analysis of non-autonomous model
In this section, dynamical properties of the non-autonomous model (1) will be explored. The non-autonomous model (1) has a unique trivial equilibrium point denoted by T∗0=(E∗,L∗1,L∗2,L∗3,L∗4,P∗,V∗, W∗,U∗)=(0,0,0,0,0,0,0,0,0) and positive periodic solution(s) denoted by T∗1=(E∗(t),L∗1(t),L∗2(t),L∗3,L∗4(t), P∗(t),V∗(t),W∗(t),U∗(t)) which satisfies the unique periodic system:
|
dE∗(t)dt = ψU(t)[1−U∗(t)KU]U∗(t)−[σE(t)+μE(t)]E∗(t),dL∗1(t)dt = σE(t)E∗(t)−[ξ1(t)+μL(t)+δLL∗(t)]L∗1(t),dL∗i(t)dt = ξ(i−1)(t)L∗(i−1)(t)−[ξi(t)+μL(t)+δLL∗(t)]L∗i(t); i=2,3,4,dP∗(t)dt = ξ4(t)L∗4(t)−[σP(t)+μP(t)]P∗(t),dV∗(t)dt = σP(t)P∗(t)+γUU∗(t)−ηVHH+FV∗(t)−μA(t)V∗(t),
|
|
dW∗(t)dt = ηVHH+FV∗(t)−[τWH+μA(t)]W∗(t),dU∗(t)dt = ατWHW∗(t)−[γU+μA(t)]U∗(t),L∗(t) = 4∑i=1L∗i(t).
|
(22)
|
4.1. Computation of vectorial reproduction ratio
The vectorial reproduction ratio, associated with the non-autonomous model (6), will be computed using the approach in [5,6,7,8,9,10,75]. The next generation matrix F(t) (of the new eggs deposited) and the M-Matrix V(t) (of the remaining transfer terms), associated with the non-autonomous model (6) (linearized at the trivial equilibrium T∗0), are given, respectively, by
|
F(t)=[00F1(t)000000]andV(t)=[V1(t)00V2(t)V3(t)00V4(t)V5(t)],
|
where 0 denotes a zero matrix of order 3, and
|
F1(t)=[00ψU(t)000000],V1(t)=[CE(t)00−σE(t)C1(t)00−ξ1(t)C2(t)],V2(t)=[00−ξ2(t)000000],V3(t)=[C3(t)00−ξ3(t)C4(t)00−ξ4(t)CP(t)],V4(t)=[00−σP(t)000000],V5=[C5(t)0−γU−η∗VC6(t)00−ατ∗WC7(t)],
|
where τ∗W,η∗V,Ci(t) (i=E,P,1,…,7) are as defined in (7). The linearized version of the model (1), at T∗0, can be expressed as
where x(t)=(E(t),L1(t),L2(t),L3(t),L4(t),P(t),V(t),W(t),U(t)). Following [75], let Y(t,s), t≥s, be the evolution operator of the linear ω-periodic system dydt=−V(t)y. Thus, for each s∈R, the associated 9×9 matrix Y(t,s) satisfies [75]
|
dY(t,s)dt=−V(t)Y(t,s)∀t≥s,Y(s,s)=I.
|
where I is the 9×9 identity matrix.
Suppose that ϕ(s) (ω-periodic in s) is the initial distribution of new eggs. Thus, F(s)ϕ(s) is the rate of generation (hatching) of new eggs in the breeding habitat at time s [1,75]. Since t≥s, it follows that Y(t,s)F(s)ϕ(s) represents the distribution of new eggs at time s, and became adult at time t. Hence, the cumulative distribution of new eggs at time t, produced by all female adult mosquitoes (ϕ(s)) introduced at a prior time s=t, is given by
|
Ψ(t)=∫t−∞Y(t,s)F(s)ϕ(s)ds=∫∞0Y(t,t−a)F(t−a)ϕ(t−a)da.
|
Let Cω be the ordered Banach space of all ω-periodic functions from R to R9, which is equipped with maximum norm and positive cone C+ω{ϕ∈Cω:ϕ(t)≥0,∀t∈R} [75]. Define a linear operator L:Cω→Cω [75]
|
(Lϕ)(t)=∫∞0Y(t,t−a)F(t−a)ϕ(t−a)da∀t∈R,ϕ∈Cω.
|
The vectorial reproduction ratio of the model (22) (R0TR) is then given by the spectral radius of L, (i.e., R0TR=ρ(L)). It can be verified that system (6) satisfy the assumptions A1−A7 in [75]. Hence, the result below follows from Theorem 2.2 in [75].
Theorem 4.1. The trivial equilibrium (T∗0), of the non-autonomous model (6), is LAS in C([0],R9+) if R0TR<1, and unstable if R0TR>1.
The global asymptotic stability of the trivial equilibrium T∗0 of the model is now considered.
Theorem 4.2. The trivial equilibrium T∗0 of the non-autonomous model (1) is GAS in C([0],R9+) whenever R0TR<1.
The proof of Theorem 4.2, based on using comparison theorem [69], is given in Appendix B. The epidemiological implication of Theorem 4.2 is that the mosquito population (both immature and mature) can be effectively controlled (or eliminated) if the associated vectorial reproduction threshold, R0TR, can be brought to (and maintained at) a value less than or equal to unity.
4.2. Existence of non-trivial positive periodic solution
In this section, the possibility of the existence of a non-trivial positive periodic solution for the non-autonomous system (1) will be explored using uniform persistence theory [40,72,81,82] (see also [55]). Following and using notations in, Lou and Zhao [40], it is convenient to define the following sets (X, X0 and ∂X0)
|
X= Ω,X0= {ϕ=(ϕ1,ϕ2,ϕ3,ϕ4,ϕ5,ϕ6,ϕ7,ϕ8,ϕ9)∈X:ϕi(0)>0 for all i∈[1,9]},∂X0= X∖X0={ϕ∈X:ϕi(0)=0forsomei∈[1,9]}.
|
Theorem 4.3. Consider the non-autonomous model (2.1). Let R0TR>1. The model has at least has at least one positive periodic solution, and there exists a φ>0 such that any solution u(t,ϕ) of the model with initial value ϕ∈X0 satisfies
|
lim inft→∞(E,L1,L2,L3,L4,P,V,W,U)(t)≥(φ,φ,φ,φ,φ,φ,φ,φ,φ).
|
Proof. The proof is based on using the approach in [40,55]. Let u(t,ϕ) be the unique solution of model (1), with u(0,ϕ)=ϕ. Let Φ(t)ψ=u(t,ψ) and let P:X→X be the Poincaré map associated with (1) i.e., P(ϕ)=u(ω,ϕ) for all ϕ∈X. Then, using similar approach as in Lemma (2.1), it is easy to see that X0 is a positively invariant compact set. Hence, since solutions of model (1) are uniformly (ultimately) bounded, P is point dissipative [40]. It then follows from Theorem 1.1.2 in [82] that P admits a global attractor in X.
Thus, it suffices to show that model (1) is uniformly-persistent with respect to (X0,∂X0) [40]. It is convenient to define
|
K∂= {ϕ∈∂X0:Pn(ϕ)∈∂X0forn≥0},D1= {ϕ∈X:ϕi(0)=0 for all i∈[1,9]},∂X0∖D1= {ϕ∈X:ϕi(0)≥0 for some i∈[1,9]}.
|
(23)
|
We claim that K∂=D1 [40,55]. This claim can be proved by, first of all, seing that for any ψ∈D1, ui(t,ψ)=0 for all i∈[1,9], (hence, D1⊂K∂). Furthermore, for any ψ∈∂X0∖D1, we can choose ψi(0)>0 for all i=1,…,9, so that u(t,ψ)∈X0. This implies that for any ψ∈∂X0∖D1, there exist some n with nω>t0, such that Pn(ϕ)∉∂X0. Hence, K∂⊂D1. This concludes the proof of the claim.
Thus, from (23), it can be verified that Pn(ϕ), n≥0 contains exactly one trivial equilibrium:
Hence, the set A:={T∗0} is a compact and isolated invariant set for the Poincaré map P in K∂ [40] and ∪ϕ∈K∂ω(ϕ)=A [40]. Furthermore, {A} does not form a cycle in K∂ (and hence in ∂X0). In addition, since M∗(t) is a positive periodic solution with respect to X0, then it follows from the proof of Theorem 3.2 in [40] that there exists a ϵ>0 such that
|
lim supt→∞|Φ(nω)ϕ−T0|≥ϵ for all ϕ∈X0.
|
Thus, it follows that A is an isolated invariant set for P in X and Ws(A)∩X0=∅ where Ws(A) is the stable manifold of A for P [40]. Hence, every trajectory in K∂ converges to A, and {A} is acyclic in K∂ [82]. It then follows from Theorem 1.3.1 in [82] that P is uniformly persistent with respect to X0. Thus, from Theorem 3.1.1 in [82], the periodic semiflow Φ(t):X→X is also uniformly persistent to X [40] where Φ(t)ψ=ut(ψ). It then follows from Theorem 4.5 in [42] (see also Theorem 4.6 in [71] and Theorem 3.1 in [83]) that the model (1) admits a positive ω-periodic solution T∗1=Φ(t)ϕ∗ with ϕ∗∈X0.
It follows, from Theorem 4.5 in [42] (see also Theorem 2.1 in [84]), that P:X0→X0 has a compact global attractor, denoted by A0. Hence, A0 is invariant for P (that is, A0=P(A0)=Φ(ω)A0). Furthermore, using the notation in [55,84], let A∗0:=⋃t∈[0,ω]Φ(t)A0. Then, ψi(0)>0 for all ψ∈A∗0,i=1,…,9 [40]. Since X0 is invariant, it follows that Φ(t)X0⊂X0. Thus, A∗0⊂X0 and lim supt→∞d(Φ(t)ϕ,A∗0)=0 for all ϕ∈X0 [40,84]. Also, it follows, by the continuity of Φ(t)ϕ for (t,ϕ)∈[0,∞)×X0 and the compactness of [0,τ]×A0 [84], that A∗0 is compact in X0 [40,84]. Thus, infϕ∈A∗0d(ϕ,∂X0)=minϕ∈A∗0d(ϕ,∂X0)>0 [40,84]. Consequently, there exists φ>0 such that
|
lim inft→∞min(E(t,ϕ),L1(t,ϕ),L2(t,ϕ),L3(t,ϕ),L4(t,ϕ),P(t,ϕ),V(t,ϕ),W(t,ϕ),U(t,ϕ))=lim inft→∞d(ϕ,∂X0)≥φ, for all ϕ∈X0.
|
In particular, lim inft→∞min(Φ(t)ϕ∗)≥φ. Hence, ui(t,ϕ)>0, i=1,…,9 for all t≥0.
5. Numerical simulations
The non-autonomous model (6) is simulated to illustrate the effect of the two climate variables (temperature and rainfall) on the population dynamics of adult mosquitoes in a community. Suitable functional forms for the temperature-and rainfall-dependent functions, relevant to Anopheles mosquitoes (mostly given in [2,47,55,60]) as defined in Section 2.1, will be used. For these simulations, water temperature (ˆT) is taken to be ˆT=T+30C. Furthermore, the simulations are carried out using the parameter values in Table 4 (with a fixed nutrient value of N=100000).
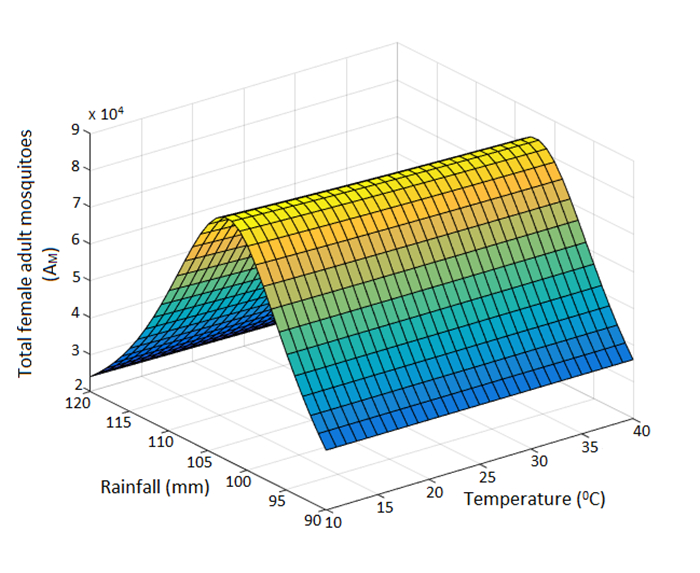
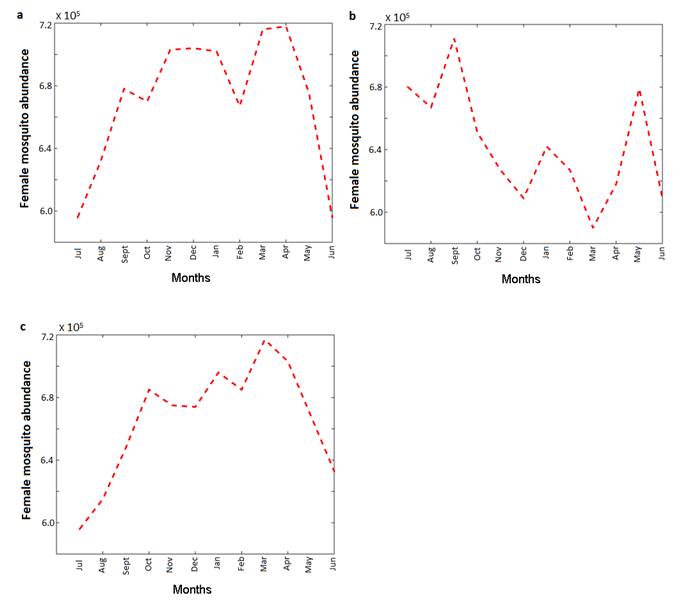
The combined effect of mean monthly temperature and rainfall is assessed by simulating the non-autonomous model using various mean monthly temperature and rainfall values in the range [16,40]0C and [90−120] mm, respectively (the temperature ranges for most tropical and sub-tropical regions of the world lie within this temperature range [11]). The results obtained (as measured in terms of the total number of female adult mosquitoes), depicted in Figure 5, show that the total mosquito population (of a typical community with the aforementioned temperature and rainfall ranges) is maximized when the mean monthly temperature and rainfall values lie in the range [20−25]0C and [105−115] mm, respectively. Furthermore, simulations were carried out using weather (temperature and rainfall) data for three cities in Africa, namely, KwaZulu-Natal, South-Africa (Southern Africa); Lagos, Nigeria (Western Africa) and Nairobi, Kenya (Eastern Africa) (see profiles Tables 7, 8 and 9, respectively). While the peak mosquito abundance for KwaZulu-Natal (Figure 6a) and Lagos (Figure 6b) occur when temperature and rainfall values lie in the range [22−25]0C, [98−121] mm (occurring during the months of January, March, April, November and December) and [24−27]0C [113−255] mm (occurring during the months of May, July, August, September and October) respectively, the peak mosquito abundance for Nairobi (Figure 6c) occurs for temperature and rainfall ranges [20.5−21.5]0C and [50−120] mm (occurring during the months of January, February, March and April).
Table 7. Monthly mean temperature (in 0C) and rainfall (in mm) for KwaZulu-Natal, South Africa [25].
| Month |
Jul |
Aug |
Sept |
Oct |
Nov |
Dec |
Jan |
Feb |
Mar |
Apr |
May |
Jun |
| Temperature (
∘
C) |
17.5 |
18.5 |
20 |
21.0 |
22.5 |
22.0 |
25 |
25 |
25.5 |
22.5 |
20 |
17.5 |
| Rainfall (
mm
) |
48.2 |
32.3 |
65.2 |
107.1 |
121 |
118.3 |
124 |
142.2 |
113 |
98.1 |
35.4 |
34.7 |
Table 8. Monthly mean temperature (in 0C) and rainfall (in mm) for Lagos, Nigeria [36].
| Month |
Jul |
Aug |
Sept |
Oct |
Nov |
Dec |
Jan |
Feb |
Mar |
Apr |
May |
Jun |
| Temperature (
∘
C) |
25.5 |
25 |
24 |
25.5 |
26 |
26.5 |
25.5 |
26 |
27 |
27.5 |
27 |
26.5 |
| Rainfall (
mm
) |
255 |
115 |
162 |
113 |
57 |
15 |
20 |
55 |
80 |
150 |
210 |
320 |
Table 9. Monthly mean temperature (in 0C) and rainfall (in mm) for Nairobi, Kenya [50].
| Month |
Jul |
Aug |
Sept |
Oct |
Nov |
Dec |
Jan |
Feb |
Mar |
Apr |
May |
Jun |
| Temperature (
∘
C) |
17.5 |
18 |
19 |
20.5 |
20 |
19.5 |
20.5 |
20.5 |
21.5 |
20.5 |
19.5 |
18.5 |
| Rainfall (
mm
) |
14.5 |
29.8 |
21.3 |
36.7 |
151 |
79.1 |
73.9 |
48.8 |
89.2 |
119.9 |
129.4 |
15.8 |
6. Conclusions
This study presents a new mathematical model for the population biology of the mosquito (the world's deadliest animal, which accounts for 80% of vector-borne diseases of humans). Some of the notable features of the new model are:
(ⅰ) incorporating four developmental stages of the mosquito larvae (L1,L2,L3,L4);
(ⅱ) including density dependence for the eggs oviposition process and larval mortality rates;
(ⅲ) including the dispersal states of female adult mosquitoes(U,V and W).
The model, which takes the form of a non-autonomous deterministic system of non-linear differential equations, is used to assess the impact of temperature and rainfall on the population dynamics of the mosquito. The main theoretical and epidemiological findings of this study are summarized below:
(ⅰ) The trivial equilibrium of the autonomous model (6) is globally-asymptotically stable whenever the associated vectorial reproduction number (R0) is less than unity. For the case when the associated vectorial reproduction number (R0) exceeds unity, the autonomous model (6) has at least one non-trivial equilibrium. Furthermore, it is shown that the autonomous model has a unique non-trivial equilibrium for the special case with no density-dependent larval mortality (i. e., δL=0). This unique non-trivial equilibrium is shown to be globally-asymptotically stable under a certain condition (i.e., when 1<R0<RC0) (this equilibrium bifurcates into a limit cycle, via a Hopf bifurcation at R0=RC0).
(ⅱ) Uncertainty and sensitivity analysis of the autonomous version of the model shows that the top five parameters that have the most influence on the dynamics of the model (with respect to various response functions) are the probability of female adult mosquito of type W successfully taking a blood meal (α), the natural mortality rate of female adult mosquitoes (μA), the natural mortality rate of female larvae (μL), the deposition rate of female eggs (ψU) and the maturation rate of female larvae from Stage 1 to Stage 2 (ξ1). Hence, this study suggests that the population of adult mosquito in a community can be effectively-controlled using mosquito-reduction strategies, as well as personal protection against mosquito bites.
(ⅲ) The trivial periodic solution of the non-autonomous model (1) is shown to be globally-asymptotically stable, whenever the spectral radius of a certain linear operator (denoted by R0TR) is less than unity. Furthermore, it is shown, using uniform persistence theory, that the non-autonomous model (1) has at least one positive periodic solution whenever R0TR>1.
Numerical simulations of the non-autonomous model, using relevant functional forms (given in Section 2.1) and parameter values associated with the Anopheles species (which causes malaria in humans), show the following:
(ⅰ) For mean monthly temperature and rainfall values in the range [10,40]0C and [90−120] mm, respectively, the peak mosquito abundance lie in the range [20−25]0C and [105−115] mm, respectively.
(ⅱ) For mean monthly temperature and rainfall data for three cities in Africa, namely, KwaZulu-Natal, South-Africa; Lagos, Nigeria and Nairobi, Kenya (Tables 7, 8 and 9). The peak mosquito abundance for KwaZulu-Natal (Figure 6a) and Lagos (Figure 6b) occur when temperature and rainfall values lie in the range [22−25]0C, [98−121] mm (occurring during the months of January, March, April, November and December) and [24−27]0C, [113−255] mm (occurring during the months of May, July, August, September and October) respectively. The peak mosquito abundance for Nairobi (Figure 6c) occurs for temperature and rainfall ranges [20.5−21.5]0C and [50−120] mm (occurring during the months of January, February, March and April).
Acknowledgments
One of the authors (ABG) is grateful to National Institute for Mathematical and Biological Synthesis (NIMBioS) for funding the Working Group on Climate Change and Vector-borne Diseases (VBDs). NIMBioS is an Institute sponsored by the National Science Foundation, the U.S. Department of Homeland Security, and the U.S. Department of Agriculture through NSF Award #EF-0832858, with additional support from The University of Tennessee, Knoxville.
7. Appendices
7.1. Appendix A: Coefficients of Equations (14) and (16)
7.1.1. Coefficients of Equation (14)
|
b1 = [(1R0−1)Q1X3+Q2X5X6]δL+1,b2 = [(1R0−1)Q1X2+Q2(X5X3+X4X6)](δL)2,b3 = [(1R0−1)Q1+Q2(X1X6+X2X4+X3X4)](δL)3,b4 = Q2(X1X3+X2X4+X5+X6)(δL)4,b5 = Q2(X1X2+X3+X4)(δL)5,b6 = Q2(X1+X2)(δL)6,b7 = Q2(δL)7,
|
where,
|
Q1= σECPDKUατ∗Wη∗VB, Q2=KU(CPD)2σECE(ατ∗Wη∗VB)2ψU, X1=C1+C2+C3+C4,X2= C2+C3+C4+ξ1, X3=C2C3+C2C4+C3C4+C3ξ1+C4ξ1+ξ1ξ2,X4= C1C2+C1C3+C1C4+C2C3+C2C4+C3C4, X5= C1C2C3+C1C2C4+C1C3C4+C2C3C4, X6=C2C3C4+C3C4ξ1+C4ξ1ξ2+ξ1ξ2ξ3,
|
with τ∗W,η∗V,B,C,Ci (i=E,P,1,…,7) and D as defined in (7).
7.1.2. Coefficients of Equation (16)
|
A1=D(C1C2C3C4CE+C1C2C3C4CP+C1C2C3CECP+C1C2C4CECP+C1C3C4CECP+C2C3C4CECP)+C(C5C6+C5C7+C6C7)>0,
|
|
A2=2∑i=1Ci3∑j=i+1Cj4∑k=j+1Cj5∑l=k+1Cl6∑m=l+1Cm7∑n=m+1Cn(CE+CP+7∑q=n+1Cq)+CECP(3∑i=1Ci4∑j=i+1Cj5∑k=j+1Ck6∑l=k+1Cl7∑m=l+1Cm−ατ∗Wη∗VγU3∑iCi4∑j=i+1Cj)−ατ∗Wη∗VγU2∑i=1Ci3∑j=i+1Cj4∑k=j+1Ck(4∑l=k+1Cl+CE+CP)>0,A3=3∑i=1Ci4∑j=i+1Cj5∑k=j+1Cj6∑l=k+1Cl7∑m=l+1Cm(CE+CP+7∑n=m+1Cn)+CECP(4∑i=1Ci5∑j=i+1Cj6∑k=j+1Ck7∑l=k+1Cl−ατ∗Wη∗VγU4∑iCi)−ατ∗Wη∗VγU3∑i=1Ci4∑j=i+1Cj(4∑k=j+1Ck+CE+CP)>0,A4=4∑i=1Ci5∑j=i+1Cj6∑k=j+1Cj7∑l=k+1Cl(CE+CP+7∑m=l+1Cm)+CECP(5∑i=1Ci6∑j=i+1Cj7∑k=j+1Ck−ατ∗Wη∗VγU)−ατ∗Wη∗VγU3∑i=1Ci(4∑j=i+1Cj+CE+CP)>0,A5=5∑i=1Ci6∑j=i+1Cj7∑k=j+1Cj(CE+CP+7∑l=k+1Cl)+CECP6∑i=1Ci7∑j=i+1Cj−ατ∗Wη∗VγUC>0,A6=6∑i=1Ci7∑j=i+1Cj(CE+CP+7∑k=j+1Ck)+CECP7∑i=1Ci−ατ∗Wη∗VγU>0,A7=7∑i=1Ci(CE+CP+7∑j=i+1Cj)>0,A8=CE+CP+7∑i=1Ci>0,
|
where τ∗W,η∗V,B,C,Ci (i=E,P,1,…,7) and D are as defined in (7).
7.2. Appendix B: Proof of Theorem 3.11
Proof. Consider the model (6) with δL=0 and sgn(U∗∗−U(t))=sgn(E∗∗−E(t)) for all t≥0. Furthermore, let 1<R0<RC0, so that the unique non-trivial equilibrium T1 exists and is LAS (in line with Theorem 3.10). Consider, further, the following non-linear Lyapunov function of Goh-Volterra type:
|
K2= E−E∗∗lnE+d1(L1−L∗∗1lnL1)+d2(L2−L∗∗2lnL2)+d3(L3−L∗∗3lnL3)+d4(L4−L∗∗4lnL4)+d5(P−P∗∗lnP)+d6(V−V∗∗lnV)+ d7(W−W∗∗lnW)+d8(U−U∗∗lnU),
|
where,
|
d1=CEσE, d2=C1CEξ1σE, d3=C2C1CEξ2ξ1σE, d4=C3C2C1CEξ3ξ2ξ1σE,d5=C4C3C2C1CEξ4ξ3ξ2ξ1σE, d6=CB, d7=C5Cη∗VB, d8=C6C5Cατ∗Wη∗VB,
|
(24)
|
with τ∗W,η∗V,B,C,Ci (i=E,P,1,…,7) and D as defined in (7). The following steady state relations will be used to simplify the derivative of the Lyapunov function K2.
|
CEE∗∗=ψU(1−U∗∗KU)U∗∗,C1L∗∗1=σEE∗∗, CiL∗∗i=ξ(i−1)L∗∗(i−1); i=2,3,4,CPP∗∗=ξ4L∗∗4,C5V∗∗=σPP∗∗+γUU∗∗, C6W∗∗=η∗VV∗∗,C7U∗∗=ατ∗WW∗∗.
|
(25)
|
The Lyapunov derivative of K2 is
|
˙K2= (1−E∗∗E)[ψU(1−UKU)U−CEE]+d1(1−L∗∗1L1)[σEE−C1L1]+d2(1−L∗∗2L2)[ξ1L1−C2L2]+d3(1−L∗∗3L3)[ξ2L2−C3L3]+d4(1−L∗∗4L4)[ξ3L3−C4L4]+d5(1−P∗∗P)[ξ4L4−CPP]+d6(1−V∗∗V)[σPP−C5V+γUU]+d7(1−W∗∗W)[η∗VV−C6W]+d8(1−U∗∗U)[ατ∗WW−C7U],
|
(26)
|
Substituting (24) and (25) into (26), and simplifying, gives
|
˙K2= −ψUUEKU(E∗∗−E)(U∗∗−U)+γUd6U∗∗(3−UV∗∗U∗∗V−VW∗∗V∗∗W−U∗∗WUW∗∗)+CEE∗∗(9−L∗∗1EL1E∗∗−L∗∗2L1L2L∗∗1−L∗∗3L2L3L∗∗2−L∗∗4L3L4L∗∗3−P∗∗L4PL∗∗4−V∗∗PVP∗∗−W∗∗VWV∗∗−U∗∗WUW∗∗−E∗∗UEU∗∗).
|
(27)
|
The first term of (27) is automatically negative in Ω∖{T0}, since sgn(U∗∗−U(t))=sgn(E∗∗−E(t)) for all t≥0. Furthermore, since the arithmetic mean exceeds the geometric mean, it follows that the second and third term of (27) are also negative. Hence, ˙K2≤0. The proof is concluded as in the proof of Theorem 3.2.
The assumption sgn(U∗∗−U(t))=sgn(E∗∗−E(t)) for all t≥0 can be justified by noting the fact that, in order to maintain a non-trivial equilibrium for the adult mosquito population, it is necessary that each reproducing female mosquito must produce at least one egg during its entire reproductive life period. Thus, if the population of the reproduction female adult mosquitoes (U(t)) increases, so does the population of eggs laid (E(t)) for all t≥0.
7.3. Appendix C: Proof of Theorem 4.2
Proof. Consider the non-autonomous model (1) with R0TR<1. Using the fact that (and noting that L(t)=4∑i=1Li(t)),
|
ψU(1−U(t)KU)U(t)≤ψUU(t) (since KU>U(t) for all t≥0),
|
and,
|
Ci(t)+δLL(t)≥Ci(t), for all t≥0,
|
it follows that the non-autonomous model (1), subject to the aforementioned assumptions, can be re-written as
|
dEdt ≤ ψUU−CE(t)E,dL1dt ≤ σE(t)E−C1(t)L1,dLidt ≤ ξ(i−1)(t)L(i−1)−Ci(t)Li ; i=2,3,4,dPdt = ξ4(t)L4−CP(t)P,dVdt = σP(t)P+γUU(t)−C5(t)V,dWdt = η∗VV−C6(t)W,dUdt = ατ∗WW−C7(t)U.
|
(28)
|
Following [75], the equations in (28), with equalities used in place of the inequalities, can be re-written in terms of the next generation matrices F(t) and V(t), as follows
|
dX(t)dt=[F(t)−V(t)]X(t).
|
(29)
|
It follows, from Lemma 2.1 in [80], that there exists a positive and bounded ω-periodic function, x(t)=(ˉE(t),ˉL1(t),ˉL2(t),ˉL3(t),ˉL4(t),ˉP(t),ˉV(t),ˉW(t),ˉU(t)), such that
|
X(t)=eθtx(t), with θ=1ωlnρ[ϕF−V(ω)],
|
is a solution of the linearized system (28). Furthermore, it follows from Theorem 2.2 in [75] that R0TR<1 if and only if ρ[ϕF−V(τ)]<1. Hence, θ is a negative constant. Thus, X(t)→0 as t→∞. Thus, the unique trivial solution of the linear system (28), given by X(t)=0, is GAS [40,55,66]. For any non-negative initial solution (E,L1,L2,L3,L4,P,V,W,U)(0))T of the system (29), there exists a sufficiently large Q∗>0 such that [55,66],
|
((E,L1,L2,L3,L4,P,V,W,U)(0))T≤Q∗((ˉE,ˉL1,ˉL2,ˉL3,ˉL4,ˉP,ˉV,ˉW,ˉU)(0))T.
|
Thus, it follows, by comparison theorem [37,69], that
|
(E(t),L1(t),L2(t),L3(t),L4(t),P(t),V(t),W(t),U(t))≤Q∗X(t)for all t>0,
|
where Q∗X(t) is also a solution of (29).
Hence,
|
(E(t),L1(t),L2(t),L3(t),L4(t),P(t),V(t),W(t),U(t))→(0,0,0,0,0,0,0,0,0),
|
as t→∞.









 DownLoad:
DownLoad: