1.
Introduction
T cell-mediated, delayed-type hypersensitivity to dental metals is becoming prevalent in the general population, and the prevalence is still increasing worldwide [1]. The condition is characterized by contact or systemic dermatitis that is caused by chronic exposure to cations released from dental metals [2],[3]. Furthermore, dental metal hypersensitivity has a close pathogenetic relationship with palmoplantar pustulosis [4], lichen planus [5], dyshidrotic eczema [6], and autoimmune diseases that include systemic lupus erythematosus, rheumatoid arthritis, and Sjögren's syndrome [7],[8].
For the diagnosis of metal hypersensitivity, skin patch testing has been used most frequently owing to its high reproducibility and simplicity; however, it tends to have a high false-positive rate and/or a high false-negative rate [9]. In addition, patch testing carries the potential risk of allergen-primed sensitization of subjects, as evidenced by the previous reports describing flare-up of delayed-type hypersensitivity dermatitis triggered by patch testing [10]–[13]. In contrast, the lymphocyte transformation test (LTT) is an in vitro method based on the activation of peripheral blood lymphocytes upon re-exposure to the suspected metal allergen. Previous studies have demonstrated a strong correlation between results obtained from patch testing and the LTT and established the LTT as an alternative tool for detecting metal sensitization [14]–[17]. The LTT also has a high false-positive rate because certain metal cations can potently stimulate lymphocytes [17]–[19].
To overcome these problems, we evaluated a genetic method for detecting metal sensitization, focusing on single nucleotide polymorphism (SNP) rs2367563 within the intron 1 of the netrin-4 (NTN4) gene, which has been reported to have a possible genome-wide association with nickel hypersensitivity in a subset of the Korean population [20]. Nickel has been regarded as the most common allergenic metal. In dentistry, nickel, gold, palladium, and tin, which have been frequently used for dental alloys, have drawn much attention as the most common dental allergens [21]–[23]. We thus explored the efficacy of using SNP rs2367563 as a genotyping test for hypersensitivity to these dentally important metals. The primary aim of the current study is to test the feasibility of SNP rs2367563 genotyping in detecting hypersensitivity to multiple metals in a cohort of patients with signs and symptoms associated with dental metal hypersensitivity.
2.
Materials and methods
2.1. Ethics statement
This study was carried out in accordance with The Code of Ethics of the World Medical Association (Declaration of Helsinki). All procedures were reviewed and approved by the Ethics Committee of Takanawa Clinic (approval number: 2018-2). A signed informed consent form was obtained from each participant prior to inclusion in this study.
2.2. Subjects
The subjects were 154 Japanese (59 males and 95 females, ages 5 to 79 years, mean 48.3 years at tests) who visited the outpatient departments of Takanawa Clinic from October 2016 through July 2017 with a variety of complaints, 31.8% (49 subjects) of which exhibited symptoms suggestive of metal hypersensitivity. Their predominant symptoms were localized or systemic skin lesions such as dryness (6.12%), itch (69.4%), pain (14.3%), erythema (10.2%), blister (14.3%), eczema (18.4%), rough skin (14.3%), and/or skin peeling (6.12%). A subset of the subjects also complained of headaches (2.04%), fatigue (4.08%), and abdominal discomfort (2.04%). The diagnoses included contact dermatitis (1.64%), atopic dermatitis (9.84%), palmoplantar pustulosis (10.7%), psoriasis (9.84%), and dyshidrotic eczema (pompholyx, 4.10%), all of which are known to be associated with metal hypersensitivity [1]–[4],[6],[24]–[26]. The complaints of the undiagnosed subjects were not medically explained; however, these unexplained physical complaints are also known to be signs of metal hypersensitivity [27],[28]. For subjects without subjective symptoms of metal hypersensitivity, their diagnoses were diverse, which included Sjögren's syndrome (15.6%), irritable bowel syndrome (13.1%), ulcerative colitis (10.7%), Crohn's disease (1.64%), diabetes mellitus (0.820%), and ureteral calculus (0.820%). Sjögren's syndrome, irritable bowel syndrome, and ulcerative colitis are known to have a pathophysiological association with metal hypersensitivity [7],[8],[29],[30]. Patients who were over 80 years old, who were pregnant, or who used any drugs until blood sampling at the initial visit were excluded.
2.3. LTT
Tested metals were selected according to the examination of dental prostheses of the subjects. The LTT was outsourced to SRL, Inc. (Tokyo, Japan). Briefly, lymphocytes were isolated from 30 mL of heparinized peripheral blood of each subject by density gradient centrifugation using Ficoll-Conray media (Lymphosepar I, Immuno-Biological Laboratories Co., Ltd., Fujioka, Japan) according to the manufacturer's instructions. The lymphocytes were washed twice with phosphate-buffered saline (−) and resuspended at 1 × 106/mL in RPMI1640 medium (DS Pharma Biomedical Co., Ltd., Suita, Japan) supplemented with 20% autologous plasma. The 200 µL aliquots (2 × 105 cells) were treated with metal cations (a sequential 5-fold dilution series of 0.1% NiSO4, 0.004% HAuCl4, 0.02% PdCl2 or 0.02% SnCl4, Torii Pharmaceutical Co., Ltd., Tokyo, Japan), phytohemagglutinin (PHA, 7 µg/mL, Cosmo Bio Co., Ltd., Tokyo, Japan) or vehicles in triplicate in a 96-well UniFilter microplate (PerkinElmer Inc., Waltham, USA) at 37 °C for 72 hours in a 5% CO2 incubator. PHA- and vehicle-treated cells were used as a positive and a negative control, respectively. Then, cells were cultured with [Methyl-3H]thymidine (10.57 kBq/well, Moravek Inc. Brea, USA) for additional 18 hours and harvested on the UniFilter using the FilterMate cell harvester (PerkinElmer Inc., Waltham, USA). Radioactivity retained on the UniFilter was measured using a microplate scintillation counter (PerkinElmer Inc., Waltham, USA). Stimulation index (SI) was calculated as a ratio of incorporated 3H between metal- and vehicle-treated cultures: the amount (cpm) of 3H (metal-treated)/the amount (cpm) of 3H (vehicle-treated). Any subject with a SI of 1.8 or more was regarded as a LTT-positive (i.e. hypersensitive) person [31].
2.4. SNP rs2367563 genotyping
Genomic DNA was prepared from 3 hair bulbs of each subject using the DNA Extract All Reagents kit (Thermo Fisher Scientific, Inc., Waltham, USA) and genotyped with the TaqMan SNP Genotyping Assays (Assay ID: C__16216164_10; Thermo Fisher Scientific, Waltham, USA) according to the manufacturer's instructions. The genotyping PCR mix (10 µL) contained 2 µL (10 ng) of genomic DNA, 1 × TaqMan™ GTXpress™ Master Mix (Thermo Fisher Scientific, Inc., Waltham, USA), and 1 × TaqMan SNP Genotyping Assays. The PCR conditions were as follows: initial denaturation at 95 °C for 20 s; 40 cycles of denaturation at 95 °C for 3 s and annealing/elongation at 60 °C for 20 s. Genotyping was performed using StepOne Real-time PCR System (Thermo Fisher Scientific, Inc., Waltham, USA).
2.5. Statistical analysis
No outliers were taken into account, and all collected data were subjected to the statistical analysis. The normality of the LTT data was tested using the Shapiro-Wilk test. Since the yielded P-values were lower than the significance level of 0.05 in the majority of sample populations in the Shapiro-Wilk test, we employed the two-tailed Mann-Whitney U test at the significance level of 0.05 for subsequent statistical analysis. All statistical analyses were performed with EZR version 1.53 (Saitama Medical Center, Jichi Medical University, Saitama, Japan), which is a graphical user interface for R (The R Foundation for Statistical Computing, Vienna, Austria) [32]. All experimental procedures and data analyses were conducted by investigators who were blinded to the subjects' clinical information using a de-identified dataset.
3.
Results
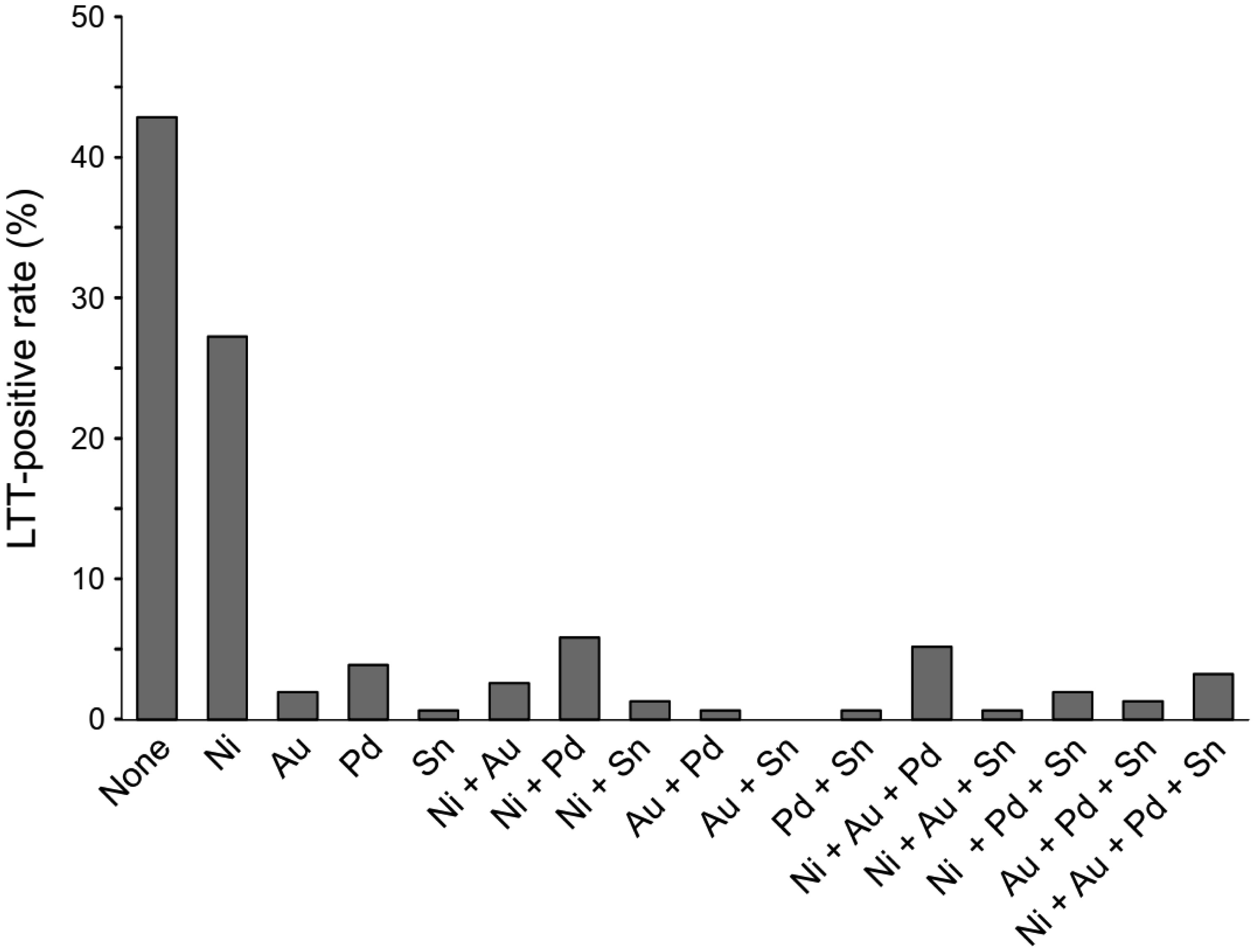
For the LTT, 66 subjects were negative for hypersensitivity to any metals examined, whereas 88 individuals were hypersensitive to at least one metal. The subjects hypersensitive to nickel alone were observed most commonly (27.3%, Figure 1). Hypersensitivity to multiple metal species such as nickel/gold, nickel/palladium, and nickel/gold/palladium was observed in 2.6–5.8% of the subjects, and 3.2% of the subjects were hypersensitive to all four metals examined (Figure 1). The overall rates of nickel, gold, palladium, and tin hypersensitivity were 48.1%, 15.6%, 22.7%, and 9.7%, respectively.
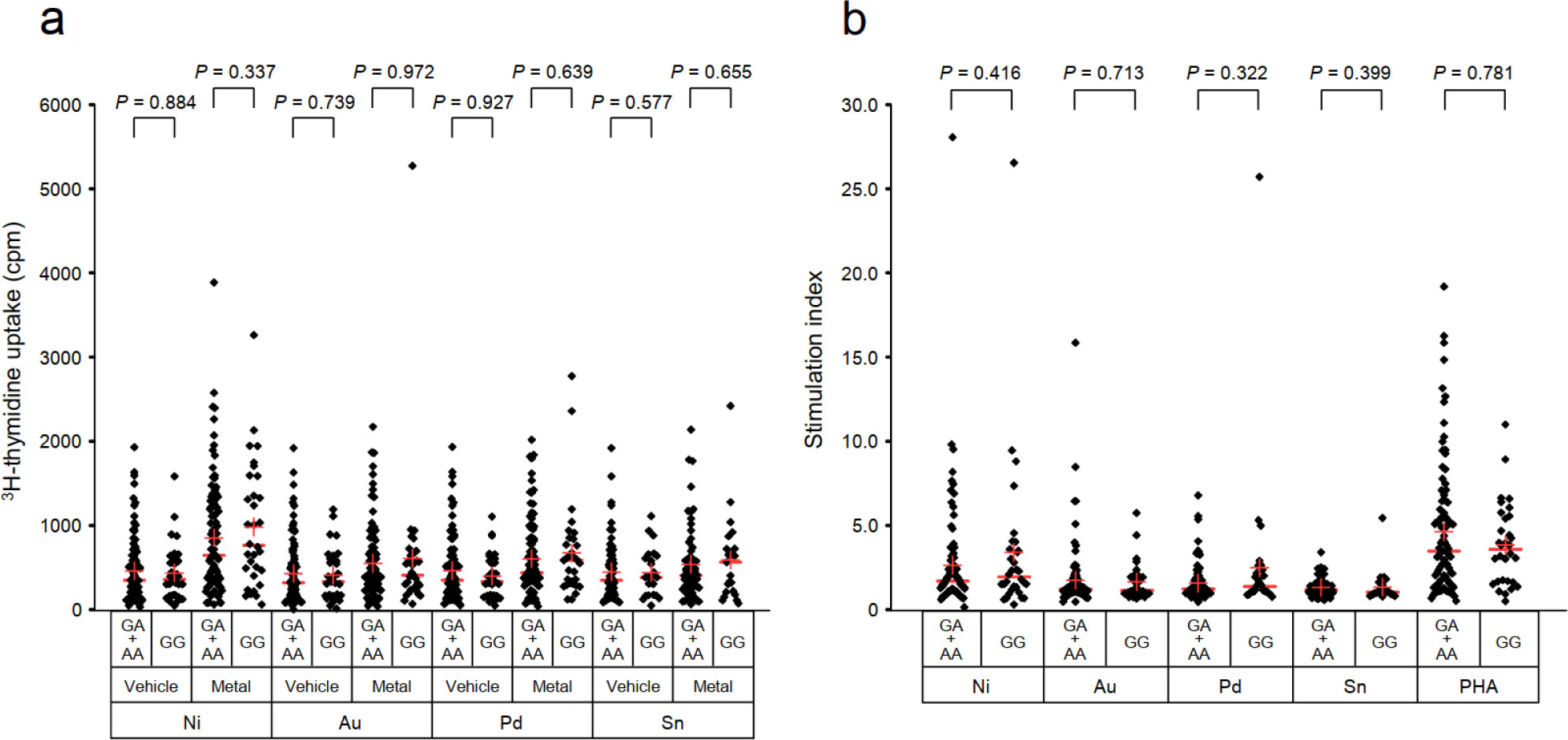
The SNP rs2367563 has two alternative alleles, a major G and a minor A alleles, the latter of which is known to be associated with the risk of nickel hypersensitivity [20]. The theoretical frequencies of the risk allele carriers (genotypes: GA and AA) and non-carriers (genotype: GG) in East Asian population are 73.1% and 26.9%, respectively. There was no significant difference in 3H-tymidine uptake and SI value between risk allele carriers and non-carriers (Figure 2). This result suggests that lymphocytes are stimulated by metals to the same degree irrespective of rs2367563 genotypes, and thus the results of the LTT can be utilized as a reference in the subsequent sensitivity and specificity analyses.
We then evaluated the sensitivity (the number of risk allele carriers/the number of LTT-positive subjects) and specificity (the number of risk allele non-carriers/the number of LTT-negative subjects) of rs2367563 genotyping using the LTT as a reference (Table 1). Of 74 subjects who were hypersensitive to nickel, 57 carried at least one risk allele (A) of rs2367563, which yielded the sensitivity of 77.0%. In contrast, of 77 individuals who were LTT-negative for nickel, 19 were non-carriers of the risk allele, resulting in the specificity of 24.7%. Notably, rs2367563 genotyping in subjects who were LTT-positive or -negative for gold, palladium, or tin also showed comparable sensitivity (62.5%, 68.6%, and 80.0%, respectively) and specificity (21.1%, 21.2%, and 26.9%, respectively) to those for nickel hypersensitivity (Table 1). The overall sensitivity and specificity were 73.9% and 19.7%, respectively.
4.
Discussion
Currently, metal hypersensitivity is one of the most common allergic disorders worldwide, and an increasing number of individuals with this condition is becoming a threat to public health [1]. However, there have been limited detection tools available for metal hypersensitivity over the years. Kim et al. reported that the association of rs2367563 with nickel hypersensitivity did not reach the genome-wide significance threshold [20]. Our finding suggests that SNP rs2367563 genotyping might detect potential risk for hypersensitivity to multiple dental metals, not only nickel but also gold, palladium, and tin. Owing to its low specificity, the rs2367563 genotyping test may be suitable for the adjunctive diagnosis that supports and complements patch testing and the LTT (e.g. primary screening or susceptibility prediction).
The SNP rs2367563 is located within the intron 1 of the NTN4, approximately 4.2 kb downstream from the boundary with the exon 1. There has been no information about the biological effect of the intronic SNP on NTN4 such as transcription activity, splicing efficiency, or pre-mRNA stability. Netrin-4 protein disrupts laminin-integrin networks and basement membrane assembly to regulate cell adhesion and migration during angiogenesis, lymphangiogenesis, and branching morphogenesis [33]–[37]. Furthermore, netrin-4 promotes tumor cell invasion and metastasis by regulating epithelial-mesenchymal transition [38],[39]. Collectively, netrin-4 may contribute to the migration of immune cells during delayed-type hypersensitivity reaction.
Patch testing has been widely accepted as a standard diagnostic tool among allergists for many years owing to its high sensitivity and specificity (70–80%) [9]. However, patch testing inevitably involves exposure to metals that elicits local contact dermatitis and carries the potential risk of unexpected sensitization of subjects [10]–[13]. The sensitivity and specificity of the LTT has been estimated to be relatively lower (40–50%) [14]–[19]. In addition, the LTT involves blood sampling and time-consuming procedures with radioactive materials. In contrast, rs2367563 genotyping can be completed in a short time without any invasive procedure and potential risk of harmful effects on the subjects. The rs2367563 genotyping test may therefore play an adjunctive role in detecting dental metal hypersensitivity such as primary screening and risk prediction if the sensitivity and specificity can be more improved. Since this method involves only simple PCR procedures and can be performed rapidly in general laboratory settings at a substantially lower cost, the low specificity may not be a critical limitation.
5.
Conclusions
Our finding suggests that rs2367563 genotyping can detect hypersensitivity to not only nickel but also other allergenic dental metals with substantially high sensitivity. However, despite its non-invasiveness and quickness, the rs2367563 genotyping test may be currently limited to the adjunctive use such as primary screening and risk prediction due to its low specificity.









 DownLoad:
DownLoad: