Influenza remains one of the major infectious diseases that target humankind, therefore, understand transmission mechanisms and control strategies can help us obtain more accurate predictions. There are many control strategies, one of them is vaccination. In this paper, our purpose is to extend the incidence rate of a two-strain flu model with a single vaccination, which includes a wide range of incidence rates among them, some cases are not monotonic nor concave, which may be used to reflect media education or psychological effect. Our main aim is to mathematically analyze the effect of the vaccine for strain 1, the general incidence rate of strain 1 and the general incidence rate of strain 2 on the dynamics of the model. Four equilibrium points were obtained and the global dynamics of the model are completely determined via suitable Lyapunov functions. We illustrate our results by some numerical simulations. Our results showed that the vaccination is always beneficial for controlling strain 1, its impact on strain 2 depends on the force of infection of strain 2. Also, the psychological effect is always beneficial for controlling the disease.
1.
Introduction
Synchronization [1,2,3,4,5] and propagation [6,7,8,9,10], as the typical interesting and important dynamical behaviors in complex networks [11,12,13,14,15,16,17,18,19,20], arouse a hot study in various fields in recent decades. When a disease is discovered and diffused from the affected area, the information about and appraisal of an epidemic is also transmitted along the connective networks. In other words, if there exists relationship between two individuals, one person can get the message from another, so that the message about disease can diffuse along with the relationship networks. While, the transmission of epidemic is through the contact network among individuals. Furthermore, many outstanding works are taken which have looked at epidemic spread as an important aspect of transmission behavior in complex networks from the mathematical biology field.
A thought is taken it for granted that synchronization and propagation almost disappear simultaneously in a complex network, but many examples and phenomena show that situations are opposite in fact. Especially when a kind of epidemic disease transmission, the masses' behavior always reach to consensus and tackle diseases, which can be claimed to achieve the synchronous behaviors for nodes in the complex network. As a matter of fact, we always see or do the same things such as washing hands with soap frequently, doing exercise to enhance our health and avoiding to go to the crowded place and so on, to refrain from infected and to combat the disease when we get the information about epidemic diseases. This kind of consistent behaviors in a complex network is so called behavior synchronization aroused by the epidemic spreading. In recent years, there are many excellent works concerned about such kind of synchronization induced by contagious diseases [21,22,23,24,25], while in which synchronization and spreading of epidemic disease are discussed in combination from the aspect of numeric. Therefore, it is so interesting about the interaction among synchronization and epidemic spread in complex networks that we will also go on discussing the behavior synchronization induced by propagation of disease in this work.
From the view of mathematical biology, several interesting models have been analyzed qualitatively on dynamical synchronization aroused by epidemic spread. The adaptive mechanism between dynamical synchronization and epidemic behavior as well as the interplay between collective behavior and spreading dynamics were discussed respectively, where the effect about individuals' awareness was introduced in epidemic models in the later one [26,27]. And then mutually restrictive conditions among dynamical synchronization and epidemic transmission were derived from sternly theoretical methods. Follow on, with the assistance of the quenched mean-field theory, behavioral synchronization induced by epidemic spread was addressed under the constructed mathematical models without delay, with a coupling delay and with double delay [28]. And Sun et al. [29] taken an exploration and simulation of epidemic spread and its control in multiplex networks, and found that the epidemic control strategy from the perspective of behavioral control is extremely relevant for epidemic control.
While those works are all about complete synchronization patterns induced by epidemic spread, the cluster collective behavior in complex networks are more general. And there are many successful efforts on the cluster synchronization in complex networks, such as [30,31] and references therein. However, few works paid attention to grouped collective behaviors induced by disease propagation in a complex networks with community structure. The collective behaviors induced by epidemic spread are firstly considered under community structure of complex networks, and obtained corresponding results [32]. So universal and significant as the cluster collective behaviors are that we will consider the grouped collective behaviors aroused by epidemic transmission in our work. On the other hand, because of distinct survival conditions and food resources distributed in space, there are agammaegation of individuals in different areas and then forming patches [33,34]. And it is common phenomenon that individuals can take dispersal or migration in the patch environment, thus in our discussion there will also consider the effect of dispersal among patches in the epidemic model, and further consider the grouped collective behaviors induced by patchy epidemic spread. Different from other cluster characteristic collective behaviors, the cluster numbers are corresponding to the number of patches in our consideration, and the information about diseases in each patch will be utilized to design the behavioral state feedback pinning controllers in the behavior dynamical systems which familiar with the control strategy [35].
Inspired by the above discussions, the cluster collective behaviors in behavioral synchronization systems aroused by epidemic spread under patchy population will be studied in our work. In the problem we considered, the epidemic models with input rates and remove rates under patchy dispersal environment different from the above mentioned, are constructed in view of the quantity of population, while the total population is guaranteed as a constant. In which we assume that the dispersal only appear among the susceptible in patches. Then we consider the relation network of individuals under this constant population, and assume that the relationship is inheritable, even though there are input and remove rates in epidemic models, which means the fixed relation network. In other words, the new input one will fill the lost relation position in the relation network. It should be noticed that the spatial structures of individuals are not concerned, just concerning the relation. And then, dividing the relation network into several subetaoup same as the number of patches, named as behavioral pattern relation group induced by patches. Called the individual belongs to the group k if it lies in the kth behavioral pattern relation group. On the basis of above, the main purpose of our work is to achieve behavioral consistence in each group under the transmission of disease by using so called behavior feedback controlling strategy related with the information about diseases and the whole behaviors for all individuals.
The main contribution of this work are listed as follows. First, we construct the coupling system about patch epidemic disease-behavior synchronization models based on population, in which the effect of dispersal only appears in the susceptible while the infected are limited to migration. And a function of contact willing related with information about disease in each patch and whole behavior state is added before the incidence as a kind of cofactor. Then, we design the disease relative feedback pinning controllers by using the diseases' information for each patch and the states of behavior in each group. In other words, a part of nodes in each group are needed to control. Finally, we obtain conditions about global asymptotical stability for disease-free equilibrium by using Lyapunov stability analysis method, and prove the existence of positive equilibrium, and derive the corresponding criteria. On the other hand, we verify the global asymptotical stability of the positive equilibrium for epidemic systems by Lyapunov function, and meanwhile, obtain the criteria that achieve the cluster behavioral synchronization, related with the cluster relation network structures and patch characteristic.
The rest of this paper is organized as follows. The mathematical models and necessary preliminaries are shown in Section 2. In Section 3, the global stability of disease-free equilibrium and the existence of positive equilibrium are analyzed in the patch epidemic-behavior synchronization systems, and the global stability of positive equilibrium as well as the cluster behavioral synchronization under the designed feedback pinning control strategy are discussed. The numerical simulation is performed in Section 4 to demonstrate effectiveness of the theoretical results. Finally, the conclusion is presented in Section 5.
Notations: Trough out this paper, R+ is the set of nonnegative real numbers, Rn represents n dimensional Euclidean space, and Rn×m denotes the set of n×m dimensional real matrix. A matrix P is claimed as positive (negative) if P>0(<0). And the unit matrix is denoted as Em×m with m×m dimension.
2.
Models and preliminaries
2.1. Mathematical models
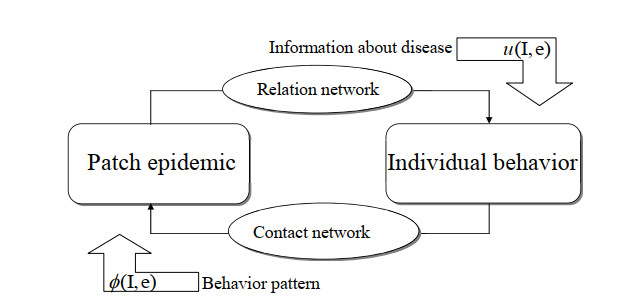
As shown in Figure 1, the mutual influence between patch epidemic and individual behaviors includes two processes, such as, the one is the transmission of information about epidemic diseases, and the behavioral contact among individuals. In which the message about patch epidemic disease will be transferred along with the relation network of the individuals, meanwhile the information about patch disease will be used to design the state feedback controllers for individuals' behavior pattern. The relation network mentioned here is a kind of network about information exchange among individuals, and there exist also reinforcement of transmission, such as more frequent exchange. On the other hand, the spreading for epidemic diseases occurs by the full probability contact network, where considering the bilinear incidence, while the behavior pattern will be as one part for a kind of cofactor function to affect the actual infected population. In this framework, the mutual interaction coupling systems can be formed. It should be noticed that we model the patchy epidemic spreading based on the number about total population of the susceptible and the infected in each patch, and it is taken into consideration that the uniform contact or identical probability contact among the susceptible and the infected. Thus, the concrete topological construction about the contact network leading to disease transmission is not reflected in the population patch epidemic model.
In this paper, we consider the fixed topology structure of the relation network A=(aij). Because the input and remove are considered in the epidemic model (shown below in the system (2.1)), we assume that the new individuals fill up the leaves one's relation site and remain the origin relation unchange. Even though dispersal is also considered in the epidemic model, we assume that the relation network among individuals is unchanged with the time going, and the subetaoups of relationship are divided from the patch disease information not the individuals' numbers in each patch, which means that the numbers for the subetaoup of relationship are same as the patch numbers. In the same subetaoup of relationship, there will be a enhancer coefficient that reinforces the relationship in the same subetaoup. We name these groups consisting of the individuals in such relationship subetaoup as behavior pattern relation group induced by the corresponding information of patch diseases. Which can be understandable that some individuals in different places that are feedback by one patch so called that they belong the same behavior pattern relation group induced by the information of patch diseases. In each behavior pattern group induced by patch diseases, we will take the patch disease information to design the feedback control tactic to achieve a desired behavior consistence. Maybe these feedbacks are added to a part of individuals in the behavior pattern group.
We now construct the following m patch epidemic models with dispersal
Where Sk(t) and Ik(t) represent the susceptible and infective population in kth patch at t, respectively. And the total population N(t)=∑mk=1(Sk(t)+Ik(t)). In the epidemic models, we assume that the dispersals of the susceptible population are balance, which means that the dispersal matrix B=(bkl) satisfies ∑mk=1∑ml=1bklSl(t)=∑mk=1∑ml=1blkSk(t), where bkl is the rate of dispersal with bkl≥0, and B=(bkl) is assumed to be irreducible. μS0k is the constant input in the kth patch, μ is the natural death rate, and the diseased death is not considered in this model. And suppose that ∑mk=1S0k=N(t). In addition, ϕk(x(t),Ik(t)) represents the contact willing function that is relative with the behavior states and information about patch diseases, which reflects the case that the more similar between individuals' behavior pattern, the more willing to contact with each other, or the more severe the disease, the less likely they are to be exposed. And the actual expression will be defined later.
Discuss the models (2.1), and with the assumption ∑mk=1S0k=N(t) assistance, we find that
Therefore, the population N(t) is a constant, denoting as N, i.e., N(t)≡N.
Based on the above finding, we introduce the individuals'(or nodes') behaviors, and then construct the coupling systems about cluster individual behavior network systems and patch epidemic models with dispersal under constant population, as following
In which, corresponding to the number of patches there also be divided into m behavior pattern groups induced by the information of patch diseases under the relation network. Let K represents the kth behavior pattern group induced by kth patch epidemic, and K={rk−1+1,⋯,rk} is the nodes set of individuals in kth behavior pattern group. In the system (2.3), xi(t)∈Rn represents the ith individual's behavior state vector, fk(xi(t)):R+×Rn→Rn denotes the local behavior dynamics in the kth group. If the node i and j exist relationship then aij>0, otherwise aij=0. cij denotes the intra-group enhancement factor, which means that cij=ck>0 if ˉi=ˉj, where ˉi is the group that i belongs, otherwise cij=1 when ˉi≠ˉj. ui(t) is the state feedback controllers related with information about patch diseases which will be designed later.
And from the models (2.3), one can know that local behavior of nodes in the whole network are non-identical and each subetaoup has distinct behavioral target pattern. What's more, the division for nodes relies on their relationship network, do not on their actual spatial position, which means that if individuals in distinct places are impacted from the same patch's disease information, we will classify them as the same relationship subetaoup. Therefore, in models (2.3), the first one equation represents the node i's dynamical behavior process in k's relationship subetaoup K that aroused by the k's patch disease. Then when the patch disease spreading, the behavioral control ui(t) for each node i in corresponding subetaoup will be activated to make node's behavior pattern trend the desired state.
So far, we define the expression of contact willing function ϕk(x(t),Ik(t)) as
where the αk∈(0,1) is the consciousness strength in the kth patch. Let x(t)=(xT1(t),⋯,xTN(t))T and y(t)=(yT1(t),⋯,yTm(t))T, and denote the behavioral error for each node as ei(t)=xi(t)−yk(t), then there are e(t)=(eT1(t),⋯,eTN(t))T, in which yk(t)∈Rn is the target in each subetaoup. For writing convenient, rewriting the ϕk(x(t),Ik(t)) as ϕk(t), i.e., there are
The system (2.3) is a kind of compound models mixes with the behavioral equation for individuals' states and patch epidemic spread equations. xi(t),i∈K represents the individual's state vector at t for the node belongs to the kth behavior pattern relation group, which reflects the individual's actions such as washing hands, wearing a mask and having a rest, etc.. fk(⋅) is the local dynamics for the group k that shows the summation of distinct behaviors for the individuals in the subetaoup, in other words, the nodes are not identical. And fk(⋅) for each k is active, dynamic, as well as complex. Sk(⋅) and Ik(⋅) are the population of the susceptible and the infective, and bilinear incidence is adopted here. The contact willing function ϕk for each patch, determined by patch information and total behavior state error, is introduced as a factor to affect the incidence. ϕk is affected by the behavior equations, in which the more less the behavior error is, the more willing to contact with others. The controllers in the behavior equation of system (2.3), ui, are added to the single node and will use the patch epidemic information and single node's behavior errors, which means that only when epidemic transmission the controllers can work to synchronize behaviors. What's more, the controllers are even pinning that only a part of nodes need to be controlled. It is meaningful to design the controllers ui in this way. Notice a fact that two processes occur, the one is the transmission of information about patch disease along with the relation network A, which will influence individuals' behavior pattern by external controllers. Another is the epidemic spread through the contact network adopting the bilinear incidence affected by behavior related cofactor, which will impact the epidemic spread from contact willing function. Therefore, in models we realize the coupling between behavior equations and patch epidemic spread equations by the external controllers ui, as well as the ϕk.
2.2. Preliminaries
Definition 1. It is said a network contains N nodes achieve cluster synchronization if the network consists of N is divided into m subetaoups, such as i∈K={rk−1+1,⋯,rk},k=1,⋯,m, for any i and j belong to the same cluster, there are limt→∞||xi(t)−xj(t)||=0.
Remark 1. Usually, we do not compute the errors between any two nodes xi(t) and xj(t) directly. In order to achieve cluster synchronization, it is only needed to obtain limt→∞||xi(t)−yk(t)||=0, for i∈K under the given synchronization target yk(t) for each cluster. And in this work, we want to use the patchy disease information Ik(t) to design nodes' controllers in each subetaoup to achieve cluster behavior synchronization. Which means only when disease spreading controllers can be activated to work.
Definition 2. A matrix L is claimed to belong the A1, denoted as L∈A1, if A satisfies
1. lij≥0,j≠i,lii=−∑Nj=1,j≠ilij,
2. L is irreducible.
If the L∈A1 and L is symmetric, it is said L belongs to A2, denoted as L∈A2. Furthermore, for any matrix L∈Rn×m, if satisfies the row-sum zero, it can be called that Ln×m belongs to A3, denoted as Ln×m∈A3.
Definition 3. A continuous function [36] f(x(t)):[0,∞]×Rn→Rn is said to be QUAD class of function, denoted as f∈QUAD(P,Δ,η), if there exist positive definite diagonal matrix P=diag{p1,⋯,pn} and the diagonal matrix Δ={δ1,⋯,δn}, and a positive constant η such that for f there holds
for any x(t),y(t)∈Rn.
Which also implies that there exists positive constant ξ and a positive diagnose matrix P=diag{p1,p2,⋯,pn} such that
Remark 2. It can be easily verified that almost chaotic systems satisfied the QUAD class of function, for instant, the famous Lorenz system, the Chua's circuit, Rössler system, Chen system, and so on.
Lemma 1. For any vectors x,y∈Rn, there exists a positive constant θ, such that
The relation between the above inequalities is actually derived from the Cauchy inequality for the vector. Under the positive constant θ, using the Cauchy inequality can easy to obtain above result [37].
3.
Main results
In this section, we will consider the boundedness and nonnegativity of the m patches epidemic models in the system (2.1). Obviously, the boundedness of the system (2.1) has been verified from the discussion in Eq (2.2).
For the nonnegativity of system (2.1), which means that for any given initial values Sk(0)≥0,Ik(0)≥0, there will hold Sk(t)≥0,Ik(t)≥0, for all k=1,2,⋯,m, and t≥0.
Assume that for any initial values Sk(0)>0, there exists k and t1, such that
In other aspect,
Therefore, when t∈[0,t1), we get the Sk(t) satisfies that
then, when t→t1, we obtain
But from the assumption Sk(t1)=0, there is contradiction. Therefore, for any initial values Sk(0)>0, there are Sk(t)>0 for k=1,2,⋯,m,t≥0. Combined with the continuity of solution to initial value, when Sk(0)≥0, there always hold Sk(t)≥0 for any t≥0 and k=1,2,⋯,m.
For the Ik(t), we get Ik(t)=Ik(0)e∫t0(ϕk(s)bkSk(s)−μ)ds. When the initial values Ik(0)≥0, there exists that Ik(t)≥0 for all t≥0,k=1,2,⋯,m.
Remark 3. It should be noticed that it is just a kind of qualitative analysis way to discuss the nonnegativity of solutions for the epidemic system, and the concrete solutions expression for the system can not be derived in this process. It is merely a method to analyze character of sign for solutions that we want to know.
3.1. The disease-free equilibrium of patch epidemic systems
We now analyze the disease-free equilibrium of the system (2.1). We first introduce some notations. Let S(t)=(S1(t),S2(t),⋯,Sm(t))T∈Rm, b=(μS01,μS02,⋯,μS0m)∈Rm, and
Under the situation of the disease-free equilibrium, we discuss the equation
Therefore, we obtain the compact form,
Then the problem about the solution for Eq (3.1) can be transformed into the solution for matrix Eq (3.2). Which means that we want to obtain the matrix equation's solution such that S(t)>0 for Eq (3.2). In other words, the current aim is to get the positive solution for the system of inhomogeneous linear Eq (3.2).
For the Eq (3.2), assume
Then there exists positive solution for Eq (3.2).
The following is simple proof about the existence of positive solution for Eq (3.2).
Proof. At first, let BD=diag{μ+∑l≠1bl1,μ+∑l≠2bl2,⋯,μ+∑l≠mblm}, since bkl≥0, then μ+∑l≠kblk>0,k=1,2,⋯,m, therefore, BD>0 and BD is invertible as well as B−1D≥0, where B−1D=diag{1μ+∑l≠1bl1,1μ+∑l≠2bl2,⋯,1μ+∑l≠mblm}.
Let D=E−BB−1D, then B=(E−D)BD. From the (H1), we obtain that C≡(E−D)b>0. And according to b>0,D≥0, we get ρ(D)<1, where ρ(D) represents the spectral radius of D [38]. By the Perron-Frobenius theorem there exists a vector v≥0, such that DTv=ρ(D)v. Thus, there is 0=vTρ(D)−vTD=vT(Eρ(D)−D)<vT(E−D). Combining with b>0, we have vT(E−D)b=vTC>0. On the other hand, vT(E−D)b=(1−ρ(D))vTb, which implies 1−ρ(D)>0.
To sum up, we can claim that E−D is invertible, and then with the representation of B, B is also invertible. Therefore, for the Eq (3.2), there are
Which means there exist positive solution for the Eq (3.2) when (H1) hold.
Then, denote by E0=(ˉS01,0,ˉS02,0,⋯,ˉS0m,0) the disease-free equilibrium, we have
Therefore, we obtain the following results for the disease-free equilibrium E0=(ˉS01,0,ˉS02,0,⋯,ˉS0m,0).
Theorem 1. Assumption that B=(bkl)m×m is irreducible and (H1) hold.
1. When ˉR0k=ˉS0kαkbkμ≤1,k=1,2,⋯,m, then the disease-free equilibrium E0 is globally asymptotically stable.
2. When R_0k=ˉS0kαk(1−1N)bkμ>1,k=1,2,⋯,m, then the disease-free equilibrium E0 is unstable, and if there are ˜R0k=S0kαkbkμ+∑l≠kblk>1,k=1,2,⋯,m, then there exist positive equilibrium E∗=(S∗1,I∗2,S∗2,I∗2,⋯,S∗m,I∗m).
Proof. Firstly, denote the Lyapunov candidate function
where vk is the kth cofactor of the kth diagonal entry for the Laplacian matrix of ˜B=(˜bkl)m×m, and ˜bkl=bklˉS0l. Due to the B=(bkl)m×m is irreducible, so as the ˜B, then vk>0,k=1,2,⋯,m.
Then, take the derivative of L1(t) along the system (2.1), and according to the equation that disease-free equilibrium E0 satisfies as shown in Eq (3.3), we obtain
From the fact that
and the equality holds if and only if Sk(t)=ˉS0k, then there is
Let ˜bkl=bklˉS0l, then ˜B=(˜bkl)m×m. And then denote that
Therefore, from Eq (3.5) we obtain that
On the other hand, there is 1−x+lnx≤0 and the equal hold if and only if x=1. Which means that 1−x≤−lnx holds. Then
Then
where Fk(Sk(t),ˉS0k)=−Sk(t)ˉS0k+lnSk(t)ˉS0k.
Then we have
Therefore, there exists the following result according to [39]
To sum up, we have ˙L1(t)≤−∑mk=1vk(μ−ˉS0kϕk(t)bk)Ik(t).
In addition, Ik(t)≥0 for each k that has been verified, as well as the fact that
Let
then when ˉR0k≤1, we get μ−ˉS0kαkbk≥0. On the other hands, μ−ˉS0kϕk(t)bk≥μ−ˉS0kαkbk. Thus when ˉR0k≤1, there is ˙L1(t)≤0. And ˙L1(t)=0 if and only if Ik(t)=0,Sk(t)=ˉS0k. Which means that the disease-free equilibrium E0 is the single point compact invariant set for the ˙L1(t)=0. Therefore by the LaSalle's Invariant Principle, we can claim that the disease-free equilibrium E0 is globally asymptotically stable.
From the other aspect, let
Then when R_0k>1, we have −μ+ˉS0kαk(1−1N)bk>0, which implies that −μ+ˉS0kϕk(t)bk>0. It means that ˙L1(t)>0, and the disease-free equilibrium E0 is unstable in the neighborhood of E0. Combined with the boundedness of the system, there exists positive equilibrium.
From the system (2.1), we can easily obtain the nonzero solution, denote the nonzero solution as E∗=(S∗1,I∗1,S∗2,I∗2,⋯,S∗m,I∗m) that holds
where ϕk(t)|I∗k=αk due to the equilibrium state. In which the S∗k and I∗k equal to
Denote
Then when ˜R0k>1, e.g., S0k−μαkbk−∑ml=1,l≠kblk1αkbk>0. On the other hand,
Therefore, ˜R0k>1 implies that there exists the positive solution for the system (2.1). The proof of the theorem is then completed.
3.2. The stability of positive equilibrium and behavior system's behavioral pattern synchronization
In this subsection, we will analyze the behavior pattern cluster synchronization induced by the patch disease under the case of positive equilibrium existence for epidemic systems, implying the epidemic disease spreading, and address the stability of positive equilibrium at the same time. For this purpose, we assume the relationship network is fixed, even though there are input and removing as well as the dispersal among patches, as for the input and death, the new individuals will fill up the removed one's relation site and remain the origin relationship unchanged. Assume there are m patches, and we divide the relation network into m behavior pattern relation groups induced by the patch disease information and let K={rk−1+1,⋯,rk},k=1,2,⋯,m represents the kth group with rk−rk−1 numbers that individuals belong to, where r0=0,rm=N. Specially, the individuals' numbers in the kth behavioral pattern relation groups do not need to be same with kth patch's population. Under this situation, we just focus on the behavior pattern of individuals, not the spatial position, that is to say the individuals from different places can have the same behavior pattern, so that we divide them into the same behavior pattern group. Corresponding to this division, when we divide the relationship network the individuals are also divided in fact and then utilize the patches disease information to design the feedback controllers for individuals in corresponding behavior pattern group, while this feedback control would be added to a part of the individuals in each group, named pinning.
Next, we divide the relationship network. Let
then we have the matrix L as the relationship network A's Laplacian matrix L=(lij)N×N
Blocking L according to the behavioral pattern relation groups, obtain
Additionally, combined with the intra-group enhancement factor, we have
where ¯Lkk=ckLkk,k=1,2,⋯,m, and Lkqk=Lkqk,k=1,2,⋯,m,qk=N−(rk−rk−1). And the matrix block ¯Lkk belongs to A1 and Lkqk belongs to A3 for each k.
Now, we use the patch disease information to design the feedback controllers ui(t) in the system (2.3) for individuals in each behavior pattern group to achieve behavior pattern grouped synchronization. And the controllers may add to apart of individuals in each behavior pattern group. We design the ui(t),i∈K,k=1,2,⋯,m as following
where cˉi is the intra-group enhancement factor in the group that i belongs, and di represents the control strength with di>0 for i=rk−1+1,⋯,rk−1+l, otherwise di=0. ei(t) has been denoted in the expression about ϕk(t) in subsection 2.1 called the behavior pattern grouped synchronization error for each individual i in the group k, and yk(t) is the behavior pattern target in the kth behavior pattern group that satisfies the uncoupled system
Then the whole error denotes as e(t)=(eT1(t),eT2(t),⋯,eTN(t))T, and eT(t)e(t)=∑mk=1∑i∈KeTi(t)ei(t). According to the behavior pattern error's definition, we get the patch epidemic-behavior error systems corresponding to the systems (2.3)
in which, from the ¯Lkk∈A1 and Lkqk∈A3, there are
Then the problem about the stability of positive equilibrium for epidemic systems and the behavior pattern synchronization of the system (2.3) is transferred to the issue about the positive equilibrium stability and the zeros stability for the error system (3.9).
Therefore, we denote the patch epidemic-behavior cluster synchronization manifold D for patch epidemic-behavior cluster synchronization error network system (3.9) as shown
Then, we obtain the following result.
Theorem 2. Assume that the B=(bkl)m×m is irreducible and the positive equilibrium exists for the epidemic system in (3.9). And assume that the fk∈QUAD for each k. If there exists constant θ>0, such that
where ˆck represents the kth cofactor of the kth diagonal entry for the Laplacian matrix of ˆB=(ˆbkl)m×m, ˆbkl=bklS∗l, δ(k)=maxj{δ(k)j} about Δk=diag{δ(k)1,⋯,δ(k)n}, and ¯Dk=diag{ckdrk−1+1,⋯,ckdrk−1+l,0,⋯,0}. Then the patch epidemic-behavior cluster synchronization manifold D is globally asymptotically stable. In other words, patch epidemic-behavior synchronization network system (2.3) achieve behavior pattern cluster synchronization induced by the patch disease spreading, as well as the positive equilibrium E∗ for epidemic systems is unique and globally asymptotically stable.
Proof. Denote the Lyapunov function as
where
in which
Firstly, take the derivative of V1(t) along the behavior error equation, and obtain
Next, handling three terms in the above equation.
From the QUAD class of function, we get
where Δk=diag{δ(k)1,⋯,δ(k)n}, δ(k)=maxj{δ(k)j},
˜e(k)j(t)=(erk−1+1,j(t),erk−1+2,j(t),⋯,erk,j(t))T∈Rrk−rk−1,
˜e(q)j(t)=(e1,j(t),⋯,erk−1,j(t),erk+1,j(t),⋯,eN,j(t))T∈RN−(rk−rk−1),
that also be used in later analysis.
For the second term, we have
According to Lemma 1, we get
On the other hand,
Therefore, substitute the Eqs (3.17) and (3.18) into Eq (3.16), we obtain
where Erk−rk−1 is identity matrix with dimension rk−rk−1.
From the assumption that there exists positive equilibrium for epidemic systems, then there holds limitation
which means that for any ε>0 there is t0>0, when t>t0 there holds
e.g.,
So there are
where
In conclusion, substitute the Eqs (3.15), (3.19) and (3.20) into the Eq (3.14), we obtain
Then taking the derivative of the V(k)1(Sk(t)) and V(k)2(Ik(t)) along with the epidemic model in system (2.3), respectively, and according to Eq (3.6) that positive equilibrium satisfies, we obtain
In addition, there exist the fact that
and the equality holds if and only if Sk(t)=S∗k.
Then, from the expression of V2(t), there are
Be similar to Theorem 1, let ˆbkl=bklS∗l, and ˆck represents the kth cofactor of the kth diagonal entry for the Laplacian matrix of ˆB=(ˆbkl)m×m.
Then denote
We get
where
On the other hand,
Thus, according to the result in [39], one obtain
From above, we get
In conclusion, combined Eqs (3.14) and (3.25) as well as the V(t)'s denote in Eq (3.11), there are
Then, we obtain when Eq (3.10) holds, the ˙V(t)<0. Therefore, from the Lyapunov stability theorem, there are results that when positive equilibrium exists for the epidemic-behavior synchronization model (2.3), it is unique and globally asymptotically stable, meanwhile behavior systems achieve the behavior pattern cluster synchronization induced by patch diseases. In other works, under the conditions of positive equilibrium existence for epidemic systems, combined with conditions (3.10), then the patch epidemic-behavior cluster synchronization manifold D for the patch epidemic-behavior synchronization network is globally asymptotically stable. Then the theorem is completed.
To achieve the conditions (3.10) in Theorem 2, we can carry out from the following steps.
Step 1. Firstly, we obtain the largest eigenvalue of the (−ηkλmax(P)+δ(k)+m−12θ+mNˆckαkbkλmin(P))Erk−rk−1+θ2LkqkLTkqk, denote as ρk.
Step 2. Then, we also get the least eigenvalue of Lkk+Dk(I∗k−ε) when given the strength of controlling, denote as wk, where
Step 3. Naturally, in order to making condition (3.10) be satisfied, it is needed to select the appropriate ck, which implies that the ck is just selected larger than ρkwk, i.e., ck>ρkwk.
From the steps we conclude that, on the one hand, the internal group enhance factors ck are working as an important role in synchronizing the same group individuals, in other words, behavior cluster synchronization and stability of positive equilibrium positive can achieve needed to select the ck as large as possible. Which means that we can strengthen subetaoup connection to realize the desired target. On the other hand, it is unrealistic to choose any large ck due to the limited resource, therefore this procedure also provides a feasible method to select the advisable ck working among the internal group individuals.
Remark 4. Notice that from the QUAD class of function in the Definition 3 the conditions (3.10) can also be represented as
which is convenient to compute in the numerical simulation. Furthermore, it is obvious that conditions (3.10) are relative to the relation sub-group network's structure, susceptible population's dispersal rates, and the scale of patchy epidemic diseases. In other words, in view of cluster conditions (3.10), the behavior pattern cluster synchronization is codetermined by topological structure of individuals' relation network and the migration for the susceptible population as well as the appropriate external controlling based on the epidemic disease spreading.
Remark 5. In conditions (3.10), ¯Lkk is inner-group relation network structure containing relation enhance factor, that is to say the relation sub-networks among nodes in the same group are weighted networks. Thus, combined with appropriate the strength of controlling, it is easily to achieve conditions (3.10). What's more, from the designed control strategy shown in Eq (3.7), the external control can work well only when epidemic disease spreading, thus, conditions (3.10) will be satisfied when giving appropriate strong of control.
4.
Numerical simulations
In this section, we give the numerical simulation to demonstrate the effectiveness of our results obtained in the previous sections.
As for the local dynamics in the behavior system, we consider the unified system as shown in the early work [40] and its generation [41]
From the reference [40], we know that for all τ∈[0,1], the unified systems are all chaotic. And for 0≤τ<129, there is the positive invariant set for the above system shown in [40],
Then,
We denote that f1(x,τ)=(25τ+10)(x2−x1),f2(x,τ)=(28−35τ)x1−x1x3−(29τ−1)x2,f3(x,τ)=x1x2−8+τ3, then f(x,τ)=(f1(x,τ),f2(x,τ),f3(x,τ))T. Let e=x−y, when p2=p3, then there are
where ξ(τ)1=−(25τ+10)p1+ϵ(25τ+10)p1+(M+56−70τ)p22+vp2M2, ξ(τ)2=(29τ−1)p2+(25τ+10)p1+(M+56−70τ)p22ϵ, ξ(τ)3=−8+τ3p2+p2M2v.
In this numeric simulation, we set τ=0,0.01,0.03 to get three chaotic systems as the local dynamical behavior in the behavior dynamic systems. And from the QUAD class of function, we just need to obtain the positive value ξk for k=1,2,3. Thus, we set P=diag{0.099,0.1,0.1} and ϵ=1, v=1. Then we get these values
Then we let ξ1=maxk=1,2,3{ξ(0)k}=5.1923, ξ2=maxk=1,2,3{ξ(0.01)k}=5.3821, ξ3=maxk=1,2,3{ξ(0.03)k}=8.4266.
Therefore, we obtain the following relationship for every local behavior dynamics when k=1,2,3 corresponding to the Definition 3
for any x(t),y(t)∈Rn.
We consider 18 nodes network and each subetaoup contains six nodes, and the local behavior dynamics for each group are shown in above, then we denote the relationship network structure's Laplacian matrix corresponding to the relationship network is defined as
where {{
}} {{
}} Then we select the intra-group enhancement factors c1=32,c2=35,c3=50.
Then, we select the parameters in the epidemic system, and let the natural death rate as μ=0.5, the awareness coefficients for each group denote as α1=0.2,α2=0.15,α3=0.2, and the infective rates b1=0.06,b2=0.05,b3=0.06. And the dispersal matrix for the susceptible individuals denote as
Select S01=5,S02=7,S03=6. Then we can verify the condition (H1) holds as
Then, the disease-free equilibrium can be derived as
so that one can get
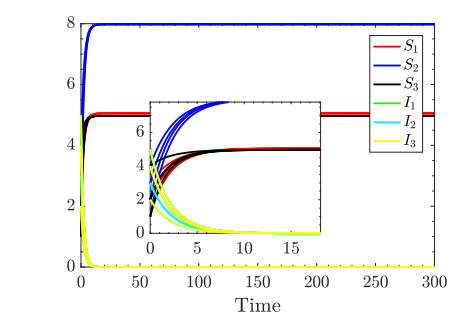
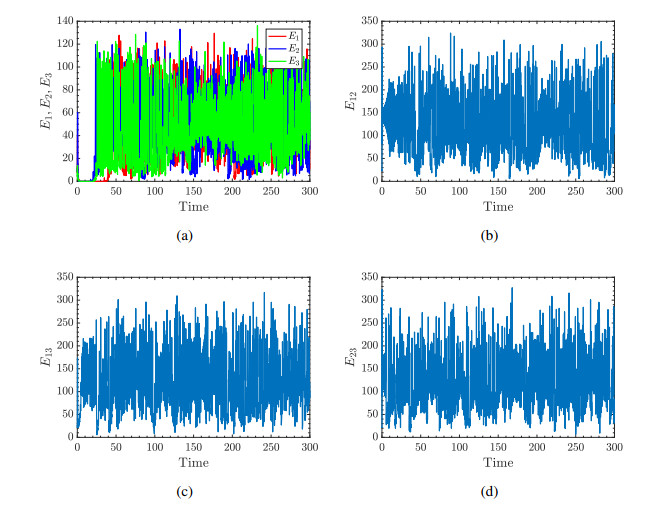
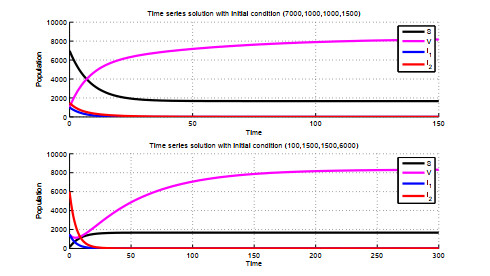
thus they are all less than 1, so E0 is globally asymptotically stable from the Theorem 1. When select any 4 different initial values for the epidemic systems, then the state graphs for the epidemic system under the different initial values are shown in Figure 2, in which we use different colors to reveal the different state variables for susceptible and infective individuals, that is to say, the same color curves represent the same state variable curves with different initial values. In Figure 2, the infective states curves all trend to the zeros states and the susceptible states curve trend to positive stable states, which means that the states of susceptible and the infective all trend to the stable one, i.e., the disease-free equilibrium E0. Meanwhile, the behavior states are not synchronization under this time due to the controllers unworked ultimately, and the errors between states and target are shown in Figure 3, in which neither the intra-group behaviors nor between-group behaviors trend to synchronization, i.e., the corresponding errors curves toward nonzero, where the intra-group errors and the between-group errors are defined as Ek=√∑i,j∈K‖xi(t)−xj(t)‖2,k=1,2,3, E12=√∑6i=1∑12j=7‖xi(t)−xj(t)‖2, E13=√∑6i=1∑18j=13‖xi(t)−xj(t)‖2, E23=√∑12i=7∑18j=13‖xi(t)−xj(t)‖2, respectively.
When we reset the αk, μ and bk,k=1,2,3, such as α1=0.2,α2=0.1,α3=0.15, μ=0.4, b1=0.6, b2=0.8, b3=0.7. In this situation, the (H1) also holds. And we can compute that
which means that R_0k>1 for k=1,2,3. Then from the Theorem 1, one can claim that the disease-free equilibrium is unstable. Further, one obtain that ˜R0k=S0kαkbkμ+∑j≠kbjk>1,k=1,2,3, where
Therefore, according to the Theorem 1, there are positive equilibrium, and E∗=(S∗1,I∗1,S∗2,I∗2,S∗3,I∗3)=(3.3333,1.756,5,2.9286,3.8095,1.1726).
Select the θ=2, and only added controllers to first three nodes in each subetaoup, and the control strength for each group's nodes are selected as
In addition, the cofactor can also be computed as ˆc1=0.0083,ˆc2=0.0101,ˆc3=0.0871.
Then, according to the Remark 4, the conditions in the Theorem 2 can be verified easily, and when k=1,2,3, there are
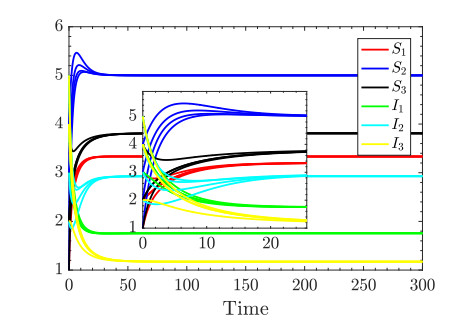
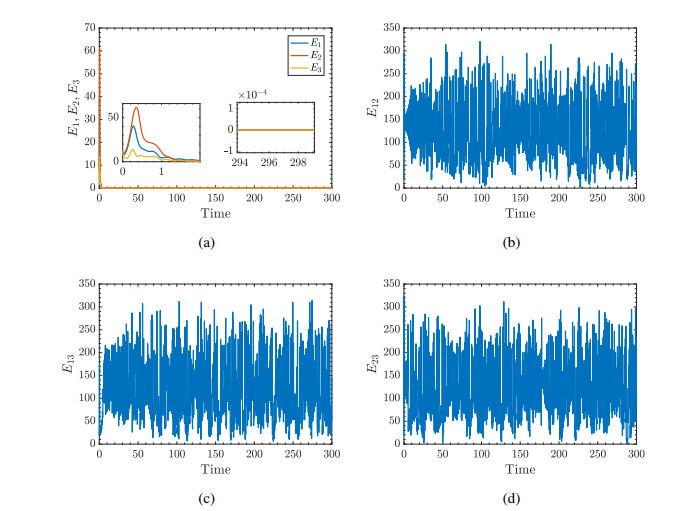
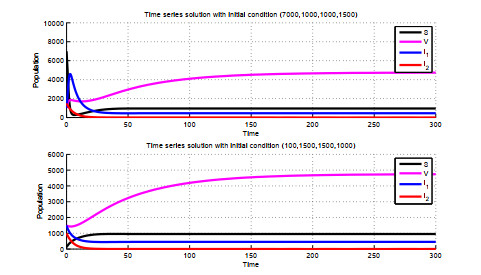
With these parameters, the epidemic states' curves can be shown as in Figure 4, meanwhile, the behavior errors curves are also shown in Figure 5. In this situation, we also use 4 different initial values for the epidemic systems as given in the case of disease-free, and as shown in Figure 4, one can see that the susceptible states' curves and infective states' curves under different initial values all trend to the same stable nonzero constant states with the time goes on, ultimately. In other words, the positive equilibrium is globally asymptotically stable. As well as the behavior states errors in Figure 5 can achieve the desired states, which means that the behavior errors in the same subetaoup achieve the behavior synchronization, such as the first subfigure in Figure 5 with each subetaoup's behavior errors states curve trending to zeros, ultimately, and the other three subfigures representing the errors among different subetaoup do not trend to zeros. It is to say that the nodes intra-group achieve behavior synchronization, while the between's ones are not.
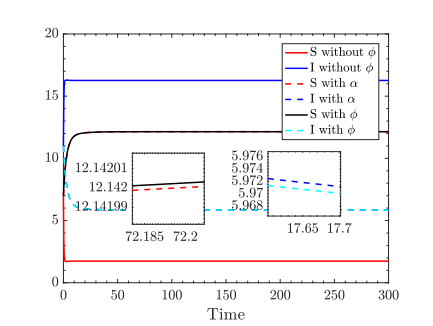
Besides, the simple comparison about the effectiveness of behavior awareness to epidemic states is also shown. Under the situation of positive equilibrium existing, and the parameters are same as in corresponding cases, we compare three cases about the infected term in each patch, such as bkSk(t)Ik(t), αkbkSk(t)Ik(t) and ϕk(t)bkSk(t)Ik(t), for k=1,2,3, respectively. And plotting their states' curves as shown in Figure 6. There are different marked states' curves corresponding to represent distinct cases, and one can see the stable infected states with cofactor α and ϕ before incidence are lower than the without cases, i.e., the cofactor is 1. And comparing the effect among α and ϕ, we see that their curves are almost the same, but the susceptible curves with ϕ is upper than the α curves and the infected curves with ϕ are lower than the one with α. Which means that there exists tiny difference in effect between α and ϕ that can not ignore. Those two cases trend to the same stable states, ultimately. This also shows that the behavior of individuals can impact the process of epidemic.
Remark 6. Notice that from the range of αk and ϕk, we get bkSk(t)Ik(t)>αkbkSk(t)Ik(t)>ϕk(t)bkSk(t)Ik(t), which means the numbers of infected individuals in the unit time under the later two cases are less than the first case. From Figure 6, and under the influence about parameters αk and ϕk, the infected number level are becoming lower. Furthermore, when errors of behavior trend to zero, then ϕk trend to αk, so, their ultimate states will be same, while the process may not the same due to the ϕk contains behavior pattern.
Remark 7. To be notice that in our simulation part, we just list some parameters values in systems to demonstrate our main results and it is not based on the practical data. In the future work, there will be a trying direction to introduce the real epidemic disease data to simulation and even forecast the disease trend, such as the COVID-19 spread. And structure about the real relationship network is a vast work that will be our aim in the next work.
5.
Conclusions
In this paper, we investigate the problem about behavior pattern cluster synchronization aroused by patchy epidemic transmission based on external feedback pinning control strategy, in which the coupled models combined with behavior synchronization systems and patchy dispersal epidemic systems with constant population are constructed, where so called contact willing functions are introduced in the epidemic systems and the dispersal is only concerned among the susceptible. Firstly, in view of the constant population the boundedness is obvious, and the nonnegativity is also discussed by the qualitative analysis for epidemic systems. And then we concern the stability of disease-free equilibrium for the patchy epidemic systems and obtain the patchy related conditions that guarantee globally asymptotically stable by using the Lyapunov analysis method. As well as, conditions that insure the existence of positive equilibrium for epidemic systems are also derived. Next, behavior pattern cluster synchronization aroused by patchy epidemic disease under the case of disease spreading, as well as the global stability of positive equilibrium for epidemic systems are addressed at the same time by means of Lyapunov function and the Lyapunov stable theory, meanwhile, sufficient criteria, related to the structure of inner-group relation, dispersal matrix of the susceptible and scale of diseases, making individuals to achieve behavior pattern cluster synchronization, are derived. The simulation example is exhibited to demonstrate the effectiveness of the main results obtained here.
Acknowledgments
This work was jointly supported by the NSFC grants under Grant Nos. 11572181 and 61873171.
Conflict of Interests
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: