Model of strategy control for delayed panic spread in emergencies

1.   Introduction

In recent years, emergencies have frequently occurred such as stampede events ^[1], infectious diseases ^[2,3] and disruptive political rallies ^[4], which put a psychological burden on the public and have a serious negative impact on society ^[5]; such events also cause the spread of negative emotions such as panic and anxiety in groups ^[6,7,8]. Therefore, it is of great importance to reduce the damage and harm caused by emergencies.

Epidemiological models were used to study information transmission ^[9] and emotion ^[10] and rumour spreading ^[11] because of their unique characteristics. Based on an epidemiological model, the SIR-UA dynamic system was developed to analyze the possibility of the spread of conscious information, which allows the probability of infection to be reduced and recovery to be accelerated through appropriate behavior ^[12]. In combination with complex networks, a layered SIRS model was developed to analyze the impact of online opinions on information spread ^[13]. To explore the role of population topology in the spread of panic, a new network model was proposed to simulate the interactions between virus propagation and patch propagation, taking into account a central node and a multiplex network ^[14]. Considering the interaction of information dissemination with epidemic spreading and the partial mapping between two-layered networks, the kinetic equations of epidemic dynamics were obtained using the micro Markov chain method to establish the disease related information dissemination in favor of suppressing the outbreak of epidemics ^[15]. For COVID-19, which has been rampant in recent years, the relative risk of infection with the virus can be assessed by probabilistic epidemiological models in the initial stages, for which data and literature are scarce ^[16]. There are some discrete situations in the real life. Hence, to simulate the evolution of the spread of COVID-19, a non-Markovian SIR epidemic spread model was developed and numerically validated for both continuous and discrete situations ^[17]. Note that viruses have incubation periods. The SNIS model was developed and the impact of various strategies on the epidemic spreading process was analyzed ^[18]. In the case of epidemic diseases, the government should take feasible measures in the initial stage so that a disease-free state can be achieved more quickly ^[19]; maintaining a certain social distance can also control the spread of the disease ^[20].

In reality, the essence of natural phenomena is complex and nonlinear. Therefore, nonlinear systems can be used to study these ^[21]. For the epidemiological model of COVID-19, a continuous-time nonlinear control law synthesized by an exact feedback input‒output linearization method can be used to establish a vaccination strategy and, thus, gradually track the recovery population ^[22,23]. It is difficult to obtain the numbers of susceptible and infected individuals, so vaccination control can be generated from relevant information provided by an observer ^[24]. Since there are many lurkers, i.e., groups with infectivity but no symptoms of infection, continuous-time SEIR models with a distributed delay can be developed to analyze the feedback effects of groups under vaccination rules ^[25]. A SEIR-type epidemic model with time delay and vaccination control under a basic reproduction number was investigated to determine the presence or absence of vaccination control ^[26]. Discrete phenomena are common in life; therefore, Micken's discretization method was used to build the SEIR model, and an implicit approach was applied to construct the observer of the model and analyze the asymptotic stability of the observer for validity ^[27]. To explore the reasons for disease mortality, the SEIR epidemiological model was considered for discretization and control and an impulse inoculation strategy adjusting the free parameters was designed to ensure the positivity of the model ^[28]. The production and provision of vaccinations was controlled by the government ^[29] and the number of infected individuals can be controlled well by inventions such as the vaccination ^[30]. Nonlinear system control is used to analyze epidemic models and, currently, there are variable structure control ^[31,32] and fuzzy control guidelines ^[33] in addition to exact linearization methods. To establish prevention strategies effectively, it is crucial to explore the evolution of the virus ^[34]. Whether it is the spread of viruses or negative emotions, the aim of developing prevention strategies effectively to control them is to make the infected population decrease or even disappear ^[35]. To achieve this aim, the costs and the elimination of the infection are controlled according to the Ponterian principle of minimal values in optimal control theory, i.e., isolation and treatment of infected individuals ^[36].

Some research has shown that emotion can spread in groups. Based on data from the Framingham Heart Study ^[37], it was concluded that emotion could spread through social networks like an epidemic, which is very similar to the process of spreading emotions during emergencies ^[38]. An improved SIRS model of panic propagation was developed under self-organizing circumstances to simulate that panic caused by subway emergencies can spread rapidly and have an adverse impact on the society ^[39]. In emergency, emotion plays an important role in the decision making of an individual. Based on cellular automata and the SIR epidemic model, the CA-SIRS model was proposed to simulate the dynamics of emotional contagion in crowds ^[40]. The model of emotional contagion and the control of personality integrated the effects of individual personality and interpersonal relationships, according to the epidemic model that simulated crowd queuing ^[41]. Individual panic behavior in emergencies is contagious and leads to collective panic behavior, which can be particularly destructive. An ILSAR panic spreading model was proposed to describe the dynamics of panic propagation in real emergencies ^[42]. When emergencies occur, the government should set up strategies to control the spread of panic. Research on emergencies can provide guidance to the government in developing programs and strategies in response to emergencies.

In summary, it is necessary to explore the transmission mechanism and decision-making behavior of panic in the group under emergencies. Therefore, the combined approach of modeling and numerical simulation is adopted for the research in this paper. Based on epidemic models, there are researchers who have explored the spread process of emotion under emergencies and analyzed its dynamical behavior. Thus, the spread of panic in emergencies can be simulated by classical epidemic models. However, in natural and social phenomena, trends depend not only on the current situation but also on past development dynamics. Thus, the introduction of a time delay can effectively describe the dynamical behavior of the model. The main work of this paper is shown below:

(Ⅰ) A SEIR delayed panic spread model is established, which introduces a time delay between susceptible and exposed individuals and considers the infection rate of panic as a time-varying variable.

(Ⅱ) A government strategy is proposed in this paper to control the spread of panic.

(Ⅲ) The control strategy is to use the exact linearization of nonlinear control systems. The control law for the system is determined and its stability is proven.

(Ⅳ) Simulation of the proposed strategy to control the spread of panic to verify theoretical results.

The rest of the paper is organized as follows. In Section 2, a SEIR delayed panic spread model is developed and the basic reproduction number of the model is obtained. The feedback linearization approach is used to obtain the control law of the model for the government strategy in Section 3. In Section 4, we simulate the control of the government strategy under emergencies. A short conclusion is given in Section 5.

2.   SEIR delayed panic spread model

In the emergencies, motivated by ^[23], the total population $N(t)$ can be divided into four compartments. $S(t), E(t), I(t)$ and $R(t)$ are defined as the susceptible (people who are susceptible to the spread of panic), exposed (people who have only symptoms of infection without the ability to spread panic), infected (people who can spread panic) and recovered individuals (people who know panic but never spread panic) at time t, respectively.

According to the SEIR epidemic model (where S denotes susceptible people, E denotes exposed people, I denotes infected people and R denotes recovered people), the SEIR delayed panic spread model is constructed and some parameters are chosen. All of these parameters are nonnegative. The detailed explanation is summarized in Table 1.

In the process of panic spread, $\beta (t)$ denotes the infection rate of panic, which responds to the rate of the spread of panic in the group. In previous studies of spread models, infection rate of panic $\beta (t)$ has been used as a fixed parameter in the construction of the model ^[43,44]. In this section, we consider that the infection rate is not a fixed value due to changes in the external environment. Therefore, it is more realistic to consider the rate of spread of panic $\beta (t)$ as a time-varying variable by setting it to increase with the number of infected individuals and automatically decay with time. The formula is shown as follows:

In Eq (1), $\lambda$ is an increasing ratio with the number of infected. $\delta$ is the ratio of panic disappearing.

In the real world, the trends of matter development are related not only to the current situation but also to past development dynamics. Therefore, time delay is introduced to describe this phenomenon ^[45]. Consider that there is a delay effect $\tau$ between the transformation of susceptible individuals to exposed individuals in this paper.

In the group, the changes in the four compartments, susceptible, exposed, infected and recovered, are described and are shown as follows:

There are ${d_e}N[1-u(t)]$ individuals into the group, then the susceptible individuals contact the exposed individuals. The exposed group at moment $t - \tau$ is infectious at moment t and the susceptible and exposed group share a transmission medium. The number of transformed individuals is $\beta (t)\frac{{S(t)I(t - \tau)}}{N}$. The number of people who leave the group due to death rate is ${d_e}S(t)$. The number of recovered individuals transformed into susceptible individuals is $wR(t)$ because they do not have permanent immunity. Therefore, the trend of change of susceptible individuals can be shown as follows: ${d_e}N[1-u(t)] - \beta (t)\frac{{S(t)I(t - \tau)}}{N} - {d_e}S(t) + wR(t)$.

There exists a time delay in the transformation process between the susceptible and exposed group and the number of transformations into exposed group is $\beta (t)\frac{{S(t)I(t - \tau)}}{N}$. At the same time, exposed individuals will be removed from the group due to death rate by the number of ${d_e}E(t)$. The number of exposed individuals who will change to recovered individuals due to recovery rate is $\theta E(t)$. The number of exposed individuals who will change into infected individuals with the ability to become infected is $\mu E(t)$, then the trend of exposed individuals can be expressed as $\beta (t)\frac{{S(t)I(t - \tau)}}{N} - ({d_e} + \mu + \theta)E(t)$.

The number of infected individuals who will transform into exposed individuals with panic but without the ability to transmit due to exposed individuals probability is $\mu E(t)$. Due to the recovery rate, the number of infected individuals who will become rehabilitated is $\gamma I(t)$. The number of people who will be removed from the group due to their own mortality is ${d_e}I(t)$. Therefore, the change trend of infected individuals can be expressed as: $\mu E(t) - ({d_e} + \gamma)I(t)$.

Due to the strategy control adopted by the government, the recovered group tracks the whole group asymptotically with the number of ${d_e}Nu(t)$. Owing to the recovery rate, there is a conversion of exposed individuals to recovered individuals in the number of $\gamma I(t)$. The number of infected individuals who will transform into recovered individuals due to recovery rate is $\theta E(t)$. The recovered individuals are removed from the group by the probability of person death by the amount of ${d_e}R(t)$. The recovered individuals are not permanently immune and can become susceptible individuals again in the amount of $wR(t)$. Thus, the trend of recovered individuals can be expressed as: ${d_e}Nu(t) + \gamma I(t) - ({d_e} + w)R(t) + \theta E(t)$.

Notation $R_{0 + }^n$ denotes the first closed $n$th real orthant, while $R_ + ^n$ denotes the first open $n$th real orthant. $x \in R_{0 + }^n$ denotes a positive real $n$-vector and all its components are nonnegative, and ${R_{0 + }}$ is used instead of $R_{0 + }^1$ for scalar.

Based on this, a SEIR epidemic model with time delay and strategy control is developed, which is expressed as the following functional differential equation:

In the Model (2), $u(t)$ can be seen as the control strategy used by the government in emergencies. The total population dynamics can be obtained by summing up the first four equations on both sides of Model (2), yielding: $\dot S(t) + \dot E(t) + \dot I(t) + \dot R(t) = \dot N(t) = 0$ so that the total population $N(t) = N(0) = N$ is constant at any time. For Model (2), supposing that the death and birth rates are the equal, the total population may be considered constant for all time $\forall t \in {R_{0 + }}$.

We consider Model (2) with initial conditions:

When $u(t) = 0$, the government does not take control measures and the positive invariant set of Model (2) is obtained:

According to reference ^[46], the basic reproduction number of Model (2) is obtained as

3.   Strategy control

In emergencies, the spread of uncertain information triggers group panic. In this situation, the government should take corresponding measures to reassure the group at once in response to this emergency. In this section, the aim is to design a strategy control $u(t)$ that can be adopted by the government by which the group of recovered people will asymptotically track the whole population. In other words, as time passes, infected people will disappear from the group. Exact linearization, a method using differential geometry as a tool developed in nonlinear control systems, is used to solve this system.

Model (2) can be written as the following nonlinear control affine system:

where $x(t) = {[\begin{array}{*{20}{c}} {I(t)} & {E(t)} & {S(t)} \end{array}]^T} \in R_{0 + }^3$, $y(t) = I(t) \in {R_{0 + }}$.$R(t) = N - I(t) - E(t) - S(t)$ is used with

where ${\beta _1}{\text{ = }}\frac{\beta }{N}$. Note that $\forall$$t \geqslant (i - 1)\tau, i = 1, 2, \ldots {x_{i\tau }}$ uses ${x_{i\tau }}(t) = x(t - i\tau)$ and ${u_{i\tau }}(t) = u(t - i\tau)$. In addition, ${u_{i\tau }}(t)$ satisfies $t \geqslant i\tau$.

From Eq (5), according to the theory of Lie derivatives ^[47] and obtained by calculation, ${L_g}h(x(t)) = {L_g}{L_f}h(x(t)) = 0$, while ${L_g}L_f^2h(x(t)) = - {d_e}\mu \beta I(t - \tau) \ne 0$. Therefore, the relative degree of the system (4) is three in $D = \{ {[\begin{array}{*{20}{c}} {I(t)} & {E(t)} & {S(t)} \end{array}]^T} \in R_{0 + }^3|I \ne 0\}$, i.e. $\forall x \in D$; that is, there is a relative degree equal to the dimensionality of the state space. Thus, the nonlinear coordinate change is defined as follows:

For the neighborhood of any $\forall x \in D$, in regular form it is represented by the model

where $x(t) = {[\begin{array}{*{20}{c}} {\bar I(t)} & {\bar E(t)} & {\bar S(t)} \end{array}]^T}$, and

where

By calculation, the reverse transformation is obtained as

Theorem 1 The state feedback control law is defined as

Around any point $\forall x \in D$, ${\lambda _0}, {\lambda _1}, {\lambda _2}$ satisfies the linear closed-loop dynamics and is given by

Proof. The state equation for the closed-loop system can be represented in the following form:

Considering control law (10) and system (7) and taking into account coordinate transformation (6), ${L_g}L_f^2h(x(t)) = - {d_e}\mu \beta I(t - \tau) \ne 0$ is satisfied. In addition, by calculation we obtain

We adopt the form of $\bar x(t)$ to define the coordinate transformation $L_f^3h(x(t))$ in the state space, which yields $L_f^3h(x(t)) = \psi (\bar x(t))$. Thus, the state equation of the closed-loop system under $\bar x(t)$ can be expressed as

Parameters ${\lambda _0}, {\lambda _1}, {\lambda _2}$ must to be designed.

Remark 1 Since the control law $u(t)$ is defined for all $x \in R_{0 + }^3$, we consider the infection will disappear when the number of infected people is strictly greater than zero and smaller than one individual. Hence, the control measure may be stopped when $0 < I(t) < \varepsilon < 1$. Therefore, an effective control law can be expressed as

where ${t_f} \triangleq \min \{ t \in R_0^ + |I(t) < \varepsilon {\kern 1pt} {\kern 1pt} {\kern 1pt} for{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} some{\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < \varepsilon < 1\}$.

Remark 2 The parameters ${\lambda _0}, {\lambda _1}, {\lambda _2}$ depend on the roots of the closed-loop system (11) characteristic polynomial $P(s) = Det(sI - A)$, where ${r_i}(i = 1, 2, 3)$ are the desired roots of $P(s)$. If the closed-loop system (11) is asymptotically stable, then the characteristic roots of $P(s) = (s + {r_1})(s + {r_2})(s + {r_3})$ have negative real parts, then the values ${\lambda _0} = {r_1}{r_2}{r_3}$, ${\lambda _1} = {r_1}{r_2} + {r_2}{r_3} + {r_1}{r_3}$, and ${\lambda _2} = {r_1} + {r_2} + {r_3}$ are greater than zero.

The control law (10) can be written as

The control law is an equation with a delay, so we must ensure that $S, E, I, R$ are nonnegative. Thus, the parameters ${\lambda _0}, {\lambda _1}, {\lambda _2}$ are chosen such that ${r_i}(i = 1, 2, 3)$ must satisfy Theorem 2.

Theorem 2 Note that Model (2) with initial condition (3) and ${r_1}, {r_2}, {r_3}$ must satisfy the following conditions:

(1) ${r_1} \leqslant \min \{ {d_e} + \gamma, {d_e} + \mu + \theta \}$, ${r_2} = {d_e} + \gamma$, ${r_3} \geqslant \max \{ {d_e} + \gamma, {d_e} + \mu + \theta \}$ and ${r_1} < {r_2} < {r_3}$,

(2) $({r_3} - {r_1})({r_3} - {d_e} - \gamma) - \mu \beta \geqslant 0$, ${r_1} + {r_3} > 2{d_e} + \mu + \theta$,

${r_1}{r_3}{ \geqslant _1}({r_1} + {r_3})({d_e} + \mu + \theta) - (2{d_e} + \mu + \gamma + \theta)(\mu + \theta - \gamma) - {({d_e} + \gamma)^2}$.

Proof. The dynamics (11) of Model (2) can be specified in the state space defined by $\bar x(t) = {[\begin{array}{*{20}{c}} {y(t)} & {\dot y(t)} & {\ddot y(t)} \end{array}]^T}$ as in (14).

where ${r_1}, {r_2}, {r_3}$ are the eigenvalues of A, so it follows that ${c_1}, {c_2}, {c_3}$ can be obtained by the following equation

Equation (18) can be written as $R \cdot C = M$, where

The matrix R is the Vandermonde matrix. Thus, when ${r_1} \ne {r_2} \ne {r_3}$, R is an invertible matrix. By calculation, we have $C = {R^{ - 1}} \cdot M$.

If ${r_2}{r_3} - ({r_2} + {r_3})({d_e} + \gamma) + {({d_e} + \gamma)^2}{\text{ = }}0$, ${r_1} < {r_2} < {r_3}$, ${r_3} - {d_e} - \mu - \theta > 0$, ${d_e} + \gamma - {r_1} > 0$ and $I(0) > 0, E(t) > 0, S(t) > 0$, then ${c_1} = \frac{{\mu ({r_3} - {d_e} - \mu - \theta)E(\tau) + \mu {\beta _1}I(- \tau)S(0)}}{{({r_3} - {r_1})({d_e} + \gamma - {r_1})}} > 0$ and ${r_2} = {d_e} + \gamma$.

Since the ranges of ${c_2}$ and ${c_3}$ cannot be determined, the following four cases need to be discussed: (1) ${c_2} > 0, {c_3} > 0$; (2) ${c_2} > 0, {c_3} < 0$; (3) ${c_2} < 0, {c_3} \geqslant 0$; (4) ${c_2} < 0, {c_3} < 0$.

(Ⅰ) For the first two cases, i.e., ${c_2} > 0$, we obtain

(Ⅱ) For the case (ⅲ); that is, ${c_2} < 0$ and ${c_3} \geqslant 0$,

Because $I(0) \leqslant I(\tau), S(\tau) \leqslant N$, we have

where $I(\tau) - {c_3}{\kern 1pt} \geqslant 0$ holds when conditions (1) and (2) in Theorem 2 are satisfied.

(Ⅲ) For the case (ⅲ); that is ${c_2} < 0$ and ${c_3} < 0$, we calculate

By Eqs (11) and (19), we know that

Since ${r_2} = {d_e} + \gamma$, $E(t) = \frac{{{c_1}({d_e} + \gamma - {r_1}){e^{ - {r_1}(t - \tau)}} + {c_3}({d_e} + \gamma - {r_3}){e^{ - {r_3}(t - \tau)}}}}{\mu }$.

If ${c_3}({d_e} + \gamma - {r_3}) = \mu E(\tau) - {c_1}({d_e} + \gamma - {r_1})$, then

From the second equation in (25), we can obtain

From the fourth equation of Model (2) and $R({t_0}) = 0$, we know that

Since $S({t_0}) \leqslant N, \varepsilon \leqslant I({t_0}) \leqslant N, R({t_0}) \leqslant N$, we can obtain

If condition (2) of Theorem 2 holds, then $\dot R({t_0}) \geqslant 0$.

The parameters ${\lambda _0}, {\lambda _1}, {\lambda _2}$ are related to the roots ${r_1}, {r_2}, {r_3}$ of the closed-loop characteristic polynomial P(s). We can obtain

By calculation, control law (16) can be expressed in the following form:

If conditions (1) and (2) of Theorem 2 hold, then $u(t) \geqslant 1$.

In summary, a strategy control is designed for the control of governmental measures based on linearization control techniques for nonlinear systems in this section. Moreover, under Model (2) with initial condition (3), Theorem 2 holds. The control law is proposed to ensure that the panic disappears after moment t_f.

4.   Simulation results

4.1.   Numerical simulations

We select parameters ${d_e} = 0.001$, $\mu = 0.4$, $\gamma {\text{ = }}0.4$, $\theta = 0.0006$, $w = 0.1$, $\lambda = 0.01$, $\beta = 0.2$ and $N = 1000$ to study the evolution of the SEIR delayed spread model. The initial values are chosen as $(S(t), E(t), I(t), R(t), \beta (t)) = (800, 60,100, 40, 0.5)$.

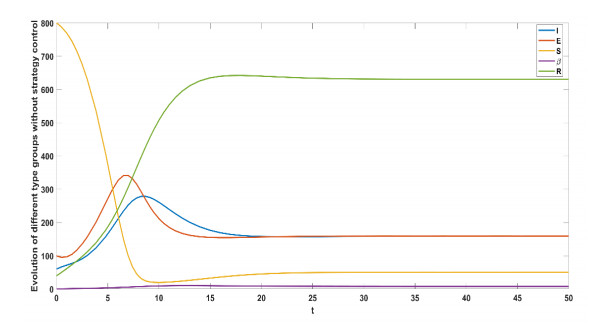
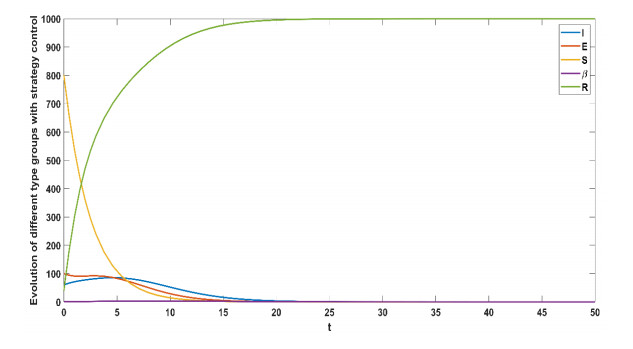
Figure 1 shows the evolution process of Model (2) without strategy control. In the initial stage, the number of susceptible people sharply, the exposed people, infected people and recovered people show a rapid increase in a very short time. The model tends to reach equilibrium as time passes. To make the panic disappear, we should adopt a corresponding strategy control. Figure 2 depicts the evolution of the different groups under strategy control.

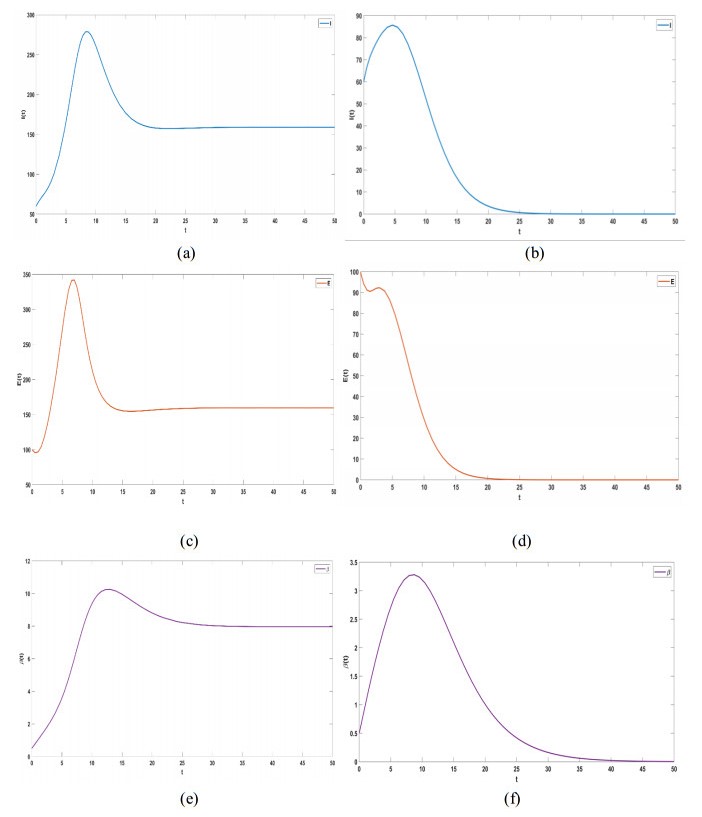
The aim of Figure 3 is to contrast the exposed people, infected people and the trend of panic under control with and without strategy control to illustrate the effectiveness of strategy control. There are four types of the group, susceptible, exposed, infected and recovered individuals, as shown in Figure 3(a) and (c). It shows that the panic has not disappeared, as shown in Figure 3(e). Both the exposed and the infected individuals eventually converge to zero, as shown in Figure 3(b), (d) and (f). i.e., the panic disappears and the recovered group tracks the whole group asymptotically. Strategy control is effective.

From Figures 1–3, we can derive that there are some differences in the process of population evolution with and without strategy control. It is concluded that the strategy control adopted by the government makes panic disappear within the group, indicating that strategy control should play an important role in the control of panic. Therefore, when an emergency occurs, the government responds quickly and releases official information to calm the public panic.

4.2.   Numerical simulations with different delays

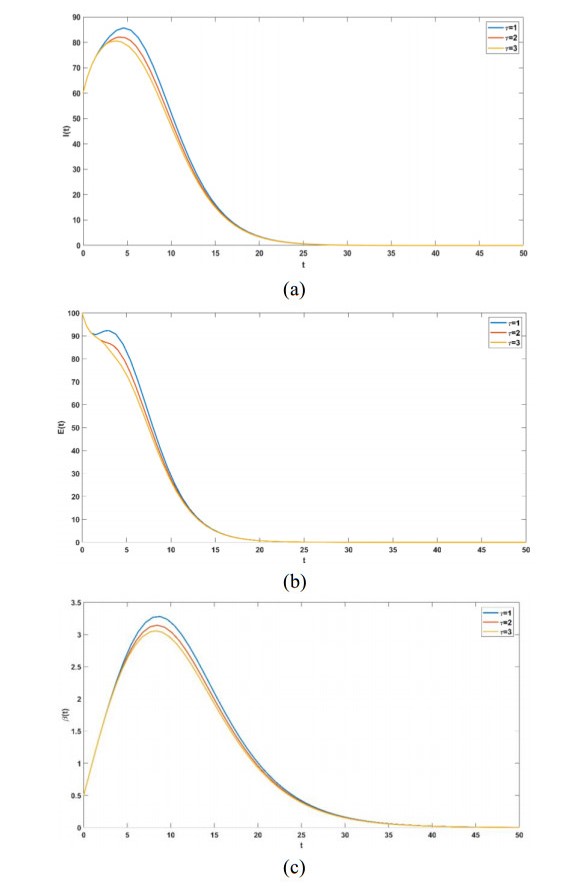
In this section, we simulate the influence of different time delays on infected individuals, exposed individuals and the spread ratio of panic in the model with and without strategy control. The time delay $\tau$ takes different values ($\tau = 1, 2, 3$).

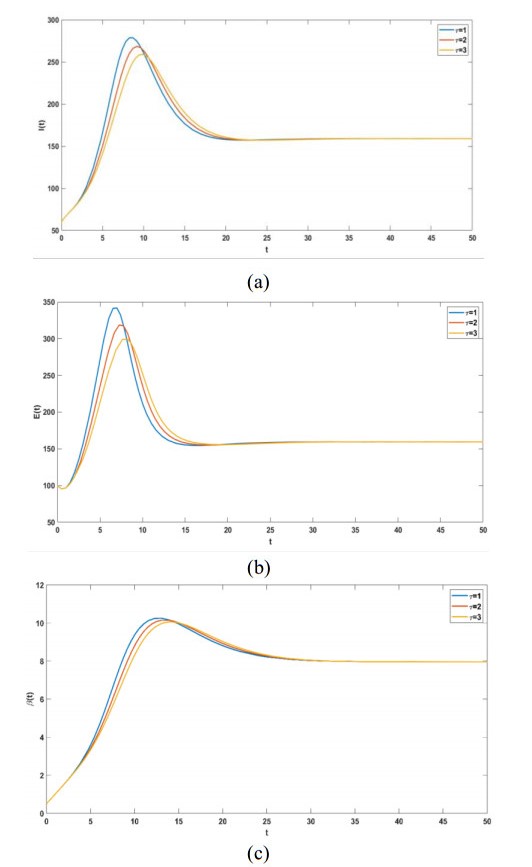
Figure 4 simulates the effect of different time delays on the model with no control strategy. As can be seen from Figure 4, in the initial stage of emergency, infected people, exposed people and the spread ratio of panic show a rapid increase in a very short time. The model ultimately reaches a stable state over time. As the time delay increases, the peak of infected people, exposed people and the spread ratio of panic decreases.

The aim is to make panic disappear. Thus, Figure 5 illustrates the effect of delay on the exposed, infected and panicked groups with different delays $\tau$ ($\tau = 1, 2, 3$). We observe that the trend of exposed, infected and panicked decreases as $\tau$ increases, and the same is true for the peak (see Figure 5(a), (b) and (c)).

It is observed from Figures 4 and 5 that the peak of each group decreases as time delay increases with and without strategy control. However, the number of groups under strategy control is smaller than without strategy control, as shown in Figures 4(a) and 5(a), Figures 4(b) and 5(b) and Figures 4(c) and 5(c). Moreover, the adoption of strategy control makes the number of infected people, the number of exposed people and the spread ratio of panic disappear and drop to zero within the groups, indicating that strategic control is effective. Therefore, a longer delay, i.e., a longer latency period, can reduce the number of infected individuals and effectively control the spread of panic.

4.3.   Sensitivity analysis

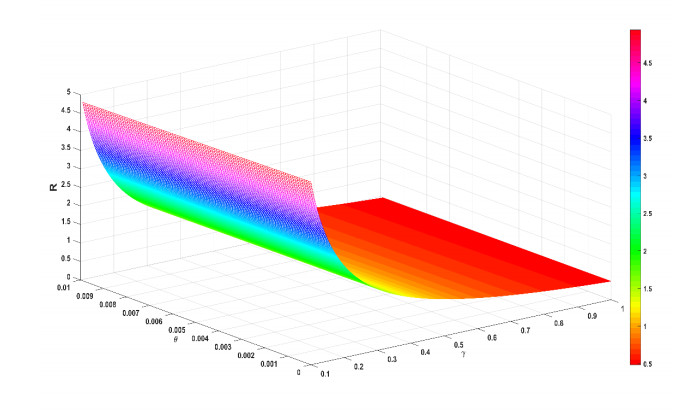
The basic reproduction number is an important standard of the presence of panic within the group, to which we perform sensitivity analysis. We analyze the dependence of the basic reproduction number $R$ on $\theta$ and $\gamma$ and obtain

If $\frac{{\partial R}}{{\partial \theta }} < 0$ and $\frac{{\partial R}}{{\partial \gamma }} < 0$, then they are monotonically decreasing; i.e., the basic reproduction number decreases as $\theta$ and $\gamma$ increase, as shown in Figure 6. Therefore, the rate of recovery and rehabilitation of the population is important to eliminate panic. When an emergency occurs, the government takes measures (releasing information about the event and its progress) so that individuals in the group can be transformed into recovered individuals more quickly due to the timely response of the government, i.e., the rate of recovery and rehabilitation of the population can be increased. Therefore, the government can achieve exactly this goal by control measures.

5.   Conclusions

This paper presented a type of strategy control for reducing the spread of panic in groups in emergencies. Based on an epidemiological model, a delayed SEIR model was developed taking into account delay and the time-varying panic rate. The spread of false or uncertain information in a group in an emergency leads to group panic. The government should take corresponding strategy control to counteract this. Our aim was to make the exposed, infected and panicked individuals disappear from the group, which the recovered group asymptotically tracked the whole group. Therefore, we take an exact linearization approach for the nonlinear system to design the control law and prove its stability. We simulated the evolution of the model with and without strategy control, and the simulation results are consistent with the theoretical results. At present, the reason for numerical simulations is that there are no databases to find out the real data on the spread of panic under emergencies. At the same time, there are no conditions for obtaining experimental data because real scenarios are complicated and difficult to simulate. Moreover, since the simulation results rely heavily on experimental data, the accuracy of experimental data is very high and the flexibility and adaptability are very poor. Thus, the application of experimental data to explore the propagation mechanism of emotions needs to be further explored. The spreading model established in this paper is a continuous model, but there is much discrete phenomena in the real life. The problems related to discrete were also the major research topic. Therefore, it is necessary to establish discrete epidemic models to explore the transmission mechanism of emotions in future research. In this paper, we studied the evolutionary process of panic in the group from a macroscopic perspective. In future research, we will analyze the individual-individual interactions and visualization at a microscopic level. Thus, a combination of macroscopic perspective and microscopic perspective was used to simulate crowd evacuation in emergencies.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by Natural Science Foundation of China (71771112) and Project of Liaoning Provincial Federation Social Science Circles of China (L20BGL047).

Conflict of interest

The authors declare there is no conflict of interest.