A cholera transmission model incorporating the impact of medical resources

In Memory of Geoffrey J. Butler and Herbert I. Freedman

1.   Introduction

Cholera has been endemic in South Asia, Central America, and a number of countries in Africa, remaining a significant threat to the public health in these places. A water- and food-borne disease caused by the bacterium Vibrio cholerae, cholera can be transmitted either from the contaminated aquatic environment, or through the human-to-human contact ^[1,2]. Currently in its seventh pandemic, cholera continues devastating populations in developing countries, particularly those places where sanitation facilities and access to clean drinking water are limited. Large-scale cholera outbreaks in recent years, such as those in Zimbabwe (2008–2009, with nearly 100,000 reported cases), Haiti (2010–2012, with 545,000 reported cases), and Yemen (2016–2018, with suspected cases exceeding 1 million), have received worldwide attention.

An important factor in the cholera epidemics and endemics in developing countries is that the medical resources are insufficient to meet the needs of fighting the cholera outbreaks. Indeed, one of the common characteristics among the recent, large-scale cholera outbreaks, including those from Zimbabwe, Haiti and Yemen, is the difficulty in providing an adequate medical response due to shortages in health professionals and medical supplies ^[3,4,5,6,7]. Consequently, massive surge of cases occurred in these outbreaks, underscoring the importance of medical resources in shaping the cholera epidemics.

Under normal situations, cholera is relatively easy to treat. Oral rehydration therapy using clear water and modest amount of salt and sugar has saved millions of lives and reduced overall case fatality rates below $1\%$ ^[8,9]. Antibiotics are used to treat severe infections, while their effects in mass administration are unclear as they contribute to increasing antimicrobial resistance ^[8]. In addition, cholera vaccines, especially the recently introduced two-dose oral vaccine that is less expensive and more convenient to deliver than its predecessor ^[10,11], have been effective in both the prevention and intervention of disease outbreaks. For many developing countries, however, the availability of medical resources significantly limits the implementation of these control measures. Antibiotics, vaccines and other medicine may not be available or may be in severe shortage compared to the demands. There may not even be sufficient clean drinking water, salt and sugar for the basic rehydration practice ^[7,12,13,14].

Due to the inadequate medical resources, the infection may rapidly spread, leading to unusually high prevalence and attack rates. The risk of transmitting cholera from the environment as well as among human hosts could be significantly increased. Meanwhile, as a result of insufficient medical treatment and sanitation and as a feedback of increased infection levels, human contribution (e.g., through shedding) to the environmental pathogen could also increase. These factors worsen and elongate the cholera epidemics.

There have been many mathematical models published for cholera ^{[5,15,16,17,18]}. These studies have emphasized the dual routes (environment-to-human and human-to-human) for cholera transmission, the impact of seasonal fluctuations on cholera dynamics, the role of the free-living water-borne pathogens, and the effects of media reports and awareness programs on cholera epidemics. The focus of the present paper, however, is to investigate how the availability of medical resources would impact the cholera transmission and shape the pattern of a cholera epidemic. To that end, we formulate a system of differential equations to describe cholera transmission dynamics, using a compartmental modeling approach. In addition to the typical compartments involved in cholera models (i.e., the susceptible hosts, the infected/infectious hosts, the recovered hosts, and the pathogen), we introduce another compartment to represent the strength, or availability level, of the medical resources. Our model will then describe the interaction among the hosts, the pathogen, and the medical resources, incorporating both direct and indirect transmission pathways. Particularly, several model parameters, including the direct and indirect transmission rates and the host shedding rate, will explicitly depend on the medical resources.

As an application of our model, we study the Yemen cholera outbreak during the period of April 2017 to May 2018. Yemen has experienced years of heavy conflicts and wars, severely disrupting the society and the public health infrastructure. In particular, 55% of the health facilities in Yemen are no longer fully functional ^[19]. In October 2016, a small cholera epidemic started in Yemen which, by March 2017, was apparently in decline. However, the outbreak resurged on April 27, 2017 and remained on-going since then, leading to the largest documented cholera epidemic of modern times. By the end of 2017, cumulative cases exceeded 1 million, and by May 2018, more than 1.1 million cases were reported ^[20]. We conduct data fitting of our model by using the weekly epidemiological reports published by the World Health Organization (WHO) ^[21]. We particularly emphasize the role of limited medical resources in shaping the Yemen cholera outbreak, by examining the data fitting results at both the national and governorate levels. Our findings contribute to deeper understanding of the transmission dynamics underlying the Yemen cholera outbreak, and provide useful guidelines for the design of future prevention and intervention strategies.

The remainder of this paper is organized as follows. In Section 2, we present the mathematical model and conduct a careful equilibrium analysis, studying both local and global stabilities. In Section 3, we apply our model to the Yemen cholera outbreak using data fitting and numerical simulation. In Section 4, we conclude the paper with some discussion.

2.   Model formulation and analysis

We use the following differential equations to describe the impact of available medical resources on cholera transmission:

Here $S$, $I$ and $R$ are the the numbers of susceptible, infected and recovered individuals, respectively, and $B$ is the concentration of the pathogenic vibrios in the environment. Meanwhile, $M$ denotes the strength (or, availability) of related medical resources and facilities, normalized to $0\le M\le 1$; these could include, in a broad (and abstract) sense, medicines, health centers, sanitation systems, etc. The parameter $\mu$ is the natural birth and death rate for the human hosts, $K$ is the half saturation concentration of the vibrios, $\gamma$ is the rate of recovery from cholera infection, and $\delta$ is the removal rate of vibrios from the environment. We neglect the disease induced death rate in our model, since the mortality rate for cholera is generally lower than $1\%$ ^[8]; in particular, the overall case fatality rate for the Yemen cholera outbreak from April 2017 to May 2018 is $0.21\%$ ^[20].

The parameter $\Gamma$ represents the outflux rate of the medical resources due to socioeconomic factors such as conflicts, wars, and economic collapse. Meanwhile, the availability of medical resources is stimulated by the disease prevalence at a rate $\eta$ (for example, through international assistance from WHO, CDC, UNICEF, etc.). We additionally assume that its self growth is described by a function $\lambda(M)$, which is introduced to ensure that a positive number of medical facilities and infrastructures are available at any time, as a minimal requirement of public health. The parameters $\beta_1$ and $\beta_2$ are the direct (or, human-to-human) and indirect (or, environment-to-human) transmission rates, respectively, and $\xi$ is the rate of human contribution (e.g., through shedding) to the environmental vibrios. We assume that $\beta_1 \,$, $\beta_2$ and $\xi$ all explicitly depend on $M$ and increase while $M$ decays, reflecting the impact of the collapsing public infrastructure on cholera transmission and spread. Specifically, we make the following assumptions on these three parameters:

(H1) $\beta_1(M)$, $\beta_2(M)$, $\xi(M)\in C^1[0, 1]$ and are all positive;

(H2) $\beta_1'(M)\le 0$, $\, \beta_2'(M) \le 0$, $\, \xi'(M)\le 0$.

We also assume that the function $\lambda(M)$ satisfies:

(H3) $\lambda(M)\in C^1[0, 1]$ and $\lambda'(M) < 0$;

(H4) $\lambda(0) > \Gamma > \eta N+\lambda(1)$.

The condition (H3) states that when the available medical resource ($M$) increases, its self-growth rate would decrease. The condition (H4) is introduced to ensure that $M$ remains in the range $[0, 1]$.

2.1.   Basic reproduction number

We will make use of the basic reproduction number ^[22], commonly denoted as $\mathcal{R}_0$, in the analysis of our model (2.1). Let us first determine $\mathcal{R}_0$ by the standard next generation matrix technique ^[23,24].

Note that $\lambda(M)$ is invertible since $\lambda'(M) < 0$. The system (2.1) has a unique disease-free equilibrium (DFE) at

The infection components in this model are $I$ and $B$. We find that the new infection matrix $F$ and the transition matrix $V$ are given by

It follows that the next generation matrix is given by

The basic reproduction number of model (2.1) is then defined as the spectral radius of the matrix $FV^{-1}$, and we find that

which provides a quantification of the disease risk during a cholera outbreak. The first term $\mathcal{R}_{01}$ comes from the direct transmission route, and the second term $\mathcal{R}_{02}$ represents the contribution from the indirect transmission route.

2.2.   Equilibrium analysis

We now analyze the equilibria of the system (2.1) which will provide essential information regarding the transmission dynamics of the disease. Let $(S, I, R, B, M)$ be an equilibrium of model (2.1), which satisfies the following equations

Solving (2.6) yields

Note that $\Gamma-\eta I > 0$ based on the condition (H4). It follows from $S+I+R = N$ that the third equation of (2.7) implies

Meanwhile, in view of the first equation of (2.7), we obtain

where

Let us now consider curves $S = \phi(I)$ and $S = \psi(I)$. In particular, any intersection of these two curves in $\mathbb{R}^2_{+}$ determines a non-DFE equilibrium. Note that

Using assumption (H2) and the fact $\chi'(I) = -\eta/\lambda'(\chi(I)) > 0$, we see that $h'(I)\le 0$. This implies that $\psi(I)$ is an increasing function. In contrast, $\phi(I)$ is strictly decreasing. Additionally, one can easily verify that $\psi(0) = N/\mathcal{R}_0$, $\; \phi(0) = N$, $\; \psi(N/a) > 0$ and $\phi(N/a) = 0$. Hence, we conclude:

$(1)$ If $\mathcal{R}_0 > 1$, these two curves have a unique intersection lying in the interior of $\mathbb{R}^2_{+}$, due to $\psi(0) < \phi(0)$ and $\psi(N/a) > \phi(N/a)$. Furthermore, at this intersection point, equation (2.7) yields $M, R, B > 0$ (since $I > 0$).

$(2)$ If $\mathcal{R}_0\le 1$, the two curves have no intersection in the interior of $\mathbb{R}^2_{+}$ as $\psi(0)\ge \phi(0)$.

Therefore, by equation (2.7), we find that the model (2.1) admits a unique equilibrium, the DFE, if $\mathcal{R}_0 \le 1$; and it admits two equilibria, the DFE and an endemic equilibrium (EE), if $\mathcal{R}_0 > 1$.

In what follows, we perform a study on the global stability of the DFE. By a simple comparison principle, we find that $0\le B\le B_{max}$ and $M_0\le M\le 1$, where $B_{max} = \xi(0)N/\delta$. Thus, it leads to a biological feasible domain

Theorem 2.1. The following statements hold for the model (2.1).

(1) If $\mathcal{R}_0\le 1$, the DFE of system (2.1) is globally asymptotically stable in $\Omega$.

(2) If $\mathcal{R}_0 > 1$, the DFE of system (2.1) is unstable and there exists a unique endemic equilibrium. Moreover, the disease is uniformly persistent in the interior of $\Omega$, denoted by $\mathring{\Omega}$; namely, $\liminf\limits_{t\to\infty} (I(t), B(t)) > (c, c)$ for some $c > 0$.

Proof. Let $\mathbf{x} = (I, B)^T$. One can verify that

where the matrices $F$ and $V$ are given in equation (2.3). Take $\mathbf{u} = (\beta_1(M_0)N, \; \beta_2(M_0)N/K)$. It then follows from the fact $\mathcal{R}_0 = \rho(FV^{-1}) = \rho(V^{-1}F)$ and direct calculation that $\mathbf{u}$ is a left eigenvector associated with the eigenvalue $\mathcal{R}_0$ of the matrix $V^{-1}F$; i.e., $\mathbf{u} V^{-1}F = \mathcal{R}_0 \mathbf{u}$. Let us consider a Lyapunov function

Differentiating $\mathcal{L}$ along the solutions of (2.1), we have

Case 1: $\mathcal{R}_0 < 1$.    The equality $\mathcal{L}' = 0$ implies that $\mathbf{u} \mathbf{x} = 0$. This leads to $I = B = 0$ by noting the positive components of $\mathbf{u}$. Hence, when $\mathcal{R}_0 < 1$, equations of (2.6) yield $S = S_0, \; M = M_0$ and $I = R = B = 0$. Therefore, the invariant set on which $\mathcal{L}' = 0$ contains only one point which is the DFE.

Case 2: $\mathcal{R}_0 = 1$.    The equality $\mathcal{L}' = 0$ implies that $\beta_1(M)SI = \beta_1(M_0)NI$, $\, \beta_2(M)S B/(B+K) = \beta_2(M_0)N B/K$ and $\xi(M)I = \xi(M_0)I$. Thus, either $I = B = 0$, or $B = 0$, $S = N$ and $\beta_1(M) = \beta_1(M_0)$ and $\xi(M) = \xi(M_0)$ hold. The former can proceed as above. Suppose the latter holds, then $\frac{dB}{dt} = \xi(M)I\equiv 0$ which implies $I = 0$. Once again this would yield the same conclusion as before.

Therefore, in either case, the largest invariant set on which $\mathcal{L}' = 0$ consists of the singleton $E_0 = (N, 0, 0, 0, M_0)$. By LaSalle's Invariant Principle ^[25], the DFE is globally asymptotically stable in $\Omega$ if $\mathcal{R}_0\le 1$.

In contrast, if $\mathcal{R}_0 > 1$, then it follows from the continuity of vector fields that $\mathcal{L}' > 0$ in a neighborhood of the DFE in $\mathring{\Omega}$. Thus the DFE is unstable by the Lyapunov stability theory. The last part can be proved by the persistent theory ^[26] which is similar to the proof of Theorem 2.5 in Gao and Ruan ^[27].

In addition, we have carried out an analysis on the global asymptotic stability of the endemic equilibrium. We remark that, in general, this would be a nontrivial task for an epidemic system of dimension higher than two. Our model (2.1) is essentially four-dimensional, after we remove the equation for $R$. We have managed to conduct the endemic stability analysis using the geometric approach based on the third additive compound matrix ^[28,29]. Below we first briefly describe this method.

The third additive compound matrix for a $4\times4$ matrix $A = (a_{ij})$ is defined as

Now consider a dynamical system

where $F: D\mapsto\mathbb{R}^n$ is a $C^1$ function and where $D\subset\mathbb{R}^n$ is a simply connected open set. Let $X(t, X_0)$ denote the solution of (2.13) with the initial condition $X(0) = X_0$. We assume:

(a1) There exists a compact absorbing set $K\subset D$;

(a2) The system (2.13) has a unique equilibrium point $X^*$ in $D$.

The linearized system of system (2.13) is

and the associated third compound system is

where $J^{[3]}$ is the third compound matrix of the Jacobian $J$ for equation (2.13).

Theorem 2.2. Assume that (a1), (a2) hold and there are a Lyapunov function $V(X, Z)$, a function $\kappa(t)$, and positive constants $c, k$, and $C$ such that

(i) $c|Z|\le V(X, Z)\le C|Z|, \; c\le\kappa(t)\le C$;

(ii) $V'\le(\kappa'(t)-k)V$,

where the total derivative $V'$ is taken along the direction of (2.15). Then the interior equilibrium $X^*$ of system (2.13) is globally asymptotically stable.

Proof. If $\kappa(t)$ is a constant, this is the case covered by Corollary 3.2 in ^[29]. For a general differentiable function $\kappa(t)$, the conclusion follows from a similar proof, since the modified Lyapunov function $\tilde{V} = V(X, Z)/\kappa(t)$ satisfies all the conditions to establish Corollary 3.2 in ^[29].

We now prove the main result in this section; i.e., the global stability of the endemic equilibrium, using the geometric approach described above. To simplify our notations, we will adopt the abbreviations

Furthermore, we will assume that each of these four functions is subject to saturation effects, a common assumption for disease-related rates, mathematically characterized by a non-positive second derivative.

Theorem 2.3. If $\mathcal{R}_0 > 1$ and the following inequalities hold for all $M\in[0, \; 1]$

then the unique endemic equilibrium of the system (2.1) is globally asymptotically stable in $\Omega$.

Proof. It is clear that the equation for $R$ can be decoupled from the system (2.1). As a result, we obtain a four-dimensional system associated with $S$, $I$, $B$ and $M$, for which the Jacobian matrix is given by

The third additive compound matrix of $J$ is

where

The associated linear compound system is

We need to show the uniform global stability of the linear compound system (2.17). To this end, we choose an associated Lyapunov function

where

It is easy to see that the following estimate hods

Based on the uniform persistence of the system, we see that there exist positive constants $c_1$ and $c_2$ such that

Meanwhile, note that $\beta_1, \; \beta_2 > 0$ for $M\in[0, \; 1]$, we can choose a small positive constant $k$ such that

Other than that, we have the following inequalities by (2.16):

Now, we can estimate the total derivative of $V$ along the trajectory of the compound system (2.17) by inequalities (2.20) and (2.21). We need to discuss the following cases.

Case 1: $V = V_1$. Then $B|Y|\le M|X|$, $\, I |Z+W| \le M|X|$. We have

Case 2: $V = V_2$. Then $I|Z+W|\le B|Y|$, and

Case 3-a: $V = I|Z+W|$. Then $M|X|, B|Y|\le I|Z+W|$, and

Case 3-b: $V = I|Z|$. Then $|W|\le|Z|, \; \; M|X|, B|Y|\le I|Z|$, and

Case 3-c: $V = I|W|$. Then

Now, let $\kappa(t) = \ln(IBM)$. Then it follows from (2.22) to (2.26) that the following inequality hods

In view of the uniform persistence, we can actually choose $c_1$ and $c_2$ from (2.19) such that

for sufficiently large $t$. Therefore, we conclude from (2.19), (2.27), (2.28) and Theorem 2.2 that the endemic equilibrium of the system (2.1) is globally asymptotically stable.

Essentially, the stability results in Theorems 2.1 and 2.3 establish $\mathcal{R}_0 = 1$ as a forward transcritical bifurcation point, or, a sharp threshold for disease dynamics, and indicate that reducing $\mathcal{R}_0$ to values at or below unity will be sufficient to eradicate the disease. In other words, the cholera model (2.1) exhibits regular threshold dynamics.

3.   Numerical results

In order to verify our mathematical modeling framework, we apply our model to study the recent cholera outbreak in Yemen, where heavy conflicts and wars have led to a collapsed public health system and severe shortage of medical resources. Using our model, we aim to gain insight into the transmission pattern of this large-scale cholera outbreak under the impact of limited medical resources.

We utilize the outbreak data in the Yemen Situation Reports published weekly by WHO ^[21]. These data sets contain the weekly reported new cases and cumulative cases for each governorate as well as the entire country. We implement our model and conduct numerical simulation for an epidemic period slightly over one year, starting from April 2017 (when the cholera epidemic resurged in Yemen and went on to become the worst cholera outbreak in modern history) and ending in May 2018 (when the cholera epidemic significantly slowed down already and only a small number of new cases were reported since then).

We first describe how the values of the model parameters are determined in our numerical simulation. The entire population in Yemen is about $N = 27.5\;$million as of 2016 ^[30]. The average life expectancy in Yemen is about $64$ years ^[31], and so we may estimate the natural human death rate $\mu$ by $\mu \approx (64\; {\rm year})^{-1} \approx 0.0003 \; {\rm week}^{-1}$. Vibrio cholerae can typically survive in the aquatic environment for about $30$ days ^[2], thus we calculate the natural death (or, removal) rate of the bacteria by $\delta \approx (30\; {\rm day})^{-1} \approx 0.233 \; {\rm week}^{-1}$. An individual with a moderate cholera infection could recover in about $5$ days ^[1], and so we estimate the recovery rate by $\gamma \approx (5\; {\rm day})^{-1} \approx 1.4 \; {\rm week}^{-1}$. Based on the recent WHO survey on Yemen's health system ^[19], only $45\%$ of the medical facilities in Yemen remain fully functional after two years of wars. Then we may roughly estimate the decay rate of the medical resources by $\Gamma \approx 0.5 * 0.55 \; {\rm year}^{-1} \approx 0.00529 \; {\rm week}^{-1}$. Additionally, the half saturation rate of Vibrio cholerae is commonly accepted as $K \approx 10^6 \, {\rm cells\cdot ml}^{-1}$ ^[1].

On the other hand, the direct transmission rate $\beta_1(M)$, the indirect transmission rate $\beta_2(M)$, the average individual shedding rate $\xi(M)$, and the self-growth rate of medical resources $\lambda(M)$ all depend on $M$ (where $0 \leq M \leq 1$) and are more difficult to calibrate. For simplicity, we consider the following representations of these rates, as decreasing functions of $M$:

Using the base values from ^[5] for the cholera transmission rates and individual shedding rate, we set the lower bounds of these parameters as $\beta_1(1) = c_1- d_1 = 1.099\times10^{-4} \; {\rm week}^{-1}\, {\rm person}^{-1}$, $\; \beta_2(1) = c_2- d_2 = 0.0077 \; {\rm week}^{-1}$, and $\; \xi(1) = c_3- d_3 = 70 \; {\rm cells} \cdot {\rm ml}^{-1}\, {\rm week}^{-1}\, {\rm person}^{-1}$. By using these conditions as well as the assumption (H4), we are left with five independent parameters $c_i$ ($1 \leq i \leq 4$) and $\eta$, whose values will then be determined through data fitting.

We conduct data fitting to a number of time series that include the weekly reported cases at the country level and the individual governorate level, based on the standard least squares method. We also note that the country of Yemen can be divided into three major regions (the Northwest, the Southwest, and the East) which differ from each other in climatic and geographical conditions ^[32,33]. The three regions can be roughly defined as – East: Longitude + Latitude $>$ $60^{\circ}$; Northwest: Longitude + Latitude $<$ $60^{\circ}$ & Latitude $>$ $14.5^{\circ}$; Southwest: Longitude + Latitude $<$ $60^{\circ}$ & Latitude $<$ $14.5^{\circ}$. In our numerical simulation, we have chosen one or more governorates from each of the three regions.

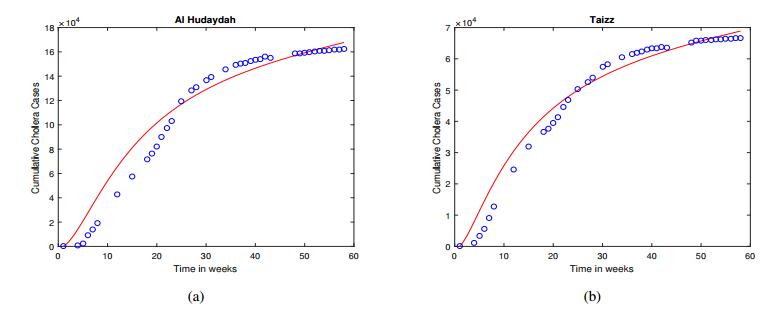
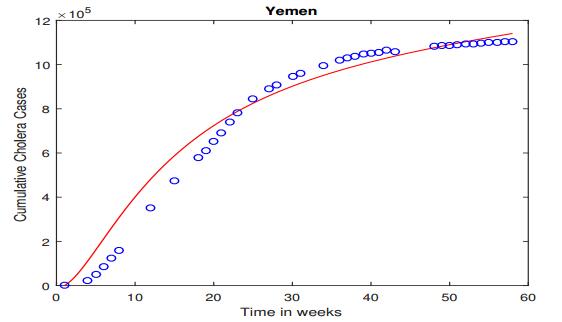
Figure 1 shows the number of cumulative infections from the WHO reports and from our numerical simulation, for the entire country of Yemen. The parameters $c_i$ ($1 \leq i \leq 4$) and $\eta$ are determined from the data fitting; their values and $95\%$ confidence intervals are shown in Table 2 in the Appendix. From Figure 1, we observe reasonably good fitting results based on our numerical simulation (red curve) to the reported data (blue circles). To quantify the goodness of fit, we have calculated the Normalized Mean Square Error (NMSE), which provides an estimate of the overall deviation between the predicted and measured values. The NMSE in this case is computed by

where

and where $x_i$ ($1 \leq i \leq n$) are the WHO reported data, $y_i$ ($1 \leq i \leq n$) are the fitted data, and $n$ is the number of data points used. In general, a lower value of NMSE indicates a better fitting result. The values of the NMSE for the cholera data fitting of Yemen (as well as four of its governorates) are presented in Table 1.

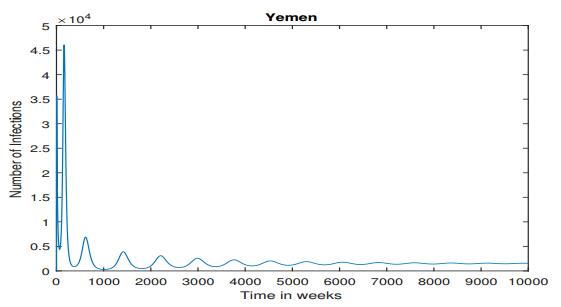
In Figure 1, we see that the the increase of the cumulative cholera cases was very fast during the first 20 weeks or so (starting from April 27, 2017), but gradually slowed down afterwards (ending in May 2018). Based on the data fitting result, we are able to evaluate the basic reproduction number from equation (2.5). We find that $\mathcal{R}_0 = 1.344$, consistent with our prediction of a cholera epidemic when $\mathcal{R}_0 > 1$. Moreover, Figure 2 shows the long-term behavior of the infection (or, prevalence) curve which approaches a positive endemic state (i.e., the endemic equilibrium) over time, an evidence for the global stability of the endemic equilibrium when $\mathcal{R}_0 > 1$, as predicted by Theorem 2.3.

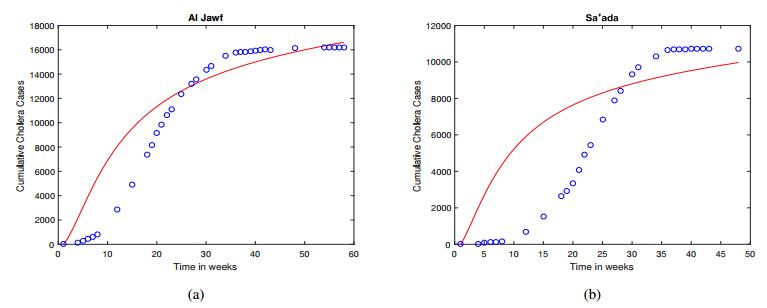
In order to conduct a deeper investigation into the transmission dynamics of this cholera outbreak, we have also carried out numerical simulation and data fitting for a number of individual governorates in Yemen. Figures 3 and 4 show some typical results, where one governorate is chosen from each of the Northwest and Southwest regions, and two chosen from the East region. The parameter values for $c_i$ ($1 \leq i \leq 4$) and $\eta$ are again determined through data fitting in each scenario; see Tables 3-6 for their values and confidence intervals. We observe that Al Hudaydah in the Northwest has the highest cumulative infection cases among the four governorates, followed by Taizz in the Southwest, and the lowest are Al Jawf and Sa'ada in the East. Correspondingly, the value of the basic reproduction number $\mathcal{R}_0$ (evaluated based on the data fitting result for each governorate) is the highest for Al Hudaydah, and the lowest for Al Jawf and Sa'ada, indicating the different levels of disease risk in these places. More specifically, the numbers of cumulative cases in Al Jawf and Sa'ada are about one order lower than those in Al Hudaydah and Taizz. For each of the two governorates in the East, the reported number of cumulative cases remains pretty flat during the first 10 weeks or so, indicating that the onset of the major cholera outbreak in the East region lags behind, and is possibly caused by, that in the Northwest and Southwest regions. Meanwhile, when $t \ge 30$ weeks, the reported cumulative cases in Al Jawf and Sa'ada essentially level off, a strong indication that the cholera epidemic has been contained in these places after about 30 weeks. As a result, the reported cumulative cases in each of these two governorates in the East (especially Sa'ada) show an approximate 'S' shape. These factors contribute to the fact that our least squares data fitting results for the eastern governorates (especially Sa'ada) are not as good as those for the northwestern and southwestern governorates. Indeed, Table 1 shows the values of the NMSE for each case, which quantifies the goodness of fitting, and we clearly observe that the NMSE value for Sa'ada is the highest, followed by that for Al Jawf, and those for Al Hudaydah and Taizz are the lowest.

Based on the parameters estimated in each scenario, we have calculated the two parts $\mathcal{R}_{01}$ and $\mathcal{R}_{02}$ in equation (2.5), which represent the contribution from the direct and indirect transmission routes, respectively, to the overall disease risk. We observe that the ratio of $\mathcal{R}_{01} / \mathcal{R}_{02}$ is high for the two governorates in the Northwest and Southwest, showing that the direct transmission route plays the dominant role in shaping the transmission pattern in these places. Particularly, for Al Hudaydah in the Northwest, the value of $\mathcal{R}_{01}$ is almost 8 times of that of $\mathcal{R}_{02} \,$. On the other hand, for Al Jawf and Sa'ada in the East, the values of $\mathcal{R}_{01}$ and $\mathcal{R}_{02}$ are much closer, indicating that the indirect transmission route plays a more significant role there. A possible explanation for this difference is that in the country of Yemen, the population density in the Northwest and Southwest is much higher than that in the East ^[32,30], thus the direct, human-to-human, transmission route may contribute more to the cholera epidemic in the Northwest and Southwest, but less in the East.

In addition, we have examined the variation of $M$ in our simulation. We find that the value of $M$ is generally decreasing throughout the course of the epidemic, indicating the continuing decline of the available medical resources and deterioration of the public health system due to the conflicts and wars, despite the stimulation from the on-going cholera outbreak. Particularly, we have calculated the value of $M_0\,$, the level of medical resources at the disease-free equilibrium, for these four governorates under consideration (see the caption under each figure). We see that the values of $M_0\,$ in Al Hudaydah and Taizz are much higher than those in Al Jawf and Sa'ada, implying that a much higher level of medical resources is required to attain the disease-free state in the Northwest and Southwest regions, than that required in the East region. This is possibly caused by the larger populations (that demand more medical supplies/facilities) and the higher degrees of outbreak severity (characterized by the high levels of prevalence and accumulated cases) in the Northwest and Southwest.

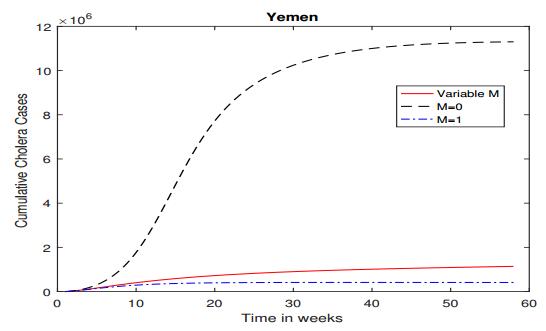
To further demonstrate the impact of the available medical resources, which interact with the disease transmission dynamics and vary with time, on the Yemen cholera outbreak, we consider two extreme cases with fixed $M$: $M = 0$ (no resources available throughout the epidemic) and $M = 1$ ($100\%$ resources available throughout the epidemic). In each of these two scenarios, the disease transmission rates $\beta_1(M)$ and $\beta_2(M)$, and the rate of human contribution to the bacterial growth, $\xi(M)$, are all reduced to constants; i.e., independent of $M$. When $M = 0$, the host transmission and pathogen growth rates are fixed at their maximum values, so that higher disease prevalence and severity are expected. When $M = 1$, these transmission and growth rates remain at their minimum values for the entire course, which would lead to a less severe epidemic. Figure 5 plots the numbers of infected human hosts in Yemen for $M = 0$ and $M = 1$, and compare those to the scenario emphasized in our model where $M$ is a variable with respect to the time. An implication of these results is that without considering the impact of the dynamic, time-dependent medical resources, we might either over-estimate or under-estimate the disease risk.

4.   Discussion and conclusion

In this study, we have formulated a mathematical model to investigate cholera transmission under the impact of limited medical resources. Our model includes both the human-to-human (direct) and environment-to-human (indirect) transmission pathways. In particular, we have incorporated the strength of the medical resources as a key component in the model, on which the transmission rates explicitly depend. Our model thus represents the interaction among the human hosts (susceptible, infectious, and recovered), the environmental pathogen, and the available medical resources, which shapes the transmission pattern of a cholera epidemic. We have carefully analyzed the dynamical properties of our model. Particularly, using the geometric approach based on the third compound matrix, we are able to establish the global asymptotic stability of the endemic equilibrium for our model (which essentially constitutes a four-dimensional system). Our analytical results show that under this model setting, cholera transmission follows regular threshold dynamics that are characterized by the basic reproduction number $\mathcal{R}_0\,$; i.e., the disease is eradicated when $\mathcal{R}_0 \leq 1$ and persists when $\mathcal{R}_0 > 1$.

We have applied our model to the simulation of the recent cholera outbreak in Yemen, as a means to demonstrate the application of our model and to verify our analytical predictions. We fit the model parameters using the realistic data published by WHO for both the whole country level and individual governorate level, with a few typical governorates from the three major regions of Yemen (the Northwest, the Southwest and the East). The findings from our numerical simulation and data fitting show significant differences of transmission structures among the three regions; these are reflected by the degrees of outbreak severity, disease risk quantifications, relative roles played by the direct and indirect transmission routes, and demand levels of medical resources. The results help us to better understand the complex, and heterogeneous, disease dynamics involved in this extremely severe and long-lasting cholera epidemic.

It is well known that the transmission and spread of cholera involve complicated biological, environmental and socioeconomic processes, and the underlying mechanism for a cholera outbreak may vary from place to place. Our work puts an emphasis on the availability of medical resources and its contribution to the overall transmission pattern of cholera. The Yemen cholera outbreak provides a realistic case study for this model, as the high prevalence and severity of this cholera epidemic are widely believed to stem from the collapsed health system and limited medical resources in this country. We obtain reasonably good results in fitting our model to the reported cholera data. Moreover, we find that different degrees of epidemic severity are linked to different geographical regions, which in term leads to different levels of demands for necessary medical resources in order to reach a disease-free state. These findings indicate that cholera prevention/intervention efforts should be implemented strategically with respect to different locations. Particularly for Yemen, stronger control measures should be planned, and more attention should be paid to the reduction of the direct disease transmission, for the Northwest and Southwest regions than that for the East region. Above all, the improvement of public health infrastructure and recovery of medical facilities and supplies are of fundamental importance in fighting future cholera outbreaks.

There are, however, a few limitations in our study. Our model does not consider the intrinsic dynamics of the pathogenic vibrios in the contaminated water, by assuming that the growth of the vibrios in the aquatic environment is predominantly refueled by the infected hosts ^[1,5,6,34]. Several cholera models (e.g., ^[17,35]) published in recent years have incorporated some bacterial intrinsic growth terms, though their potential impact on the transmission dynamics of the Yemen cholera outbreak remains unclear (but is worth exploring). Meanwhile, the intense conflicts and wars in Yemen and their devastating effects on the country's social, political and economic conditions certainly played a large role in this cholera outbreak. The significant reduction and shortage in medical resources represent one angle to investigate the complex dynamical interaction, and that is what our current paper is focused on, though there are many other socioeconomic factors which may have contributed to the Yemen cholera outbreak and which are not considered in our model. Furthermore, such factors are most likely random and discontinuous, and might be better represented in a stochastic modeling framework.

Acknowledgments

This work was partially supported by the National Science Foundation under Grant No. 1557739. The authors are grateful to the two anonymous referees for their valuable comments that have improved the original manuscript.

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Appendix

We present the parameter values and their confidence intervals in the tables below (A1 - A5) for the cholera data fitting of Yemen and its four governorates: Al Hudaydah in the Northwest, Taizz in the Southwest, and Al Jawf and Sa'ada in the East. The 95% confidence intervals listed in these tables imply that the corresponding $p$-values are greater than $0.05$. They also indicate that the standard deviations are large. This may be caused by the fact that our sample size is relatively small, as our data fitting is based on the weekly reported cases from WHO for about 39 weeks in the period from April 2017 to May 2018 (there are a number of weeks in this period that WHO did not report the data).