Mathematical modeling of the influence of cultural practices on cholera infections in Cameroon

1.   Introduction

Human resource management practices play an important role in the success of a company by allowing them to achieve their goals in a timely manner (Nishii & Wright, 2007). Multinational companies, as well as local companies, face challenges in implementing different approaches and processes to diversity management in the workplace (Dupuis, 2014, Savaneviciene, 2015). With the focus on global business and global competition, complex issues have forced multinational companies, as well as local organizations, to implement strategic management practices such as HRMPs. The training of skilled workers, a plan to increase the unity and benefits of the workforce, as well as ways to find employment increase the level of enrollment. Global advancements encourage the forces behind the organization to use employee-oriented approaches. HRM aims to improve the performance of various business sectors in context to the company’s goal. HRM not only advises employees but also recognizes the need for technology. Therefore, it strengthens people’s long-term relationships between organizations (Madison, 2012). In general, procurement means that purchasing partners develop and maintain long-term relationships (Moore, 1998). It focuses on lasting relationships based on trust, respect, devotion, and friendship. This was built on the foundation of friendship and trust through RC (Inkpen and Tsang, 2005). Trust is based on the exchange of information through the ease of access, improving communication, and describing the behavior, which can be achieved through relationship commitment (Dyer and Singh, 1998). In the same way, friendship, respect, and understanding are formed through lasting relationships (Kale et al., 2000). When reported together, the parties can resolve their weaknesses and turn them into successes (Villena et al., 2011). RC promotes long-term partnerships that build trust, friendship, and collaboration and reduce partnership costs in addition to partnerships.

Previous researchers have shown that HRMPs can improve RC and enhance performance (Naz et al., 2016; Stavrou & Brewster, 2005). Previous research has developed a framework for identifying and assessing the impact of HR work processes and performance (Ali et al., 2017). RC goal is to develop emotional connections between the company and its employees (Şendoğdu et al., 2013). The organizational strategies should be consistent with HRMP and represented by HRM (Tang et al., 2015). Today, organizations are said to be under the influence of technology, e.g., “Internet of Things” which enables companies to increase in value. Developing the service sector in emerging markets is currently a major challenge, and many service companies want to achieve and maintain a competitive advantage by evaluating the quality management process (Shabbir et al., 2016). Many studies have shown a high quality of service that can be achieved through customer satisfaction, customer loyalty, employee satisfaction, and effective staff experience improvisation (Lytras and Pablos, 2008). Moreover, sustainability has affected the ways firms operate, e.g., previous researchers suggest that sustainable firms and their supply chains differ from traditional ones (Syed et al., 2019). Therefore, it is a challenge for firms HR to cope with guidelines for sustainability and environmental management (EMS) practices for smooth operations. Relationship commitment is said to be a source for achieving higher sustainable performance (Tensie and Fink, 2016). The system of the enterprise must be fully involved and respected in the implementation of human resources for growth and development in the field of services, and therefore requires honest and dedicated staff. In addition, the quality of customer service is a good reflection of positive HRM practices prevalent in the workplace to create a link between the goals of the organization and the employee. Loyalty to the organization is an unexpected outcome of HRM and is important in retaining employees and recognizing their potential over time (Ahmad and Schroeder, 2003). Relationship commitment provides the basis for coping with social, environmental, and economic challenges (Parmigiani et al., 2011).

Although there is copious research on HRM and researchers have explained its importance and usage; however, when it comes to sustainable firms, these practices are rarely seen. There is very little research available on HRMPs and its application to sustainable supply chains. It is believed that HRMPs increase relationship commitment among the various partners, which in turn increases a firm’s performance. Regarding previous literature, no research has identified the relationship between HRMPs, relationship commitment, and sustainable performance. This leaves several questions unanswered, such as, what is the role of HRMPs in relationship commitment? How HRMPs affect firm performance through relationship commitment? The previous literature fails to answer these questions and lacks in clarifying the relationship among these concepts. Moreover, this study, for the first time, examines the meditative nature of relationship commitment relative to HRMPs and sustainable performance. Hence, this research provides a detailed examination of the relationship between HRMPs, relationship commitment, and sustainable performance.

The next section provides a literature review and discusses various concepts, illustrates hypotheses, and presents a conceptual model. Section 3 discusses the methodology, i.e., data collection tools, measurement of constructs, and provides reliability and data validity, while Section 4 outlines the results. Finally, discussion and conclusions are presented in section 5.

2.   Review of literature

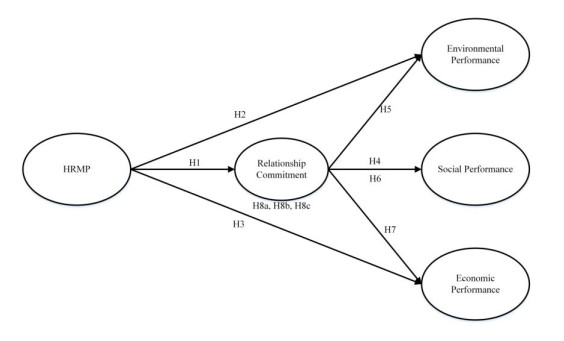
This section provides a review of the literature for the various concepts used in this study, such as; human resource management practices, relationship commitment, environmental performance, social performance, and economic performance. The relationship among these factors is briefly explained, and hypotheses are generated. Figure 1 summarizes the discussion and further provides the basis for the conceptual model derived from the data.

2.1.   Human resource management practices

Kok et al. (2003) defined HRM as the process of appealing, maintaining, and developing skilled and active staff to assist the firm’s objective, mission, and strategies. The conventional comprehension of HRM concentrates on measuring and managing and controlling a firm’s workforce. Technical and strategic HRM comprises on recruitment and selection, training, evaluation, and benefits of administration, while aspects of HRM events include: staff participation, communication, empowerment, work design on team-based, and growth of the managers in the firm. Therefore, HR depends on a commitment that concentrates on the emotional connections between employees and firms’ goals as well as it increases the participation of managers, which offers better rewards and training to the subordinate. Furthermore, it can be said that HR remains concentrated on straight evaluation and rewarding the employee’s performance (Arther, 1994). Kotey and Slad (2005) describe HRMPs as being comprised of recruitment and selection, training, performance appraisal, designing the policies of HR, and maintaining HR records. After reviewing the literature on HRMPs it can be deduced that it increases the workforce skills and motivation levels and that HRMPs helps to achieve business goals through technical competence and innovation (Huselid and schuler, 1997). Efficient HRMPs are gaining more attention in the contemporary business community knowledge-based economy as firms face challenges with the requirement of highly qualified human resources and lack of skilled labor.

2.1.1.   Recruitment and selection

It is one of the most important components of HRMPs, which is to find a skilled and qualified workforce for the organization, who can assist the organization in achieving its strategic and financial goals (Derous & Fruyt, 2016). In the planning section of human resources, it requires ensuring that the best workforce is available when organizations require them. During the recruitment process, a pool of people who are interested and appropriate for the job is created. Among these, the best and most suitable candidates are selected for further selection. Therefore, it creates the foundation of the selection process. If the recruitment process is performed appropriately), it benefits the organization to find out the most sophisticated and capable workforce for the organization (Nielsen et al., 2011). In the selection process, qualified candidates are chosen from the pool formed during the recruitment process. Where different candidate’s applications are received either from internal or external sources of the recruitment process, some organizations prefer to recruit and select employees from known sources, and some prefer to recruit through proper channels recommend by their panel of interviewers. “Recruitment is a process of searching for prospective employees and stimulating them to apply for jobs” by Edward Flippo (Chaturvedi, 2015). The recruitment and selection, which is comprised of a variety of processes start with the application letter.

2.1.2.   Training and development

Training and development (TD) is described as a formal process of making efforts that increase the firm performance and satisfy its workforce through different programs and educational training that improve their skills. In the contemporary working environment, there are multiple types of applications which can be implemented for highly qualified human resources or an unskilled or semi-skilled workforce, to enhance productivity (Ahlstrom et al., 2001). Recent research and development have become recognized business functions and a very important portion of the strategy, and apart from this acknowledgment as a profession with apparent methodologies and theories. An increasing number of firms, regardless of their size, either small and big, have adopted this methodological approach as continual learning. There is another aspect of TD; it can be related to the growth of the employee and an improved, highly qualified human resource workforce (Kam et al., 2010). Generally, training and development is considered as the education and improvement of the employees of the firm. Though there is little difference between training and development when observed closely. For instance, training is related to quantifiable and specific goals, like comprehensive knowledge about a particular process, operating a specific machine, or executing defined procedure with complete focused. While development, conversely, is focused on a variety of skill sets, which can be appropriate on a bigger perspective, such as goal setting, decision making, and leadership skills (Menon, 2010).

2.1.3.   Performance management

Performance management (PM) is the combination of Human Resources along with the record of the employee’s performance as it relates to goals, descriptions, and the objective and specific position. This process ensures that allocated activities and results similar to the firm’s objective are the final outcomes. It is a tool that assists the executive in evaluating and tracking employees’ work. PM’s main goal is to set up an atmosphere where the workforce can utilize its utmost capabilities for the organization effectively and efficiently (Ahlstrom et al., 2001). A proper PM course of action enables the executives and workforce to evaluate their career progress and objective and align work with the firm’s overall vision. Some firms use PM as a conventional tool, similar to measuring and creating objectives, milestones, and goals. They also set a target for the performance regarding how it should be measured. Although they should set a paradigm for annual appraisal, instead they convert it into interaction and thus, they can measure employee performance. PM can be used as a tool by executives, and therefore, they can manipulate workflow, suggest new plans, and can make the right decisions, which further leverages the employees to achieve their goals. Alternatively, by utilizing this process strategically, firms can successfully achieve their targets (Menon, 2010).

2.2.   Relationship commitment

RC in the supply chain is generally understood as the supply relationship for building and maintaining stable and lasting relationships (Moore, 1998). This means that supply chain partners can invest in relationships, physical resources. RC provides a theoretical view of exploring the benefits that service providers derive through social media. A long-term relationship between partners is based on trust, respect, determination, and friendship. Trust is the basis of building relationships (Inkpen and Tsang, 2005). Faith is based on a transaction that repeatedly reduces risks, promotes open communication, and increases transparency in behavior between the parties (Dyer and Singh, 1998). Similarly, friendship, respect, and mutual understanding develop through repeated transactions and long-term relationships (Kale et al., 2000). RC believes that the parties are not exploiting their vulnerabilities, thereby creating mutual understanding for buyers and suppliers of autonomous partners who are members of a shared value relationship (Villena et al., 2011). In short, RC is based on long-term, reciprocal relationships that develop trust, respect, friendship, and mutual understanding and facilitate collaboration while reducing transaction costs.

2.3.   Relationship between HRMP and relationship commitment

There are various HR practices which firms use to increase efficiency and effectiveness, such as; recruitment and selection, training and development, performance management, etc. Darrag and Mohamed (2010) stated successful companies need to use basic recruitment methods to attract the attention of relevant employees. However, the details of the recruitment and selection process have an impact on the RC of employees and reflect the response of the recruitment and selection system for various companies (Loganathan & Dharmaraj, 2017). Various researchers have explained that there is a positive relationship between recruitment and selection, and RC (Bisharat et al., 2017; Lamba & Choudhary, 2013; Obeidat et al., 2014). It does not just impact the RC, but, in turn, increases the firm’s overall performance (Bimpitsos and Petridou, 2012). Improving staff training skills through training and development leads to an increase in RC (Paşaoğlu, 2015). According to Maheshwari and Vohra (2015), training is related to staff skills which improve their understanding and increase the level of commitment towards tasks. Several studies have shown an important linkage between training and development, and RC (Bisharat et al., 2017; Obeidat et al., 2014; Paşaoğlu, 2015). It should be noted that this was proposed by Chen and Eldridge (2010) to review the organization’s HR practices, e.g., performance management. Satisfactory performance evaluation systems provide a comprehensive basis for analyzing employee performance and giving appraisals according to their strengths and weaknesses (Sripirabaa and Krishnaveni, 2009). It is seen that when employees see they are treated fairly by their firm through performance appraisal and proper rewards are given based on their performance, and then they feel positive about their job and the company, which in turn increases their job satisfaction. A high level of job satisfaction leads to higher RC, which in turn increases a firm’s performance. In view of the above discussion, the following hypothesis is proposed:

H1: There is a positive relationship between HRMPs and relationship commitment.

2.4.   Relationship between human resource management practices and sustainable performance

Recently HRMPs have been linked with sustainability and TBL perspectives (Randev and Jha, 2019). In which the HRMPs orientation and its relationship with environmental, social, and economic perspectives are explained. HRM along with sustainability promotes sustainable practices through the implementation of HRMPs, which reduce the negative impact of business on the environment and improves the firm’s supply chain as well as environmental performance (Mishra, 2017). A set of HRMPs which comply with environmental standards helps firms in reducing the fragility of the system and enhances a firm’s environmental business activities (Tang et al., 2018). Previous researchers have proposed that HRMPs such as recruitment and selection, training and development, performance management have a positive impact on the environmental aspects of the business (Likhitkar and Verma, 2017; Renwick et al., 2016; Randev and Jha, 2019). In regard to the above discussion, we propose the following hypothesis:

H2: There is a positive relationship between HRMPs and environmental performance.

Numerous researchers (e.g., Lund-Thomsen & Jeppesen, 2017; Weerts et al., 2018; Randev and Jha, 2019) have explored the relationship between corporate social responsibility (CSR) and TBL. HRMPs play a vital role in achieving sustainable goals of the firm and enhance its TBL performance (Randev and Jha, 2019). Voegtlin and Greenwood (2016) proposed a combined CSR-HRMP approach, which explains that the involvement of employees in CSR enhances the firm’s TBL performance. The social side of CSR-HRMP integration explains that both social and business demand are integrated because society and businesses are interdependent for growth and continuity. HRMPs can effectively enhance the social performance of the firm by boosting employee morale, well-being, loyalty and productivity. A significant positive association of HRMPs with social performance can be seen (Celma et al., 2018). Therefore, we propose the following hypothesis:

H3: There is a positive relationship between HRMPs and social performance.

Implementation of HRMPs enhance the ability of firms in achieving goals and provides it with a competitive advantage, which in turn increase a firm’s economic performance (Randev and Jha, 2019). Various HRMPs contribute positively to firms such as efficient and cost-effective recruitment, development of staff skills and managing employee performance (Browning & Delahaye, 2011). They also provide a structure for an organization that motivates employees to participate in organizational activities resulting in continuous feedback (Ehnert, 2009). Performance management allows firms to evaluate each employee’s performance, which helps the firm in building employee strength, which ultimately leads to higher performance of the firm (Wells, 2011). Among the literature on HRMPs and economic performance, a positive relationship can be observed due to cost reductions and goal completion, resulting in enhanced financial performance (Randev and Jha, 2019). Therefore, we propose the following hypothesis:

H4: There is a positive relationship between HRMPs and economic performance.

2.5.   Relationship between relationship commitment and sustainable performance

Previous literature supports the view that commitment to long-term relationships plays a decisive role in improving the performance of the entire supply chain (Krause et al., 2007; Nahapiet and Ghosal, 1998). RC, based on long terms, reduces the expectations for opportunistic behavior and decreases the transaction costs, which in turn increases performance (Dyer and Singh, 1998). Customers and suppliers can work together for a long time, build mutual trust, begin to understand the details and barriers that exist to enhance collaboration, and make the changes when needed (Cousins, 2006). These promises made by RC can reduce fears about sharing of information, which encourage customers and suppliers to work in teams to achieve shared ambitions and goals, and provides more opportunities to increase innovation and enhance performance (Carey et al., 2011). RC enhances relationships that facilitate knowledge sharing and creates a framework for developing innovative solutions to social, economic, and environmental problems (Krause et al., 2007; Parmigiani et al., 2011). Finally, long-term relationships with key suppliers, generate new ideas, find new solutions, solve complex problems, and improve the environment, social and economic performance. In view of the above discussion, the following hypotheses are proposed:

H5: There is a positive relationship between relationship commitment and environmental performance.

H6: There is a positive relationship between relationship commitment and social performance.

H7: There is a positive relationship between relationship commitment and economic performance.

2.6.   Mediating effects of relationship commitment

RC focuses on stronger relationships based on trust, respect, devotion, and friendship among partners (Inkpen and Tsang, 2005). Trust is based on the exchange of information by the ease of access, improving communication, and describing the behavior, which can be achieved through relationship commitment (Dyer and Singh, 1998). When reported together, the parties can resolve each other’s weaknesses and turn into success (Villena, et al., 2011). RC promotes long-term partnerships that build trust, friendship, and collaboration and reduce partnership costs in addition to partnerships. Previous researchers have shown that HRMP can improve RC and enhance performance (Naz et al., 2016; Stavrou & Brewster, 2005). Previous research has developed a framework for identifying and assessing the impact of HR work processes and performance (Ali et al., 2017). RC goal is to develop emotional connections between the company and its employees (Şendoğdu et al., 2013). HRMPs can significantly improve RC, which in turn enhances firm’s sustainable performance. Therefore, we develop the following hypotheses:

H8a: Relationship commitment mediates the relationship between HRMPs and environmental performance.

H8b: Relationship commitment mediates the relationship between HRMPs and social performance.

H8c: Relationship commitment mediates the relationship between HRMPs and economic performance.

3.   Material and methods

3.1.   Sample selection

There are 425 manufacturing organizations listed on the Pakistani Stock Exchange (PSX). Initially, we have selected all the firms to take part in this study. Later, we have checked that some of the firms are delisted from the stock exchange, and some are merged with other firms. Therefore, we had left behind a total of 404 firms, and we have decided to send questionnaires to all these firms and make personal visits where possible. The selected firms belong to 19 different industry sectors, including textile, cement, technology and communication, chemical, automobile, electric goods, transport, and logistics, etc.

3.2.   Questionnaire design and data collection

The items for the survey were carefully selected after close collaboration with HRM, relationship commitment, and sustainable performance literature. A seven-point Likert scale questionnaire, for instance (strongly disagree to strongly agree), was sent to SC practitioners and two professors in the field of SCM to discuss and evaluate the questions and their consistency with the research objective. The questionnaire comprised of four parts, the first section consists of the name of the company and respondent, along with designation, experience, qualification, and department. In the second part, the question regarding HRMP is presented. In the third part, question-related to relationship commitment is provided. In the last part, relationship commitment to sustainable performance (Economic, Social, and Environment) is presented.

The target respondents for our study are HR managers/supply chain managers/relationship managers. We sent out 425 questionnaires and received 246 questionnaires back with a response rate of 58%.

3.3.   Measurements

This section explains the constructs and items used in this research, such as HRMP, relationship commitment, and sustainable performance. Based on literature (Das, 2017), HRMP is measured through six items (e.g., “HRMP1: Our firm follows a selection method, recommended by the interview panel”). Relationship commitment is measured through four items (e.g., “RC1: Our firm and our client both trust each other”). This study aims at measuring firm sustainable performance, which is a triple bottom line. Triple bottom line performance includes three measures of performance, e.g., environment, social, and economic. Environmental performance is measured through three items (e.g., “EP1: Our firm adopts processes and procedures to decrease air emission”). Social performance is measured through three items (e.g., “SP1: Our firm focuses on worker safety and health”). Economic performance is measured through four items (e.g., “ECP1: Production cost”). The items were turned into questions, which are explained in Table 1.

3.4.   Analysis of constructs validity and reliability

We have performed EFA first in which we have checked factor loadings of the items of the constructs, and all the items have higher factor loadings. In factor analysis, seven factors were identified, and they have eigenvalues greater than 1, such as 3.573, 2.104, 1.745, 1.515, and 1.148, respectively. After confirmation from EFA, we have performed CFA for cross-validation. CFA results for all constructs represent that the data and constructs fit well with the model. The obtained fit indices for CFA for all constructs are Chi-square/df = 1.495, p < 0.57 GFI = 0.95, PGFI = 0.86, CFI = 0.95, NFI = 0.90, RMSEA = 0.045, RMR = 0.045.

Afterward, we checked the constructs convergent and construct validity through composite reliability and average variance extracted. The AVEs for five constructs are 0.60, 0.55, 0.77, 0.57 and 0.52, which is higher than the cut-off value of 0.50 (Fornell and Larker, 1981). The CRs are 0.75, 0.83, 0.91, 0.80 and 0.81 which are greater than the threshold value of 0.60 (Kline, 2015). We have checked the reliability through Cronbach alpha, and obtained values are 0.82, 0.75, 0.92, 0.76, and 0.77, respectively, which are higher than the cut-off value of 0.70. Therefore, we suggest that reliability and validity exist in the construct and overall conceptual model. Hence, we can proceed for further analysis. The correlations, mean, and SD are presented in Table 2.

4.   Results

4.1.   Analysis of overall measurement model

For analysis purpose we employed the collected data to AMOS 26 and the results shows (χ2/df = 1.246, NFI = 0.913, CFI = 0.979, TLI = 0.975, IFI = 0.980, GFI = 0.930 and RMSEA = 0.032) which is a decent model fit. Value of χ2/df = 1.246 is less than 2.00, which is considered as cut-off value and was recommended by (Kline and Rosenberg, 2010) CFI = 0.979 TLI = 0.975 and NFI = 0.913 are larger than threshold value 0.900 described by (Fornell and Larker, 1981); RMSEA = 0.032 is less than 0.080, a cut off value suggested by Kline and Rosenberg (2010) and Lee (2007). The obtained results of fit indices are presented in Table 3.

The hypothesis H1 measures the impact of HRMPs on relationship commitment. Results (βeta = 0.179, prob. = 0.033) of H1 display that HRMPs has a positive relationship with relationship commitment. The hypothesis H2 measures the impact of HRMPs on environmental performance. Results (βeta = 0.456, prob. = 0.000) of H2 display that HRMPs has a positive relationship with environmental performance. The hypothesis H3 measures the impact of HRMPs on social performance. Results (βeta = 0.043, prob. = 0.584) of H3 display that HRMPs have a non-significant relationship with social performance. The hypothesis H4 measures the impact of HRMPs on economic performance. Results (βeta = 0.009, prob. = 0.904) of H4 display that HRMPs have a non-significant relationship with economic performance.

Similarly, we have measured relationship commitment with environmental, social and economic performance. The hypothesis H5 measures the impact of relationship commitment on environmental performance. Results (βeta = 0.124, prob. = 0.089) of H5 display that relationship commitment has a moderate positive relationship with environmental performance. H6 measures the impact of relationship commitment on social performance. Results (βeta = 0.042, prob. = 0.603) of H6 display that relationship commitment have insignificant relationship with social performance. H7 measures the impact of relationship commitment on economic performance. Results (βeta = 0.497, prob. = 0.000) of H7 display that relationship commitment have a positive relationship with economic performance.

4.2.   Analysis of mediation analysis

To measure the mediation effect of relationship commitment as formulated in hypotheses H8a, H8b and H8c, a bootstrapping bias-corrected confidence interval procedure was adopted (Preacher and Hayes, 2008; Strizhakova et al., 2011). We assessed 2000 samples using AMOS 26 to obtain the confidence intervals in bootstrapping for mediation effects. 95% confidence intervals were generated in this method and the results of mediation effects are presented in Table 4.

The mediation results performed in AMOS 26 through bootstrapping procedure shows a significant indirect effect of HRMPs on environmental performance through relationship commitment, supporting the predicted hypothesis H8a (βeta = 0.059, prob. = 0.045). Alternatively, H8b, which is about HRMPs on social performance through relationship commitment, shows that the predicted hypothesis H8b is insignificant (βeta = 0.008, prob. = 0.456). On the other hand, HRMPs shows a significant indirect effect on economic performance through relationship commitment, supporting the predicted hypothesis H8c (βeta = 0.156, prob. = 0.022). Hence, relationship commitment mediates the relationship between HRMPs and environmental and economic performance but it fails to mediate the relationship between HRMPs and social performance.

5.   Discussion and conclusions

Though there is a plethora of research on HRM and researchers have explained its importance and usage, when it comes to sustainable firms, these practices are rarely seen. There is very little research available on HRMPs and its application to sustainable supply chains. It is believed that HRMPs increase relationship commitment among various partners, which in turn increases the firm’s performance (Randev and Jha, 2019). Concerning previous studies, we have found no study that identifies the relationship between HRMPs, relationship commitment, and sustainable performance. Therefore, this research aimed at identifying the relationship between HRMPs, relationship commitment, and sustainable performance through a triple bottom line. The results of the study suggest that HRMPs have a significant positive correlation with relationship commitment, supporting the view that effective recruitment and selection, training and development, and performance management increase the relationship commitment. Moroever, HRMPs are positively linked to sustainable performance but its relationship with social performance and economic performance remains insignificant. It states that HRMPs have a direct positive impact on environmental performance only, which confirms the view of Mishra (2017) that HRM along with sustainability promotes sustainable practices through implementation of HRMPs which reduce the negative impact of business on the environment and improves firm’s environmental performance (Mishra, 2017). Similarly, this study measures the effects of relationship commitment on sustainable performance and the results suggest that relation commitment has a positive and significant relationship between environmental and economic performance. The results support the view that when the relationship commitment among employees and partners increases trust, decreases transaction cost, enhance motivation and increase innovation, which in turn increase the firm’s performance. To clarify the mediation concept of relationship commitment towards HRMPs and sustainable performance, we have used a bootstrapping technique following the pattern of Preacher and Hayes (2008). The results of the mediation analysis suggest that relationship commitment mediates the relationship between HRMPs and environmental performance and economic performance. While it failed to mediate the relationship between HRMPs and social performance. Hence, we can say that relationship commitment plays a vital role in achieving sustainable performance.

It is substantially important for supply chain managers and HR managers to understand the role of HRMPs, in addition to sustainability and triple-bottom-line performance in the world’s current business settings (Westerman et al., 2020). Moreover, the relationship between HRMPs and relationship commitment is also an important factor for enhancing trust and building commitment among employees and supply chain partners. Through effective HRMPs, HR can increase relationship commitment and also sustainable performance. Moreover, this study shows the significant positive mediation effects of relationship commitment among HRMPs and sustainable performance. Therefore, this study is important for managers as it clarifies the relationships among HRMPs, relationship commitment and sustainable performance. This study also provides a foundation for future research on HRMPs and sustainable performance.

Apart from various practical implications, this study has some limitations. The data used in this study was collected from manufacturers and their suppliers, data collection from other partners, were not included in this study. Further research could examine the significance of including customers and suppliers, for example. Furthermore, the data used in this study is limited to Pakistan. The cross-national comparison would provide a more complete picture in regards to the relationship between HRMPs, RC, and performance.

Overall, the study contributes to our understanding of human resource management practices and sustainable performance. Our results indicate that HRMPs, along with relationship commitment among employees and supply chain partners, are critical factors in achieving sustainable performance.

Conflict of interest

The authors declare no conflict of interest.

Acknowledgment

The authors acknowledge Maurice JM Lineman for providing editing assistance and proofreading the manuscript. He has published several articles on “Ecology Wetland Conservation and Public Awareness” and is a Canadian Expat working in China.