| 1.
|
Jinliang Wang, Min Guo, Xianning Liu, Zhitao Zhao,
Threshold dynamics of HIV-1 virus model with cell-to-cell transmission, cell-mediated immune responses and distributed delay,
2016,
291,
00963003,
149,
10.1016/j.amc.2016.06.032
|
|
| 2.
|
Yu Yang,
Stability and Hopf bifurcation of a delayed virus infection model with Beddington-DeAngelis infection function and cytotoxic T-lymphocyte immune response,
2015,
38,
01704214,
5253,
10.1002/mma.3455
|
|
| 3.
|
Hongquan Sun, Jin Li,
A numerical method for a diffusive virus model with general incidence function, cell-to-cell transmission and time delay,
2020,
545,
03784371,
123477,
10.1016/j.physa.2019.123477
|
|
| 4.
|
A. M. Elaiw, N. H. AlShamrani,
Dynamics of viral infection models with antibodies and general nonlinear incidence and neutralize rates,
2016,
4,
2195-268X,
303,
10.1007/s40435-015-0181-2
|
|
| 5.
|
Zhiting Xu, Youqing Xu,
Stability of a CD4+ T cell viral infection model with diffusion,
2018,
11,
1793-5245,
1850071,
10.1142/S1793524518500717
|
|
| 6.
|
Jinliang Wang, Jiying Lang, Xianning Liu,
Global dynamics for viral infection model with Beddington-DeAngelis functional response and an eclipse stage of infected cells,
2015,
20,
1531-3492,
3215,
10.3934/dcdsb.2015.20.3215
|
|
| 7.
|
A. M. Elaiw, A. S. Alsheri,
Global Dynamics of HIV Infection of CD4+T Cells and Macrophages,
2013,
2013,
1026-0226,
1,
10.1155/2013/264759
|
|
| 8.
|
Jia Liu, Qunying Zhang, Canrong Tian,
EFFECT OF TIME DELAY ON SPATIAL PATTERNS IN A AIRAL INFECTION MODEL WITH DIFFUSION,
2016,
21,
1392-6292,
143,
10.3846/13926292.2016.1137503
|
|
| 9.
|
A. M. Shehata, A. M. Elaiw, E. Kh. Elnahary, M. Abul-Ez,
Stability analysis of humoral immunity HIV infection models with RTI and discrete delays,
2017,
5,
2195-268X,
811,
10.1007/s40435-016-0235-0
|
|
| 10.
|
M.L. Mann Manyombe, J. Mbang, G. Chendjou,
Stability and Hopf bifurcation of a CTL-inclusive HIV-1 infection model with both viral and cellular infections, and three delays,
2021,
144,
09600779,
110695,
10.1016/j.chaos.2021.110695
|
|
| 11.
|
A. M. Elaiw, N. H. AlShamrani,
Global Properties of General Viral Infection Models with Humoral Immune Response,
2017,
25,
0971-3514,
453,
10.1007/s12591-015-0247-9
|
|
| 12.
|
Adrianne Jenner, Chae-Ok Yun, Arum Yoon, Peter S. Kim, Adelle C.F. Coster,
Modelling heterogeneity in viral-tumour dynamics: The effects of gene-attenuation on viral characteristics,
2018,
454,
00225193,
41,
10.1016/j.jtbi.2018.05.030
|
|
| 13.
|
Ting Guo, Haihong Liu, Chenglin Xu, Fang Yan,
Dynamics of a Delayed HIV-1 Infection Model with Saturation Incidence Rate and CTL Immune Response,
2016,
26,
0218-1274,
1650234,
10.1142/S0218127416502345
|
|
| 14.
|
Xiulan Lai, Xingfu Zou,
Modeling HIV-1 Virus Dynamics with Both Virus-to-Cell Infection and Cell-to-Cell Transmission,
2014,
74,
0036-1399,
898,
10.1137/130930145
|
|
| 15.
|
A. M. Elaiw, N. A. Alghamdi,
Global Stability of Humoral Immunity HIV Infection Models with Chronically Infected Cells and Discrete Delays,
2015,
2015,
1026-0226,
1,
10.1155/2015/370968
|
|
| 16.
|
Hai-Feng Huo, Rui Chen,
Stability of an HIV/AIDS Treatment Model with Different Stages,
2015,
2015,
1026-0226,
1,
10.1155/2015/630503
|
|
| 17.
|
Hui Miao, Zhidong Teng, Xamxinur Abdurahman,
Stability and Hopf bifurcation for a five-dimensional virus infection model with Beddington–DeAngelis incidence and three delays,
2018,
12,
1751-3758,
146,
10.1080/17513758.2017.1408861
|
|
| 18.
|
Chengjun Kang, Hui Miao, Xing Chen, Jiabo Xu, Da Huang,
Global stability of a diffusive and delayed virus dynamics model with Crowley-Martin incidence function and CTL immune response,
2017,
2017,
1687-1847,
10.1186/s13662-017-1332-x
|
|
| 19.
|
Hui Miao, Zhidong Teng, Zhiming Li,
Global Stability of Delayed Viral Infection Models with Nonlinear Antibody and CTL Immune Responses and General Incidence Rate,
2016,
2016,
1748-670X,
1,
10.1155/2016/3903726
|
|
| 20.
|
Hui Miao, Zhidong Teng, Xamxinur Abdurahman, Zhiming Li,
Global stability of a diffusive and delayed virus infection model with general incidence function and adaptive immune response,
2018,
37,
0101-8205,
3780,
10.1007/s40314-017-0543-9
|
|
| 21.
|
Jinliang Wang, Xinxin Tian, Xia Wang,
Stability analysis for delayed viral infection model with multitarget cells and general incidence rate,
2016,
09,
1793-5245,
1650007,
10.1142/S1793524516500078
|
|
| 22.
|
A. M. Ełaiw, N. H. AlShamrani,
Global stability of a delayed virus dynamics model with multi-staged infected progression and humoral immunity,
2016,
09,
1793-5245,
1650060,
10.1142/S1793524516500601
|
|
| 23.
|
A. M. Elaiw, N. A. Almuallem,
Global dynamics of delay-distributed HIV infection models with differential drug efficacy in cocirculating target cells,
2016,
39,
01704214,
4,
10.1002/mma.3453
|
|
| 24.
|
A. M. Elaiw, N. H. AlShamrani,
Global stability of a delayed humoral immunity virus dynamics model with nonlinear incidence and infected cells removal rates,
2017,
5,
2195-268X,
381,
10.1007/s40435-015-0200-3
|
|
| 25.
|
Hongquan Sun, Jinliang Wang,
Dynamics of a diffusive virus model with general incidence function, cell-to-cell transmission and time delay,
2019,
77,
08981221,
284,
10.1016/j.camwa.2018.09.032
|
|
| 26.
|
Liang Zhan, Jiayu Zhou, Yalin Wang, Yan Jin, Neda Jahanshad, Gautam Prasad, Talia M. Nir, Cassandra D. Leonardo, Jieping Ye, Paul M. Thompson, ,
Comparison of nine tractography algorithms for detecting abnormal structural brain networks in Alzheimer’s disease,
2015,
7,
1663-4365,
10.3389/fnagi.2015.00048
|
|
| 27.
|
Yan Geng, Jinhu Xu,
Stability and bifurcation analysis for a delayed viral infection model with full logistic proliferation,
2020,
13,
1793-5245,
2050033,
10.1142/S1793524520500333
|
|
| 28.
|
Jinliang Wang, Jingmei Pang, Toshikazu Kuniya, Yoichi Enatsu,
Global threshold dynamics in a five-dimensional virus model with cell-mediated, humoral immune responses and distributed delays,
2014,
241,
00963003,
298,
10.1016/j.amc.2014.05.015
|
|
| 29.
|
A.M. Elaiw, N.H. AlShamrani,
Global stability of humoral immunity virus dynamics models with nonlinear infection rate and removal,
2015,
26,
14681218,
161,
10.1016/j.nonrwa.2015.05.007
|
|
| 30.
|
A. M. Elaiw, N. H. AlShamrani,
Global properties of nonlinear humoral immunity viral infection models,
2015,
08,
1793-5245,
1550058,
10.1142/S1793524515500588
|
|
| 31.
|
Zhijun Liu, Lianwen Wang, Ronghua Tan,
Spatiotemporal dynamics for a diffusive HIV-1 infection model with distributed delays and CTL immune response,
2022,
27,
1531-3492,
2767,
10.3934/dcdsb.2021159
|
|
| 32.
|
Ke Guo, Songbai Guo,
Lyapunov functionals for a general time-delayed virus dynamic model with different CTL responses,
2024,
34,
1054-1500,
10.1063/5.0204169
|
|
| 33.
|
Hui Miao,
Global stability of a diffusive humoral immunity viral infection model with time delays and two modes of transmission,
2025,
10,
2473-6988,
14122,
10.3934/math.2025636
|
|










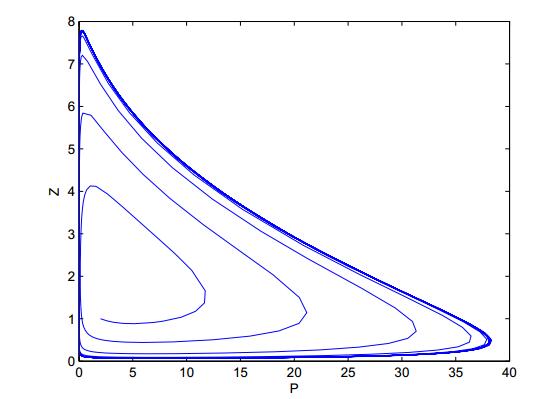
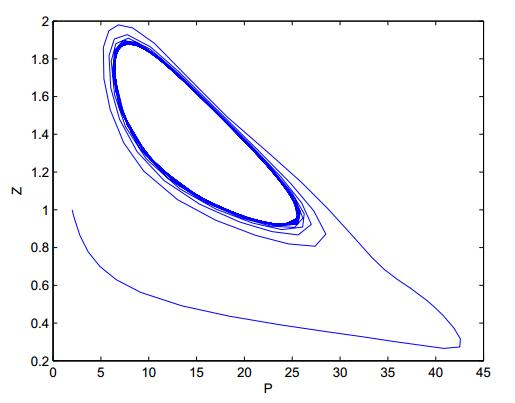
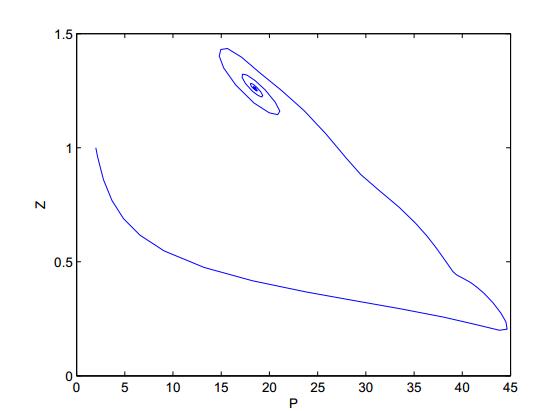
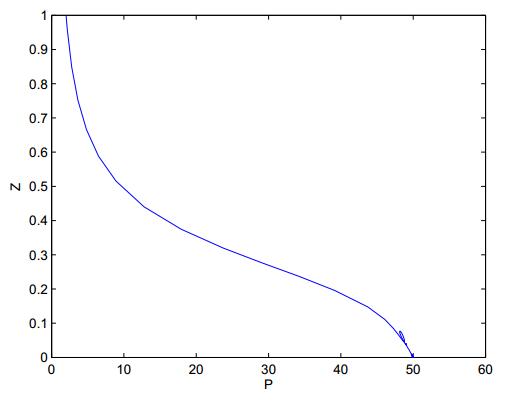


 DownLoad:
DownLoad: