In this paper, a mathematical model is formulated to investigate the effect of cytotoxic T lymphocyte (CTL) immune response on human immunodeficiency virus (HIV) infection dynamics. The model includes latently infected cells, antiretroviral therapy, cell-free virus infection and cell-to-cell viral transmission. By constructing Lyapunov functionals, the global stability of three equilibria is obtained. More specifically, the infection-free equilibrium Ef is globally asymptotically stable when the basic reproductive numbers R0<1, implying that the virus can be eventually cleared; the infected equilibrium without immune response Ew is globally asymptotically stable when the CTL immune response reproduction number R1 is less than one and R0 is greater than one, implying that the infection becomes chronic, but CTL immune response has not been established; the infected equilibrium with immune response Ec is globally asymptotically stable when R1>1, implying that the infection becomes chronic with persistent CTL immune response. Numerical simulations confirm the above theoretical results. Moreover, the inclusion of CTL immune response can generate a higher level of uninfected CD4+ T cells, and significantly reduce infected cells and viral load. These results may help to improve the understanding of HIV infection dynamics.
1.
Introduction
Acquired immunodeficiency syndrome (AIDS) is a fatal infectious disease. It is caused by HIV, which is a retrovirus and targets crucial components of the immune system (i.e. CD4+ T cells) [1,2]. According to the world health organization (WHO), HIV infection continues to be a serious global public health issue, particularly in low- and middle-income countries [3]. Indeed, there were approximately 36.7 million people living with HIV at the end of 2016, and 1.8 million people becomes newly infected in 2016 globally [4].
Because of destructiveness and complexity of HIV infection, researchers have been trying to find a way to cure HIV since it was discovered in 1981. Different classes of antiretroviral drugs have been developed, including fusion/entry inhibitors, reverse transcriptase inhibitors (RTIs), integrase inhibitors and protease inhibitors (PIs) that act on different steps of the HIV life cycle. RTIs can prevent HIV RNA from being converted into DNA, and PIs can inhibit infected cells to produce mature virus particles. For this reason, RTIs can be assumed to reduce the viral infection rate and PIs can decrease the number of new infectious virions as shown in existing mathematical models [5,6,7,8].
Although current therapy regimens have proven to be very effective in suppressing the viral load to below the detection threshold of standard clinical assays (50 copies/mL) [9,10], low-level viremia can be detected in most patients even after years of treatment using ultrasensitive assays [9,11]. In addition, a number of patients experience intermittent episodes of detectable viremia (i.e. blips) during treatment [10] or rapid viral rebound after stopping treatment [12]. These phenomena indicate that the virus has not be successfully eradicated from infected individuals. Latently infected cells that persist during therapy and can release infectious virions when activation by relevant antigens are now considered as a major barrier to viral eradication [7,13,14]. To study the effect of latently infected cells on HIV infection dynamics, Pankavich [15] developed the following model:
where state variables S, L, I and VI represent the concentrations of uninfected CD4+ T cells, latently infected CD4+ T cells, productively infected CD4+ T cells and infectious virions, respectively. εRTI and εPI are the drug efficacy of RTIs and PIs, respectively. Uninfected cells are produced at a constant rate λ, die naturally at rate d1, and are infected by cell-free virus at rate β. A fraction f of infection events lead to latency, latently infected cells die at rate d2 and are activated at rate α. The parameter N denotes the total number of viruses produced by one productively infected CD4+ T cell in its lifespan. Constants d3 and d4 are the death rate of productively infected CD4+ T cells and infectious virions, respectively. All parameters are positive constants and 0<f,εRTI,εRTI<1, existing mathematical models [5,6,7,8].
Obviously, the model (1) includes only cell-free virus infection route presented in many mathematical models [6,13,16]. However, cell-to-cell viral transmission through the formation of virological synapses, has been estimated to be several orders of magnitude more efficient than infection by free virus [17,18,19]. Moreover, cell-to-cell viral transmission permits the transfer of HIV without exposing the virus to extracellular environment, which may increases the probability of escaping from antiretroviral therapy and neutralization by antibodies. In other words, cell-to-cell viral transmission may be the reason why virions can persist in the presence of therapy for a long time [20]. Therefore, in [5], Mojaver and Kheiri studied following model by incorporating the two ways of viral infection:
obtained the two equilibria of system (2) and proved their global stability by constructing Lyapunov functionals. Here state variable V represents the concentration of free virions. ε=1−(1−εRTI)(1−εPI) is overall drug efficacy. The cell-to-cell viral transmission is modeled by aSI. The other variables and parameters are the same as those in model (1).
As stated in paper [21], the normal host immune responses, including antibodies, cytokines, natural killer cells and T cells, will be activated to fight viral infections. In particular, CTLs are considered to be a major branch of immune system because they generally lack CD4+ receptor [22,23,24]. Additionally, the authors of [25] concluded that CTL can lead to better immune responses in HIV-infected patients on antiretroviral therapy. These findings suggest that CTL immune response play an indispensable role in HIV infection. Thus, we combine CTL immune response and (2) to have the following set of differential equations,
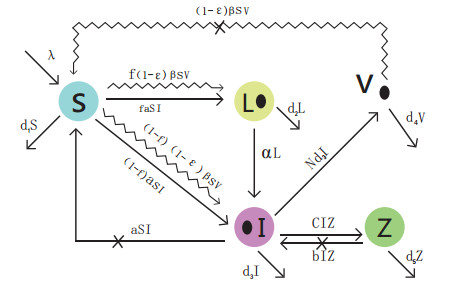
where state variable Z denotes the concentration of CTLs. CTLs expand at rate c and decay at rate d5. Productively infected cells are killed by CTLs at rate b. Table 1 gives the definitions and values of parameters. The model diagram is shown in Figure 1 existing mathematical models [5,6,7,8].
In this paper, we attempt to explore the effect of CTL immune response on viral infection dynamics. Our model also includes antiretroviral therapy, latently infected cells and cell-to-cell viral transmission. In the next section, the well-posedness of solutions, reproduction numbers and existence of the equilibria are introduced. In Section 3, we prove the local or global stability of three equilibria. In Section 4, we carry out some numerical examples to confirm our theoretical results and explain the role of CTL immune response. Finally, a brief discussion and conclusion are given in Section 5.
2.
Basic results
In this section, we establish the well-posedness of solutions of model (3) because this model describes the evolution of cells and free viruses. Furthermore, we give the reproduction numbers R0, R1 and existence conditions of the positive equilibria of the model (3).
2.1. Well-posedness of solutions
We assume that initial conditions associated with system (3) are
The following theorem shows that for nonnegative initial values, the solutions are nonnegative and bounded.
Theorem 2.1. For any nonnegative initial conditions (S(0),L(0),I(0),V(0),Z(0)), system (3) has a unique solution. Moreover, this solution is nonnegative and bounded for all t≥0.
Proof. By the classical differential equations theory, we confirm that model (3) has a unique local solution (S(t),L(t),I(t),V(t),Z(t)) in t∈[0,tp), where 0<tp<+∞. S(t) is positive for all t∈[0,tp). Indeed, assuming the contrary, let t1∈[0,tp) represent the first time such that S(t1)=0 and ˙S(t1)≤0. From the first equation of model (3), we obtain ˙S(t1)=λ>0, which contradicts with ˙S(t1)≤0. Thus, S(t)>0 for all t∈[0,tp). We have
when Z(0)≥0. In particular, Z(t)>0 if Z(0)>0. From the fourth equation of system (3), we obtain
Thus, V(t)≥0 for all t≥0 as long as I(t)≥0. Then, it is critical to show the nonnegativity of L(t) and I(t). Similar to the arguments in S(t)>0, we assume that t2∈[0,tp) and t3∈[0,tp) are the first times when L(t) and I(t) reach zero respectively, and t0=min{t2,t3}. If t0=t2, then L(t2)=0, ˙L(t2)≤0 and I(t2)>0. According to the second equation of system (3), we obtain ˙L(t2)=f(1−ε)βS(t2)V(t2)+faS(t2)I(t2)>0 which contradicts ˙L(t2)≤0. Similarly, if t0=t3, from the third equation of (3), we can find another contradiction. Therefore, the solutions of system (3) satisfying the nonnegative initial conditions are non-negative.existing mathematical models [5,6,7,8].
Next, we prove the boundedness of solutions. It follows from the first equation of model (3) that ˙S(t)≤λ−d1S(t). This implies lim supt→∞S(t)≤λd1. Thus, S(t) is ultimately bounded. To prove that L(t), I(t) and Z(t) are bounded, we define a Lyapunov functional
Obviously, Q(t)≥0 for t≥0. Differentiating Q(t) along the solution of model (3) yields that
where m=min{d1,d2,d3,d5}, thus lim supt→∞Q(t)≤λm. This implies that Q(t) is eventually bounded and hence L(t), I(t) and Z(t) are bounded, denote by M1, M2 and M3. From the fourth equation of (3), we have ˙V(t)≤Nd3M2−d4V(t), which means that lim supt→∞V(t)≤Nd3M2d4. Thus, V(t) is also ultimately bounded. Hence, every local solution can be prolonged up to any time tp>0, which means that the solution exists globally. This completes the proof.
2.2. Reproduction numbers and equilibria
It is obvious that model (3) always has an infection-free equilibrium Ef=(Sf,Lf,If,Vf,Zf)=(λd1,0,0,0,0), implying HIV infection die out. Using the next-generation method [37], the matrices for the new infection term F and the remaining transfer term V are given by:
Thus, the basic reproduction number under treatment, R0, is computed to be:
where ρ indicates the spectral radius of the next-generation operator F⋅V−1. Clearly, the first part of R0 denotes the average number of productively infected cells from the cell-free virus infection, whereas the second part is the average number of productively infected cells from the cell-to-cell viral transmission. When R0>1, in addition to equilibrium Ef, model (3) admits another equilibrium Ew,
Ew is called infected equilibrium without immune response, meaning that HIV infection is successful but CTL immune response is absent in this case.
We define the CTL immune response reproduction number R1 of model (3) by
In (5), cIw represents the amount of CTLs produced from productively infected cells at Ew per unit time, and 1d5 is the average survival time of CTLs. By multiplying the above quantities together, we can obtain that the expected number of CTLs generated from one CTL during its life time through the stimulation of productively infected cells, that is R1. If R1>1, there exists an infected equilibrium with immune response (except for Ef and Ew),
where
and
This equilibrium denotes the state in which both the viruses and CTLs are present.
3.
Stability of the equilibria Ef, Ew and Ec
In this section, we will classify the local or global stability of the three equilibria of (3).
3.1. Stability of the infection-free equilibrium Ef
Firstly, we have the following local stability result for the infection-free equilibrium Ef.
Theorem 3.1. The infection-free equilibrium, Ef, is locally asymptotically stable for R0<1.
Proof. The Jacobian matrix of model (3) at Ef is
From this, the characteristic equation can be written in the form
where
It is easy to see that (6) has eigenvalues δ1=−d1 and δ2=−d5, which are negative. The remaining eigenvalues are determined by the following equation,
Because R0<1, the inequalities d3−aλ(1−f)d1>0 and d3(α+d2)−aλ(α+d2(1−f))d1>0 hold. Consequently, we have
and
We can conclude that
By the Routh-Hurwitz criterion, we show that all roots of (6) have negative real parts. Hence, the infection-free equilibrium Ef is locally asymptotically stable when R0<1.
Theorem 3.1. only establishes the local stability of infection-free equilibrium Ef. However, the research about global stability of equilibrium is crucial in answering the question of whether this equilibrium is induced ultimately. Thereby, we focus on the global stability analysis of Ef in the next section. For the global stability of Ef, we have the following theorem.
Theorem 3.2. If R0<1, then the infection-free equilibrium Ef is globally asymptotically stable.
Proof. Consider the following Lyapunov functional
Calculating the time derivative of Hf along the positive solutions of model (3) and using the equalities λ=d1Sf and α+d2(1−f)=(α+d2)(1−f)+fα, we derive
Thus, we have that dHfdt|(3)≤0 under the assumption that R0<1. Furthermore, it is easy to verify that when dHfdt|(3)=0, Z=I=0 and S=Sf hold. This implies L=V=0. Thus, the largest compact invariant set in {(S,L,I,V,Z)∈R5+:dHfdt|(3)=0} is the singleton set {Ef}. From LaSalle invariance principle [38], we conclude that the infection-free equilibrium Ef is globally asymptotically stable when R0<1.
3.2. Global stability of the infected equilibrium without immune response Ew
According to the above analysis, we know Ef becomes unstable and a new equilibrium Ew emerges when R0>1. For the global stability of Ew, we have the following theorem.
Theorem 3.3. If R1<1<R0, then the infected equilibrium without immune response Ew is globally asymptotically stable.
Proof. Define
Calculating the derivative of Hw along solutions of system (3) yields
Substituting equalities λ=(1−ε)βSwVw+d1Sw+aSwIw and Nd3Iw=d4Vw into (11), we have
Since
it follows that
Since the arithmetic mean is greater than or equal to geometric mean (1nn∑i=1xi≥n√n∏i=1xi), the last four terms of (13) is non-positive. Hence, when R1<1<R0, the inequalitydHwdt|(3)≤0 holds. We note that dHwdt|(3)=0 if and only if S=Sw, L=Lw, I=Iw, V=Vw and Z=0. Thus, the largest invariant set in {(S,L,I,V,Z)∈R5+:dHwdt|(3)=0} is the singleton set {Ew}. This proves the global stability of Ew by applying LaSalle invariance principle.
3.3. Global stability of the infected equilibrium with immune response Ec
In this section, we will focus on the stability of the infected equilibrium with immune response Ec. Thus, we always assume that R1>1.
Theorem 3.4. If R1>1, then the infected equilibrium with immune response Ec is globally asymptotically stable.
Proof. Let
Then, the time derivative of Hc along solutions of model (3) is given by
where the equalities
and
have been used.
The arithmetic-geometric mean inequality (1nn∑i=1xi≥n√n∏i=1xi) implies dHcdt|(3)≤0 with equality if and only if S=Sc, L=Lc, I=Ic, V=Vc and Z=Zc. Thus, the largest invariant set in {(S,L,I,V,Z)∈R5+:dHcdt|(3)=0} is the singleton set {Ec}. It follows from LaSalle invariance principle that the equilibrium Ec is globally asymptotically stable when R1>1. This completes the proof of the theorem.
4.
Numerical simulations
In this section, we give some numerical simulations to validate our theoretical results and show the effect of CTL immune response on HIV infection dynamics. The parameter values or ranges used in the numerical simulations are presented in Table 1 existing mathematical models [5,6,7,8].
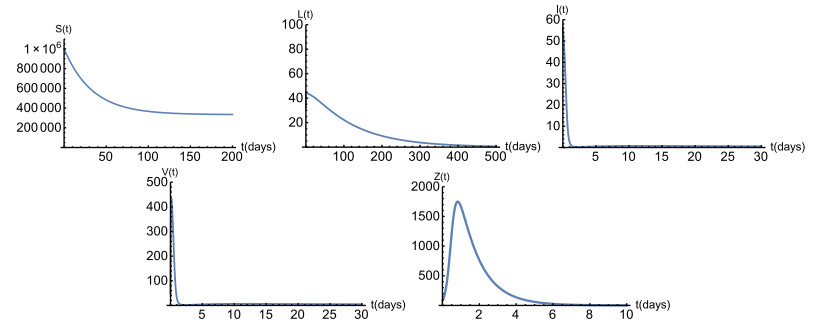
When β=2.4×10−8, a=10−6, N=200, c=0.15, d5=0.9, ε=0.87, and the other parameter values are the same as those in Table 1, we can compute that R0=0.3268<1. In this case, model (3) has a unique infection-free equilibrium Ef:(Sf,Lf,If,Vf,Zf)=(333333,0,0,0,0). Numerical simulations for equilibrium Ef are shown in Figure 2, which indicate that all state variables, except for S, converge to zero and S converges to 333333. This supports our results in theorem 3.2 that Ef is globally asymptotically stable when R0<1.
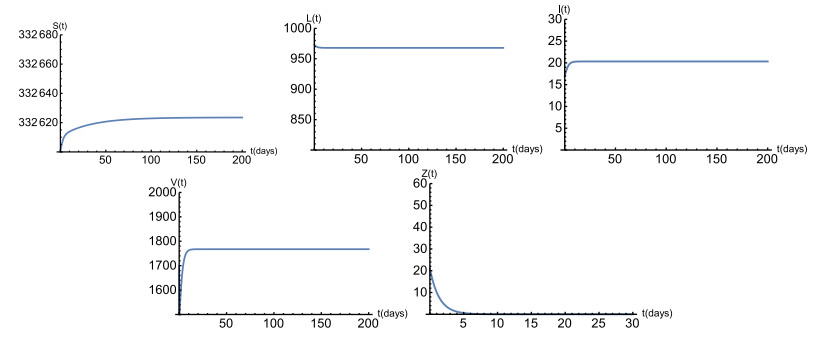
For the case where β=2.4×10−7, a=10−6, N=2000, c=0.01, d5=0.9 and ε=0.897, we have the basic reproduction number R0=1.0021>1 and the CTL immune response reproduction number R1=0.2259<1. According to theorem 3.3, the infected equilibrium without immune response Ew:(Sw,Lw,Iw,Vw,0)=(332623,968.11,20.33,1767.85,0) is globally asymptotically stable. That is, the HIV infection becomes chronic but CTL immune response is absent in such a situation [39]. This result is numerically demonstrated in Figure 3.
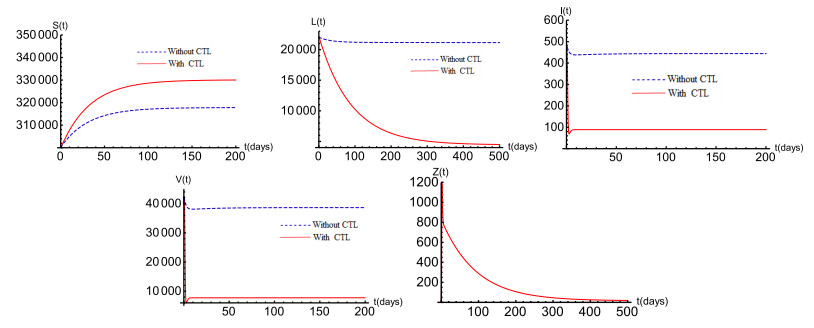
If the drugs are less effective than the previous scenario, for example, choosing ε=0.89, then the basic reproduction number becomes R0=1.0486>1 and the CTL immune response reproduction number becomes R1=4.9173>1. From theorem 3.4, the infected equilibrium with immune response Ec:(Sc,Lc,Ic,Vc,Zc)=(330070,4450.07,90,7826.09,15.9794) is globally asymptotically stable. This means that both CTL immune response and viral infection have been successfully established in this case. The numerical result in Figure 4 agrees with the theoretical result (see the case with CTL). In order to show the effect of CTL immune response, the infected equilibrium without immune response also be plotted in Figure 4. We found that CTL immune response reduces viral load by 4.75 times, and increases uninfected CD4+ T cells by 1.04 times. Moreover, in the presence of CTL immune response, the concentrations of infected cells are reduced obviously (decrease 4.2 times and 4.6 times for latently and productively infected cells, respectively). These findings suggest that CTL immune response plays an indispensable role in the dynamics of virus infection.
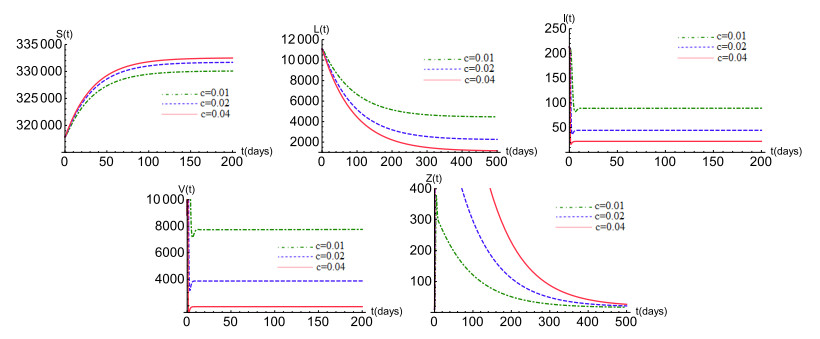
Through the above numerical analysis, we can qualitatively and quantitatively obtain the relationships between CTL immune response and HIV infection. However, how CTL-related parameters affect the dynamical behavior of system (3) remains unclear. Thus, taking the production rate of CTLs c as example, we will carry out some numerical simulations to examine its influence on HIV infection dynamics. When c=0.01,0.02,0.04, we observe that all solution trajectories converge to the infected equilibrium with immune response. For the case c=0.01, the concentration of uninfected CD4+ T cells and CTLs are at their lowest level, but the levels of the infected cells (latently and productively infected cells) and virus are maximum in this situation. As c increases, we found that the stabilized level of infected cells and viruses decrease, while CTLs and uninfected cells increase. We also examine the effect of the death rate of CTLs, d5, on the system's dynamics. Contrary to the above case, increasing d5 in model (3) reduces the concentrations of uninfected cells and CTLs, but increases the level of infected cells and viruses (figure not shown). Generally speaking, CTL immune response contributes to viral inhibition.
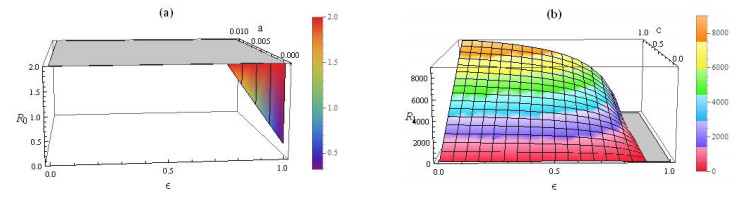
Based on the analysis in Section 3, we know that the stability of equilibria Ef, Ew and Ec is determined by the reproduction numbers R0 and R1. When the basic reproduction number R0 is less than one, the viruses are cleared and the infection dies out (i.e., the case in which Ef is globally asymptotically stable). When the basic reproduction number R0 is greater than one, viruses cannot be eradicated. However, adding CTLs to system (2) (i.e. R1>1) has a positive role in the reduction of infected cells and the increase of uninfected cells (see Figure 4). Thus, in order to prevent the risk of HIV infection, we should seek for the strategies that decreases the basic reproduction number R0 to below one or increases the CTL immune response reproduction number R1 to above one. Figure 6a shows the relationship among R0, the overall drug efficacy ε and the cell-to-cell viral transmission rate a. We found that the drug efficacy should be maintained at a constant greater than 0.857 to satisfy R0<1, even if a is small enough (a=10−6 ml⋅cell−1day−1). In other words, maintaining constant drug effectiveness of at least 85.7% may theoretically eradicate virus from infected individuals, but it is unattainable at present. This is because the efficacy of current therapy may be as low as 68% [40], and additional viral compartments and sanctuary sites may exist in infected individuals [7,9]. To relax the requirement on drug efficacy, the production rate of CTLs c should increase, as shown in Figure 6b. This suggests CTL immune response is important, which should not be ignored in studying HIV infection dynamics.
5.
Conclusion and discussion
In the last decades, a number of mathematical models with respect to HIV infection have been introduced [5,7,15,21,22,25,41,42], and these models have greatly improved our understanding of HIV pathogenesis and antiretroviral treatment. A HIV infection model, including uninfected CD4+ T cells, latently infected CD4+ T cells, productively infected CD4+ T cells, free virus and antiretroviral therapy, has been analyzed by Perelson et al. [42]. In addition to cell-free virus infection, cell-to-cell viral transmission is another route of HIV infection and is thought to be more efficient than cell-free virus infection [17,18,19]. Thus, Mojaver et al. [5] studied the extended one of model developed by Perelson et al. [42] by including cell-to-cell viral transmission. In Ref. [43], Wang et al. investigated the global properties a mathematical model considering uninfected CD4+ T cells, infected CD4+ T cells, free virus and CTLs, and found that CTL immune response play a critical role in antiviral defense. However, the importance of these factors was rarely discussed in a model. For this purpose, we develop a HIV infection model with CTL immune response, antiretroviral therapy, cell-to-cell viral transmission and latently infected cells in this paper.existing mathematical models [5,6,7,8].
For this mathematical model, the positivity and boundedness of the solutions have been established firstly. Secondly, we show that this model exists three possible equilibria: infection-free equilibrium Ef, infected equilibrium without immune response Ew and infected equilibrium with immune response Ec, depending on the basic reproduction number R0 and the CTL immune response reproduction number R1. Furthermore, R0 and R1 also determine the local or global properties of the model (3). More specifically, we have proven that, (i) if R0<1, then equilibrium Ef is globally asymptotically stable, implying that the virus can be eventually cleared; (ii) if R1<1<R0, then equilibrium Ew is globally asymptotically stable, implying that the infection becomes chronic but CTL immune response has not be successfully activated; (iii) if R1>1, equilibrium Ec is globally asymptotically stable, implying that the infection becomes chronic and there are persistent CTL immune response. Finally, some numerical simulations are carried out, in which we found that the numerical results are in good agreement with theoretical results.existing mathematical models [5,6,7,8].
Adding CTLs to system (2) causes some changes in the theoretical and numerical results. Indeed, the number of steady states increases from two to three compared with the results given in [5], which affects the overall dynamics analysis of the system (3). For example, a new threshold, the CTL immune response reproduction number R1 is introduced to clearly explain the existence and stability of equilibria. The numerical results show that CTL immune response plays an essential role in HIV control by increasing uninfected cells and reducing infected cells and free viruses (see Figure 4). This implies that in the presence of CTL immune response, the control of infection is better than only drug treatment. We also demonstrate the effect of CTL-associated parameter c on cells and virus dynamics (see Figure 5). A larger production rate of CTLs leads to a lower level of infected cells, a lower viral load, and a higher level of uninfected cells. These suggest that although the activation of CTL immune response is unable to eradicate virus, it plays an important role in the increase of the uninfected cells and the reduction of the infected cells and virus.existing mathematical models [5,6,7,8].
From the stability analysis of equilibria, we know that the infection dies out if R0<1. Thus, a strategy to eradicate HIV should focus on reducing R0 to lower one. To this end, the overall drug efficacy need to be maintained in at least 85.7%, despite the negligible cell-to-cell viral transmission rate (see Figure 6a). However, this constant drug efficacy is difficult to achieve for some patients infected with HIV. Moreover, many patients cannot physically tolerate antiviral therapy and afford the cost, the immune therapy (such as, antigenic boost and structured treatment interruption) may be a way that controls HIV infection.existing mathematical models [5,6,7,8].
In conclusion, both theoretical and numerical results show that CTL immune response is a important factor, and should not be ignored in HIV infection. In this paper, we assume that the drug efficacy is a constant. However, the drug concentration in plasma varies widely, depending on the half-life of drugs, the amount of drug intake and the adherence of patients. How these will affect the viral load dynamics remains to be further investigated.
Acknowledgments
The authors express gratitude to the anonymous referee for his/her helpful suggestions and the partial supports of the Postgraduate Research and Practice Innovation Program of Jiangsu Province (KYCX18_0375), the CSC (201806840119) and the National Natural Science Foundations of China (11671206).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: