1. Introduction
1.1. Background
In global financial markets, the pricing of a bond becomes more complicated due to different credit rating and different interest rate. A change of credit rating or a change of interest rate may cause drastic swing of bond prices. To manage the complication, one needs to understand how the credit risk impacts on the bond markets and how it can be measured. There are two types of credit risks: defaults and credit rating migrations. In the previous researches, the defaults are paid more attentions. However, in the financial crisis in 2008 and European debt crisis in 2010, the credit rating migrations played a much more important role in the finance and economics than what people expected. Therefore, the study of credit rating migrations becomes significant. Another observed factor in a financial market is that bond prices strongly depend on the interest rate. This leads to a crucial question of how to price a corporate bond with credit rating migration risks and interest rate change.
1.2. Literature review
There are many existing research papers on bond pricing models, see examples, Briys and de Varenne (Briys and Varenne, 1997), Tsiveriotis and Fernandes (Tsiveriotis and Fernandes, 1998).To measure default risks, there are two basic frameworks: a structure model, and a reduced form one. It is well-known that the first structure model for credit default proposed by Merton (Merton, 1974) is under the assumption that the firm's value follows a geometric Brownian motion process and the corporate bonds are considered as contingent claims. The default event may only occur at the maturity of the claim. In 1976, Black and Cox extended Merton's model to a first-passage-time model by introducing safety covenants. This extends the original model which gives bondholders the right to recognize a firm's value if its asset falls below some exogenously given threshold. In the modified model(Black and Cox, 1976), the default is allowed to occur any time up to the debt's maturity. By the reduced form framework, the credit events are considered to be governed by exogenous reason stochastically, see (Duffie and Singleton, 1999; Jarrow and Turnbull, 1995; Lando, 1998; Leland and Toft, 1996).
In study of credit rating migration, a major tool is the Markov chain. Most researchers mainly adopted a transfer intensity matrix. By this approach, the reduced form framework is naturally developed for the dynamic process of credit rating migrations, see Jarrow et al. (1997), Das and Tufano (1996), Hurd and Kuznetsov (2007), Lando (1998), Thomas et al. (2002) and so forth. The transfer intensity matrix usually comes from general statistical data, which do not include any particulary firm's information. However, a firm's own value plays a key role of its credit rating migration. In this situation, the Markov chain alone cannot fully capture the credit-rating mitigation for a firm. From the existing literatures, few research took this into account. Liang et al. (2015) in 2015 used a structure model for pricing bonds with credit rating migrations at first time. They gave a predetermined migration threshold where a firm's value is divided into high and low rating regions, under the assumption that the value of the firm follows a stochastic process. By using Feynman-Kac theorem, these models can be reduced to certain boundary value problems of partial differential equations. This PDE method is very different from the traditional approaches in the research field of corporative bond modelling. However, the rating migration boundary is usually not predetermined in the real financial world. It depends on the proportion of the debt and the value of the firm. From this point of view, the migration boundary should be a free boundary. Recently, Hu et al. (2015) and liang et al. (2016) proposed a new model to reflect this fact under the fixed-interest rate. They obtained the existence and uniqueness for the free boundary problem. Also, they proved that there is a travelling wave in the problem.
For pricing a bond, interest rate is a sensitive factor. Many stochastic models are used for the model, see Longstarff and Schwartz (1995) as an example. However, when a stochastic interest rate is considered, the bond model becomes two dimensions, which is much harder to analyze.
1.3. Result description
So far, all valuations for credit rating migration via pricing a corporate bond by structure model are assumed a constant interest rate. However, the stochastic interest rate for a bond is essential. So the extension for the model to stochastic interest rate is necessary. However, the extension meets a great difficult that the original free boundary model from one dimension to a higher one. That is the main contribution and solved problem in this paper.
In the present paper, we follow the ideas from (Hu et al., 2015) to derive a new model for a bond price in which credit-rating may change and the interest rate follows a stochastic process. To be more precise, we assume that the interest rate follows a Vasicek's stochastic process and the bond price follows a geometric Brownian motion with a different volatility in different credit-rating region. A coupled system of PDEs is derived. By employing a dimension-reduction technique we are able to simplify the coupled system to a single equation with a nonlinear jump coefficient in the leading term of the equation. Under certain conditions, the existence and uniqueness are established for the new model. We would like to indicate that our approach is different from that in (Hu et al., 2015; Liang et al., 2016). Moreover, the uniqueness proof in Section 4 is new to our knowledge. The method is also suitable for n-dimensional problems. Furthermore, the regularity of the free boundary is also considered. By transforming the problem to a Stefan-like problem, we prove that the free boundary is smooth. Some numerical results are also illustrated in the present paper. Those numerical results are well matching the theoretical analysis.
1.4. Paper structure
The paper is organized as follows: In Section 2, a new model with credit-rating migration and stochastic interest rate is rigorously derived under usual assumptions. In Section 3, we use the dimension reduction technique to simplify the model to a free boundary problem. In Section 4, we first use various PDE techniques to derive uniform estimates for the approximate problem. The existence and uniqueness are then established by using a compactness argument. Uniqueness is proved via an energy method. In Section 5, further properties of the solution are shown. In Section 6, some numerical results are presented. Some concluding remarks are given in section 7.
2. The Derivation of the Model
2.1. Basic assumptions
Let (Ω,F,P) be a complete probability space. We assume that the firm issues a corporate bond, which is a contingent claim of its value on the space F.
Assumption 2.1.
Interest rate rt follows Vasicek process:
|
drt=a(t)(θ(t)−rt)dt+σr(t)dWrt,
|
where a(t), θ(t) and σr(t) are given positive functions, which are supposed to be positive constants a,θ,σr for the simplification in this paper. Wrt is the Brownian motion which generates the filtration {Ft}.
We would like to point out that our model is a big improvement from the assumption of a constant interest rate to the stochastic one. There are many stochastic models for the interest rate, Vesicek model is popular one. The advantage point of this model is simply and easily calculable, while the weak point is the possibility of negative interest rate, which is proved to be very low. We assume that the interest rate follows Vesicek model also because that in our dimension reducing technique, only Vesicek model works.
Assumption 2.2 (the firm asset with credit rating migration).
Let St denote the firm's value in the risk neutral world. It satisfies
|
dSt={rtStdt+σH(t)StdWt,inhighratingregion,rtStdt+σL(t)StdWt,inlowratingregion,
|
where rt is the risk free interest rate, and
represent volatilities of the firm under the high and low credit grades, respectively. They are assumed to be deterministic and differentiable on [0,T] and have a positive lower bound:
|
0<˜σ0≤σH(t)<σL(t)≤˜σ1<∞,0≤t≤T.
|
(2)
|
Wt is the Brownian motion which generates the filtration {Ft}, and
where −1<ρ<1 is a constant.
It is reasonable to assume (1), namely, that the volatility in high rating region is lower than the one in the low rating region. This implies that there is a jump for the volatility when the rating changes.
Assumption 2.3 (the corporate bond).
The firm issues only one corporate zero-coupon bond with face value F. Denote Φt the discount value of the bond at time t, which is also the function of rt. Therefore, on the maturity time T, an investor can get ΦT=min{ST,F}.
Assumption 2.4 (the credit rating migration time).
High and low rating regions are determined by the proportion of the debt and value. The credit rating migration time τ1 and τ2 are the first moments when the firm's grade is downgraded and upgraded, respectively, as follows:
|
τ1=inf{t>0|Φ0/S0<γ,Φt/St≥γ},τ2=inf{t>0|Φ0/S0>γ,Φt/St≤γ},
|
where Φt=Φt(St,r,t) is a contingent claim with respect to St and
is a positive constant representing the threshold proportion of the debt and value of the firm's rating.
2.2. Cash flow
Once the credit rating migrates before the maturity T, a virtual substitute termination happens, i.e., the bond is virtually terminated and substituted by a new one with a new credit rating. There is a virtual cash flow of the bond. Denoted by ΦH(y,r,t) and ΦL(y,r,t) the values of the bond in high and low grades respectively. Then, they are the conditional expectations as follows:
|
ΦH(y,r,t)=Ey,t[e−∫Ttrsdsmin(ST,F)⋅1τ1≥T+e−∫τ1trsdsΦL(Sτ1,rt,τ1)⋅1t<τ1<T|St=y>1γΦH(y,t),rt=r],
|
(4)
|
|
ΦL(y,r,t)=Ey,t[e−∫Ttrsdsmin(ST,F)⋅1τ2≥T+e−∫τ2trsdsΦH(Sτ2,rt,τ2)⋅1t<τ2<T|St=y<1γΦL(y,t),rt=r],
|
(5)
|
where 1event={1, if "event" happens ,0, otherwise.
2.3. Mathematical model
By Feynman-Kac formula (Dixit and Pindyck, 1994), it is not difficult to drive that ΦH and ΦL are the function of the firm value S, interest rate r and time t. They satisfy the following partial differential equations in their regions:
|
∂ΦH∂t+12σ2HS2∂2ΦH∂S2+σrσHρS∂2ΦH∂S∂r+12σ2r∂2ΦH∂r2+rS∂ΦH∂S+a(θ−r)∂ΦH∂r−rΦH=0,S>1γΦH,0<t<T,
|
(6)
|
|
∂ΦL∂t+12σ2LS2∂2ΦL∂S2+σrσLρS∂2ΦL∂S∂r+12σ2r∂2ΦL∂r2+rS∂ΦL∂S+a(θ−r)∂ΦL∂r−rΦL=0,S<1γΦL,0<t<T,
|
(7)
|
with the terminal condition:
|
ΦH(S,T)=ΦL(S,T)=min{S,F}.
|
(8)
|
(4) and (5) imply that the value of the bond is continuous when it passes the rating threshold, i.e.,
|
ΦH=ΦL=γSon the rating
migration boundary.
|
(9)
|
Also, as in (Hu et al., 2015; Jin et al., 2016), we have
|
∂ΦH∂S=∂ΦL∂Son the rating migration
boundary.
|
(10)
|
This is a two-dimensional free boundary problem of an terminate value parabolic problem with discontinuous leading coefficient.
3. A PDE Problem
3.1. Reduction of dimension
The equations (6) and (7) are two-dimensional. For the purpose of simplifying the problem, we could use a technique to reduce the dimension.
Denote P(rt,t:T) to be the value of a zero-coupon bond faced 1 at time T. So that, it satisfies
|
∂P∂t+12σ2r∂2P∂r2+a(θ−r)∂P∂r−rP=0,
|
(11)
|
which admits a unique solution (Hall, 1989)
|
P(r,t:T)=A(t)e−rB(t),
|
(12)
|
where
|
A(t)=e{1a2[B2(t)−(T−t)](a2θ−σ2r2)−σ24aB2(t)},B(t)=1a(1−e−a(T−t)).
|
Now make a transform by
|
y=SP(r,t;T),VH(y,t)=ΦH(S,r,t)P(r,t;T),VL(y,t)=ΦL(S,r,t)P(r,t;T).
|
Then V(y,t) satisfies
|
∂VH∂t+12ˆσ2Hy2∂2VH∂y2=0,y>1γVH, 0<t<T,
|
(13)
|
|
∂VL∂t+12ˆσ2Ly2∂2VL∂y2=0,y<1γVL, 0<t<T,
|
(14)
|
|
VH(y,T)=VL(y,T)=min{y,F},
|
(15)
|
where
|
ˆσi=√σ2i+2ρσiσrB(t)+σ2rB2(t),i=H,L.
|
(16)
|
And on credit rating migration boundary, there holds
|
VH(y,t)=VL(y,t)=γy,∂VH∂y=∂VL∂y.
|
(17)
|
3.2. A free boundary problem
Using the standard change of variables x=logy and renaming T−t as t, and defining
|
ϕ(x,t)={VH(ex,T−t) in high rating region,VL(ex,T−t) in low rating region,
|
using also (6) and (7), we then derive the following equation from (6), (7):
|
∂ϕ∂t−12σ2∂2ϕ∂x2+12σ2∂ϕ∂x=0,(x,t)∈QT∖ΓT
|
(18)
|
where
|
QT=(−∞,+∞)×(0,T],ΓT={(x,t)|ϕ(x,t)=γex}
|
(19)
|
and σ is a function of ϕ and (x,t), i.e.,
|
σ=σ(ϕ,x,t)={ˆσHifϕ<γex,ˆσLifϕ≥γex.
|
(20)
|
The constant γ is defined in (3), and ˆσH,ˆσL are defined in (16). There exist constants σ0,σ1, such that
Without loss of generality, we assume F=1. Equation (18) is supplemented with the initial condition (derived from (8))
|
ϕ(x,0)=ϕ0(x)=min{ex,1},−∞<x<∞.
|
(22)
|
The domain will be divided into the high rating region QHT where ϕ<γex and a low rating region QLT where ϕ>γex. We shall prove that these two domains will be separated by a free boundary x=s(t), and
|
QHT={x>s(t),0<t<T},QLT={x<s(t),0<t<T}.
|
(23)
|
In another word, s(t) is apriorily unknown since it should be the solved by the equation
where the solution ϕ is apriorily unknown.
4. Existence and Uniqueness
4.1. Approximation
Let H(ξ) be the Heaviside function, i.e., H(ξ)=0 for ξ<0 and H(ξ)=1 for ξ>0. Then we can rewrite (20) as
|
σ(t,ϕ)=ˆσH+(ˆσL−ˆσH)H(ϕ−γex).
|
We use a standard approximation for H(ξ) and ϕ0(x) such that
|
Hε(ξ)∈C∞(R1)andHε(ξ)=H(ξ)for|ξ|≥ε,ϕ0ε(x)∈C3(R1)∩W1,∞(R1),ϕ′0ε(x)−γex<0,for0<x<ln1γ.
|
Now we consider the following approximated problem
|
∂ϕε∂t−12σ2ε(∂2ϕε∂x2−∂ϕε∂x)=0,(x,t)∈QT,
|
(24)
|
|
ϕε(x,0)=ϕ0ε(x),−∞<x<∞,
|
(25)
|
where
|
σε=ˆσH+(ˆσL−ˆσH)Hε(ϕε−γex).
|
(26)
|
4.2. Estimates
Lemma 4.1. The problem (24)-(25) admits a unique solution
|
ϕε(x,t)∈C2,1(QT)∩Cα,α2(¯QT),forforallα∈(0,1)
|
Moreover, the following estimates hold uniformly with respect to
ε:
a) 0≤ϕε(x,t)≤1, 0≤ϕεx(x,t)≤C1
b) sup0≤t≤T∫+∞−∞ϕ2εxdx+∬QT(ϕ2εxx+ϕ2εt)dxdt≤C2
where C1 and C2 depend only on known data.
Proof. By the theory of parabolic equation, we know that the problem (24)-(25) admits a unique classic solution ϕε∈C2,1(QT)∩Cα,α2(¯QT).
Now we derive the uniform estimates. First of all, by the maximum principle for Cauchy problem, we see
Let ψε(x,t)=ϕεx(x,t), then
|
ψεt−∂∂x[12σ2ε(ψεx−ψε)],(x,t)∈¯QT,ψε(x,0)=ϕ′0ε(x)≥0,−∞<x<+∞
|
Again, since ϕ′0ε(x)≥0, by maximum principle, we obtain
On the other hand,
|
ψεt−∂∂x(12σ2εψεx)=−∂∂x(12σ2εψε)
|
(27)
|
We multiply equation (27) ψpε for any p≥1, to obtain
|
ddt1p+1∫+∞−∞ψp+1εdx+p∫+∞−∞12σ2εψ2εxψp−1εdx=p∫+∞−∞12σ2εψpεψεxdx≤δ∫+∞−∞p⋅12σ2εψp−1εψ2εxdx+C(δ)p∫+∞−∞12σ2εψp+1εdx.
|
If we choose δ sufficiently small, we have
|
ddt1p+1∫+∞−∞ψp+1εdx+12p∫+∞−∞12σ2εψ2εxψp−1εdx≤C∫+∞−∞12σ2εψp+1εdx
|
Since 0<σ0≤σε≤σ1<+∞, we have
|
∫+∞−∞ψp+1εdx+∫+∞−∞∫t0ψ2εxψp−1εdxdt≤∫+∞−∞ϕ′0ε(x)2dx+C∫t0∫+∞−∞ψp+1εdxdt
|
Gronwall's inequality yields,
|
∫+∞−∞ψp+1εdx+∫+∞−∞∫T0ψ2εxψp−1εdxdt≤C,
|
where C depends only on known data and p, but not on ε.
Now from equation (27),
|
ψεt−∂∂x(12σ2εψεx)=−∂∂x(12σ2εψε),(x,t)∈QTψε(x,0)=ϕ′0ε(x),−∞<x<+∞
|
where σ2εψε∈Lp(R1) for any p>1. Then ||ψε||L∞(QT)≤C. To derive the W2,12(QT)−estimate, we multiply equation (24) by ϕεxx and integrate over Qt to obtain
|
σ0∬Qtϕ2εxxdxdt+∫+∞−∞ϕ2εxdx−∫+∞−∞ϕ2εx(x,0)dx=∬Qt12σ2εϕεxϕεxxdxdt≤δ∬Qtϕ2εxxdxdt+C(δ)∬Qtϕ2εxdxdt
|
By choosing δ sufficiently small, we have
|
σ0∬Qtϕ2εxxdxdt+∫+∞−∞ϕ2εx(x,t)dx≤∫+∞−∞ϕ2εx(x,0)dx+C∬Qtϕ2εxdxdt
|
Gronwall's inequality yields
|
sup0≤t≤T∫+∞−∞ϕ2εxdx+∬Qtϕ2εxxdxdt≤C.
|
From the equation (24), we see
Lemma 4.2. The solution ϕε(x,t)∈C1+α,1+α2(QT) uniformly with respect to ε, for some α∈(0,1). Moreover, for any ρ>0
there exists a constant C(ρ) such that
|
||ψε||Cα,α2(ˉQT∖Bρ(0,0))≤C(ρ),
|
where Bρ(0,0)={(x,t):−ρ<x<ρ,0<t<ρ}
and C(ρ) depends only on known data and ρ.
Proof. Indeed, we see ψε(x,t) is a solution of the following problem:
|
ψεt−∂∂x[12σ2(ψεx−ψε)]=0,(x,t)∈QT,ψε(x,0)=ϕ′ε0(x)≥0,−∞<x<+∞.
|
By the standard theory for parabolic equations, we see that ψε(x,t) is Hölder continuous in QT. Moreover, the Hölder continuity of ψε holds up to the initial time t=0 except a neighborhood of the singular point (0,0). Hence, for any ρ>0, we have
|
||ψε||Cα,α2(ˉQT∖Bρ(0,0))≤C(ρ),
|
where Bρ(0,0) defined above and C(ρ) depends only on known data and ρ, but not on ε.
4.3. Existence
Theorem 4.1. The problem (17), (21) admits a solution ϕ(x,t)∈W1,0∞(QT)∩W2,12(QT)∩Cα,α2(¯QT), for any
α∈(0,1). Furthermore, the solution satisfies
a) 0≤ϕ(x,t)≤1, 0≤ϕx(x,t)≤C1,
b) ∫+∞−∞ϕ2xdx+∬QT(ϕ2xx+ϕ2t)dxdt≤C2,
where C1 and C2 are constants which depend only on known data.
Proof. By the standard compactness argument, we see that there exists a function ϕ(x,t)∈Cα,α2(¯QT)∩W2,12(QT) such that
|
ϕε(x,t)→ϕ(x,t)uniformly in Cα,α2(¯QT),ϕε(x,t)→ϕ(x,t)weakly in W2,12(QT).
|
Moreover, 0≤ϕ(x,t)≤1, 0≤ϕx(x,t)≤C1. For the limit function ϕ, and (x0,t0) with (x0,t0)∉ΓT and t0>0, where ΓT is defined in (19), there exists a small neighborhood Pδ(x0,t0)={(x,t)|(x−x0)2+(t−t0)2<δ} such that Pδ(x0,t0)∩ΓT=∅. In Pδ(x0,t0),
σε(x,t,ϕ)=σ(x,t,ϕ). By regularity theory of parabolic equation, ϕ(x,t)∈C2,1(Pδ(x0,t0)), and
It follows that for any (x,t)∉ΓT
|
ϕt−12σ2(ϕxx−ϕx)=0,in the classical sense in QT∖ΓT,ϕ(x,0)=ϕ0(x),−∞<x<+∞.
|
Notice also by Lemma 4.2, ϕ,ϕx are continuous across ΓT. That is, ϕ(x,t) is a solution in QT.
We can obtain a better regularity for the strong solution obtained in Theorem 4.1.
Theorem 4.2. The solution ϕ(x,t)∈C1+α,1+α2(QT) for some α∈(0,1). Moreover, ϕx(x,t) is Hölder continuous up to the initial time t=0 except a neighborhood of (0,0).
Proof. Indeed, we see ψ(x,t)=ϕx(x,t) is a weak solution of the following problem:
|
ψt=∂∂x[12σ2(ψx−ψ)],(x,t)∈QT,ψ(x,0)=ϕ′0(x)≥0,−∞<x<+∞.
|
By the standard regularity theory of parabolic equations, we see that ψ(x,t) is Hölder continuous in QT. Moreover, the Hölder continuity of ψ holds up to the initial time t=0 except a neighborhood of the singular point (0,0).
4.4. Uniqueness
In this section we use a novel approach to prove the uniqueness. This method is also suitable for a general n-dimensional problem.
Theorem 4.3. The solution obtained in Theorem 4.1 is unique.
Proof. We rewrite Eq.(18) as follows:
where
|
k(ϕ,x,t)={2/ˆσ2L(t), if ϕ>γex,2/ˆσ2H(t), if ϕ<γex.
|
Define
|
e(ϕ,x,t)=(1/ˆσ2L(t)+1/ˆσ2H(t))(ϕ−γex)+(1/ˆσ2L(t)−1/ˆσ2H(t))|ϕ−γex|={2(ϕ−γex)/ˆσ2L(t), if ϕ>γex,2(ϕ−γex)/ˆσ2H(t), if ϕ<γex.
|
(29)
|
which satisfies that
|
k(ϕ,x,t)=∂e∂ϕ={2/ˆσ2L(t), if ϕ>γex,2/ˆσ2H(t), if ϕ<γex.
|
(30)
|
Therefore,
|
∂∂t[e(ϕ,x,t)]−[ϕxx−ϕx]=∂e∂t≡f(ϕ,x,t),
|
(31)
|
where
|
f(ϕ,x,t):=(1/ˆσ2L(t)+1/ˆσ2H(t))′(ϕ−γex)+(1/ˆσ2L(t)−1/ˆσ2H(t))′|ϕ−γex|.
|
We also have
where
|
e0(x)=(1/ˆσ2L(0)+1/ˆσ2H(0))(ϕ0(x)−γex)+(1/ˆσ2L(0)−1/ˆσ2H(0))|ϕ0(x)−γex|,
|
To prove the uniqueness, we assume that there are two solutions ϕi(x,t), i=1,2 of the problem (17), (21), which satisfy the estimates in Theorem 4.1. Set
|
ϕ(x,t)=ϕ1(x,t)−ϕ2(x,t),(x,t)∈QT.
|
Now we multiply ∫τtϕ(x,s)ds in the both sides of (31), where τ∈[0,T], and then integrate it in R, we have
|
∂∂t∫R[(e(ϕ1,x,t)−e(ϕ2,x,t))∫τtϕds]dx+∫R[(e(ϕ1,x,t)−e(ϕ2,x,t))ϕ]dx=∫R[(ϕxx−ϕx)∫τtϕds]dx+∫R[(f(ϕ1,x,t)−f(ϕ2,x,t))∫τtϕds]dx:=A1(x,t,τ)+A2(x,t,τ),
|
where
|
A1(t,τ)=∫R[(ϕxx−ϕx)∫τtϕds]dx,A2(t,τ)=∫R[(f(ϕ1,x,t)−f(ϕ2,x,t))∫τtϕds]dx.
|
Now,
|
A1(t,τ)=−∫R[(ϕx−ϕ)∫τtϕxds]dx=12∂∂t∫R[∫τtϕxds]2dx+∫R[ϕ∫τtϕxds]dx.
|
|
A2(t,τ)=∫R[(fϕ(ξ,t)ϕ)∫τtϕds]dx,
|
where ξ is the mean-value between ϕ1 and ϕ2.
We take integration to the above equation with respect to t from 0 to τ to obtain:
|
∫τ0∫R[e(ϕ1,x,t)−e(ϕ2,x,t)]ϕdxdt+12∫R[∫τ0ϕxds]2dx=∫τ0∫R+[ϕ∫τtϕxds]dxdt+∫τ0∫R(fϕ(ξ,x,t)ϕ)∫τtϕdsdxdt≤2ε∫τ0∫Rϕ2dxdt+C(ε)∫τ0∫R([∫τ0ϕds]2+[∫τ0ϕxds]2)dxdt.
|
Here at the final step we have used the uniform boundedness of fu(u,t) and Cauchy-Schwarz's inequality with small parameter ε.
Notice (29), we have
|
[e(ϕ1,x,t)−e(ϕ2,x,t)]≥c0(ϕ1−ϕ2)=(2/σ21)ϕ,
|
where σ1 defined in (21) has a positive lower bound. We choose ε sufficiently small to obtain
|
∫τ0∫Rϕ2dxdt+∫R[∫τ0ϕxds]2dx≤C[∫τ0[∫t0∫Rϕ2dxds]dt+∫τ0∫R[∫τ0ϕxds]2dxdt].
|
Consequently, Gronwall's inequality yields ϕ(x,t)≡0 on Qτ. As τ is arbitrary over [0,T], we have ϕ(x,t)≡0 on QT.
Thin concludes the proof of uniqueness.
5. Free Boundary and its Regularity
In this section, we show that ΓT is the graph of a smooth free boundary x=s(t).
Lemma 5.1. There exists a number T0>0, such that ΓT0 defined in (19)
is the graph of a function
x=s(t),0≤t≤T0 with s(0)=s0=ln1γ.
Proof. Note that ϕ0(x)=min{ex,1}, then s0:=s(0)=ln1/γ>0, it follows that ϕ′0(x)=0, for x>0; ϕ′0(x)=ex, for x<0. It follows that if x>0,
Since ϕx(x,t) is Hölder continuous except (0,0), there exists small numbers t0>0 and δ0>0 such that
|
ϕx(x,t)−γex≤m0<0,s0−δ0<x<s0+δ0,0≤t≤t0,
|
where m0 depends on t0 and δ0.
By the implicit function theorem, there exists a function, denoted by x=s(t) solves ϕ(s(t),t)=γes(t) such that
|
Γt0={(x,t)|x=s(t),0≤t≤t0}.
|
It will be seen in the next theorem that we can extend t0 as long as ϕ−x(s(t),t)−γes(t)<0.
Theorem 5.1. There exists a function x=s(t)∈Cβ[0,T] with β∈(12,1) such that
Moreover, there exists a constant ε0>0 such that
|
ϕx(s(t),t)−γes(t)≤−ε0<0,0≤t≤T.
|
Proof. From Lemma 5.1, we know that there exists at least a small internal [0,T0] such that
Moreover,
|
ϕx(s(t),t)−γes(t)<0,t∈[0,T0].
|
Since F(x,t):=ϕ(x,t)−γex is differentiable in QT with respect to x, by the implicit function theorem, the set
|
Γt0={(x,t);F(x,t)=0,0≤t≤t0}
|
can be extended as the graph of a curve x=s(t) as long as
|
Fx(x,t)<0,for all (x,t)∈ΓT.
|
Moreover, x=s(t) is decreasing on [0,T].
Define
|
T∗=sup{T0:ϕx(s(t),t)−γes(t)<0,0≤t≤T0}.
|
We claim T∗=T. Assume the contrary with T∗<T. It is clear by the definition of T∗ and the continuity of ϕx(x,t) that
|
limt→T∗(ϕ−x(s(t),t)−γes(t))=0.
|
We define W(x,t)=ϕ(x,t)−γex, then
|
Wt=ϕt,Wx=ϕx−γex,Wxx=ϕxx−γex
|
Therefore, W(x,t) satisfies
|
Wt−12σ2H(Wxx−Wx)=0,−∞<x<s(t),0<t<T∗,W(s(t),t)=0,0<t<T∗,W(x,0)=W0(x),−∞<x<s0,
|
where W0(x):=ϕ0(x)−γex≥0 on (−∞,s0].
Since s(t) is decreasing on [0,T∗), Hopf's lemma holds at (s(T∗),T∗). Hence, by Hopf's lemma, there exists a number ε0>0 such that Wx(s(T∗),T∗)≤−ε0<0, which contradicts with the definition of T∗. It follows that T=T∗. Consequently, there exists a curve, denoted by x=s(t), such that
Moreover, there exists a constant ε0>0 such that
|
ϕx(s(t),t)−γes(t)≤−ε0<0,0≤t≤T.
|
(33)
|
To prove the Hölder continuity of s(t) on [0,T], we take any t1<t2 in [0,T] with |t1−t2| sufficiently small,
|
ϕ(s(t2),t2)−ϕ(s(t1),t1)=γ(es(t2)−es(t1)).
|
Then,
|
ϕ(s(t2),t1)−ϕ(s(t1),t1)−γ(es(t2)−es(t1))=ϕ(s(t2),t1)−ϕ(s(t2),t2).
|
We use the mean-value theorem to obtain
|
|s(t2)−s(t1)|≤|ϕ(s(t2),t2)−ϕ(s(t2),t1)||Fx(θ,t1)|,
|
where θ is the mean-value between s(t1) and s(t2).
Since |Fx(x,t)| is bounded and |Fx(x,t)| has a positive lower bound in a neighborhood of x=s(t),0≤t≤T, we find that there exists a constant C such that
where β=1+α2.
It follows that s(t) is Hölder continuous on [0,T] with a Hölder exponent β∈(12,1).
Theorem 5.2.
The free boundary s(t) satisfies
|
s′(t)=−σH(t)(ϕxx(s(t)−,t)−ϕx(s(t)−,t))ϕx(s(t),t)−γes(t),0≤t≤T.
|
Moreover, s(t)∈C∞[0,T], provided that σL(t) and σH(t) are smooth on
[0,T].
Proof. By Theorem 5.1, we can define QLT and QHT as in Section 3. From the theory of parabolic equations (Ladyženskaja et al., 1968), we know that ϕ(x,t) is smooth in QLT and QHT, respectively. Moreover, ϕx(x,t) is continuous up the boundary x=s(t) from the left-hand side and the right-hand side on [0,T].
To prove the further regularity of s(t), we note that ψ(x,t)=ϕx(x,t) is a classical solution of the following free boundary problem
|
ψt=∂∂x[12σ2(ψxx−ψ)],(x,t)∈QT∖ΓT,ψ(s(t)−,t)=ψ(s(t)+,t),0<t<T,σH(ψx(s(t)−,t)−ψ(s(t),t))=σL(ψx(s(t)+,t)−ψ(s(t)+,t)),0≤t≤T,s′(t)=−σH(t)(ψx(s(t)−,t)−ψ(s(t),t))ψ(s(t),t)−γes(t),0≤t≤T,ψ(x,0)=ϕ′0(x),−∞<x<∞.
|
We can apply the classical technique for the Musket problem Evans (1978) to obtain s(t)∈C∞[0,∞].
Theorem 5.3. s(t) is non-increasing on [0.T].
Proof. We go back the approximate problem (24)-(25). Note that ϕ′0(x)−ϕ0(x)=0 if x<0 and ϕ′0(x)−ϕ0(x)=−1 if x>0. We can construct a smooth approximation for ϕ0(x) such that
Let w(x,t)=ϕεt(x,t). Then w(x,t) satisfies
|
wt=12σ2[wxx−wx]+a(x,t)w,(x,t)∈QT.
|
where
|
a(x,t):=(σ2(t,ϕ))tσ2(t,ϕ).
|
Moreover,
|
w(x,0)=12σε(0,ϕ0)2[ϕ″0ε(x)−ϕ′0ε(x)]<0,−∞<x<∞.
|
By the maximum principle, we see w(x,t)≤0 on QT. After passing the limit, we see
|
ϕxx(x,t)−ϕx(x,t)≤0,(x,t)∈QT,
|
in the L2-sense. On the other hand,
|
ϕx(s(t),t)−γes(t)<0,0≤t≤T,
|
we see from the representation of s(t) that
6. Numerical Example
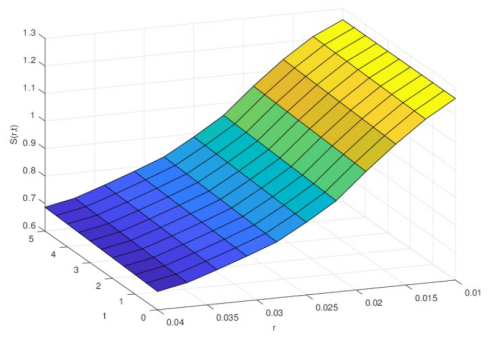
The numerical solution of the Eq.(17), (21) can be calculated by using a standard PDE method. However, we are more interested in the. For convenience, the free boundary is denoted by s(r,t), which depends on the interest rate r.
In order to draw the graph s(r,t), we use the explicit difference scheme (Jiang, 2005), which is equivalent to the well-known the Binomial-Tree method. The steps of the computation are as follows:
1. Discrete t∈(0,T) by ti=T−iΔt, where T=t0,...,tI=0, I=10, Δt=tI−t0I; r∈(0.01,0.04) by rk=0.01+kΔr, where 0.01=r0,...,rK=0.04, Δr=rK−r0K; in space using a mesh with difference Δx: 0=x0,...,xj=2. And at every point (ti,xj,rk), denote the function ϕ(ti,xj,rk) by ϕi,j,k.
2. For t0=T,
ϕ0,j,k=min(xj,F), then solve ϕi,j,k by finite difference scheme:
|
ϕi,j,k=ϕi−1,j,k+σ2Δt2Δx2x2j[ϕi−1,j−1,k+ϕi−1,j+1,k−2ϕi−1,j,k]+σ2rΔt2Δr2r2k[ϕi−1,j,k−1+ϕi−1,j,k+1−2ϕi−1,j,k]+rkxjΔt2Δx[ϕi−1,j+1,k−ϕi−1,j−1,k]+a(θ−rk)Δt2Δr[ϕi−1,j,k+1−ϕi−1,j,k−1]−rkϕi−1,j,kΔt+σσrΔtρxj4ΔrΔx[ϕi−1,j+1,k+11−ϕi−1,j+1,k−1−ϕi−1,j−1,k+1+ϕi−1,j−1,k−1],
|
where
|
σ={σL, if ϕi−1,j,k>γxk,σH, otherwise,
|
Denote the joint points to be sj,k, which represents the approximated credit rating migration joints.
3. Repeat the above process.
4. Draw the graph based on {sj,k} in space r.S,t.
Now we have the 2-d free boundary interface.
The numerical solution of the free boundary is shown in Figure 1, where the parameters and the ranges of the variables are chosen as follows
|
a=1,θ=0.03,F=1,γ=0.8,σL=0.4,σH=0.2,σr=0.3,ρ=0.5,T=5,r∈(0.01,0.04), t∈(0,5).
|
From the graphs, we see that a free boundary y=s(r,t) divides the region into two parts: high and low rating regions. Moreover, the free boundary is decreasing with respect to r and increasing with respect to t as expected (see Theorem 4.1 and Theorem 5.2), where t is the original life time of the bond. From the graph Fig. 1, we also see that the change of free boundary is more sensitive with respect to the interest rate than that of time.
7. Conclusion
In this paper, we derived a new model for pricing corporate bonds with credit-rating migration and a stochastic interest rate. The new model consists of a coupled system of partial differential equations. By employing a dimension-deduction technique, we obtain a new free boundary problem. By using various analysis techniques for partial differential equations, we established the existence, uniqueness and regularities of the solution under certain assumptions. Moreover, some properties of the solution are derived. A C∞-regularity of the free boundary is proved. Their financial implications are explained. The model is new to our knowledge and is a big improvement for the current model. The analysis is delicate. Finally, numerical simulations are also presented.
Acknowledgement
This work is supported by National Natural Science Foundation of China (No.11671301).The authors would like to thank Professor Bei Hu for some discussions during the preparation of the paper. Many thanks also go to anonymous referees for their comments and suggestions. Chen and Yin would like to thank the hospitalities of Tongji University during their visiting where the part of this work was completed.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: 



