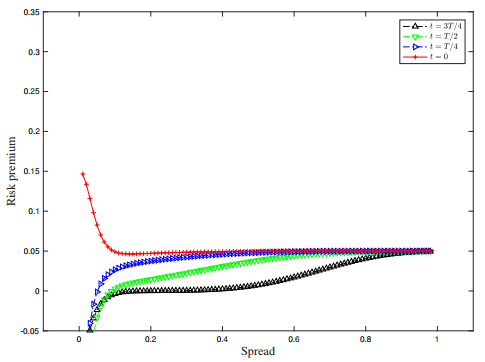
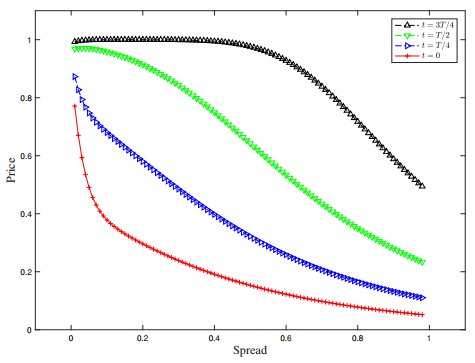
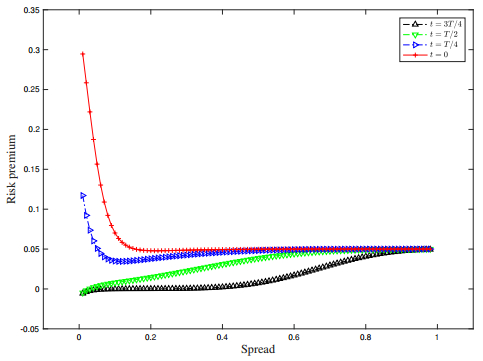
Taking arbitrage opportunities into consideration in an incomplete market, dealers will price bonds based on asymmetric information. The dealer with the best offering price wins the bid. The risk premium in dealer's offering price is primarily determined by the dealer's add-on rate of change to the term structure. To optimize the trading strategy, a new equilibrium trading model is introduced. Optimal sequential estimation scheme for detecting the risk premium due to private inforamtion is proposed based on historical prices, and the best bond pricing formula is given with the according optimal trading strategy. Numerical examples are provided to illustrate the economic insights under the certain stochastic term structure interest rate models.
1.
Introduction
Hippocampus detection is a critical activity in the medical industry because it provides anatomical data on the size and structure of the hippocampus, which subsequently aids doctors in patient planning, treatments, and follow-ups. The hippocampus plays a vital role in the formation, consolidation, and retrieval of memories. It receives information from various sensory systems and processes it before sending it to other regions of the brain for long-term storage. Specifically, the hippocampus is associated with the formation of declarative memories, which are memories of facts and events. It helps to organize and integrate information from different brain regions to create coherent memories. Damage to the hippocampus can result in memory impairment, specifically in the formation of new memories, which is often observed in conditions such as Alzheimer's disease and other forms of amnesia. Accurate segmentation of the hippocampus is a critical task in medical imaging, particularly for diagnosing and monitoring conditions such as Alzheimer's disease. Traditional methods, including deformable shape models and multi-atlas-based segmentation techniques, have significantly advanced the field. However, these approaches often struggle with complex cases that involve significant pathological variations, variability across imaging modalities, and the need for extensive manual intervention. While deep learning techniques, such as Convolutional Neural Networks (CNNs) and Generative Adversarial Networks (GANs), have shown promise in enhancing the segmentation accuracy, they still face limitations in handling challenging cases and require large amounts of labeled data for training.
To address this, the Semi-Supervised Deep Neuro-Fuzzy Iterative Learning (SS-DNFIL) method introduces a novel approach that combines deep learning with fuzzy logic in a semi-supervised framework. This innovative method effectively utilizes both labeled and unlabeled data, thus reducing the dependency on extensively annotated datasets and improving the generalization across diverse imaging conditions. By leveraging a semi-supervised learning paradigm, SS-DNFIL enhances the robustness and adaptability of segmentation models, particularly in cases where labeled data is either scarce or difficult to obtain. The hippocampus' intricate limits and undetectable location make it difficult for humans to accurately segment it, hence a computer-aided process is required to identify it. To normalize the hippocampus volume, four potential approaches are suggested, including the head circumference, sphere volume, block volume, and intracranial volume [1]. A Deformable Shape Model [2] should be used to estimate the hippocampus' size and shape in MR images. The overlap error and mean volume were said to be within the bounds of accuracy and dependability. The normal neuroanatomic atlas of the hippocampus divides the surface of the hippocampus into zones. Hippocampal surface alterations [3] are shown using surface-based measures and surface-based mesh modeling. This approach allows for the detection of regional changes from the subcortical systems. Based on the findings in [4], Ada-Support Vector Machine (Ada-SVM) is considered superior to AdaBoost, SVM, and FreeSurfer in terms of hippocampal border detection. A multi-atlas segmentation approach with joint label fusion [5] was proposed for the segmentation of the hippocampus and its subfields in Magnetic Resonance Imaging (MRI) images. In this technique, the joint label fusion was used after the atlases were registered with the target image. Joint label fusion reduces the expected label error by considering the interdependencies among the atlases. In the SS-DNFIL System for hippocampus segmentation, multiple atlases and their components are strategically integrated to enhance the segmentation accuracy and robustness. Anatomical atlases provide prior knowledge and initial segmentation references, while classifiers, such as deep neural networks, label different brain tissues based on the features extracted through Deep Hierarchical Self-Organizing Feature Maps (DHSOFM) and Fuzzy C-Means (FCM) clustering. Label fusion techniques, such as Joint Label Fusion, aggregate outputs from multiple atlases to produce a consensus segmentation map, thus reducing errors and improving the reliability. Optimizers fine-tune model parameters to enhance the performance, while iterative refinement processes continuously improve the segmentation results by addressing inaccuracies and adapting to pathological variations. This hybrid approach effectively combines deep learning with fuzzy logic, thereby leveraging the strengths of each to achieve precise and adaptive segmentation of the hippocampus in MRI images. Using a two-layer Independent Subspace Analysis model, the manually built features are replaced in 7.0 tesla pictures with hierarchical features [6], thus introducing the Unsupervised Deep Learning Hippocampus (HC) segmentation methodology. Discriminative dictionary learning and sparse patch representation have been implemented to surpass the limitations of the multi-atlas techniques used to measure the volume of the hippocampus [7]. After atlases have been registered with the resulting image, the patch-based features are retrieved. The patch set dictionaries are learned using classifiers and dictionaries. Then, a fully automatic hippocampal segmentation method which uses subject-specific sets and three-dimensional optimal local maps [8] was proposed.
The feature extraction is performed based on the Gray Level Co-occurance Matrix (GLCM) once the GLCM [9] of the picture has been determined. The GLCM is a prominent method for a texture analysis in image processing, thereby capturing the spatial dependencies between pixel intensities and generating a matrix where each entry quantifies the frequency of occurrence of specific pixel intensity pairs under defined spatial relationships. Key texture features derived from the GLCM, including contrast, correlation, energy, and homogeneity, provide critical insights into the image texture. In practical applications such as brain tumor segmentation from MRI images, GLCM features are computed to form detailed feature vectors that encapsulate the textural information of different regions. These vectors are subsequently utilized in clustering algorithms, such as k-means, to group pixels with similar texture patterns, thereby facilitating the accurate isolation of tumor regions from the surrounding tissues. The efficacy of this approach is validated through comparisons with either expert annotations or ground truth data, thus demonstrating that a GLCM-based texture analysis significantly enhances the precision of segmentation tasks in medical imaging. The mean, correlation, kurtosis, contrast, standard deviation, inverse difference moment, energy, skewness, entropy, and homogeneity are the features that are extracted from the brain MR images. In the proposed method, a GLCM is employed for a texture analysis by capturing the spatial relationships between the pixel intensities in MRI images. The GLCM creates a matrix that quantifies how often pairs of pixel intensities occur at specific spatial relationships within the image. Important texture features such as contrast, correlation, energy, and homogeneity are derived from this matrix. These features provide valuable information about the textural patterns of different regions in the brain, thus making it easier to differentiate between tissues such as the hippocampus, gray matter, and white matter. Once the GLCM features are extracted, they are fed into the Fuzzy C-Means clustering algorithm, where they help group pixels with similar textural patterns. The clusters formed correspond to different anatomical structures in the brain. For instance, the hippocampus exhibits specific textural characteristics that are different from the surrounding tissues, allowing the GLCM-derived feature vectors to contribute to more accurate segmentation. Thus, the extracted GLCM features play a pivotal role in enhancing the accuracy of the segmentation process by providing a rich set of descriptors that capture the textural diversity of the brain tissues.
For the segmentation of the hippocampus, a few atlases, including classifiers, label-fusion, optimizers, and non-linear registration methods such as Automatic Registration Toolkit (ART) and Symmetric Normalization (SyN) [10], are used to obtain prior knowledge about the medical image before segmentation. Atlases in medical image segmentation serve as prior knowledge sources, thus providing reference segmentations that guide the automatic segmentation process. In the proposed method, multiple atlases are used as the initial segmentation references. Once aligned with the target MRI image through a registration process, these atlases provide a rough segmentation that outlines the hippocampus and other brain regions. Each atlas acts as a classifier, thereby labeling different tissues based on the features extracted from the image. However, since each atlas may have variations due to differences in anatomy or imaging modalities, relying on a single atlas may lead to errors. The proposed method employs label fusion techniques, specifically Joint Label Fusion, to overcome this limitation. This technique aggregates the segmentation results from multiple atlases, thereby combining their outputs to produce a consensus segmentation map. The label fusion process helps mitigate the errors that may arise from individual atlases by considering their interdependencies and agreements. Optimizers, such as the Adam optimizer, are applied during the deep neural network training to fine-tune the model's parameters. The role of the optimizer is to adjust the model weights to minimize the loss function and to improve the segmentation accuracy. The iterative refinement process further enhances the segmentation by continuously improving the results with each iteration, correcting inaccuracies, and adapting to variations in the dataset. The deep learning techniques dramatically enhanced the effectiveness of image identification and semantic segmentation techniques [11]. Data-driven techniques are included in hierarchical feature learning and are simple to apply to medical images. The NiftyNet architecture [12] makes it possible to apply deep learning to big and complicated data sets. A patch extraction technique and the Classification-Guided Boundary Regression approach were developed for the HC segmentation of newborn brain MRI images [13]. Using the two-stage ensemble CNN, the displacement vectors are incorporated in the sample position to determine the output position based on the hough ranking approach for hippocampal localization. The left and right hippocampi prediction errors were 2.32 and 2.31 mm, respectively [14]. The deep CNN for HC segmentation with obvious segmentation and error-fixing steps was presented by incorporating the edge information into the loss function [15]. Then the Replace and Refine networks [16] were combined to correct incorrect labels, thus increasing the dice values mean on the MICCAI and EADC-ADNI Harp datasets.
The use of specialized layers such as Convolution layers, location pooling, and abstraction were enabled for modeling using generators and discriminators in Generative Adversarial Networks [17]. To segment medical images, various deep learning network architectures such as Convolutional Residual Networks (CRNs), Recurrent Neural Networks (RNNs), U-Net, V-Net, and several other Convolutional Neural Networks [18] have been implemented. In combination with Bayesian techniques, deep learning was shown [19] to outperform traditional methods in segmenting unclear areas of the image. An autonomous level set method combined with a CNN was used to adjust the contour to two levels, and a training was performed on the images. The suggested system yielded a dice similarity coefficient of 0.864 [20]. The multi-model CNN [21] was first used for HC segmentation and AD to classify the disease and to learn the 3D patch features using segmentation data. In the field of neuroimaging, deep learning approaches are effective tools for automated brain segmentation, outperforming traditional methods. A brain MRI with noise was used to illustrate a hippocampal segmentation method using the clustering method known as Subspace Patch-Sparsity Clustering [22,23,24,25,26]. A spatial Fuzzy C-Means (sFCM) method [27] was proposed for clustering the nearby pixels, thus resulting in better image segmentation due to the inclusion of spatial context. The spatial information in the membership function produced better results for segmentation with the proposed method dealt. A new fuzzy-level set algorithm for automated medical image segmentation was proposed in which the method used Fuzzy clustering with spatial information [28] that had defined boundaries. The proposed method removed boundary leakage issues and manual intervention during the process of image segmentation. Segmenting masses from the multi-parametric MRI using sFCM [29] automatically segmented breast cancer-affected parts. Alternatively, a better option than the conventional U-Net architecture is U-Net++ [30]. U-Net++ employs dense and stacked skip connections to close the semantic gap between the feature maps of the encoder and the decoder. ResNet-50 [31] is a significant advancement in deep learning, thereby solving the vanishing gradient problem through residual learning and enabling the training of very deep networks, which has made it a foundational model in computer vision tasks such as object detection and image classification. DenseNet [32] builds upon this by establishing feed-forward connections between all layers, which minimizes the redundancy and increases the feature propagation, thus resulting in more effective parameter usage and a superior performance. The Swin Transformer [33], applies a hierarchical vision transformer using shifted windows, thus enabling scalability to high-resolution images, and achieving state-of-the-art results in tasks such as object detection and segmentation. Squeeze-and-Excitation (SE) Networks [34], enhance the representational power of CNNs by explicitly modeling channel interdependencies, thus leading to an improved accuracy across various models. HRNet [35], maintains high-resolution representations throughout the network, thus setting new benchmarks in visual recognition tasks that require precise spatial information, such as object detection and semantic segmentation.
Existing hippocampus segmentation methods face several drawbacks. Traditional techniques, such as deformable shape models and multi-atlas-based approaches, often struggle with complex pathological variations and variability across imaging modalities, thus leading to inconsistent and less accurate results. Additionally, these methods require extensive manual interventions, making them time-consuming and prone to human error. While promising, these methods demand large amounts of labeled data for training, which can be difficult to obtain and lead to overfitting issues that impact the generalization to new data Deep learning techniques. Additionally, these advanced models are computationally intensive, thus requiring significant resources that may not be available in all medical settings. Furthermore, the complexity of deep learning models can hinder interpretability, thus making it challenging for clinicians to understand and trust the segmentation results. Issues such as boundary leakage and the need for manual corrections persist even with advanced methods, thus affecting the overall automation and accuracy. Recent advancements in Semi-Supervised Learning (SSL) for medical image segmentation highlight significant progress in addressing challenges related to limited labeled data and complex imaging scenarios. The framework proposed in [36] leveraged shape encoding for neonatal ventricular segmentation from 3D ultrasound images, thus enhancing the segmentation accuracy by incorporating the anatomical shape information. This method is valuable in neonatal imaging, where acquiring labeled data is difficult due to the complexity and variability of the neonatal anatomy. In [37], the Dual-Contrastive Dual-Consistency Dual-Transformer model was introduced, by combining contrastive learning with a dual-transformer architecture to improve medical image segmentation. This model enhances feature representation and consistency, by employing dual-contrastive and dual-consistency learning strategies, thus demonstrating a robust performance in scenarios with limited labeled data. This approach underscores the effectiveness of combining advanced learning techniques to address the challenges of medical image segmentation. Further advancements are seen in [38,39], which proposed innovative SSL approaches for brain tumor segmentation. The method [38] used a semi-supervised multiple evidence fusion approach, thereby combining information from various sources to improve the segmentation accuracy. Meanwhile, [39] introduced the Exigent Examiner and Mean Teacher framework, thereby integrating adaptability and consistency regularization in 3D CNN-based segmentation. Additionally, [40] addressed motion artifacts in brain tumor segmentation by incorporating these artifacts into a motion-artifact-augmented pseudo-label network, thus enhancing the robustness and accuracy. These studies collectively highlight how SSL techniques improve the segmentation performance by effectively utilizing both labeled and unlabeled data in challenging medical imaging contexts.
It was discovered that the issue of hippocampal segmentation can be successfully addressed by a semi-`supervised clustering strategy. For the healthcare organization to deliver a diagnosis based on volume, accurate and automatic segmentation is needed [40]. This research suggests an SS-DNFIL to segment the hippocampus. An SS-DNFIL algorithm combines elements of deep neural networks, fuzzy logic, and iterative refinement to perform segmentation in a semi-supervised manner. The Deep Neuro-Fuzzy System is a hybrid Deep Artificial Neural Network and a Fuzzy Logic based Artificial Intelligence System. Here, the FCM algorithm and the Deep Hierarchical Self DHSOFM based on ANNs were developed to classify the image layer by layer. Different tissues, including the Grey Matter (GM), White Matter (WM), Cerebrospinal Fluid (CSF), and the Hippocampus (HC), are detected by the DHSOFM and FCM. DHSOFM uses multi-scale segmentation to achieve the feature space at various levels of abstraction. Grey matter will be represented at one level of abstraction, and white matter at a higher level; therefore, extracting all the features on a multi-space makes the clinical diagnosis simpler. The SS-DNFIL method integrates two powerful techniques: DHSOFM and FCM clustering. DHSOFM facilitates multi-scale and multi-level feature extraction, thus allowing for the detection of different brain tissues such as WM, GM, CSF, and the HC at various levels of abstraction. This hierarchical feature extraction enables a more accurate and detailed segmentation by capturing the complex anatomical structures of the hippocampus and its surrounding tissues. Meanwhile, the FCM clustering algorithm incorporates fuzzy logic to handle the inherent uncertainties and variations in medical images, thus further enhancing the precision of segmentation. A key innovation of SS-DNFIL is its iterative refinement process, which progressively improves the segmentation results through multiple iterations. This iterative approach addresses common issues such as boundary leakage and inaccuracies in the initial segmentations. SS-DNFIL enhances the method's ability to accurately delineate the hippocampus, by continuously refining the segmentation output, even in the presence of significant atrophy, lesions, or abnormal shapes. This iterative learning process improves the segmentation accuracy and makes the method more adaptable to various pathological conditions.
The SS-DNFIL method integrates deep neural networks (DNNs), fuzzy logic, and iterative refinement, each selected for their respective complementary strengths in enhancing the segmentation performance. DNNs are leveraged for their robust capability to extract complex, high-level features from medical images, which is essential for accurate segmentation. However, given the scarcity of labeled medical data, a semi-supervised learning approach is employed, allowing the model to effectively utilize both labeled and unlabeled data, thus improving its generalization, and reducing the dependency on large annotated datasets. Fuzzy logic is incorporated to address the inherent uncertainties and ambiguities in medical imaging, where traditional binary logic systems fall short. By allowing for degrees of truth, fuzzy logic enhances the model's ability to handle imprecise data, particularly in cases where anatomical boundaries are not delineated, such as in hippocampus segmentation. The iterative refinement process further augments this framework by enabling the model to progressively enhance its predictions through multiple iterations. Unlike static, one-shot learning methods, this iterative approach allows the model to continuously refine its segmentation output continuously, leading to a higher accuracy and reliability. The synergistic combination of DNNs for feature extraction, fuzzy logic for uncertainty management, and iterative refinement for continuous improvement results in a method that is highly effective in producing precise and robust segmentation outcomes in complex medical imaging scenarios. The combination of deep learning and fuzzy logic is particularly advantageous in medical image segmentation, especially for intricate structures such as the hippocampus, where challenges such as boundary uncertainty and limited annotated data are significant. Deep learning, specifically using CNNs, excels in extracting complex hierarchical features from high-dimensional data such as MRI scans. [41,42] CNNs are proficient at identifying patterns and structures, such as textures and shapes within medical images, though their performance heavily relies on the availability of a large amount of labeled data. However, obtaining such annotated data in medical imaging is often difficult, particularly for structures such as the hippocampus, which may exhibit significant variation across patients. Moreover, CNNs can struggle with cases where anatomical boundaries are unclear or where the image contains noise and irregularities, thus leading to an inaccurate segmentation. This is where fuzzy logic, particularly the Fuzzy C-Means (FCM) clustering algorithm, plays a crucial role. Fuzzy logic is designed to handle uncertainty and imprecision by allowing either soft or partial membership of data points to different classes or clusters, rather than forcing a binary decision. In the context of hippocampus segmentation, FCM enables the method to assign pixel degrees of membership to different regions, such as GM, WM and the HC itself. This soft partitioning is particularly effective in cases where the boundaries between regions are ambiguous. The innovation of the proposed method lies in how it integrates deep learning with fuzzy logic through an iterative learning process. The CNN extracts detailed features, while the FCM uses these features to segment the image based on the fuzzy memberships. The iterative learning approach refines the segmentation over multiple cycles, thereby revisiting regions of ambiguity where pixels belong to multiple clusters and adjusting the segmentation output accordingly. This combination improves the segmentation accuracy by leveraging the strengths of deep learning for feature extraction and fuzzy logic to manage the uncertainty and imprecision, thus leading to a more robust and reliable performance, even with limited annotated data.
2.
Semi supervised deep neuro-fuzzy iterative learning system
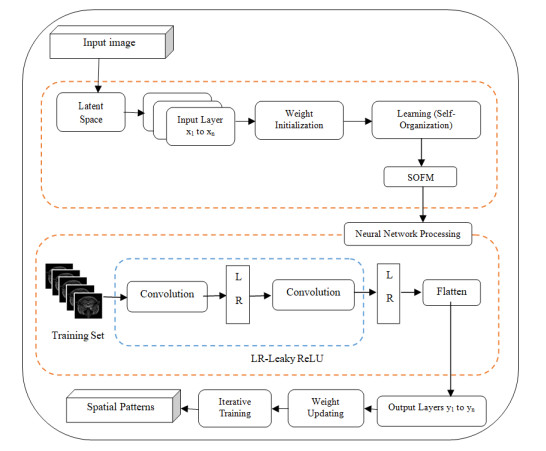
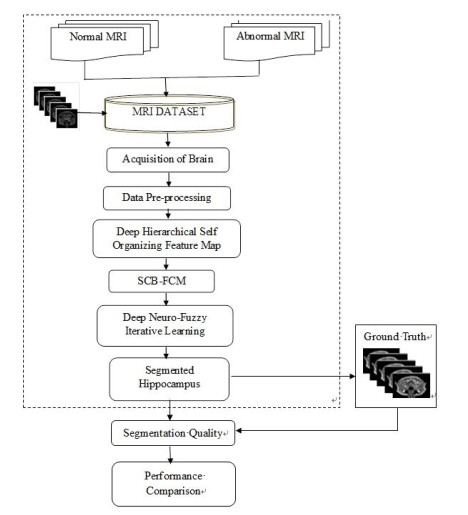
The similarities of several objects with mathematical processes that are described by a member function to partition the categories quantitatively are decided by the Fuzzy clustering schemes. The FCM is the most used algorithm among all the fuzzy clustering schemes. It is the most widely used scheme since it preserves much more information and because of its advantages of robustness for ambiguity than any other clustering schemes. Figure 1 depicts the proposed flow for the Neuro-Fuzzy Technique for Hippocampus Detection. The SS-DNFIL System involves several key steps to enhance hippocampus segmentation. Initially, MRI images are collected and preprocessed to standardize and normalize the data. Then anatomical atlases are integrated to provide prior knowledge and initial segmentation references. This is followed by a feature extraction thereby, utilizing techniques such as DHSOFM and FCM clustering to capture the relevant details. The system employs a semi-supervised learning framework that combines labeled and unlabeled data, thus reducing the reliance on extensive annotations and leveraging additional information for an improved performance. The deep learning model is trained using this combined data, and label fusion techniques, such as Joint Label Fusion, are applied to aggregate outputs from multiple atlases and classifiers, thus enhancing the segmentation accuracy. Iterative refinement processes continuously improve the results by addressing inaccuracies and adapting to variations. The system is validated and tested against the ground truth data to ensure reliability, and the final optimizations are performed to fine-tune the model [43]. Ultimately, the trained model is deployed and integrated into clinical workflows to aid in the diagnosis and monitoring of the hippocampal conditions. The SS-DNFIL algorithm is a cutting-edge method developed to tackle the complexities of medical image segmentation, with a particular focus on hippocampus segmentation from MRI scans. This algorithm leverages the strengths of deep neural networks (DNNs) for the feature extraction, fuzzy logic for managing uncertainties in the data, and an iterative refinement process to enhance the accuracy of the segmentation. By combining these elements, the algorithm is designed to deliver high precision and reliability, even when labeled data is scarce, which is a common challenge in medical imaging. The various steps involved in the SS-DNFIL are as follows.
Step 1: Data preparation
In the data preparation phase, MRI images of the hippocampus are preprocessed to ensure the consistency and quality. Normalization is applied to adjust the image intensity values to a standard range. For example, if I represents the raw image and I′ the normalized image, then normalization can be denoted as Eq (1) [43]:
where μ is the mean, and σ is the standard deviation of the pixel values. The images are resized to a uniform dimension Iresized to facilitates the batch processing by Eq (2) [43]:
Data augmentation includes techniques such as scaling, rotation, and flipping, applied via affine transformations. For instance, a rotation transformation Irot can be defined as Eq (3) [43]:
where θ is the rotation angle. These steps enhance the model's ability to generalize across diverse imaging conditions.
Step 2: Feature extraction
Feature extraction uses a CNN to transform the MRI images into feature maps. For a given input image I, the convolution operation can be mathematically represented as Eq (4) [43]:
where Fl is the feature map at I, the Wl,k layer denotes the convolutional filter at layer I, ∗ represents the convolution operation, bl is the bias term, and σ is the activation function. This step extracts hierarchical features from the images, thereby capturing spatial patterns and anatomical structures essential for accurate segmentation.
Step 3: Fuzzy logic integration
FCM clustering is applied to classify features into distinct clusters based on the membership values. The objective function of FCM, which must be minimized, is provided by Eq (5) [43]:
where μik represents the membership degree of feature xi in cluster ck, m is the fuzziness parameter, and C is the number of clusters. The membership values are iteratively updated using Eq (6) [43]:
This allows the algorithm to handle uncertain and overlapping regions by assigning partial membership to different clusters.
Step 4: Iterative learning and label fusion
In iterative learning, the model is refined by integrating predictions from both labeled and pseudo-labeled data. Pseudo-labels are generated by applying the current model to the unlabeled data. The label fusion process uses multiple models to produce a consensus segmentation map. If Si represents the segmentation map from model i, then the fused segmentation map S is computed as Eq (7) [43]:
where M is the number of models, and Argmax selects the class with the highest average probability across models. This consensus approach reduces the segmentation errors and improves the overall accuracy.
Step 5: Model optimization
Model optimization is performed using gradient-based methods to minimize the loss function. For a set of images, the loss function L can be defined for {(Ii,Gi)}Ni=1 as Eq (8) [43]:
where Si is the predicted segmentation map, Gi is the ground truth, and Loss is a suitable loss function, such as the cross-entropy or Dice loss. The optimization process updates the model parameters θ using the gradient descent Eq (9) [43]:
where η is the learning rate, and ∇θL is the gradient of the loss function concerning θ. This step fine-tunes the model to improve the performance on both the labeled and unlabeled data.
Step 6: Evaluation and post-processing
Evaluation involves calculating performance metrics such as the Dice coefficient D, the Jaccard index J, the sensitivity S, and the specificity Sp. For instance, the Dice coefficient is calculated as Eq (10) [43]:
where ∣⋅∣ denotes the number of voxels in the segmentation S and ground truth G. Post-processing techniques such as morphological operations are applied to refine the segmentation boundaries. For example, a dilation operation can be mathematically expressed as Eq (11) [43]:
where structuring_element defines the shape and size of the dilation kernel. These steps enhance the segmentation result's visual and quantitative qualities, thus making it more applicable for clinical use.
2.1. Deep hierarchical self-organizing feature map
Segmentation of the brain is a challenging task and can be achieved by semi-supervised SOM, and the probability-based clustering method, and the salient dimension for automatic SOM labeling can also be extracted. Object tracking can be achieved with the help of self-organizing maps using saliency maps and FCM segmentation [44,45]. The DHSOFM is a computational model inspired by the organization and function of the human brain, particularly the hippocampus, which plays a crucial role in memory formation and spatial navigation. DHSOFM is designed to perform segmentation tasks, such as hippocampus segmentation, by learning the underlying structure and patterns in the input data. The DHSOFM model consists of multiple layers of Self-Organizing Feature Maps (SOFMs) that are hierarchically arranged. Each layer represents a different level of abstraction, thus capturing increasingly complex features as the information flows through the network. The SOFM is a type of unsupervised learning algorithm that organizes the input data based on their similarities and forms a topological map. In the context of hippocampus segmentation, the DHSOFM model can be trained using a large dataset of brain images, where the hippocampus is labeled. The model can learn to recognize the characteristic features and spatial relationships of the hippocampus from the input data.
During the training process, the DHSOFM model undergoes a competitive learning phase, where neurons within each layer compete for the representation of input patterns. The winning neurons adjust their weights to better represent the input, while neighboring neurons also undergo slight adjustments, thus promoting the formation of a topological map that preserves the spatial relationships of the input features. Once trained, the DHSOFM model can be used for hippocampus segmentation by presenting it with unlabeled brain images. The model will process the input through its hierarchical layers, thereby gradually extracting the complex features and identifying the regions that correspond to the hippocampus. The model's ability to capture spatial relationships and feature representations enables it to generate segmentation maps that highlight the hippocampus region in the input image. DHSOFMs are semi-supervised neural networks that cluster high-dimensional data. The transformation of complex input data into easily understandable 2D output data is performed by DHSOFM. It uses processing units called neurons to place centroids on an adjustable map. As the processing units develop, they maintain a spatial proximity. The model self-organizes through learning rules and interactions [44,45]. The main advantages of using DHSOFM include its ability to find clusters in large datasets, thus making it effective for a dimensionality reduction. Additionally, it offers powerful data visualization capabilities and can identify patterns by integrating diverse datasets. DHSOFM is highly versatile, is applicable across various fields, and simplifies complex data analysis. Additionally, it updates its weights through learning based on inputs and supports the construction of 2D/3D images using the Euclidean distance. These features make it a robust tool to handle large-scale, multidimensional data.
2.1.1. Training process of DHSOFM
The training process of DHSOFM falls under five steps:
1) Initialization of neural network weights.
2) Selection of a random input.
3) Find the winning neuron using Euclidean Distance.
4) Update the weights of neurons.
5) Repeat from Step 2 until training is done.
Deep learning involves the use of neural networks with multiple layers ie., DNNs to learn hierarchical representations from data. A hierarchical structure in a neural network involves organizing the layers in a hierarchical manner, where each layer captures different levels of abstraction or features. A self-organizing feature map is a type of neural network that employs unsupervised learning to produce a low-dimensional representation (map) of input data. It organizes neurons in a way that preserves the topology of the input space. DHSOFM combines deep learning principles with a hierarchical structure and incorporates self-organizing feature maps. DHSOFM is applied to tasks where hierarchical and hippocampus-structured representations are crucial in complex datasets. The structure of DHSOFM has input layers x1 to xn, neural network weights x1 to xn, and DHSOFM output layers y1 to yn. This structure illustrates the simplified process by which the DHSOFM handles input data, learns hierarchical features through self-organization, and adapts its weights during training. The random selection of input data during each iteration introduces stochasticity, thus enhancing the model's ability to generalize to diverse patterns in the data. Here, the input data is randomly selected from the input layer. For an MRI of a human head, xi represents voxel intensities and other features at position i in the image. In the first step, the weights of the neural network are randomly initialized from w1 to wn. These weights can be adjusted during the training process to capture patterns in the input data.
The input data x1 to xn is fed into the neural network, which includes multiple layers, possibly organized hierarchically. Each output layer yi corresponds to the self-organizing feature map output at position i. These output layers represent the organized features that the DHSOFM learns. The DHSOFM undergoes unsupervised learning, where the self-organizing feature maps are organized to capture patterns and representations in the input data. Hierarchical feature extraction occurs in each layer of the neural network, thus allowing the model to learn increasingly abstract and complex representations. In the next step, the input data x1 to xn is randomly selected from the input layer for processing. This randomness introduces variability during training. The weights w1 to wn are iteratively updated during training based on the input data, self-organization, and supervised fine-tuning. The entire process is repeated for multiple iterations or epochs, thus allowing the DHSOFM to refine its representations and learn spatial patterns within the input data.
The Euclidean Distance between the weight vector and the input layer is calculated by Eq (12) [44]:
The winning neuron is selected based on the smallest Euclidean Distance. The next step is to update the neuron weights in the neural network. Breaking down of the weight update is performed by Eq (13) [44]:
where the epoch is t, the neuron is i, another neuron is j, and the winning neuron is I(x). The learning rate is calculated by Eq (14) [44]:
The topological neighborhood between the pixels on the feature space is analyzed by Eq (15) [44]:
The lateral distance between the neurons is computed by Eq (16) [44] as follows:
Then, the features of the input sample, such as energy, entropy, and standard deviation, are extracted using Eqs (17)–(19) [44]:
The size of the neighborhood neuron is calculated by Eq (20) [44]:
Furthermore, an abstraction tree is constructed after analyzing the winning neuron. The Deep Hierarchical Self Organizing Map Feature vector is generated and the input images are mapped to clusters in the output feature space. Figure 2 depicts the Hierarchical Structure of the Organizing Feature Map (DHSOFM) to the MRI Dataset.
2.2. Spatial content-based fuzzy C-Means clustering for HC segmentation
The FCM clustering algorithm is applied to the image obtained after HSOFM. The advantage of fuzzy-based clustering is that the pixels will be grouped into more than one cluster, whereas the pixels will be clustered in only one group for intensity-based clustering. Therefore, the FCM technique belongs to the soft partitioning of pixels in a dataset. There are many variants in Spatial Fuzzy C-Means. In the proposed approach, Human Brain MRI images are used for the automatic segmentation of the hippocampus. Since the Human MRI images are with more noise, Spatial Content Based Fuzzy C-Means (SCB-FCM) is used in the proposed research work. Compared to other variants, SCB-FCM is specifically designed for image segmentation with noisy images. As SCB-FCM combines spatial information and pixel intensities and considers content-based features of brain MRI images, which ultimately provides better-enhanced results for segmenting the hippocampus. Moreover, SCB-FCM is an extension of the traditional FCM algorithm that incorporates spatial information into the clustering process. MRI images can be prone to noise, and traditional FCM might produce noisy segmentations. SCB-FCM considers spatial smoothness, which helps to reduce the impact of noise on the segmentation results. In this paper, SCB-FCM is implemented for MRI image segmentation because it considers the spatial information inherent in these images, thus leading to an improved accuracy, a reduced noise sensitivity, and a better preservation of structural details. This makes it particularly well-suited for MRI medical image analysis tasks, where precise segmentation is essential for a diagnosis and treatment planning. When compared to the traditional FCM, SCB-FCM provides the following benefits: preservation of spatial information, improved edge detection, enhanced segmentation accuracy, and clinical relevance. The proposed system begins by enhancing the image and then extracts fuzzy properties using a hyperbolized histogram function. Fuzzy weighted median filtering is designed and applied, followed by a multi-scale fuzzy membership modification. The main goal of image enhancement is to modify an image so that it is better suited for a given application than it was originally. The Contrast Improvement with Intensification-Operator (INT-Operator) involves the following steps.
Step:1 Define the membership function using Eq (21) [45]:
Step:2 Modify the membership values using Eq (22) [45]:
Step:3 Generate new enhanced values using Eq (23) [45]:
Then, the Fuzzy Property Extraction is performed with the Fuzzy Histogram Hyperbolization Function (FHHF). The steps involved in FHHF are as follows:
● Step 1: Regard the membership function's form to the real image
● Step 2: Change the value of the linguistic hedge known as the fuzzifier Beta
● Step 3: Include calculating the membership values
● Step 4: Change them to account for linguistic hedges in the spatial domain.
● Step 5: Create new grey levels using Eq (24) [28]:
Randomly initialize the fuzzy membership matrix using Eq (25) [45]:
Then, the center vector is calculated using Eq (26) [45]:
The dissimilarity between the data points and the center vectors is measured using the Euclidean distance by Eq (27) [45]:
Finally, the new fuzzy membership matrix is generated by using Eq (28) [45]:
where the value of m ranges from [1.25, 2]. Repeat steps 1 to 5, where every iteration involves two passes for the clustering process. The membership function in the spectral domain is calculated using the same first pass as is in the normal FCM. In the subsequent pass, each pixel's membership data is transferred to the spatial domain, and then the spatial function is calculated. The FCM iteration continues with the new membership integrated with the spatial function, The iteration is terminated when the largest difference between two cluster centers during two consecutive iterations is less than a threshold ( = 0.02). Defuzzification is used to assign each pixel to a certain cluster for which the membership is maximal after the convergence.
2.3. Deep neuro fuzzy iterative learning
The deep Neuro-Fuzzy Iterative Learning technique is comprised of noisy label refining and uncertainty-aware segmentation network training. To provide predictions that are resilient to random spatial hold space disruptions, DHSOFM and SFCM are cooperatively trained using multi-view in each iteration. Then, instead of eliminating the noisy labels outright, the trained networks are utilized to assess the uncertainty of the pixel annotations and then rectify them. Based on the dice coefficient in the iterative learning, an automatic halting method is created to prevent overfitting. Extensive testing on publicly available datasets demonstrates the reliability and efficiency of this technique in handling high-noise environments. Even as the noise levels increase, the segmentation performance remains consistently strong. Results from the private dataset indicate that this technique can be used to segment the hippocampus with an enhanced accuracy. The SS-DNFIL Segmentation Algorithm is given in Table 1.
3.
Results and discussion
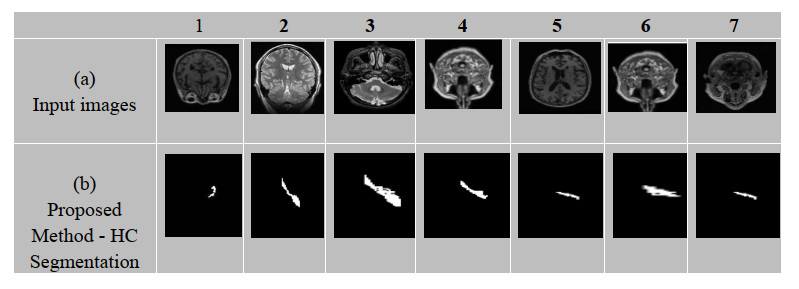
The dataset used in the experiments comprised 18,900 images across 100 classes, sourced from the Kaggle repository (SaberMalekzadeh). These images were divided into three subsets: 13,230 images (70%) for training, 2835 images (15%) for validation, and 2835 images (15%) for testing. Each image, originally sized at 197 × 233 pixels, was uniformly scaled to 197 × 197 pixels as provided in Table 2. The Adam optimizer was used for the training procedure, and the starting learning rate was set at 0.001, which decreased by 0.1 every 10 epochs. Over 50 epochs, the training was performed in batches of 32 images. The utilized Dice loss function is good at controlling class imbalances in segmentation tasks. To avoid overfitting, the best-performing model was saved based on the validation accuracy and an early halting with patience of 5 epochs based on the validation loss. The experiments were run on a high-performance Desktop with a configuration of Intel Core i7 14700 vPro, Windows 11 Professional OS, Intel UHD Graphics 770, Storage: 512GB M.2 PCIeNVMe SSD, Memory: 8 GB: 1 × 8 GB, DDR5, 4400 MT/s. The software environment included is Python 3.8, the Keras deep learning library, TensorFlow 2.4.1, PyTorch 1.8.0, and other supporting libraries such as NumPy, Pandas, and OpenCV. This setup ensured the efficient training and evaluation of the models, thereby leveraging both CPU and GPU resources to optimize the performance. Figure 3 represents the results obtained by using the SS-DNFIL technique. The performance of the proposed method was compared with state-of-the-art segmentation methods, including U-Net, DenseNet, and ResNet-50. The proposed method consistently outperformed these models across several performance metrics, including Dice, Jaccard, sensitivity, specificity, and accuracy.
The experimental assessment was completed using the Python deep learning library Keras. The fidelity criteria of the various methodologies were measured using different performance metrics such as the Dice Coefficient, the Jaccard Coefficient, Specificity, Sensitivity, FPR, and FNR for the performance evaluation. Accuracy, sensitivity, and specificity were used to evaluate the performance. The parameters are denoted in Table 3.
Table 4 shows the comparative analysis of the results of various performance metrics with the proposed schemes. The proposed method exhibited a superior performance across various metrics, including Dice (0.97), Jaccard (0.93), Sensitivity (0.95), Specificity (0.97), and Accuracy (0.97), thus demonstrating a clear advancement over other models such as U-Net++, ResNet-50, and DenseNet. The high Dice and Jaccard scores indicate that the proposed method excels in accurately segmenting the regions of interest, thus achieving a higher degree of overlap between the predicted and ground truth segments compared to its counterparts. This can be attributed to the method's likely incorporation of advanced feature extraction techniques, such as improved convolutional layers or an enhanced network depth, which enable it to capture finer details and complex patterns in the data. The equilibrium between Sensitivity and Specificity indicates that the model successfully distinguishes between positive and negative cases, thus resulting in a decrease in both false positives (FPR of 0.09) and false negatives (FNR of 0.08). This reflects a strong performance across diverse data samples. The superior performance of the proposed method, particularly in terms of the Dice coefficient (0.97) and Jaccard index (0.93), can be attributed to the innovative combination of deep learning and fuzzy logic, as well as the use of iterative learning for a continuous refinement of the segmentation results. The use of DHSOFM allows the model to extract multi-scale features that capture the complex anatomical structures of the hippocampus, while Fuzzy C-Means (FCM) handles the inherent uncertainties in the data by allowing for partial memberships in different clusters. This combination leads to a more accurate segmentation, particularly in cases where the boundaries are ambiguous or where the hippocampus exhibits abnormal shapes. The high specificity (0.97) and sensitivity (0.95) scores indicate that the model is effective at differentiating between positive and negative instances, thus reducing both false positives and false negatives. However, the increased complexity of the proposed method, particularly due to the use of multiple atlases and iterative refinement, comes with potential limitations. The method may require more computational resources and time compared to simpler models, which could make it less practical for real-time or resource-constrained environments. Additionally, the model's performance may be highly dependent on the characteristics of the dataset used for training, thus potentially limiting its generalizability to other imaging datasets.
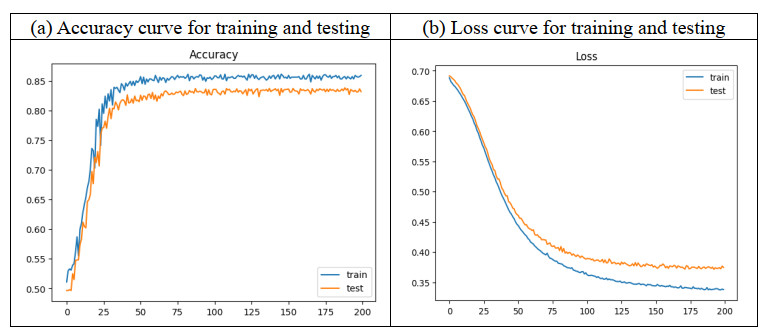
Additionally, the proposed method's enhanced performance might stem from architectural innovations such as attention mechanisms or multi-scale feature aggregation, which can improve the model's capacity to focus on relevant features and capture long-range dependencies within the data. The use of advanced training techniques, including data augmentation, transfer learning, and refined loss functions, likely contributes to the model's improved accuracy and robustness. These methodologies not only help to improve the generalization to new data, but also to optimize the model's learning process, thus resulting in superior overall performance metrics. The integration of these advanced strategies positions the proposed method as a highly effective tool for complex segmentation tasks, thus outperforming traditional and recent models. However, the increased complexity of the proposed method could result in higher computational costs, thus making it less practical for real-time or resource-constrained environments. Additionally, there is a risk of overfitting, especially if the model's performance is closely tied to the specific characteristics of the dataset used, thus potentially limiting its generalizability to other domains. Figure 4 shows the accuracy curve for training and testing alongside the loss curve for training and testing of the proposed method. The Loss curve shows the actual variation between the model's predicted and actual true output, while the accuracy curve shows how accurate the model is in predicting the provided data.
4.
Conclusions
In this work, a robust automated segmentation of the SS-DNFIL System for extracting the hippocampus from brain MRI images was presented based on the DHSOFM and the FCM technique with iterations. The concept of a fuzzy set was found to be successfully applied to MRI images. The addition of FHHF using the FPE served to enhance the image to more desired levels. The dataset was enough to evaluate a deep learning-based strategy that produced encouraging results. After a rigorous training process, significant results were obtained for each of the six metrics that were used to test the model. Particularly, both the hippocampus areas demonstrated very good accuracies in segmentation. The false positive and false negative rates of the image reflected the kind of quantitative measure of its quality and were seen to be reduced with segmentation. Thus, it can be concluded that the proposed system can be used for the HC segmentation of any brain MRI image. The experimental results showed that the system had a high specificity, sensitivity, Jaccard coefficient, and Dice coefficient. Additionally, the proposed updated architecture is useful for a variety of biomedical image processing applications.
In the future, a computer-assisted tool that aids in the work of doctors and biologists may be suggested. Service continuity can be improved by building self-organized systems with a flexible structure, which will tighten the security and availability restrictions. Therefore, it is possible to design any bio-inspired management approach [46] that analyses medical image data utilizing specialized computing environments that make use of Service Oriented Networks and produce automated clinical outcomes after scanning using a suggested picture segmentation algorithm. The bio-inspired method forbids the use of stimulation to produce phony medical outcomes and to manipulate MRI scans.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: