1. Introduction
Batteries have long been a very important commodity for satisfying the world’s mobile energy storage needs. But more than ever before, advanced lithium-ion batteries are receiving an increased level of interest due to expanded power capabilities and the near limitless assortment of application opportunities, from vehicles and laptop computers to orbiting satellites and electric tools. As transportation markets are coming into play, the environmental impact of lithium-ion batteries and durability characteristics against climate variation are becoming very important in both the component material selection and design [1,2,3,4,5]. In 1997, the concept of LiFePO4 as a possible cathode for today’s Li-ion batteries came to life [6]. This material, which has an olivine structure, has been a focal point for much experimentation and discussion, as it boasts several attractive qualities including a relatively high theoretical capacity of 170 mAh/g, great structural stability, long cycle life, environmentally benign qualities, and most importantly, safety due to great thermal stability [6,7]. However, LiFePO4 has a very low electronic conductivity, a property essential for battery design, but it has been greatly improved through the successful application of conductive coatings or cation doping, making it comparable with other cathode materials [8,9,10,11]. In addition to these attributes, the constituent materials are abundant and widely available at a relatively low cost [12], making LiFePO4 extremely attractive for high-power vehicles, military and space flight operations [13,14], and everyday consumer electronics.
Phase transformation from lithium-poor (FePO4) to lithium-rich (LiFePO4) during intercalation induces different strains in each lattice direction: a, b, and c [15,16,17,18,19]. Stresses induced by the phase transformation create flaws or cracks that may become stress concentration areas when further cycling occurs [20,21,22,23,24,25,26]. As a result, cracks are often observed along the phase boundary on the ac-plane [15,27]; structural failure due to fracturing of active material is a primary factor in battery degradation [7,22,27,28,29,30]. A combination of tensile and compressive stresses will induce microscopic crack propagation if critical values are reached. Over time, crack propagation will continue until the crack reaches a critical length, at which time complete fracture initiates. When this active electrode material is fractured away, the battery will effectively lose capacity and maximum power output diminishes. Thus, understanding the relationship between stresses and imperfections during lithium ion intercalation can be beneficial to better advance the current battery technology.
Olivine LiFePO4 is a brittle material and linear elastic fracture mechanics could be applied to better understand mixed-mode fractures in lithium-ion battery materials. Extensive theoretical and computational studies have focused on the growth of interfacial cracks of bi-materials, and on quantifying the extension of a crack and the elastic field near a crack tip [31,32]; the energy release rates (G) and stress intensity factors (K1 and K2) of engineering materials are generally discussed in this regard. Hutchinson and Suo have provided analytical energy release rates and stress intensity factors for interfacial cracks in isotropic bi-materials under mixed-mode loading [33]. Qian and Sun have extended the mixed-mode study to monoclinic and orthogonal bi-materials [34,35]. Sequentially, the development and application of the finite element-based virtual crack closure technique (VCCT) facilitated the analyses on fracture mechanics for orthogonal (orthorhombic) bi-materials [36,37,38,39,40]. Raju has calculated energy release rates via the VCCT with higher order and singular finite elements for isotropic materials [41]. Agrawal and Karlsson utilized the VCCT to obtain mixed-mode energy release rates and stress intensity factors for isotropic materials [40]. For details about the overview of the VCCT, please refer to studies by Krueger et al., Rybicki, Dattaguru, Xie and Agrawal [36,37,38,39,40].
The current study aims to identify an optimal combination of the particle- and crack-size of LiFePO4 for better battery performance. Because reducing the LiFePO4 electrode particle size could effectively decrease stress inside the particles, in addition to reducing the diffusion path during electrochemical cycling [42,43]. The current study is designed to provide insight into the sub-micro scale fracture mechanisms within the cathode material by accomplishing the following objectives to help aid in the understanding and development of a longer lasting and more powerful battery: (1) Perform a finite element simulation to evaluate fracture mechanisms inside a single LiFePO4 particle due to the phase transformation; and (2) establish an energy-based approach to estimate the propensity of crack extension for lithium-ion battery materials.
We achieve these objectives by utilizing the VCCT to study fracture mechanics in LiFePO4 battery materials under mixed-mode loading. Pre-existing cracks at the interface of orthotropic bi-materials are incorporated. Various particle and crack sizes are considered to illustrate the effects on the cracking information in LiFePO4 due to phase transformation. Our aim is to present an approach towards improving battery structural design by providing a better understanding of the micromechanics, as well as a basis for future fatigue analyses, which may incorporate a variety of other battery chemistries and additional fatigue life parameters.
2. Materials and Method
2.1. Model development
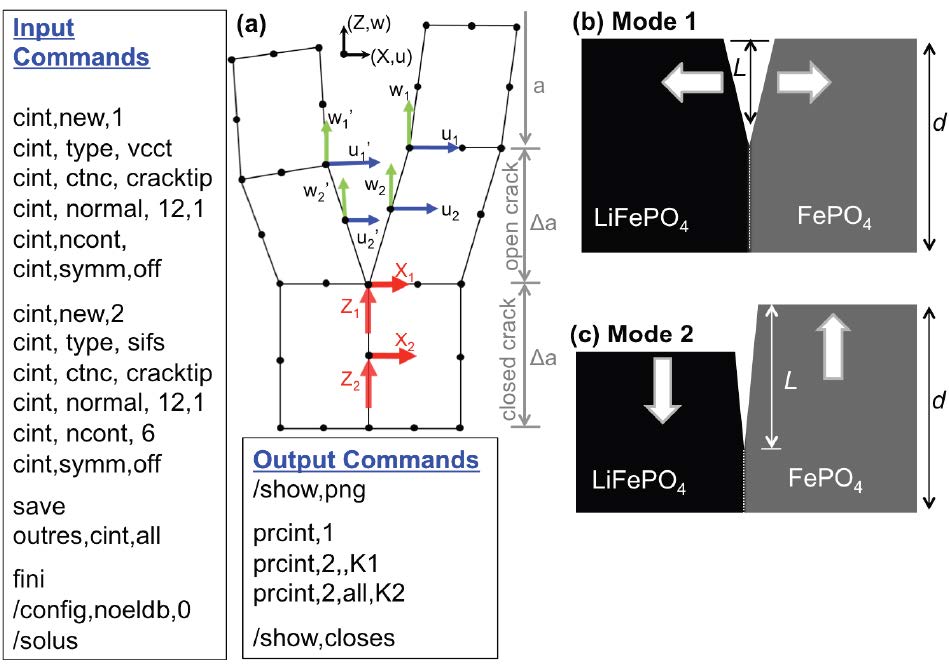
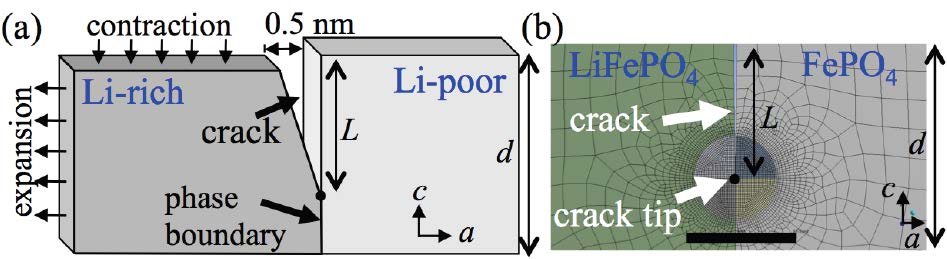
To study fracture mechanics in LiFePO4 particles, VCCT with the ANSYS finite element software (ANSYS, Inc. Canonsburg, Pennsylvania) is utilized to obtain the energy release rates and stress intensity factors. Two-phase plate-like LiFePO4 finite element models are generated based on the separate experimental observations [15,27,44] and different orthotropic material properties are adopted for both phases [28]. An interfacial crack is considered to run parallel to the bc-plane (along the c-axis) where phase boundaries are present (Figure 1). Although crack extension is possible in other planes, literature and experimentation have reported that cracks are observed in the bc-plane between phases while advancing in the c-axis [15]. In the current study, an assumption was made that the cracks will extend along their original direction. Moreover, the only experimental data that was available was for the surface energy and the prediction of crack turning or kinking was beyond the scope of the investigation. However, there exists a slight possibility that the shear mode fracture toughness may be very small in these materials and the crack path may deviate from a straight line. Therefore, we assume that a crack extends along the interface and remains parallel to the bc-plane [15,27,29] (Figure 1). Based on the experimental observation [15], previous simulations [45,46,47,48], and LiFePO4 lattice constants of the unit cell—a = 10.3 Å, b = 6.0 Å, and c = 4.7 Å [49]—three differently sized plate-like LiFePO4 finite element models on the ac-plane are generated as follows: (a) 500 nm × 225 nm, (b) 200 nm × 90 nm, and (c) 100 nm × 45 nm, respectively. In general, a continuum mechanics-based finite element method is valid when the model size is above 25 nm, as several nano-scaled studies presented by Zhao et al. [22,50,51]. Furthermore, lithium-ions diffuse into LiFePO4 particles along the b-axis during the phase transformation; the elastic model is reduced to 2D by assuming plane stress and neglecting stresses in the b-direction, as described by Hu et al. [29]. A total of 21 finite element simulations are conducted, wherein the initial crack is considered to start from the top face with variable lengths of crack sizes 0.05-0.8 L/d, in which L represents the crack length and d represents the particle size along the c-axis (Figure 1). The initial crack mouth opening is set at 0.5 nm in the a-axis in the range of experimentally observed crack dimensions [27]. Strains were applied to the LiFePO4 phase according to the misfit strains previously measured and reported in the literature: expansion occurs along the a-direction (εa = 5.03%) and contraction occurs along the c-direction (εc = −1.9%) (Figure 1a) [52]. Of note, εb = 4.5%). Two-dimensional quadrilateral elements are used in the finite element analysis. Such eight-node parabolic elements allow for more flexibility and improved accuracy in contrast to four-node elements That is, the 8 noded parabolic quadrilateral element uses quadratic functions for the displacements, and the simulation shows the exact analytic solution for pure bending dominated problems even with a coarse mesh with only one element in depth [53,54]. The finite element models are densely meshed around the crack tip to a size of 50 nm (Figure 1b).
2.2. Finite element method-based virtual crack closure technique (VCCT)
The VCCT is used along with the finite element modeling package ANSYS to determine the energy release rates and stress intensity factors under mixed-mode loading. The theory behind the VCCT is that the energy needed to separate or slide a crack surface is the same as the energy needed to close the surface back on itself [36]. The tendency of a crack to extend, the energy release rates, and the stress intensity factors are calculated through command options in ANSYS [55] (Figure 2a), and they are currently not available on the graphical user interface of ANSYS. Stress intensity factors have been derived analytically for orthotropic bi-materials, as detailed in published studies [34,56,57]. Energy release rates can be calculated with relative displacements (u, w), reaction forces (X, Z), and a unit thickness t = 1, as shown in Equation 1 and Figure 2 [39]. From the VCCT and a few commands in ANSYS, the Mode 1 (tension mode) and Mode 2 (sliding shear mode) strain energy release rates for a flaw of given size in a two-phase LiFePO4 particle could be determined (Figure 2b-c):
|
G1=−[X1(Δu1)+X2(Δu2)]2ΔαG2=−[Z1(Δw1)+Z2(Δw2)]2Δα
|
(1) |
2.3. Crack extension
A crack will advance if the total energy release rate for Mode 1 and Mode 2, GT= G1 + G2 , is larger than approximately twice the surface energy of the particle, i.e., GT > 2 g [29,58]. A first-principle analysis by Wang et al. has reported a g value of 0.66 N/m for LiFePO4 in the (100) crack face orientation [29,58]. In the current study, we collect finite element results satisfying GT > 2g, and the difference between these two energies (GT−2g) is used to predict crack extension. That is, crack extension is eminent and a crack will advance until the surface energy from the newly-formed crack faces bring the particle back to be equal to or larger than the strain energy release rate (Figure 3). In the current work, we follow steps in “Linear Elastic Fracture Mechanics” detailed by Fischer-Cripps [59]: for a crack to extend, the rate of strain energy release per unit of crack extension must be at least equal to the rate of surface energy requirement [60]. Therefore, a 0.01-nm crack extension is set as a unit growth and the resulting crack growth (da) would be determined as follows: First, we calculate the difference between the GT and 2g. Second, the additional energy release rate for a unit of 0.01 nm crack extension is determined based on the crack surface areas. Third, the updated additional surface energy for a 0.01 nm crack extension is determined. Fourth, the crack extension is calculated since the relieved internal energy due to crack propagation should be balanced by the additional strain energy release rate, as shown in Figure 3.
3. Results and Discussion
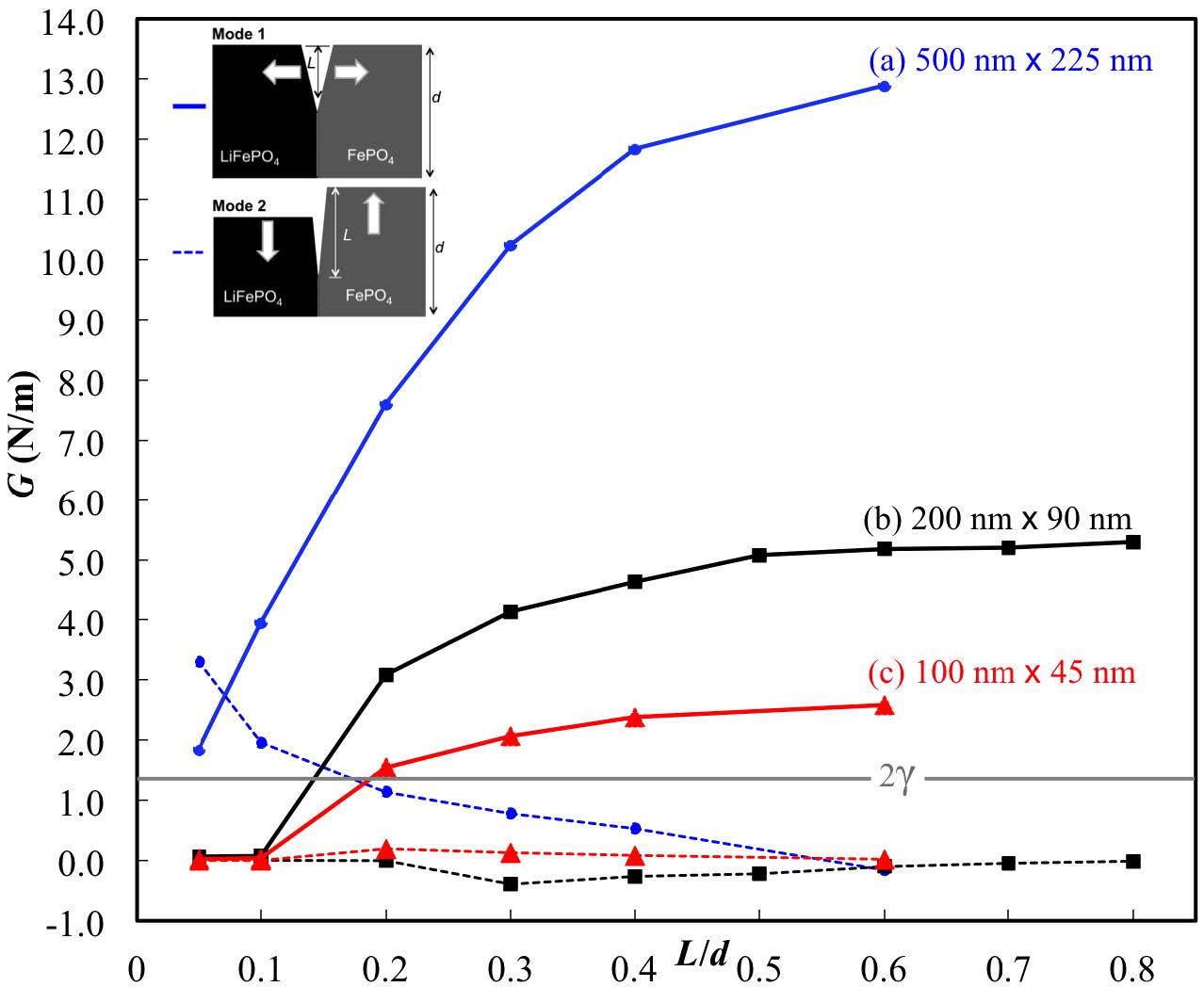
The results of the finite element method-based VCCT indicate that normal stresses dominate as compared to shear stress throughout the particle (stress fields not shown). In particular, the Mode 1 fractures predominated for all models, as the energy release rate G1 is much larger than G2 for all particle sizes (Figure 4). The fracture mode is a result of applied boundary conditions (misfit strains due to phase transformation in the current study: εa = 5.03% and εc = −1.9%), anisotropic elastic moduli for LiFePO4 and FePO4 [28], and as a result, the energy release rates and the stress intensity factors are indicators of the state of energy or stress around the crack tip. Since the stiffness value of LiFePO4 from [28] along the a-axis is much smaller than in the other orthorhombic directions, the material is weaker in this direction, giving way to the splitting or opening Mode 1 type of fracture. Therefore, in the current study we focus on the discussion of Mode 1 fractures in LiFePO4 battery materials from the mixed-mode boundary condition.
Several studies have shown that the energy release rate is proportional to the crack size since the energy release rate is the energy dissipated during fracture per unit of newly created fracture surface area [33]. The variation of energy release rates with respect to the crack-to-particle ratios for two fracture modes are shown in Figure 4. It is revealed that G1is highly dependent on the crack size for all three particle sizes. Comparing to the 2g = 1.32 N/m, smaller particles (100 nm × 45 nm) are able to better accommodate initial flaws without the crack propagation, i.e., L/d ≤ 0.2. In contrast, particles with a larger size (500 nm × 225 nm) could only accommodate initial flaws as small as L/d ≤0.03 by a linear extrapolation. Therefore, it is the L/d point that needs to be considered to determine if crack propagation occurs during the lithiation/delithiation process. Below L/d = 0.5 and 0.6, the energy release rates increase with the increased crack lengths and then begin to level off. It is concluded that crack propagation acts to relieve internal stresses due to misfit strain during the phase transformation of LiFePO4 materials, and it is particle-size and initial flaw-size dependent. Crack propagation due to mixed-mode loading is possible in other planes; however, experimentation has reported that cracks are observed between phases while propagating in the c-axis [15]. The olivine crystal structure of LiFePO4 and the Pauling's third rule support this observation: (100) planes are linked through stable, shared corner bonds between FeO6 octahedra and PO4 tetrahedra, while (010) planes are connected by weaker, edge-sharing bonds between FeO6 octahedra [27,52,61]. Lower energy release rates are observed in the Mode 2 fracture and exhibit less dependency on particle sizes. However, G1 and G2 both contribute to the GT for the crack extension. In contrast to the study by Hu et al. [29], a maximum value of the normalized energy release rate was identified; however, it is not clear which fracture mode is considered in their study. The approach in their study was to inversely look for a critical particle size d by solving boundary value problems, and the normalized energy release rate is a function of one component of the anisotropic stiffness matrix (c11) and the volume misfit along the c-axis (ec). The decreasing normalized energy release rate after L/d = 0.5 from Hu et al. could be attributed by several simplifications [29], such as the choice of the normalization where the other anisotropic effects of volume expansions were not incorporated.
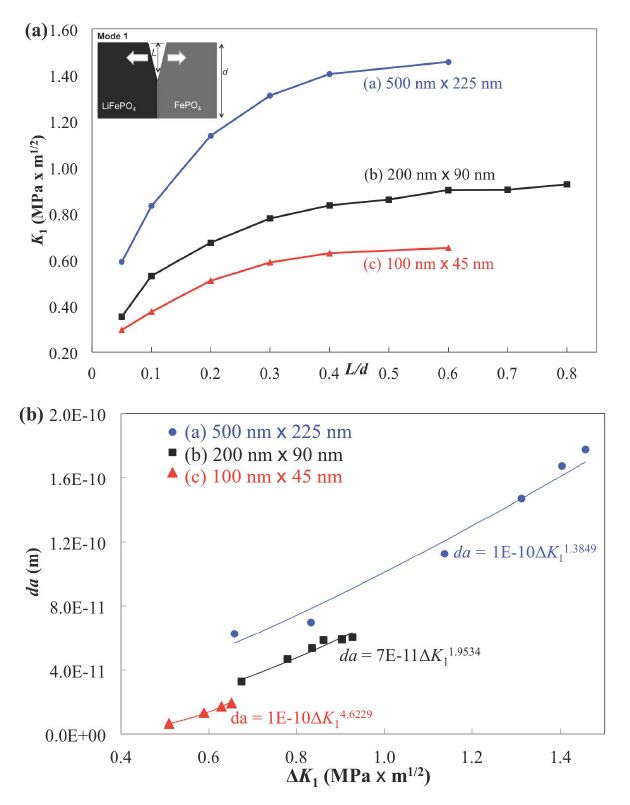
Stress intensity factors (K) are also obtained from the command-coding interface of ANSYS via the VCCT (Figure 2a), and the particle-size-dependent relationship of stress intensity factors and L/d is shown in Figure 5a. For larger particles (500 nm × 225 nm), it is observed that K1reaches a relative maximum value of 1.4 MPa-m1/2. For a particle size of 200 nm × 90 nm, K1 reaches a relative maximum value of 1.0 MPa-m1/2. For smaller particles (100 nm × 45 nm), it is observed that K1 reaches a relative maximum value of 0.6 MPa-m1/2 (Figure 5a). Our results indicate that K1is particle-size dependent, which is consistent with the observations made by Krstic and Khaund [62].
Further, to reveal the relationship between the crack advancement (da) and the change in the Mode 1 stress intensity factor for LiFePO4, the estimation is depicted in Figure 5b. The da is determined via the method described in Figure 3, and ΔK1 is determined from ranges of the stress intensity factor of Mode 1. It is observed that da vs. ΔK1 curves are particle-size dependent, wherein smaller particles exhibit faster crack extension (i.e., a higher value for the exponent of ΔK1 in the best-fit equations appearing in Figure 5b): the crack growth is proportional to the DK1 to the power of 4.6229 for particle size of 100 nm × 45 nm, and for particle size of 500 nm x 225 nm, the crack growth is related to the DK1 to the power of 1.3849 (Figure 5b). Detailed calculated data from the FEM-based VCCT are listed in Table 1.
Table 1. Results from the FEM-based VCCT of lithium-ion battery materials for each particle size with various crack-to-particle ratios: Mode 1 stress intensity factor (K1), total energy release rate (GT), twice of the surface energies (2γ), the energy difference between them (ΔE = GT - 2γ), the required additional strain energy release rate per 0.01 nm crack growth (ER), the required additional strain energy release rate per 0.01-nm crack growth (Es), and the required crack advancement (da).
| a × b × c = 500 nm × 300 nm × 225 nm |
| L/d | KI (MPa-m1/2) | GT (N/m) | 2γ (N/m) | ΔE (N/m) | ER per 0.01 nm (Joules) | ES per 0.01 nm (Joules) | da (m) |
| 0.05 | 0.659 | 5.462 | 1.32 | 4.142 | 2.485×10-17 | 3.960×10-18 | 6.275×10-11 |
| 0.1 | 0.833 | 5.922 | 1.32 | 4.602 | 2.761×10-17 | 3.960×10-18 | 6.972×10-11 |
| 0.2 | 1.136 | 8.744 | 1.32 | 7.424 | 4.454×10-17 | 3.960×10-18 | 1.125×10-11 |
| 0.3 | 1.310 | 11.027 | 1.32 | 9.707 | 5.824×10-17 | 3.960×10-18 | 1.471×10-11 |
| 0.4 | 1.403 | 12.373 | 1.32 | 11.053 | 6.632×10-17 | 3.960×10-18 | 1.675×10-11 |
| 0.6 | 1.456 | 13.053 | 1.32 | 11.733 | 7.040×10-17 | 3.960×10-18 | 1.778×10-11 |
|
| a × b × c = 200 nm × 120 nm × 90 nm |
| L/d | KI (MPa-m1/2) | GT (N/m) | 2γ (N/m) | ΔE (N/m) | ER per 0.01 nm (Joules) | ES per 0.01 nm (Joules) | da (m) |
| 0.05 | 0.354 | 0.068 | 1.32 | -1.252 | - | - | - |
| 0.1 | 0.531 | 0.079 | 1.32 | -1.241 | - | - | - |
| 0.2 | 0.674 | 3.481 | 1.32 | 2.161 | 5.185×10-18 | 1.584×10-18 | 3.273×10-11 |
| 0.3 | 0.779 | 4.400 | 1.32 | 3.080 | 7.393×10-18 | 1.584×10-18 | 4.667×10-11 |
| 0.4 | 0.836 | 4.850 | 1.32 | 3.530 | 8.472×10-18 | 1.584×10-18 | 5.348×10-11 |
| 0.5 | 0.861 | 5.176 | 1.32 | 3.856 | 9.254×10-18 | 1.584×10-18 | 5.842×10-11 |
| 0.6 | 0.902 | 5.220 | 1.32 | 3.900 | 9.361×10-18 | 1.584×10-18 | 5.910×10-11 |
| 0.7 | 0.903 | 5.211 | 1.32 | 3.891 | 9.337×10-18 | 1.584×10-18 | 5.895×10-11 |
| 0.8 | 0.926 | 5.305 | 1.32 | 3.985 | 9.564×10-18 | 1.584×10-18 | 6.038×10-11 |
|
| a × b × c = 100 nm × 60 nm × 45 nm |
| L/d | KI (MPa-m1/2) | GT (N/m) | 2γ (N/m) | ΔE (N/m) | ER per 0.01 nm (Joules) | ES per 0.01 nm (Joules) | da (m) |
| 0.05 | 0.297 | 0.029 | 1.32 | -1.291 | - | | - |
| 0.1 | 0.375 | 0.042 | 1.32 | -1.278 | - | | - |
| 0.2 | 0.510 | 1.740 | 1.32 | 0.420 | 5.044×10-19 | 7.920×10-19 | 6.369×10-12 |
| 0.3 | 0.589 | 2.200 | 1.32 | 0.880 | 1.055×10-19 | 7.920×10-19 | 1.332×10-12 |
| 0.4 | 0.629 | 2.470 | 1.32 | 1.150 | 1.380×10-19 | 7.920×10-19 | 1.742×10-12 |
| 0.6 | 0.652 | 2.607 | 1.32 | 1.287 | 1.545×10-19 | 7.920×10-19 | 1.951×10-12 |
Though the particle sizes chosen for the study retain the same aspect ratio, it is believed the surface energy has greater effects for smaller particles [63], where the same surface energy for three particle-size models are adopted, i.e., g = 0.66 N/m [58]. That is, for a particle with a smaller size, the newly created surface area has a stronger effect since crack propagation in a smaller particle acts to relieve more internal stresses. As a result, less strain energy release rates and stress-intensity factors are found in smaller particles (Figures 4 and 5a). In addition, a convergence test was performed in our finite element analysis. It has been observed that models beyond L/d = 0.6 provide similar strain energy release rates and stress intensity factors, suggesting that L/d = 0.6 is the critical value for both computational simulations and battery materials design.
In general, an empirical Paris’ Law is used to describe crack propagation in engineering materials. However, fatigue experiments are not currently available for nanosized LiFePO4 particles. The current study specifically aims to provide a method that estimates crack advancement based on the effects of particle and crack sizes under mixed-mode loading. The current study does not aim to estimate material parameters from the Paris’ Law for LiFePO4 particles. Our approach is in contrast to that of Deshpande et al. [64], who utilized Paris’ Law and incorporated material parameters for LiFePO4 to predict battery life (i.e., numbers of cycles). In their study, an isotropic core-shell model incorporating chemical and mechanical degradation was implemented, considering a surface crack that grows with each charge-discharge cycle [64].
The rate of discharge will determine the resultant stresses within the material, which will in turn alter the energy release rates and stress intensity factors at a crack in the particle. Therefore a current-rate-dependent crack propagation analysis for LiFePO4 is currently being developed in our research group. In general, larger stresses over a shorter period of time may induce cracking more readily than for slower discharging rates; this is due to the limited volumetric expansion rate being unable to satisfying the rate of lithium diffusivity during fast discharging, similar to rush hour traffic in limited highway space. Zhu et al. [20] have reported current density dependent fracture mechanic characteristics for another battery chemistry, LiMn2O4, wherein isotropic spherical and ellipsoidal particles are considered. They have concluded that crack propagation occurs at the center of the particle even during relatively low current density discharging [20].
Molecular dynamic (MD) simulation has been a powerful tool to numerically solve the classical equations of motion for a system at a smaller-scale. It has been widely used to understand the behavior of liquid electrolytes for lithium-ion batteries to improve the performance of portable electronics devices, electric vehicles, and hybrid electric vehicles. However, such considerations represent limitations of our study, as we did not have the computational tools in the present study. We have chosen to conducta continuum mechanics-based finite element analyses based available experimental and computational results from the literatures in which particles and models are on the same size order of ours. In this case, we could use the available surface energy values from the literature to calculate the crack extension, as shown in Table 1. Moreover, since our current study mainly focuses on interface-diffusion limited lithium-ion battery materials, an improved model by using MD could be developed to better predict interface diffusion and failure. Another limitation in the current study lies on the small element size at the crack tip in which a MD simulation is regarded as a better choice. To this matter, the logical approach in the desire to create truly multiple scale simulations that exist at disparate length and timescales has been to couple MD and FE. Unfortunately, the coupling of these methods is not straightforward since the major problem in multi-scale simulations is that of pathological wave reflection, which occurs at the interface between the MD and FE regions. We did not have the coupled MD and FE computational tools in the present study. Therefore, the idea of meshing the finite element region down to a small-scale was one of our first attempts to eliminate spurious wave reflections, which has been generally reported at the MD-FEM interface. To this end, we are in the process by adopting MD simulations to improve our computational technique.
4. Conclusions
To the best of the authors’ knowledge, this is the first study utilizing the finite element method-based VCCT to obtain cracking information in LiFePO4 battery materials. Various lengths of interfacial cracks in orthotropic bi-materials are incorporated. A method is established to calculate the amount of crack propagation for lithium-ion battery materials (Figure 3 and Figure 5b). It is observed that energy release rates, stress intensity factors, and crack propagation are all particle- and crack-size-dependent (Figures 4-5). Therefore, one potential future consideration is to reduce the LiFePO4 electrode particle size to allow initial flaws during material processing (Figure 4) and to effectively decrease stress inside the particles (Figure 5a) in addition to reducing the diffusion path for better battery performance [42,43].
The current study provides an approach towards improving battery structural design by providing a better understanding of the micromechanics, as well as a basis for future fatigue analyses, which may incorporate a variety of other battery chemistries and additional fatigue life parameters. Thus, the current study has identified factors that play an important role in inducing fracture, and the study also provides insight into factors that can be optimized to minimize any detrimental capacity loss in a battery. This research will hopefully elucidate a relationship between micro-mechanics and battery usage so as to help in the design of a higher performance, longer lasting battery for the future.
Conflict of Interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: