Analysis of a simplified model of the urine concentration mechanism

1.   Introduction

A time delay widely exists in many fields such as chemistry, biology, industry, and so on. Since a time delay arising in a system may cause instability, the stability analysis of time-delay systems has been wildly studied in the past few decades ^[1,2]. The main purpose is paid to determine the admissible delay, for which the systems remain stable.

It is well known that the LKF method has been widely used to obtain stability conditions for time-delay systems ^[3,4]. The main purpose of the LKF method is to estimate the integral term arising in the time derivative of double integral term in the LKF. Therefore, to get less conservative stability criteria, many integral inequality methods are derived. Those inequality methods include Jensen inequality ^[5,6], Wirtinger inequality ^[7,8,9], double integral inequlity ^[10,11,12], various improved integral inequalities ^{[13,14,15,16,17,18,19,20,21,22,23,24,25,26]}. The Jensen inequality expressed as $ V_{ab}(\dot y) = \int_a^b\dot y^T(t)R\dot y(t)dt\geq \frac{1}{b-a}\Omega_0^TR\Omega_0 = V_{Jensen} $, where $ a < b, R = R^T > 0, \Omega_0 = y(b)-y(a) $. The Wirtinger-based inequality expressed as $ V_{ab}(\dot y)\geq V_{Jensen}+\frac{3}{b-a}\Omega_1^TR\Omega_1 = V_{Seuret} $, where $ \Omega_1 = y(b)+y(a)-\frac{2}{b-a}\int_a^by(t)dt $. The further improved inequality expressed as$ V_{ab}(\dot y)\geq V_{Seuret}+ \frac{5}{b-a}\Omega_2^TR\Omega_2 $, $ V_{ab}(\dot y)\geq V_{Seuret}+ \frac{5}{b-a}\Omega_2^TR\Omega_2 +\frac{7}{b-a}\Omega_3^TR\Omega_3 $, $ V_{ab}(\dot y)\geq V_{Seuret}+ \frac{5}{b-a}\Omega_2^TR\Omega_2 +\frac{7}{b-a}\Omega_3^TR\Omega_3 +\frac{9}{b-a}\Omega_4^TR\Omega_4 $ in ^[13,14,15], respectively, where $ \Omega_2, \Omega_3, \Omega_4 $ are defined in Lemma 4 ^[15]. However, these results only estimate the integral term arising in the time derivative of double integral term in the LKF. This paper presents a generalized double integral inequality which includes those in ^[10,11,12] as special cases. A new stability criterion is proposed by choosing a new LKF and using the generalized double integral inequality. Both the generalized integral inequality and the new LKF include fourth integrals, which may yield less conservative results. Two examples are introduced to show the effectiveness of the proposed criterion. The contributions of our paper are as follows:

$ \bullet $ The integral $ -\int_a^b\int_u^b\dot x^T(s)P\dot x(s)dsdu $ is estimated as$ -\int_a^b\int_u^b\dot x^T(s)P\dot x(s)dsdu\le \zeta^T\omega\zeta $, where $ \omega $ and $ \zeta $ are defined in Lemma 3. The above inequality includes those in ^[10,11,12] as special cases.

$ \bullet $ Both the new double integral inequality and the new LKF include fourth integrals, which may obtain more general results.

$ \bf{Notation} $: See Table 1.

2.   Preliminary

Consider the time delay systems as

where $ y(t)\in R^{n} $ is the state vector, $ h > 0 $ is constant time-delay and the initial condition $ \phi(t) $ is a continuous function.

Lemma 1. ^[15] For a matrix $ P\in S^n_+ $, and any continuously differentiable function $ x:[a, b]\longrightarrow R^n $, then we can obtain

where

Lemma 2. ^[27] For a positive define matrix $ P\in S_+^{n} $, a integrable function $ \left\{ {x(s)\left| {s \in \left[ {a, \; b} \right]} \right.} \right\} $, and any auxiliary functions $ \left\{ {f_i(s)\left| {i \in \left[0, n\right]}, {s \in \left[ {a, \; b} \right]} \right.}, f_0(s) = 1 \right\} $ satisfying $ \int_a^b\int_u^bf_i(s)f_j(s)dsdu = 0 $, $ (0\le i, j\le n, i\ne j) $ with $ f_i(s)\ne 0, i = 1, 2, \cdots, n $. Let $ \lambda_i\in R^{n\times k}, i = 0, 1, \cdots, n $ and a vector $ \zeta\in R^k $, such that$ \int_a^b\int_u^bf_i(s)x(s)dsdu = \lambda_i\zeta $. Then for any matrices $ M_i\in R^{k\times n}(i = 0, 1, \cdots, n) $, the following inequality holds

Proof. Define $ M = \left[ {

$$\begin{array}{*{20}c} {M_0^T} & {M_1^T} & {\cdots} & {M_n^T} \\ \end{array}$$ } \right]^T $, $ \xi(s) = \left[ { $$\begin{array}{*{20}c} {f_0(s)\zeta^T} & {f_1(s)\zeta^T} & {\cdots} & {f_n(s)\zeta^T} \\ \end{array}$$ } \right]^T $.

It is easy to obtain that

Integrating the inequality (2.5) from $ \left[ {a, b} \right]\times \left[ {u, b} \right] $ yields

This completes the proof.

Lemma 3. For a differential function $ x: \left[a, b\right]\to R^n $, a matrix $ P\in R_+^n $, a vector $ \zeta\in R^k $, and any matrices $ M_i\in R^{k\times n}(i = 1, 2, 3, 4) $, then the following inequality holds:

where

Proof. The result can be easily obtained by choosing $ n = 3 $, $ f_1(s) = \frac{3}{b-a}\left(s-\frac{2b+a}{3}\right) $, $ f_2(s) = \frac{10}{(b-a)^2}\left[\left(s-\frac{3b+2a}{5}\right)^2-\frac{3(b-a)^2}{50}\right] $, $ f_3(s) = -4+30\frac{s-a}{b-a}-60\left(\frac{s-a}{b-a}\right)^2+35\left(\frac{s-a}{b-a}\right)^3 $in (2.4). So the details of proof is omitted.

Remark 1. The inequality (25) of Lemma 5.1 in ^[10] is a special case of Lemma 3 by setting $ M_1 = -\frac{2}{b-a}\lambda_1^TR $, $ M_2 = -\frac{4}{b-a}\lambda_2^TR $, $ M_3 = 0 $, and $ M_4 = 0 $. The inequality (4) of Lemma 2.3 in ^[11] is a special case of Lemma 3 by setting $ M_1 = -\frac{2}{b-a}\lambda_1^TR $, $ M_2 = -\frac{4}{b-a}\lambda_2^TR $, $ M_3 = -\frac{6}{b-a}\lambda_3^TR $, and $ M_4 = 0 $. In addition, the inequality (12) of Lemma 5 in ^[12] is a special case of Lemma 3 by set ting $ M_1 = -\frac{2}{b-a}\lambda_1^TR $, $ M_2 = -\frac{4}{b-a}\lambda_2^TR $, $ M_3 = -\frac{6}{b-a}\lambda_3^TR $, and $ M_4 = -\frac{8}{b-a}\lambda_4^TR $.

3.   Results

Based on Lemma 1 and Lemma 3, a new stability condition can be obtained.

Theorem 1. System (1) is asymptotically stable if there exist matrices $ P\in S_+^{5n} $, $ R_1, R_2, R_3\in S_+^{n} $, and any matrices $ M_1, M_2, M_3, M_4\in R^{6n\times n} $ such that

where

$ \Pi_1 = \left[ {

$$\begin{array}{*{20}c} \delta_1^T & \delta_3^T & \delta_4^T & \delta_5^T & \delta_6^T \end{array}$$ } \right]^T $,

$ \Pi_2 = \left[ {

$$\begin{array}{*{20}c} \delta_0^T & \delta_1^T- \delta_2^T&h \delta_1^T- \delta_3^T & \frac{h^2}{2} \delta_1^T- \delta_4^T & \frac{h^3}{6}\delta_1^T- \delta_5^T \\ \end{array}$$ } \right] $,

$ \Pi_3 = \delta_1-\delta_2 $,

$ \Pi_4 = \delta_1+\delta_2-\frac{2}{h}\delta_3 $,

$ \Pi_5 = \delta_1-\delta_2+\frac{6}{h}\delta_3-\frac{12}{h^2}\delta_4 $,

$ \Pi_6 = \delta_1+\delta_2-\frac{12}{h}\delta_3+\frac{60}{h^2}\delta_4-\frac{120}{h^3}\delta_5 $,

$ \Pi_7 = \delta_1-\delta_2+\frac{20}{h}\delta_3-\frac{180}{h^2}\delta_4+\frac{840}{h^3}\delta_5-\frac{1680}{h^4}\delta_6 $,

$ \Pi_8 = \delta_1-\frac{1}{h}\delta_3 $,

$ \Pi_9 = \delta_1+\frac{2}{h}\delta_3-\frac{6}{h^2}\delta_4 $,

$ \Pi_{10} = \delta_1-\frac{3}{h}\delta_3+\frac{24}{h^2}\delta_4-\frac{60}{h^3}\delta_5 $,

$ \Pi_{11} = \delta_1+\frac{4}{h}\delta_3-\frac{60}{h^2}\delta_4+\frac{360}{h^3}\delta_5-\frac{840}{h^4}\delta_6 $,

$ \delta_0 = A\delta_1+B\delta_2+C\delta_3 $,

$ \delta_i = \left[ {

$$\begin{array}{*{20}c} 0_{n\times (i-1)n} & I_n & 0_{n\times (7-i)n} \\ \end{array}$$ } \right] $, $ i = 1, 2, \cdots, 6. $

Proof. Introduce a LKF as

where

$

$$\begin{array}{l} \zeta(t) = \left[ {\begin{array}{*{20}c} y^T(t) & \int_{t-h}^ty^T(s)ds & v_1^T(t) & v_2^T(t) & v_3^T(t) \end{array}} \right]^T \\ \end{array}$$ $

$ v_1^T(t) = \int_{t-h}^t\int_{u_1}^ty^T(s)dsdu_1 $

$ v_2^T(t) = \int_{t-h}^t\int_{u_1}^t\int_{u_2}^t y^T(s)dsdu_2 du_1 $

$ v_3^T(t) = \int_{t-h}^t\int_{u_1}^t\int_{u_2}^t\int_{u_3}^t y^T(s)dsdu_3 du_2du_1 $

Then, the time derivative of $ V(y_t) $ along the trajectories of system (1) as follows

where

$

$$\begin{array}{l} \eta(t) = \left[ {\begin{array}{*{20}c} y^T(t) & y^T(t-h) & \int_{t-h}^ty^T(s)ds & v_1^T(t) & v_2^T(t) & v_3^T(t)\\ \end{array}} \right]^T \\ \end{array}$$ $

By Lemma 1, we have

By Lemma 3, we have

Thus, according to (3.2)–(3.5), we have $ \dot V(y_t)\le \eta^T(t)\Psi \eta(t) $. Thus, if (3.1)holds, then, for a sufficient small scalar $ \varepsilon > 0 $, $ \dot V(y_t)\le -\varepsilon\left\| {y(t)} \right\|^2 $ holds, which ensures system (1) is asymptotically stable. The proof is completed.

Remark 2. Both the double integral inequality and the new LKF include fourth integrals, which may yield novel stability results. Furthermore, in order to fully consider relevant information of the double integral inequality in Lemma 3, the $ \int_{t-h}^t\int_{u_1}^t\int_{u_2}^t\int_{u_3}^t y^T(s)dsdu_3 du_2du_1 $ is added as a state vector.

4.   Numerical examples

In this section, we demonstrate the advantages of our proposed criterion by two numerical examples.

Example 1. Consider system(1) with:

$ A = \left[ {

$$\begin{array}{*{20}c} 0.2 & 0\\ 0.2 & 0.1 \end{array}$$ } \right] $, $ B = \left[ { $$\begin{array}{*{20}c} 0 & 0 \\ 0 & 0\\ \end{array}$$ } \right] $, $ C = \left[ { $$\begin{array}{*{20}c} -1 & 0 \\ -1 & -1\\ \end{array}$$ } \right] $.

Table 2 lists the allowable upper bounds of $ h $ by different methods. Table 2 shows that the maximum delay bounds of $ h $ obtained by our method are much larger than those in ^[4,6,7,9,11].

Example 2. Consider system(1) with:

$ A = \left[ {

$$\begin{array}{*{20}c} 0 & 1 \\ -100 & -1 \end{array}$$ } \right] $, $ B = \left[ { $$\begin{array}{*{20}c} 0.0 & 0.1 \\ 0.1 & 0.2\\ \end{array}$$ } \right] $, $ C = \left[ { $$\begin{array}{*{20}c} 0 & 0 \\ 0 & 0\\ \end{array}$$ } \right] $

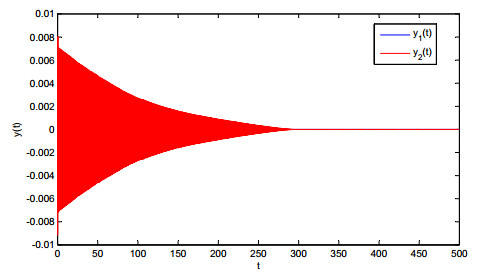
Table 3 lists the allowable upper bounds of $ h $ by different methods. Table 3 shows that the maximum delay bounds of $ h $ obtained by our method are much larger than those in ^{[4,7,9,10,11,14]}. For $ h = 0.750 $, $ y(0) = (0.001, -0.001)^T $, the state trajectories of the system(1) is given in Figure 1.

Remark 3. According to Example 1 and Example 2, although our method can reduce the conservatism of the system effectively, it increases the computational burden.

5.   Conclusion

This paper focus on a new stability condition for a class of time delay systems. By using two generalized integral inequalities and a new augmented LKF, a new stability criterion is obtained. Both the double integral inequality and the new LKF include fourth integrals, which may yield more general results. Two numerical examples are proposed to show the effectiveness of the proposed criterion.

Acknowledgments

This work was supported by New Academic Talents and Innovation Exploration Project of Department of Science and Technology of Guizhou Province of China under Grant (Qian ke he pingtai rencai [2017] 5727-19); Innovative Groups of Education Department of Guizhou Province (Qian jiao he KY [2016] 046).

Conflict of interest

The authors declare that there are no conflicts of interest.