1. Cardiac development and congenital heart disease
The heart, in addition to being one of the most important organs and the first to develop, is also one of the organs most susceptible to disease and dysfunction and hence extremely widely studied. Heart development begins with the appearance of two distinct mesodermal heart fields; the First Heart Field (FHF) and the Second Heart Field (SHF) both with a common origin contributing to cells of the developing heart in a spatio-temporal manner. While the SHF precursors contribute to the distal developing outflow tract (OFT) myocardium, the proximal smooth muscle cells that give rise to the tunica media of the great arteries, parts of the inflow, ventricular septum and the right ventricle, cells from the FHF contribute to mainly the left ventricle [1,2,3,4]. Both lineage precursors are regulated by a complex network of signaling pathways involving factors of the bone morphogenic pathway (BMP), sonic hedgehog pathway (Shh), Wnt, NOTCH, fibroblast growth factor (FGF) and the TGFβ pathway, some of which emanate from the adjacent endoderm although the exact role and nature of these signals remain unknown [5]. Cells of the FHF differentiate at the cardiac crescent stage while the SHF exhibits delayed differentiation. This delayed differentiation of the SHF is due to the presence of inhibitory Wnt signals rising from the ventral midline [6]. In addition to the FHF and SHF precursors, there exists another key player; the Cardiac Neural Crest Cells (cNCCs). The cNCCs originate from neural crest cells (NCCs) which are derived from the dorsal aspect of the developing neural tube [7]. These cells possess the ability to differentiate into two populations of cells namely the cranial and truncal neural crest. Cells from both the cranial and truncal neural crest give rise to the peripheral nervous system and melanocytes but only the cranial neural crest gives rise to a unique derivate of cells known as the ectomesenchyme. These ectomesenchyme derived from the preotic cranial neural crest contributes to the skeletal structures of the head, face and neck while the ectomesenchyme derived from the postotic cranial neural crest, also known as the cNCC region, contributes to the development of the cardiovascular structures [8,9].
The NCCs that populate the pharyngeal arches are responsible for the development of all arch derivatives. A sub population of these NCCs, destined to contribute to cardiac development, continue to migrate via the circumpharyngeal region to pharyngeal arches 3, 4 and 6 and into the outflow tract forming both the aortopulmonary septum and the conotruncal portions of the outflow septation complex [10,11]. Depending on which region of the pharyngeal arches the cNCCs migrate from, they contribute different parts of the septation complex and conotruncus at different times. Along with contributing to septation of the OFT, the cNCCs differentiate into smooth muscle cells (SMCs) of the tunica media layer of the aortic arteries distally while the SHF contributes proximally to the SMC layer of the great arteries, this region-specific contribution is crucial to its structure and function. In mice, the migration of the cNCCs occurs at around E9.5, shortly after cardiac looping. Between E8.5 and E9.5, the first signs of valvulogenesis appear. This is marked by the formation of endocardial cushions or local tissue swellings in the lumen of the atrioventricular canal (AVC) and OFT of the looped and segmented heart. A number of signaling molecules produced by the myocardium inhibit the expression of chamber specific gene in the AVC and proximal OFT and instead trigger an increased synthesis of extracellular matrix (ECM) between the endocardium and myocardium [12]. This increased deposition of ECM, also known as the cardiac jelly, leads to protrusions into the lumen of the AVC and OFT giving rise to valve precursors. As the endocardial cushions move into the lumen, signals emanating from the OFT myocardium or the AVC, for example secretion of VEGF, TGβ or BMP factors, trigger a subset of endocardial cells that line the cushions undergo a highly complex and tightly regulated process termed as endothelial-mesenchymal transition (End-MT) causing the specified cells to break away and migrate into the cardiac jelly where they complete their mesenchymal transition in order to populate the precursor valves with mesenchymal cells [12]. In the lumen of the distal OFT localised tissue swelling, termed as truncal cushions arise. These are subsequently populated by the mesenchymal cells originating from the neural crest and form the aortopulmonary septum [13]. Apart from the fact that the AVC valves develop approximately one day earlier than the OFT valves, another distinguishing factor between the two valves is the relative contribution of cells to these valves. While the AVC valves consist of cells that are primarily of endothelial endocardial origin, the semilunar valves are complicated by the presence of cNC progenitor derivatives [12].
Given that the SHF contributes to progenitor cells of the OFT, small perturbations in this cell lineage can lead to defects involving not only of the OFT but also the OFT valves. Furthermore, the SHF contributes to the OFT myocardium, responsible for the secretion of a number of signaling molecules that trigger Endo-MT/EMT in the conal endocardial cushions aiding in OFT valve and septum development. Additionally, the SHF derived OFT myocardium expresses chemoattractant molecules like SEMA3C which is responsible for cNCC migration and guidance upon entry into the OFT [14,15,16]. At the base of the aorta and pulmonary trunk, the SHF contributes to the vascular smooth muscle cells which supports segregation of the arteries from their respective left and right ventricular outlets [13,17]. Studies targeting SHF factors like Isl1, Mef2c, Tbx20, Tbx1 revealed disruption of a number of signaling pathways namely, TGFβ, Wnt/B-catenin, BMP, FGF, NOTCH, eNOS, Sonic Hedgehog, Retinoic Acid, Nfatc1 and calcineurin and the recently described Robo-Slit pathway [18,19,20,21,22,23,24,25]. Mutations in components of these pathways can lead to a spectrum of phenotypes affecting cardiac septation and valve development (Table 1) [26,27,28].
Table 1. Genes associated with syndromic and non-syndromic forms of BAV in humans.
| Gene |
Identified via |
Phenotype |
Mutations observed |
Reference |
| NOTCH1 |
Familial Sequencing, NGS |
BAV, calcific aortic valve disease, left side congenital heart disease, left hypoplastic heart disease |
√ |
[83,112,113,114] [108] |
| MATR3 |
CNV analysis and Sequencing |
LVOTO, BAV, CoA, PDA |
√ |
[85] |
| GATA4 |
Sequencing |
AR, pulmonary stenosis, BAV |
√ |
[86,87,88,89,115,116] |
| GATA5 |
Sequencing |
Autosomal dominant pattern of BAV inheritance |
√ |
[90,91,92] |
| GATA6 |
Sequencing |
Tetralogy of Fallot (TOF), persistent truncus arteriosus and atrial septal defects |
√ |
[95,97] |
| NKX2.5 |
Sequencing |
BAV, ASD, VSD, AVSD, TOF, SVAS, LVNC, PA, PS, PDA, MV anomalies, AV conduction defects, DORV, PAPVR, TAPVR, heterotaxy, TGA |
√ |
[93,117,118,119,120] |
| SMAD6 |
Sequencing |
BAV and/or aortic stenosis, coarctation of the aorta and with thoracic aortic aneurysms |
√ |
[106,107] |
| FBN1 |
Direct sequencing along with comprehensive assessment of BAV phenotype and function using Doppler echocardiography |
Atypical mutations associated with BAV, aortic dilation, aneurysm |
√ |
[98,99] |
| AXIN/PDIA2/ENG |
Gene Network Analysis on BAV probands |
Associated with BAV |
|
[121] |
| ACTA2 |
Sequencing |
BAV, thoracic aneurysm and dissection (TAAD) (BAV, CoA or PDA observed) |
|
[122], [109] |
| MAT2A |
Sequencing |
Thoracic aortic aneurysms, variable presentation of BAV |
√ |
[123] |
| UF1DL |
Protein analysis |
Reduced levels of UF1DL in BAV aortas |
|
[124] |
| EGFR |
Targeted Sequencing of nine genes |
Associated with BAV |
√ |
[125] |
| TGFBR1, TGFBR2 |
Sequencing |
Non syndromic BAV and proximal aortic aneurysm |
√ |
[104] |
| TGFBR1/2, TGFB2, TGFB3, SMAD3 |
Sequencing, NGS |
Loeys-Dietz Syndrome (LDS) or phenotypes within the LDS spectrum |
√ |
[37,100,101,102,103] |
| COL1A2 |
Sequencing |
Ehlers Danlos Syndrome (skin and bone abnormalities as well as mitral and aortic valve dysfunction observed) |
√ |
[126] |
| KCNJ2 |
Familial sequencing |
Andersons Syndrome (Cardiovascular abnormalities: polymorphic ventricular tachycardia and periodic paralysis and semilunar valve abnormalities including BAV) |
√ |
[81] |
| HOXA1 |
Sequencing |
Bosley-Salih-Alorainy syndrome and Athabascan Brainstem Dysgenesis syndrome (Cardiovascular abnormalities observed: interrupted aortic arch type B, subclavian artery abnormalities, VSD, TOF, and BAV) |
√ |
[127] |
| Abbreviations: BAV: Bicuspid Aortic Valve; LVOTO: Left ventricular outflow tract obstruction; CoA: Coarctation; PDA: Patent ductus arteriosus; AR: Aortic regurgitation; ASD: Atrial septal defect; VSD: Ventricular septal defect; AVSD: Atrioventricular septal defect; TOF: Tetralogy of Fallot; SVAS: Supravalvular aortic stenosis; LVNC: Left ventricular non-compaction; PA: Pulmonary atresia; PS: Pulmonary stenosis; PDA: Patent ductus arteriosus; MV: Mitral valve; AV: Atrioventricular; DORV: Double outlet right ventricle; PAPVR: Partial Anomalous Pulmonary Venous Return; TAPVR: Total anomalous pulmonary venous return; TGA: Transposition of the great arteries |
Signals emanating from the myocardium trigger Endo-MT/EMT and constitute a number of pathways and factors like BMP2/4, TGFB2/3 and VEGF. The sensitivity of the endocardium to these factors, in turn initiating Endo-MT/EMT, requires the expression of receptors and effectors of downstream myocardial signaling pathways such as Alk1, Alk3, Alk5, B-catenin, VEGF, NOTCH1, Twist1, Sox9, Tbx20, Gata4, Pitx2 and Hedgehog signaling [29]. Increased ECM production for valve development requires the suppression of chamber specific genes at the myocardium of the cushions. This process is specified and programmed by Tbx2, Nfatc2-4 and Bmp2 among others to suppress chamber-specific genes, produce factors important for EMT and to increase ECM synthesis creating a support for EMT [30,31]. Both the myocardium and endocardium at the cushion is different from that in the cardiac chambers. These tissues at the cushion express genes that are essential for valve and septal development like Nfatc1 [31]. This regional specificity of EMT is defined by the temporal pattern of co-ordinated yet distinct and specific gene programming events and expression of an array of signaling factors and receptors at the endocardium and myocardium cushions of the OFT and AVC.
Given the complexity and intricacy of the pathways and signaling molecules that orchestrate cardiac development in a spatio-temporal manner, slight dysregulation at any stage can lead to serious consequences on the development of the heart and embryo, sometimes fatal. Defects in gene expression of factors governing development, differentiation, migration and proliferation in either of the two myocardial lineages (FHF and SHF) and cNCC can lead to an array of cardiac phenotypes (Table 1 and 2)
Table 2. Animal models of valvular defects including BAV and great artery defects.
| Gene |
Expression |
Organism |
Genotype |
Phenotype |
Reference |
| NOS3 |
Endocardium, myocardium, SL valves |
Mouse, Syrian Hamster |
Nos –/– |
Congenital heart defects with BAV |
[45,46,132] |
| GATA5 |
AV and OFT Endocardial cushions, endocardium |
Mouse |
Gata5–/–, eGATA5–/–, Tie2Cre; Gata5F/F |
BAV |
[131] |
| NOTCH1 |
OFT and AV endocardial cushions |
Mouse, Zebrafish |
Notch1–/– |
Septation defects, valve atrophy |
[134] |
| GATA6 |
AV and OFT, endocardial cushions, endocardium, myocardium |
Mouse |
Targeted deletion in VSMCs and NCCs; Conditional knockout; SMCre+GATA-6F/F; Wnt1Cre+GATA-6F/F |
DORV, VSD, aortic arch patterning defects |
[130] |
| FGF8 |
Heart, OFT, endocardial cushions, great arteries, pharyngeal endoderm |
Mouse |
Fgf8; hoxa3-IRESCre (Ablation in the 3rd and 4th pharyngeal endoderm and ectoderm) |
BAV, parathyroid and thymic defects |
[130] |
|
|
|
Fgf8; AP2α-IRESCre (Ablation in the pharyngeal arch extoderm) |
Postnatal lethality, Failed formation of the 4th pharyngeal arch artery, aortic arch defects, IAA |
|
| Nkx2.5 |
SHF, cNCCs, OFT endocardial cushions |
Mouse |
Nkx2.5GFPhet, Nkx2.5HDneohet |
BAV, AV block, ASD |
[135] |
| MATR3 |
cNCCs, heart, great arteries |
Mouse |
Matr3GT-ex13–/– |
Lethal |
[85] |
|
|
|
Matr3GT-ex13+/– |
BAV, PDA, CoA |
|
| ROBO1 and ROBO2 |
Endothelial cells, endocardium. OFT Endocardial cushions |
Mouse |
Robo 1–/– |
VSD, Overriding Aorta (OA) |
[21] |
|
|
|
Robo1–/–Robo2–/– |
VSDs, OA, BAV, |
|
| SLIT2 |
Endocardium lining |
Mouse |
Slit2–/– |
VSD, thickening of SL valves |
[21] |
| SLIT3 |
OFT and myocardium adjacent to endocardial cushions |
Mouse |
Slit3–/– |
VSD, hypoplastic aortic valves |
[21] |
| Alk2 (Acvr1) |
cNCC, OFT endocardial cushions |
Mouse |
Targeted deletion in endocardial cushions; Alk2–/–/Gata5-Cre |
BAV, AS, AI |
[136,137] |
|
|
|
Targeted deletion in NCCs Wnt-Cre Alk2–/– |
PTA, abnormal morphogenesis of the aortic arch, impaired migration of cNCCs into the OFT and loss of cNC derived smooth muscle cell differentiation around the aortic arteries. |
|
| ALK6 |
cNCC, OFT endocardial cushions |
Mouse |
Targeted deletion in NCCs Wnt-Cre Bmpr1a–/– |
shortened outflow tract and septation defects including reduced proliferation of the ventricular myocardium |
[138] |
| SMAD4 |
cNCCs, myocardium, SHF |
Mouse |
Targeted deletion in NCC Wnt-Cre Smad4fl/fl |
Embryonic lethality, reduced cNCC migration into OFT, PTA, OFT hypoplasia and septation defects |
[139] |
| TBX20 |
cNCCs, SHF, OFT endocardial mesenchyme |
Mouse |
Tbx20–/– |
Embryonic lethality, OFT defects |
[140,141] |
|
|
|
Targeted deletion in the endocardial cushions; Nfatc1-Cre Tbx20–/– |
Dysmorphic and hypoplastic valve, endocardial cushion proliferation defects |
|
| ET-A |
cNCCs, OFT endocardial cushions, endocardium, |
Mouse |
ETA–/– |
IAA, DA, aortic arch patterning defects, OA, DORV, PTA, TGA |
[18,142] |
| ET-1 |
Endothelium of great arteries and OFT, cNCCs, OFT endocardial cushions, endocardium, epithelium of pharyngeal arches |
Mouse |
ET-1-/- |
IAA, VSD, tubular hypoplasia of the aortic arch, OFT malformations |
[143] |
| ECE1 |
OFT endocardial cushions, endocardium |
Mouse |
Ece1–/– |
IAA, PTA, VSD, DORV |
[144,145] |
|
|
Mouse |
Ece1–/–: Ece2–/– |
AV and OFT dysplasia, DORV, VSD, hypoplastic endocardial cushion |
|
| ECE2 |
Endocardial cushion mesenchyme |
Mouse |
Ece2–/– |
No detectable phenotype |
|
| NF1 |
cNCC, SHF, endocardial OFT endocardial cushions, myocardium, endothelium |
Mouse |
NF1–/–, Endothelial specific deletion NF1ec (Tie2-Cre NF1–/–) |
Enlarged endothelial cushions, DORV, VSD, impaired EMT |
[146] |
| NFATC1 |
OFT endocardial cushions, endothelium |
Mouse |
NFATC1–/– |
Embryonic lethality, hypoplastic valves, impaired SL valve development |
[147,148] |
| Ltbp1L |
cNCC, OFT endocardial cushions |
Mouse |
Ltbp1L–/– |
PTA, IAA |
[149,150] |
| SEMA3C |
cNCC, SHF, endocardial OFT endocardial cushions, myocardium |
Mouse |
Sema3c–/– |
Quadricuspid Aortic valve, CoA, PTA, septal defects abnormal migration of cNCCs |
[14] |
| CXCR4 SDF1 |
cNCC, SHF, endocardial OFT endocardial cushions, myocardium |
Chick |
miRNA-CXCR4 silencing, Dominant negative-CXCR4 (DN-CXCR4) to inhibit SDF1 signaling |
delayed cNCC migration and increased cNCC death cNCC migration defects, severe conotruncal and cardiac defects |
[151] |
| CXCR7 |
cNCC, OFT endocardial cushions |
Mouse |
CxCr7–/– |
Severe SL valve stenosis |
[152] |
| Cnb1 |
SHF, OFT endocardial cushions |
Mouse |
Targeted deletion in SHF Mef2c-Cre Cnb1–/– |
Absent SL valves, reduced conal cushions |
[26] |
| Rac 1 |
cNCCs |
Mouse |
Wnt-Cre Rac1–/– |
Abnormal patterning of the aortic arteries, absence of VSMC differentiation.OFT septation failure |
[153] |
| Rae 28 |
cNCC, OFT endocardial cushions |
Mouse |
Rae28–/– |
TOF, DORV and aortic valve stenosis |
[154,155] |
| Ets1 |
OFT septum |
Mouse |
Ets1–/– |
Septal defects |
[156] |
| HOXA1 |
NCCs, OFT myocardium, endocardium, SHF |
Mouse |
HOXA1–/– |
BAV and heart defects |
[157] |
Congenital heart defects involving the OFT, aortic arch and the ductus arteriosus constitute about 20–30% of all congenital heart disease. The presence of a bicuspid aortic valve (BAV), a common congenital cardiac anomaly with a relatively high prevalence in the general population, results in an increased risk of complications later on in life. Due to the significant associated morbidity and mortality, these congenital heart defects prove to be a continuing medical challenge for prognosis and treatment, most of the time demanding invasive approaches of therapy.
2. Bicuspid aortic valve associated thoracic aortic aneurysm
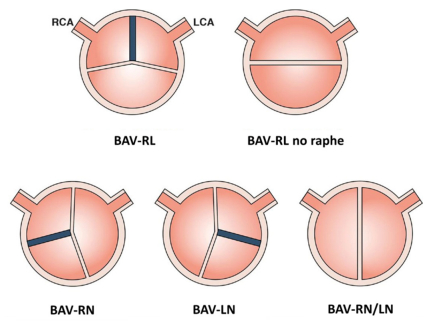
The normal aortic valve is tricuspid and comprises three semilunar shaped leaflets or cusps, each of which housed within a small dilation of the proximal aorta called the Sinus of Valsalva or the aortic sinus. Each of these sinuses and the leaflets arising from them are annotated relative to their relationship to the coronary arteries; right, left and non-coronary sinuses/cusps. The outward edges of the semicircular border of each cusp attach it to the wall of the aorta via an attachment point called a commissure. The bicuspid aortic valve is defined as a congenital cardiac abnormality that arises due to perturbations in tightly regulated process involved in valve formation and OFT septation during cardiogenesis. These perturbations result in an aortic valve comprised of only two asymmetrical valve leaflets, as a consequence of fusion of two out of the three valve leaflets, instead of three distinct valve leaflets. The region at which the fusion between two leaflets occurs is marked by a raphe, commonly present with most fusion patterns, although rarely fusion of leaflets without a marked raphe does occur, giving rise to symmetrical valve leaflets. The most common fusion pattern observed in BAV is the fusion of the right and left (R-L) coronary cusps and this occurs in 80% of individuals that present with BAV while the right-noncoronary cusp fusion (R-N) occurs in ~17% followed by the rarest fusion pattern, the left-noncoronary cusp (L-N) fusion in about ~2% of BAV patients (Figure 1) [32,33]. With a prevalence of 1–2% in the general population and a male to 138 female preponderance of ~3:1, BAV is one of the most common congenital malformations as compared to a total of 0.8% for all other forms of congenital cardiac disease combined. This large prevalence is reflective of the immense clinical burden that BAV imposes for the vast majority of the cases that will develop serious complications later on in life, such as aortic dilation and dissection. As a consequence of BAV, some of the serious and common complications like aortic stenosis (AS) and aortic regurgitation (AR) may occur. Dilation involving any or all segments of the proximal aorta right from the aortic root to the arch, termed as BAV related/associated aortopathy is observed in about 50% of the affected individuals [34,35]. Abnormalities of the aortic wall are common in BAV patients and, from a developmental perspective, can be explained by the relative contribution of NCCs to both, the semilunar valves and the tunica media of the distal great arteries. Hence, defects of the NC can result in an abnormal valve in combination with ascending aorta or aortic arch abnormalities. In fact, studies have shown that impaired differentiation and contraction of the cNCC derived smooth muscle cells contribute to aortopathy observed in BAV individuals [36]. Craniofacial abnormalities have also been observed in patients with syndromic aneurysms, with BAV as one of the cardiovascular anomalies, reflective of defects in the neural crest that also contribute to the craniofacial mesenchyme [37,38,39,40,41].
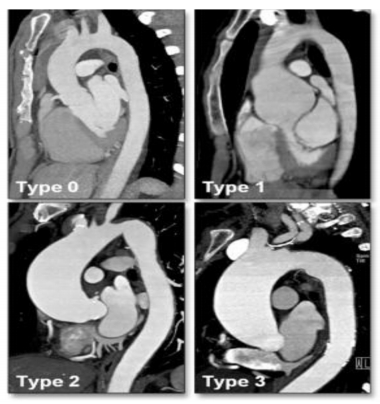
BAV individuals present with an 8-fold increased risk of aortic dissection and a 53% risk of valve replacement over a 25-year period. In addition, affected individuals carry a 26% risk for aneurysm formation and a 25% risk for aortic surgery [42]. Almost 75–80% of the stenotic valves in children and at least 50% of aortic valve stenosis in adults is due to the presence of BAV [43]. BAV associated aortopathy can be classified into 3 different subtypes (Figure 2): Aortic root dilation (Type 1), Aortic enlargement involving the tubular portion of the ascending aorta (Type 2) and diffuse involvement of the complete ascending aorta and the transverse aortic arch (Type 3) [44]. A normal non-dilated aorta is classified as Type 0. Studies have hypothesized that while the different valve fusion subtypes have distinct etiologies which are reflective of the defects in molecular and genetic mechanisms involved in the developmental processes of valve development and OFT septation, the subsequent BAV associated aortopathy observed later on in life, may be different depending on the valve fusion subtype observed [44,45,46,47]. BAV associated aortopathy follows a heterogeneous pattern with variable presentation within affected members of families and isolated individuals. This suggests that the underlying pathomechanism of BAV associated aortopathy may consist of a complex interplay of genetic, hemodynamic and epigenetic factors.
3. Hemodynamics in relation to valvular fusion
The altered hemodynamics of blood flow through the aorta as a result of a morphologically or functionally defective aortic valve, has been one of factors, suggested to lead to BAV-associated aortopathy. Several studies have established the presence of a nonaxial transvalvular turbulent jet flow within the aortic root, as a result of the restricted mobility of the fused cusps [48,49,50]. This turbulent jet flow creates altered biomechanics and fluid dynamics within the proximal aorta causing uneven wall stress distribution along the aortic wall, in turn leading to aortic dilation or aneurysm formation and subsequent dissection and rupture. As consequence of this hemodynamic stress, the dilation protrudes asymmetrically towards the right anterior aortic wall due to the aortic convexity [51]. A correlation has been established between the degree of restrictive mobility of the fused cusp and the eccentricity of the transvalvular systolic flow, with the severity and rate of dilation at the root and ascending aorta [50,52]. In addition to determining the rate of progression of aortic dilation due to turbulent flow patterns, the BAV cusp fusion subtypes have been shown to produce unique jet orientations in the proximal aorta [51]. The different BAV subtypes lead to different degrees and orientations of asymmetry in aneurysms that in turn leads to varying rates of dilation progression and altered signatures of matrix metalloproteinases (MMPs) and tissue inhibitors of metalloproteinases (TIMPs) [53,54]. Comprehensive studies involving MDCT imaging and transthoracic echocardiography of BAV patients with varying BAV subtypes and associated aortopathy, reported that, the R-L fusion subtype was most commonly associated with a normal aorta followed by type 2 aortopathy, while the R-N/L-N fusion subtype was most frequently associated with type 3 aortopathy. In addition, although both subtypes showed hemodynamically significant valvular dysfunction in terms of stenosis and regurgitation, moderate-to-severe aortic stenosis (AS) is predominantly associated with R-N/L-N subtype as compared to moderate-to-severe aortic regurgitation (AR) in R-L subtypes [44]. This study also confirmed the R-L subtype as being the most common valve fusion phenotype among patients. 4D cardiac MRI also showed that the R-L subtype produced a right-anteriorly directed helical systolic jet flow with considerable peripheral skewing towards the ascending aortic convexity, which may explain the asymmetrical dilation of the mid-region of the ascending aorta along with increased aortic root dimensions [48,51,53]. These patients also show severe degeneration of the aortic wall accompanied by higher proteolytic indices. The less frequent R-N subtype is associated with a left-posteriorly directed eccentric flow jet towards the proximal aortic arch which explains the diffuse involvement of the ascending aorta and the transverse arch leaving out the aortic root [48,55]. Interestingly, phase locked particle image velocimetry experiments on non-dilated ascending BAV aortas subjected to different flow patterns observed in TAV, R-L BAV, R-N BAV and N-L BAV revealed significant flow abnormalities measured by degree of jet skewness, velocity, turbulence and shear stress. These substantial flow abnormalities observed in non-dilated aortas, although different from dilated aortas, have been shown to coincide with regions of the aortic wall prone to dilation [56]. Abnormal shear stress created as a result of cusp fusion, can exert an effect on molecular events and modulate genes responsible for ECM remodeling, MMP production and apoptosis of VSMCs hereby increasing the predisposition to aneurysm formation [57]. Levels of global MMP activity including MMP-2, MMP-9 were increased while expression of MMP-7, MMP-8, TIMP-1 and TIMP-4 was decreased in BAV patients [53,58]. MMP and TIMP levels in the R-L patients were consistent with the overall expression observed in BAV patients. In the case of L-N patients, although elevated levels of global MMPs were observed, only MMP-8 and TIMP-4 expression levels showed a decrease. The R-N subgroup showed only a decrease in levels of MMP-7, MMP-8, TIMP-1 and TIMP-4. In addition, the R-L subgroup showed higher proteolytic balance indices for MMP-1, MMP-9 and MMP-12 relative to the R-N and L-N subtypes. This further highlights the unique MMP and TIMP signatures specific to BAV subtypes, and implicating the R-L subtype as associated with the most aggressive deterioration of aortic wall requiring early surgical intervention. Differential profiles of circulating MMPs, TIMPs and recently implicated miRNAs (eg; miRNA-21, miRNA-1, miRNA-29a) may prove to be important biomarkers to predict progression of aortopathy and to distinguish between different BAV associated aortopathy etiologies [59]. Apart from the differential MMP and TIMP expression levels, differential levels of endothelial nitric oxide synthase (eNOS) have also been reported in aortic walls from BAV patients as compared to individuals with TAV [60,61,62,63]. While a reduction in levels of eNOS was observed in the proximal aorta (above the sinotubular junction), eNOS levels in the concavity and distal aorta were increased. This site-dependent variation is probably reflective of aggressive and variable shear stress along the aortic wall [60].
Although valvular dysfunction along with hemodynamic factors, as a result of BAV, can explain some of the progressive, typically asymmetric aortic enlargement observed in these patients, it cannot entirely describe the full spectrum of BAV-associated aortopathy. Understanding not only the hemodynamic factors but also the developmental mechanisms and the underlying genetics, that govern this congenital abnormality, will be essential to explain the phenotypic heterogeneity and the propensity to develop BAV associated aortopathy seen in these patients.
4. Genetics
The "genetic" hypothesis around BAV and its associated aortopathy evolved from the observation that pediatric patients with BAV had larger aortic root and ascending aorta measurements indicating that the inherent structural fragility of the aortic wall was determined early on life [64,65]. Furthermore, progressive aortic dilation is seen in patients both with a normally functioning BAV and following valve replacement indicating an inherent weakness of the aortic wall leading to vascular complications independent of valvular dysfunction [62,66]. Familial studies also demonstrated that within families, BAV can occur independently of any vascular complication or aortopathy and vice versa [67]. Histopathological examination of dilated aortas from BAV individuals revealed localized regions of matrix disruption, VSMC apoptosis, altered collagen content, increased elastic fragmentation and MMP levels and accumulation of mucopolysaccharide ground substance. These findings were strikingly similar to aortas analyzed from Marfan syndrome (MFS) patients caused by a deficiency in fibrillin-1 (FBN1) and was also observed in non-dilated aortas [68,69,70]. Interestingly, loss of aortic elasticity, increased MMPs and fibrillin-1 deficiency has been observed independent of aortic diameter in BAV individuals [71,72]. FBN1 deficiency triggers the activation of MMPs, degrading the structural integrity of the aorta. Notably, decreased fibrillin-1 expression has been observed in the aortic wall of BAV individuals and it is postulated that a microfibrillar gene defect causes increased VSMC detachment from the elastic laminae leading to VSMC apoptosis, subsequently resulting in an increase of MMP and proteolytic factors [72,73,74,75]. This MMP and proteolytic factor activation accelerates the degeneration of the aortic wall and causes loss of structural integrity and elasticity, resulting in progressive dilation prior to aneurysm development even after valve replacement or in the presence of a normally functioning BAV. The FBN-1 deficiency and dilation is also observed in the walls of the pulmonary artery in the absence of any pulmonary valve abnormality in BAV individuals, indicating an underlying developmental abnormality since the great arteries originate from a common embryonic trunk [72]. Interestingly, a recent study observed and upregulation of fibrillin 2 (FBN2) in the ascending aorta of patients with BAV irrespective of dilation [76]. These observations suggest a genetic contribution to the pathogenesis of BAV associated aortopathy. In addition, familial clustering studies and echocardiography screening revealed a high incidence of BAV with 9% prevalence in first degree relatives of BAV patients and about 24% in families with more than 1 affected individual, proposing an autosomal dominant pattern of inheritance with reduced penetrance and variable expressivity [77,78]. A heritability of 89% was estimated indicating that BAV was almost entirely genetically determined with mutations in a number of different genes responsible for the phenotypic heterogeneity observed in BAV patients [43].
The genetics of BAV and its associated aortopathy remain elusive and largely uncharacterized. Linkage analysis in BAV families using microsatellite markers have identified regions on chromosome 5q, 13q and 18q linked to BAV and cardiovascular malformations, while a region on 15q25-26 has been linked particularly to BAV and ascending aortic aneurysms. The specific genes within these regions have not yet been identified [79,80]. One of the first genes to be associated with BAV was KCNJ2, identified via ascertainment of a 41-member pedigree presenting with polymorphic ventricular tachycardia and periodic paralysis and semilunar valve abnormalities including BAV [81]. However, the strongest association came shortly after with the identification of mutations in NOTCH1 in non-syndromic BAV and calcification in a small number of families and ~4% of sporadic cases [82,83]. Missense and loss of function mutations in NOTCH1 in affected individuals with BAV and/or aneurysms revealed haploinsufficiency as a probable mechanism of aortic valve disease. NOTCH1 is expressed in the OFT mesenchyme and aortic valve leaflets highlighting the role of Notch signaling in aortic valve development and morphogenesis. NOTCH1 has been shown to regulate Sox9 expression; a chondrogenic transcription factor influencing the expression of genes involved in ECM remodeling and valve development. Inhibition of NOTCH1 signaling results in decreased Sox9 expression causing aortic valve calcification while overexpression of Sox9 curbs the calcific process associated with Notch1 inhibition [84]. Hence, NOTCH1 mutations drive the dysregulation of developmental processes involved in aortic valve development and remodeling probably via a Sox9 dependent and Runx2 upregulation mechanism leading to calcification/stenosis of the aortic valve [82,84]. Recently, MATR3 was identified at a translocation breakpoint in a 46, XY, t(1:5)(p36.11;q31.2) dn translocation carrier with pervasive developmental delay and left ventricular outflow tract obstruction (LVOTO) defects, including BAV, coarctation of the aorta and patent ductus arteriosus [85]. The 5q translocation breakpoint resulted in the disruption of the 3' UTR of MATR3, which encodes for the nuclear matrix protein; Matrin 3. The 3'UTR disruption of the MATR3 transcripts resulted in polyadenylation defects affecting transcript and protein expression [85]. The GATA family of transcription factors have long been known to be essential for development and morphogenesis of the cardiac system (Table 1). Mutations in GATA4, an essential transcription factor in OFT development lead to atrial septal defects and valve abnormalities like aortic regurgitation, mitral valve regurgitation and pulmonary stenosis [86,87,88]. Some of the mutations identified have been shown to disrupt GATA4 binding to Smad4 or Tbx5 indicating the conserved function of these Gata complexes in AV and OFT valve development [86,89]. GATA5, has been shown to be essential for aortic valve development. Mutations in GATA5 were identified in families presenting with an autosomal dominant pattern of inheritance of BAV. Few of the identified rare GATA5 variants resulted in significantly decreased transcriptional activity as compared to wildtype when tested via functional assays [90,91,92]. Nkx2.5 maps to region 5q34 which has been linked to BAV and recently, the first mutation in Nkx2.5 was found in a family with BAV, segregating in an autosomal dominant pattern. As a consequence of the mutation, the interaction of Nkx2.5 with GATA5 was abolished rendering Nkx2.5 incapable of regulating downstream effectors in a GATA5 dependent manner [93]. In addition, Nkx2.5 is also known to be a modulator of ECM remodeling through collagen type 1 (COL1A1). The activation of collagen type 1 is dependent on the interaction between Nkx2.5 and GATA6 [94]. Mutations in GATA6, a transcription factor expressed in the developing heart, OFT and VSMC, are associated with Tetralogy of Fallot (TOF), persistent truncus arteriosus and atrial septal defects [95]. Gata6 is involved in OFT development and has been shown to transcriptionally activate SEMA3C and PLXNA2 to aid the migration of NCC into the OFT, which is important for OFT septation [96,97]. Some of the identified mutations in patients with persistent truncus arteriosus have been known to disrupt the binding of GATA6 to SEMA3C and PLXNA2 promoters abrogating its transcriptional activity and nuclear localization [97]. Although, GATA6 maps to chromosome 18q, a region already known to be linked to BAV, no mutations have been reported in BAV individuals so far. Direct sequencing along with comprehensive assessment of BAV phenotype and function using Doppler echocardiography in 10 BAV individuals revealed novel mutations in FBN1 in the absence of Marfan syndrome (MFS) [98,99]. Mutations in genes involved in the TGFβ signaling pathway, TGFBR1, TGFBR2, SMAD3,
TGFB2 and more recently TGFB3 are known to cause Loeys-Dietz Syndrome (LDS) or phenotypes within the LDS spectrum [37,100,101,102,103]. A TGFBR2 mutation was identified in a patient with BAV and aneurysm without a LDS presentation [104]. Analysis of global expression levels between BAV and tricuspid aortic valve (TAV) individuals with and without an aneurysm revealed a significant increase of TGFβ binding proteins; particularly LTBP3/4, ADAMTSL1 and an alternatively spliced isoform of fibronectin-1 (FN1) exclusively in BAV patients with aortic dilation [105]. Additionally, non-synonymous variants in SMAD6 have been observed in patients with BAV and/or aortic stenosis, coarctation of the aorta and with thoracic aortic aneurysms [106,107]. Recently, whole exome sequencing of 182 individuals of 51 pedigrees with congenital heart disease including BAV identified mutations in NOTCH1 and other factors of the NOTCH signaling cascade including MAML1, JARID2,
SMARCA4 and JAG1. Furthermore, mutations were also identified in ARHGAP31 and MYH6 [108]. Linkage analysis of family members with BAV and/or aortic aneurysms identified the ACTA2 gene [109]. ACTA2 encodes for α-smooth muscle actin and analysis of tissues obtained from the aortas of these patients show proteoglycan accumulation, fragmentation of elastic fibers and loss of VSMCs. Although it is clear that mutations in ACTA2 can lead to thoracic aneurysm and dissection (TAAD) as a result of increased fragility and degeneration of the aortic wall, it is unclear if these mutations can cause BAV [109]. A class of small noncoding RNAs that regulate gene expression, microRNAs (miRNAs) have been shown to be differentially expressed in BAV patients. miR-26a, miR-30b, and miR-195 are downregulated in BAV patients with aortic stenosis as compared to aortic regurgitation [110]. In vitro studies, transfecting each of the above miRNAs into aortic valve interstitial cells activated a number of genes like Bmp2,
Runx2, SMAD3, SMAD1 and alkaline phosphatase (ALPL)
[110]. Stenotic valves also have a reduced expression of miR-41, a repressor of Bmp2 [111]. The above studies highlight the complexity and the genetic heterogeneity that confound the molecular dissection of this disease.
Although the studies mentioned above are in humans, the largest contribution to understanding the development and pathogenesis of BAV-TAA comes from animal studies (Table 2). Tissue specific ablation of Notch1 in either cNCCs or the SHF leads to developmental abnormalities of the semilunar valves [28,128,129]. Interestingly, SHF specific inhibition of Notch1 causes a dysregulation of Fgf8 signaling leading to VSMC abnormalities of the great arteries and BAV thus suggesting a common mechanism underlying both valve defects and the associated aortopathy [130]. Gata5 knockout mice showed a downregulation of endothelial nitric oxide synthase (eNOS) expression levels in the OFT endocardial cushions. Of note, the R-N cusp fusion subtype observed in Gata5 knockout mice was identical to the valve phenotype observed in Nos3 knockout mice suggesting that R-N fusion is a result of perturbations in early developmental processes, prior to OFT septation, and may rely on the nitric oxide (NO)-dependent differentiation/migration of endocardial cells during EMT [46,131]. Studies in eNOS knockout mice and inbred syrian hamsters have shown that while the R-N fusion subtype is reflective of an early EMT defect, the R-L fusion subtype is a late defect caused due to abnormal cNCC migration resulting in impaired septation of the proximal OFT [45,46,132]. The abnormal migration of the neural crest could explain the severe aortopathy in the R-L fusion subtype associated with accelerated degeneration of the aortic wall as compared to the R-N fusion subtype. This study for the first time shed light on the different etiological identities of the BAV subtypes, which may play an important role in understanding the genetic and haemodynamic mechanisms at play. These observations re-instate the importance of Nos3 in valve development but also suggest a dose dependent role during valve morphogenesis. Gata4, Gata5 and Gata6 expression has been shown to overlap during cardiac development. Gata4+/– Gata5+/– and Gata5+/– Gata6+/– double knockout mice die perinatally or embryonically due to severe cardiac defects including double outlet right ventricle (DORV) and ventricular septal defects (VSD)
[133]. Examination of Gata4+/– Gata5+/– mice revealed an extremely high pressure gradient through the aortic valve along with the presence of BAV. The prevalence of BAV in Gata5+/– Gata6+/– mice was ~25%. Collectively, the above data suggest a dose-dependent sensitivity for GATA factors during cardiogenesis and aortic valve formation.
The above mentioned findings provide a foundation for the genetic basis of the pathogenesis of BAV and highlights the complex crosstalk between hemodynamic, developmental, environmental and genetic factors.
5. Epigenetics
In addition to mutations in the genes themselves, another important heritable factor in regulating or modulating the expression of genes involves the modification of chromatin. The higher order structure containing packaged DNA around histone proteins serves not only a structural purpose but also one that is critical for gene expression controlling the access of certain factors to specific regions in the genome in a temporal manner. Regulation at the chromatin level is mediated by three different processes; DNA methylation and acetylation, ATP dependent chromatin remodeling and covalent histone modifications. Combinations of specific histone modifications coupled with nucleosome structure at defined regions provide a histone code or mark which act as docking sites for transcription factors and other chromatin regulators exerting an array of specificity and complexity on gene expression control.
One of the important molecules known to play a role in cardiac and OFT development is the Brg1/Brm-associated factor (BAF) complex. The BAF complex consists of 12 subunits and is part of the family of SWI-SNF type of chromatin remodeling complexes. One of two highly homologous genes, Brg1 and Brm encode for the ATPase subunit of the BAF complex. Brg1 aids in the binding of the myocardin family of coactivators to promoters of genes involved in the expression of smooth muscle contractile proteins [158,159]. Targeted deletion of Brg1 in VSMCs in mice results in patent ductus arteriosis causing cyanosis and dilation of the cardiac chambers in 1/3 of the mice [160]. Furthermore, in vitro studies on VSMCs have shown that knockdown of Brg1 or Brm results in decreased expression of SMC contractile proteins which could provide an explanation for the patent ductus arteriosus phenotype. While the patency of the ductus arteriosus is essential for fetal circulation, its closure, mediated by the contraction of SMCs of the DA is essential for adult circulation, hence disorganization of SMCs as a result of Brg1 deficiency can lead to PDA due to absent perinatal closure of the ductus arteriosus. Deletion of Brm, does not recapitulate any of the Brg1 knockout defects and neither does it exacerbate the patent ductus arteriosus phenotype of Brg1 deficient mice. This highlights the fact that Brg1 is the dominant ATPase of the BAF complex and is crucial for smooth muscle cell maturation. These studies have brought to light the importance of factors involved in VSMC maturation and homeostasis, dysregulation of which could possibly contribute to the underlying aortopathy observed in BAV individuals including increased VSMC apoptosis, aberrant ECM remodeling and loss of elasticity and contractile ability resulting in a weakened aortic wall.
While mutations in NOTCH1 are known to be associated with BAV and calcific valve disease, recently, human disease modelling in induced pluripotent stem cells (iPSCs) derived from endothelial cells, revealed a complex network of transcriptional and epigenetic mechanisms governing NOTCH1 haploinsufficiency [161]. This study showed that NOTCH1 haploinsufficiency caused by heterozygous nonsense mutations in NOTCH1, affected H3K27 acetylation at NOTCH1-bound enhancers leading to disruption of the transcriptional process of almost 1000 genes involved in osteogenesis, inflammation and oxidative stress. This suggests that the altered epigenetic architecture caused an activation of the pro-osteogenic factors exacerbated in the presence of hemodynamic shear stress leading to calcification of the aortic valves [161]. This study highlights the complex interplay between genetic, epigenetic and hemodynamic factors, in addition to transcription factor dosage effect leading to human disease. Acetylation and deacetylation of lysine residues on Notch1 intracellular domain (NICD) act as important modulators of NOTCH signaling and response by regulating NICD protein turnover shuttling between NICD stabilization and degradation respectively. Interestingly, endothelial specific deletion of the lysine deacetylase Sirt1, important for the deacetylation of NICD, caused increased sensitivity to Notch signals and aberrant cell signal response due to the activation of downstream Notch target genes leading to impaired vascular growth and sprout elongation [162]. Further studies are required to determine the exact role of Sirt1 in vascular development. The involvement of the mixed lineage leukemia (MLL) complexes in cardiovascular development has also been suggested. Mutations in MLL2, known to cause Kabuki syndrome, are characterized by an array of birth defects including cardiac defects. Patients with kabuki syndrome show a high incidence of LVOTO defects and aortic dilation at approximately 46% with the most common defects being coarctation of the aorta, ventricular septal defects and atrial septal defects [163]. While de novo and partial deletions of the X chromosome gene, KDM6, which encodes a histone demethylase that interacts with MLL2 have been shown to also cause Kabuki Syndrome, loss of function mutations in MLL2 remain the major cause of Kabuki Syndrome. Recently, a Kabuki patient presented with BAV as the only cardiac defect observed [164]. Impaired histone methylation due to deficiency of MLL2 causing reduced expression of the downstream targets provide a mechanism of pathogenesis in Kabuki Syndrome patients. Another important factor in chromatin remodeling is the histone deacetyltransferase; EP300. P300 proteins act as transcriptional coactivators bridging communication between the transcriptional activators located at enhancer sites and the basal transcription machinery at promoter sites. Crucial to myocardial cell differentiation, EP300 is known to act as a coactivator of GATA5, via physical interaction of the two proteins, to regulate the transcription of the cardiac restricted atrial natriuretic factor (ANF) gene expressed in cells committed to the cardiac lineage early on in embryonic development [165]. Interestingly, mutations in EP300 are known to be associated with Rubenstein-Taybi Syndrome (RSTS) characterized by delayed development, microcephaly and dysmorphic facial features. Several secondary complications are observed in patients with RSTS including cardiovascular malformations like BAV, ASD, VSD, PDA, coarctation of the aorta and hypoplastic left heart [166]. Given the role of the TGFβ superfamily in cardiac development, with mutations in various signaling factors and receptors causing an array of syndromic cardiovascular phenotypes, adding another layer of complexity, studies have shown that alternative TGFβ splicing patterns driven by diverse epigenetic modification mechanisms at specific loci can contribute to the phenotypic heterogeneity of TAA aortopathy observed in BAV patients [167].
6. TGFβ, BMP and NOTCH-The crosstalk
6.1. TGFβ pathway
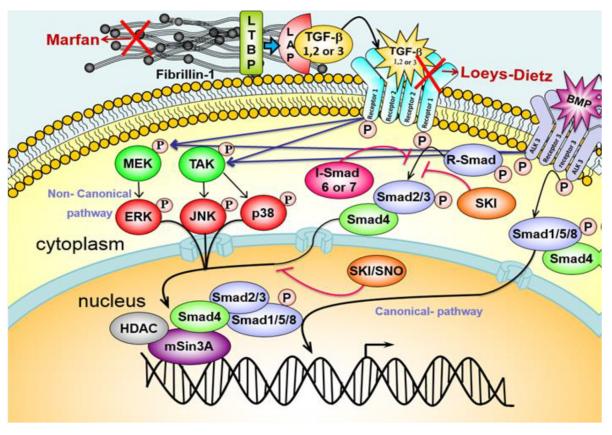
A few of the first signaling molecules shown to be involved in EMT were the TGFβ signaling factors [168,169,170,171,172]. Studies have shown a number of differentially spliced TGFB isoforms are expressed in the developing endocardial cushions in mice [173]. These isoforms are highly redundant, which could highlight the existence of a number of compensatory mechanisms which may uncover an important role for TGFβ ligands in cardiogenesis. On binding to their corresponding TGFβ type 2 receptors, TGFβ ligands activate them, hereby triggering the transphosphorylation of type 1 receptors within the receptor ligand complex. The phosphorylated type 1 receptor in turn acts as a serine/threonine kinase to phosphorylate and activate the cytosolic smad proteins which act as important intracellular mediators and enhancers of TGFβ signaling. The TGFβ ligands also exert their effects on downstream gene expression and regulation via the non-canonical signaling pathway via ERK, JNK and MEKK proteins (Figure 3). During EMT, the TGFβ ligands are known to signal through the canonical signaling pathway, particularly through SMAD2/3, hereby activating the expression of downstream genes including Snail and Slug. These are two important transcriptional repressors that can tightly modulate EMT in the developing heart valves [174,175,176,177]. Slug/Snail trigger endothelial cell activation, in the endocardial cushions, and invasion. Another important molecule is VE-cadherin. Its expression is reciprocal to that of Slug and Snail. The maintenance of low levels of VE-cadherin is essential for the developing mesenchyme of the heart valves [134]. TGFβ2 acts downstream of Notch, TBX5 and Bmp2 pathways to activate the WNT/β-catenin pathway [30,178,179]. Important for the transduction of signals in the TGFβ pathway are the SMAD proteins. Targeted deletion of SMAD4 in NCCs results in defects of the pharyngeal arch including OFT cushion hypoplasia and patent truncus arteriosus [139]. SMAD4 deficient NCCs exhibit increased apoptosis and reduced presence in OFT along with decreased expression of Bmp4, SEMA3C and PLXNA2; signals that are all required for OFT septation. Another member of the TGFβ family of inhibitory SMADs, SMAD6 is expressed in the endocardial cells of the AVC and OFT. Interestingly, knockdown of Madh6, which encodes for SMAD6 and acts as a repressor of BMP signaling, results in hyperplasia of the atrioventricular canal and OFT cushions leading to hyperplastic valves and reduced endothelial cell mediated vasodilation due to an increase in BMP signaling [180]. In vitro studies have shown BMP signaling may be regulated via a SMAD6 dependent physiological feedback loop and hence might play a role in maintaining the number of endothelial cells that undergo EMT [181]. Knockdown of Erk2/Mapk1, a non-canonical TGFβ signaling factor known to be expressed in the pharyngeal arches, in mice causes cardiovascular defects including double outlet right ventricle, patent truncus arteriosus and ventricular septal defects [182,183].
6.2. BMP pathway
The TGFβ cytokine superfamily includes the bone morphogenic proteins (BMPs) that signal mainly through the activation of Smad1/5/8. BMPs have a number of roles in OFT septation and valve development. Myocardially expressed Bmp2 activates the expression of hyaluronic acid synthetase 2 (Has2), important for the production of cushion ECM, and other genes (Twist1, Msx2 and Msx1) that are important for EMT [184,185]. In vitro studies on atrioventricular canal endothelial explants from mice, following treatment with Bmp2, indicated an increase in TGFB2 suggesting that Bmp2 triggers an endocardial autocrine TGFβ loop promoting EMT [186]. Bmp4 is strongly expressed in the OFT and is required for septation. Mice deficient in Bmp4 exhibits atrial septal defects, ventricular septal defects and patent truncus arteriosus [187]. BMP6 is expressed in the endocardium, myocardium and the developing valve mesenchyme and shows functional redundancy with BMP7 with a similar pattern of expression.
Bmp6–/–/Bmp7–/– double knockout mice exhibit hypocellular OFT cushions with a delay in OFT formation uncovering for the first time the role of BMP signaling in OFT and valve development [188]. Some of the important BMP receptors expressed in the developing heart are Alk2,
Alk3 and Bmpr2. Hypomorphic Bmpr2 alleles in mice present with interrupted aortic arch, patent truncus arteriosus and absent semilunar valves [189]. Knockdown of Bmpr2 in endothelial cells results in atrial septal defects, hyperplastic semilunar and atrioventricular valve leaflets and ventricular septal defects while myocardial knockdown or NCC knockdown of Bmpr2 causes double outlet right ventricle or overriding aorta, indicating a cell specific role of Bmpr2 [190]. Conditional deletion of Alk3, a BMP type 1A receptor, resulted in hypoplastic cushions. Further analysis of the endocardial cushions showed a decrease of TGFβ2 and p-Smad1/5/8 suggesting that the hypoplasia observed in the valves might be secondary to TGFβ mediated endocardial cushion EMT [191].
6.3. Notch pathway
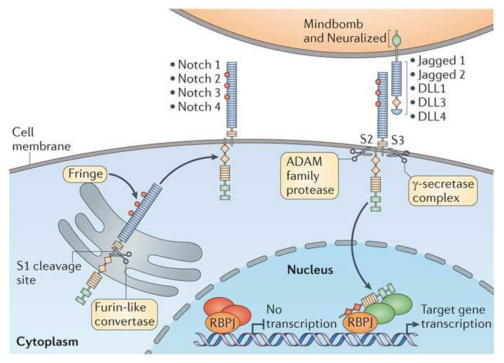
The Notch signaling pathway (Figure 4) is important for a larger number of developmental processes particularly cell fate determination and differentiation and is highly conserved [192]. As described before, NOTCH signaling has been shown to be involved in BAV and its related aortopathy. Notch signaling is important for EMT. Endocardial and OFT expression of Notch1 is indicative of its role in EMT and valve development. Mutations in NOTCH1 or its effector RBPj-κ results in aberrant EMT. In humans, the NOTCH family comprises 4 type 1 receptors (Notch1-4) and 5 type 1 transmembrane ligands (Jagged 1-2, Delta like (DLL) 1, DLL3 and DLL4) [193]. Ligand binding to the Notch receptors triggers the cleavage of NICD by gamma secretase, followed by the translocation of NICD to the nucleus activating gene expression via binding to RBPj-κ. Initiation of EMT requires the Notch1 induced TGFβ2 activation of Snail1 and Snail2, which in turn represses VE-cadherin disrupting cell-cell contact [134,176]. Endocardial cells exposed to Notch1/TGFβ2 require Bmp2 to trigger EMT. This Bmp2 expression is repressed by the myocardial Notch1 indicating a tissue specific reciprocal effect of myocardial and endocardial Notch1 adding a layer of complexity to the EMT and septation processes involved in early development [179]. In the SHF, Notch1 inhibition has been shown to be associated with a reduction in Fgf8, aberrant EMT in OFT cushions and abnormal migration of NCC consistent with thick, asymmetric semilunar valve leaflets [27,128]. These defects are reversed by the overexpression of Fgf8 indicating that Notch1 acts through Fgf8 to trigger EMT in the OFT [27]. Deletion of Notch in the SHF in mice leads to atrial septal defects, double outlet right ventricle, ventricular septal defects and patent truncus arteriosus [27]. While Notch1 mutations, in humans, are associated with calcified aortic valve disease, mutations in JAG1 or NOTCH2 cause Alagille syndrome comprising heart defects that are recapitulated in mice deficient in Hey2, a downstream target of Notch [194,195,196].
Given the crosstalk between these large pathways and the multitude of genes and signaling factors involved, dissecting the molecular mechanisms leading to the pathogenesis of BAV associated aortopathy requires gene discovery strategies ranging from candidate gene association and linkage to next generation sequencing.
7. Future directions and conclusions
The complexity of BAV, along with the underlying predisposition to secondary cardiac complications coupled with increased morbidity, poses both a research and clinical challenge. While experimental animal models, linkage analysis and more recently next generation sequencing approaches have broadened the existing knowledge of the underlying genetics of BAV associated aortopathy, the exact mechanisms by which these networks of factors interact with each other leading to the development of disease and influencing disease progression remains to be understood. However, data from these large candidate gene identification studies does suggest a complex interplay of genetic factors synergistically involved in OFT and aortic valve development perturbations leading to the development of BAV-associated aortopathy. In addition to current next generation sequencing approaches, identification of rare copy number variants in congenital heart disease may also provide further insight into the genetics and the molecular mechanisms involved in disease pathogenesis. It is important to note that although much of the candidate gene discovery strategies have been applied to mainly familial cases, these constitute only a fraction of the total BAV cases with a large number of cases being isolated or sporadic. Implication of candidate genes in causality requires not only careful functional downstream analysis but also validation in replication cohorts using a case-control approach. Large sample sized case and control cohorts are essential in order to account for low frequency disease causing variants especially given the prevalence and heterogeneity of BAV, both phenotypically and genetically. Furthermore, loci identified in human cohorts can be tested in animal models to determine their causative link to disease. BAV is a risk factor for early onset of serious cardiovascular complications however, the molecular basis and tools (such as biomarkers) to monitor disease progression remain largely undefined. Moving forward, the results of these candidate gene approaches and biomarker studies will be pertinent in influencing clinical practice via translation into better diagnosis, follow up and early intervention of secondary complications in individuals with family history of valve disease.
Acknowledgements
The authors are supported by funding from the Fund for Scientific Research, Flanders (FWO, Belgium, G.0221.12), the Fondation Leducq (MIBAVA – Leducq 12CVD03). BL is senior clinical investigator of the Fund for Scientific Research, Flanders and holds a starting grant from the European Research Council (ERC-StG-2012-30972-BRAVE).
Conflict of Interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: