Two-scale homogenization of nonlinear reaction-diffusion systems with slow diffusion

1.   Introduction

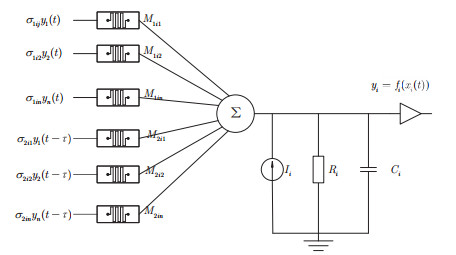
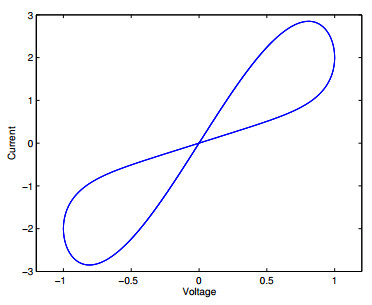
The concept of memristor was proposed by Chua ^[1,2]. The characteristic of memristive systems is shown in Figure 1. Until more than 30 years later, Hewlett Packard laboratory ^[3,4] announced the realization of the physical devices of the memristor. The theory and application of memristor have attracted the attention of scholars again. Memristor has the advantages of smaller size, lower energy consumption, and larger information storage capacity. Memristor is Therefore, memristor is the best choice to construct the next generation neural network instead of resistor and improve the efficiency of intelligent algorithm in machine learning ^[5,6,7]. Therefore, memristor-based neural networks can be constructed (see Figure 2). In Figure 2, $ M_{1i1}, ..., M_{1in} $ and $ M_{2i1}, ..., M_{2in} $ are memristor, other parameters are same as traditional neural networks with resistor ^[8]. Shi and Cao et al. ^[9] first investigated exponential stability of complex-valued memristive neural networks. In ^[10], Yang and Ho analyzed the robustness of the memristive neural network. In ^[11], a more general situation of mixed delays is discussed. Mehrabbeik ^[12] et al. investigate synchronization of the m-Rulkov model. In addition, memristive neural networks with time delay ^[13,14], time-varying delay ^[15,16], mixed delays ^[17,18] and switching jumps mismatch ^[8,19] are discussed.

Fractional calculus which was proposed in 1695, appears almost at the same time as classical calculus. In later research, scholars found that some models can not be well described by using classical integral calculus. On the contrary, fractional calculus can well describe those models. In recent years, the theory of fractional calculus has been successfully applied to various fields. There are more and more works on fractional order dynamical systems. Wang and Yang ^[23] first discussed the quasi-synchronization problem of fractional-order systems with different structures. In ^[24], Bifurcations of fractional complex-valued neural networks with delays is investigated. The synchronization of fractional order systems with discontinuous activation functions is studied in ^[25]. In addition, the fractional order system is also analyzed from the mathematical point of view ^[20,21,22].

Synchronization is one of the most common collective behaviors of dynamical systems ^[26,27]. Synchronization usually refers to the phenomenon of phase consistency among dynamical systems. Synchronization not only exists widely in nature, but it is also very important in practical applications. There are a lot of results about synchronization. In these published results, some control strategies are used to achieve synchronization, such as predictive control ^[28], adaptive control ^[29], iterative learning control ^[30], fuzzy control ^[31], sliding-mode control ^[32], event-triggered control ^[33,34,35], sampled-date control ^[36], impulsive control ^{[37,38,39,40]}, intermittent control ^[41,42,43] and so on. Among those control strategies, intermittent control strategy is the most representative one, and also the one most in line with actual needs. So, intermittent control attracts more and more attention. The intermittent strategy can be divided into periodically intermittent and aperiodically intermittent. Synchronization of integer order systems via periodically intermittent control or aperiodically intermittent control has been widely studied ^[41,42,43]. Synchronization of fractional order systems via periodically intermittent strategy has been investigated in ^[41,42]. However, as far as we know, there are no literatures on fractional order dynamical systems via aperiodically intermittent strategy.

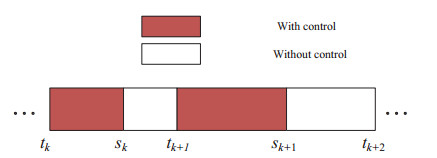
Inspired by the idea of aperiodically intermittent strategy of integer order, aperiodically intermittent strategy is extended to fractional order systems. In the works of integer-order dynamical behavior, both periodically intermittent control and aperiodically intermittent control are widely studied. Among those works, The advantages of aperiodically intermittent control are proven. In addition, unlike periodically intermittent control with fixed width control interval and non-control interval, aperiodically control has fewer interval constraints(see Figure 3), which makes aperiodically intermittent control more flexible and more in line with application requirements. This paper investigates synchronization of fractional order memeristive neural networks via aperiodically intermittent control. Firstly, according to the characteristics of memristive neural networks, dynamical systems with differential inclusion is obtained. Then, in the sense of Filipov's solution, systems with differential inclusion are transformed into conventional forms that can be processed. Finally, based on the periodically intermittent control theory, sufficient conditions of synchronization of memeristive neural networks via aperiodically intermittent control are derived. The structure of this paper is organized as follows: In Section 2, some useful definitions, basic assumptions and lemmas are recalled. In Section 3, based on the theory of fractional order periodically control, sufficient conditions for synchronization are derived by constructing appropriate Lyapunov functional. In addition, Some comparisons with existing results are given verify advantages of the derived conditions. In Section 4, a numerical example is given to demonstrate the derived conditions. Conclusions are given in Section 5.

Notations. This paper is a conducted in the sense of Filippov's. $ \mathbb{R}^{m\times n} $ denote the $ m\times n $ real-valued matrix set. $ co\{x, y\} $ represents convex hull of x and y. $ \lambda_{\max}(\cdot) $ denotes the max eigenvalue of a matrix. T denotes the matrix transposition. $ \mathrm{Inf}(\cdot) $ and $ \mathrm{Sup}(\cdot) $ denote the upper bound and lower bound. $ ||\cdot|| $ denotes the norm of a matrix vector.

2.   Preliminary

The Captuto calculus is the most common of many types of calculus. The properties of some integer-order differentials can be applied directly, which is one of the reasons for the wide application of Caputo calculus. In this article, Captuto calculus is used for analysis.

Definition 1. ^[23] For any integrable function $ f(t)\in \mathbb{C} $, the fractional integral of order $ \alpha $ of function f(t) is defined as

where $ \alpha > 0 $, and $ \Gamma(\cdot) $ is Gamma function.

Definition 2. ^[23] For any function f(t), Caputo's derivative of order $ \alpha $ is defined by

where $ n $ is a positive number and $ n-1 < \alpha < n $. Particularly, when $ n = 1 $,

Fractional-order memristive neural networks of Caputo's derivative are defined by

where $ \alpha $ is the order of Captuto's derivative, $ x(t) = (x_{1}(t), x_{2}(t), \cdot\cdot\cdot, x_{n}(t))^{T}\in\mathbb{C}^{n} $, $ x_{i}(t) $ is the complex-valued state variable. $ C = diag \{c_{i}\}_{n\times n}\in\mathbb{R}^{n\times n \\} $ is the $ i $th self-feedback connection weight with $ c_{i} > 0\; (i = 1, 2, ..., n) $. $ A(x(t)) = a_{ij}(x_{ij}(t))_{n\times n} $ are connection weights $ f(x(t)) = (f_{1}(x_{1}(t)), f_{2}(x_{2}(t)), ..., f_{n}(x_{n}(t)))^{T} $ are activation function. $ I(t) = (I_{1}(t), I_{2}(t), ..., I_{n}(t))^{T}\in\mathbb{C}^{n} $ are external input.

Similarly, the slave-systems are denoted as follows:

where $ u(t) = (u_{1}(t), u_{2}(t), ..., u_{n}(t))^{T} $ are controller.

For the convenience of discussion, Figure 4 is used for discussion. Figure 4 is a simplified model of Figure 1. In this case, the connection weight $ a_{ij}(x_{j}(t)) $ of (2.1) are defined as follows ^[15]

where $ T $ is the switching threshold value with master-systems (2.1) and slave-systems (2.2). $ a' $ and $ a'' $ denote two states of $ a_{ij}(v_{j}(t)) $.

Lemma 1. ^[42] If $ x(\cdot):[t_{0}, \infty)\rightarrow R $ is a continuous differential function and

where a and b are positive constants, then

where $ E_{\alpha}(-a(t-t_{0}^{\alpha})) $ is one-parameter Mittag-Leffler function which is defined by

Lemma 2. ^[41] For $ x(\cdot) $ and $ y(\cdot) $ are two continuous differential functions, if $ \alpha, \; \beta > 0 $, then

Lemma 3. ^[25] Let $ f(t) = (f_{1}(t), f_{2}(t), ..., f_{n}(t))^{T} $ is a n-dimensional vector differentiable function, for any positive definite symmetric matrix $ Q\in R^{n\times n} $. The following inequalities can be derived

where $ \alpha\in[0, 1], 0\leq s. $

Assumption 1. ^[24] For the aperiodically intermittent strategy, the control interval and non-control interval satisfy the following equations

where $ h $ and $ H $ are two positive scalars and satisfy $ 0 < h < H < +\infty. $

Based on the Assumption 1, (2.1) can be rewritten as the following differential inclusion:

Under the Assumption 1, define $ e_{j}(t) = y_{j}(t)-x_{j}(t) $ for $ j = 1, 2, ..., n. $ So, error systems can be obtained:

where $ K $ are gain coefficients.

Lemma 4. ^[42] For any activation functions $ f(\pm T) = 0 $, then one can derive that

where $ l_{j} $ is the Lipschitz condition and $ a_{ij}^{*} $ is the maximum of $ a' $ and $ a'' $.

3.   Main results

In this section, the synchronization problems of fractional order memristor-based neural netwroks via aperiodically intermittent control strategy would be investigated. Sufficient conditions will be derived.

Theorem 1. Under the Lemmas 1–4, and Assumption 1, fractional-order master-system (2.1) and slave-systems (2.2) can achieve synchronization under controller (2.5), if

where, $ \gamma_{1} = -||C||+||A||||L||-||K|| $ and $ \gamma_{2} = -||C||+||A||||L|| $ are two positive scalers.

Proof. Constructing the following Lyapunov functional

For, $ t_{k}\leq t < s_{k} $, deriving derivative of $ V(t) $ along along with (2.3), one can get

Combining the error systems (2.4) and Lemma 3,

According to the Theorem conditions, $ -\gamma_{1} = -||C||+||A||||L||-||K|| < 0 $, so

Based on the Lemma 4, the following equalities can be derived

Similarly, For, $ s_{k}\leq t < t_{k+1} $ Deriving derivative of $ V(t) $ along along with (2.4), one can get

Combining the error system (2.4) and Lemma 3,

According to the Theorem conditions, $ \gamma_{2} = -C+Al > 0 $, so

Based on the Lemma 4, the following equalities can be derived

According to the principle of mathematical induction, combining the control period $ s_{k}-t_{k} $ and non-control period $ t_{k+1}-s_{k} $, when $ k = 0 $, one can get that:

For $ 0 = t_{0}\leq t < s_{0} $, based on the Lemma 2, one can get

so, one can derive

For $ s_{0}\leq t < t_{1} $,

so, one can derive

For $ t_{1}\leq t < s_{1} $,

so, one can derive

For $ s_{1}\leq t < t_{2} $,

so, one can derive

For $ t_{2}\leq t < s_{2} $

so, one can derive

For $ s_{2}\leq t < t_{3} $,

so, one can derive that

According to the principle of mathematical analogy, when $ k = m $, one can assume

For $ t_{m}\leq t < s_{m} $,

so, one can derive that

For, $ s_{m}\leq t < t_{m+1} $,

so, one can get that

Suppose the Eqs (3.13)–(3.16) are hold. According to the principle of mathematical recursive reasoning, when $ t_{m+1}\leq t < s_{m+1} $, one can get

One can derive

For $ s_{m+1}\leq t < t_{m+2} $,

Based on the Assumption 1, one can have that the lower bound of $ s_{k}-t_{k} $ is h and the upper bound of $ t_{k+1}-t_{k} $ is H. The upper bound of $ t_{k}-s_{k} $ is $ H-h $. Therefore, one can obtain that:

For $ t_{m+1}\leq t < s_{m+1} $,

For $ s_{m+1}\leq t < t_{m+2} $,

From the condition $ (E_{\alpha}(-\gamma_{1}h^{\alpha})^{m}E_{\alpha}(\gamma_{2}(H-h)^{\alpha}))^{m} < 1 $ and $ 0\leq t-h-t_{m} < H-h $, we can derive that $ (E_{\alpha}(-\gamma_{1}h^{\alpha})^{m}E_{\alpha}(\gamma_{2}(t-h-t_{k})^{\alpha}))^{m} $ is bounded. So, one can obtain

Then, $ \lim_{t\rightarrow \infty}V(t) = 0 $, the proof of theorem is over.

This completes the proof of Theorem.

Remark 1. In Theorem 1, by using aperiodically intermittent controller, synchronization problem is investigated. Based on the property of Mittag-Leffler function, through strict mathematical reasoning, we can derive $ V(t)\rightarrow0 $ when $ t\rightarrow \infty $. Therefore, we can get that the theorem holds.

Remark 2. Intermittent synchronization strategy has been studied ^[41] and ^[42]. In ^[41], synchronization via aperiodically intermittent strategy is first given in the form of a theory. Compared with ^[41] and ^[42], aperiodically intermittent strategy is more general. In Theorem 1, if the control interval $ t_{k}-s_{k}\equiv h $ and $ t_{k}-s_{k}\equiv H $, aperiodically intermittent strategy is degraded to periodically intermittent control. That is to say, periodically intermittent control is a special form of aperiodically intermittent strategy. Aperiodically intermittent strategy owns more practical characteristics. In this case, a corollary (see Corollary 1) is given.

Remark 3. Synchronization of integer order dynamical systems via aperiodically intermittent control has been investigated. As far as we know, there are no works on fractional order. As is known to all, integral order derivative is a special case of fractional order derivative. When the fractional order derivative a = 1, the derived conclusion can be directly applied to the integral order works. That is to say, the works of integer order on aperiodically intermittent are a special case of Theorem 1.

Corollary 1. When $ t_{k}-s_{k}\equiv h $ and $ t_{k}-t_{k+1}\equiv J $, the controller (2.5) is degenerated into

Controller (3.22) is rewritten as

Under the Lemmas 1–4, and Assumption 1, fractional-order master-system (2.1) and slave-systems (2.2) can achieve synchronization under controller (3.22) or (3.23), if

where, $ \gamma_{1} = -||C||+||A||||L||-||K|| $ and $ \gamma_{2} = -||C||+||A||||L|| $ are two positive scalers. All the parameters are the same as Theorem 1.

4.   Simulation

In this section, an example is given to verify the validity of the sufficient conditions derived by the Theorem 1.

Example 1. Considering three-neuron fractional-order MRNNs, the master-systems are as follows:

where $ \alpha = 0.95 $, $ I_{j}(t) = (0, 0, 0), \; j = 1, 2, 3 $

and

The slave-systems of MRNNs are considered as follows:

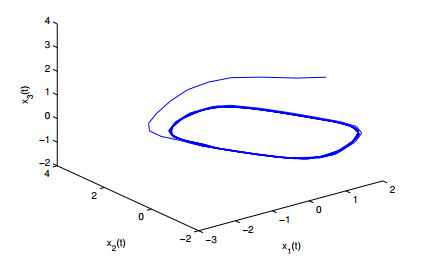
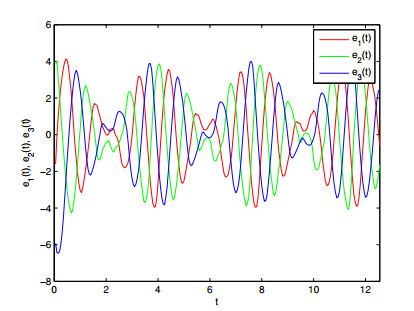
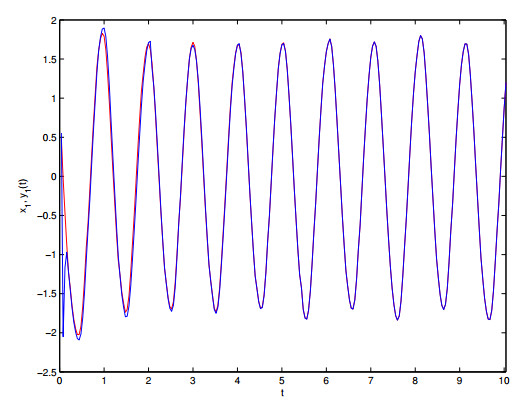
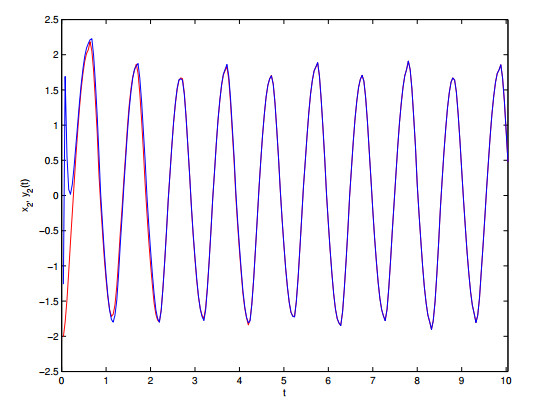
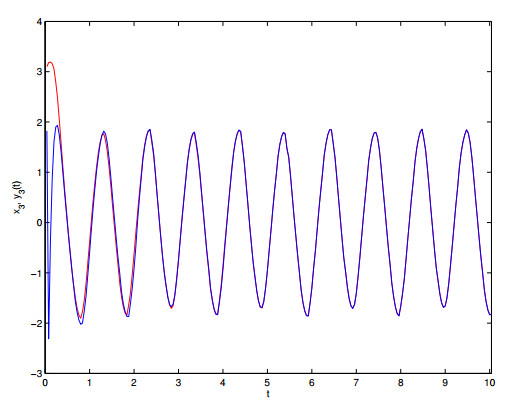
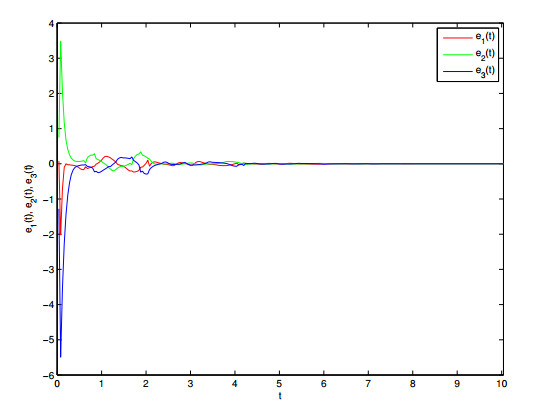
some parameters are given as follows: $ H = 2, \; h = 1.4 $, $ K = 18 $, $ l_{1} = l_{2} = l_{3} = 1 $, one can get $ \gamma_{1} = -||C||+||L||||A||-K < 0 $, $ \gamma_{2} = 7.5357 > 0 $ $ E_{\alpha}(-\gamma_{1}h^{\alpha})E_{\alpha}(\gamma_{2}(H-h)^{\alpha}) = 0.5730 < 1 $. The state trajectories of $ x_{1}(t), x_{2}(t), x_{3}(t) $ are depicted on Figure 5 with initial condition $ x(0) = [1,-2,3]^{T} $. Under the initial condition of $ y(0) = [-1,2,-3]^{T} $, Figure 6 depicts the errors of $ x(t) $ and $ y(t) $ without control. Figures 7–9 depict synchronization state trajectories of $ (x_{1}(t), y_{1}(t))) $, $ (x_{2}(t), y_{2}(t)) $ and $ (x_{3}(t), y_{3}(t)) $ with control. Each dimensional synchronization error is described in Figure 10. From synchronization states Figures 7–9, one can derive that master-slave systems can get synchronization with designed controller. Synchronization error Figure 10 also verifies the derived theory.

5.   Conclusions

In this paper, by using aperiodically intermittent controller, the synchronization problem of fractional-order memristor-based recurrent neural networks is investigated. Although there have been some results about aperiodically intermittent control, those results are studied in integer domain. In the case of fractional calculus, as far as we know, there are only some works on periodically intermittent control. With reasonable assumptions and suitable lemmas, by means of Lyapunov method, synchronization is obtained via aperiodically intermittent control. A simulation example is presented to illustrate the validity of derived sufficient conditions which. Delays are widespread in dynamical systems. Different kinds of delay will have different effects on the dynamical system. It is of great significance to study the influence of delay on dynamical system. In this paper, system are considered without delay. Therefore, in the future, we consider the situation with delays. Furthermore, In addition, the selection of parameters usually depends on experience, resulting in high control costs. Therefore, in the future, optimization algorithm is considered to find the optimal parameter.

Acknowledgments

This work was jointly supported by the Natural Science Foundation of Jiangsu Province of China under Grant No. BK20170171, Postgraduate Research & Practice Innovation Program of Jiangsu Province under Grant No. KYCX18_1857, No. KYCX18_1858.

Conflict of interest

The authors declare there is no conflict of interest.