1.
Introduction
Ovarian cancer is the most lethal gynecological malignancy worldwide [1]. The most common type of ovarian cancer is epithelial ovarian cancer and is the substantial cause of death in female cancer patients every year [2]. At the diagnosis stage, 58% of ovarian cancers are metastatic with a 5-year relative survival of only 30% of patients [2]. Ovarian surface epithelial carcinoma cells are capable of initiating ovarian cancer cells and are crucial for the malignant progression of cancer [3]. In the tumor microenvironment, epithelial component from high grade serous ovarian cancer is associated with cancer invasion, progression, and pathogenesis [4]. The differentially expressed genes of the epithelial component in ovarian cancer are associated with cell proliferation, invasion, motility, chromosomal instability, and gene silencing [5]. The epithelial component of ovarian cancer tissue also provided the prognostic factors, immunological factors, and molecular factors [6]. In ovarian cancer, key immune cells and soluble molecules in the TME regulated the prognosis [7]. These studies provide the clue that the human ovarian cancer epithelial-derived transcriptomes are associated with cancer initiation, invasion, migration, and metastasis.
Previous studies revealed the association of coding and non-coding biomarkers including differentially expressed genes (DEGs), mRNA, and miRNA on ovarian cancer pathogenesis. Ting Gui et al identified biomarkers including key hub genes and signaling pathways that are involved with epithelial ovarian cancer progression [8]. Another study identified the biomarkers including DEGs, key hub genes, prognostic genes, significant clusters of genes, and functional enrichment analysis in epithelial ovarian cancer [9]. Daniela Matei et al identified mRNA levels that are significantly deregulated in primary cultures of ovarian epithelial cells derived from epithelial ovarian carcinoma [10]. Immunogenic mRNA and protein expression by cell cultures of epithelial ovarian cancer are also crucial factors to identify the disease progression [11]. MicroRNA (miRNA), the substantial onco-regulators in cancer, is associated with clinicopathological characteristics of epithelial ovarian cancer [12]. MiRNA regulating the initiation, proliferation, cell cycle, survivability, and resistance of chemosensitivity in ovarian cancer [13]. Some studies demonstrated the significance of bioinformatics analysis, data mining, gene regulatory networks, and prediction of biomarkers in human diseases [14,15,16,17]. Altogether, these studies provide the clue that the bioinformatics strategies could identify the epithelial-derived transcriptomes that are associated with the pathogenesis of ovarian cancer.
Herein, we identified the deregulated transcriptional signatures in laser capture microdissected human ovarian cancer epithelia. Then we identified the TFs that are associated with regulating the deregulated transcriptional signatures in ovarian cancer epithelia. Moreover, we identified the key hub genes and hub genes associated clusters from the PPI network. Furthermore, we investigated the correlation of key genes with survival prognosis and immune infiltrations. Finally, we investigated the genetic alterations of key prognostic hub genes and their diagnostic efficacy in ovarian cancer. The study may provide novel insights to investigate the functional regulatory mechanisms of immune-related biomarkers and help to develop immune-related targeted therapy in the treatment of ovarian cancer. Also, this study will help the experimental biologists to further carry out their research to explore the clinical association of these identified biomarkers to treat ovarian cancer patients.
2.
Materials
2.1. Datasets
We searched the NCBI gene expression omnibus (GEO) database (https://www.ncbi.nlm.nih.gov/geo/) using the keywords "epithelial", "ovarian epithelial", "ovarian surface epithelium tumor", "cancer-associated epithelial", "ovarian cancer", and "tumor epithelial", and identified five ovarian epithelial gene expression datasets from the same platform. These included five datasets have the following criteria: the datasets extracted from the same platform (Affymetrix human genome U133 plus 2.0 array), the study organisms had to be Homo sapiens, the datasets had to contain ovarian epithelial cancer and normal ovarian epithelial tissue samples, and the sample size is greater than 20 with minimum 5 control samples. The five selected datasets are GSE14407 [3], GSE27651 [18], GSE38666 [19,20], GSE40595 [4], and GSE54388 [21]. The total samples included 120 ovarian epitheial tumors and 43 control epithelial. Moreover, we downloaded the TCGA ovarian cancer cohort (n = 307) (https://portal.gdc.cancer.gov/) and normalized it by base-2 log transformation. Finally, we downloaded the clinical data of the TCGA ovarian cancer cohort for analyzing the survival differences between the two groups (https://portal.gdc.cancer.gov/).
The GEO datasets (GSE14407, GSE27651, GSE38666, GSE40595, and GSE54388) used in this study are available in The National Biotechnology Information Center Gene (NCBI-Gene) database (https://www.ncbi.nlm.nih.gov/gene). TCGA-OV cohort is downloaded from the Cancer Genome Atlas (TCGA) database (https://portal.gdc.cancer.gov/). Genetical data of OV was utilized from the cBioPortal (http://www.cbioportal.org/).
2.2. Identification of differentially expressed genes (DEGs)
We used Network Analyst [22] to identify the DEGs between ovarian epithelial tumor and normal samples by a meta-analysis of five epithelial gene expression profiling datasets (GSE14407 [3], GSE27651 [18], GSE38666 [19,20], GSE40595 [4], and GSE54388 [21]). Datasets were normalized by quantile normalization or base-2 log transformation. We removed the batch effects of multiple datasets by using the ComBat method [23]. A total of 20, 184 common genes were found by integrating the datasets from five datasets using the Network Analyst [22] tool. We used the R package "limma" for identifying the DEGs between tumor and normal samples, and Cochran's combination test for performing the meta-analysis [24]. The false discovery rate (FDR) [25] was used to adjust for multiple tests. We identified the DEGs using a threshold of absolute combined effect size (ES) > 1.50 and FDR < 0.05.
2.3. Identification of master transcriptional regulators (MTRs) that are significantly associated with the DEGs
We utilized Cytoscape [26] plug-in iRegulon [27] to identify the MTRs for the upregulated and downregulated DEGs. In the Cytoscape plug-in iRegulon [27], a minimum normalized enrichment score (NES) > 3.0 was selected for each TFs. For this purpose, we used an extensive collection of TF motifs and a large collection of ChIP-seq tracks. The iRegulon method depends on a ranking-and-recovery system where all genes of the human genome are scored by a motif discovery step integrating the clustering of binding sites within cis-regulatory modules (CRMs) and the potential distal location of CRMs upstream or downstream of the transcription start site (TSS ± 10 kb). The recovery step calculates the normalized enrichment score (NES) of TFs for each set of genes, input for each of the individual analyses, leading to the prediction of the TFs based on NES and their putative direct target genes which exist in the input lists. This methodology optimizes the linking of TFs to motifs using both explicit annotations and predictions of TF orthologs and motif similarity. A transcription factor NES was computed for each group where an NES > 3.0 corresponds, and the maximum false discovery rate (FDR) on motif similarity was set as 0.001 [28].
2.4. Gene-set enrichment analysis
We performed gene-set enrichment analysis of the DEGs by using the GSEA [29]. We inputted all significant upregulated and downregulated DEGs into the GSEA tool [29] for identifying deregulated pathways. The KEGG [30] pathways significantly associated with the upregulated DEGs and the downregulated DEGs were identified, respectively. The P-value < 0.05 was considered significant when selecting the pathways.
2.5. Identifying hub genes and modular analysis from protein-protein interaction (PPI) network of DEGs
To better know the relationship among these identified DEGs, the PPI network was established using the STRING-based analysis [31]. To identify the rank of hub genes, we used Cytoscape plug-in tool cytoHubba [32]. Hub genes were identified based on the degree of interactions with neighbor genes. We selected the minimum required interaction score is 0.40 for identifying the PPI of DEGs. Hub genes were defined as a gene that was connected to a minimum of 10 other DEGs in the PPI. We visualize the PPI networks by utilizing the Cytoscape 3.6.1 software [26]. A Cytoscape plug-in molecular complex detection (MCODE) was employed to detect the modules from the PPI network [33]. We identified the significant modules based on the MCODE score and node number. The threshold of the MCODE was Node Score Cut-off: 0.2, Haircut: true, K-Core: 2, and maximum depth from Seed: 100.
2.6. Survival analysis of key hub genes
We used the R package "survival" to investigate the survival prognosis of ovarian cancer patients [34]. We used the clinical data of the TCGA OV cohort for analyzing the survival differences. We compared the overall survival (OS) of ovarian cancer patients that are classified based on gene expression levels (expression levels > median versus expression levels < median). Kaplan-Meier survival curves were used to show the survival differences, and the log-rank test (P < 0.05) was utilized to evaluate the significance of survival differences between the groups.
2.7. ESTIMATE algorithmic for quantifying immune score and stromal score
ESTIMATE is an algorithmic tool based on the R package for predicting tumor purity, immune score (predicting the infiltrations of immune cells), and stromal score (predicting the infiltrations of stromal cells) which uses the gene expression profiles of 141 immune genes and 141 stromal genes [35]. The presence of infiltrated immune cells and stromal cells in tumor tissues were calculated using related gene expression matrix data, represented by immune score and stromal score, respectively [35]. Then we calculated the correlations of key genes with immune scores and stromal scores. The threshold value of correlation is R > 0.20, and P-value is not less than 0.001 (Spearman's correlation test).
2.8. Single-sample gene-set enrichment analysis (ssGSEA) and correlation of immune signatures with prognostic genes
One of the extension packages of GSEA, single-sample gene-set enrichment analysis (ssGSEA) was used to identify the enrichment scores of immune cells for each pairing of a sample and gene set in the tumor samples [36]. We collected the marker gene set for immune signatures and utilizing each gene set to quantify the ssGSEA scores of specific immune signatures [37,38,39,40]. We identified the enrichment levels (ssGSEA scores) of ten immune signatures included TILs, B cells, CD8+ T cells, CD4+ regulatory T cells, cytolytic activity, T cells activations, CAFs, pDC, macrophages, and neutrophils. All of the marker genes are displayed in Supplementary Table S1. Then we investigated Spearman's correlation between the ssGSEA scores and specific prognostic genes. The threshold of correlation of immune cells is the absolute value is not less than 0.20 with P-value < 0.05.
2.9. Genetic alterations analysis of prognostic hub genes
We identified the genetic alterations associated with prognostic hub genes by using the cBioPortal (http://www.cbioportal.org/), an open-access tool for exploring and analyzing genetical alterations of multidimensional cancer studies [41]. In this study, we selected the TCGA OV epithelial data that contains 311 samples with mutation data and copy number alteration data (https://www.cbioportal.org/study/summary?id=ov_tcga).
2.10. Diagnostic efficacy evaluation for prognostic key genes
To assess diagnostic values of the prognostic genes, the receiver operating characteristic (ROC) curve was plotted and the area under the ROC curve (AUC) was calculated using the "pROC" R package [42] to evaluate the capability of distinguishing ovarian cancer epithelia and normal epithelia. The greater AUC value of individual genes indicated the differences between tumor and normal samples, and the key gene of AUC > 0.5 in the integrated five datasets was defined as a diagnostic efficiency of the gene [43]. If the P-value < 0.05, the selection of the prognostic genes are considered statistically significant.
2.11. Statistical and computational analysis
We evaluated Pearson's or Spearman's correlation test to verify the significant levels between the two variables. For analyzing the correlations between the expression levels of hub genes and the enrichment levels (ssGSEA scores) of immune signatures, we used Spearman's correlation test because these data were not normally distributed [44]. For analyzing the correlations between the expression levels of hub genes with the expression levels of other marker genes, we utilized Pearson's correlation test because these data were normally distributed [44]. We utilized the Network Analyst [22] tool for calculating the average expression of a gene having multiple probes in the same expression dataset. We used the R package "ggplot2" for plotting the graphs in this study [45].
3.
Results
3.1. Identification of differentially expressed genes in ovarian epithelium by a meta-analysis
We identified 1339 differentially expressed genes (DEGs) between the ovarian epithelial tumor and normal epithelial, which included 541 upregulated (Tables 1 and S2) and 798 downregulated (Tables 2 and S3) genes in the tumor ovarian epithelial when compared with normal ovarian epithelial based on combined Effect size (ES). ES is the difference between two group means divided by standard deviation, which is considered combinable and comparable across different studies [22]. Table 1 describes the regulatory status of the top 25 (The highest combined effect size) upregulated genes including SOX17, CENPF, CD24, INAVA, MECOM, NEK2, DTL, WFDC2, PAX8, MUC1, and CXXC5. Lin Zhao et al reported that the expression of SOX17, INAVA, WFDC2, and CD24 are upregulated in ovarian cancer [46]. It was found that PAX8 and SOX17 regulate tumor angiogenesis in vitro and in vivo in ovarian cancer [47]. NEK2, another upregulated gene in ovarian tumor epithelia, is associated with drug resistance in ovarian cancer [48].
In addition, Table 2 describes the regulatory status of the top 25 (The lowest combined effect size) downregulated genes including ITLN1, SILC1, ABCA8, PRG4, AOX1, BCHE, ALDH1A2, NPY1R, ADH1B, and REEP1. It was found that the downregulation of mesothelial cell-derived ITLN1 in the omental tumor microenvironment facilitates ovarian cancer progression [49]. In the ovarian cancer cell line, ABCA8 was significantly downregulated and is associated with drug-resistant [50]. A tumor suppressor, ALDH1A2, was strongly downregulated 36-fold in 779 epithelial ovarian cancer cases compared with 18 normal controls [51]. Altogether, it indicates that the ovarian cancer epithelia-derived deregulated transcriptomes are associated with ovarian cancer pathogenesis.
3.2. Master transcriptional regulators (MTRs) are significantly associated with the DEGs
MTRs are crucial cancer-associated biomarkers and targets for metabolism-targeted cancer therapy [52]. To identify the significant MTRs that regulating the DEGs, we used the Cytoscape plug-in iRegulon tool. We identified 21 (E2F4, FOXM1, TFDP1, E2F1, SIN3A, PIR, SMAD1, E2F7, UBP1, NFYC, BDP1, E2F1, NFYA, MYBL2, TCF12, MTHFD1, TEAD4, MZF1, EP300, FHL2, and GRHL1) and 11 (JUN, DDX4, FOSL1, NOC2L, HMGA1, JUND, TCF12, EP300, NFIC, ZSCAN9, and FOS) MTRs for the upregulated and the downregulated genes in ovarian tumor epithelial, respectively (Table S4). We built the regulatory networks between the top 5 MTRs and upregulated DEGs (Figure 1A). In addition, we built the regulatory networks between the top 5 MTRs and downregulated DEGs (Figure 1B). In the networks, E2F4, top MTRs for upregulated genes, targeted 267 upregulated genes, and JUN, top-scored MTRs for downregulated genes, targeted 146 downregulated genes. Interestingly, three members of the E2 factor (E2F) family of transcription factors (E2F1, E2F7, and E2F1) were the MTRs that regulated the upregulated genes in ovarian tumors epithelium (Figure 1A). Deregulation of E2F transcription factors is associated with both proliferation-promoting and proliferation-inhibiting and their cross-talk is involved in the tumor biology of ovarian cancer and influences the clinical outcome of ovarian cancer [53,54]. Transcription factor JUN is associated with cellular proliferation, malignant transformation, and invasion in various tumors including ovarian cancer [55].
3.3. Epithelium-derived transcriptomes are associated with the enrichment of KEGG pathways
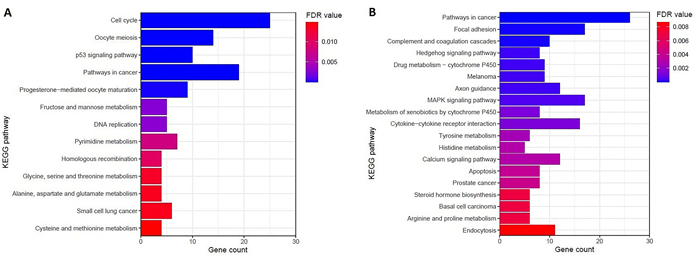
The significantly enriched upregulated and downregulated biological pathways were identified by using the GSEA tool (Figure 2). GSEA identified 13 KEGG pathways that are significantly associated with upregulated DEGs (Figure 2A). The upregulated pathways included cell cycle, Oocyte meiosis, pathways in cancer, progesterone-mediated oocyte maturation, DNA replication, homologous recombination, and small cell lung cancer (Figure 2A). Besides, we identified the 42 KEGG pathways that are significantly linked with downregulated DEGs (Table S5). Some of these downregulated pathways are involved with immune regulation, including complement and coagulation cascades, cytokine-cytokine receptor interaction, Fc gamma R-mediated phagocytosis, apoptosis, and endocytosis (Table S5 and Figure 2B). Moreover, metabolic pathways including drug metabolism - cytochrome P450, metabolism of xenobiotics by cytochrome P450, tyrosine metabolism, histidine metabolism, arginine and proline metabolism, and steroid hormone biosynthesis are downregulated in the epithelium of ovarian cancer (Figure 2B).
3.4. STRING-based PPI analysis identified epithelial-derived hub genes and significant modules in ovarian cancer
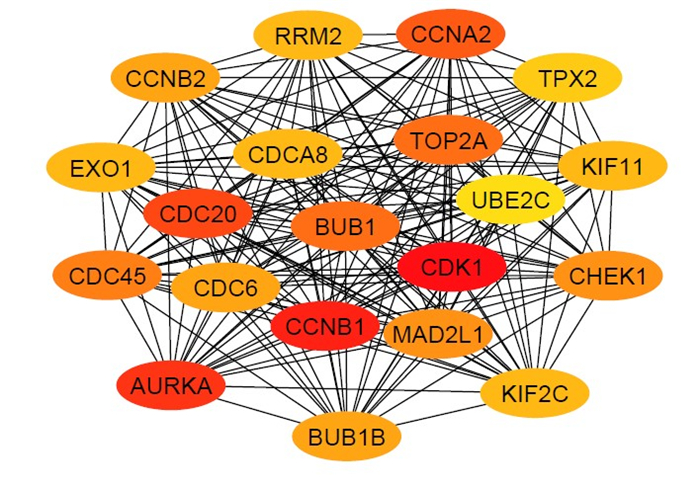
We investigated the PPI of all significant epithelial-derived DEGs. The PPI information of STRING is inputted into the Cytoscape for identifying and visualizing the hub genes and significant clusters. We identified the 460 hub genes (minimum degree of interaction is 10 with other DEGs) (Table S6). The top 20 hub genes (with the maximum degree of interaction) including CDK1, CCNB1, AURKA, CDC20, CCNA2, BUB1, TOP2A, BUB1B, CCNB2, and CDC45 are shown in Figure 3. The overexpression of CDK1 is associated with cancer growth and survival rate in epithelial ovarian cancer [56]. CCNB1, another top hub gene, is abnormally expressed and significantly involved in carboplatin-resistant epithelial ovarian cancer [57]. The expression level of CCNB2 is distinguished between ovarian cancer and normal tissues [58].
We investigated the significant cluster-based analysis of 460 hub genes. The MCODE-based analysis identified 7 clusters (Score of MCODE > 5.0) from the original PPI networks. The description of MCODE derived clusters with their interacting gene lists is illustrated in Table 3. The top significant cluster 1 included 103 nodes and 4571 edges (Table 3). We identified the functional enrichment of KEGG pathways for all clusters by using the GSEA [29]. Interestingly, we found that all seven of the clusters are associated with the enrichment of KEGG pathways (FDR < 0.05). Gene set of cluster 1 is associated with the enrichment of the cell cycle and other cellular differentiation pathways (Table 3). Gene set of cluster 2 is mainly involved with immune regulation and cellular signaling (Table 3). Gene set of clusters 4 and 5 is mainly involved with cancer-associated pathways including pathways in cancer, Hedgehog signaling pathway, basal cell carcinoma, melanoma, Wnt signaling pathway, endocytosis, cytokine-cytokine receptor interaction, focal adhesion, regulation of actin cytoskeleton, MAPK signaling pathway, and TGF-beta signaling pathway (Table 3). Altogether, these results indicate that the epithelial tumor tissue-derived transcriptomes are contributed to ovarian cancer pathogenesis.
3.5. Epithelial derived hub transcriptomes are correlated with survival prognosis in ovarian cancer
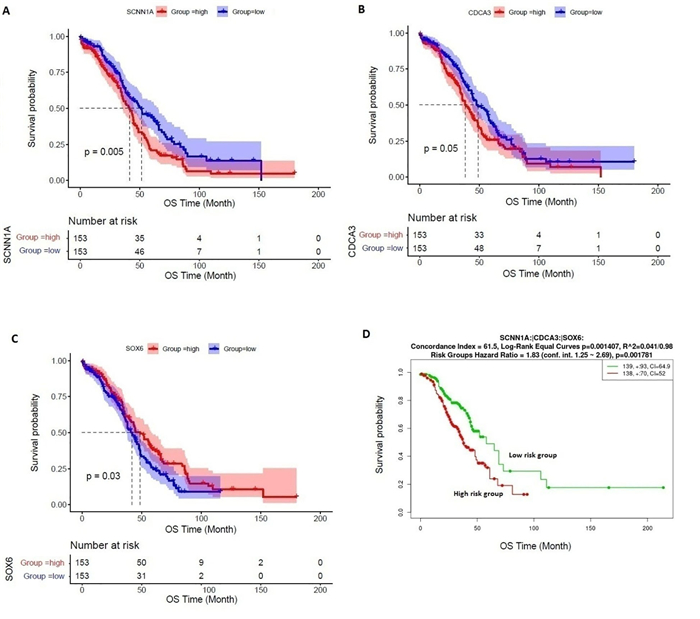
We investigated the survival significance of the epithelium-derived all 460 significant hub genes in TCGA OV data. Our analysis revealed that the epithelium-derived upregulated genes included SCNN1A and CDCA3 (Figure 4A, B) and downregulated SOX6 gene (Figure 4C) is significantly correlated with shorter survival time of ovarian cancer patients (Figure 4). The overexpression of SCNN1A exerts substantial roles in cell growth, invasion, and migration in ovarian cancer through regulating the epithelial to mesenchymal transition, and is a potential indicator for a patient's prognosis [59]. Chongxiang Chen et al. reported that the expression of the CDCA3 gene is associated with the survival and tumorigenesis through the PLK1 pathway in ovarian cancer [60]. SOX6, a tumor suppressor, is downregulated in various cancers and associated with the inhibition of cellular proliferation, invasion, and tumor cell-induced angiogenesis of ovarian cancer cells [61].
To verify the survival significance of the key three genes (SCNN1A, CDCA3, and SOX6), we inputted these prognostic three gene signatures into the SurvExpress tool (http://bioinformatica.mty.itesm.mx/SurvExpress) [62]. We used a GEO dataset GSE9891 (n = 285) [63] that is a built-in dataset in the SurvExpress tool (http://bioinformatica.mty.itesm.mx/SurvExpress). SurvExpress split the samples into two groups (high-risk group and low-risk group) based on the prognostic index and identify the significant survival differences between the two groups. Interestingly, we found that the three gene signatures are prognostic in overall survival (Figure 4D). The high-risk group patients had significantly lower survival times than low-risk group patients (Figure 4D).
3.6. Epithelial tumor-derived prognostic hub genes are associated with immune infiltrations in ovarian cancer
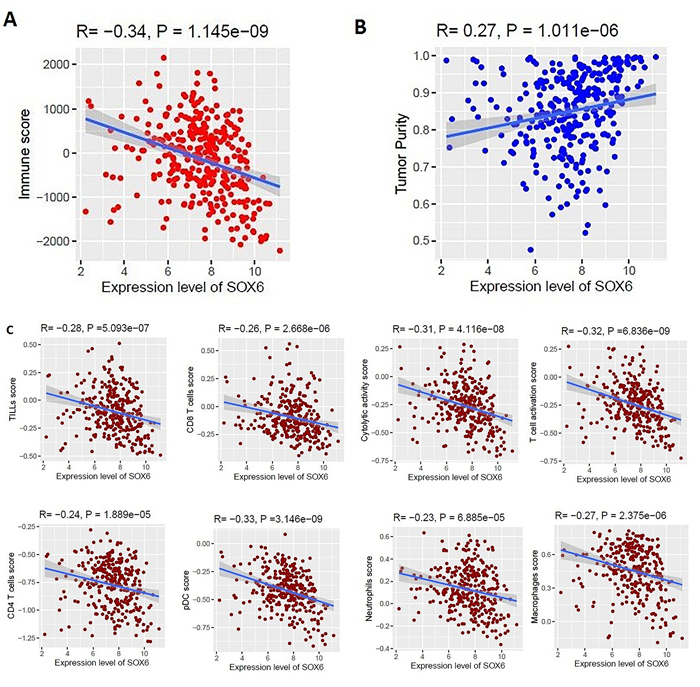
Since survival time of patients is correlated with immunological responses in human cancers [64], it is essential to identify the correlation of prognostic hub genes with the immune infiltrations. We investigated the correlations between the expression levels of three hub genes (SCNN1A, CDCA3, and SOX6) and the levels of immune signatures and tumor purity in the TME of OV. Interestingly, we found that the expression level of SOX6 is negatively correlated with immune scores (R = -0.34, P < 0.001) (Figure 5A), and positively correlated with tumor purity (R = 0.27, P < 0.001) (Figure 5B), but the expression level of SCNN1A and CDCA3 are not correlated with immune scores and tumor purity. Then, we investigated the correlation of three prognostic hub genes (SCNN1A, CDCA3, and SOX6) with the several immune stimulatory and inhibitory signatures including B cells, TILs, CD8+ T cells, CD4+ Regulatory T cells, cytolytic activity, T cell activation, pDC, neutrophils, CAFs, and macrophages. We found that the expression of SOX6 is negatively correlated with the infiltration of TILs, CD8+ T cells, CD4+ Regulatory T cells, cytolytic activity, T cell activation, pDC, neutrophils, and macrophages (Figure 5C). The expression level of SCNN1A and CDCA3 is not correlated with immune infiltrations. Therefore, we identified the correlations of SOX6 with the immune markers (all markers selected from the significant immune signatures). Interestingly, we found that the expression of SOX6 negatively correlated with 68 immune markers including CD8A, PRF1, GZMA, GZMB, NKG7, PRF1, CCL3, CCL4, CST7, CXCR3, and IL10RA in ovarian cancer (Table 5). Tumor immune infiltration is a key indicator in the progression of ovarian cancer [65]. In epithelial ovarian cancer, tumor-infiltrating T cells are predictors of prognosis and biological basis of treatment outcomes [66]. In intratumoral TME, the accumulation of CD8+ T cells is associated with the survival of high-grade serous ovarian carcinoma patients [67]. Our immunological analysis indicated that the epithelial-derived-transcriptomes are associated with the modulation of the immune microenvironment in ovarian cancer.
3.7. Three prognostic hub genes are mutated in ovarian cancer
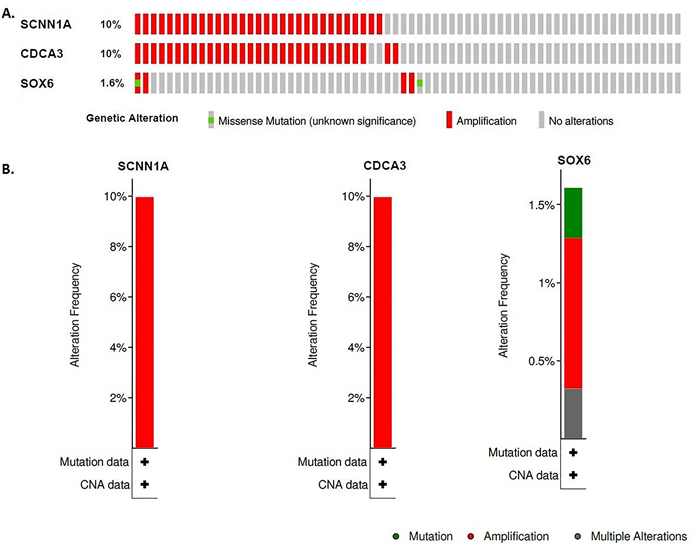
We used the OV epithelial tumor data (n = 311) in cBioPortal (http://www.cbioportal.org/) to identify the genetic alterations of three prognostic hubs genes (SCNN1A, CDCA3, and SOX6). Queried SCNN1A, CDCA3, and SOX6 genes are altered in 36 (12%) of queried patients/samples.
We found that the SCNN1A and CDCA3 are altered in 10 % of patients (Figure 6A). In addition, SOX6 is altered in 1.6 % of patients (Figure 6A). The genetic alterations of SCNN1A and CDCA3 included amplification and the genetic alterations of SOX6 included mutation, amplification, and multiple alterations (Figure 6B).
3.8. Diagnostic efficacy evaluation of prognostic in combined 5 datasets of ovarian epithelium
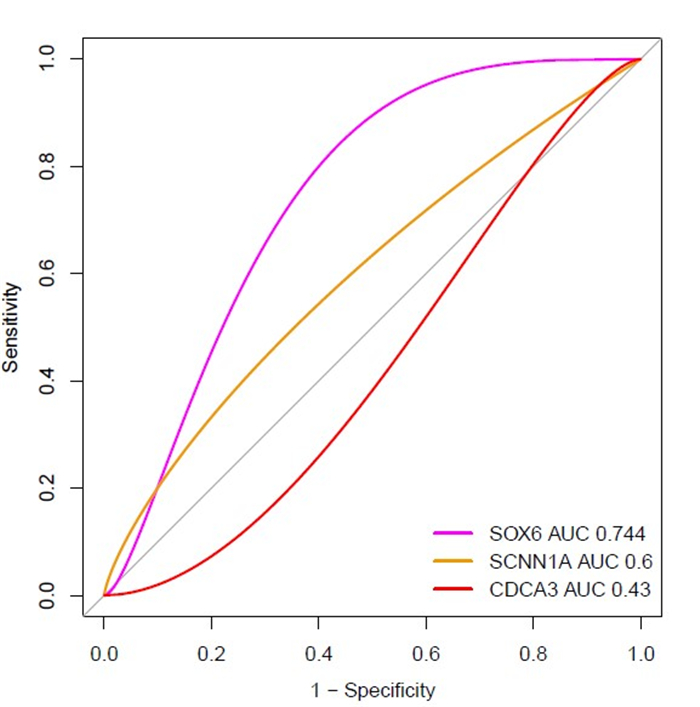
We speculate that these six genes (SCNN1A, CDCA3, and SOX6) have diagnostic value in combined 5 datasets of ovarian epithelium. We used the combined 5 datasets (GSE14407 [3], GSE27651 [18], GSE38666 [19,20], GSE40595 [4], and GSE54388 [21]) of the ovarian epithelium to validate our hypothesis, and the results showed that the ROC curve of the expression levels of SCNN1A (AUC = 0.60) and SOX6 (AUC = 0.744) showed excellent diagnostic value for ovarian epithelial tumor and normal ovarian epithelial cells (Figure 7).
The receiver operating characteristic (ROC) curve of prognostic genes in combined 5 datasets (GSE14407 [3], GSE27651 [18], GSE38666 [19,20], GSE40595 [4], and GSE54388 [21]) of ovarian tumor epithelium and normal ovarian epithelium. The expression levels of SCNN1A (AUC = 0.60) and SOX6 (AUC = 0.744) showed diagnostic value in the ovarian epithelial tumor.
4.
Discussion
Since bioinformatic studies are crucial for identifying the key signaling genes and pathways in human diseases [68,69,70,71], we aimed to explore the ovarian cancer epithelium-derived transcriptomes for identifying the substantial biomarkers. We identified DEGs in ovarian tumor epithelium by a meta-analysis of five gene expression datasets (Tables S2 and S3). Based on the significant DEGs, we identified pathways that are associated with the significant DEGs. The upregulated pathways were mainly involved in cellular development, cancer, and metabolism, and the downregulated pathways involved in immune-regulation and metabolism (Figure 2). The cell cycle, the top enriched upregulated pathway, is involved in ovarian cancer pathogenesis [68]. The downregulation of immune cells is directly associated with enhancing the pathogenesis of ovarian cancer through the release of various cytokines and chemokines [72]. Therefore, our investigated results are consistent with the role of DEGs in the enrichment of pathways that cause ovarian cancer pathogenesis. These results revealed the abnormal alterations of cellular development, immune regulation, and metabolism-related pathways in the compartment of the ovarian cancer epithelium. In addition, we identified hub genes that are interacted with other DEGs. We identified 21 and 11 transcription factors that are associated with regulating the upregulated and downregulated DEGs, respectively (Table S4). In ovarian epithelial cancer, TFs are substantial contributors to cancer risk and somatic development [73]. These TFs could be a unique target for the development of novel precision medicine strategies for ovarian cancer.
Moreover, we found that several clusters are associated with the hub gene signatures. These clusters are associated with the enrichment level of KEGG pathways (Table 3). Pathway analysis revealed that the significant clusters are mainly involved with cancer, immune regulation, and cellular signaling (Table 3). Then, we found that the expression of three hub genes (SCNN1A, CDCA3, and SOX6) are significantly correlated with the shorter overall survival time of ovarian cancer patients (Figure 4). Since the level of immune infiltration is an independent predictor of a patient's survival in cancer [74], we analyzed the correlation of SCNN1A, CDCA3, and SOX6 with the immune infiltration levels in the ovarian tumor. First, we revealed the association of these three hub genes with the ovarian tumor microenvironment. The expression level of SOX6 is negatively correlated with immune scores, indicating that SOX6 is associated with lower the immunity (Figure 5A, B). Second, the expression level of SOX6 is negatively correlated with infiltrations of TILs, CD8+ T cells, CD4+ Regulatory T cells, cytolytic activity, T cell activation, pDC, neutrophils, and macrophages in epithelial ovarian cancer, suggesting that the SOX6 expression is linked with lowering the immune infiltrations in ovarian cancer (Figure 5C). Third, the 68 immune markers (we selected all markers of the significant immune signatures (Figure 4C)) including CD8A, GZMA, PRF1, GZMB, NKG7, CCL3, CCL4, and CCL5 are negatively correlated with the expression levels of SOX6, demonstrating that the SOX6 expression is related to the reduced expression levels of immune markers (Table 4). Altogether. It indicates that the expression of SOX6 is associated with the suppression of tumor immunity in ovarian epithelial cancer. The expression of SCNN1A and CDCA3 is not associated with the regulation of immune infiltrations in epithelial cancer. In addition, SCNN1A, CDCA3, and SOX6 are genetically altered in ovarian cancer. The genetic alteration of SCNN1A and CDCA3 is amplification and the genetic alterations of SOX6 are mutation, amplification, and multiple alterations in ovarian cancer (Figure 6).
We downloaded and integrated publicly available five datasets for this study. Some of the previous studies scatteredly used these datasets to implement various purposes [75,76,77]. For example, Dan Yang et al identified hub genes and therapeutic drugs by using the four datasets including GSE54388 and GSE40595 [75]. However, none of the authors specifically using these five datasets together for identifying the key biomarkers in the epithelial compartment of ovarian cancer. As per our knowledge, this is the first time, we have integrated the five transcriptomic datasets from the same platform. One of the major advantages of this study is that we selected only laser capture microdissected human ovarian cancer epithelial samples with control. Another advantage of this study is that we integrated the microarray datasets from the same platform (Affymetrix Human Genome U133 Plus 2.0) to reduce the data platform heterogeneity. Moreover, we did a meta-analysis to identify the key genes in ovarian tumor epithelial samples. This meta-analysis method usually gives more conservative results (less DEGs but more confident) [22]. The major drawback of this study is that the ovarian epithelial-associated key genes and networks identified by bioinformatics analysis have not been validated by experimental analysis. Thus, although our findings could provide potential biomarkers for ovarian cancer diagnosis and prognosis, as well as therapeutic targets, further experimental and clinical validation is necessary to transform these results into practical application in ovarian cancer treatments.
5.
Conclusions
The identification of ovarian cancer epithelial-derived key biomarkers may provide insight into the association of these genes with survival prognosis and tumor immunity. Epithelial-derived key transcriptomes may be crucial indicators of the effectiveness of ovarian cancer diagnosis and treatment.
Acknowledgments
All authors have contributed to the research concept, design, and interpretation of the data. All authors review and approved the final version of the manuscript.
The external fund was not collected for this project.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: