1.
Introduction
With the rapid development of the global economy and the continuous growth of the population, the proportion of building energy consumption in global energy consumption has increased yearly, becoming an important part of it. Building energy consumption refers to the energy used in the construction and operation of buildings, including the energy consumed in the production of building materials, construction processes, building operation, and maintenance. According to the International Energy Agency (IEA) [1], the share of building energy consumption in global energy consumption has risen from about 30% in the 1970s to approximately 40% today, and it is expected that buildings will account for more than half of global energy consumption by 2050. In China, as of 2021, building operation energy consumption accounted for 21% of the country's total energy consumption, with CO2 emissions constituting 19% of China's total CO2 emissions [2], as shown in Figure 1. In response to the increasing energy consumption of buildings, many scholars are studying the supervision and prediction of building energy consumption.
In an effort to address the issue of building energy consumption, numerous country leaders have advocated for the monitoring and management of building energy usage, alongside the implementation of pertinent regulations and standards aimed at reducing energy consumption, enhancing building energy efficiency, mitigating environmental pollution, and fostering sustainable development. Through the scrutiny of building energy consumption data, patterns and anomalies in energy use are identified, thereby providing a foundation for effective building energy management and facilitating the optimization of energy utilization and efficiency. Concurrently, researchers have embarked on the prediction of building energy consumption, with the aspiration of refining energy management through the anticipation of future energy consumption data, thereby contributing to energy conservation and emission reduction. Data-driven technologies are employed to conduct a comprehensive analysis of various factors, including the building environment, energy consumption, and geographical location, thereby offering data support for green building design and optimizing building design schemes.
To attain precision in building energy consumption prediction, researchers have proposed methodologies categorized as white-box, black-box, and gray-box approaches. Leveraging the granularity of IoT-enabled smart meter data, Natarajan et al. [3] utilized deep learning models to achieve accurate predictions of energy consumption in residential and commercial spaces. Ahmad et al. [4] introduced four machine-learning models to ensure the robustness and high accuracy of energy consumption predictions. Given the often complex and nonlinear nature of energy time series, a single model is typically insufficient for achieving satisfactory prediction results. Consequently, in recent years, an increasing number of scholars have endeavored to develop hybrid models to address this challenge. Xiao et al. [5] proposed constructing a hybrid prediction model based on the point selection ensemble group method, while Neo et al. [6] suggested the integration of XGboost into hybrid prediction methodologies. Building upon the research of these scholars, building energy consumption is effectively analyzed through data-driven and other methodologies, thereby enhancing building energy efficiency and reducing energy consumption. Furthermore, data-driven technologies can elucidate the relationship between various determinants of building energy consumption and actual energy usage, thereby enabling more targeted and precise energy consumption predictions.
In the literature, most researchers looking at building energy consumption prediction have focused on data-driven models, such as Ahmad et al. [7], who reviewed data-driven and large-scale building energy consumption, and Mohamad et al. [8], who researched machine learning, deep learning, and statistical analysis models for building energy consumption prediction. Mathieu et al. [9] directed their attention towards the attributes of input data and the methodologies employed in data preprocessing, subsequently conducting a comprehensive review of the advancements in novel data-driven models tailored for building-scale applications. Yin et al. [10] conducted a comprehensive review of the application of Artificial Neural Networks (ANNs) in predicting building energy consumption, with a particular emphasis on the evolution of ANNs for this purpose. Kadir et al. [11] focused on the scope of energy consumption prediction, the attributes of data employed, the methodologies of data preprocessing, and the machine learning algorithms utilized for predictive tasks. Most of these review articles introduce the application of data-driven approaches in building energy consumption prediction, allocating substantial consideration to aspects such as data-driven methodologies, algorithmic accuracy, and data preprocessing. Nevertheless, in practical scenarios, both intra-building and extra-building factors exert significant influence on the energy consumption of buildings. Consequently, we adopt a holistic approach, integrating the insights from prior research, to synthesize establishment and optimization strategies for building energy consumption prediction models, taking into account the multifaceted influences of building energy consumption factors, as informed by advancements in the field. Our purpose of this paper is to review the research progress of building energy consumption supervision and prediction and to discuss the practical significance of the research on building energy consumption supervision and prediction to green development.
2.
Methodology
To attain building energy efficiency and develop a more precise prediction methodology for building energy consumption, this study is primarily segmented into three phases: Delineating the scope of the literature review; establishing the criteria for literature selection; and categorizing and discussing the content of the selected literature.
2.1. Research scope
This paper primarily encompasses an examination of the regulatory landscape governing building energy consumption, an analysis of the factors influencing building energy consumption, and an exploration of prediction methodologies for building energy consumption. Various factors influence the energy consumption of buildings, originating from the building's inherent characteristics such as design, structure, and materials, all of which impart a significant impact. Moreover, external factors, including climate, building equipment, and usage habits, also contribute to varying degrees of influence on the building, thereby correspondingly affecting energy consumption. The energy consumption values attributed to these diverse influencing factors are monitored by an energy consumption supervision system, which analyzes the data collected to facilitate short-term or long-term predictions of building energy consumption, thereby informing the formulation of targeted building energy conservation strategies. Accordingly, we focus on the selection of literature pertaining to the factors influencing building energy consumption, the supervision of building energy consumption, and the prediction of energy consumption.
2.2. Literature selection
During the initial phase of literature collection, a total of 232 articles were identified and screened from relevant websites and journals based on specific keywords. The primary keywords included: Building energy consumption prediction, building energy consumption supervision, and data-driven approaches. Owing to the substantial volume of retrieved literature, the selection of articles was guided by the following criteria: (ⅰ) Publication within the past decade to ensure the incorporation of the most up-to-date research content; (ⅱ) a focus on the forecasting of building energy consumption and load demand; and (ⅲ) research pertaining to energy consumption prediction and optimization grounded in building influencing factors. Furthermore, relevant laws and regulations enacted by various countries to manage building energy consumption were also reviewed. These studies encompass the research contributions of scholars from diverse countries in the field of building energy, and they collectively reflect a comprehensive consideration of the latest research developments in energy consumption forecasting.
2.3. Discussion of literature content classification
Given the extensive volume of literature, these documents were categorized into distinct thematic areas at the outset of the screening process. The primary categories are as follows:
(ⅰ) The Current Status of Building Energy Consumption Supervision
We synthesize the regulatory frameworks of various countries, providing exemplars of pertinent regulatory provisions from representative nations. Accordingly, we introduce scholarly research on building energy consumption monitoring systems, discuss the developmental status of these systems with respect to architectural framework and system integration applications, and summarize the structural configuration of contemporary building energy consumption monitoring systems, thereby establishing a foundation for building energy consumption prediction.
(ⅱ) Categorization of Influencing Factors of Building Energy Consumption
A multitude of factors influence building operation energy consumption, including architectural design, construction materials, building equipment energy management, usage patterns, and environmental factors. While architectural design and construction materials are extensively discussed within the domains of civil engineering and architecture, building equipment energy management is intrinsically linked to occupant behavior. Consequently, we identify climatic conditions, occupant behavior, and urban morphology as emblematic factors influencing building operation energy consumption.
(ⅲ) Inquiry into Building Energy Consumption Forecasting
Research methodologies in the realm of building energy consumption prediction are predominantly classified into three categories: White-box methods (physical methods), black-box methods (data-driven methods), and gray-box methods (hybrid methods). We elaborate on the predictive processes of these three methodologies based on operational energy consumption factors, juxtaposing their respective advantages and disadvantages. Furthermore, given the diversity of methods within these three categories and the inherent limitations of relying on a single method for accurate building energy consumption prediction, we also explore optimization research in energy consumption prediction. By analyzing the procedural steps of building energy consumption prediction, two focal areas for optimization are selected for discussion: Algorithmic optimization and model optimization.
2.4. Future research discussions
Through the synthesis, analysis, and summarization of the extant literature, a more precise methodology for forecasting building energy consumption is ascertained. As a proactive approach, building energy consumption prediction elucidates the intrinsic correlations between energy consumption determinants and actual energy usage via data-driven techniques, thereby furnishing a scientific foundation for formulating precise energy conservation strategies. In the realm of optimization research, investigations into algorithmic and model optimization reveal substantial potential for energy savings, facilitate the development of more refined building energy consumption optimization strategies, and enable the implementation of personalized and differentiated energy management practices.
3.
The current situation of energy consumption supervision in building operation
With global energy consumption on the rise, building energy consumption, as a major contributor to overall energy use, has garnered significant attention. Many countries have implemented various measures to regulate and reduce building energy consumption. To address the increasing energy demands of buildings, governments worldwide have introduced a range of policy measures, including building energy efficiency standards, promoting renewable energy use, and green building evaluation systems. These policies are aimed at enhancing the energy efficiency of buildings, reducing energy consumption, and fostering sustainable development. Additionally, to decrease building energy consumption and improve energy efficiency, developing a building energy consumption monitoring system has been the subject of increasing research and attention. Researchers utilizing information technology are investigating various aspects of the monitoring system's general design framework, including IoT-based data collection modes, data transmission technologies, and database deployment strategies, with the goal of establishing a comprehensive and scientific energy consumption monitoring system for public buildings.
3.1. The development status of building energy consumption supervision at home and abroad
In China, the regulatory status of energy consumption in building operations has garnered widespread attention. The Chinese government has implemented various measures to control energy use in building operations, including setting standards, conducting energy efficiency assessments, providing financial support, and promoting green building practices. These actions are aimed at steering the development of the building industry towards greater energy conservation and environmental protection. To achieve this, the Chinese government has enacted several laws, regulations, and policies to enhance energy efficiency and promote sustainable development in the building sector.
China has developed a series of building energy efficiency standards, including the Design Standards for Building Energy Efficiency [12,13] and the Implementation Rules for Building Energy Efficiency Projects. These standards establish energy use limits and energy-efficient design requirements for buildings, aimed at ensuring that buildings operate with the lowest possible energy consumption. Additionally, China has implemented a mandatory energy efficiency rating system for building energy consumption. This system requires building owners to conduct energy efficiency assessments and ratings for new buildings and large-scale renovation projects, to ensure compliance with national energy efficiency standards. The Chinese government also encourages the construction industry to adopt advanced energy-saving technologies and equipment and has provided a range of fiscal and tax incentives to motivate building entities to implement energy management and energy-saving renovation measures [14]. Concurrently, China has established a special fund for building energy efficiency, which supports building energy management and technological innovation. China is actively promoting green building certification systems, such as the China Green Building Evaluation Standard (GB/T 50378) and the Green Building Evaluation Mark (three-star, four-star, and five-star), to encourage the adoption of sustainable design and construction practices in the construction industry. As shown in Table 1, from 2007 to the present, the Chinese government has issued a series of standards and policies for building energy management and energy-saving renovation measures.
In Europe and the United States, a range of regulations and standards for building energy efficiency have been established to promote the development of the building industry towards greater sustainability and energy efficiency. For instance, Europe's Building Energy Performance Directive (EPBD) mandates that EU member states develop and implement building energy performance requirements and encourage the use of renewable energy. Member states are required to ensure that new buildings meet certain energy efficiency standards and to conduct energy audits of buildings. Additionally, the U.S. Energy Policy Act (EPACT) sets energy efficiency requirements for buildings owned by the U.S. federal government and requires states to develop building energy codes. Each state in the United States has its own energy efficiency standards that apply to both commercial and residential buildings. These regulations and standards are part of the framework for regulating building energy consumption in Europe and the United States, promoting the adoption of energy-saving measures in the building industry to reduce energy use and carbon emissions by establishing energy efficiency standards, certification systems, and policy incentives. For examples, Table 2 lists the policies and standards for building energy efficiency and energy management issued by Japan, Germany, and the United States.
In summary, a growing number of policies and legal provisions have been established for the supervision of building energy consumption both domestically and internationally. These initiatives collectively aim to contribute to the reduction of building energy consumption and to the global energy consumption reduction effort. Furthermore, it is evident that the awareness of building energy efficiency in European and American countries is ahead of China. Nevertheless, China's building energy efficiency policy has seen rapid development in recent years, keeping pace with the construction industry's growth. The Chinese government has revised its policies in line with current events, making a meaningful contribution to reducing global building energy consumption. These measures related to building energy efficiency provide a data foundation for the building energy consumption monitoring system and offer a reference range for further enhancing the accuracy of building energy consumption predictions.
3.2. Research on building energy consumption monitoring system
In addition to the regulations for the supervision of building energy consumption both domestically and internationally, an in-depth study of building energy consumption supervision systems is warranted. Such studies can provide new measures for reducing building energy consumption when using cooling and heating equipment in buildings. Among the various building energy consumption monitoring systems, researchers primarily focus on the integration and application of system architecture, functional design, and system capabilities.
3.2.1. System architecture and functional design
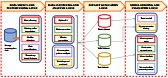
Starting from the overall design framework of the monitoring system, scholars have investigated the design method, data transmission technology, and database deployment method for the data collector in the Internet of Things (IoT), with the aim of constructing a scientific and comprehensive energy consumption monitoring system for public buildings, as depicted in Figure 2. Boris et al. [15] introduced a conceptual architecture for an integrated performance monitoring system that can facilitate planning, execution, inspection, and action modes. Zhao et al. [16] devised a comprehensive system tailored for the surveillance of energy consumption in large public edifices, meticulously engineered from six strategic dimensions: The strategic selection of building monitoring points, the sophisticated design of data collection protocols, the implementation of measures to preclude data loss, and the development of both top-level database architectures and application software. The creation of application software is tantamount to the visualization of data and the administration of the system, thereby necessitating a multi-faceted examination in the design of an integrated building energy monitoring system.
The current building energy consumption monitoring system can be roughly divided into five sections (Figure 2). The first section involves defining the objectives and requirements of the monitoring system based on the building's energy usage, designing the system, and selecting suitable sensors and data collectors. The second section entails installing sensors and data acquisition equipment at critical locations within the building, such as electricity meters, water meters, and temperature sensors. The third section involves collecting real-time building energy consumption data through sensors, including electricity, water, gas, and heat consumption, and then transmitting the collected data wirelessly to the processor. The fourth section utilizes computers for data clarification, storage, and analysis and calculates building energy consumption indicators, such as total energy consumption, sub-item energy consumption, and energy efficiency ratios. The fifth section involves displaying the generated energy consumption report on a device such as a mobile phone. Furthermore, in response to the inherent instability of the data, Ma et al. [17] introduced a methodology to ascertain latent erroneous energy consumption data utilizing the building energy consumption monitoring platform. They categorized energy utilization patterns, employed cluster analysis to detect anomalous data, and conducted a comparative analysis between real-time and historical energy consumption data to validate the precision of the methodology and enhance the overall data quality.
In addition, with the rapid development of emerging technologies such as the Internet of Things, the design of building energy consumption detection systems can also be based on this. For example, Malkawi et al. [18] designed a building energy management system based on data collection based on the Internet of Things architecture. Arun et al. [19] combined the Internet of Things technology to propose a safe and energy-saving intelligent building system architecture, which can effectively reduce building energy consumption through simulation analysis. Garín et al. [20] described an approach to a building environment monitoring system based on an open-source platform and the Internet of Things, which first collects data based on sensors and then analyzes and evaluates the collected data. In addition, the design of building energy consumption systems is carried out in combination with BIM tools, and Gökc et al. [21] have developed a system for building energy monitoring and management through sensor facilities, BIM tools, etc.
The architecture and design of building monitoring systems have garnered increasing attention with the rise of big data. By integrating big data with the supervision system, the energy consumption of building operations can be accurately tracked. Subsequently, based on the energy consumption values obtained from the building energy consumption monitoring system, researchers can make more precise predictions of building energy consumption equipment, enhancing the accuracy of their predictions and thereby reducing building energy consumption.
3.2.2. System integration and application
In the design of building energy monitoring systems, they will also be integrated with other systems or technologies. In this paragraph, the combination of building automation systems and energy management systems and building energy consumption monitoring systems is reviewed to obtain higher-quality building energy consumption monitoring data.
The Building Automation System (BAS) is an important part of the intelligent building, which automates the management of various mechanical and electrical equipment and systems in the building through centralized monitoring and remote control. Its core goal is to provide an efficient, safe, comfortable and economical living and working environment. Vandenbogaerde et al. [22] analyzed the building automation and control system for building energy consumption, such as heating, cooling, and ventilation of buildings, combined with the European standard EN 52120-1, and reflected the limitations of EN 52120-1 and the key parameters that need to be considered in the practical application of building automation and control systems. Morshed et al. [23] investigated a data mining method based on using K-means clustering analysis on building management systems to identify sources of waste in buildings.
An Energy Management System (EMS) is a systematic solution for monitoring, controlling, and optimizing energy consumption. By collecting and analyzing energy usage data, the system helps businesses or organizations manage energy consumption more effectively, thereby reducing costs, reducing environmental impact, and improving energy efficiency. Muhammad et al. [24] developed a method for optimizing building energy management systems that uses multi-criteria decision-making techniques to balance the demand and consumption of buildings.
In addition to the integrated application of the above two systems, there are also the applications of artificial intelligence technology, sensor network monitoring systems, etc. Rajalakshmi et al. [25] proposed the application of artificial intelligence technology in the monitoring of energy management in intelligent buildings to monitor energy consumption and utilization. Wang et al. [26] used a sensor network-based monitoring system to analyze the performance of building energy-saving parameters.
In summary, the research progress related to the design of building energy consumption monitoring systems has achieved certain results. The design of building energy consumption monitoring systems can mainly provide a new management scheme for building energy conservation, so as to achieve energy conservation and emission reduction from the demand side. However, there are some challenges in the design of building energy consumption monitoring systems, such as efficient operation and maintenance of the system, data security, and privacy protection. Future research can continue to focus on these issues and seek more efficient and reliable design methods to provide technical support for building energy efficiency and green building development.
4.
Factors influencing the energy consumption of building operations
As research into building energy consumption supervision systems progresses, the understanding of the factors influencing building energy consumption has similarly evolved. Building energy consumption primarily encompasses expenditures in heating, cooling, lighting, and electrical appliances. The principal determinants of such consumption include architectural design, construction materials, equipment usage patterns, environmental conditions, and occupant behaviors. Within individual buildings or complexes, the specific factors influencing energy consumption vary with the architectural style. Consequently, architectural design must be considered within the broader context of urban morphology for a holistic evaluation. For isolated structures, indoor and outdoor meteorological conditions, as well as occupant behavior, are critical variables contributing to energy consumption fluctuations. In the context of urban clusters, the morphology shaped by urban planning and design, along with the urban green belt coverage ratio, influences urban heat emissions, thereby impacting building energy consumption. Thus, the primary factors examined in this discourse are climatic conditions, occupant behavior, and urban morphology.
4.1. Climatic conditions
Climatic conditions are an important external factor influencing a building's energy consumption. For example, Thomas et al. [27] analyzed the impact of urban microclimate on building energy consumption based on the monthly urban energy consumption data of New York in the past three years, and Chen [28] AutoBPS was used to establish 22 different urban buildings, and the total energy use intensity of these 22 types of urban buildings in 2050 and 2080 under the scenario of low emissions in the future was compared, and the energy intensity of buildings increased by climate change was obtained. Luo et al. [29] proposed a model predictive control (MPC) system that relies on weather forecasting. This system is used to select the mode of renewable energy generation and building energy consumption. Furthermore, Nowak et al. [30] conducted a systematic review of the impact of microclimate on energy consumption, albeit with a focus on delineating Eco-feedback technology as a mechanism for energy conservation aimed at enhancing household awareness regarding energy usage.
Climatic conditions that typically affect a building's energy consumption include temperature, wind direction and speed, sunlight, and climate zones, as shown in Figure 3. However, depending on the region, the climatic conditions that affect the energy consumption of buildings are also different. For example, heating in cold areas accounts for a large proportion of energy consumption, while cooling energy consumption in hot areas accounts for a large proportion. Therefore, according to the local climatic conditions, the energy consumption of buildings can be reduced by adopting appropriate energy-saving technologies and measures.
Temperature is one of the most direct factors affecting a building's energy consumption. In cold regions, buildings require a lot of heating energy to maintain indoor temperatures, while in hot areas, air conditioning energy consumption is relatively high. In areas with large temperature differences, the energy consumption of buildings will also increase accordingly. Verichev et al. [31] studied the changes in heating energy consumption of residential buildings in three regions of southern Chile under two scenarios of increased temperatures and found that the increase in temperature led to a decrease in the heating energy consumption of residential buildings. Li et al. [32] studied the variation of cooling energy consumption of office buildings in different climatic zones in China and concluded that the annual cooling load is mainly affected by dry-bulb temperature in severely cold regions, while wet-bulb temperature is affected in other regions.
Wind direction and velocity significantly influence the natural ventilation of a building. During the architectural design phase, it is imperative to consider the local wind direction and velocity to optimize the building's layout and morphology, thereby mitigating the energy consumption associated with ventilation and air conditioning systems. A favorable wind direction can facilitate the exchange of air between the interior and exterior, thereby diminishing the reliance on air conditioning and mechanical ventilation systems and subsequently lowering energy consumption. The velocity of the wind enhances the convective heat transfer effect, which in turn impacts the heat exchange on the building's external surfaces. Du et al. [33] conducted an analysis of the coupling relationship between the rugged topography of coastal cities, urban heat islands, land-sea breezes, and related local wind patterns, as well as their collective impact on the energy consumption of urban buildings. Mikulik [34] investigated the correlation between various meteorological parameters—including wind speed, irradiation, humidity, and air temperature—and observed energy consumption, revealing a correlation coefficient of no more than 0.25 between energy demand and wind speed. Liu et al. [35] identified that the wind velocity at the building's corner significantly influenced the energy consumption of high-rise buildings during renovations in severe cold regions. The renovation notably mitigated the strong wind zones in winter and the calm wind areas in summer. In summary, wind direction and velocity are pivotal factors affecting building energy consumption, and through judicious design and strategic interventions, it is possible to effectively reduce building energy consumption and enhance energy efficiency.
Sunlight conditions have a direct impact on a building's energy consumption for lighting and heating. Adequate sunlight can reduce the energy consumption of lighting, while in areas with insufficient sunlight, the energy consumption of buildings will increase accordingly. In addition, sunlight can also provide free heating energy for the building, reducing heating energy consumption. Mitja et al. [36] studied that slender buildings are more effective at harvesting solar energy than compact buildings in Central European climates, saving the need for heating energy.
The energy consumption characteristics of buildings in different climate zones are different. For example, the energy consumption of buildings in tropical regions is mainly used for air conditioning and lighting, while the energy consumption of buildings in temperate regions is mainly used for heating and air conditioning. Duan et al. [37] studied the influence of climatic conditions on building energy consumption under the conditions of five thermal climate distributions in China and concluded that the influence of climatic conditions on building energy consumption is greater due to the greater energy consumption of building operations in severe cold areas and hot summer and cold winter areas. Ayoub et al. [38] selected six typical cities in Morocco to compare building energy consumption, and found that buildings in the Mediterranean climate have the largest energy demand, while those in the desert climate have the least energy demand. Wang et al. [39] analyzed measures to reduce hospital energy consumption in areas with hot summers and warm winters and proposed two measures to save energy and reduce emissions: Photovoltaic power generation and green roofs.
In summary, climatic conditions are an important factor affecting the energy consumption of buildings, but the climatic conditions listed in this paragraph are far less than the impact of actual climatic conditions on building energy consumption, and specific analysis is required in combination with the actual building. For example, Kim et al. [40] used experimental reference years to study the impact of climate parameters on the energy demand of buildings in 18 regions of South Korea and concluded that temperature has a greater impact on building energy consumption in winter and solar irradiance has a greater impact on building energy consumption in summer. Therefore, in the analysis of the energy consumption of the actual building, it is often necessary to consider the influence of multiple climatic conditions on it to ensure the accuracy of the building energy consumption prediction.
4.2. Occupant behavior
The impact of occupant behavior on building energy consumption is often multifaceted, and the mode of energy consumption, the amount of energy consumed, and the distribution of consumption time all affect the prediction of building energy consumption. The use behavior of the occupant directly determines the switching status and running time of the internal equipment of the building, including lighting, air conditioning, heating, refrigeration, and electrical appliances. For example, excessive lighting use will increase electricity consumption, and inappropriate air conditioning and heating use will increase fossil energy consumption, which will directly affect the energy consumption of buildings. Generally, the influence of occupant behavior on building energy consumption can be primarily categorized into three aspects: Occupancy, interaction, and behavioral efficiency. A high occupancy rate tends to elevate the frequency of interaction between individuals and building systems, thereby affording greater opportunities to optimize energy consumption through these interactions. Moreover, well-designed interaction mechanisms, such as intuitive control systems and real-time energy consumption feedback, have the potential to enhance the behavioral efficiency of occupants, thereby incentivizing more energy-efficient practices. Additionally, at a constant occupancy rate, a higher level of behavioral efficiency is likely to result in reduced energy consumption. Conversely, lower behavioral efficiency may exacerbate the energy consumption issues associated with high occupancy levels. as shown in Figure 4 [41].
Occupancy mainly refers to the occupancy rate of occupants in the building, and factors such as the number of people in the building, the time distribution of activities, and the nature of activities (e.g., different energy consumption needs of offices and gyms) will affect the total amount of energy consumption. For example, the peak energy consumption of domestic buildings usually occurs from the evening to night, while the peak energy consumption of commercial buildings may occur during the day on weekdays. Hu et al. [42] analyzed the composition and floor area of 4964 households in China based on a questionnaire survey, and concluded that the larger the unit size of the household, the greater the energy consumption of the building. Osman et al. [43] studied the energy use intensity of six types of households: Single working individuals, single retired individuals, working couples, retired couples, nuclear families, and single-parent families and found that regions with more retirees had higher energy intensity at noon and larger households. Luo et al. [44] studied the impact of hotel occupancy rate on the efficiency of building photovoltaic cell energy consumption and proposed a new scheme for hotel energy cost savings.
Interaction refers to the behavior and habits of the occupants in the use of the building, such as: The interaction of the occupants with lighting, the interaction with the air conditioning system, the interaction with the heating system, the interaction with electrical appliances, etc. Moreover, regulating indoor temperatures, using lighting and appliances wisely, and avoiding wasting energy can reduce building energy consumption. Duan et al. [45] divided the energy consumption of households living in high-rise buildings into five categories, namely, households with high energy consumption for heating and cooling, households with low energy consumption for heating and cooling, households with high cooling energy consumption and low heating energy consumption, households with low cooling energy consumption, households with high heating energy consumption, and households with medium energy consumption for heating and cooling. For university buildings, Deng et al. [46] calculated the electricity consumption of university dormitory buildings in China's hot summer and cold winter areas for two consecutive years, and concluded that the frequency of computer use by men and women is different, and the height and orientation of the floors lead to different electricity consumption in the dormitories. Zhang et al. [47] proposed an improved building energy consumption prediction system, which uses the duration of occupant behavior as an input parameter to more accurately reflect the relationship between building users and building energy consumption.
Behavioral efficiency refers to consciously improving the awareness and awareness of building users on energy conservation and emission reduction through publicity, which is also one of the effective ways to reduce building energy consumption. Rational usage mode can reduce ineffective energy waste and improve energy efficiency by optimizing the operating state of the equipment. For example, the intelligent control system can effectively reduce energy waste by adjusting the temperature of the air conditioner according to the temperature difference between indoor and outdoor and the needs of personnel. Zhou et al. [48] established a model of residents' behavior in government office buildings, analyzed the specific causes of residents' energy consumption behavior, and reduced the energy intensity of buildings as a basis for improving building energy efficiency. Yoon et al. [49] designed a new building energy consumption model based on the energy consumption of individual rooms, offices, and retail tenants in commercial buildings, focusing on the different energy consumption caused by different tenants to achieve energy conservation and emission reduction.
According to the above research and analysis results on occupant behavior, it was found that the use behavior of occupants greatly affects the consumption of building energy, and different family structures will lead to different consumption of building energy. Therefore, in the prediction of building energy consumption, the behavior habits of occupants need to be considered. In addition, in order to better save energy and reduce emissions, it is advisable to consider taking into account the behavior and habits of occupants in the future building design and functional layout, so that occupants can use reasonable equipment, reduce the consumption of ineffective energy, and reduce energy intensity to improve the prediction accuracy in the prediction of building energy consumption.
4.3. Urban form
The impact of urban form on a building's energy consumption is multifaceted. The urban form mostly includes the density, type, and spatial layout of the buildings, as shown in Figure 5. Different urban forms will have an impact on solar radiation, wind direction, and speed, which impact the energy consumption of buildings.
First, the density and height of buildings in cities are often higher, which leads to the heat island effect between buildings, where temperatures are higher in urban areas than in surrounding rural areas. This heat island effect increases the cooling demand of the building, which in turn increases energy consumption. Du [50] categorized the urban morphological parameters into three distinct groups—urban structure, vegetation coverage, and impervious surface thermal characteristics—under mesoscale climatic conditions, and subsequently investigated the impact of these three urban forms on building energy consumption.
Furthermore, buildings in cities tend to be more concentrated, which can lead to poor heat exchange and ventilation between buildings, further increasing energy consumption. Rostami et al. [51] studied the energy consumption and solar energy utilization in urban canyons and neighborhoods in three different regions under semi-arid climate conditions, and the results showed that different urban morphologies had an impact on both solar energy utilization and energy consumption in cities. Liu et al. [52] proposed a framework for multi-objective urban form design optimization to combine urban form with building energy consumption and solar energy potential, and summarized the optimal energy-saving building form in Jianhu City. The concentration of urban form signifies a concentration of population residences, where the flow of people is substantial, leading to increased demand for building energy consumption.
The existence of an urban green environment also affects the generation of building energy consumption. Wang et al. [53] analyzed the correlation between the layout of different building environments around urban parks and building energy consumption, and concluded that water bodies and roads have a positive effect on compact high-rise buildings and a negative effect on sparse high-rise buildings. Zhu et al. [54] analyzed the relationship between urban vegetation morphology and urban building energy consumption, and concluded that urban vegetation morphology can significantly reduce the energy consumption of urban buildings. Shareef et al. [55] aimed to explore urban forms suitable for the local climate in the UAE region to reduce the indoor energy consumption of buildings, and concluded that building orientation is the main factor affecting the energy consumption of urban blocks.
A well-designed spatial layout can enhance the accessibility and connectivity of a building or area. Similarly, a well-designed public space can offer a venue for leisure and social interaction, which can encourage residents' engagement, promote outdoor activities, enhance resident satisfaction and lead to increased occupancy. Xie et al. [56] analyzed the impact of different urban forms on the energy consumption and solar power generation potential of university dormitory buildings, and the results showed that different block patterns would lead to different energy use intensities. Ge et al. [57] analyzed the impact of vertical meteorological models on the energy consumption of different urban blocks, and obtained a regression equation for the relationship between building energy consumption and urban block morphology. Nasrollahi et al. [58] studied the influence of urban morphological parameters on building energy consumption in the Ilang region, and concluded that building height had the greatest impact on building energy consumption. High-density cities can offer a wider array of housing options to cater to the diverse needs of various income levels and lifestyles. A rich housing supply can help draw in diverse groups of people. However, it is important to recognize that excessive urban density can have a detrimental effect on environmental quality. Yu et al. [59] studied the inter-building effect (EBI) of energy consumption of high-rise office buildings in high-density cities, and in order to ensure the accuracy of the data, the impact of shutters on EBI was considered, and the results showed that the impact of EBI on the total energy consumption of buildings was as high as 13.1%.
In summary, urban forms increase the energy consumption of buildings and provide more opportunities to save energy and reduce emissions. In the early stage of urban construction, the urban form should be taken into account to fundamentally reduce the energy consumption of urban buildings and improve the accuracy of building energy consumption prediction.
In the prediction of building energy consumption, the above factors do not completely summarize the fluctuation of building energy consumption, but whether it is climatic conditions, building use behavior, or urban form, as shown in Table 3 and Figure 6, they are important factors affecting building operation energy consumption, which provide prerequisites for predicting building energy consumption. For the energy use of specific buildings, it is necessary to conduct multi-party investigation and research, this paragraph only provides a relevant analysis for predicting building energy consumption, and on the basis of these influencing factors, researchers can more accurately study new energy consumption prediction models and improve the accuracy of building energy consumption prediction.
5.
Research on building energy consumption prediction model
Accurate building energy forecasting can help building managers understand future energy needs, so they can develop more effective energy conservation measures and energy use strategies. In the prediction of building energy consumption, it can be seen from the previous paragraph that there are many influencing factors, such as building type, building heating mode, internal personnel behavior, and urban form, which can affect the prediction of building energy consumption. Therefore, the establishment and optimization of prediction models for building energy consumption is an important research topic. Constructing an accurate building energy consumption prediction model is an effective measure for building energy conservation, which can help managers control operating costs and optimize energy scheduling by predicting building energy consumption. When there is an anomaly in the building energy system, the building energy consumption forecast can also help to carry out maintenance and repair in a timely manner. Therefore, it is crucial for research content to do a good job in the prediction and optimization of building energy consumption.
In the past few decades, many scholars have conducted a lot of research on the prediction of building energy consumption, aiming at the prediction algorithms, models, and characteristics of building energy, etc., and now the research methods of building energy consumption prediction are mainly divided into three categories: physical model (white box method), data-driven method (black box method), and hybrid method (gray box method) [98].
5.1. Physical methods
Physical models, also known as white box methods, typically evaluate a building's energy consumption based on comprehensive data, including the building's construction details, HVAC system specifications, physical characteristics of equipment, and occupant behavior patterns. The physical modeling approach necessitates the establishment of a detailed building physics model, which encompasses the geometric structure, material properties, thermal characteristics, and internal equipment systems of the building. Additionally, it is imperative to account for the heat exchange between the building and the external environment, thereby maintaining energy balance. Utilizing the developed physical model, in conjunction with input meteorological parameters and other relevant data, the predicted energy consumption of the building is calculated through simulation. Consequently, physical models generally rely on computer simulation tools and software, such as EnergyPlus, eQUEST, DOE-2, Trnsys, and Matlab, to forecast energy consumption by simulating the building's thermal environment and air conditioning load.
EnergyPlus is a building energy consumption simulation engine jointly developed by the U.S. Department of Energy and Lawrence Berkeley National Laboratory, which is a detailed software that can simulate building energy consumption, suitable for simulation and evaluation of building heating, cooling, lighting, ventilation and other energy consumption. Wang et al. [99] used a dynamic coupling of the physical model (VCWG) with EnergyPlus, which provides the prediction conditions of the urban microclimate to EnergyPlus, and EnergyPlus predicts the heat dissipation and exterior surface temperature of the building. Bilous et al. [100] established a dynamic simulation model of the room in EnergyPlus to analyze the influence of these factors on the thermal state of the building. Based on meteorological data, Wang et al. [101] established the EnergyPlus simulation model under two climatic conditions to analyze and predict the overall energy consumption, heating energy consumption, and cooling energy consumption of office buildings.
Design Builder is a comprehensive user interface simulation software developed based on EnergyPlus, which can perform simulation calculations and analyses for building heating, carbon emissions, building incremental costs, light simulation, indoor and outdoor CFD simulations, and LEED scores. Wang et al. [102] used Design Builder to simulate the annual dynamic energy consumption of three models: The target single building, the target building and the building group within 50 m, and the target building and the building group within 200 m, and analyzed the energy consumption difference of the target building under three different conditions.
Trnsys is an instantaneous system simulation program that simulates and evaluates building energy consumption by entering a building model to simulate the built environment. Hu et al. [103] used Trnsys to simulate and predict the energy consumption of rural residential buildings and analyzed the carbon emissions and their economics under three different heating methods: Natural gas, biomass and standard plum, and biomass and air conditioning. In addition, Trnsys can also analyze the hourly energy consumption of buildings throughout the year, simulate and calculate solar heat pump systems or ground source heat pump systems, etc., and can establish links with other software such as EnergyPlus and Matlab to provide strong support for building energy consumption data prediction. Cao et al. [104] proposed a method combining WRF and Trnsys, which uses the data provided by WRF to make corrections in Trnsys and then predict the cooling and heating loads of commercial buildings. Alibabaei et al. [105] studied the development of a joint Matlab and Trnsys simulator for more advanced and accurate predictive control and verified the effectiveness of the simulator on the energy saving of actual residential HVAC systems under three different types of prediction strategies: load shifting, intelligent dual-fuel switching system, and load shifting and intelligent dual-fuel switching system.
eQUEST is a DOE-2 engine-based building energy simulation tool, which can be applied to building energy simulation and economic analysis of various building types. The software can output graphical results intuitively, which is convenient for users to analyze the results of building energy consumption. Zhao et al. [106] proposed a building energy consumption prediction method based on monitoring data and Bayesian theory, and used eQUEST software to establish a campus building energy consumption model and output the results, which verified the applicability of the method. Xing et al. [107] used eQUEST software to conduct energy simulation analysis of hotel buildings, studied the major factors affecting the energy consumption of hotel buildings, and proposed energy-saving renovation measures.
The white box method uses the laws of physics (e.g., thermodynamics, heat transfer, etc.) to simulate and predict building energy consumption through detailed building information, including the building's structure, material properties, equipment performance, and operating mechanisms. The white box method is based on physical processes so that the model can be adapted and optimized to suit the energy consumption characteristics of different buildings in the face of different building types, designs, and operating modes. In addition, the white box method not only simulates the energy consumption under known conditions but also predict the energy consumption response of the building under changing environmental and operation strategies, providing a scientific basis for the energy management and energy-saving measures of the building. However, since the white box method is mostly based on physical processes for prediction, researchers need to have professional knowledge of physics, which is difficult for people who lack physical knowledge. In recent years, due to the rise of big data, data-driven applications in building energy consumption prediction have become more and more extensive.
5.2. Data-driven methods
The data-driven method, also known as the black box method, is a simplified approach commonly used in building energy simulations. This method does not delve into the detailed physical processes of a building's energy consumption, but instead treats the building as a "black box", focusing only on the relationship between inputs (time series characteristics, meteorological conditions, building physical parameters, etc.) and outputs (building heating and cooling loads, electricity consumption, etc.). When using the black box method to simulate the energy consumption of a building, it is not necessary to have an in-depth understanding of the details of the building's internal structure, material properties, equipment performance, etc., but only to focus on the overall energy consumption characteristics of the building. The black box method can improve the efficiency of the simulation, lower the technical threshold, and provide scientific and practical analysis results for building energy efficiency in the simulation of building energy consumption.
According to Sun et al. [108], the classification of data-driven models for building energy forecasting can be divided into two categories: statistical models and machine learning models, as shown in Figure 7.
5.2.1. Statistical modeling
Statistical analysis is a method of collecting, analyzing, interpreting, and presenting data using mathematical and statistical methods. In the field of data science, statistical analysis is the basis for building machine learning models and conducting data exploration, providing theoretical support and data processing methods for machine learning algorithms. The purpose of this method is to establish a statistical relationship between energy consumption and influencing parameters by analyzing historical energy consumption data to make energy consumption predictions. Such methods mostly include linear regression models and time series models.
Linear regression models are common in the field of machine learning and are mainly used to predict the linear relationship between a continuous target variable and one or more independent variables. The linear regression model mainly combines the historical eigenvalues and model parameters of building energy consumption to predict building energy consumption. Linear regression models are typically noted as:
thereinto:
● y is the prediction function;
● w is the model parameter;
● x is the feature input;
● b is the paranoid quantity.
R2 (coefficient of determination), MAE (mean absolute error), MSE (mean square error), RMSE (root mean square error), MAPE (mean absolute percentage error), and so on are used as metrics to evaluate the predicted performance of the linear regression model. In the linear regression model, when the coefficient of determination is high, and the mean square error and root mean square error values are low, it is indicative that the method can be effectively utilized as a prediction model for building energy consumption. As a typical example, Ciulla et al. [109] developed an alternative white-box method, a reliable multiple linear regression method, to predict building energy. This method selects several suitable variables for sensitivity analysis and then develops simple linear relationships to determine the cooling and heating load requirements of buildings. Bilous et al. [100] established a multiple nonlinear regression model, which used the modified coefficient of determination as the prediction criterion and the indoor air temperature as the eigenvalue. This model was verified to have high applicability and accuracy and can be used for other performance parameters of indoor and outdoor buildings.
Time series models are primarily suited for processing time series data and predicting energy consumption trends. Similarly, the prediction criteria for time series models are derived from metrics such as MAE (mean absolute error), MSE (mean square error), RMSE (root mean square error), and MAPE (mean absolute percentage error). Li et al. [110] developed a time series energy consumption prediction model for five campus buildings in northern China. They proposed an energy consumption evaluation method based on sub-projection and overall forecasting and conducted a comprehensive comparison of MAE (mean absolute error), RMSE (root mean square error), and CV-RMSE (coefficient of variation of root mean square error). They concluded that the accuracy of building energy consumption sub-prediction was higher than that of the overall prediction. In time series analysis, there are also autoregressive moving average models (ARMA) and differential autoregressive moving average models (ARIMA). Alexander et al. [111] proposed a genetic algorithm to optimize the regression wavelet neural network to predict the daily gas consumption of buildings, which uses the multiple nonlinear autoregressive model modeling of the s-shaped neural network and performs wavelet decomposition on the time series of outdoor average temperature regression, which effectively reduces the prediction error compared with the traditional autoregressive moving average error model. Jahanshahi et al. [112] employed an autoregressive composite moving average model to predict energy consumption in residential buildings across the EU, revealing an improvement in energy efficiency. Transformer models have great advantages in analysis and time series forecasting models because of their powerful sequence modeling capabilities and ability to capture long-distance dependencies in time series. Li et al. [113] proposed the Transformer model to establish a building load prediction model based on the dependence between time series information in building load data, and compared with the latest methods of the XGBoost model, deep learning model (LSTM model), and hybrid model (CLM model), the TRN model has higher prediction accuracy.
The linear regression model is well-suited for capturing the linear relationship between building energy consumption and static factors such as floor area, number of floors, geographical location, etc. Moreover, the time series model predicts that building energy consumption is influenced by various dynamic factors, including seasonality, calendar effects, weather changes, etc., and can effectively capture the patterns of these changes. In the evaluation of the predictions from these two models, the coefficient of determination (R2), adjusted R2, mean square error (MSE), root mean square error (RMSE), and mean absolute error (MAE) are used as metrics for assessing prediction errors. The linear regression model is typically used for long-term forecasting, while the time series model is more suitable for short-term forecasting. In practical building energy consumption forecasting, it may be beneficial to combine time series models and linear regression models to leverage the strengths of both. For instance, a time series model could be used for short-term forecasting, followed by a linear regression model for long-term forecasting. Alternatively, a linear regression model could be used to extract static features, which could then be combined with a time series model to capture dynamic changes.
In summary, the building energy consumption prediction model based on statistical analysis primarily performs linear analysis on characteristic parameters, which can intuitively depict the variability of building energy consumption. However, due to the prevalence of many nonlinear relationships in building energy consumption data, statistical analysis methods are not fully applicable for building energy consumption prediction. Consequently, prediction accuracy may be compromised. As a result, machine learning methods have become increasingly prevalent in recent years.
5.2.2. Machine learning models
Machine learning is a branch of artificial intelligence that enables computers to learn from data to improve performance without the need for explicit programming. Machine learning models predict the output of unknown data by learning patterns from data. These models can be statistically based, such as linear regression, logistic regression, or complex algorithms, including decision trees and support vector machines. The goal of machine learning is to build models that can learn from historical data and make predictions or decisions. Researchers use machine learning models to analyze building energy consumption data, including deep learning (DL), artificial neural networks (ANN), random forests (RF), and support vector machines (SVMs). Similar to the statistical analysis model, the machine learning approach to building energy consumption prediction also relies on metrics such as the coefficient of determination (R2), adjusted R2, mean square error (MSE), root mean square error (RMSE), and mean absolute error (MAE).
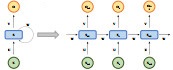
Deep learning (DL) is a subfield of machine learning (ML) that focuses on learning complex patterns and features of data using neural networks with multi-layered structures. These neural networks mimic how the human brain works, passing and processing information layer by layer, extracting useful features from raw data. Common deep learning architectures encompass Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), Long Short-Term Memory (LSTM) frameworks, and Artificial Neural Networks (ANNs). These architectures are individually examined as representative methodologies within the domain of deep learning, while the respective advantages and disadvantages of the latter three deep learning methodologies are delineated in Table 4.
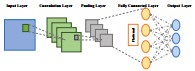
An artificial neural network (ANN) comprises numerous interconnected neurons, each possessing a specific input-output relationship. These neurons are typically organized into three layers: The input layer, the hidden layer, and the output layer (Figure 8). The input layer receives external data, the hidden layer processes and transforms the data, and the output layer delivers the final result. Despite the nonlinear nature of most building energy consumption data, ANNs possess adaptive learning capabilities, enabling them to automatically extract features from input data without the need for complex feature engineering. They are adept at handling complex and nonlinear data, capturing intricate relationships among various factors, and thereby predicting building energy consumption with greater accuracy. Moreover, ANNs are robust and can tolerate a certain level of data noise and outliers. Afzal et al. [161] employed three extended ANN frameworks and a regression model to predict cooling and heating loads, comprehensively analyzed the correlation coefficients of the cooling and heating loads, and optimized the data to develop an optimal hybrid model. Talib et al. [162] employed artificial neural network (ANN) models to accomplish multi-step forecasting of building thermodynamics utilizing historical and contemporary data. To mitigate the overfitting phenomenon inherent in ANN models, the dataset underwent cross-validation, thereby facilitating effective generalization of the dataset. Consequently, the root mean square error (RMSE) of the ANN model was determined, demonstrating commendable performance.
ANNs typically demand a significant number of computational resources, particularly when dealing with large datasets. Moreover, due to the multitude of ANN parameters, if the training data is insufficient, the risk of overfitting increases, which can diminish the model's generalization ability and lead to a reduction in prediction accuracy. Lu et al. [163] employed a geographically weighted regression model to analyze the influencing factors of energy consumption in commercial buildings in Singapore. They utilized K-means clustering and an artificial neural network to predict energy consumption, significantly enhancing the fitting effect. However, the analysis lacked comprehensive data, and the number of datasets for each cluster was not equal, resulting in inaccuracies in cross-sectional data comparison.
Artificial neural networks (ANNs) generally possess robust capabilities for predicting building energy consumption. Their multi-layer architecture is adept at processing nonlinear data, and their capacity for automatic feature extraction mitigates reliance on intricate feature engineering, while exhibiting a certain degree of robustness. Nevertheless, ANNs are not without the common shortcomings inherent to neural network models, including substantial computational resource demands, a propensity for overfitting owing to many parameters, and limited interpretability. Consequently, despite their potential in forecasting building energy consumption, ANNs necessitate further optimization to holistically account for their strengths and weaknesses, thereby enhancing the accuracy and practicality of predictions.
Random Forest (RF) is an ensemble learning method that is based on decision trees (Figure 9), it holds significant application value in building energy consumption prediction. Random Forest randomly selects a subset of the original feature set and constructs multiple decision trees based on that subset. Each decision tree is independently trained on the training set, which enhances the training and prediction speed of the model and results in the optimal segmentation scheme. Finally, the prediction results of the multiple decision trees are aggregated by voting or averaging to derive the final prediction results. Throughout this process, Random Forest can handle high-dimensional data with numerous features and can manage noise and outliers to enhance the robustness of the model. Lei et al. [164] proposed combining the entropy weight K-means and the Random Forest method to establish a prediction model for building energy consumption and to facilitate the classification and selection of influencing factors. Ahmad et al. [98] utilized three methods—Nonlinear autoregressive model (NARM), stepwise regression linear model (LMSR), and Random Forest (LSBoost)—To analyze the power consumption and climate data of the target building on a monthly, quarterly, and annual basis. However, Random Forest requires the construction of multiple decision trees, each of which is built independently. Additionally, there are numerous feature selections and parameter quantity selections, which lead to a significant computational burden in the Random Forest and increase the training and prediction cost of the model.
The Support Vector Regression (SVR) model is a powerful machine learning algorithm. It first requires the selection of features related to energy consumption, such as indoor and outdoor temperature, humidity, light intensity, and human activity, which will be used as inputs for the SVR model in the prediction of building energy consumption. Second, the SVR algorithm is employed to conduct regression analysis on the training data, and the optimal model is determined by adjusting the model parameters (such as the penalty parameter C and the kernel function type) during the training process. The performance of the model is then evaluated using cross-validation methods, such as mean square error (MSE), coefficient of determination (R2), and other metrics. Finally, the model is optimized and adjusted based on the evaluation results. SVR identifies the optimal hyperplane by optimizing the objective function, enabling it to capture complex relationships in the data and provide high prediction accuracy when dealing with nonlinear data. Hamed et al. [165] selected the SVR method and the combination of a meta-heuristic algorithm to predict the heating energy consumption of residential buildings. They comprehensively compared the coefficients of determination of the training dataset and the test data of the model and concluded that the model exhibits high prediction accuracy. The SVR has relatively few parameters and supports various kernel functions, making it suitable for different data types and prediction tasks. Li et al. [166] proposed a hybrid prediction model based on Multivariate Empirical Mode Decomposition (MEMD) and SVR. This model decomposes the eigenvalues and building heat load into several components using MEMD and maintains these components constant, then uses SVR to predict the building heat load. The model compares metrics such as MAPE, NMBE, CVRMSE, and R2 to enhance the accuracy of the heat load prediction. Jain et al. [167] d developed a sensor-based prediction model using SVR to forecast building energy consumption. However, the SVR training process is time-consuming, especially in the absence of high-performance computing resources, and the scale of data collection cannot be effectively utilized.
All four machine learning models can process nonlinear data and capturing complex relationships in building energy forecasting. This implies that they can handle seasonality, weather changes, and other factors in building energy consumption data, and can automatically extract features from these factors. By employing data-driven techniques, they address the uncertainty in building energy consumption forecasting and enhance prediction accuracy. In addition, both random forests and support vector regression are ensemble learning methods that build multiple models to improve prediction accuracy. This also enables them to enhance the robustness of predictions and deal with noise and outliers. However, the process of extracting data features often necessitates a large number of datasets, especially when working with large-scale datasets. Different parameter adjustments can lead to errors in building energy consumption predictions. Deep learning models, in particular, have high requirements for data preprocessing, demand a substantial amount of labeled data, and their parameter adjustment is more complex. If the training data is insufficient, it is prone to overfitting.
Whether it is a statistical model based on the linear relationship of building energy consumption data or a machine learning model based on the nonlinear relationship of building energy consumption data, it focuses only on the input of historical building energy data or eigenvalues and then makes relevant predictions. Both black box methods focus more on the end result of a building's energy consumption, i.e., the relationship between input energy and output energy, and are more helpful in identifying key issues in building energy consumption without considering the intricate details of the building's interior. In general, the application of the black box method in building energy consumption simulation can improve the efficiency of simulation, reduce the technical threshold, and provide scientific and practical analysis results for building energy efficiency. However, the black box method also has limitations, and the premise of using the black box method is that there is a sufficient data set and a wide range of types, so the black box method cannot accurately predict the influencing parameters of the building's energy consumption behavior.
5.3. Mixed methods
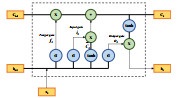
The mixed methods (also known as the gray box method, Figure 10) is a method commonly used in the simulation and analysis of building energy consumption, which combines detailed simulations based on physical models (white box method) and simplified simulations based on statistical or empirical models (black box method). The gray box method approximates the prediction of building energy consumption by abstracting and simplifying complex processes in the physical model, using fewer input data and a simplified simulation process.
Mao et al. [168] proposed an Elman neural network prediction model based on the improved Harry Eagle algorithm, which mostly uses the entropy weight method and the grey correlation method to select the eigenvalues, and then uses the improved Elman neural network model to predict the cooling load of the building. Talib et al. [162] used a resistor-capacitance thermal network to predict the thermal dynamics of buildings and compared it with the artificial neural network model prediction; the gray box model was more accurate. Fan et al. [169] developed a new hybrid model for short-term prediction of power load, which predicts energy consumption based on several models such as gray mutation, random forest, and support vector regression, and optimizes the prediction results of the model using genetic algorithms, and the conclusion proves that the model has high prediction accuracy.
To sum up, the gray box method combines the white box method and the black box method and combines the advantages of the two methods to process a large amount of data, find the relationship between the input variables and the output variables, and predict the building energy consumption more accurately. In addition, a new hybrid method combining a white box method and a black box method can be found to adjust model parameters, etc., and to reduce the building's energy consumption by comparing it with a single method. The gray box method is more widely used in the application of actual building energy consumption, which can effectively reduce building energy consumption, improve the energy efficiency of buildings, and contribute to energy conservation and emission reduction.
From the perspective of actual building energy consumption prediction, the gray box model generally exhibits superior prediction accuracy compared to both the black box and white box models. Nevertheless, irrespective of the method employed, it is imperative to investigate the role of influencing factors on building energy consumption. The white box method, grounded in the physical model of the building, necessitates consideration of the building's physical characteristics. Conversely, the black box method is highly dependent on the accuracy and completeness of historical data, with the selection of appropriate characteristic parameters—Such as temperature, humidity, and lighting—Being crucial to the model's accuracy. The gray box method, however, integrates both the physical characteristics of the white box method and the characteristic parameters of the black box method. Consequently, it is essential to consider the influencing factors of building operation energy consumption in the prediction process to enhance the accuracy of building energy consumption forecasts, thereby creating pivotal conditions for building energy conservation and optimization of energy management. Building managers, armed with this enhanced accuracy, can more precisely control building energy consumption, contributing to reductions in energy use and furthering efforts to save energy and reduce emissions. To this end, optimizing these three methods remains a focal point for researchers, as refining building energy consumption prediction enables a deeper understanding of energy flow, fundamentally mitigates energy waste, and facilitates the achievement of energy conservation and emission reduction in buildings.
6.
Optimization study of building energy consumption forecasting
Building energy consumption prediction constitutes a critical facet of building energy conservation strategies, wherein precise predictions can facilitate enhancements in energy efficiency and the attainment of energy conservation and emission reduction objectives. Within the extant body of research, aside from the prediction of building energy consumption, there are researchers who focus on the optimization of such predictions. The optimization of building energy consumption prediction not only has the potential to transform the predictive modalities of current research and propose novel model-based inquiries but also to further elevate the accuracy of building energy consumption demand forecasts, thereby enabling more precise energy conservation and emission reduction outcomes. The optimization of building energy consumption forecasting is an iterative process, encompassing multiple stages aimed at enhancing the accuracy, stability, and utility of the predictive model. Moreover, the prediction and optimization phases are intricately linked to the influencing factors of building operational energy consumption, with both algorithmic and model optimization necessitating the consideration of input characteristic parameters, which typically derive from historical climate data, equipment usage data, and historical energy consumption data, among other sources. Consequently, the optimization process must also place emphasis on these influencing factors.
The optimization procedures for building energy consumption are inherently complex (Figure 11), initially requiring the determination of the temporal scope, type of energy consumption, and the granularity of the prediction. Subsequently, data collection and preprocessing are undertaken to gather building energy consumption data, meteorological data, and building usage data, followed by the standardization of data through the cleanup and conversion of missing values, outliers, and duplicate data. The selection of an appropriate prediction model involves the construction of model architecture and the specification of network layers, neuron counts, and activation functions. The model is then trained using historical data, and the resulting structure is validated and refined. The analysis of the discrepancy between predicted results and actual energy consumption is conducted using appropriate evaluation metrics, such as Mean Square Error (MSE), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE). The optimization strategy—Whether feature optimization, model optimization, or otherwise—Is determined by analyzing these results. Conclusions are drawn based on the optimization strategy employed. From the optimization workflow, it is evident that the process involves data processing and adjustment, followed by algorithmic optimization, and culminates in optimizing the prediction model. An examination of the optimization process reveals that building energy consumption data, meteorological data, and building use data are integral to the entire workflow of building energy consumption prediction and optimization, necessitating the consideration of data anomalies. Consequently, the influencing factors of building energy consumption are inherently linked to the optimization process. To enhance the accuracy of building energy consumption prediction, the focus of optimization efforts can be directed toward two fundamental components: The algorithm and the model.
6.1. Algorithm optimization research
Algorithm optimization of building energy consumption prediction refers to improving the accuracy, efficiency, and reliability of energy consumption prediction by improving the design of the algorithm, adjusting the parameters, or combining multiple algorithms. The energy consumption optimization based on optimization algorithm mainly optimizes the energy consumption of buildings through optimization algorithms such as genetic algorithm, particle swarm optimization algorithm, and simulated annealing algorithm. The optimization process for this category of algorithms predominantly follows a similar sequence of steps. Initially, data preprocessing is undertaken, which entails data cleaning and the elimination of aberrant elements. Subsequently, an appropriate algorithm is selected based on the intrinsic characteristics of the data, followed by the optimization of its parameters. The dataset is then utilized to train the model, thereby accomplishing the objective of optimization. Consequently, data serves as the foundational element for algorithmic optimization, with high-quality data significantly contributing to the enhancement of predictive accuracy. During the collection and collation of energy consumption data, it is imperative to ensure the veracity, completeness, and precision of the data. Ju et al. [170] used the AHU data collected from the operating buildings to evaluate the performance of the locally calibrated building heat source energy consumption prediction model, and compared with the uncalibrated building heat source energy consumption prediction model, the calibrated prediction model has a coefficient of determination (R2) of 0.95, which is more suitable for model predictive control. Abbass et al. [171] proposed a comprehensive framework based on artificial neural networks, which optimizes the scenario parameters of building energy consumption, evaluates them completely, and finally selects appropriate artificial neural networks for prediction.
Zheng et al. [172] proposed an interpretable system for predicting building energy consumption based on energy consumption pattern recognition and time fusion transformers, which experimentally proved that the system had a lower average absolute percentage error than other traditional prediction models. Zhang et al. [173] proposed an ensemble model using the Exponentially Weighted Moving Average (EWMA) algorithm for energy consumption prediction optimization for the energy consumption prediction of building heating systems, and selected four basic machine learning to compare with it, and the ensemble model effectively improved the accuracy of heating energy consumption prediction. Cao et al. [174] proposed an improved particle swarm optimization overlay ensemble model (PStIE) and a preferred feature selection method to solve the problem that it is difficult to determine the optimal combination of parameters of the ensemble algorithm when using the ensemble model to predict building energy consumption, and the root mean square error of the model is 1.71 lower than that of the ordinary machine learning method.
Selecting the right features is also an important step in optimizing the algorithm. Through the analysis of the influencing factors of building energy consumption, the characteristics closely related to energy consumption are selected, such as outdoor meteorological parameters, building parameters, and equipment performance. After selecting the appropriate features, they are combined with the optimized algorithm to improve the accuracy of building energy consumption prediction. Zhang et al. [47] proposed an improvement of the building energy consumption prediction system, which includes the modification of the input system and the modification of the operation algorithm. The behavioral relationship between sockets, lighting, air conditioners, and people is proposed as input parameters, and the swarm intelligence algorithm with circle mapping is used to predict energy consumption. The method is used to predict building energy consumption with a determination coefficient of 0.9588–0.9901 and an average absolute percentage error of 4.44%~11.60%, and the performance of the building energy consumption prediction model is optimized. In addition, Table 5 lists some scholars' research on algorithm optimization. It can be observed that the essence of algorithm optimization lies in the processing of energy consumption data. Effective data processing can lead to accurate predictions of building energy consumption, which aligns with the above-mentioned demonstration of building energy consumption prediction and optimization steps.
Most of the algorithm optimization for building energy consumption prediction is data-driven. The optimized algorithm can more accurately predict the energy demand of the building, which helps managers allocate energy rationally and reduce waste. With accurate energy forecasting, building operators can make more economical purchasing decisions and reduce operating costs when energy prices fluctuate. However, advanced energy consumption prediction algorithms may require complex data analysis and model building, which requires a high level of expertise and skills. Moreover, optimization algorithms often rely on large amounts of historical data, and the quality and availability of data may affect the accuracy of predictions. Therefore, the optimization algorithm is not fully applicable to all buildings, and it is necessary to conduct practical research based on the building.
6.2. Model optimization studies
Building energy consumption prediction model optimization refers to improving the prediction accuracy, stability, and generalization ability of the model on energy consumption data by improving the structure, parameters, or training process of the prediction model. Choosing the right predictive model is also the key to improving the accuracy of the forecast. In numerous studies, it has been found that scholars have improved the performance of predictive models through machine learning, the use of artificial intelligence, and algorithm selection.
With machine learning algorithms, complex nonlinear relationships can be processed, and patterns and features in the data can be automatically learned. Vasanthkumar et al. [181] proposed an improved Mustang optimization deep learning method model for the prediction of energy consumption of residential buildings, and according to the experimental results, the method is better than the prediction of other deep learning methods. Alymani et al. [182] introduced an improved Moth Flame Optimized Weighted Voting Ensemble Learning (IMFO-WVEL) model based on machine learning methods.
Khan et al. [183] proposed an AI-based efficient hybrid framework to accurately predict building electricity consumption and power generation in response to the mismatch between building supply and demand, and experimentally reduced the hourly mean square error of the method by 0.012 and 0.045 compared with the latest technology (SOTA). Zhang et al. [184] developed an interpretable artificial intelligence model that integrates building features, building geometry, and urban morphology to accurately predict building energy consumption and greenhouse gas emissions, and experiments have proved that this method is feasible. Based on machine learning and artificial neural networks, Aruta et al. [185] proposed a model framework that can predict energy demand in advance and plan the optimal set value of building energy consumption based on meteorological data.
While establishing the building energy consumption prediction model, the feature selection algorithm is optimized or selected. In order to improve the efficiency of building energy consumption prediction, Afzal et al. [186] combined multi-layer perceptron with eight meta-heuristic algorithms to obtain that the MLP-PSOGWO hybrid model has the best performance and the highest accuracy in building energy consumption prediction. Sun et al. [187] proposed a Thermal Comfort Control Strategy for Buildings (PTCN-ICHOA) that combines temporal convolutional neural networks with chimpanzee optimization algorithms, which predicts the energy consumption of buildings in both winter and summer with the smallest error. Liu et al. [188] proposed a Data-Driven Evidence Regression (EVREG) model based on feature selection and model parameter learning, which can predict the point and interval prediction of building energy consumption, which can better describe the fluctuation of building energy consumption and achieve better prediction than the traditional EVEG model.
For the company or system that provides energy, the building energy consumption prediction model is designed to achieve energy saving. Wang et al. [189] proposed a GRU-GTO model for HVAC energy consumption prediction, which uses different communication protocols to reduce transmission efficiency and improve the accuracy of building energy consumption prediction. Irankhah et al. [190] designed a model based on bidirectional gated recurrent units (BiGRUs) and particle swarm optimization (PSO) methods for energy consumption prediction of power companies, which can effectively improve the accuracy of energy consumption prediction. Cai et al. [191] used the support vector regression model combined with six meta-heuristic algorithms to select the optimal model SVR-AEO to predict the cooling and heating load of buildings.
Table 6 lists the research on using deep learning for model optimization in building energy consumption prediction over the past decade. From this table, it is evident that model prediction optimization has garnered increasing attention from many scholars in recent years, which is conducive to a comprehensive understanding of building energy consumption. The optimization of the model can help building managers gain a better understanding of energy consumption patterns, enabling them to optimize energy management, reduce waste, cut costs, and promote sustainable development. Compared to algorithms, the model can more accurately control indoor environmental factors such as temperature and humidity, thereby enhancing the comfort of the living or working environment. To build accurate prediction models, a substantial amount of high-quality historical energy consumption data and related variable data, such as weather and usage patterns, is often necessary, and the combination of simulation software and computer simulations is required. During this process, researchers must collect a large amount of high-quality historical data and relevant variable parameters to prevent data anomalies and ensure accurate model predictions.
Through the optimization of building energy consumption forecasting, energy use can be adjusted with greater precision, facilitating the rational allocation and utilization of energy, thereby enhancing energy use efficiency. The optimization of algorithms in building energy consumption prediction leverages the flexibility and stability of mathematical algorithms, taking into account various building-related influencing factors. This process involves the optimization and adjustment of diverse building feature data and the extraction and processing of effective data, thereby mitigating the impact of random errors and enhancing the stability of predictions. By selecting influencing factors and readily interpretable features that are highly correlated with operational energy consumption as the basis for algorithm optimization, the comprehensibility of the model is augmented, thereby improving the accuracy of the prediction model and reducing prediction errors. Research indicates that both the optimization of mathematical algorithms and model optimization necessitate the collection of a substantial volume of high-quality historical data and relevant characteristic parameters, which are derived from factors influencing building operational energy consumption. To enhance the accuracy of building energy consumption prediction, this approach provides a more precise direction for energy-saving transformations in building energy consumption.
7.
Summary
We primarily address the significance of building energy consumption supervision and prediction and explore methods for optimizing building energy consumption prediction models through mathematical algorithms and data feature selection. The supervision and prediction of building energy consumption are pivotal in achieving energy conservation and emission reduction, reducing operating costs, and enhancing living comfort. By identifying the influencing factors of building energy consumption and subsequently employing suitable mathematical algorithms and model selection techniques, the accuracy of building energy consumption prediction can be enhanced, thereby providing robust support for building energy management.
Global Emphasis and Systematic Design in Building Energy Regulation: Numerous nations persistently concentrate on the formulation of regulations and standards pertaining to building energy regulation. Regarding the design of building energy consumption supervision systems, the optimization and integration of system architecture have facilitated the precise extraction of data and the comprehensive analysis of building energy-saving parameters. This has intuitively delineated the trends in energy consumption and their underlying factors, thereby providing robust data support for the prediction of building energy consumption. Nevertheless, there remains a deficiency in reliable research methodologies within the domains of system maintenance and data security, necessitating urgent further exploration.
Multivariate Analysis of Building Energy Consumption Influencing Factors: We systematically synthesize the intricate effects of climatic conditions, occupant behavior, and urban morphology on building energy consumption. Divergent climatic conditions exert varying influences on energy consumption within buildings, while the air conditioning habits and window opening behaviors of occupants engender substantial discrepancies in household energy usage. Furthermore, urban morphology, block scale, and the density of surrounding buildings also exert a range of impacts on building energy consumption. These aforementioned factors delineate the trajectory for research on building energy consumption prediction and robustly facilitate the profound advancement of energy conservation and emission reduction initiatives.
Three-Dimensional Analysis of Building Energy Consumption Prediction Methodologies: Building energy consumption prediction methodologies are primarily categorized into three classes: Physical methods, data-driven methods, and mixed methods. Although the physical method is predicated on computer technology and simulation software, it necessitates a high level of physical knowledge on the part of the researchers. The black-box method, a subset of data-driven methods, can process vast datasets, extracting pertinent information, and enhancing prediction accuracy through data-driven and algorithmic leveraging; however, it requires the support of extensive and diverse datasets, presenting challenges in the training phase. The mixed method is extensively employed in the prediction of building energy consumption, integrating physical models with data-driven techniques, and has been shown to significantly augment prediction accuracy in comparison to single-method approaches.
Dual-Track Examination of Building Energy Consumption Prediction and Optimization: To further enhance the precision of building energy consumption forecasting, we conduct a succinct analysis of prediction process optimization methodologies. The optimization trajectory primarily concentrates on refining mathematical algorithms and predictive models. The optimization of data algorithms can augment data quality, albeit necessitating extensive data collection and profound analysis, thereby imposing stringent requirements on researchers' mathematical proficiency. While model optimization can be realized through feature selection, it also mandates substantial data support. Consequently, both algorithmic optimization and model optimization are inherently linked to data analysis and collation, warranting researchers' meticulous attention.
In the analysis of the aforementioned literature, it is evident that factors related to building operation energy consumption form the foundation of energy consumption prediction. Data-driven approaches are a crucial element in achieving accurate predictions of building energy consumption. Looking ahead, for the prediction and optimization of building energy consumption, a new model could be developed by integrating the influencing factors of building operation energy consumption with a prediction model based on mathematical algorithms. This integration would enable a more precise estimation of building energy use intensity and contribute to further research on energy conservation and emission reduction.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to acknowledge the financial support from the Natural Science Foundation of Liaoning Province of China (Grant No. 2024-BSLH-251).
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Author contributions
The authors confirm contribution to the paper as follows: study conception and design: Zhongjiao Ma, Zichun Yan; data survey collection: Zhongjiao Ma, Zichun Yan, Mingfei He, Haikuan Zhao; analysis and interpretation of results: Zhongjiao Ma, Zichun Yan; fund support: Zhongjiao Ma; draft manuscript preparation: Jialin Song, Zichun Yan. All authors reviewed the results and approved the final version of the manuscript.










 DownLoad:
DownLoad: