Professional and personal experiences of workplace violence among Italian mental health nurses: A qualitative study

1.   Introduction

Nonlinear partial differential equations (PDEs) are often used to describe some significant problems in natural science and engineering technology. The analysis of nonlinear waves has garnered increasing attention in the fields of shallow water, plasma, nonlinear optics, Bose−Einstein condensates, and fluids. The nonlinear PDEs in these fields can be solved using lump solutions. The lump solution and interaction hybrid solutions were first discovered by Zakharov in ^[1] and Craik in ^[2], respectively. These special solutions are of great significance for the study of nonlinear integrable equations ^[3,4,5]. To obtain these analytical solutions, the scholars have proposed a variety of methods, including Ansatz technique ^[6], Hirota's bilinear method (HBM) ^[7], and the inverse scattering transform (IST) ^[8]. The HBM proposed by Hirota, has been widely used as an effective approach to study the nonlinear dynamics wave equation, resulting in numerous richer solutions, such as solitons solutions, novel breather waves, lump solutions, two-wave solutions, and rogue wave solutions (^{[9,10,11,12,13,14]}). These solutions are visualized in three-dimensional graphics via numerical simulations, making it easier to understand the propagation of nonlinear waves.

The study of the stability of integrable equations, such as the KPI equation, the Ishimori equation, the nonlinear Schrödinger (NLS) equation and the KdV equation have further enriched the theory of nonlinear wave equations. Spectral methods can effectively solve the problem of linear stability. In ^[15], Degasperis et al. proposed the construction of the eigenmodes of the linearized equation using the associated Lax pair and provided the computation of both analytical and numerical solutions with the example of two coupled NLS equations. In ^[16], Ablowitz provided a comprehensive review of research methods for integrability and nonlinear waves, including Bäcklund transformations, Darboux transformations, direct integral equations or Riemann−Hilbert or Dbar methods, and HBM. By combining the KdV and NLS equations, the author further elaborated on the ideas and background of the IST method.

The computation of nonlinear PDEs has become a very active research topic. With advancements in traditional methods like finite element (^[17,18]), finite difference (^{[19,20,21,22,23,24]}), finite volume (^[25,26,27]), and spectral methods (^[28,29,30]), numerous outstanding research results have been achieved in the numerical approximations of nonlinear PDEs. In ^[31], the authors developed a time-two-grid difference scheme for nonlinear Burgers equations. In ^[32], a method combining the barycentre Lagrange interpolation collocation technique with a second-order operator splitting approach was proposed for the purpose of solving the NLS equation. Based on novel shifted Delannoy functions, Ansari et al. ^[33] employed a matrix collocation technique to numerically approximate the singularly perturbed parabolic convection−diffusion−reaction problems.

In recent years, for the treatment of nonlinear terms, there have been a lot of unconditionally energy dissipative numerical schemes for Allen−Cahn and Cahn−Hilliard gradient flows models, such as:

(ⅰ) CSS (convex splitting) scheme ^[34,35,36];

(ⅱ) IMEX (stabilized semi-implicit) scheme ^[37,38];

(ⅲ) ETD (exponential time differencing) scheme ^[39,40];

(ⅳ) IEQ (invariant energy quadratization) scheme ^[41];

(ⅴ) SAV (scalar auxiliary variable) scheme ^[42,43];

(ⅵ) E-SAV (exponential scalar auxiliary variable) scheme ^[44].

The idea of (ⅰ) is to decompose the energy function into convex and concave parts, handling the convex part implicitly and the concave part explicitly. The advantage is that it can achieve second-order unconditional stability. However, the drawback is that it still requires solving nonlinear equations. The method of (ⅱ) yields extra error, which makes it difficult to construct a higher-order scheme. The (ⅳ) and (ⅴ) approaches make it easier to handle nonlinear terms by defining auxiliary variables that transform the nonlinear potential function into a simple quadratic form. Nevertheless, an inner product must be calculated before obtaining the next time value. Compared with (ⅳ) and (ⅴ), the variable defined in (ⅵ) does not require any assumptions. And the E-SAV method can easily construct an explicit scheme that can preserve energy stability. But this physical property can not be satisfied with the explicit SAV scheme.

In addition, Huang et al. ^[45] studied a new SAV method to approximate the gradient flows, which is an improvement of the SAV method. By defining an auxiliary variable in the new SAV method as a shifted total energy function, instead of focusing on the nonlinear parts of the classic SAV method, we replace the dynamic equation for that variable with the energy balance equation of the gradient flow. This facilitates the construction of high-order and energy-stable discrete schemes. In ^[46], Liu et al. further developed an exponential semi-implicit scalar auxiliary variable (ESI-SAV) method for the phase field equation. The ESI-SAV method can preserve the advantages of both the new SAV and E-SAV methods and be applied more effectively to other dissipative systems.

On the basis of the above methods, researchers began to apply the above nonlinear processing techniques to approximate semi-linear wave equations. Jiang et al. ^[47] proposed an IEQ approach and established an energy-preserving linear implicit scheme for the sine-Gordon equation. In ^[48], based on the SAV method with a combination of the Gauss technique and the extrapolation method, Li et al. provided a high-order energy-conserving and linearly implicit scheme. Wang et al. ^[49] developed a second-order SAV Fourier spectral method to solve a nonlinear fractional generalized wave equation.

The primary objective of this paper is to develop second-order and Hamiltonian conserved semi-discrete schemes for semi-linear wave equations. Following the superiorities of the E-SAV and ESI-SAV methods, two different numerical schemes are given by utilizing the Crank−Nicolson scheme for temporal approximation. Furthermore, the convergence order and the evolution curve of the Hamiltonian function are validated through numerical experiments.

The paper is organized as follows: In Section 2, by introducing scalar auxiliary variables, we obtain two equivalent forms for the semi-linear wave equation in the continuous case. In Sections 3 and 4, by using the Crank−Nicolson scheme, we propose two semi-discrete schemes corresponding to the equivalent forms and provide proof of the convergence order. Two numerical examples are implemented to test the effectiveness of the theoretical analysis in Section 5.

2.   Preliminary results

We consider the following semi-linear wave equation:

where $\Omega \subset \mathbb{R}^{d} (d = 2, 3)$ is a bounded convex domain, $T > 0$ is a fixed number, $f(y) = -F'(y)$ is a nonlinear term, and $F(y)$ satisfies $F(y)\in\mathcal{C}^{3}(R)$. The Hamiltonian function is defined as

Proposition 2.1. The system (2.1) holds the following Hamiltonian conservation law:

Proof. Multiplying the first equation of the system (2.1) by $y_{t}$ yields

By using the continuous Leibniz rule, we obtain

and

Inserting (2.5) and (2.6) into (2.4), we obtain

Integrating (2.7) over the spatial domain $\Omega$ and combining the boundary conditions leads to

From (2.8) and (2.2), we can deduce that

The proof is complete. □

We introduce two scalar auxiliary variables as

Then the system (2.1) can be equivalently rewritten as

where

For the system (2.10)–(2.14), we have the following lemma:

Lemma 2.1. (Hamiltonian conservation) The above system (2.10)–(2.14) satisfies

where the modified Hamiltonian function

Proof. Taking the inner product of (2.11) by $\omega$, then combining (2.10) and (2.12), we obtain

Obviously, we can deduce

The proof is complete. □

Next, introducing a new variable

which satisfies the dissipation law

and defining $\xi = \frac{\exp (\mathcal{R})}{\exp (H(y))}$, we can know that $\xi\equiv1$ in the continuous case. Replacing the factor $q^{y, r}$ in (2.11) by $Q(\xi)$, where $Q(\xi)$ is a polynomial function of $\xi$, the system (2.1) can be transformed into the following equivalent form:

Furthermore, (2.17) and (2.22) imply that the system (2.18)–(2.24) is Hamiltonian conserved.

3.   CN-E-SAV scheme

Let $0 = t_{0} < t_{1} < ... < t_{N} = T$ be a uniform partition of the time interval $[0, T]$ with the time steps $\Delta t = T/N$ and $t^{n} = n\Delta t$. Then, utilizing the Crank−Nicolson scheme to discretize the system (2.10)–(2.14), a second-order Carnk−Nicolson E-SAV (CN-E-SAV) scheme can be formulated as follows:

where

and $\hat{q}^{n+\frac{1}{2}} > 0$ with $(\hat{y}^{n+\frac{1}{2}}, \hat{r}^{n+\frac{1}{2}})$ being generated by the first-order scheme with the time step size $\dfrac{\Delta t}{2}$, i.e.,

In order to better understand this scheme, by plugging (3.1) into (3.2) and (3.4) into (3.5), respectively, we can get

So we can implement the CN-E-SAV scheme as follows:

3.1.   Hamiltonian conservation

We show the conservation of the CN-E-SAV scheme by the following theorem:

Theorem 3.1. The CN-E-SAV scheme (3.1)–(3.3) is Hamiltonian conserved:

Proof. Taking the inner product with (3.1) and (3.2) by $y^{n+\frac{1}{2}}$, $\omega^{n+\frac{1}{2}}$, we have

and

Substituting (3.10) into (3.11) and combining (3.3), we obtain

The proof is complete. □

3.2.   The error of the CN-E-SAV scheme

We will follow the next two steps to complete the error estimation of the CN-E-SAV scheme:

step (ⅰ): complete the error between (2.10)–(2.14) and (3.4)–(3.6);

step (ⅱ): with the help of the results of step (ⅰ), the error of (2.10)–(2.14) and (3.1)–(3.3) is further estimated.

For simplicity, we define

It follows from (2.10)–(2.14) that the exact solution $(\omega, y, r)$ satisfies

where the truncation functions are defined as

and satisfy

For the purposes of theorem proving, we present the following assumptions and lemmas:

Assumption 3.1. There exist constants $Q^{*}$, $Q_{*}$, $\tilde{Q}^{*}$, and $\tilde{Q}_{*}$ independent of $\Delta t$ such that $Q_{*} \leq q^{n}\leq Q^{*}$, $\tilde{Q}_{*} \leq\hat{q}^{n+\frac{1}{2}}\leq \tilde{Q}^{*}$ for all n.

Lemma 3.1. Denote

then the following holds:

where the constant $C > 0$ depends on $Q^{*}, Q_{*}, \tilde{Q}^{*}$, $\tilde{Q}_{*}, |\Omega|, y_{0}$, and $||f||_{C^{1}(R)}$.

Proof. Similar to the proof of Lemma 4 of ^[51], the results can be proved by applying Poincaré's inequality to $||e_{y}^{n}||, ||\hat{e}_{y}^{n+\frac{1}{2}}||$ once more. □

Lemma 3.2. Assume $\Delta t$ is sufficiently small and satisfies

Then, we have

Proof. Subtracting (3.4)–(3.6) from (3.12)–(3.14), we have the error equations as

Taking the inner product of (3.19) with $\hat{e}_{\omega}^{n+\frac{1}{2}}$ and combining (3.18), we have

For the first term on the right-hand side of (3.21), according to Lemma 3.1, we obtain

Then for $\Lambda_{2}, \; \Lambda_{3}, \; \Lambda_{4}$, using Young's inequality and (3.15), one has

Combining (3.22)–(3.25) with (3.21), we can have

Multiplying (3.20) by $\hat{e}_{r}^{n+\frac{1}{2}}$, we can obtain

According to $q^{n}\leq Q^{*}, \; F\in \mathcal{C}^{3}(R)$, and Poincaré's inequality, we can derive the following estimate for $\Psi_{1}$:

The estimate for $\Psi_{2}$ is similar to (3.22), so we obtain

For the last two terms of (3.27), by utilizing (3.16), we have that

Therefore, injecting (3.28)–(3.30) into (3.27) leads to

Multiplying (3.26) by $C^{*}$ and adding it to (3.31) implies

The proof is completed when $C^{*}\geq1$ and $(\Delta t)^{2}\leq\frac{C^{*}}{\tilde{C}_{1}C^{*}+\tilde{C}_{2}}$. □

Next, we will derive the convergence order of the CN-E-SAV scheme (3.1)–(3.3). Clearly, the exact solution $(\omega, y, r)$ satisfies

where the truncation functions are defined by

The truncation functions satisfy the following lemma:

Lemma 3.3. (^[50]) The following estimates hold

Theorem 3.2. Let $(\omega(t_{n}), y(t_{n}), r(t_{n}))$ and $(\omega^{n}, y^{n}, r^{n})$ be the solutions of (2.10)–(2.14) and CN-E-SAV scheme (3.1)–(3.3), respectively. Suppose that the assumptions in Lemma 3.2 hold and assume further

Then, we have

Proof. Subtracting (3.1)–(3.3) from (3.32)–(3.34), we derive the following error equations:

Taking the inner product of (3.36) with $e_{\omega}^{n+\frac{1}{2}}$ and combining (3.35), we have

According to Lemma 3.1, we obtain

For the last four terms of (3.38), it follows from Lemma 3.3 that

Substituting (3.39)–(3.43) into (3.38), we can obtain

Multiplying (3.3) by $e_{r}^{n+\frac{1}{2}}$, we obtain

Next, we estimate the right-hand side of (3.45). Applying Lemma 3.1, Lemma 3.3, and Young's inequality, we deduce that

Combining the above estimates of (3.46)–(3.48) together, one has

By adding (3.44) and (3.49) and summing the index $k$ from $0$ to $n-1$, we obtain

Applying Lemma 3.2 and the discrete Gronwall's inequality, we can complete the proof. □

4.   New-CN-E-SAV scheme

For the system (2.18)–(2.24), we obtain the semi-discrete new Crank−Nicolson E-SAV (New-CN-E-SAV) scheme by adopting the Crank−Nicolson scheme as

where $\hat{y} ^{n+\frac{1}{2}}$ is obtained by solving the following equation:

From (4.5), we can find that the New-CN-E-SAV scheme (4.1)–(4.5) also enjoys the same conservation as the CN-E-SAV scheme (3.1)–(3.3).

Theorem 4.1. The New-CN-E-SAV scheme (4.1)–(4.5) is Hamiltonian conserved in the sense that

Further, according to Theorem 4.1, the Eq (4.3) can be simplified as

In order to better illustrate the calculation process of the New-CN-E-SAV scheme (4.1)–(4.5), plugging (4.1) and (4.6) into (4.2) and (4.7), respectively, we obtain

So the New-CN-E-SAV scheme can be implemented as follows:

For the convergence order of the New-CN-E-SAV scheme, from (4.6) and (4.7), we can obtain

Referring to ^[46] and combining (4.11) and (4.12), we obtain

Then, we derive that

which means that the New-CN-E-SAV scheme can achieve second-order approximation.

5.   Numerical experiments

In this section, two examples are presented to test the validity of the theory. We set

and consider different nonlinear functions $F(y)$ to simulate the order of convergence and the Hamiltonian conservation. Discretize the physical space by the Fourier spectral method with a spatial step $h = L/2^9$. Since we do not have the exact solution, we thus select the sufficiently small time step $\Delta t = 1/1024$ as the reference solution.

Example 5.1. In this example, we choose the nonlinear function $F(y)$ and initial values $r_{0}, \mathcal{R}_{0}$ as follows:

Example 5.2 In this example, we select

For the CN-E-SAV and New-CN-E-SAV schemes, the error between the numerical solution and the exact solution in the sense of $L^{2}$-norm is listed in Tables 1–6, where Tables 1–3 and 4–6 show the numerical results for Examples 5.1 and 5.2, respectively.

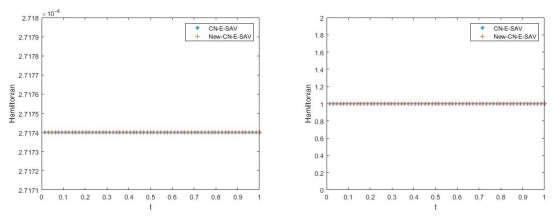
The evolution of the Hamiltonian function with respect to the CN-E-SAV and New-CN-E-SAV schemes in Examples 5.1 and 5.2 is depicted in Figure 1.

From the analysis of the data presented in Tables 1–6, it is evident that the error decreases as the time step $\Delta t$ decreases. And the numerical results for the convergence order of the variables $\omega, y, r$ in Examples 5.1 and 5.2 are consistent with the theoretical results. This thereby further illustrates the effectiveness of the CN-E-SAV and New-CN-E-SAV schemes.

Figure 1 clearly shows that, regardless of the different nonlinear functions selected in the two examples, the CN-E-SAV and New-CN-E-SAV schemes successfully maintain the conservation property of the Hamiltonian function.

6.   Conclusions

In this work, we develop the CN-E-SAV and New-CN-E-SAV schemes to approximate a semi-linear wave equation with the following advantages: (ⅰ) it preserves Hamiltonian conservation; (ⅱ) it is efficient; and (ⅳ) it is easy to implement. The further topic can also involve designing the high-order BDFk-E-SAV schemes or applying them to other nonlinear problems. It is also meaningful to consider the construction of numerical schemes for the nonlinear localized wave equations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Granted No. 11961008) and Guizhou University Doctoral Foundation (Granted NO. 15 (2022)).

Conflict of interest

The authors declare there is no conflict of interest.