1. Introduction
The definition of impulsive semi-dynamical system and its properties including the limit sets of orbits have been investigated [1,9]. The generalized planar impulsive dynamical semi-dynamical system can be described as follows
|
{dxdt=P(x,y),dydt=Q(x,y),(x,y)∉M,△x=a(x,y),△y=b(x,y),(x,y)∈M,
|
(1)
|
where (x,y)∈R2, △x=x+−x and △y=y+−y. P,Q,a,b are continuous functions from R2 into R, M⊂R2 denotes the impulsive set. For each point z(x,y)∈M, the map or impulsive function I:R2→R2 is defined as
|
I(z)=z+=(x+,y+)∈R2, x+=x+a(x,y), y+=y+b(x,y)
|
and z+ is called as an impulsive point of z.
Let N=I(M) be the phase set (i.e. for any z∈M,I(z)=z+∈N), and N∩M=∅. Let (X,Π,R+) or (X,Π) be a semi-dynamical system, where X=R2 is a metric space, R+ is the set of all non-negative reals. For any z∈X, the function Πz:R+→X defined by Πz(t)=Π(z,t) is clearly continuous such that Π(z,0)=z for all z∈X, and Π(Π(z,t),s)=Π(z,t+s) for all z∈X and t,s∈R+. The set
is called the positive orbit of z. For all t≥0 and z∈X, we define F(z,t)={w:Π(w,t)=z}, and further for any set M⊂X, let
Based on above notations, the definition of impulsive semi-dynamical system is defined as follows [1,9,23].
Definition 1.1. An planar impulsive semi-dynamic system (R2,Π;M,I) consists of a continuous semi-dynamic system (R2,Π) together with a nonempty closed subset M (or impulsive set) of R2 and a continuous function I:M→R2 such that for every z∈M, there exists a ϵz>0 such that
|
F(z,(0,ϵz))∩M=∅ and Π(z,(0,ϵz))∩M=∅.
|
Definition 1.2. Let (R2,Π) be a dynamical system. An open set V in R2 is called a tube if there exist an s>0 and a subset S⊂V such that
1. Π(z,t)∈V for all z∈S and −s<t<s, and
2. for each z∈V there is a unique s(z), |s(z)|<s such that Π(z,s(z))∈S.
It is clear that V=[Π(z,t)|z∈S,−s<t<s]. The set S is called an (s,V)-section of the tube V. It is well known that if z0∈R2 is not a rest point, that is, Π(z0,t)≠z0 for all t, then there exists a tube containing z0.
Definition 1.3. Let (R2,Π) be a dynamical system. A subset M⊂R2 is said to be well placed in R2 if every point z∈M lies in some tube whose section lies in M.
Denote the points of discontinuity of Πz by {z+n} and call z+n an impulsive point of zn. A function Φ from R2 into the extended positive reals R+∪{∞} is defined as follows: let z∈X, if M+(z)=∅ then Φ(z)=∞, otherwise if M+(z)≠∅ then Φ(z)=s, where Π(z,t)∉M for 0<t<s but Π(z,s)∈M. Obviously, this function describes the times of meeting impulsive sets, and its continuity plays an important role in impulsive semi-dynamical system. In 1990 [9], Kual defined the time function (denoted as Φ)-the time of reaching impulsive points in the given impulsive semi-dynamical system (X,π;M,I). And he also provided a theorem that the function Φ is continuous on X when the impulsive set M is well placed. That is, the following main results on the continuity of function Φ have been provided in [1,9] (i.e. Theorem 2.1 in [1] and Theorem 4 in [9]).
Theorem 1.4. Let (R2,Π) be a dynamical system. Let M be a closed and well placed subset of R2. Suppose that (R2,Π,M,I) is an impulsive semi-dynamical system. Then Φ is continuous on R2.
2. Example and main results
In 2004 [2], the author pointed out some errors on Theorem 1.4, that is, it need not be continuous under the assumptions. And the main aspect concerned in the paper [2] is the continuality of Φ on the impulsive set M. In another word, the author has proved that the function Φ sometimes is not continuous (actually not low semicontinuous) on some points in the impulsive set M and more conditions are needed to guarantee its continuity. They concluded that Φ just continuous on X∖M under the assumptions in [9]. And in paper [1], the authors have adopted this result. In this note, we have make further efforts that the function would not be continuous on X∖M under the assumption in the paper [9]. We first address this in the following by a realistic example in pest control and discuss generally what extra condition should be added to guarantee the continuity of Φ on X∖M.
In the following we will provide an example to show this Theorem is not true for some special cases. Considering the following model with state-dependent feedback control
|
{dx(t)dt=ax(t)[1−x(t)K]−βx(t)y(t)1+ωx(t),dy(t)dt=ηβx(t)y(t)1+ωx(t)−δy(t),}x<ET,x(t+)=(1−θ)x(t),y(t+)=y(t)+τ,}x=ET.
|
(2)
|
where x(t+)≐x+ and y(t+)≐y+ denote the numbers of pests and natural enemies after an integrated control strategy is applied at time t [11,17]. The definitions of all parameters and their biological meanings please refer to literatures [11,17]. For convenience, we assume that the initial density of the pest population is always less than the economic threshold (ET) (i.e. x(0+)≐x+0<ET,y(0+)≐y+0>0) and ET<K. In model (2), 0≤θ<1 is the proportion by which the pest density is reduced by killing and/or trapping once the number of pests reaches ET, while τ (τ≥0) is the constant number of natural enemies released at this time t.
Define four curves as follows
|
L0:x=δηβ−δω; L1:y=rβ[1−xK](1+ωx);
|
|
L2:x=ET; and L3:x=(1−θ)ET.
|
The intersection points of two lines L1 and L2, L1 and L3 are QET=(ET,yET) and QθET=((1−θ)ET,yθET), respectively, where
|
yET=rβ[1−ETK](1+ωET), yθET=rβ[1−(1−θ)ETK](1+ω(1−θ)ET).
|
Define the open set in R2+ as follows
|
Ω={(x,y)|x>0,y>0,x<ET}⊂R2+={(x,y)|x≥0,y≥0}.
|
(3)
|
In the following we assume that model (2) without impulsive effects exists an unstable focus E∗ with
|
E∗=(xe,ye)=(δηβ−δω,rη(Kηβ−Kδω−δ)K(ηβ−δω)2),
|
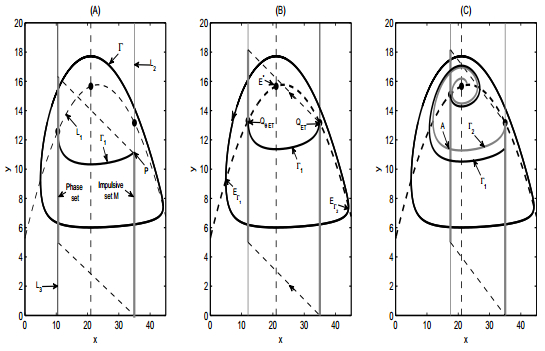
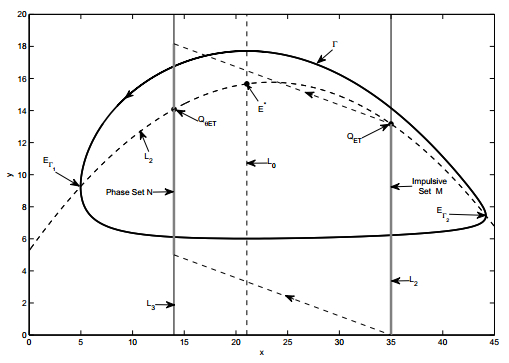
which means that model (2) without impulsive effects has a unique stable limit cycle (denoted by Γ)[11,17], as shown in Fig. 1. Note that the Γ intersects with the isocline L1 at two points EΓ1(xΓ1,yΓ1) and EΓ2(xΓ2,yΓ2) with xΓ1<xΓ2.
In the following we show that model (2) defines an impulsive semi-dynamical system. From a biological point of view, we focus on the space R2+ to discuss model (2). As an example, we only focus on the special case, i.e. xΓ1<(1−θ)ET<ET<xΓ2, as shown in Fig. 1, and the trajectory initiating from the point QθET (denoted by Γ1) plays a key role in defining the impulsive set and determining the continuity of the function Φ. There are three cases: (A) Γ1 reaches the section SET={(x,y)|x=ET,y≥0} without crossing the curve L1; (B) Γ1 reaches the section SET={(x,y)|x=ET,y≥0} just on the point QET; and (C) Γ1 will cross the curve L1 several times before reaching the section SET, shown in Fig. 2(A), (B) and (C), respectively.
Further, we define the section SθET={(x,y)|x=(1−θ)ET,y≥0} and assume that it does not involve the rest point E∗ in it. Choosing the section SθET as a Poincaré section. Assume that the point P+k=((1−θ)ET,y+k) lies in the section SθET (here E∗∉SθET), and the trajectory Ψ(t,t0,(1−θ)ET,y+k)=(x(t,t0,(1−θ)ET,y+k),y(t,t0,(1−θ)ET,y+k)) initiating from P+k will reach at the section SET in a finite time t1 (i.e. x(t1,t0,(1−θ)ET,y+k)=ET and Φ(y+k)=t1), denote the intersection point as Pk+1=(ET,yk+1). This indicates that yk+1 is determined by y+k, i.e. we have yk+1=y(t1,t0,(1−θ)ET,y+k)≐P(y+k). One time state dependent feedback control action is implemented at point Pk+1 such that it jumps to point P+k+1=((1−θ)ET,y+k+1) with y+k+1=yk+1+τ on SθET. Therefore, we can define the Poincaré map PM as
|
y+k+1=P(y+k)+τ=y(t1,t0,(1−θ)ET,y+k)+τ≐PM(y+k), and Φ(y+k)=t1.
|
(4)
|
Now define the impulsive set M for three cases shown in Fig. 1 as
|
M={(x,y)| x=ET,0≤y≤YM},
|
(5)
|
which is a closed subset of R2+, where YM=P(yθET) for cases (A) and (B), and YM=yET for case (C). It is easy to see that any solution of model (2) without impulsive effects initiating from Ω will reach in the impulsive set M in a finite time except for the rest point E∗. Define the continuous function I:(ET,y)∈M→(x+,y+)=((1−θ)ET,y+τ)∈Ω. Thus, the phase set N can be defined as follows
|
N=I(M)={(x+,y+)∈Ω| x+=(1−θ)ET,τ≤y+≤P(yθET)+τ}.
|
(6)
|
Therefore, (R2+,Π;Ω,M,I) or (R2+,Π;M,I) with respect to model (2) defines an impulsive semi-dynamical system.
According to the Definition 1.3 and topological structure of orbits of model (2) without impulsive effects, it is easy to see that M defined in (5) is a closed and well placed subset of R2+, and further no initial point in (R2,Π) belongs to the impulsive set M. This indicates that according to Theorem 1 the function Φ is continuous for the three cases shown in Fig. 2. For the cases shown in Fig. 2(A) and (B) it is easy to see that the results are true.
However, this is not true for case (C) shown in Fig. 2(C). In fact, for case (C) there exists a trajectory (denoted by Γ2) initiating from Ω will tangent to the section SET at point QET, and the orbit Γ2 will intersect with the section SθET at several points, for example, point A=((1−θ)ET,yA) as shown in Fig. 2(C). Now we consider this point A and choose an open set U which contains the point A. Taking any two points Ai∈U∩SθET(i=1,2) with yA1<yA<yA2, we see that the trajectory starting from the point A2 will cross the curve L1 at least one time before hitting the impulsive set M, and the trajectory starting from the point A1 will reach the impulsive set M directly. This confirms that both trajectories initiating from the set U∩SθET can not simultaneously reach the tube V of the impulsive set M for small s, and consequently the function Φ is not continuous at the point A.
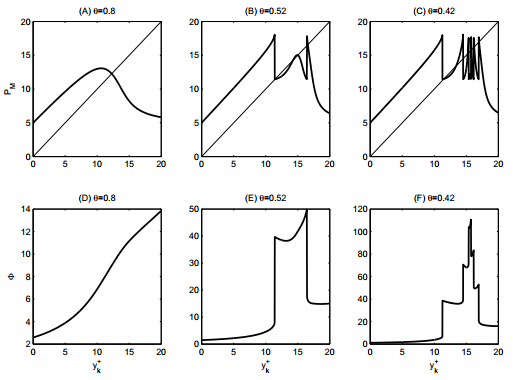
If we fixed all the parameter values as those shown in Fig. 3, then we can see that the continuities of the Poincaré map and the function Φ depend on the parameter θ. For larger θ values both the Poincaré map and the function Φ are continuous, and for smaller θ values both the Poincaré map and the function Φ exist several discontinuous points, as shown in Fig. 3. Moreover, we can show that the function Φ is continuous when the E∗ is stable equilibrium or E∗ does not exist. Thus, this counter example shows that more exact conditions are needed to show the continuity of the function Φ[1,9]. Based on above discussion, we can see that if the impulsive set M is transversal, i.e. there is no trajectory of model (2) without impulsive effect which tangents to the set M, then the function Φ is continuous. Therefore, we have the following result on the continuity of the function Φ which can be proved by using the similar method as those in[1,2,9].
Theorem 2.1. Let (R2,Π) be a dynamical system and consider an impulsive semi-dynamical system (R2,Π,M,I). Let M be a closed and well placed subset of R2 which is transversal. Then Φ is continuous on R2 if and only if z∉M.
Note that the transversality condition in Theorem 2.1 may exclude the case (B) in Fig. 2(B). In fact, based on our example we can conclude that the function Φ is continuous on phase set provided that the Poincaré map reaches its maximal value at yθET. This confirms that the conditions shown in Theorem 2.1 could be further improved.
3. Dicsussion
Recently, impulsive semi-dynamical systems or state dependent feedback control systems arise from many important applications in life sciences including biological resource management programmes and chemostat cultures [5,6,10,12,17,18,19,20,21,22,24], diabetes mellitus and tumor control [8,13], vaccination strategies and epidemiological control [14,15], and neuroscience [3,4,7]. In those fields, the threshold policies such as ET and threshold glucose level for closed-loop treatment play the pivotal role in the pest control and medications to treat diabetes. For example, control actions such as spraying pesticides and releasing natural enemies for pest control and drug administrations (such as insulin and glucose-lowering pills) for disease treatment depend on the threshold levels including density of pest population and glucose level [8,16,17,24].
The above state-dependent feedback control strategies can be defined in broad terms in real biological problems, which are usually modeled by the impulsive semi-dynamical systems. The continuity of the function Φ describing the times of meeting impulsive set which is equivalent to the continuity of the Poincaré map determined by the impulsive points in phase set (as shown in Fig. 3) plays an important role in investigating the qualitative theories of the impulsive semi-dynamical system. In particular, it is very useful for determining the existence and stability of order one periodic solution or order one limit cycle [21,23]. However, in order to guarantee the continuity of this function, only some special cases for the proposed models have been discussed in literatures [11,12,16,23]. For example, the proposed models without impulsive effects do not have any positive equilibrium in the first quadrant, or the threshold level must be less than the values of the steady state once the models exist the interior equilibrium. Moreover, the Poincaré map can also help us to study the dynamic complexity of impulsive semi-dynamical system and its application in reality. Therefore, determining the continuity of the function describing the times of meeting impulsive set and then the Poincaré map are crucial for proposed models arising from different fields.









 DownLoad:
DownLoad: