1.
Introduction
1.1. Natural background of the Amur river basin
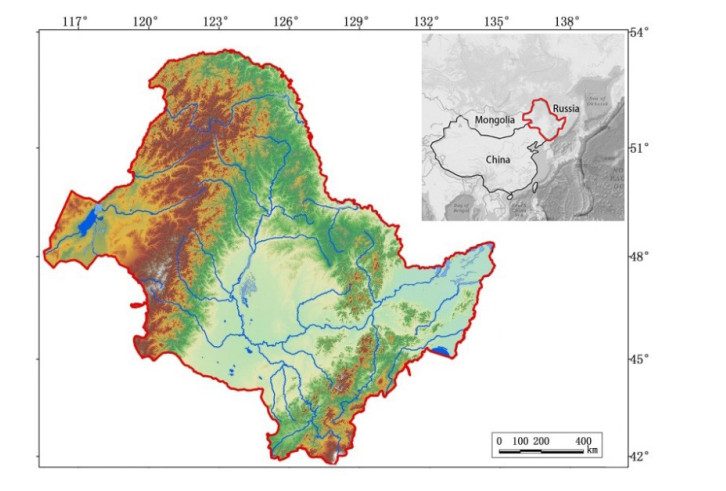
Accurate documentation and mapping of archaeological data of human sites contribute to a better understanding of temporal and spatial information of ancient lifestyles, cultural and economic exchange pathways, migration routes, and process of social development [1,2,3,4]. Furthermore, information at a cross-regional scale could also provide valuable contribution to a broad range of scientific projects that focus on human environmental interactions, evolution of landscape, and land-use [5,6,7,8]. The spatial and temporal distribution of archaeological sites and their environment background in many areas of China has been studied intensively [9,10,11,12,13,14,15,16,17,18]. These Summarizing studies based on primary archaeological data promote people's cognition of regional culture and environment evolution process [19,20,21,22,23], but similar studies in north east China, especially in the Amur river basin and surrounding areas, are scarce [24,25]. The Amur river is the tenth longest river in the world with a length over 4, 400 km, and it flows along the borders of China, Russia, and Mongolia. The Amur river is an important river in the central region of the Northeast Asia and its basin covers an area of over 1.8 million Km2, 48% of which is in China [26]. As shown in Figure 1, the Amur River Basin in Northeast China is the study area of this paper.
The development and maturation of large ancient civilizations required adequate material resources and a secure external environment as a guarantee. The isolated geographical space created by the fertile soil of the great river basin and the enclosed mountains allowed the Amur River basin to become an ideal place for ancient human habitation. More than 200 rivers originate from the Amur river, and more than 50 of these tributaries have a basin area of more than 10, 000 Km2. The river plains along the Songhua river, Nengjiang river, Ussuri river and Mudan river provided ample environmental capacity for the construction of human settlements derived from ancient agricultural civilization. In addition, the extensive forest and grassland areas also provide sufficient material resources for the construction of human settlements derived from ancient fishing, hunting and nomadic civilizations.
1.2. Archaeological progress of Human habitation sites in the Amur river basin
The spatial and temporal distribution of habitation sites, with the support of various archaeological information, is an essential component of settlement archaeology, landscape archaeology, and other branches of archaeology [27,28,29,30,31,32,33]. Archaeological work on human settlement sites in the Amur River basin has been carried out for more than a century since the end of the 19th century. Previous related archaeological studies have gradually increased, contributing to a reassessment of regional chronology and a deeper understanding of human-land relations in the Amur River basin.
Archaeological research in the Amur River basin can be broadly divided into three phases. The first phase was the period of colonial archaeology phase from the late 19th century to the founding of the People's Republic of China in 1949, which was dominated by Russia and Japan in the macro context of the construction of the Siberian railway and the Manchukuo invasion program. The capital cities of the Balhae state (698-926 AD), the Jin dynasty (1115-1234 AD), and a number of other large habitation sites were the major investigation and research targets during that period, and some excavations that did not follow archaeological rules led to a range of irreversible damage.
The second phase was from 1949 to the 1980s, when Chinese scholars began to take over the archaeological work in the Amur River basin. During this period, a large number of field surveys and some small-scale excavations were carried out under the guidance of the theory of cultural regionalism. Along some tributaries of the Amur River, several critical ancient sites from the Liao and Jin periods and the Balhae Kingdom period were investigated. Moreover, some specific sites with rich material remains were excavated, such as the Yinggeling site (3000 B.C.) and the Tuanjie site (2000 B.C.). However, the types of excavation were not comprehensive enough, and some critical technical archaeological methods were not used.
The third phase was from the 1980s to 2020s, when the third national census of cultural relics in China began and the awareness of archaeological research in frontier areas raised. A large number of habitation sites were excavated and studied under the guidance of processual archaeological theory. Many important archaeological programs, such as the research program on the Qixing River coastal settlement groups during the Han-Wei period [34], the sites of three capital cities of the Bohai kingdoms [35], the sites of the Khitan nomadic camps, and many other important settlement sites were carried out orderly [36]. In addition, international cooperation between Russia, Mongolia, and China has made it possible to study habitation sites in the surrounding areas of the Amur River Basin, which is essential to keep the regional integrity of this study.
Based on the research mentioned above, the collection of comprehensive data on the chronology, location, scale, and cultural composition of human habitation sites in the Amur River Basin is practicable. These information is essential for interpreting the spatial and temporal distribution of ancient habitation sites and the human-land relationship in them.
2.
Materials and method
2.1. The sources of archaeological information
The archaeology data of human habitation sites I adopted is mainly from The Atlas of Chinese Cultural Relics of Jilin, Heilongjiang provinces, and Inner Mongolia autonomous region volumes, and these atlases are compiled based on the second national archaeological field survey, launched and organized by the State Council of China in 1981. The other supplementary information derives mainly from The Unmovable Cultural Relics Directories, these directories were compiled according to results of the third national archaeology field surveys which started in 2007 and was the most comprehensive archaeology surveys in China, in which a lot of original information on the location, scale, material remains and dating of habitation sites was registered. The habitation sites included in the database only include those that have been discovered through archaeological survey, and do not include predictions of possible sites. The location accuracy of most sites is at the level of villages and streets, which are the smallest administrative units in China. The coordinates of the sites are then picked up through Google Maps, and some sites have precise GPS positioning coordinates, such as the Qixing River Site Group in the Sanjiang Plain [34]. Despite limitations in the accuracy of location coordinates and the dating of habitation sites, it provides the most authoritative information on ancient sites in the Amur River Basin and a basis for the study of habitation sites. More precise data information depends on future archaeological investigations with a larger scope and more refined methods.
The raster file of digital elevation model (DEM) is derived from the open-source data of geospatial data cloud website of Chinese Academy of Sciences (http://www.gscloud.cn/) with a horizontal resolution of 30 × 30 m. After mosaicking and clipping operations in ArcGIS 10.2 software, the digital elevation file of the Amur river basin with the latitude spanning 53°N-41°N and longitude spanning 115°E-135°E was obtained. On the basis of this elevation map, other georeferenced information and archaeology information could be loaded as new layers. Due to the lack of micro-scale remote sensing analysis in this article, medium-precision raster data is adopted, which is suitable for the research needs of macro-scale regions. In the future, more precise raster data will be essential for small-scale analysis, but without official open-source data, it will be more difficult to obtain.
The habitation sites used in this paper covered two main types. The first type is sites directly and closely related to ancient human habitation activities, it contains sites of ancient cities, ancient buildings and structures. The second type is human sites without obvious building remains within the site boundaries. The first type covered relatively stable human settlement sites, especially the existence of large cities and buildings is an important sign of long-term settled life; the second type covered unstable human activity sites with a large number of artificial remains in its scope, and the scale of habitation sites is often bounded by the distribution range of artificial remains. For the second type, if the site is large enough and densely occupied with relics, it is likely to be the result of settled life. Small and temporary habitation sites may also exist in small human sites, but the probability of their existence is much lower than that of large human sites, so these sites were excluded from the database. In this paper, according to the common way of dividing human settlement size in archaeological research [37], human sites with an area of more than 50, 000 m2 are considered as habitation sites. After selection and statistics, based on the above determination criteria, 1944 site points were obtained, which include almost all the habitation sites found in archaeological field surveys of the Amur River basin in China.
2.2. Research methods
In order to get a comprehensive understanding of the distribution situation and its evolution progress in different time and regions of the Amur river basin, we transformed the attribute data of 1944 points into vector data in ArcGIS 10.2 software and formed a spatial database of habitation sites of. After geographic coordinate transformation, these points were overlaid on the DEM (Digital elevation model) layer. By calculating and analyzing the quantities and densities of site points, it is applicable to obtain a spatial-temporal distribution of habitation sites. Then, spatial analysis tools of ArcGIS are adopted to study the distribution ways of site points in different periods and regions under different geospatial factors and reveal their integration patterns with water system, topographic landforms and other surface landscapes. Finally, the site points layers are overlaid with the vegetation resource layer and annual mean temperature layer to explain the coupling relationship between the habitation sites and the natural environment. The detailed data operation process and analysis steps is shown in Figure 2.
3.
Results
3.1. The temporal distribution characteristics of habitation sites in six periods
The chronology of habitation sites in the Amur River basin is mainly attributed to three archaeological phases: The Stone Age, the Bronze Age, and the Iron Age. Based on the archaeological theory of cultural zones or the perspective of the development level of iron handicrafts [10,11,12], scholars hold many different views on the division of Iron Age in this region. According to these views and historical background, the Iron Age in the Amur River basin could be further divided into four periods. The Early Iron Age corresponds to the Han-Wei periods (220 BC-AD 534), the Mature Iron Age corresponds to the Sui-Tang periods (AD 581-907), the Early Advanced Iron Age corresponds to the Liao-Jin periods (907-AD 1234), and the Late Advanced Iron Age corresponds to the Yuan-Ming-Qing periods (1271-1898AD). As shown in Figure 2, it reflects the spatial distribution pattern of habitation sites in six different periods in the Amur River basin.
Statistical analysis suggests that the total number of sites in the six periods shows a trend of growth followed by a decline, forming a clear cyclical development pattern. As shown in Table 1, the evolutionary process of habitation sites in the Amur River Basin can be grouped into six phases: The germination stage (Stone Age) - the development stage (Bronze Age) - the first peak stage (Early Iron Age) - the adjustment stage (Mature Iron Age) - the second peak stage (Early Advanced Iron Age) - the decline stage (Later Advanced Iron Age). The habitation sites in Stone Age are scattered mainly in the central region, and in the following Bronze Age, sites concentrated in the central and south-eastern regions. The Iron Age was a period of rapid development and exchange between the Amur River basin's ancient civilizations and the period with the most significant number and density of habitation sites. During the Early and Late Iron Age, the Yilou people and Mohe people established a large number of settlements in the north-eastern and central parts of the Amur River basin, forming the most densely area of sites distribution. As shown in Figure 4, an analysis of the density of habitation sites indicates that the density is close to 0.3 sites/km2 in middle and lower regions of the Qixing River in Sanjiang Plain, as well as close to 0.2 sites/km2 in parts of the Woken River and West Songhua River basins, and this high concentration of density is even higher than that of contemporary settlements. During the mature Iron Age, the Mohe people learned from central China and built a large number of cities in the south-eastern part of the Amur River basin with a density of 0.1sites/km2, and many of the large cities and palace sites could reflect the highest level of building technology in north-eastern China.
The cultural inheritance index is the proportion of the number of early sites with multiple cultural period properties to the total number of sites in a given area, indicating the degree to which the site had been continuously used in different historical periods, and aiming at assessing the inheritance degree of archaeological sites as well as the essential indicator of the stability of human settlements [13]. Corresponding to multi-cultural sites, single-cultural sites refer to sites that only contain cultural relics from a specific historical period, indicating that the site was only used during a specific historical period, and human culture at that time was not able to continue through these sites to subsequent eras. Based on this, the formula for calculating the cultural inheritance index of habitation sites in the Amur River Basin is summarized as Eq (1).
·CI means cultural inheritance index.
·Si-multi means the amount of multi-cultural habitation sites.
·Si-single means the amount of single-cultural habitation sites.
The cultural inheritance index for all the periods of habitation sites in the Amur River Basin is shown in Table 1. For the whole region, both the cultural inheritance index and the stability of sites are at a low level, with an average cultural inheritance index of 0.217 for the six different phases, meaning that only slightly more than 20% of early habitation sites were continued by later periods. The habitation sites of The Han-Wei and Liao-Jin periods account for over 80% of the total sites number, but nearly 90% of these sites were not continued by later generations. These indicators suggest that there was not a stable long-term settlement area for ancient humans in the Amur river basin, people at different times chose different habitation areas, and the spatial distribution of habitation sites was characterized by discontinuity. This situation is closely linked to the historical context of the nomadic fishing and hunting civilization that prevailed in the Amur River basin in ancient times, where mobility and migration in response to environmental resources contributed to the difficulty of anchoring human settlements.
Table 1 above contains the results of calculating the gravity center of habitation sites of six periods in the Amur River Basin. The gravity center of sites in a given area could represent the balanced and stable point of sites distribution, and the location of the gravity center depends on the average value of the x and y coordinates of all habitat sites. As shown in Figure 5, the center of gravity points for six periods, from the Stone Age to the Late Advanced Iron Age, were extracted by ArcGIS software and overlaid on the distribution map, which facilitates our understanding of site distribution trends and transfer paths across the different periods. In general, gravity centers of sites never appeared in the western and northern parts of the Amur River basin. Sometimes, for example in the Early and Mature Iron Age, gravity centers were in the eastern and southern parts of the basin, and in the other periods, the gravity centers were always in the central part. The location of gravity center indicates a flowing and changing trend, migrating from the central region to the north-eastern region first, and then from the south-eastern region to central region. This migration route of gravity center reflects the unbalanced spatial and temporal distribution of habitation sites. In most periods, the Songnun Plain in the central region was the main distribution area for sites with a higher cultural inheritance index than other areas, and other areas were only short periods of site concentration with a lower cultural inheritance index.
3.2. The spatial distribution of habitation sites in four geographical plates
Amur river basin is mainly constituted by four geography plates: The Songnen plain of the middle area, the eastern part of the Mongolian plateau, the Sanjiang plain of the east area, and the mountainous area along the coast in south east area, and the habitation sites in these plates is more than 90% of the total number. As shown in Figure 6 and Table 2, each of the four geographic plates has its own characteristic way of distributing sites: the highest number of habitat sites shows in the Songnen Plain, the highest concentration of habitat sites shows in the Sanjiang Plain, low quantity and density of sites is in other two plates.
As shown in Figure 6(a), the Songnun Plain, located in the heart of the Amur River Basin, is the largest part of the Northeast China Plain, and the habitation sites in this plate are mostly distributed along the large and small Xing'an Mountains, the Changbai Mountains, the Songhua River water system, and the Neng River water system. Among these areas, the second Songhua River system in west of the Changbai Mountains is the most densely settled area, as it is the black soil plain area with the most fertile soil in China, which could produce large ancient agricultural civilization. The dispersion and scarcity of habitation sites in the central part of the Songnen Plain relates to the ancient geographical condition, large inland lakes were spread out and unsuitable for ancient humans to live [38]. The chronologies of sites varies from the Paleolithic period to the late stage of advanced Iron age, and the site of Liaojin dynasties is more than 650, which was much higher and more concentrated than other periods, and these sites are mainly located along the Ash River and the West Songhua River, as this was the birthplace of the Jin dynasty, which had built a large number of human settlements there.
As shown in Figure 6(b), the Sanjiang Plain in the northeastern part of the Amur River Basin is surrounded by three long rivers and several mountains, with only one outlet to the outside world and the largest area of wetlands in China scattered in it. Habitation sites in this region are mainly located along the foothills of the Wanda Mountains in the central region, with the Qixing river and Woken River systems being the most densely settled areas. The habitation sites traced back to the Han-Wei period with more than 500 sites of this period, accounting for more than 80% of the total number of sites in this region. These habitation sites constitute the largest and densest cluster of human settlements of the Early Iron Age in the Amur River basin, and the sites of other eras are very rare. In a special historical and geographical context, these habitation sites remained isolated for a long period after their rapid emerging, making the cultural context of these sites homogeneous and clear. Archaeological work has shown that the spatial distribution of these sites has a clear tendency toward groups and communities, which are typical specimens for studying the early social structure in northeast frontier region of China [34].
As shown in Figure 6(c), the coastal mountains region in the southeastern part of the Amur River basin are mainly occupied by small plains and basins enclosed by the Changbai Mountain Range, which is bordered by the Sea of Japan in the south. The climate of this region is wetter and milder than other areas, and the geographical conditions also make it rich in fishing and hunting resources, thus making it more suitable for ancient human to produce and live. The Yilou and Mohe people of the Sushen nation had flourished here for a long period and created the Balhae kingdom civilization, which was the most prosperous culture in the Amur River basin. The mountainous terrain occupies most parts of this plate, so the mountain valley is the most densely distributed area of habitation sites, with a maximum density of 0.12 sites/Km2. More than 150 habitation sites in this plate could be dated back to the Balhae Kingdom period, and more than 50% of these sites located in the areas around the capital cities and along the transportation routes.
As shown in Figure 6(d), the eastern Mongolian plateau is located in the west of Amur river basin. Since the large Xing'an mountains lies between the Mongolian plateau and the Songnen plain, this plate becomes an independent space without geospatial connection to other plates in the Amur river basin. This region is mainly covered by mountainous terrain along the large Xing'an mountains and arid grassland landform of Hulunbuir plateau, under the limitations of resources and other natural geographical conditions, there did not appear any large-scale agriculture civilization historically, and nomadic civilization has always played a dominant role. Hence, habitation sites here are not as much as the plain areas, and the distribution pattern is also more disorganized and scattered. The ages of most habitation sites, distributed in the foothills area of the Large xing'an Mountains, date back to the Liao and Jin dynasties, accounting for nearly 60% of the total. The highest density area is on the east foothill area, with maximum density value of 0.09/Km2.
3.3. The coupling relationship between habitation sites and three main natural geographical conditions
3.3.1. Topography and hydrology
Elevation values were extracted from the overlay maps and Dem files for each site by ArcGIS software and the percentage of sites within the different elevation ranges were analyzed (Figure 7). The elevation values of habitation sites in the Amur River Basin were divided into five ranges. The elevation values of sites in eastern Mongolia and coastal mountainous areas are higher than those of other areas, with 44.8% and 30.5% of the elevation values of sites in eastern Mongolia at 300-500 m and above 500 m, and 46.4%, and 26.2% of the elevation values of sites in coastal mountainous areas at 200-300 m and 300-500 m. The elevation values of sites in the Sanjiang Plain and the Songneng Plain are relatively lower, with the number of sites below 200 m and below 300 m exceeding 80% and 95%. The variability in elevation distribution is related to the macroscopic topographic characteristics of the Amur River basin, where sites are mostly distributed in lower areas such as foothills and mountainsides in mountainous areas with higher average elevations [39]. In contrast, sites are primarily distributed in riverine terrace areas with relatively higher elevations in plain areas with lower average elevations.
The hydrological data of Amur River basin is derived from the Resource and Environment Science and Data Center of Chinese Academy of Science (https://www.resdc.cn/), and the original data is transformed to identifiable geospatial information data, then the shortest distances between habitation sites and rivers were extracted from the overlaid maps of sites and river systems in Arc GIS. As shown in Figure 8, the distance values of four different plates were extracted. The range of distance values could be divided into five different sections, with most sites less than 3 km from the rivers, and the number of sites decreasing as the distance from the river increases. Sites in the eastern Mongolia and coastal mountainous plate are closer to the river than other areas, with 34.45% and 31.10% of sites less than 1 km and 1-3 km in eastern Mongolia, and the corresponding proportion in coastal mountainous plates is 40.23% and 37.16%. Sites in the Sanjiang and Songnun Plains are further from the nearest river, with 21.48% and 13.72% of sites in the Sanjiang Plain distributed within a distance of 5-8 km and more than 8 km, and the corresponding proportions in the Songnun Plain are 20.64% and 18.28% respectively. The variability of distance values is closely related to the dependence level of settlements on water resources. Fishing and hunting civilization was the main mode of production of ancient humans in mountainous areas, and the dependence on water resources was much stronger, so the settlements in these areas were closer to water systems. Agricultural civilization was the main production method of ancient humans in the plains, and their demand for water resources was more flexible, the distance between dwelling places and water systems was more variable.
The slope value of habitation sites in four plates of the Amur river basin could be extracted by the overlaid maps of sites and topography in Arc GIS. As shown in Figure 9, the slope value was also divided into five different ranges, and the slope value of most sites is less than 2°or between 2° to 6°, indicating that the proportion of sites becomes smaller as slope values increase. The slope ranges of habitation sites in four plates is similar, with the proportion of sites slope values less than 6° exceeding 80%, the proportion of sites with slope values between 6° and 10° being about 10%, and the proportion of sites slope values between 10° and 15° and above 15° being less than 5%. The average slope of eastern Mongolia and coastal mountain region is slightly higher than that of the other two plain regions, but there is no significant difference on the slope value of sites between plain and mountain regions. The distribution characteristics of slope values indicate that ancient humans in the Amur River basin were unable to modify the original terrain and had to passively adapt to the natural terrain during the settlement construction process.
3.3.2. Land vegetation
The vegetation and climatic conditions is also closely related to the spatial distribution of habitation sites, and the surface of the Amur River basin is mainly covered by forests, grasslands, marshes, and cultivated land. As shown in Figure 10, the surface vegetation data was derived from the Resource and Environment Science and Data Center of Chinese Academy of Science(https://www.resdc.cn/), by overlaying the site layers and the surface vegetation layers in ArcGIS, the vegetation type of the point where the site is located can be extracted, and the proportion of single-cultural and multi-cultural sites in each vegetation type can be identified. As shown in Figure 11, the proportions of single-cultural sites and multi-cultural sites in the cultivated land area are 72.28% and 64.67%, respectively. In the grassland-covered areas, the corresponding proportions are 15.89% and 16.77%, respectively. In areas covered by woodlands, the corresponding proportions are 9.60% and 14.98%, respectively. In areas covered by marshland, the corresponding proportions are 2.23% and 3.60%, respectively.
Cultivated land is the most concentrated area of sites, because most of the cultivated vegetation in the Amur River basin is distributed in the plain areas, where there are enough resources for agricultural development and human settlement. The other forestland, grasslands and swamps areas cannot provide enough resources to reproduce numerous large-scale settlements; instead, the quantity and density of sites in these areas are smaller and can only accommodate the development of small-scale settlements provided by fishing, hunting and nomadic civilizations. In the forestland, grassland and swampland, where geographic conditions were suitable for military defense, settlements were more likely to be sustainable even in a historical context of frequent war and conflict, with a higher proportion of multi-cultural sites than single-cultural sites. In the plains covered by cultivated vegetation, the open geographical condition is difficult for military defense, and most settlements were destroyed during frequent wars, therefore, the proportion of single-cultural sites is slightly higher.
3.3.3. Thermal climate
Temperature is an essential factor influencing the distribution of settlements, the temperature data of the Amur river basin was also derived from the Resource and Environment Science and Data Center of Chinese Academy of Science (https://www.resdc.cn/). As shown in Figure 12, the annual average temperature map of the Amur River basin at 2 pm shows that most areas are below 4 ℃, and even some northern areas are above the permafrost line with annual average temperatures below 0 ℃. The area with an annual temperature above 4 ℃ is mainly in the central and southern parts, these areas could also receive abundant rainfall and solar radiation which makes it more suitable for ancient human to settle down, and more than 80% of the habitation sites located in these areas. Some parts of these regions, including the areas along the Second Songhua river and Mudan river, are the most concentrated areas of habitation sites.
There are far fewer sites in areas with average annual temperatures below 4℃ than that of warmer areas, especially in areas above the permafrost line, such as the foothills of the Large Xing'an Mountains and the eastern part of the Mongolian Plateau, there are almost no habitation sites, especially the multi-cultural sites, because the soil in these areas freezes all year round, and it is unsuitable for farming production and human settlement. However, the area around the middle and lower reaches of the Qixing River in the Sanjiang Plain, where the average annual temperature is slightly below 4 ℃, is one of the most concentrated areas of sites. The Qixing River Basin is located in the hinterland of the plains surrounded by the Wanda Mountains, the Ussuri River and the Songhua River. The enclosed geographical space surrounded by mountains and rivers constitutes a natural military defense barrier; the densely covered wetland water system, fertile arable land, and abundant fishing and hunting resources can provide sufficient living materials. These two factors are important guarantees for the emergence and continuation of large-scale ancient settlements.
The archaeological work on settlement sites of Han Wei period in the Qixing River Basin, which began in 2008, has investigated and excavated more than 400 sites, accounting for more than 50% of the ancient settlement sites in the Sanjiang Plain. These sites are usually distributed along rivers or around hills, forming highly clustered groups, and most of the groups have large core sites in the middle area, indicating that there may have been a tribal city-state political structure at that time [34,39]. These site emerged and vanished suddenly during Han-wei period, without any credible archaeological evidence to prove that the temperature in the Sanjiang Plain was higher during the Han-Wei periods than it is now, so we can infer that human civilization with large-scale and high-density could also be bred in these colder areas.
4.
Discussions
In this paper, the spatial and temporal distribution characteristics of habitation sites in the Amur River basin are described and interpreted. With the basic information of 1944 sites and geospatial analysis, several values of distribution features were drawn and a series of distribution maps were created. The coupling relationship between sites and topographic, hydrological, vegetation, and temperature was revealed, as well as calculations including density, proportion, distances, and so on, opens a broad, long-term perspective on the evolution of habitation sites and allows some conclusions to be drawn as follows.
In terms of distribution pattern, the habitation sites in Amur River basin are mostly derived from six archaeological periods and four geographical plates. The temporal distribution indicates periodic and lagging characteristics, and its evolutionary process can be summarized into six stages with different distribution pattern and coupling relationship with geographic environment (Table 3). The Han-Wei and Liao-Jin periods are two peak stages when habitation sites concentrated in Sanjiang plain and Songnen plain with maximum values of quantity and density. The spatial distribution shows an obvious characteristic of regionalization and non-uniformity, with the gravity centers of sites in different stages have been always shifting and changing, and among the six archaeological periods, four centers concentrated in the central region and the other two centers of Han-Wei and Balhae state period distributed in the northeast and southeast of the Amur River basin.
Based on the similar productive and defensive needs, the ancient settlements in the Amur River basin have certain similarities in their integration with the geography condition. Most of these sites are concentrated at the junction of plains and mountains, and close to rivers, with average annual temperatures above 4 ℃. However, due to the geographical environmental differences between the four geospatial plates, there are also some differences in the coupling patterns of settlement with topography, climate, and vegetation conditions. Most agricultural sites are bred in the cultivated areas of warm regions, and most nomadic sites are bred in the woodlands, grasslands or swamplands of low-temperature regions, but there are almost no large settlements in extreme climate zones with permafrost.
In addition to the above factors, some sudden extreme environmental factors also have a significant impact on the spatial and temporal distribution of habitation sites, such as extreme drought and cold climate, sudden infectious or biological diseases, which can lead many people to leave their original settlements and migrating to other regions. From the distribution trend presented by the site data in the Amur River Basin, there is also a tendency for the spatial center of gravity to shift and the continuity of time to break in different periods. For example, for the four site groups in the Sanjiang Plain of the early Iron Age (Figure 13), their number and density of sites reached a peak during the Han and Wei Dynasties, and these sites were suddenly abandoned, including the huge imperial city with nine districts and an area of over 1.2 million m2; the city was not reused by subsequent ethnic groups, and the spatial center of habitation sites in the Amur River Basin also shifted to the adjacent Songnen Plain [39]. This change may be related to the above-mentioned extreme climatic conditions or sudden environmental changes, but the definitive answer depends on more detailed evidence from environmental archaeology.
From a cultural and social perspective, the distribution of habitation sites in the Amur River Basin is more complex. The central part of the Songnen plain and the western part of the Sanjiang plain constitute agricultural settlement regions, while the surrounding areas are the nomadic and hunting cultural regions (Figure 14). The opposition of nomadic and agricultural settlements played an important role in the forming process of spatial and temporal distribution of habitation sites in the Amur River Basin. On the one hand, the confrontation between nomadic and agricultural settlements promoted the emergence of garrison settlements, and many defensive settlements appeared in the border areas between agriculture and nomadism, such as along the Great Wall in the eastern foot of the Greater Khingan Mountains. During the confrontation between the Yuan Empire in the eastern part of Mongolia plateau and the Jin Empire in the Songnen Plain, many fortified fortresses appeared. On the other hand, there were no native farming peoples in the Amur River Basin. The indigenous peoples engaged in large-scale agricultural activities had transformed from early nomadic and hunting people, which led to agricultural settlement sites contains nomadic and hunting cultural factors. However, most of the time, the two were mixed together without clear boundaries. Even during the period when agricultural civilization dominated, nomadic patterns also remained an important complement to agricultural settlement. The development and growth of agricultural settlement culture required the protection of nomadic culture. For example, during the period of the Balhae state period (698-926 AD), the agricultural settlement pattern represented by large-scale plain cities could only develop safely under the protection of surrounding mountain cities in vast nomadic areas, but the elaborate and deepening development of agricultural settlement was also hindered by nomadic culture.
From the perspective of regional comparison, Xinjiang Province and the Amur River Basin in China are two regions with similar cultural and geographical attributes. Both are located in cold border areas at almost the same latitude, and there are both farming and nomadic culture zones, as well as characteristics of ancient ethnic diversity. Affected by environmental changes and the construction of the ancient Silk Road, the spatial distribution of habitation sites in Xinjiang Province showed a shift from the north to the south, and then to the north, and the change in the number of sites was not a continuous growth or decline process [40,41]. These spatial and temporal distribution characteristics were similar to habitation sites in the Amur River Basin which was more complex, mostly manifested in the irregularity, suddenness, and fluctuation of changes in the number and location of archaeological sites. The above-mentioned characteristics were more evident when compared with habitation sites in the southern Central Plains and eastern coastal areas of China. The distribution of habitation sites in the latter two regions was more closely related to the water system network, with a more stable temporal distribution, a more balanced spatial distribution, and a smaller range of changes and fluctuations in the number of sites [10,42]. From the perspective of comparing ancient and contemporary times, the circular area around the site with a radius of a given distances is the targeted area of ancient human activity, and the proportion of these areas to the whole area defines the land use efficiency of the whole area [43]. As shown in Figures 15 and 16, the land use patches of ancient and contemporary settlements were extracted in ArcGIS with the settlements as centers and with a radius of 12 km. The calculation results show that the ancient and contemporary areas of land using account for 25.83% and 46.29% of the whole Amur River basin area respectively. This data indicates that ancient humans in the Amur River Basin had much less intensity in developing geographic space than contemporary development. When the ancient ethnic groups of the Amur River had relatively weak adaptability to the natural environment, they were more cautious in choosing their place of residence. Except for some low temperature areas of high latitude and some mountainous areas, the patch area of ancient settlements covers most patches area of contemporary settlements, indicating that under the constraints of similar natural environment in the same region, there are many similarities between ancient and contemporary settlements in terms of geospatial utilization and location selecting methods, and the macro trend of human-land coupling relationship is relatively stable. In contrast to the traditional view that ancient human settlement patterns in the Amur River basin are characterized by variability and uncertainty, this paper concludes that human-land relations in the cold frontier region of high latitude could be maintained in balance and stability, if measured from a long-term perspective.
Due to the limitations of archaeological materials and research methods in this study, several relevant questions about habitation sites of the Amur river basin remain unanswered. The Amur River basin has long been a northern frontier region of China, and the spatial-temporal evolutionary process of the habitation sites is different from that of other regions of China. Under the influence of many factors, the unstable and diversified evolutionary features are prominent. In order to explain these special phenomena, we need to integrate more anthropological approaches to archaeological findings, which is the next key point to focus on. Especially, the anthropological progress in the following three aspects will provide support for further explanation of habitation sites in the Amur River Basin. First, by the technical means of physical anthropology, biological fragments with genetic information could be extracted from sites to determine which ancient human ethnic group the site belongs to, providing a basis for site type classification and ethnic origin interpretation. Second, by the method of ethnoarchaeology, the morphological characteristics of habitation sites and modern human settlement could be correlated and compared, then analyzing similarities and differences in the organizational forms to determine the inheritance and change characteristics in the evolution process. Third, by environmental archaeology techniques, the correlation between ancient human settlement sites and surface environmental changes could be explored, such as using plant fossils from sites to restore ancient surface vegetation, and then interpreting the relationship between human settlement and landscape environment.
Use of AI tools declaration
The author declares that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgements
Thank the Institute of Chinese Architectural History and Cultural Heritage Preservation of Harbin Institute of Technology for helping me on data collection and analysis. This project was supported by Social Science Planning Office of Guangdong province China [No.GD21YDXZSH01], the project of social Science for youth of Chinese ministry of education [23YJCZH142], research on innovation of online open course design in undergraduate universities in Guangdong Province [2022ZXKC164], Shantou University Scientific Research Fund [NTF21028, 470-0441182121].
Conflict of interest
There are no conflicts of interest.









 DownLoad:
DownLoad:


















