Generalized high-order iterative methods for solutions of nonlinear systems and their applications

1.   Introduction

The pursuit of constructing fixed-point iterative techniques for the solution of nonlinear equations or systems of nonlinear equations stands as a compelling and formidable challenge within the domains of numerical analysis and various applied sciences. The significance of this topic has led to the development of numerous numerical techniques, often employing iterative approaches, to yield highly precise approximate solutions for systems of nonlinear equations, represented as follows:

where $\Omega:\mathbb{D}\subseteq \mathbb{X}\to \mathbb{Y}$, with $\mathbb{X}$ and $\mathbb{Y}$ as Banach spaces, is continuously Fréchet-differentiable; and $\mathbb{D}$ is a non-empty open convex subset of $\mathbb{X}$.

One of the most prevalent iterative approaches for determining the solution $\alpha$ of (1.1) is the well-established quadratically convergent one-point Newton method ^[1], which is outlined below:

where $\Omega'(s_n)^{-1}$ denotes the inverse of the first Fréchet derivative $\Omega'(s_n)$ of the function $\Omega(s_n)$. The method's convergence relies on two crucial prerequisites. First, the initial approximation $s_0$ must be in close proximity to the desired solution $\alpha$, and second, the existence of the inverse $\Omega'(s_n)^{-1}$ of the derivative must be ensured within the neighborhood $\mathbb{D}$ centered around $\alpha$.

In pursuit of achieving a higher order of convergence, scientific literature has introduced a range of modifications to Newton's method, referred to as Newton-like techniques. These strategies have been explored extensively in both univariate and multivariate scenarios, with comprehensive discussions available in References ^{[2,3,4,5,6,7,8,9,10,11,12]} and associated citations. One of the earliest and notable yet simple modifications to Newton's method is the cubically convergent Potra-Pták method (PPM3)^[13], which is given below:

However, achieving the enhanced convergence order in (1.3) involves incurring an additional computational cost in the form of an extra function evaluation, $\Omega(y_n)$.

An interesting new development in the field is the hybridization of iterative techniques and optimization algorithms. Several optimization algorithms, including the butterfly optimization algorithm ^[14] and the sperm swarm optimization algorithm ^[15], have been applied to solve problems involving systems of nonlinear equations. However, optimization algorithms often lack accurate solutions due to their limitations, including falling into local optima and divergence problems. Only a few researchers have attempted to combine iterative methods with optimization algorithms. Recently, Sihwail et al. ^[16] and Said Solaiman et al. ^[17] proposed new hybrid algorithms by combining iterative methods and optimization algorithms for the purpose of solving systems of nonlinear equations. These hybrid approaches leverage the benefits of both methods while overcoming their drawbacks.

Aiming to contribute to this evolving landscape, we propose multipoint iterative techniques that progressively increase convergence orders while minimizing function evaluations and inverse operators. Initially, we introduce a family of three-step schemes with sixth order of convergence and then generalize it to a scheme of convergence order $p+3$. The first two steps are akin to Newton-like iterations with a convergence order of $p$ (where $p\geq3$). Building on this, we present a more generalized $(m+2)$-step scheme with an increased convergence order of $p+3m, \ m\in\mathbb{N}$. In fact, we can achieve a threefold increase in convergence order by adding only one more function evaluation for each additional step.

The subsequent sections of this paper are structured as follows. Section 2 introduces a three-step method and establishes its convergence, achieving a sixth order of convergence. Section 3 presents a generalized version of the family of methods with convergence order $p+3$, which is then further extended to an $(m+2)$-step scheme with a convergence order of $p+3m$, $m\in\mathbb{N}$. Section 4 presents a comprehensive analysis of the local convergence properties. Section 5 offers numerical examples to validate our theoretical results. Again, Section 6 applies these methods to tackle systems of nonlinear equations. Section 7 presents a graphical analysis of the dynamical behaviours of our newly proposed methods, comparing them with existing methods through the lens of their basins of attraction on the Cartesian plane. Finally, Section 8 includes some concluding remarks.

2.   Description of the proposed iterative scheme

In this section, we aim to develop new families of iterative methods of order six for the purpose of solving systems of nonlinear equations. First, we present a three-step scheme as follows:

where $k_1, k_2, k_3$, and $k_4$ are free parameters to be determined in the sequel.

To obtain the convergence order of (2.1), we first recall the following result of the Taylor's expansion on vector functions (see ^[1]).

Lemma 2.1. Let $\Omega\colon \mathbb{D}\subseteq \mathbb{R}^n\to \mathbb{R}^n$ be a $p$ time Fréchet-differentiable function with $\mathbb{D}$ as a convex set; then, for any $s, h\in \mathbb{R}^n$, we have

where $\lVert R_p\rVert\leq\frac{1}{p!}\sup\limits_{0\leq t\leq1}\lVert \Omega^{(p)}(s+th)\rVert\lVert h\rVert^p$ and $h^p = (h, h, h, \overset{p}{\dots}, h)$.

Theorem 2.1. Suppose that the function $\Omega\colon \mathbb{D}\subseteq \mathbb{R}^n\to \mathbb{R}^n$ is sufficiently Fréchet-differentiable in a neighborhood $\mathbb{D}\subseteq \mathbb{R}^n$ which contains the root $\alpha$ of $\Omega(s) = 0$. Assuming that $\Omega'(\alpha)$ is nonsingular, the sequence $\{s_n \}_{n\geq 0} (s_0\in \mathbb{D})$ produced by the family of methods given by (2.1) converges to the actual solution $\alpha$ with a convergence order of 6 if $k_2 = \frac{2+k_1}{4}, k_3 = \frac{2-k_1}{4}$, and $k_4 = -2k_1, k_1\in\mathbb{R}$. And, it satisfies the error equation given by

Proof of Theorem 2.1. The expansion of $\Omega(s_n)$ by using Taylor's series expansion given by (2.2) near $s = \alpha$ gives

where $C_j = \frac{1}{j!}\Omega'(\alpha)^{-1}\Omega^{(j)}(\alpha)$, $\varepsilon_n = s_n-\alpha$, and $\varepsilon_{n}^{i} = (\varepsilon_{n}, \varepsilon_{n}, \overset{i}{\dots}, \varepsilon_n)$, $\varepsilon_n\in \mathbb{R}^n$.

Then, it is straightforward to obtain

where $K_i$ depends on $C_2$, $C_3$, $...$, $C_7$, i.e., $K_1 = -4(2C_{2}^{3}-3C_2C_3+C_4)$, $K_2 = 16C_{2}^{4}-36C_{2}^{2}C_3+9C_{3}^{2}+16C_2C_4-5C_5$, etc.

Using (2.4) and (2.6), we have

where $M_i$ depends on $C_2, C_3, ..., C_6$, i.e., $M_1 = 4C_{2}^{3}+3C_4-7C_2C_3$, $M_2 = -8C_{2}^{4}+20C_{2}^{2}C_3-6C_{3}^{2}-10C_2C_4+4C_5$, etc.

By using (2.2) and (2.7), the expansion of $\Omega(y_n)$ gives

where $N_i$ depends on $C_2, C_3, ..., C_6$. Then, from (2.8), it follows that

where $P_i$ depends on $C_2, C_3, ..., C_6$. Also,

where $Q_i$ depends on $C_2, C_3, ..., C_6$.

Now, replacing the values of (2.4)–(2.7), (2.9), and (2.10) in the second step of (2.1), we get

where $R_i$ depends on $C_2, C_3, ..., C_6$. Then, by using (2.2), (2.11) becomes as follows:

where $S_i$ depends on $C_2, C_3, ..., C_6$.

Incorporating the values from (2.5), (2.6), and (2.9)–(2.12) in the concluding step of (2.1), we arrive at the error equation as follows:

where $T_i$ depends on $C_2, C_3, ..., C_6$, i.e.,

$T_1 = \frac{1}{2}(-(2(-1+k_1+k_2+k_3)+k_4)+(-3+3k_1+k_2+5k_3+k_4)C_2C_3-(2(-1+k_1+k_2+k_3)+k_4)C_4)$, $T_2 = \frac{1}{8}\Big(4(-8+8k_1+4k_2+12k_3+3k_4)C_2^4-4(13k_1+5(-3+k_2+5k_3)+4k_4)C_2^2C_3+3(-8+8k_1+4k_2+12k_3+3k_4)C_3^2$+$4(-4+4k_1+8k_3+k_4)C_2C_4-6(2(-1+k_1+k_2+k_3)+k_4)C_5\Big)$, etc.

Finally, by substituting $k_2 = \frac{2+k_1}{4}, k_3 = \frac{2-k_1}{4}$, and $k_4 = -2k_1$ in the above error (2.13), we get

As a result, the proof has been successfully established. □

Now, upon substituting the values of the parameters $k_1, k_2, k_3$, and $k_4$, the proposed sixth-order family of methods derived from (2.1) can be formulated as follows:

where the free parameter $k\in\mathbb{R}$. We shall denote it by PFM6.

3.   Generalization of the proposed scheme

3.1.   The iterative methods with a $p+3$ order of convergence

Our objective here is to generalize the proposed family of methods given by (2.14) by establishing a universal principle that is capable of enhancing lower-order methods with convergence order $p\geq3$. Through this approach, we aim to achieve an improvement of order $p+3$.

The generalized method is characterized by the following construction:

Here, the parameters $k_1, k_2, k_3$, and $k_4$ will be determined later. It is worth noting that $z_n = \mu_p(s_n, y_n)$ represents the iteration function with a convergence order of $p\geq3$.

Theorem 3.1. Suppose that $\Omega:\mathbb{D}\subseteq\mathbb{R}^n\to\mathbb{R}^n$ is a sufficiently Fréchet-differentiable function in a neighborhood $\mathbb{D}\subseteq\mathbb{R}^n$ which contains the root $\alpha$ of $\Omega(s) = 0$. Assuming that $\Omega'(\alpha)$ is nonsingular, the sequence $\{s_n\}$ generated by method (3.1) for $s_0\in\mathbb{D}$ converges to $\alpha$ with order $p+3$ for $p\geq3$, provided that $k_2 = \frac{2+k_1}{4}, k_3 = \frac{2-k_1}{4}$, and $k_4 = -2k_1$.

Proof of Theorem 3.1. We consider all of the assumptions made in Theorem 2.1; using (2.5), (2.6), (2.9), and (2.10), we have

Furthermore, by considering the iteration function $z_n = \mu_p(s_n, y_n)$ with convergence order of $p$, we can introduce the following definition:

Then, using (2.2) and (3.3), the expansion of $\Omega(z_n)$ about $\alpha$ is obtained as follows:

Now, using (3.2)–(3.4) in the last step of (3.1), we obtain the error equation as follows:

For $p\geq3$, the method (3.1) exhibits convergence to the root $\alpha$ with an order of $p+3$ if and only if the constants $k_1, k_2$, and $k_3$ satisfy the following system:

The only solution of the above system (3.6) is as follows: $k_2 = \frac{2+k_1}{4}, k_3 = \frac{2-k_1}{4}$, and $k_4 = -2k_1$. By substituting $k_1 = k$, the error Eq (3.5) reduces to

Hence, the theorem is proved. □

Here, it is worth highlighting that, based on the proof of Theorem 3.1, we can readily derive the following significant results:

Corollary 1. When considering a special case of $k = k_1 = 0$, solving the system (3.6) yields that $k_2 = k_3 = \frac{1}{2}$. Thus, the proposed approach given by (3.1) is reduced to the following construction given by

where $y_n, z_n$ are defined as given in (3.1). In fact, the above construction (3.8) was the technique introduced by the authors of ^[18] in the year 2018.

Remark 1. A particular case of the above approach given by (3.8) is the following sixth-order method developed by Sharma et al. ^[19] in the year 2019. We shall call it the Sharma-Sharma-Karla method (SSKM6).

Corollary 2. When considering the special case of $k = k_1 = 2$, solving the system (3.6) yields that $k_2 = 1, k_3 = 0$, and $k_4 = -4$. Thus, we obtain the following approach given by

Also, by considering the special case of $k = k_1 = -2$, solving the system (3.6) yields that $k_2 = 0$, $k_3 = 1$, and $k_4 = 4$. Then, we obtain the approach given by

Remark 2. Applying (3.10) to the third-order method of Liu et al. ^[20], developed in 2016, gives the following new sixth-order method, which is denoted by PFM6.1:

where $u_n = \frac{s_n+y_n}{2}$ and $v_n = \frac{y_n-s_n}{2\sqrt{3}}$.

Also, applying (3.11) to the third-order method of Sharma and Gupta ^[21], developed in 2013, gives the following new sixth-order method denoted by PFM6.2.

3.2.   The extended method consisting of $(m+2)$ steps

The extended form of the method given by (3.1), involving $(m+2)$ steps, can be represented as:

where $m\in\mathbb{N}$, $z_n^{(0)} = z_n$ and $\Psi(s_n, y_n) = \big(kI+\left(\frac{2+k}{4}\right)\Omega'(y_n)^{-1}\Omega'(s_n)+\left(\frac{2-k}{4}\right)\Omega'(s_n)^{-1}\Omega'(y_n)-2k(\Omega'(s_n)+\Omega'(y_n))^{-1}\Omega'(s_n)\big)\Omega'(y_n)^{-1}$.

Theorem 3.2. Given the assumptions of Theorem 3.1, the sequence $\{s_n\}$ generated by employing the method given by (3.14) with an initial value of $s_0\in \mathbb{D}$ achieves convergence toward $\alpha$ with a convergence order of $p+3m$ for cases in which $p\geq3$ and $m\in \mathbb{N}$.

Proof of Theorem 3.2. Considering the expression given in (3.2), it follows that

Utilizing Taylor's series, we can express the expansion of $\Omega(z_n^{(m-1)})$ around $\alpha$ as follows:

Then, it follows from (3.15) and (3.16) that

By applying (3.17) in the concluding step of (3.14), we acquire the following:

Referring to (3.7), it is evident that $z_n^{(1)}-\alpha = \big((4-k)C_{2}^{3}-2C_2C_3\big)\varepsilon_{n}^{p+3}+O(\varepsilon_{n}^{p+4})$. Consequently, applying (3.18) with $m = 2, 3,$ we derive the following:

Continuing by the process of induction, we obtain

This concludes the proof of Theorem 3.2. □

Remark 3. Applying the construction given by (3.14) for $m = 2$ to the Potra-Pták method described by (1.3) ^[13] of third order yields the following newly extended family of ninth-order method (PFM9).

4.   Local convergence analysis

In this section, we extend the local convergence analysis of (2.14) (PFM6) from Section 2 to the Banach space setting. To analyze this local convergence under the Lipschitz continuity condition, we make the following assumptions on all real numbers $\kappa_0 > 0$, $\kappa > 0$, and all points $s, y\in\mathbb{D}$:

where $\mathcal{L}(\mathbb{Y}, \mathbb{X})$ represents the set of linear bounded operators from $\mathbb{Y}$ to $\mathbb{X}$.

Lemma 4.1. Under the assumption that operator $\Omega$ satisfies conditions (4.1) and (4.2), the following inequalities hold for all points $s\in\mathbb{D}$:

Proof of Lemma 4.1. By applying condition (4.1), we obtain:

Again, by virtue of the mean value theorem, it follows that:

□

The following Theorem 4.1 provides the local convergence analysis of the considered scheme (2.14) (PFM6) under the Lipschitz continuity condition.

Theorem 4.1. Let $\Omega:\mathbb{D}\subseteq \mathbb{X}\to\mathbb{Y}$ be a Fréchet differentiable operator. Suppose that there exist $\alpha\in\mathbb{D}$ and $k\in(-\infty, +\infty)$ such that conditions (4.1) and (4.2) are satisfied and B$(\alpha, \rho)\subseteq\mathbb{D}$, where $\rho$ is to be determined. Then, the iterative sequence $\{s_n\}$ produced by PFM6 (2.14), starting from $s_0\in B(\alpha, \rho)$, remains in $B(\alpha, \rho) \; \forall \ n\geq0$, and converges to $\alpha$. Futhermore, the following inequalities hold for all $n\geq0$:

where the functions represented by $\eta_i$ are to be defined. Additionally, if there exists $R\in[\rho, \frac{1}{\kappa_0})$ such that B$(\alpha, R)\in\mathbb{D}$, then the limit point $\alpha$ is the unique solution in B$(\alpha, R)$.

Proof of Theorem 4.1. Given that $s_0\in\mathbb{D}$, and by assuming that $\Vert s_0-\alpha\Vert < \frac{1}{\kappa_0}$, (4.1) gives

Consequently, by applying the Banach lemma on invertible operators, $\Omega'(s_0)^{-1}$ exists, and it follows that

Therefore, $y_0$ is well defined. Now, considering the first sub-step of (2.14) for $n = 0$, we obtain

Taking the norm on both sides and using (4.2) and (4.8), we obtain

where

We define the function $\omega_1(\vartheta) = \eta_1(\vartheta)-1$. Since $\omega_1(0) < 0$ and $\omega_1(\frac{1}{\kappa_0})\to +\infty$, the intermediate value theorem guarantees that at least one root of $\omega_1(\vartheta)$ exists in the interval $(0, \frac{1}{\kappa_0})$. Let $\rho_1$ represent the smallest root of $\omega_1(\vartheta)$ within this interval. Then, we obtain

Applying (4.9) and (4.10), we arrive at the following result:

Since $y_0\in\mathbb{D}$, by using the assumption (4.1), we can deduce that

As a result, by virtue of the Banach lemma about invertible operators, $\Omega'(y_0)^{-1}$ exists and

Hence, $z_0$ is well-defined. As such, from (2.14) for $n = 0$, we have

where

We define the function $\omega_2(\vartheta) = \eta_2(\vartheta) - 1$. Clearly, there is at least one root of $\omega_2(\vartheta)$ in the interval $(0, \rho_1)$ since $\omega_2(0) < 0$ and $\omega_2(\rho_1) > 0$. Let $\rho_2$ denote the smallest root of $\omega_2(\vartheta)$ within this interval. Then, we obtain

Now, applying (4.12) and (4.13), we arrive at the following result:

Moreover, by using (4.1) and (4.10), we have

Consequently, by applying the Banach lemma on invertible operators, $\big(\Omega'(s_0)+\Omega'(y_0)\big)^{-1}$ exists and

Accordingly, $s_1$ is well-defined. As such, from (2.14) with $n = 0$, we have

where

Let us define the function $\omega_3(\vartheta) = \eta_3(\vartheta)-1$. It is evident that, with $\omega_3(0) < 0$ and $\omega_3(\rho_2) > 0$, there exists at least one root of $\omega_3(\vartheta)$ in the interval $(0, \rho_2)$. Let $\rho$ represent the smallest root of $\omega_3(\vartheta)$ within this interval. Then, we obtain

Now, applying (4.15) and (4.16), we arrive at the following result:

It follows that the theorem is valid for $n = 0$. By repeating the computations above with $s_n$, $y_n$, $z_n$, $s_{n+1}$ respectively replacing $s_0$, $y_0$, $z_0$, $s_1$, the induction will be completed and we can establish the inequalities detailed in (4.5)–(4.7). Additionally, based on the estimate $\Vert s_{n+1}-\alpha\Vert\leq\Vert s_n-\alpha\Vert < \rho$, we conclude that $s_{n+1}\in B(\alpha, \rho)$. Evidently, the function $\eta_3$ is increasing in its domain; so, we have

Using $\lim_{n\to\infty}\eta_3(\vartheta)^{n+1} = 0$, we obtained that $\lim_{n\to\infty} s_n = \alpha$; hence, the method tends to the solution.

To establish the uniqueness aspect, consider that $\alpha^{*}\in B(\alpha, \rho)$, where $\alpha^{*}\neq\alpha$ and satisfies the condition that $\Omega(\alpha^{*}) = 0$. Let $T = \int_{0}^{1}\Omega'(\alpha^{*}+\vartheta(\alpha-\alpha^{*})) d\vartheta$. Then, by using (4.1), we have

Hence, $T^{-1}$ exists, and by utilizing the following identity:

we deduce that $\alpha = \alpha^{*}$. □

5.   Numerical results

In this section, we will use a series of numerical examples to show how well our local convergence analysis works for the proposed method PFM6 (2.14).

To begin with, we will determine the radius of convergence for each example and subsequently compare our method with several established alternatives found in the literature. Specifically, we will focus on two sixth-order convergence schemes (schemes (1.2) and (1.3) from ^[22]) and one fifth-order convergence scheme (scheme from ^[23]). We will refer to these schemes as M1, M2, and M3, respectively.

Example 1. ^[24] Let us consider $\tau$ defined over the interval $\mathbb{D} = [-\frac{1}{2}, \frac{5}{2}]$ by

The zero of $\tau$ is $\alpha = 1$. Also, we have

Although the third derivative of $\tau$ is unbounded on $\mathbb{D}$, the iterative method given by (2.14) still converges, according to Theorem 4.1 with $\alpha = 1$. We found that $\kappa_0 = \kappa = 96.662907$. By setting $k = 0.1$, we calculate the radius of convergence as follows:

The comparison results for the radii of convergence are displayed in Table 1.

Example 2. ^[24] Consider a system of differential equations governing the dynamics of an object. These equations are given as follows:

with the initial conditions $\tau_1(0) = \tau_2(0) = \tau_3(0) = 0$. These equations can be collectively represented as the vector $\tau = (\tau_1, \tau_2, \tau_3)$. Let $\mathbb{X} = \mathbb{Y} = \mathbb{R}^3$ and $\mathbb{D} = \mathbb{\bar{B}}(0, 1)$. Define $\tau$ on $\mathbb{D}$ for $\nu = (\omega_1, \omega_2, \omega_3)^T$ by

The Fréchet derivative is given by

For $\alpha = (0, 0, 0)^T$, $\tau'(\alpha) = \tau'(\alpha)^{-1} = diag\{1, 1, 1\}$, and $\kappa_0 = e-1$, $\kappa = e^{\frac{1}{e-1}}$, and taking $k = 0.1$, we get

The comparison results for the radii of convergence are displayed in Table 1.

Example 3. ^[24] (Also, see ^[23] for details) Let $\mathbb{X} = \mathbb{Y} = C[0, 1]$ and the space of continuous functions defined on $[0, 1]$ be equipped with the max norm, and let $\mathbb{D} = B(0, 1)$. Consider the nonlinear integral equation of the Hammerstein type $\tau$ defined on $\mathbb{D}$ by

with $\nu(s)\in C[0, 1]$. The first derivative of $\tau$ is given by

For the solution $\alpha = 0$, we obtain that $\kappa_0 = 7.5$ and $\kappa = 15$. Then, using the iterative method given by (2.14) for $k = 0.1$, we get the radii of convergence as follows:

The comparison results for the radii of convergence are displayed in Table 1.

As evident from the data presented in Table 1, the proposed family of methods given by PFM6 (2.14) exhibits a significantly broad convergence radius. Moreover, across all three examples, it is consistently observed that PFM6 (2.14) outperforms the other three methods by exhibiting a notably larger convergence radius.

6.   Applications

In this section, we apply the proposed method PFM6 (2.14), along with PFM6.1 (3.12), PFM6.2 (3.13), and PFM9 (3.22) to solve systems of nonlinear equations in $\mathbb{R}^n$; we also compare their performance to the existing methods given by PPM3 (1.3) and SSKM6 (3.9). Also, the following two methods are considered for the comparison.

The sixth-order method established by Lotfi et al. in ^[25] (TLM6):

The ninth-order method established by Lotfi et al. in ^[25] (TLM9):

All computations were performed in the Mathematica 12.2 programming package by using multiple-precision arithmetic with 1000 significant digits. For each problem, we recorded the number of iterations ($n$) needed to converge to the root such that the stopping criterion $\Vert \Omega(s_n)\Vert < 10^{-100}$ is satisfied. Numerical tests were conducted for the following set of problems:

Problem 1. A nonlinear system with two unknowns is given by

By taking $s_0 = (-1, -1)^T$ as the initial approximation, we arrive at the root:

$\alpha = (0.367758471822148, 0.458483793003288)^T.$

Problem 2. A nonlinear system with three unknowns is given by

By choosing $s_0 = (1, 1, 1)^T$ as the initial approximation, we get the root:

$\alpha = (0.351733711249196, 0.351733711249196, 0.351733711249196)^T$.

Table 2 provides a comprehensive overview of the comparison results for the various methods applied to the test problems. The table shows the residual error (i.e., $\Vert \Omega(s_n)\Vert$), the error in the consecutive iterations $\Vert s_n-s_{n-1}\Vert$, and the approximated computational order of convergence (COC) after the methods satisfy the stopping criterion. The COC is calculated as follows ^[26]:

Moreover, the order of convergence can be confirmed through the analysis of the asymptotic behavior of the convergence rate, i.e., the asymptotic error constant ($\mu$), by using the following formula ^[26]:

Furthermore, we provide in Table 3 a comparison of the CPU time (measured in seconds) required by each method to meet the stopping criterion. We averaged the CPU running time over three trials to improve accuracy. All computations were carried out on a computer equipped with an Intel^(R) Core^(TM) i5-10210U CPU @ 2.11 GHz and 8 GB of RAM running Windows 11.

Our numerical results, as presented in Tables 2 and 3, demonstrate that the proposed methods exhibit highly competitive performance. They converge rapidly toward the root in the smallest number of iterations ($n$), achieve better accuracy in terms of minimal residual error ($\Vert \Omega(s_n)\Vert$) and the error in the consecutive iterations $\left(\Vert s_n-s_{n-1}\Vert\right)$, and consume less CPU time than well-known existing methods. Additionally, the computed COC aligns with the theoretical convergence order for the newly proposed methods.

7.   Basins of attraction

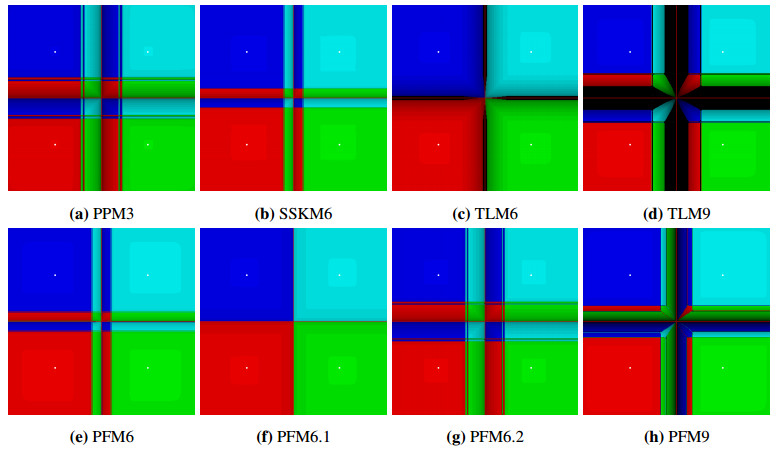
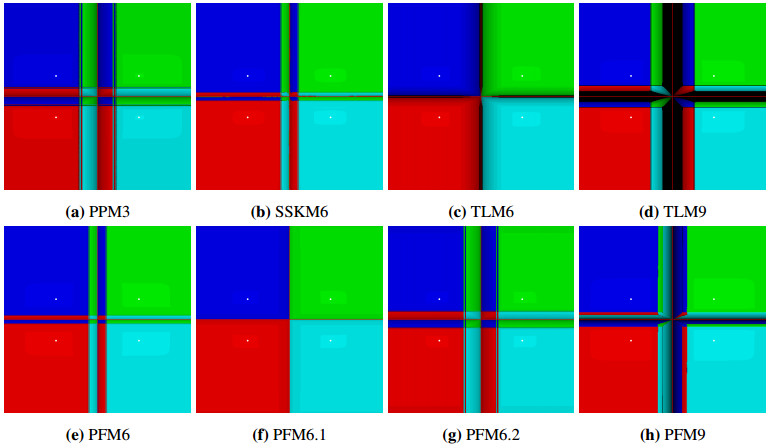
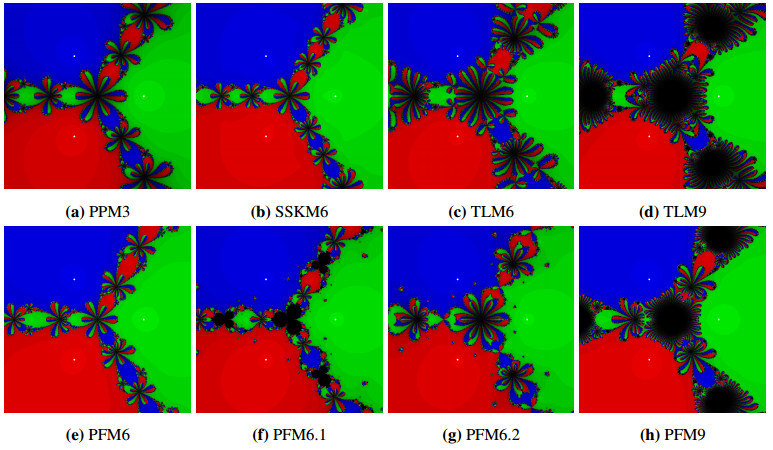
In this section, we offer a graphical analysis of our newly proposed scheme, PFM6 ($k = 0.001$) (2.14), along with PFM6.1 (3.12), PFM6.2 (3.13), and PFM9 ($k = 0.001$) (3.22), against the established methods of PPM3 (1.3), SSKM6 (3.9), TLM6 (6.1), and TLM9 (6.2). This comparison is facilitated by an analysis of their dynamical behaviors on the Cartesian plane, specifically through the lens of their basins of attraction. These basins not only serve as a visual comparative tool, they also shed light on the convergence and stability attributes of each method. We focus on the following systems of nonlinear polynomial equations for the analysis:

(i) $P_1(s) = (s_{1}^{2}- 1, s_{2}^2-1)^T$.

(ii) $P_2(s) = (s_{1}^{2}+s_{2}^{2}- 1, \frac{1}{4}s_{1}^{2}+4s_{2}^2-1)^T$.

(iii) $P_3(s) = (3s_{1}^{2}s_2-s_{2}^{3}, s_{1}^{3}-3s_1s_{2}^2-1)^T$.

For this graphical analysis, we employed a precisely defined rectangular grid $\mathbb{S} = [-2, 2]\times[-2, 2]\in \mathbb{R}^2$ within the Cartesian plane that has been subdivided into a $401\times401$ matrix of grid points. Each point on this grid serves as an initial point for iterations. These points were each assigned a unique color to indicate the specific real root to which the iterative method will converge when initialized from that point. The roots are visually demarcated by small white circles in the plot. Points that fail to converge within the set tolerance of $10^{-3}$ or before reaching a maximum of 80 iterations have been marked in black, denoting them as divergent points. Additionally, the brightness of the colour within each basin serves as an indicator of the speed of convergence, with brighter hues representing faster convergence and darker shades indicating a slower rate. The graphical illustrations of the basins of attraction for the methods under evaluation are displayed in Figures 1–3. To supplement this, Table 4 enumerates the instances of divergence, sourced from a $401 \times 401$ matrix of initial points, when the methods are applied to $P_i(s), i = 1, 2, 3$.

Figures 1–3 reveal key insights into the performance of the methods based on their basins of attraction. Our proposed methods exhibit strong performance with large basins, demonstrating their robustness by yielding a notably low count of divergent points. PFM6 emerges as the top performer, with SSKM6 following closely behind and offering a strong challenge to our proposed approach. On the other hand, PFM9 and TLM9 underperform, indicating that higher order does not guarantee better convergence or stability, as evidenced by their small basins and large number of divergent points. Intriguingly, while PFM6.1 excels and matches the performance of PFM6 and SSKM6 for $P_1(s)$ and $P_2(s)$, it struggles significantly with $P_3(s)$, lagging behind the other methods and delivering the poorest performance in this specific scenario. These observations are corroborated by the divergent point data in Table 4.

8.   Concluding remarks

In this paper, we have presented a family of three-step iterative methods with sixth-order convergence for the purpose of solving systems of nonlinear equations. The proposed methods are based on a novel approach to enhance the convergence order of iterative methods. We have also proposed a three-step scheme with convergence order $p+3$ (for $p\geq3$) and extended it to a generalized $(m+2)$-step scheme by merely incorporating one additional function evaluation, thus achieving convergence orders up to $p+3m$, $m\in\mathbb{N}$. We have provided thorough local convergence analysis and numerical experiments to validate the theoretical findings. Lastly, we have showcased the performance of these methods through the analysis of their basins of attraction and their application to systems of nonlinear equations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors gratefully acknowledge the University Grants Commission (UGC), New Delhi, India, for providing financial assistance to carry out this work. Open access of this article is supported by the Technical University of Cluj-Napoca.

Conflict of interest

The authors declare no conflict of interest.