From the binomial reshuffling model to Poisson distribution of money

1.   Introduction

The starting point of our study is to consider a system of $N$ agents with wealth denoted by $X_1, \ldots, X_N$. At each iteration, two agents picked randomly (say $i$ and $j$) reshuffle their combined wealth by flipping a sequence of fair coins. Mathematically, this exchange rule can be written as:

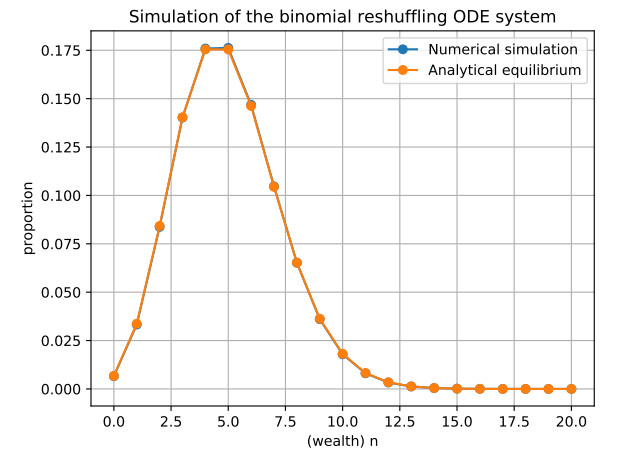
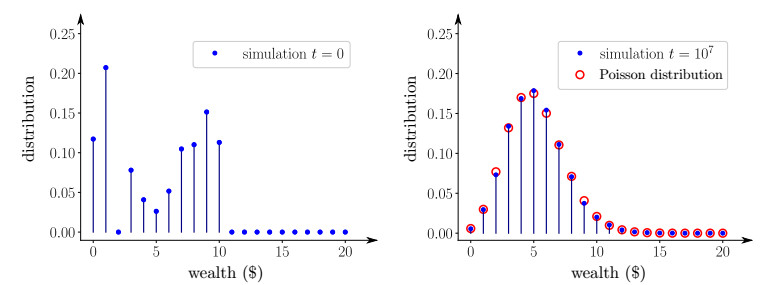
where $B \circ (X_i+X_j)$ is binomial random variable with parameters $X_i+X_j$ (combined wealth) and $1/2$ (fair coins). We refer to this dynamics as the binomial reshuffling model. Notice that the combined wealth is preserved after the exchange, and hence the model is closed (i.e., the total wealth is conserved). Our goal of this manuscript is to study the asymptotic limit of this dynamics as the number of agents and iterations become large. To gain an insight into the dynamics, we provide in Figure 1 a numerical simulation with $N = 10^4$ agents and after $10^7$ iterations. We observe the total wealth distribution is well approximated by a Poisson distribution whose rate parameter $\lambda$ is equal to the arithmetic mean of the agents' wealth ($\lambda \approx 5$ in the simulation).

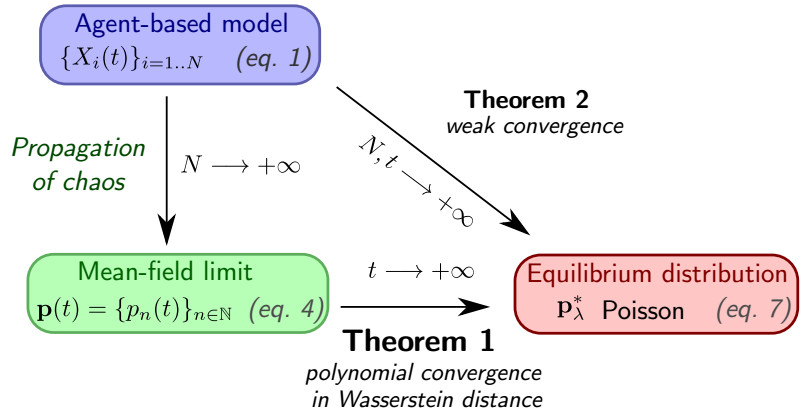
Our main result, Theorem 1, formalizes the empirical observation illustrated in Figure 1. We consider the mean-field behavior of binomial reshuffling (1.1) in the large population limit ($N \to \infty$) and prove convergence of the distribution of wealth to a Poisson distribution in the $2$-Wasserstein metric. In Theorem 2, we provide direct proof of the convergence of the agent-based model toward the Poisson distribution. However, in contrast to Theorem 1, the Theorem 2 does not provide a convergence rate toward the equilibrium distribution. We summarize our results in Figure 2.

1.1.   Related work

Before starting our investigation of the binomial reshuffling model, we would like to emphasize its link with other models in econophysics. We start by recalling the uniform reshuffling model ^[4]. In this dynamics, a pair of agents $i, j$ is chosen randomly and their combined wealth is redistributed according to a uniform distribution. Thus, the update rule is given as follows:

where $U\circ (X_i + X_j)$ denotes a uniform random variable on $[0, X_i + X_j]$. The uniform distribution has a larger variance than the binomial distribution $B\circ (X_i + X_j)$. As a result, the uniform reshuffling model generates more wealth inequality (measured by the so-called Gini index) compared to the binomial reshuffling model. The associated equilibrium is an exponential law instead of a Poisson distribution. Notice also that in contrast to the binomial reshuffling model, the wealth of the agents is a real non-negative number and no longer an integer (i.e., $X_i(t) \in \mathbb{R}^+$).

In contrast to the uniform reshuffling model, the repeated average model ^[5,13] reduces wealth inequality. In this dynamics, the combined wealth of two agents is simply shared equally, leading to the following update rule:

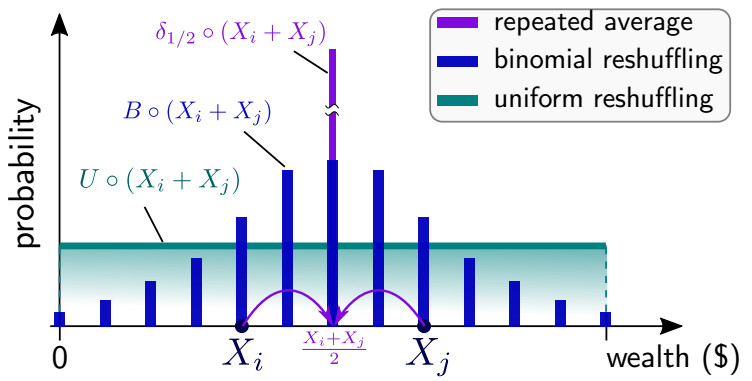
in which $\delta_{1/2} \circ (X_i + X_j)$ denotes a Dirac delta centered at $(X_i + X_j)/2$. The long time behavior of such dynamics is a Dirac distribution, i.e., the wealth of all agents are equal, and the Gini index converges to zero ^[5]. We illustrate the three different dynamics in Figure 3. The binomial reshuffling model could be seen as an intermediate behavior between the uniform reshuffling model and the repeated average dynamics.

Modifications of these models, which lead to different dynamics, also exist. For example, the so-called immediate exchange model introduced in ^[22] assumes that pairs of agents are randomly and uniformly picked at each random time, and each of the agents transfers a random fraction of its money to the other agents, where these fractions are independent and uniformly distributed in $[0, 1]$. The so-called uniform reshuffling model with saving propensity investigated in ^[11,25] suggests that the two interacting agents keep a fixed fraction $\lambda$ of their fortune and only the combined remaining fortune is uniformly reshuffled between the two agents:

The uniform reshuffling model arises as a particular case if we set $\lambda = 0$. For other models arising from econophysics (including models with bank and debt), see ^{[2,6,7,11,12,26]} and references therein.

Last, we emphasize that all the aforemention models fall into the realm of interacting particle systems ^[27] if we identify dollars as particles and agents as vertices. Thus, the binomial reshuffling model investigated here (using terminologies from econophysics) can readily be reinterpreted using languages from other communities. For instance, we refer to a recent work ^[32] for the study of a similar model on general graphs where the main focus is on the mixing time of the process.

1.2.   Main result

In order to state our main result, we need to formalize a notion of mean-field behavior as the number of agents becomes large. If we assume that updates occur at random times generated by a Poisson clock with rate $1/n$, then Eq (1.1) defines a continuous-time Markov process $\{X_1(t), \ldots, X_N(t)\}$ for $t \ge 0$, for any initial distribution of wealth. Let $\mathbf{p}(t) = \left(p_0(t), p_1(t), \ldots, p_n(t), \ldots\right)$ be the law of the process $X_1(t)$ as $N \to \infty$, that is, $p_n(t) = \lim_{N \to \infty} \mathbb{P}(X_1(t) = n)$. Then, using standard techniques, we show in Section 2 that the time evolution of $\mathbf{p}(t)$ is given by

where

for $n \ge 0$, with the usual convention that $\tbinom{0}{0}$ is interpreted as $0$. The transition between the stochastic $N$-agents dynamics (1.1) and the infinite system of ordinary differential equations (ODE) (1.4) as $n \to \infty$ is referred to as propagation of chaos ^[34] and has been rigorously justified in various models arising from econophysics, see for instance ^{[3,4,6,16,21,29]}. Given the transition from the interacting system of agents (1.1) to the deterministic system of nonlinear ODE (1.4), the natural follow-up step is to investigate the large time behavior of the system of differential equations and equilibrium solution. We refer interested readers to several monographs ^[18,35] related to infinite dimensional dynamical systems and analysis.

Finally, we also recall that the $2-$Wasserstein metric between two probability mass functions $\mathbf{p}$ and $\mathbf{q}$ is defined by

where the infimum is taken over all pairs of random variables $X$ and $Y$ distributed according to $\mathbf{p}$ and $\mathbf{q}$, respectively. Moreover, let $\mathbf{p}_\lambda^*$ denote a Poisson distribution with rate $\lambda > 0$, that is,

for $k \in \mathbb{N}$. The following Theorem is our main result.

Theorem 1. Let $\mathbf{p}(0)$ be a probability distribution on $\mathbb{N}$ with mean $\lambda$ and finite variance $\sigma^2$, and suppose that $\mathbf{p}(t)$ be defined by Eq (1.4). Then,

where $C > 0$ is a constant that only depends on the initial variance $\sigma^2$.

The proof of Theorem 1 is given in Section 3. Informally speaking, this result says that when the number of agents and the number of iterations is large, the distribution of wealth of the agents under the binomial reshuffling model converges to a Poisson distribution (Figures 1 and 2). We note that numerics indicate that it may be possible to improve the convergence rate of Theorem 1, at least for some initial probability distributions $\mathbf{p}(0)$, see the discussion in Section 5.

1.3.   Organization

The remainder of the present paper is organized as follows. In Section 2, using classical techniques, we show that the nonlinear system of nonlinear ODEs (1.4) is indeed the mean-field limit of binomial reshuffling dynamics in the large $N$ limit. In Section 3 we establish several results about the large time behavior of the nonlinear ODE system (1.4), and ultimately prove Theorem 1 using a coupling argument inspired by recent work on the uniform reshuffling model ^[4]. In Section 4, we take on a different approach similar to the methods proposed in ^[24,25,26], and show a different way to establish the convergence to the Poisson distribution. In Section 5, we discuss the presented results. The Appendix A records a qualitative way of demonstrating the large time convergence of the solution of Eq (1.4) to a Poisson distribution.

2.   Mean-field limit

2.1.   Notation

Let $\mathbb{N}$ denote the set of nonnegative integers $\mathbb{N} = \{0, 1, 2, \ldots, \}$, and bold lower case letter $\mathbf{p} = \{p_n\}_{n \in \mathbb{N}}$ denote probability distributions on $\mathbb{N}$. We say that $B$ is a Bernoulli random variable if $\mathbb{P}(B = 0) = \mathbb{P}(B = 1) = 1/2$. For random variables $X$ and $Y$ taking values in $\mathbb N$, we write $X \perp Y$ to mean that $X$ and $Y$ are mutually independent. We say that $X$ is a binomial random variable with parameters $n$ and $\gamma$ if the distribution $\mathbf{p}$ of $X$ satisfies

for $k = 0, \ldots, n$, and $p_k = 0$ otherwise. If $X$ and $Y$ are random variables taking values in the nonnegative integers, then we write $B \circ (X+Y)$ to denote a binomial random variable with parameters $X+Y$ and $1/2$, put differently,

where $\{B_n\}_{n \in \mathbb{N}}$ are independent Bernoulli random variables (which are independent from $X$ and $Y$).

2.2.   Mean-field limit

In the following, we provide a heuristic derivation of the mean-field ODE system (1.4) from the binomial reshuffling dynamics (1.1); the derivation is based on classical techniques, see for example ^[3,4,7].

Let $\mathrm{N}^{(i, j)}_t$ be independent Poisson processes with intensity $1/N$. Then, the dynamics can be written as:

with $\{B_k(t)\}_{k \in \mathbb{N}, t > 0}$ being a collection of independent Bernoulli random variables. Using our notation Eq (2.1), one can write:

As the number of agents $N$ goes to infinity, we would expect that the processes $\{X_i\}_{1\leq i\leq N}$ become (asymptotically) independent and of the same law. Therefore, the limit dynamics would be of the form:

where $\overline{Y}$ is an independent copy of $\overline{X}$ and $\overline{\mathrm{N}}_t$ is a Poisson process with unit intensity. The proof of such convergence is referred to as propagation of chaos, and it is out of the scope of the manuscript. We refer to ^{[3,6,14,16,29,34]} for the readers interested in this topic. The Kolmogorov backward equation associated with the SDE (2.4) reads as

In other words, the limit dynamics corresponds to the following pure jump process:

To write down the evolution equation for the law of the process $\overline{X}(t)$ (denoted by ${\mathbf{p}}(t)$), we need the following elementary observation:

Lemma 1. Suppose $X$ and $Y$ two i.i.d. random variables with probability mass function ${\mathbf{p}} = \{p_n\}_{n \in \mathbb N}$. Let $Z = \sum_{k = 1}^{X+Y} B_k$ where $\{B_k\}_{k \in \mathbb{N}}$ are a collection of independent Bernoulli random variables, which are independent of $X$ and $Y$. Then,

for $n \in \mathbb{N}$.

Proof. By the law of total probability, we have

which completes the proof. □

It follows from Lemma 1 that the evolution equation for the law $\mathbf{p}(t)$ of $\overline{X}(t)$ defined in Eq (2.4) satisfies

where

for $n \in \mathbb{N}$.

Remark 1. We emphasize that at the mean-field level, the nonlinear ODE system (2.7) and (2.8) turns out to be a special of a more general mean-field type ODE system motivated by biological applications and investigated in ^[1], where the authors of ^[1] rely on Fourier-based metric ^[9] for the analysis of the large time behavior. However, at the agent-based level, the binomial reshuffling dynamics cannot fit into the framework considered in ^[1]. As we will see soon in Section 3, our large time analysis of the system (2.7) and (2.8) is entirely probabilistic and the metric we use to quantify the relaxation of the solution to (2.7) and (2.8) is the Wasserstein metric rather than the well-known Fourier-based metric (introduced in a series of work on the kinetic theory of dilute gases ^[8,20]).

3.   Large time behavior

3.1.   Evolution of moments

We begin by establishing several elementary properties of the nonlinear ODE system (1.4). First, we show, through straightforward calculations, that the Poisson distribution is an equilibrium solution of Eq (1.4). At this stage, we do not argue the uniqueness of this equilibrium solution, but the argument presented in Section 4 implies that the Poisson distribution is indeed the unique equilibrium.

Lemma 2. Suppose that $Q$ is defined by Eq (1.5). Then,

where $\mathbf{p}_\lambda^*$ is the Poisson distribution defined in Eq (1.7).

Proof. The proof of Lemma 2 follows from straightforward computations and hence will be omitted. □

Lemma 3. Assume that ${\mathbf{p}}(t) = \{p_n(t)\}_{n \in \mathbb{N}}$ is a classical and global in time solution of the system (1.4) whose initial probability mass function ${\mathbf{p}}(0)$ has mean $\lambda$ and finite variance $\sigma^2$. Then

That is, the mean value of ${\mathbf{p}}(t)$ is preserved for all $t \geq 0$ and its second (non-centered) moment converges exponentially fast to $\lambda^2 + \lambda$.

Proof. Making use of the evolution equation (1.4) we deduce that

where the last identity follows from the conservation $\sum_{n = 0}^\infty p_n(t) = 1$ for all $t\geq 0$. A similar computation yields the second identity provided in Eq (3.2), whence

converges exponentially fast to $\lambda^2 + \lambda$. □

We end this subsection with a numerical experiment indicating the relaxation of the solution of Eq (1.4) to its Poisson equilibrium distribution $\mathbf{p}_\lambda^*$, as is shown in Figure 4.

3.2.   Convergence towards Poisson equilibrium

In this section, we modify a coupling method provided in ^[4] to justify the convergence of the solution of Eq (2.7) to the Poisson equilibrium distribution in the $2$-Wasserstein metric. Recall that the $W_2(\mathbf{p}, \mathbf{q})$ denotes the $2$-Wasserstein distance between two probability distributions $\mathbf{p}$ and $\mathbf{q}$ on $\mathbb{N}$ (see the definition Eq (1.6)). We begin by providing a stochastic representation of the evolution equation (2.7), on which a coupling argument relies.

Proposition 1. Assume that ${\mathbf{p}}(t)$ is a solution of Eq (2.7) with initial condition ${\mathbf{p}}(0)$ being a probability mass function whose support is contained in $\mathbb N$ having mean value $\lambda$. Defining $(X_t)_{t\geq 0}$ to be a $\mathbb N$-valued continuous-time pure jump process with jumps of the form

where $Y_t$ is an i.i.d. copy of $X_t$ and the jump occurs according to a Poisson clock running at the unit rate. If $\mathrm{Law}(X_0) = {\mathbf{p}}(0)$, then $\mathrm{Law}(X_t) = {\mathbf{p}}(t)$ for all $t\geq 0$.

Proof. The proof of Proposition 1 shares the same spirit as the proof of Proposition 3.1 in ^[4]. Taking $\varphi$ to be an arbitrary but fixed (bounded continuous) test function, we have

Let ${\mathbf{p}}(t)$ to be the probability mass function of $X_t$, we can rewrite Eq (3.4) as

Thus, ${\mathbf{p}}(t)$ satisfies the ODE system (2.7) and the proof is completed. □

Remark 2. Using a similar reasoning, we can show that if $(\overline{X}_t)_{t\geq 0}$ is a $\mathbb N$-valued continuous-time pure jump process with jumps of the form

where $\overline{Y}_t$ is an i.i.d. copy of $\overline{X}_t$ and the jump occurs according to a Poisson clock running at the unit rate. Then $\mathrm{Law}(\overline{X}_0) = {\mathbf{p}}^*_\lambda$ implies $\mathrm{Law}(\overline{X}_t) = {\mathbf{p}}^*_\lambda$ for all $t\geq 0$, where ${\mathbf{p}}^*_\lambda$ is the Poisson distribution.

3.3.   Proof of Theorem 1

We are now prepared to prove our main result.

Proof of Theorem 1. The proof strategy is based on coupling the two probability mass functions ${\mathbf{p}}(t)$ and ${\mathbf{p}}^*_\lambda$ for all $t\geq 0$. Assume that $(X_t)_{t\geq 0}$ and $(\overline{X}_t)_{t\geq 0}$ are $\mathbb N$-valued continuous-time pure jump processes with jumps of the form Eqs (3.3) and (3.5), respectively. We can take $(X_t, Y_t)$ and $(\overline{X}_t, \overline{Y}_t)$ as in the statement of Proposition 1 and Remark 2, respectively. Moreover, we require that $X_t \perp \overline{Y}_t$, $\overline{X}_t \perp Y_t$ and $(X_t, \overline{X}_t) \perp (Y_t, \overline{Y}_t)$, i.e., several independence assumptions can be imposed along the way when we introduce the coupling. We emphasize that we can employ the same set of independent fair coins in the definition of $B\circ (X_t+Y_t)$ and $B\circ(\overline{X}_t+\overline{Y}_t)$, leading us to the representations

in which $\{B_k\}$ is a collection of independent Bernoulli random variables. Due to the coupling we have just constructed, along with the notation $R_t : = |X_t+Y_t - \overline{X}_t - \overline{Y}_t|$, we deduce that

where the last identity follows from the elementary observation that

As an immediate by-product of the preceding computations, we obtain

Next, we notice that before we reach the time $T$ for which $\mathbb E[(X_T-\overline{X}_T)^2] \leq 1$, we can further deduce that

where the last inequality follows from $\mathbb E[(X_t-\overline{X}_t)^2] \geq 1$ for all $t \in [0, T]$. Consequently, we arrive at

Unfortunately, the aforementioned argument leading to the exponential decay of $\mathbb E[(X_t-\overline{X}_t)^2]$ before a finite time $T$ breaks down when the quantity of interest $\mathbb E[(X_t-\overline{X}_t)^2]$ becomes no larger than $1$ (which is guaranteed when $t$ is sufficiently large). Thus, we have to resort to a different approach in order to have a good enough upper bound for $\mathbb{E}[|X_t-\overline{X}_t+Y_t-\overline{Y}_t|]$. To this end, we will show that

for all $t \in \mathbb{R}_+$, from which we end up with the following differential inequality

holding for all $t\geq 0$. In particular, for $t \geq T = \min\{t \geq 0 \mid \mathbb E[(X_t-\overline{X}_t)^2] \leq 1\}$ the inequality (3.9) reads as

which leads us to

If we combine Eqs (3.7) and (3.10), and pick $\overline{X_0}$ with law ${\mathbf{p}}(0)$ so that $W^2_2({\mathbf{p}}(0), {\mathbf{p}}^*_\lambda) = \mathbb E[(X_0-\overline{X}_0)^2]$, we obtain Eq (1.8) and the proof will be finished. Now, it remains to justify the validity of the refined estimate Eq (3.8) for $\mathbb{E}[|X_t - \overline{X}_t + Y_t - \overline{Y}_t|]$, and we consider the following two cases:

● Case i) Suppose that $\mathbb{P}(|X_t - \overline{X}_t| = 1) \leq c\, \mathbb E[(X_t-\overline{X}_t)^2]$ for some constant $c \in (0, 1)$ to be specified later. Then we deduce that

● Case ii) Suppose that $\mathbb{P}(|X_t - \overline{X}_t| = 1) \geq c\, \mathbb E[(X_t-\overline{X}_t)^2]$, where the constant $c$ is the same one as appeared in Case i). We now proceed as follows:

Since we have assumed that $\mathbb{P}(|X_t - \overline{X}_t| = 1) \geq c\, \mathbb E[(X_t-\overline{X}_t)^2]$, without any loss of generality we may further assume that

As $\mathbb E[X_t - \overline{X}_t] = \lambda - \lambda = 0$, we also have $\mathbb E\left[|X_t - \overline{X}_t|\, \mathbb{1}_{\{X_t - \overline{X}_t < 0\}}\right] = \mathbb E\left[|X_t - \overline{X}_t|\, \mathbb{1}_{\{X_t - \overline{X}_t > 0\}}\right]$, from which it follows that

Due to the identity

we have the bound

Combining Eqs (3.11)–(3.13) yields

Combining the two lower bounds Eqs (3.11) and (3.14) leads us to

whence we finally deduce that

Setting $c = \sqrt{2/ 3}$ and combining the discussions above yield the advertised estimate (3.8), thereby completing the entire proof Theorem 1. □

Remark 3. One might have noticed that the coupling argument presented here is more sophisticated than the corresponding coupling argument used for the uniform reshuffling model ^[4]. One simple explanation is that the random variable $U\circ (X_i + X_j)$ appearing in the update of the uniform reshuffling dynamics Eq (1.2) admits a nice "factorization property", meaning that we have

where the notation $X \overset{ \mathrm{d}}{ = } Y$ is used whenever the random variables $X$ and $Y$ share the same distribution. However, it is not possible (in our opinion) to "decompose" the random variable $B\circ (X_i + X_j)$ as a product of two independent random variables similar to Eq (3.16). Loosely speaking, the noise (or randomness) introduced in the binomial reshuffling dynamics is somehow "intrinsic" while the noise rendered by the uniform reshuffling mechanism is "extrinsic".

4.   Alternative approach to convergence

In this section, we consider the discrete time version of the proposed binomial reshuffling model and we sketch the argument (in the same spirit as those used in ^[24,25]), which shows the convergence of the distribution of money to a Poisson distribution. The general strategy is to investigate the limiting behavior for each fixed number $N$ of agents as time becomes large (by focusing on the motion of dollars), and then compute the probability that a typical individual (immersed in an infinite population) has $n$ dollars at equilibrium in the limits as $N \to \infty$.

Let ${\bf X}(t) = \left(X_1(t), \ldots, X_N(t)\right)$ with $t \in \mathbb N$ and denote by

the configuration (or state) space. We will also denote $[N] = \{1, 2\ldots, N\}$ for notation simplicity. Given ${\bf Y}, {\bf Z} \in \mathcal{A}_{N, \lambda}$, it is clear that

if and only if $Y_k = Z_k$ for all $k \in [N] \setminus \{i, j\}$ and $Y_i + Y_j = Z_i + Z_j$ for some $(i, j) \in [N]^2 \setminus \{i = j\}$. By a similar argument as given in ^[24,25], one can show that the discrete time binomial reshuffling dynamics is a finite irreducible and aperiodic Markov chain, whence the process will converge to a unique stationary distribution (as $t \to \infty$) regardless of the choice of initial configuration. We now show that the process is time-reversible with the following multinomial stationary distribution

i.e., each dollar is independently in agent $i$'s pocket with probability $\frac{1}{N}$. Indeed, given ${\bf Y}, {\bf Z} \in \mathcal{A}_{N, \lambda}$ with $\mathbb{P}\left(X(t+1) = {\bf Z} \mid X(t) = {\bf Y} \right) \neq 0$ as described above, we have that

Therefore,

or

On the other hand, the detailed balance equation (4.2) holds trivially when ${\bf Y} \in \mathcal{A}_{N, \lambda}$ and ${\bf Z} \in \mathcal{A}_{N, \lambda}$ are such that $\mathbb{P}\left(X(t+1) = {\bf Z} \mid X(t) = {\bf Y} \right) = 0$. In summary, the discrete time binomial reshuffling process is (time) reversible with respect to the multinomial distribution (4.1) and the distribution (4.1) is indeed the stationary distribution of the binomial reshuffling model. Now we can prove the following convergence result.

Theorem 2. For the discrete time binomial reshuffling model, for each fixed $n$ we have that

Consequently,

Proof. The proof is similar to the proofs of Theorem 1 and Theorem 2 in ^[24] for other econophysics models. For all ${\bf X} \in \mathcal{A}_{N, \lambda}$ such that $X_1 = n$, we have that

Therefore, the stationarity of the multinomial distribution $\lambda_\infty$ and the multinomial theorem allow us to deduce that

As a consequence, taking the large population limit as $N \to \infty$ and recalling the classical result on Poisson approximation to binomial distribution, we finally obtain

This finishes the proof of theorem 2. □

5.   Conclusion

In this manuscript, we have introduced the binomial reshuffling model. We proved that, in the mean-field limit, the distribution of wealth under this model converges to the Poisson distribution. In the context of econophysics, this model is particularly natural due to the connection with coin flipping: agents redistribute their combined wealth by flipping a sequence of fair coins. We managed to show a quantitative large time convergence result to a Poisson equilibrium distribution for the solution of Eq (1.4) thanks to a coupling argument.

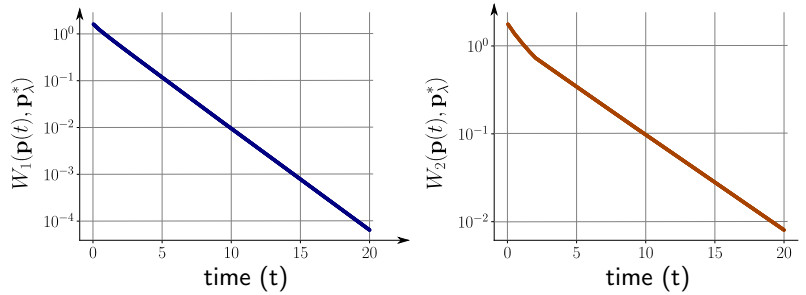
In an attempt to determine if the rate established in Theorem 1 can be improved, we can approximate the solution to the ODE system (1.4) numerically. We start the initial probability distribution $\mathbf{p}(0)$ illustrated in Figure 1 that has mean $\lambda = 5.15$. Since this initial distribution is supported on $\{0, \ldots, 10\}$, its behavior over reasonable amounts of time can be approximated by probability vectors $\mathbf{p}(t) = (p_0, \ldots, p_{55})$ truncated at $n = 55$. Indeed, when $\lambda = 5.15$, we have $p_\lambda^*(56) = \lambda^{56} \mathrm{e}^{-\lambda}/(56!) \approx 10^{-34}$ which is approximately equal to the relative precision of Quadruple-precision floating-point numbers (which is how we represent real numbers for the numerics). The system of ODEs was solved using a fourth-order Runge-Kutta method. The $W_1$ and $W_2$ metric are straightforward to compute for $1$-dimensional probability distribution, indeed, if $F$ and $G$ denote the cumulative distribution function of $\mathbf{p}$ and $\mathbf{q}$, respectively, then

where the inverse of the cumulative distribution function is defined by $F^{-1}(z) = \min \{ k \in \mathbb{N} : F(k) \ge z\}$, see for example [31, Remark 2.30]. We plot the results in Figure 5. Since the $W_1$ and $W_2$ metrics are decreasingly linearly in the log scale of the Figure, the numerics suggest that it may be possible to improve the converge rate estimate of Theorem 1 to exponential convergence, at least for some initial probability distributions. We leave this as an open problem.

Several other open questions remain to be solved in future work. For instance, it seems very difficult to find a natural Lyapunov functional associated with the Boltzmann-type evolution equation (1.4), which is pretty weird since for most of the classical econophysics models (see for instance those studied in ^{[3,4,5,7,28,30]}) natural Lyapunov functionals do exist.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

It is a great pleasure to express our gratitude to Sébastien Motsch for many helpful suggestions. We would also like to thank Augusto Santos for his answer to a question of Fei Cao on MathOverflow ^[33], where a detailed proof of Lemma 4 is provided. Nicholas F. Marshall was supported in part by NSF DMS-1903015, and a start-up grant from Oregon State University. This work was initiated as the AMS MRC conference on Data Science at the Crossroads of Analysis, Geometry, and Topology.

Conflict of interest

The authors declare that there is no conflicts of interest.

Appendix A.   Convergence to Poisson distribution via Laplace transform

We include here another (although qualitative) approach for proving the large time convergence of the solution of the ODE system (1.4) to the Poisson equilibrium, based on the application of Laplace transform. The primary motivation to present the Laplace transform approach lies in the emergence of a surprising connection between the convergence problem at hand and a closely related dynamical system. Indeed, we will need the following preliminary result on a specific dynamical system, which seems to be interesting in its own right.

Lemma 4. Assume that the following infinite dimensional ODE system

admits a unique (smooth in time) solution, whose initial datum $\{a_n(0)\}_{n\geq 0}$ satisfies $a_n(0) < a^2_{n+1}(0)$ for all $n$ and $\mathrm{e}^{-\lambda_1\, 2^{-n}} \leq a_n(0) \leq \mathrm{e}^{-\lambda_2\, 2^{-n}}$ for all large enough $n$ where $\lambda_1, \lambda_2 \in \mathbb{R}_+$. Then there exists some $\lambda \in [\lambda_1, \lambda_2]$ such that $a_n(t) \xrightarrow{t\to \infty} \mathrm{e}^{-\lambda\, 2^{-n}}$ for all $n \in \mathbb N$.

Proof. We will only provide a sketch of the proof here and refer to ^[33] for a detailed argument. We first notice that the infinite dimensional cube $[0, 1]^{\mathbb N}$ is invariant under the evolution of $\{a_n(t)\}_{n\geq 0}$, i.e., if $a_n(0) \in [0, 1]$ for all $n \in \mathbb N$, then $a_n(t) \in [0, 1]$ for all $n \in \mathbb N$ and all $t\in \mathbb{R}_+$. Moreover, the tail of the initial condition fully determines the asymptotic behavior of the system (A.1) since the state variable $a_m$ impacts the evolution of $a_n$ as long as $m > n$ but not vice versa. Furthermore, the solution of Eq (A.1) enjoys a nice monotonicity property: If $\{\bar{a}_n\}_{n\geq 0}$ is another solution of Eq (A.1) whose initial datum $\{\bar{a}_n(0)\}_{n \geq 0}$ satisfies $\bar{a}_n(0) \geq a_n(0)$ for all $n$, then $\bar{a}_n(t) \geq a_n(t)$ for all $n \in \mathbb N$ and $t\geq 0$. In particular, if there exists some $N \in \mathbb N$ for which $\mathrm{e}^{-\lambda_1\, 2^{-n}} \leq a_n(0) \leq \mathrm{e}^{-\lambda_2\, 2^{-n}}$ holds whenever $n \geq N$, then we must have $[\liminf_{t \to \infty} a_n(t), \limsup_{t \to \infty} a_n(t)] \in [ \mathrm{e}^{-\lambda_1\, 2^{-n}}, \mathrm{e}^{-\lambda_2\, 2^{-n}}]$ for all $n$. Lastly, the advertised conclusion follows from another monotonicity property of the solution of (A.1): if $a_n(0) < a^2_{n+1}(0)$ for all $n$, then $a_n(t) \geq a_n(s)$ for all $t \geq s$ and all $n$. □

Armed with Lemma 4, we are able to demonstrate the convergence of the solution of Eq (1.4) to the Poisson distribution by virtue of the Laplace transform.

Proposition 2. Assume that ${\mathbf{p}}(t) = \{p_n(t)\}_{n \geq 0}$ is a classical (and global in time) solution of the system (1.4) with a initial probability mass function ${\mathbf{p}}(0)$ having mean value $\lambda$, then ${\mathbf{p}}(t) \xrightarrow{t \to \infty} {\mathbf{p}}^*_\lambda$.

Proof. For $x \in [0, 1]$, let $\phi(x, t) = \sum_{n = 0}^\infty p_n(t)\, x^n$ to be the Laplace transform of ${\mathbf{p}}(t)$, it suffices to establish the convergence

since the function $\mathrm{e}^{\lambda(x-1)}$ is the Laplace transform of the Poisson distribution. We now show that $\phi(x, t)$ satisfies the following partial differential equation (PDE):

Indeed, we have

We remark here that the PDE (A.3) is complemented with an initial datum $\phi(x, 0)$ which satisfies $\phi(1, 0) = 1$ and $\phi'(1, 0) = \lambda$. Moreover, due to the conservation of mass and mean (recall Lemma 3), we also have

If we set $a_n(t) = \phi(1-2^{-n}, t)$ for all $n \in \mathbb N$ and all $t \in \mathbb{R}_+$, then (A.3) implies that $a'_n(t) = a^2_{n+1}(t) - a_n(t)$. Thanks to the constraint that $\partial_x \phi(1, t) \equiv \lambda$, we also have $a_n(t) \approx 1 - \lambda\, 2^{-n}$ for all large $n$. Finally, the obvious observation that $1-2^{-n} \leq \left(1 - 2^{-(n+1)}\right)^2$ allows us to apply Lemma 4, and conclude that

Therefore, by the continuity of $\phi$ (with respect to $x$) we deduce the claimed convergence $\phi(x, t) \xrightarrow{t\to \infty} \mathrm{e}^{\lambda(x-1)}$. □