1.
Introduction
The US continues to consume over 20% of the globe’s oil, with almost 70% of this going toward domestic transportation, a sector that is dominated by light duty vehicle use for personal transportation [1]. The Intergovernmental Panel on Climate Change (IPCC) [2] has recently determined that cumulative CO2 emissions must be limited to no more than 15–20 years of present-day emissions for a reasonable chance to limit global mean warming to 1.5 ℃, while perhaps 30–40 years of emissions remain for a 50% or better chance to limit warming to 2 ℃. All sectors of society must decarbonize, with net-zero emissions achieved by about 2050 or 2070 for 1.5 ℃ or ℃ warming targets, respectively [2]. Transitioning to a low-carbon passenger fleet is thus a fundamental challenge for the next several decades, and to stay broadly in line with climate goals, cumulative future emissions from the fleet must, ideally, be limited to only 15–20 years of baseline emissions with emissions rates approaching zero within 30–50 years.
Nearly all existing vehicles are conventional internal combustion vehicles (ICEVs)
[3], and ICEVs continue to make up the vast majority of new vehicle sales in the US, although alternative drivetrains, especially hybrid-electric vehicles (HEVs) and battery-electric vehicles (BEVs) have become more popular in recent years, and have the potential to appreciably reduce CO2 emissions relative to ICEVs [4]. Additionally, behavioral shifts away from passenger vehicle travel, either induced by planning and infrastructural changes, or via personal choices with respect to driving habits, can play a role in climate mitigation. Indeed, the potential for household-level changes in consumption, including mobility, for meeting climate and other environmental goals is quite significant [5,6], may be generally underappreciated, and is likely essential to meeting climate targets [7]. For example, Jones et al. [5] found that a variety of simple household-level actions, including driving reductions and vehicle trade-ins for higher efficiency models, can yield both appreciable monetary and carbon savings; such behavioral shifts are especially attractive as they can yield very rapid carbon savings without changes in infrastructure, and typically without any reduction in household well-being [8].
While they generate no emissions at the tailpipe, the lifecycle emissions associated with BEV manufacture operation and operation are far from trivial [4], due both to the upstream manufacturing footprint and the emissions associated with electricity generation, which vary geographically, seasonally, and diurnally [9,10]. Furthermore, BEVs represent an additional load on electrical grids, and so using grid-average electricity emissions factors (EFs) in analysis may also underestimate the short-term impacts of BEV deployment [11,12]. Ambient temperature (especially extreme cold) affects BEV efficiency [13], driving patterns vary regionally [4], and battery performance may degrade over time [15]. Thus, many authors have attempted more comprehensive comparisons of typical ICEVs, HEVs, and BEVs and other alternative drivertrains to determine the (geographically) optimal technology (e.g., [4,14,16,17,18,19]). Recent geographically explicit analyses by Tamayao et al. [11] and Yuksel et al. [4] compared emissions from the Toyota Prius HEV and Nissan Leaf BEV across the US, and both found the HEV to be superior in most of the Midwest and South, while the BEV tended to be better in the West and Texas.
While variations on battery-electric drivetrains are most studied, Bicer et al. [18], for example, concluded that hydrogen-powered vehicles may have a superior environmental profile, although Miotti et al. [14], on the other hand, found the lifecycle emissions of the 2016 Toyota Mirai hydrogen fuel-cell vehicle to be greater than most EVs currently on the market. Moreover, there is quite a bit of variation within electrified drivetrain classes, such that intra-class variation can appreciably overlap inter-class variation [16].
Given the fundamental need to transition away from a fossil-based energy system, nearly total electrification of the transportation sector is likely mandatory. Therefore, all vehicles must ultimately become BEVs, but it remains a question how best to orchestrate this transition, and what drivetrains (and specific vehicles) are preferable in the near-to medium-term; most existing works have not considered future changes in fleet composition under evolving electrical grids (but see, e.g., [20,21,22] for exceptions, as well as Onat et al. [23]).
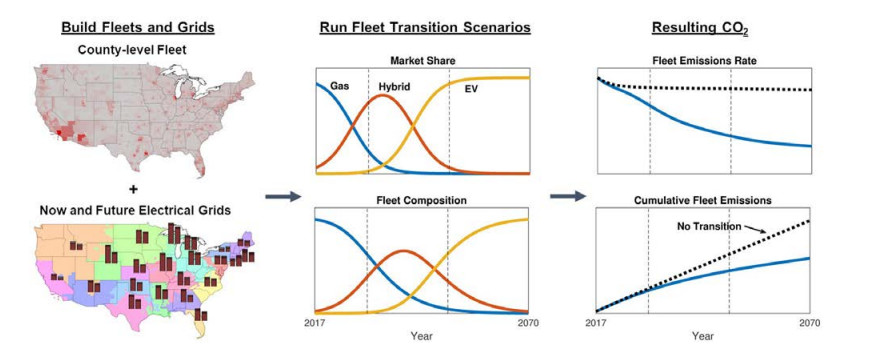
To study this question and better gain insight into the optimal roles for the two major alternative drivetrains, HEVs and BEVs, in this transition, a comprehensive modeling approach is employed that includes a county scale representation of the US passenger fleet, based upon microdata from the 2017 National Household Travel Survey (NHTS) [24], and simulates the lifecycle CO2-equivalent (CO2e) emissions associated with the maintenance, turnover, and operation of the fleet from a baseline year of 2017 through 2070, under idealized turnover scenarios. Region-specific projections from the 2019 Energy Information Administration (EIA) Annual Energy Outlook [25] are used determine the future electricity generating mix for every electricity subetaid in the continental US, while lifecycle emissions associated with electricity, fuel, and vehicle production are determined from a variety of sources.
Using this model framework, different (purely hypothetical) scenarios for the transition of new vehicle market share are imposed. These entail either an entirely high-efficiency HEV fleet, a high efficiency BEV fleet, or a transition to BEVs where HEVs are used as a transitional technology. Additionally, the utility of idealized reductions in driving (behavioral change), either alone or in combination with these transitions is examined.
Given the need the limit future cumulative emissions to 15–20 years of present emissions [2], the emissions from all scenarios are presented primarily in terms of cumulative emissions, up to the year 2070, as factors of the 2017 baseline year CO2e emissions, while the emissions rate over time is also examined. To be considered a successful low-carbon transition, a scenario must limit cumulative emissions to < 20 baseline years, and have an emissions rate approaching zero by 2070. This provides a consistent conceptual and quantitative basis for comparing and understanding possible transition scenarios.
It is found that a rapid and early transition to low carbon vehicles (LCVs) is essential to meeting climate goals. However, in general, so long as BEVs are phased in as the dominant technology by the 2050s, HEVs are a highly effective transitional technology, though they are not a valid terminal technology. That is, the internal timing of a switch from HEVs to BEVs hardly matters at all in terms of carbon emissions, so long as generally low-carbon vehicles are adopted early and there is an eventual switch to BEVs, while using HEVs as a transitional technology also markedly reduces battery production requirements. Somewhat surprisingly, this is true even if very rapid decarbonization of electricity generation is imposed on the model.
In many individual regions (mainly in the Midwest) it is actually preferable to delay the adoption of BEVs in favor of HEVs as the short-term technology. Moreover, the lifecycle emissions associated with particular ICEV, HEV, BEV models vary widely, such that many HEVs and BEVs can be similar to or even worse than economy ICEVs (over the near-term), and thus the usefulness of any individual vehicle model must be assessed for that particular model. Finally, under EIA projections for future electricity generation, at least some degree of behavioral change is needed to safely meet emissions mitigation targets.
2.
Materials and method
This work is based upon a model vehicle fleet model composed of individual vehicle “agents, ” which may either be a car, van, truck, or SUV ICEV; an HEV; or BEV, where the HEV and BEV are meant to be high-efficiency representative members of their respective classes. In brief, each county has its own fleet, the initial characteristics of which are determined from the 2017 NHTS [24], historical data on new vehicle MPG [3], and 2017 county population from the US Census [26]. Each vehicle randomly ages out of the fleet, and is randomly replaced according to a prescribed market share. The market share for ICEVs is assumed to reflect the 2017 market share indefinitely (based on [3]), while the HEV and BEV shares are imposed. Each county is assigned to an electrical subetaid (corresponding to the EIA market modules/EPA eGRID subregions), based on which subetaid the county centroid falls in, with electricity emissions factors for each subetaid determined primarily from the 2019 EIA Annual Energy Outlook [25].
The vehicle fleet turnover simulation is run with a yearly time-step for a prescribed number of years, and the lifecycle emissions from the use phase (gasoline and electricity generation) and vehicle manufacturing (from all new vehicles replacing those that age out) are recorded. Lifecycle emissions are quantified using the CO2e metric under the 100-year global warming potential (GWP) [27]. The model subcomponents and lifecycle emissions factors for gasoline, electricity, and vehicle manufacture are described in the subsequent sections. The overall methodology is summarized graphically in Figure 1.
2.1. Vehicle fleet model construction and turnover
2.1.1. Fleet construction
Partly following Yuksel et al. [4], a county-level representation of the fleet is constructed, and use- phase emissions are determined, by defining the county-level fleet according to the initial state-level conventional vehicle distribution. The initial state-level vehicle fleets are built using the 2017 NHTS [24]. Every vehicle recorded in the survey has a particular weighting; based on this weighting, this individual vehicle is replicated a number of times according to its relative weighting and the prescribed number of vehicle agents for the national fleet. Motorcycles and recreational vehicles are excluded, and it is assumed that all vehicles coded as “other truck” are pickup trucks. Now, based upon the age and class of each vehicle, MPG is also prescribed using EPA data [3] for new vehicles of each class (car, truck SUV, minivan/van, or pickup truck) and model year. Each vehicle is driven a prescribed number of miles per year (included in the NHTS data). Any vehicle data entry missing essential information is excluded from the model fleet.
Having constructed a state-level fleet of individual vehicle “agents, ” these vehicles are allocated to the individual counties based upon the relative population size of each county (using US Census population data for year 2017 [26]), and this allocation is performed randomly. Given the fuel type, MPG, and miles driven per year, it is now possible to calculate total annual fuel-cycle CO2e emissions for each county in the US, based upon the model fleet.
2.1.2. Fleet turnover
Tabulating the initial age of all vehicles to determine the age distribution yields a mean age of 10.25 years. The state-specific age distributions are, overall, well-described by a Gamma distribution, with parameters k = 2, θ = 5.5, for a mean vehicle lifetime of 11 years. This choice allows all vehicles to be modeled as existing in either a first or second age class, with aging from the first to the second an exponential random variable with mean 5.5 years, and aging out the second class resulting in replacement.
When any vehicle is retired from the fleet it is randomly replaced by a new vehicle, either a conventional ICEV or LCV, i.e., one with an alternative drive-train, according to the imposed market shares. In the case of a new ICEV, the vehicle type is selected according to the 2017 distribution of car, truck, SUV, minivan/van sales (based upon EPA figures given in [3]), which also yields vehicle MPG and weight (assumed to be the 2017 average for each vehicle class). This defines manufacturing emissions, as well as MPG over the life of the vehicle. The new conventional vehicle distribution is fixed according to the EPA data for 2017, unless otherwise stated.
If the replacement vehicle is to be an LCV, it is randomly created as either an HEV or BEV, according to the defined LCV market share, which similarly yields manufacturing emissions. Manufacturing emissions for each year’s vehicle replacements are tabulated and added to the fuel-cycle CO2e to yield total fleet-associated emissions for each year. Note that all vehicles (and their replacements) are driven the same number of miles each year of the simulation, unless driving reductions are imposed.
Finally, a single high-efficiency HEV and BEV are used in all turnover simulations, with the HEV corresponding to the 2018 Prius Eco 2 (56 MPG, curb weight 3010 lbs) and the BEV corresponding to the 2018 Nissan Leaf (112 MPGe, 40 kWh battery, curb weight 3443 lbs).
2.1.3. Turnover metrics
For all fleet turnover scenarios, annual fleet emissions in 2070 relative to the 2017 baseline, and cumulative emissions to the year 2070 as multiples of 2017 emissions, are used as the two primary metrics. That is, since the carbon budget for limiting global warming to 1.5 ℃ equates to about 15–20 years of current CO2 emissions [2], meeting climate targets should ideally entail both limiting the cumulative emissions from the passenger fleet, by 2070, to less than 20 years worth of 2017 emissions, with annual emissions approaching zero. Cumulative kWh of electric vehicle battery capacity (including 1.3 kWh per HEV) that must be produced by 2070 is also tracked as a secondary metric.
2.2. Market share model
Market share over time for LCVs, as a lumped category, is defined using a version of the logistic equation and is given mathematically as a function of time as
where klcv is a shape parameter and tlcv defines the year that the LCV market share reaches 50%. The relative fraction of the LCV share that is HEVs (with the remainder BEVs) is similarly defined as
with khev a shape parameter and thev the year that BEVs overtake HEVs as the dominant LCV. Multiplying the LCV share and relative HEV or BEV share gives the absolute market share for each drivetrain. The non-LCV market is divided among ICEV cars, vans, trucks, and SUVs according to the 2017 distribution, as previously described. For all simulations presented in the work, klcv and khev are fixed at 0.3, and only tlcv and thev are varied.
2.3. Gasoline emissions factor (EF)
The 2018 edition of Argonne National Laboratory’s GREET 1 model [28] is used to determine gasoline well-to-pump (upstream) emissions, which are equivalent to 2.175 kg CO2e/gallon (using a heating value of 33.7 kWh/gallon gasoline), such emissions are added to the standard EPA emissions factor for gasoline combustion of 8.887 kg CO2e/gallon, to yield 11.059 kg CO2e/gallon as the lifecycle emissions factor for gasoline
2.4. Electricity EFs, now and future
2.4.1. Grid-average lifecycle emissions factors
Grid-average electricity CO2 EFs are primarily based upon projections from the reference scenario from the EIA’s 2019 Annual Energy Outlook [25]. For future electricity mix and smokestack CO2 emissions, EIA projections specific to each electricity market module for each year from 2017 through 2050 are employed, while beyond 2050, it is assumed that the electricity EF continues to fall at the same average annualized rate as from 2017–2050. A hypothetical rapid decarbonization pathway that imposes a 5% annual (compounded) decrease in the electricity EF from the 2017 baseline is also considered.
EIA scenarios yield smokestack emissions for a given energy mix, but this neglects upstream and downstream lifecycle CO2e emissions. While direct emissions factors from fossil generation are known (or can be calculated) quite precisely, there is appreciable uncertainty in indirect emissions across all generating technologies, and only a “best guess” can be made for each technology, especially as these may change in the future. To estimate lifecycle EFs for fossil generation, the thermal efficiency (TE) of each fossil generating technology is estimated for each year from the reported fuel energy content and total electricity generation, and upstream emissions are determined on the basis of fuel energy content. Indirect emissions from coal mine methane, coal mining and transportation, natural gas extraction operations, and natural gas leakage are determined as discussed in a moment; indirect emissions from nuclear, hydropower, solar, wind, and biomass are estimated from a review of the literature, as also described presently.
Indirect emissions from fossil generation. For coal, 0.02638 kg CO2e/kWh(t) is taken as the upstream EF, based on [29], which in combination with the TE of generation yields an emissions factor on a per kWh(e) basis. This EF includes coal mining operations, transportation, and coal mine methane (using a GWP of 30 for methane). Since oil is only about 0.3% of the total 2017 generating mix, and just 0.1% of the EIA reference 2030 mix, upstream emissions from oil-fired electricity are neglected.
Indirect emissions for natural gas are dominated by methane leakage throughout the extraction and distribution process, and the magnitude of such rogue emissions is a matter of longstanding controversy [30,31,32]. Using 55.5 MJ/kg as the high heating value for methane, it is straightforward to calculate the mass of fugitive methane emissions for any prescribed leakage rate and fuel heat content. While US EPA inventory figures have suggested methane leak rates of about 1.4% [32], field studies and other top-down estimates [33,34] suggest much higher leakage, and that inventories have consistently underestimated methane emissions at all scales of measurement [35,36]. A point estimate of 2.3% for leakage is used based on the recent and comprehensive work by Alvarez et al. [32]. Using this leak rate, a 100-year GWP of 30 for fossil methane, and a TE of 43.7% for gas generation (2017 average) yields upstream emissions of 0.105 kg CO2e/kWh(e) from leakage. Howarth et al. [30] estimated about 13.2 g CO2/kWh(t) for gas extraction operations, giving about 0.135 kg CO2e/kWh(e) of upstream emissions as a national baseline. This figure is adjusted for each individual subetaid and year based upon the specific thermal efficiency of gas generation.
Indirect emissions for non-fossil generation. While nuclear power yields no smokestack CO2, the nuclear lifecycle has nontrivial embodied emissions, and these may increase appreciably in the future as uranium ore grades decline (see, e.g., [37] and [38]). While a relatively wide range of lifecycle emissions factors have been reported (see reviews in [38,39,40,41], the distribution of estimates is skewed to the right, with most estimates under 0.050 kg CO2e/kWh [37,42] and mean estimates hovering around 0.060 kg CO2e/kWh. The middle estimate of 0.058 kg CO2e/kWh from [41] is used as a uniform lifecycle EF for nuclear power.
All renewable electricity generation technologies have associated lifecycle emissions. Some emissions from hydropower originate in dam construction, but the most significant GHG sources are CO2 and CH4 from rotting vegetation in hydropower reservoirs [43]. Such emissions may be systematically underestimated in older literature [44], and may be extremely large in tropical regions. In temperature and boreal regions, such lifecycle emissions are likely lower, with Song et al. [43] recently estimating lifecycle emissions on the order of about 0.100 kg CO2e/kWh for (almost entirely temperate) US hydroelectric reservoir dams. However, Teodoru et al. [45] estimated net reservoir emissions equivalent to 0.158 kg CO2e/kWh over a 100-year dam lifetime for a new dam in Quebec, Canada. Furthermore, while burial of organic sediments in dams reservoir may act as a net carbon sink during the life of the dam, oxidation of such sediments may be a very large carbon source under dam dredging or decommissioning [46]. A relatively conservative lifecycle EF of 0.100 kg CO2e/kWh is used for all hydropower.
Wind power has extremely low lifecycle emissions [47,48,49] which are mainly due to the embodied emissions of steel and cement for turbine tower and base construction, and 0.019 kg CO2e/kWh is used as the baseline estimate for wind, based on Arvesen et al. [48]. Geothermal is a minor electricity source, but fugitive CO2 and CH4 emissions from geofluids averaged 0.0907 kg CO2/kWh and 0.753 gCH4/kWh (22.59 g CO2e using a GWP of 30 for fossil methane) in a survey by Sullivan et al [50], consistent with other estimates [51]; this yields 0.113 kg CO2e/kWh as the lifecycle EF for geothermal power.
Solar photovoltaic (PV) lifecycle emissions are likely on the order of 0.030–0.050 kg CO2e/kWh [52,53,54,55], with the majority of emissions from electricity use at the panel fabrication phase. The exact figure, however, varies with PV technology and panel efficiency, manufacturing process, performance factor of any particular installation, and especially with the solar insolation of the geographic region where the panels are deployed, with much of the southwestern US especially favorable to solar PV [54]. Nevertheless, a broad literature suggests no more than about 0.050 kg CO2e/kWh, with under 0.030 kg CO2e/kWh more likely for more modern systems [54]. An EF of 0.040 kg CO2e/kWh is used as the base estimate for all solar PV, this number is scaled down each year according to the change in grid-average electricity EF.
Finally, biomass and wood are minor components of renewable energy mix in all EIA projections, and determining a single lifecycle emissions factor for electricity from biomass is fraught. Depending upon system boundaries, assumptions, and feedstock, previous studies give a very broad range of lifecycle EFs (see reviews in, e.g., [56,57]), and large carbon “debts” may be incurred from converting natural land to bioenergy crops [58], and from soil organic carbon losses [59] and reductions in standing biomass in harvested forests [60]; continuous forest harvesting may undermine productivity and impair the strong carbon sink action of forests [61,62]. The long-term feasibility and sustainability of large-scale bioenergy harvests from forests has also been challenged [63]. In any case, the common assumption of instantaneous carbon neutrality for biomass cannot be supported [60,64,65], but in the face of uncertainty with respect to an exact emissions factor, a very conservative 0.1 kg CO2e/kWh(e) is used for all biomass (a rough midpoint estimate for different feedstocks in [57], but appreciably smaller than suggested by metrics used in [60,64,65]), but results are not sensitive to this parameter.
Transmission and distribution (T & D) losses. The final EFs for electricity consumption (either grid-average or marginal) are adjusted to take transmission and distribution losses into account. Values for each electrical subetaid are available from the 2016 EPA eGRID database [66], and this loss factor ranges from 4.23% to 5.35%, with 4.49% the mode.
Electric vehicle charging efficiency. The final EFs for electricity consumption are similarly ad- justed to account for the imperfect charging efficiency of electric vehicles, which may plausibly range from 80 to 95% [67]. A 90% charging efficiency is taken as a reasonable midpoint average, as also used by prior authors [67,68].
2.4.2. Marginal electricity emissions factors
EIA projections of generating mixes, smokestack CO2 emissions, and lifecycle emissions adjustments described above give, for each year from 2017 to 2050, a grid-average EF. However, as EVs represent an additional load on the system, it is also appropriate to attempt the analysis using marginal EFs, which are, for an existing grid, generally higher than grid-average, especially in the case of a relatively low-carbon grid but with fossil generation at the margin. Multiple authors have examined large-scale BEV deployment under marginal emissions scenarios, with many considering the marginal EF more appropriate than the grid-average for evaluating the actual impact of EVs [4,9]. Therefore, as a supplemental analysis, marginal EFs for 2017 in the western WECC region only are estimated, using hourly emissions data from the EPA Air Markets Program Data program [69].
To estimate marginal electricity EFs in the four subetaids (CAMX, AZNM, RMPA, NWPP) that make up the WECC region, a variant of the methodology of Siler-Evans et al. is adopted [70], who used a regression analysis on hourly fossil generating data and CO2 emissions to determine how emissions change with a marginal change in power demand. Hourly emissions data for fossil generation were obtained from the EPA Air Markets Program Data program [69] for each hour of 2017. In addition to the reported smokestack emissions, upstream lifecycle emissions were estimated from the calculated (hourly) thermal efficiency of coal and gas generation, as previously described for grid-average EFS. For each subetaid, daily marginal emissions rates are estimated by determining the daily change in fossil generation and CO2e emissions, yielding a daily marginal EF. As described for grid-average emissions, T & D losses are also factored into the final EFs.
2.4.3. Vehicle cycle EFs, now and future
Vehicle manufacture is an energy- and emissions-intensive process, with vehicle-cycle emissions a roughly linear function of vehicle weight and dependent upon the carbon-intensity of the upstream industrial activity. Argonne National Laboratory’s 2018 GREET 2 model [71] for the vehicle-cycle is used as a basis to estimate these emissions as a function of vehicle curb weight, but the battery production emissions factor is modified from the default GREET 2 value, based upon recent literature.
For ICEVs and HEVs, the following linear functions for total GHG emissions (in kg CO2e) as a function of vehicle weight and class were determined from the GREET 2 model [71],
where W is vehicle curb weight in pounds. In the case of BEVs, the battery is an especially important contributor to manufacturing emissions, with multiple studies suggesting emissions on the order of 100–200 kg CO2e/kWh battery capacity for current production methods, and with the majority of these emissions from electricity at the assembly phase. Battery-related emissions in the GREET 2 model are much lower than most of the literature suggests (discussed below), and therefore BEV vehicle-cycle GHG emissions are taken as the sum of non-battery emissions determined from the GREET 2 model (based on vehicle weight minus the battery), plus emissions due to the battery. Mathematically, this gives
where W is curb weight (lbs), Wb is battery weight (lbs), and EFbat is the EF for battery production (kg CO2e/kg). Battery capacity in kWh is converted to weight assuming 140 Wh/kg for Li-ion battery packs. Two studies on commercial battery systems both suggested about 150 kg CO2e/kWh for Li-ion batteries, with Ellingsen et al. [72] giving a minimum EF of 172.9 kg CO2e/kWh for a commercial Norweigan manufacturer of Li-ion batteries, while Kim and colleagues [73] assessed the Ford Focus EV, estimating emissions of 140 kg CO2e/kWh for the vehicle’s 24 kWh Li-ion battery pack. A recent review [74] including 36 studies gave an average embodied energy of 328 Wh and GHG emissions of 110 kg CO2e per kWh of Li-ion storage, and while estimates ranged from 38–356 kg CO2e/kWh in studies reviewed by Ellingsen et al. [75], the few studies [72,73] that have relied on primary manufacturer data give emissions on the order of 150 kg CO2e/kWh. A value of 140 kg CO2/kWh [73] is used as the baseline EF for battery production.
Finally, as a simple approximation for how future vehicle-cycle emissions may change under a changing energy system, it is assumed that vehicle-cycle emissions (including battery production emissions) scale down from the 2017 baseline in direct proportion to the grid-average electricity mix.
3.
Results
3.1. County-level electricity emissions factors
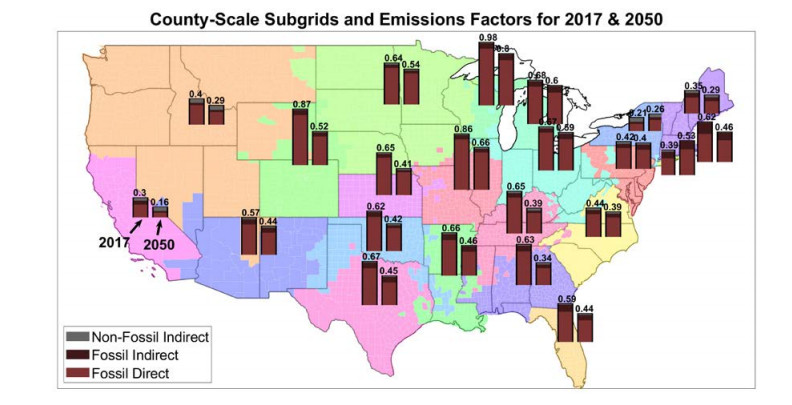
Figure 2 demonstrates how counties are apportioned to electrical grid subregions, with both 2017 and projected 2050 smokestack, upstream fossil, and other lifecycle electricity emissions factors visualized. Marginal emissions factors for the four WECC subregions are presented in the supplementary data.
3.2. Initial county-level fleet and fuel CO2e
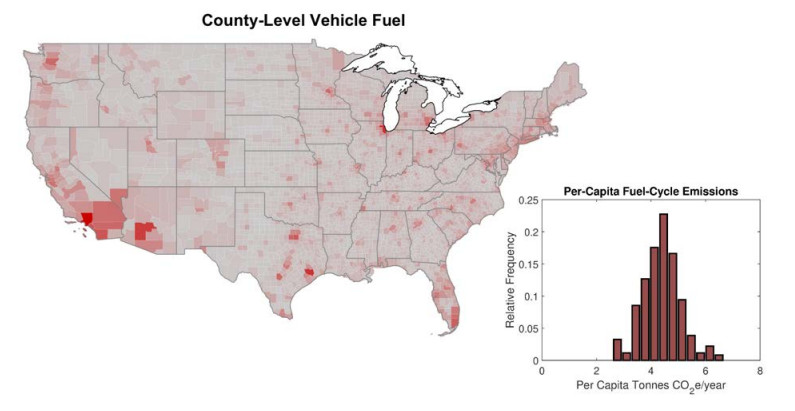
The initial county-level fleets are visualized in Figure 3, where darker red indicates more total annual CO2e emissions from vehicle fuel combustion. Note that absolute, not per capita, emissions are visualized. The per capita CO2e distribution across all counties is also given, showing that most counties are reasonably similar in their baseline emissions profile, but there is appreciable variation.
3.3. Comparisons of representative vehicles under grid-average electricity
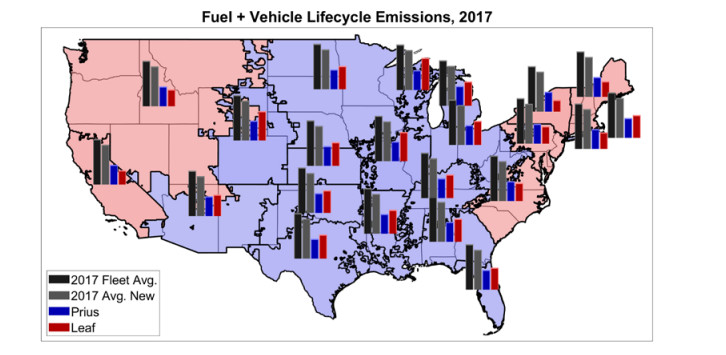
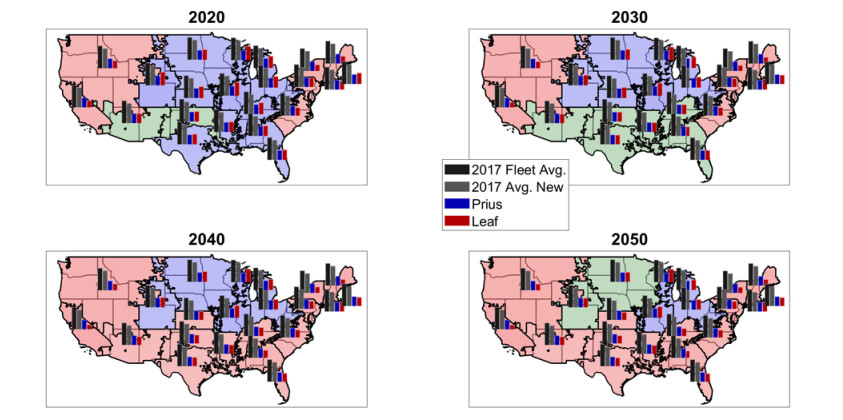
The subetaid-specific lifecycle emissions for several representative vehicles, namely an average light-duty fleet vehicle (21.5 MPG based upon the constructed fleet, and using an average curb weight of 4034 for new vehicles sold from 1998 through 2017 [3]), the average new 2017 vehicle (24.9 MPG, curb weight 4093 lbs [3]), the 2018 Prius 2 Eco (HEV), and the 2018 Nissan Leaf (BEV), are compared in this section. Lifecycle emissions are determined using vehicle manufacturer-reported curb weights and battery capacities, official EPA highway/city combined MPG (or MPGe for BEVs), and under the assumption of a 160, 000 mile vehicle lifespan amortized over 12.8 years (12, 500 miles/year). Results for the 2017 baseline year are shown in Figure 4. Results for 2020, and every decade up to 2050 conditions are given in Figure 5. Note that year and region-specific grid-average electricity EFs are used for these results, and all manufacturing emissions scale down with the change in the national average electricity EF.
In general, both the HEV and BEV are markedly superior to either the current fleet average or typical new vehicle both at baseline and in the future. In 2017, in most of the middle of the country, and especially in the upper Midwest, where the local electricity mixes are coal-heavy, the HEV is appreciably better than the BEV, while on the coasts the BEV tends to be superior. By 2050, the BEV is favorable in nearly all of the country, yet even at this late date the HEV is preferred in parts of the upper Midwest. It may be concluded that, in most of the country, HEVs and BEVs of comparable size are likely relatively similar in their lifecycle emissions profile over the relatively short-term, while BEVs become favorable in the longer-term, when grid-average emissions factors are used to calculate use-phase emissions for BEVs.
These results are generally in accord with prior work, with most previous authors concluding that BEVs are marginally superior to HEVs in the west, Texas, and northeast [10,11,17], while HEVs may be preferred in much of the southeastern region and especially the upper Midwest, where BEVs may perform worse than some ICEVs [4,13].
3.4. Comparison of representative vehicles in 2017 under marginal electricity (WECC region only)
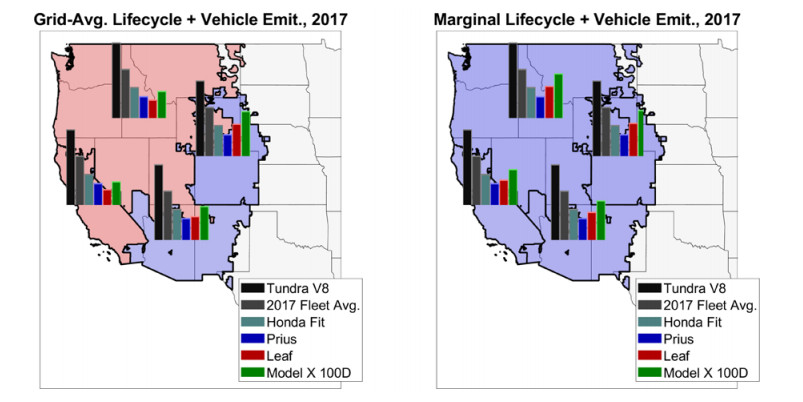
In this section, the lifecycle emissions under either grid-average or marginal electricity for a broader range of vehicles are compared. The vehicles considered include a representative low-efficiency ICEV, the V8 Toyota Tundra (14 MPG); a high-efficiency ICEV, the Honda Fit (36 MPG); the Toyota Prius and Leaf as previously described; and a representative large and relatively inefficient BEV, the Tesla Model X 100D (87 MPGe and 100 kWh battery). Marginal EFs are greater than the grid-averages in all four subregions, and the Prius consistently has the lowest lifecycle emissions using marginal EFs, contrary to the case when grid-average EFs are used. Moreover, the Leaf, while generally better than the Honda Fit, may be similar under more fossil-reliant subetaids, and the Model X 100D is actually worse than the Fit under all four subetaids. Figure 6 gives the amortized lifecycle emissions for these vehicles under both the grid-average and marginal generating mix, for 2017.
Note that previous literature has found that while marginal emissions rates are not uniformly lower than grid-average rates [11,70], marginal EFs are still larger in most grids [70] and as a national average. Therefore, the implication of this limited analysis is likely to generalize nationally, though not necessarily to every subetaid. Anticipating long-term marginal emissions factors under future grids is a challenge, and no attempt do so some is made in this work. However, these results suggest that, when grid-average emissions factors are used, there is likely at least some degree of bias toward the BEV, with this bias larger in cleaner subetaids (e.g., the CAMX subetaid centered on California) and smaller in more fossil-dependent grids.
While the Prius is uniformly superior to the Leaf under this analysis, it must be emphasized that there is a large degree of intra-class variation among all drivetrains, and this analysis does not imply that HEVs are uniformly better (at least in the WECC region) than BEVs under marginal electricity. Rather, when comparing high-efficiency representatives of the two classes, the HEV appears to be superior, and both comparatively low-efficiency HEVs and BEVs can be worse than some high-efficiency ICEVs.
Therefore, it must be kept in mind that the turnover scenarios examined presently assume transitions to highly efficient HEVs and/or BEVs: The efficacy of any given car model in reducing emissions as part of an overall drivetrain transition must be evaluated on an individual basis. Other studies have similarly found appreciable degrees of intraclass variation for vehicles with the same drivetrain technology [14,16].
3.5. Nationally uniform fleet-turnover scenarios
Fleet turnover scenarios are run for 54 years, from 2017 to 2070, with a uniform national market share for new vehicles imposed across all counties. As described in the Methods, new vehicles are drawn from an imposed market share distribution, where new vehicles are either a high efficiency HEV, BEV, or a typical 2017 ICEV. This is clearly a highly idealized turnover process, but it is meant to lend insight into strategies that minimize CO2e emissions primarily, and minimize battery production requirements secondarily.
3.5.1. No turnover, HEV-only, BEV-only and HEV-to-BEV turnovers
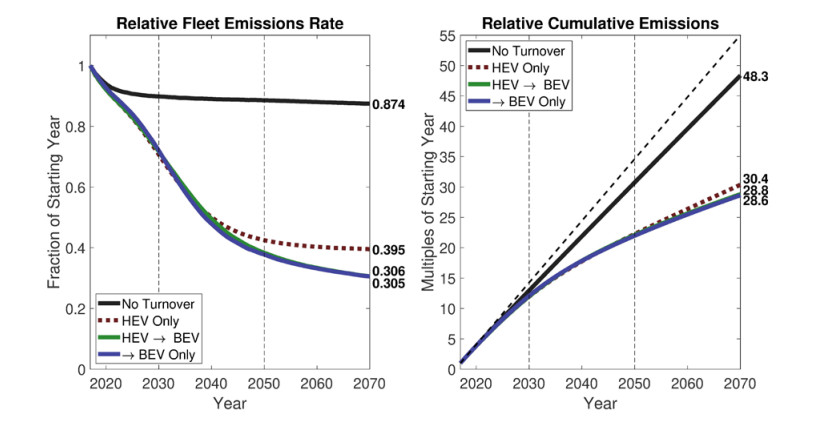
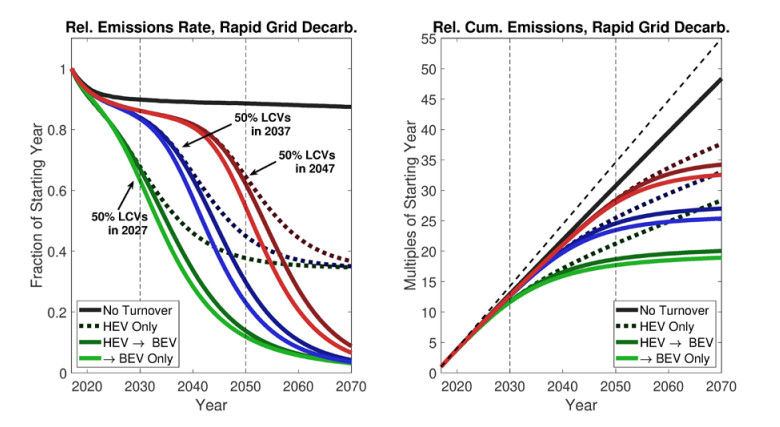
Four idealized scenarios that entail shifts in the drivetrain market share only are considered here. The first is a no turnover scenario and meant as a worst-case baseline, where all new vehicles are ICEVs that follow the same distribution of vehicle type (car, van/minivan, SUV, pickup truck) as the 2017 model year, and with the same average MPG as the respec. Results for this scenario are included in Figure 7, and as can be seen, even in this case cumulative and final emissions decrease relative to a constant 2017 fleet, as older, less efficient ICEVs age out.
Three rapid turnover scenarios are now compared. In all, low-carbon vehicle (LCV) drivetrains reach 50% market share by 2027, and entail (1) an HEV only transition, (2) a BEV-only transiton, and (3) an HEV-to-BEV transition, where HEVs are 50% of the LCV market share in 2032, and subsequently phased out in favor of BEVs. Results are visualized along with the no-turnover scenario in Figure 7. There is virtually no difference between using HEVs as a transitional technology and skipping directly to BEVs. A collection of similar transition scenarios, where LCV market share reaches 50% at different years, are considered as well, and Figure 8 summarizes how cumulative and final emissions change with this “LCV midpoint year, ” and under the three transition permutations. It is clear that an ultimate shift to BEVs is needed to reduce final emissions rates, but HEVs are effective as a transitional technology and help greatly in limiting cumulative emissions.
It is also determined that, under the scenario where LCVs reach a 50% market share by 2027, the internal transition from HEVs to BEVs is of little importance. That is, even when HEVs maintain a nearly 100% market share for several decades, there is little difference in cumulative fleet emissions to 2070, and the emissions rate falls by the endpoint so long as there is an eventual shift to BEVs.
However, even in the best cases, cumulative emissions are nearly 30 years of 2017 emissions by 2070, and emissions rates are still around 30% of the 2017 baseline: While much better than no transition, such an outcome fails to meet ambitious climate targets. As demonstrated in the subsequent sections, behavioral shifts, in terms of decreased miles, as well as eschewing new conventional low MPG vehicle types (SUV, pickup, or van/minivan), can, by themselves decrease cumulative emissions as much as a wholescale transition to LCV drivetrains, while in combination a rapid LCV transition and large-scale behavioral shift can meet climate targets. Even then, it is found that much more rapid decarbonization of the electrical grid is likely necessary to safely meet decarbonization goals, and even this requires a rapid drivetrain transition and is abetted by at least some behavioral shifts.
3.5.2. Behavioral shifts only
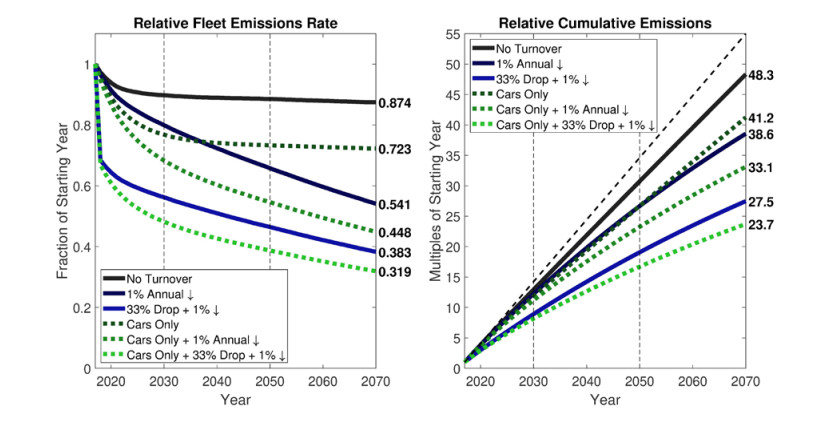
Three variations on behavioral shifts are considered: (1) annual miles driven by all vehicles fall 1% annually (compounded), such that annual miles fall a total of 42% by 2070, (2) an immediate 33% drop in all miles driven then followed by an additional 1% annual drop (and so total miles driven falls by over 60% by 2070), and (3) all new conventional vehicles sales are cars (no truck SUVs, pickups, or vans). The latter also represents a fleet transition, but it is included here to represent a more minor shift in purchasing habits compared to an alternative drivetrain. The first two driving reductions, either with or without the “car-only” condition, along with the car prohibition as a solitary measure, yield six permutations of behavioral changes (including no change), and the final emissions rates and cumulative emissions under these scenarios are given in Figure 9. As shown, ambitious behavioral changes can actually exceed a rapid drivetrain transition in limiting cumulative emissions to 2070, and are nearly as good at limiting final emissions rates.
3.5.3. Behavioral shifts + drivetrain turnover
The HEV-only and HEV-to-BEV drivetrain transition scenarios (results with the BEV-only transition are extremely similar to the HEV-to-BEV transition) are combined with the four behavioral shifts considered above. Under the most agammaessive scenarios, entailing immediate plus continued driving reductions and a rapid HEV-to-BEV transition (2027 LCV midpoint), ambitious climate targets are just barely met in the year 2070, with cumulative emissions of about 18 baseline years, and emissions rates falling to less than 20% of baseline. Since ICEVs are displaced so quickly in these scenarios, the car-only condition has little influence on the outcomes
3.5.4. Rapid electricity decarbonization, plus other changes
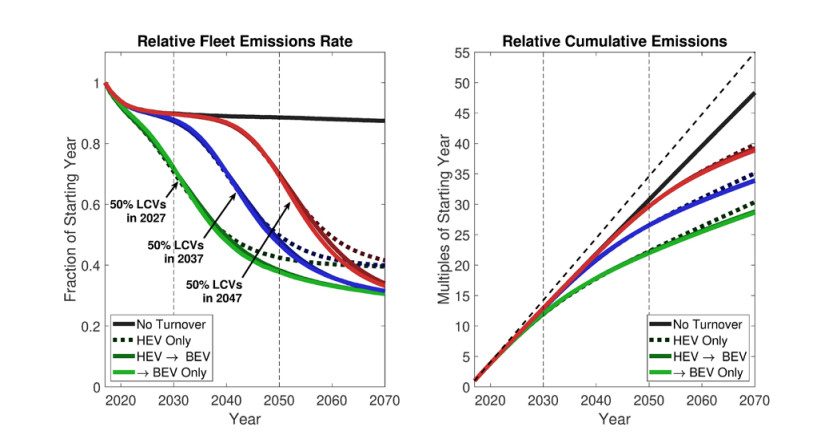
Finally, a 5% annualized reduction in all subetaid emissions factors starting from the 2017 baseline year is imposed under the previously studied drivetrain turnover and behavioral change scenarios. Such rapid decarbonization of the grid unsurprisingly results in lower cumulative and final rates when BEVs are rapidly adopted, and final emissions rates are sufficiently low that long-term decarbonization goals can be considered met, so long as LCVs exceed 50% of market share within about 10 years from the present. However, even in this case, HEVs are a surprisingly effective transitional, though not terminal, technology, with very little differences between the BEV-only and HEV-to-BEV transition scenarios, as demonstrated in Figure 10.
While these results suggest ambitious climate targets can be met by an essentially technological transition, i.e., a very rapid decarbonization of the electrical grid plus a very rapid LCV turnover, some degree of behavioral change provides breathing room, either to decarbonize the grid, or to turn the fleet over. As above, ambitious behavioral changes can compensate almost completely for a slowly decarbonizing grid, while it is also seen that, when the grid is rapidly decarbonized, maximal behavioral shifts buy roughly an extra decade of time to turn the fleet over.
3.6. Subgrid-level optimal transitions
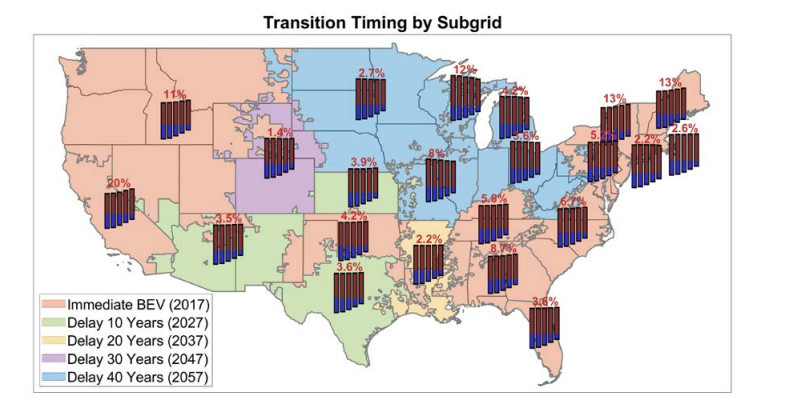
For each electricity subetaid, the optimal timing of an HEV-to-BEV transition, with respect to the timing of a shift from an HEV-dominant market to a BEV-dominant market, is examined. These simulations again assume grid-average electricity powers new BEVs and use the EIA reference scenario for the future grid. Thus, these results, like those for the nationally uniform transitions, should be considered generally (though not necessarily uniformly) biased in favor of BEVs. In all scenarios, imposed LCV market share reaches 50% in 10 years from baseline (2027), while the year at which BEV market share exceeds HEV share varies in intervals of 10 years starting from the year 2017 (i.e., hypothetical LCV sales are already 50% BEVs at the baseline year 2017) through 2057 (i.e., virtually all sales are HEVs until nearly the end of the simulation). In all cases, BEVs make up most of the market share at the end of the simulation, so the idea here is, again, to optimize the timing of HEVs as a transitional, not terminal, technology, in the turnover to an all-BEV fleet.
These turnover scenarios are run for all counties in each electricity sub-grid independently, and the optimum transition year is recorded for each subetaid. Moreover, the emissions difference between the worst- and best-case years is recorded, and compared against the cumulative emissions expected in 2070. For example, in the relatively coal-heavy RMPA subetaid (mainly Colorado and some neighboring areas), it is best to delay the adoption of BEVs somewhat, but the difference between an early and late adoption amounts to only 1.4% of the cumulative emissions generated by this subetaid up to 2070. Delaying adoption of BEVs in many areas has virtually no effect on CO2 emissions, but significantly reduces cumulative battery capacity requirements, and relative emissions and battery production profiles for all subetaids are summarized graphically in Figure 11.
It can be concluded in general that highly efficient HEVs and BEVs are both good options for new vehicles throughout the country, but early adoption of HEVs should be prioritized over BEVs thoughout much of the Midwest and center of the country (and individual HEVs and BEVs should be evaluated on the basis of their individual characteristics). HEVs are still likely an excellent alternative in the rest of the country for the next several decades, and also have the benefit of lowered battery production requirements.
4.
Conclusion
Meeting ambitious climate mitigation targets requires limiting cumulative anthropogenic CO2 emissions over the next 30–50 years, ideally to less than 20 years of present-day emissions, while emissions rates from all human activity must rapidly approach nearly zero by 2050, or 2070 at the latest [2]. This work has examined cumulative CO2e emissions under a realistic representation of the US light duty fleet and electricity grid at the county scale from 2017 through 2070, but under idealized scenarios for fleet drivetrain turnover and behavioral changes.
It is found that an early, rapid, and nation-wide transition to nearly all new vehicles being highly efficient LCVs, either as HEVs or BEVs, is necessary to limit cumulative emissions, and that even this transition must be accompanied by deep reductions in driving to meet climate targets. This is true under both EIA projections for the future electricity mix as well as a hypothetical rapid decarbonization of the electric grids. Hybrid-electric vehicles are found to be an extremely effective transitional technology for limiting emissions, regardless of the short-term evolution of the electricity grid, although limiting emissions rates requires an ultimate transition to fully electrified drivetrains (circa 2050s).
Under both national-scale and the majority of electric sub-grid scale simulations, there is virtually no difference between an early and late adoption of BEVs, so long as LCVs in general are adopted early. However, there is geographic heterogeneity, such HEVs are preferred in the shorter-term in much of the Midwest, while BEVs may be preferable on the coasts. Hybrids vehicles may have an additional short-term advantage in avoiding large additional loads upon the electrical grid expected to be met primarily with relatively dirty marginal generating sources.
Finally, it must be emphasized that the lifecycle emissions associated with individual ICEV, HEV, BEV models vary appreciably, such that the emissions associated with some HEVs and BEVs may overlap those of economy ICEVs, depending upon the geographic region. Every individual vehicle model thus must be assessed individually, but highly efficient HEVs and BEVs are both generally excellent options for limiting emissions, with the former an effective transitional technology.
Acknowledgments
The author thanks Abba B. Gumel for many useful discussions
Conflict of interest
The author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: