The fractal-fractional Atangana-Baleanu operator for pneumonia disease: stability, statistical and numerical analyses

Najat Almutairi; Sayed Saber; Hijaz Ahmad; Najat Almutairi; Sayed Saber; Hijaz Ahmad

doi:10.3934/math.20231504

AIMS Mathematics

2023, Volume 8, Issue 12: 29382-29410. doi: 10.3934/math.20231504

Previous Article Next Article

Research article

The fractal-fractional Atangana-Baleanu operator for pneumonia disease: stability, statistical and numerical analyses

1.
Department of Mathematics, College of Science, Qassim University, Buraidah, Saudi Arabia
2.
Department of Mathematics and Statistics, Faculty of Science, Beni-Suef University, Egypt
3.
Department of Mathematics, Faculty of Science and Arts in Baljurashi, Al-Baha University, Saudi Arabia
4.
Near East University, Operational Research Center in Healthcare, Nicosia, Turkey
5.
Department of Computer Science and Mathematics, Lebanese American University, Beirut, Lebanon
6.
Section of Mathematics, International Telematic University Uninettuno, Corso Vittorio Emanuele Ⅱ, 39, 00186, Rome, Italy

Received: 03 September 2023 Revised: 02 October 2023 Accepted: 11 October 2023 Published: 30 October 2023
MSC : 34C60, 92B05, 92C42, 92D25, 92D30

The present paper studies pneumonia transmission dynamics by using fractal-fractional operators in the Atangana-Baleanu sense. Our model predicts pneumonia transmission dynamically. Our goal is to generalize five ODEs of the first order under the assumption of five unknowns (susceptible, vaccinated, carriers, infected, and recovered). The Atangana-Baleanu operator is used in addition to analysing existence, uniqueness, and non-negativity of solutions, local and global stability, Hyers-Ulam stability, and sensitivity analysis. As long as the basic reproduction number $\mathscr{R}_{0}$ is less than one, the free equilibrium point is local, asymptotic, or otherwise global. Our sensitivity statistical analysis shows that $\mathscr{R}_{0}$ is most sensitive to pneumonia disease density. Further, we compute a numerical solution for the model by using fractal-fractional. Graphs of the results are presented for demonstration of our proposed method. The results of the Atangana-Baleanu fractal-fractional scheme is in excellent agreement with the actual data.

Keywords:

Citation: Najat Almutairi, Sayed Saber, Hijaz Ahmad. The fractal-fractional Atangana-Baleanu operator for pneumonia disease: stability, statistical and numerical analyses[J]. AIMS Mathematics, 2023, 8(12): 29382-29410. doi: 10.3934/math.20231504

Related Papers:

[1]	Kwang-Wu Chen, Fu-Yao Yang . Infinite series involving harmonic numbers and reciprocal of binomial coefficients. AIMS Mathematics, 2024, 9(7): 16885-16900. doi: 10.3934/math.2024820
[2]	Zhi-Hong Sun . Supercongruences involving Apéry-like numbers and binomial coefficients. AIMS Mathematics, 2022, 7(2): 2729-2781. doi: 10.3934/math.2022153
[3]	Shelby Kilmer, Songfeng Zheng . A generalized alternating harmonic series. AIMS Mathematics, 2021, 6(12): 13480-13487. doi: 10.3934/math.2021781
[4]	Wenbin Zhang, Yong Zhang, Jiachen Wu . A Ramanujan-type supercongruence related to harmonic numbers. AIMS Mathematics, 2025, 10(5): 11444-11464. doi: 10.3934/math.2025521
[5]	Xuqiong Luo . A D-N alternating algorithm for exterior 3-D problem with ellipsoidal artificial boundary. AIMS Mathematics, 2022, 7(1): 455-466. doi: 10.3934/math.2022029
[6]	Jiaye Lin . Evaluations of some Euler-type series via powers of the arcsin function. AIMS Mathematics, 2025, 10(4): 8116-8130. doi: 10.3934/math.2025372
[7]	Ling Zhu . Asymptotic expansion of a finite sum involving harmonic numbers. AIMS Mathematics, 2021, 6(3): 2756-2763. doi: 10.3934/math.2021168
[8]	Andrea Ratto . Higher order energy functionals and the Chen-Maeta conjecture. AIMS Mathematics, 2020, 5(2): 1089-1104. doi: 10.3934/math.2020076
[9]	Aleksa Srdanov . Invariants in partition classes. AIMS Mathematics, 2020, 5(6): 6233-6243. doi: 10.3934/math.2020401
[10]	Kholood M. Alsager, Sheza M. El-Deeb, Ala Amourah, Jongsuk Ro . Some results for the family of holomorphic functions associated with the Babalola operator and combination binomial series. AIMS Mathematics, 2024, 9(10): 29370-29385. doi: 10.3934/math.20241423

Abstract

1. Introduction and outline

Let $\mathbb{N}$ be the set of natural numbers with $\mathbb{N}_0 = \mathbb{N}\cup\{0\}$ . For $n \in \mathbb{N}_0$ , the following harmonic-like numbers are given by partial sums:

● The classical harmonic number and its quadratic counterpart

$\mathbf{H}_{{n}} = \sum\limits_{k = 0}^{n-1}\frac1{k+1} \quad\text{and}\quad \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle} = \sum\limits_{k = 0}^{n-1}\frac1{(k+1)^{2}}.$

● Skew harmonic number and its quadratic counterpart

$\mathbf{O}_{{n}} = \sum\limits_{k = 0}^{n-1}\frac1{2k+1} \quad\text{and}\quad \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle} = \sum\limits_{k = 0}^{n-1}\frac1{(2k+1)^{2}}.$

● Alternating harmonic number and its quadratic counterpart

$\bar{ \mathbf{H}}_{{n}} = \sum\limits_{k = 0}^{n-1}\frac{(-1)^k}{k+1} \quad\text{and}\quad \bar{ \mathbf{H}}_{{n}}^{ \langle{{{2}}}\rangle} = \sum\limits_{k = 0}^{n-1}\frac{(-1)^k}{(k+1)^{2}}.$

Among them, there are the following simple but useful relations:

$\begin{align} & \mathbf{H}_{{2n}} = \mathbf{O}_{{n}}+\frac{ \mathbf{H}_{{n}}}{2}, &\qquad& \mathbf{H}_{{2n}}^{ \langle{{{2}}}\rangle} = \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle}+\frac{ \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}}{4};\\ &\bar{ \mathbf{H}}_{{2n}} = \mathbf{O}_{{n}}-\frac{ \mathbf{H}_{{n}}}{2}, &&\bar{ \mathbf{H}}_{{2n}}^{ \langle{{{2}}}\rangle} = \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle}-\frac{ \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}}{4}. \end{align}$

Harmonic numbers and their variants have been studied since the distant past and are involved in diverse fields (cf. ^{[1,5,6,7,11,17,18]}) such as analysis of algorithms in computer science, various topics of number theory, and combinatorial analysis. In this paper, we aim at presenting several algebraic identities about infinite series involving harmonic-like numbers, the binomial coefficient $\binom{3n}{n}$ in numerators, and a free variable " $y$ ".

For $n\in\mathbb{{N}}_0$ and an indeterminate $x$ , the shifted factorials (cf. [3, §1.1])) are usually defined by

$(x)_0 = 1 \quad\text{and}\quad (x)_n = x(x+1)\cdots(x+n-1) \quad\text{for}\quad n\in\mathbb{{N}}.$

Denote by $[x^m]\phi(x)$ the coefficient of $x^m$ in the formal power series $\phi(x)$ . Then we can express harmonic-like numbers (see ^[11,18]) by extracting the initial coefficients of $x$ from the quotients of shifted factorials as below:

$\begin{align} &[x]\frac{(1+x)_n}{n!} = \mathbf{H}_{{n}}, &\qquad&[x^2]\frac{(1+x)_n}{n!} = \frac{ \mathbf{H}_{{n}}^{{2}}- \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}}{2}, \\ &[x]\frac{n!}{(1-x)_n} = \mathbf{H}_{{n}}, &&[x^2]\frac{n!}{(1-x)_n} = \frac{ \mathbf{H}_{{n}}^{{2}}+ \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}}{2}, \\ &[y]\frac{(\frac12+y)_n}{(\frac12)_n} = 2 \mathbf{O}_{{n}}, &&[y^2]\frac{(\frac12+y)_n}{(\frac12)_n} = 2( \mathbf{O}_{{n}}^{{2}}- \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle}), \\ &[y]\frac{(\frac12)_n}{(\frac12-y)_n} = 2 \mathbf{O}_{{n}}, &&[y^2]\frac{(\frac12)_n}{(\frac12-y)_n} = 2( \mathbf{O}_{{n}}^{{2}}+ \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle}). \end{align}$

There exist many infinite series identities involving central binomial coefficients (see ^{[12,14,19,25]}). However, the closed form evaluations for the known series with $\binom{3n}{n}$ are rare. In a recent paper, Sun ^[23] reported several remarkable infinite series identities, detected by numerical experimentation. Among them, the following three (see [23, Eqs (2.12), (2.13), and (2.15)]) seem rather challenging:

$\begin{align} & \sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n} \mathbf{H}_{{2n}} = \frac{1+\sqrt3}2\Big\{\sqrt3\ln2-3\ln(3-\sqrt3)\Big\}, \end{align}$

(1.1)

$\begin{align} & \sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n} \mathbf{H}_{{3n}} = \frac{1+\sqrt3}4\ln\Big(\frac{4(7+4\sqrt3)}3\Big)-\sqrt3\ln2, \end{align}$

(1.2)

$\begin{align} & \sum\limits_{n = 1}^{\infty}\Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n}\Big\{ \mathbf{H}_{{3n}}- \mathbf{H}_{{2n}}\Big\} = \frac{1+\sqrt5}{2}\ln\Big(\frac{9-3\sqrt5}{2}\Big). \end{align}$

(1.3)

When making efforts to confirm these three formulae, two substantial novelties emerged. First, not only the harmonic numbers $\mathbf{H}_{{3n}}$ and $\mathbf{H}_{{2n}}$ are separable in the third series, but also independent series involving $\mathbf{H}_{{n}}$ and $\mathbf{O}_{{n}}$ can be evaluated explicitly in closed form (cf. Corollaries 6 and 10). Another surprising novelty (see Theorems 1 and 5) lies in the fact that these series are particular cases of more general algebraic identities containing a free variable " $y$ ", corresponding to the convergent rates of these numerical series. To our knowledge, most of the infinite series identities presented in this paper have not appeared previously in the literature.

The rest of the paper is organized as follows. As preliminaries, we shall evaluate, in closed form, three series containing binomial coefficient $\binom{3n}{n}$ , harmonic number $\mathbf{H}_{{n}}$ and a free variable " $y$ " by integrating Lambert's series. Then in Sections 3–5, three classes of infinite series with harmonic-like numbers will be examined by applying the "coefficient extraction" method (see ^[8,13,24]) to cubic transformations for the $_3{F_2}$ -series, that result in several algebraic identities about these series and confirm or refine, as special numerical examples, three conjectured identities made recently by Sun ^[23]. Finally, the paper will end with Section 6, where concluding remarks and further problems are provided.

2. Lambert series weighted by harmonic numbers

In classical analysis and enumerative combinatorics, Lambert's binomial series are well-known (see Riordan [, §4.5] and ^[9,10,16]), which can be reproduced as follows: Let $T$ and $\tau$ be the two variables related by the equation $\tau = T/(1+T)^{ \beta}$ . Then

$\begin{equation} { (1+T)^{ \alpha} = \sum\limits_{k = 0}^{\infty} \frac{ \alpha}{ \alpha+k \beta} \binom{ \alpha+k \beta}{k}\tau^k \quad\text{and}\quad \frac{(1+T)^{ \alpha+1}}{1+T-T \beta} = \sum\limits_{k = 0}^{\infty} \binom{ \alpha+k \beta}{k}\tau^k.} \end{equation}$

(2.1)

As preliminaries, we are going to evaluate, in closed form, three series containing ternary coefficient $\binom{3n}{n}$ and a free variable " $y$ " by integrating across the above two equations, that will be crucial for demonstrating infinite series identities involving harmonic numbers in the subsequent sections.

2.1. Series with $\mathbf{H}_{{n}}$

For " $\alpha = 0$ and $\beta = 3$ ", performing the replacement $\tau\to{xy}/{(1+y)^3}$ in Lambert's second series, we can state the resulting equality as

$\begin{equation} { \phi(T): = \frac{1+T}{1-2T} = \sum\limits_{n = 0}^{\infty} \binom{3n}{n}\frac{(xy)^n}{(1+y)^{3n}}: \qquad {x = \frac{T(1+y)^3}{y(1+T)^3}}.} \end{equation}$

(2.2)

Since the rightmost function is monotone around $T = 0$ , it determines an implicit inverse function $T = T(x)$ in the neighborhood of $x = 0$ with particular values " $T(0) = 0$ and $T(1) = y$ ".

By expressing the harmonic number $\mathbf{H}_{{n}}$ in terms of the integral

$\mathbf{H}_{{n}} = \int_0^1\frac{1-x^n}{1-x}dx,$

we can insert $\mathbf{H}_{{n}}$ in the series (2.2) as follows:

$\begin{align*} \sum\limits_{n = 0}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}\; y^n}{(1+y)^{3n}} & = \int_0^1\frac{\phi(T(1))-\phi(T(x))}{1-x}dx\\ & = \frac{(1+y)^3}{y}\int_0^y\frac{1-2T}{(1+T)^4} \frac{\frac{1+y}{1-2y}-\frac{1+T}{1-2T}}{1-\frac{T(1+y)^3}{y(1+T)^3}}dT\\ & = (1+y)^3\int_0^y\frac{1-\frac{(1-2T)(1+y)}{(1+T)(1-2y)}}{T(1+y)^3-y(1+T)^3}dT, \end{align*}$

where the change of variable $x = \dfrac{T(1+y)^3}{y(1+T)^3}$ has been made so that the integral becomes explicit.

For the sake of brevity, the notation " $\rho$ " will be fixed, throughout the paper, for the algebraic number

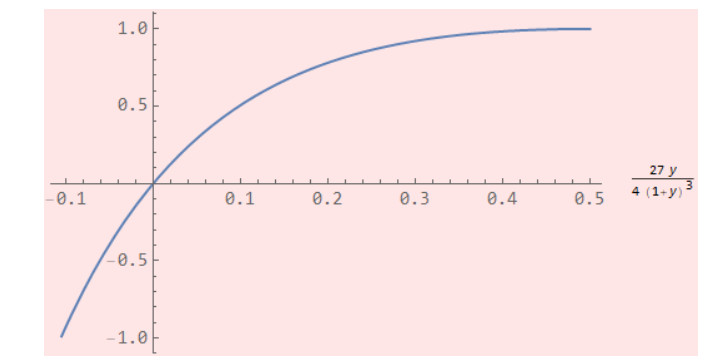
$\begin{equation} {\rho: = \frac32(\sqrt2+1)^{1/3}-\frac32(\sqrt2-1)^{1/3}-1\approx-0.105892543.} \end{equation}$

(2.3)

The convergence region of the preceding series is determined by

$-1 < \frac{27y}{4(1+y)^3} < 1, \quad \rho < y < \frac12.$

This can be illustrated graphically as below:

Figure 1. Range of convergence.

DownLoad: Full-Size Img PowerPoint

By decomposing the integrand into partial fractions

$\begin{align*} \frac{1-\frac{(1-2T)(1+y)}{(1+T)(1-2y)}}{T(1+y)^3-y(1+T)^3} & = \frac{3}{(1+T) (1+y)^2 (1-2 y)} -\frac3{2(1+y)^2(1-2y)\sqrt{4+y}}\\ &\times\Bigg\{\frac{\sqrt{4+y}+\sqrt{y}} {T+\frac{\sqrt{y}(3+y)-(1+y) \sqrt{4+y}}{2\sqrt{y}}} +\frac{\sqrt{4+y}-\sqrt{y}} {T+\frac{\sqrt{y}(3+y)+(1+y)\sqrt{4+y}}{2\sqrt{y}}}\Bigg\}, \end{align*}$

we can explicitly compute the integral

$\begin{align*} \int_0^y\frac{1-\frac{(1-2T)(1+y)}{(1+T)(1-2y)}}{T(1+y)^3-y(1+T)^3}dT & = \frac{3\ln(1+y)}{(1+y)^2(1-2y)}\\ &\; +\frac{3(\sqrt{y}-\sqrt{4+y})}{2(1+y)^2(1-2y)\sqrt{4+y}} \ln\Big(\frac{(1+y)(2-2y-y^2+y\sqrt{y^2+4y})}{2}\Big)\\ &\; -\frac{3(\sqrt{y}+\sqrt{4+y})}{2(1+y)^2(1-2y)\sqrt{4+y}} \ln\Big(\frac{(1+y)(2-2y-y^2-y\sqrt{y^2+4y})}{2}\Big). \end{align*}$

By cancelling the three terms containing $\ln(1+y)$ and then making substitution, we find the closed formula for the series as in the theorem below:

Theorem 1 ( $\rho < y < 1/2$ ).

$\begin{align*} \sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}\; y^n}{(1+y)^{3n}} & = (1+y)^3\int_0^y\frac{1-\frac{(1-2T)(1+y)}{(1+T)(1-2y)}}{T(1+y)^3-y(1+T)^3}dT\\ & = \frac{3(1+y)\ln(1-2y)}{2(2y-1)} +\frac{3(1+y)\sqrt{y}}{2(1-2y)\sqrt{4+y}} \ln\Big(\frac{2-y(2+y-\sqrt{y^2+4y})}{2-y(2+y+\sqrt{y^2+4y})}\Big). \end{align*}$

2.2. Series with $\mathbf{H}_{{n}}/(1+2n)$

For " $\alpha = 1$ and $\beta = 3$ ", performing the replacement $\tau\to{xy}/{(1+y)^3}$ , we can rewrite Lambert's first series as

$\begin{equation} { \psi(T): = 1+T = \sum\limits_{n = 0}^{\infty} \binom{3n}{n}\frac{(xy)^n}{(1+2n)(1+y)^{3n}}: \qquad {x = \frac{T(1+y)^3}{y(1+T)^3}}.} \end{equation}$

(2.4)

Analogously, by putting the harmonic number $\mathbf{H}_{{n}}$ inside the series (2.4), we have

$\begin{align*} \sum\limits_{n = 0}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}\; y^n}{(1+2n)(1+y)^{3n}} & = \int_0^1\frac{\psi(T(1))-\psi(T(x))}{1-x}dx \quad \boxed{x = \frac{T(1+y)^3}{y(1+T)^3}}\\ & = \frac{(1+y)^3}{y}\int_0^y \frac{(y-T)(1-2T)\; dT}{(1+T)^4\big\{1-\frac{T(1+y)^3}{y(1+T)^3}\big\}}\\ & = \int_0^y\frac{(1+y)^3(T-y)(1-2T)\; dT}{(1+T)\big\{T(1+y)^3-y(1+T)^3\big\}}\\ & = \int_0^y\frac{(1+y)^3(1-2T)\; dT}{(1+T)(1-T^2y-Ty^2-3Ty)}. \end{align*}$

By decomposing the integrand into partial fractions

$\begin{align*} \frac{(1+y)^3(1-2T)\; dT}{(1+T)(1-T^2y-Ty^2-3Ty)} = &3\frac{1+y}{1+T} -\frac{(1+y)(3\sqrt{y}+\sqrt{4+y})}{2\sqrt{y} \big(T+\frac{(3+y)\sqrt{y}+(1+y)\sqrt{4+y}}{2\sqrt{y}}\big)}\\ -&\frac{(1+y)(3\sqrt{y}-\sqrt{4+y})}{2\sqrt{y} \big(T+\frac{(3+y)\sqrt{y}-(1+y)\sqrt{4+y}}{2\sqrt{y}}\big)}, \end{align*}$

we can explicitly compute the integral

$\begin{align*} \int_0^y\frac{(1+y)^3(1-2T)\; dT}{(1+T)(1-T^2y-Ty^2-3Ty)} & = 3(1+y)\ln(1+y)\\ &-\frac{(1+y)(3\sqrt{y}+\sqrt{4+y})}{2\sqrt{y}} \ln\bigg(\frac{(1+y)(3\sqrt{y}+\sqrt{4+y})} {(3+y)\sqrt{y}+(1+y)\sqrt{4+y}}\bigg)\\ &-\frac{(1+y)(3\sqrt{y}-\sqrt{4+y})}{2\sqrt{y}} \ln\bigg(\frac{(1+y)(3\sqrt{y}-\sqrt{4+y})} {(3+y)\sqrt{y}-(1+y)\sqrt{4+y}}\bigg), \end{align*}$

which is simplified into the closed formula as in the theorem below:

Theorem 2 ( $\rho < y < 1/2$ ).

$\begin{align*} \sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}\; y^n}{(1+2n)(1+y)^{3n}} = &\int_0^y\frac{(1+y)^3(1-2T)\; dT}{(1+T)(1-T^2y-Ty^2-3Ty)}\\ = &\frac{(1+y)\sqrt{4+y}}{2\sqrt{y}} \ln\Big(\frac{2-y(2+y+\sqrt{y^2+4y})}{2-y(2+y-\sqrt{y^2+4y})}\Big) -\frac32(1+y)\ln(1-2y). \end{align*}$

2.3. Series with $\mathbf{H}_{{n}}/n$

Alternatively, rewriting Lambert's first series

$\frac{(1+T)^{ \alpha}-1}{ \alpha} = \sum\limits_{n = 1}^{\infty} \frac{1}{ \alpha+n \beta} \binom{ \alpha+n \beta}{n}\tau^n: \; \quad{\tau = T/(1+T)^{ \beta}}$

and letting " $\alpha\to0$ and $\beta = 3$ ", we deduce the identity

$\begin{equation} { { \sigma(T)}: = 3\ln(1+T) = \sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{(xy)^n}{n(1+y)^{3n}}: \quad {x = \frac{T(1+y)^3}{y(1+T)^3}}.} \end{equation}$

(2.5)

By inserting $\mathbf{H}_{{n}}$ in the above series, we obtain an integral expression

$\begin{align*} \sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}(xy)^n}{n(1+y)^{3n}} & = \int_0^1\frac{ \sigma\big(T(1)\big)- \sigma\big(T(x)\big)}{1-x}dx \qquad\boxed{x\to\frac{T(1+y)^3}{y(1+T)^3}}\\ & = 3\int_0^y\ln\Big(\frac{1+T}{1+y}\Big) \frac{(1-2 T) (1+y)^3}{(1+T) (T-y)(1-T^2 y-T y^2-3 T y)}dT\\ & = 3\int_0^y\ln\Big(\frac{1+T}{1+y}\Big)\bigg\{\frac{1}{T-y}-\frac{3}{1+T} +\frac{y^2+3 y+2 T y}{T^2 y+T y^2+3 T y-1}\bigg\}dT. \end{align*}$

In view of the partial fraction decomposition

$\begin{align*} \frac{y^2+3 y+2 T y}{T^2 y+T y^2+3 T y-1} = \frac1{T+\dfrac{\sqrt{y}(3+y)+(1+y)\sqrt{4+y}}{2\sqrt{y}}\big)} +\frac1{T+\dfrac{\sqrt{y}(3+y)-(1+y)\sqrt{4+y}}{2\sqrt{y}}\big)}, \end{align*}$

it suffices to evaluate, for a parameter $\lambda$ subject to $T+ \lambda\not = 0$ for $T\in(0, y)$ , the parametric integral

$\begin{align*} J( \lambda, y) = \int_0^y\ln\Big(\frac{1+T}{1+y}\Big)\frac{dT}{T+ \lambda} & = \mathrm{Li}_2\Big(\frac{1+y}{1- \lambda}\Big) - \mathrm{Li}_2\Big(\frac{1}{1- \lambda}\Big) +\ln\Big(\frac{ \lambda}{ \lambda-1}\Big)\ln(1+y), \end{align*}$

with particular cases

$J(1, y) = -\frac12\ln^2(1+y) \quad\text{and}\quad J(-y, y) = \frac{\pi^2}6 +\ln(1+y)\ln\Big(\frac{y}{1+y}\Big) - \mathrm{Li}_2\Big(\frac1{1+y}\Big).$

Hereafter, the dilogarithm function (see Lewin [, §1.1]) is defined for all complex values of $z$ by

$\mathrm{Li}_2(z) = \int_0^z\frac{\ln(1-\tau)}{-\tau} \quad\text{and}\quad \mathrm{Li}_2(z) = \sum\limits_{n = 1}^{\infty}\frac{z^n}{n^2} \quad\text{for}\quad |z|\le1.$

By making substitution and then simplifying the terms concerning logarithms and dilogarithms in the resulting expression, we find the explicit formula as in the following theorem:

Theorem 3 ( $\rho < y < 1/2$ ).

$\begin{align*} \sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}\; y^n}{n(1+y)^{3n}} & = \int_0^y\frac{-3\; dT}{1+T}\ln\Big(1-\frac{T(1+y)^3}{y(1+T)^3}\Big)\\ & = {\frac{\pi^2}2+3\Theta(y)+3\ln(1+y)\ln\Big(\frac{y}{\sqrt{(1+y)^3}}\Big)}, \end{align*}$

where, for simplicity, $\Theta(y)$ denotes the sum of five dilogarithmic values

$\begin{align*} \Theta(y)& = \mathrm{Li}_2\Big(\frac{y-\sqrt{y^2+4y}}2\Big) + \mathrm{Li}_2\Big(\frac{y+\sqrt{y^2+4y}}2\Big)\\ &- \mathrm{Li}_2\Big(\frac{y-\sqrt{y^2+4y}}{2+2y}\Big) - \mathrm{Li}_2\Big(\frac{y+\sqrt{y^2+4y}}{2+2y}\Big) - \mathrm{Li}_2\Big(\frac{1}{1+y}\Big). \end{align*}$

3. Series with $\binom{3n}{n}$ and harmonic-like numbers

According to Bailey ^[3], the classical hypergeometric series reads as

${_{1+p}F_p}\left[ \begin{array}{{r}}{a_0, a_1, a_2, \cdots, a_p}\\{b_1, b_2, \cdots, b_p} \end{array}{\Big|{z}}\right] = \sum\limits_{k = 0}^{\infty}\frac{z^k}{k!} \frac{(a_0)_k(a_1)_k(a_2)_k\cdots(a_p)_k}{(b_1)_k(b_2)_k\cdots(b_p)_k}.$

We shall confine ourselves only to examining the series with $|z| < 1$ and none of the parameters in the numerator and denominator being a non-positive integer, which imply that the corresponding series is well-defined and convergent.

There are many transformation and summation formulae for hypergeometric series (see Bailey ^[3] and Brychkov [4, Chapter 8]) in the literature. In 1928, Bailey ^[2] discovered an important cubic transformation (see the next section). Half a century later, Gessel and Stanton [15, Eq (5.4)] found the following counterpart

$_3{F_2}\left[ {\begin{array}{*{20}{c}} {\frac{{1 + a}}{3},\frac{{2 + a}}{3},\frac{{3 + a}}{3}}\\ {\frac{{1 + a + c}}{2},\;\frac{{2 + a - c}}{2}} \end{array}|\;\frac{{27y}}{{4{{(1 + y)}^3}}}} \right]\; = \frac{{{{(1 + y)}^{1 + a}}}}{{1 - 2y}}{ \times _4}{F_3}\left[ {\begin{array}{*{20}{c}} {1 + \frac{a}{3},a,\;c,\;1 - c}\\ {\frac{a}{3},\frac{{1 + a + c}}{2},\;\frac{{2 + a - c}}{2}} \end{array}|\frac{{ - y}}{4}} \right].$

(3.1)

Under the parameter replacements " $a\to 6ax, \; c\to2cx$ ", this transformation can be reformulated as

$\begin{equation} \begin{aligned}[{c}]&\sum\limits_{n = 0}^{\infty} \Big(\frac{y}{4(1+y)^3}\Big)^n \frac{(1+6ax)_{3n}}{n!(1+3ax-cx)_n(\frac12+3ax+cx)_n}\\ &\; = \frac{(1+y)^{1+6ax}}{1-2y} \Bigg\{1+6cx\sum\limits_{k = 1}^{\infty}\Big(\frac{-y}4\Big)^k \frac{(k+2ax)(1+6ax)_{k-1}(1+2cx)_{k-1}(1-2cx)_k} {k!(1+3ax-cx)_k(\frac12+3ax+cx)_k}\Bigg\}, \end{aligned} \end{equation}$

(3.2)

where " $y\in(\rho, \tfrac12)$ ", or equivalently, $\dfrac{27y}{4(1+y)^3}\in(-1, 1)$ so that the series are convergent.

The above transformation is an analytic equality with respect to $x$ in the neighborhood of $x = 0$ . Equating the constant terms on both sides yields the algebraic identity below:

$\sum\limits_{n = 0}^{\infty} \binom{3n}{n}\frac{y^n}{(1+y)^{3n}} = \frac{1+y}{1-2y}.$

As illustrated in the introduction, harmonic-like numbers can be expressed in terms of $x$ -coefficients from quotients of shifted factorials. By examining the coefficients of $x$ across the above equation, we find that the corresponding equation involving harmonic numbers can be written as

$\begin{align*} &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \Big\{6a \mathbf{H}_{{3n}}-(3a-c) \mathbf{H}_{{n}}-2(3a+c) \mathbf{O}_{{n}}\Big\}\\ &\; = 6a\frac{1+y}{1-2y}\ln(1+y) +6c\frac{1+y}{1-2y}\sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{(\frac12)_k}\Big(\frac{-y}4\Big)^k. \end{align*}$

The rightmost series admits the closed form expression, as in the lemma below:

Lemma 4 ( $-4 < y < 4$ ).

$\mathrm{W}(y) = \sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{(\frac12)_k}\Big(\frac{-y}4\Big)^k = -\sqrt{\frac{4y}{4+y}} \mathrm{ArcTanh}\sqrt{\frac{y}{4+y}} = \sqrt{\frac{4y}{4+y}}\ln\frac{\sqrt{4+y}-\sqrt{y}}{2}.$

Proof. Recall the beta function (see [21, §16])

$B(a, b) = \int_0^1x^{a-1}(1-x)^{b-1}dx = \frac{ \Gamma(a) \Gamma(b)}{ \Gamma(a+b)}, \quad\text{where}\quad \Re(a) > 0 \quad\text{and}\quad \Re(b) > 0.$

We can express $\mathrm{W}(y)$ as a definite integral

$\begin{align*} \mathrm{W}(y)& = \sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{(\frac12)_k}\Big(\frac{-y}4\Big)^k = \sum\limits_{k = 1}^{\infty}B\Big(k, \frac12\Big) \Big(\frac{-y}4\Big)^k\\ & = \sum\limits_{k = 1}^{\infty} \Big(\frac{-y}4\Big)^k \int_0^1\frac{x^{k-1}dx}{\sqrt{1-x}} = \int_0^1\frac{dx}{x\sqrt{1-x}} \sum\limits_{k = 1}^{\infty}\Big(\frac{-xy}4\Big)^k\\ & = \int_0^1\frac{-y\; dx}{\sqrt{1-x}(4+xy)} = \int_0^1\frac{-2y}{4+y-T^2y}dT, \end{align*}$

where the last line is justified by the change of variable $\sqrt{1-x}\to T$ . Then the formula in the lemma follows by evaluating the last integral explicitly. □

Therefore, we find the general formula below:

By specifying two parameters, $a$ and $c$ , we deduce four independent series

$\begin{align} &a = 0: &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\bar{ \mathbf{H}}_{{2n}} = 3\frac{1+y}{1-2y} \mathrm{W}(y), \\ &c = 0: &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\Big\{ \mathbf{H}_{{3n}}- \mathbf{H}_{{2n}}\Big\} = \frac{1+y}{1-2y}\ln(1+y), \\ &c = 3a: &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\Big\{ \mathbf{H}_{{3n}}-2 \mathbf{O}_{{n}}\Big\} = \frac{1+y}{1-2y}\ln(1+y) -3\frac{1+y}{1-2y} \mathrm{W}(y), \\ &c = -3a: &\quad&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \Big\{ \mathbf{H}_{{3n}}- \mathbf{H}_{{n}}\Big\} = \frac{1+y}{1-2y}\ln(1+y) +3\frac{1+y}{1-2y} \mathrm{W}(y). \end{align}$

Combining the above formulae with Theorem 1 and then keeping in mind the equalities

$\begin{align*} \mathbf{H}_{{2n}}& = \bar{ \mathbf{H}}_{{2n}}+ \mathbf{H}_{{n}}, \\ \mathbf{O}_{{n}}\; & = \bar{ \mathbf{H}}_{{2n}}+\frac{ \mathbf{H}_{{n}}}2, \\ \mathbf{H}_{{3n}}& = ( \mathbf{H}_{{3n}}- \mathbf{H}_{{n}})+ \mathbf{H}_{{n}}, \end{align*}$

we establish further closed formulae for four series with a free variable " $y$ ".

Theorem 5 ( $\rho < y < 1/2$ ).

$\begin{align} &\text{(a)} &&\sum\limits_{n = 1}^{\infty} \binom{3n}{n} \frac{\bar{ \mathbf{H}}_{{2n}}\; y^n}{(1+y)^{3n}} && = \frac{3+3y}{1-2y}\sqrt{\frac{4y}{4+y}} \ln\frac{\sqrt{4+y}+\sqrt{y}}{2}, \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty} \binom{3n}{n} \frac{ \mathbf{H}_{{2n}}\; y^n}{(1+y)^{3n}} && = \frac{3+3y}{2-4y}\sqrt{\frac{y}{4+y}} \ln\Big(\frac{2(1+y+\sqrt{y^2+4y})} {2-y(2+y+\sqrt{y^2+4y})}\Big) -\frac{(3+3y)\ln(1-2y)}{2(1-2y)}, \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty} \binom{3n}{n} \frac{ \mathbf{O}_{{n}}\; y^n}{(1+y)^{3n}} && = \frac{3+3y}{2-4y}\sqrt{\frac{y}{4+y}} \ln\Big(\frac{1+y+\sqrt{y^2+4y}} {\sqrt{1-2y}}\Big) -\frac{(3+3y)\ln(1-2y)}{4(1-2y)}, \\ &\text{(d)} &\quad&\sum\limits_{n = 1}^{\infty} \binom{3n}{n} \frac{ \mathbf{H}_{{3n}}\; y^n}{(1+y)^{3n}} && = \frac{1+y}{2-4y}\ln\Big(\frac{(1+y)^2}{(1-2y)^3}\Big) +\frac{3+3y}{2-4y}\sqrt{\frac{y}{4+y}} \ln\Big(\frac{2(1+y+\sqrt{y^2+4y})} {2-y(2+y+\sqrt{y^2+4y})}\Big). \end{align}$

Numerous infinite series identities with different convergence rates can be derived by assigning particular values for $y$ in Theorems 1 and 5. Five groups of representative examples are recorded as corollaries. In particular, the second formula (b) and the last formula (e) displayed in Corollary 6 confirm (1.1) and (1.2) conjectured by Sun [23, Eqs (2.12) and (2.13)].

Corollary 6 ( $y\to\tfrac{3\sqrt3-5}{2}$ in Theorems 1 and 5).

$\begin{align} &\text{(a)} &\quad&\sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n}\bar{ \mathbf{H}}_{{2n}} && = \frac{\sqrt3-3}2\ln\big(\sqrt3-1\big), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n} \mathbf{H}_{{2n}} && = \frac{1+\sqrt3}2\Big\{\sqrt3\ln2-3\ln(3-\sqrt3)\Big\}, \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n} \mathbf{H}_{{n}} && = \frac{3-\sqrt3}{4}\ln\Big(\frac43\Big) +\sqrt3\ln\Big(\frac{2+\sqrt3}3\Big), \\ &\text{(d)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n} \mathbf{O}_{{n}} && = \frac{3+\sqrt3}2\bigg\{\ln\Big(\frac{1+\sqrt3}{\sqrt2}\Big) -\frac{\sqrt3}4\ln3\bigg\}, \\ &\text{(e)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n} \mathbf{H}_{{3n}} && = \frac{1+\sqrt3}4\ln\Big(\frac{4(7+4\sqrt3)}3\Big)-\sqrt3\ln2. \end{align}$

Corollary 7 ( $y\to\sqrt5-2$ in Theorems 1 and 5).

$\begin{align} &\text{(a)} &\quad&\sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\bar{ \mathbf{H}}_{{2n}} && = \frac{3 (1-\sqrt{5}) }{\sqrt5}\ln \bigg(\frac{\sqrt{5}-1}{2} \bigg), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n} \mathbf{H}_{{2n}} && = \frac{3 (2+\sqrt{5}) }{\sqrt5} \ln \bigg(\frac{3+\sqrt5}{2}\bigg)-\frac{3 \ln5}{\sqrt5}, \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n} \mathbf{H}_{{n}} && = \frac32 \ln\bigg(\frac{3+\sqrt5}{2} \bigg)+\frac{3 }{\sqrt5}\ln \bigg(\frac{11+5 \sqrt5}{10} \bigg), \\ &\text{(d)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n} \mathbf{O}_{{n}} && = \frac{3(1+\sqrt5)}{2 \sqrt5} \ln(2+\sqrt5)-\frac{3 \ln5}{2 \sqrt5}, \\ &\text{(e)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n} \mathbf{H}_{{3n}} && = \ln (11+5 \sqrt5)+\frac{3 }{\sqrt5}\ln \bigg(\frac{4+2\sqrt5}{5} \bigg). \end{align}$

Corollary 8 ( $y\to\tfrac{\sqrt5-2}{\sqrt5}$ in Theorems 1 and 5).

$\begin{align} &\text{(a)} &\quad&\sum\limits_{n = 1}^{\infty}\Big(\frac5{64}\Big)^n \binom{3n}{n}\bar{ \mathbf{H}}_{{2n}} && = \frac{6 (\sqrt{5}-1) }{11}\ln \bigg(\frac{5-\sqrt{5}}{2} \bigg), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac5{64}\Big)^n \binom{3n}{n} \mathbf{H}_{{2n}} && = \frac{6\sqrt5}{11} \ln\bigg(\frac{25+9 \sqrt5}{22} \bigg) -\frac{3}{11} \ln \bigg(\frac{23-3 \sqrt5}{10} \bigg), \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac5{64}\Big)^n \binom{3n}{n} \mathbf{H}_{{n}} && = -\frac{3\sqrt5}{11} \ln\bigg(\frac{267-119\sqrt5}{2} \bigg) -\frac{6}{11} \ln \bigg(\frac{7+ \sqrt5}{10} \bigg), \\ &\text{(d)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac5{64}\Big)^n \binom{3n}{n} \mathbf{O}_{{n}} && = \frac{3(1+\sqrt5)}{11} \ln\bigg(\frac{4+ \sqrt5}{11} \bigg) +\frac{3\sqrt5 }{11 }\ln5, \\ &\text{(e)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac5{64}\Big)^n \binom{3n}{n} \mathbf{H}_{{3n}} && = \frac{6\sqrt5}{11} \ln\bigg(\frac{4(4+ \sqrt5)}{11} \bigg) +\frac1{11}\ln\bigg(\frac{200(2667-73\sqrt5)}{11^6}\bigg). \end{align}$

Corollary 9 ( $y\to-\tfrac1{10}$ in Theorems 1 and 5).

$\begin{align} &\text{(a)} &\quad&\sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n}\bar{ \mathbf{H}}_{{2n}} && = -\frac38\sqrt{\frac{3}{13}} \mathrm{ArcCos}\Big(\frac{161}{200}\Big), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n} \mathbf{H}_{{2n}} && = -\frac98\ln\Big(\frac65\Big) -\frac38\sqrt{\frac{3}{13}} \mathrm{ArcCos}\Big(\frac{67}{80}\Big), \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty} \Big(-\frac{100}{729}\Big)^n \binom{3n}{n} \mathbf{H}_{{n}} && = -\frac98\ln\Big(\frac65\Big) +\frac38\sqrt{\frac{3}{13}} \mathrm{ArcCos}\Big(\frac{7987}{8000}\Big), \\ &\text{(d)} &&\sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n} \mathbf{O}_{{n}} && = -\frac9{16}\ln\Big(\frac65\Big) -\frac3{16}\sqrt{\frac{3}{13}} \mathrm{ArcCos}\Big(\frac{7}{20}\Big), \\ &\text{(e)} &&\sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n} \mathbf{H}_{{3n}} && = -\frac3{8}\ln\Big(\frac{32}{15}\Big) -\frac3{8}\sqrt{\frac{3}{13}} \mathrm{ArcCos}\Big(\frac{67}{80}\Big). \end{align}$

Corollary 10 ( $y\to\tfrac{7-3\sqrt5}{2}$ in Theorems 1 and 5).

$\begin{align} &\text{(a)} &\; &\sum\limits_{n = 1}^{\infty}\Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n}\bar{ \mathbf{H}}_{{2n}} && = \sqrt{\frac{6\sqrt5-6}{\sqrt5}} \ln\Big(\frac{1+\sqrt{15+6\sqrt5}}{3+\sqrt5}\Big), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n} \mathbf{H}_{{2n}} && = \frac{3(1+\sqrt5)}4\ln\Big(\frac{2+\sqrt5}{3}\Big) +\frac{\sqrt{3/2}}{\sqrt{5+\sqrt5}} \ln\Big(\frac{3\sqrt5-1+\sqrt{30-6\sqrt5}}{4}\Big), \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty} \Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n} \mathbf{H}_{{n}} && = \frac{3(1+\sqrt5)}4\ln\Big(\frac{2+\sqrt5}{3}\Big) +{\frac{\sqrt{3/2}}{\sqrt{5+\sqrt5}} \ln\Big(\frac{11\sqrt3+\sqrt{185-82\sqrt5}} {11\sqrt3-\sqrt{185-82\sqrt5}}\Big)}, \\ &\text{(d)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n} \mathbf{O}_{{n}} && = \frac{3(1+\sqrt5)}8\ln\Big(\frac{2+\sqrt5}{3}\Big) +\frac{\sqrt{3/8}}{\sqrt{5+\sqrt5}} \ln\Big(3\sqrt5-4+2\sqrt{15-6\sqrt5}\Big), \\ &\text{(e)} &&\sum\limits_{n = 1}^{\infty}\Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n} \mathbf{H}_{{3n}} && = \frac{1+\sqrt5}4\ln\Big(\frac{11+5\sqrt5}{6}\Big) +\frac{\sqrt{3/2}}{\sqrt{5+\sqrt5}} \ln\Big(\frac{3\sqrt5-1+\sqrt{30-6\sqrt5}}{4}\Big). \end{align}$

We remark that the second formula (b) and the last series (e) in this corollary refine identity (1.3) conjectured by Sun [23, Eq (2.15)]:

$\sum\limits_{n = 1}^{\infty}\Big(\frac{3+\sqrt5}{54}\Big)^n \binom{3n}{n}\Big\{ \mathbf{H}_{{3n}}- \mathbf{H}_{{2n}}\Big\} = \frac{1+\sqrt5}{2}\ln\Big(\frac{9-3\sqrt5}{2}\Big).$

4. Series with $\binom{3n}{n}\Big/(2n+1)$ and harmonic-like numbers

Now, we turn to examine Bailey's cubic transformation (Bailey [2, Eq (4.05)])

$\begin{equation} {_3{F_2}}\left[ \begin{array}{{c}}{\frac{a}3, \frac{1+a}3, \frac{2+a}3}\\{\\[-3.5mm]\frac{1+a+c}2, \; \frac{2+a-c}2} \end{array}{\Big|{\; \frac{27y}{4(1+y)^3}\; }}\right] = (1+y)^{a}\times{_3{F_2}}\left[ \begin{array}{{c}}{a, \; c, \; 1-c}\\{\frac{1+a+c}2, \; \frac{2+a-c}2} \end{array}{\Big|{\; \frac{-y}4\; }}\right]. \end{equation}$

(4.1)

Under the parameter replacements " $a\to 1+6ax, \; c\to2cx$ ", it can be reformulated as

$\begin{equation} \begin{aligned}[{c}]&\sum\limits_{n = 0}^{\infty} \Big(\frac{y}{4(1+y)^3}\Big)^n \frac{(1+6ax)_{3n}}{n!(1+3ax+cx)_n(\frac32+3ax-cx)_n}\\ &\; = (1+y)^{1+6ax}\times \Bigg\{1+2cx\sum\limits_{k = 1}^{\infty}\Big(\frac{-y}4\Big)^k \frac{(1+6ax)_{k}(1+2cx)_{k-1}(1-2cx)_k} {k!(1+3ax+cx)_k(\frac32+3ax-cx)_k}\Bigg\}, \end{aligned} \end{equation}$

(4.2)

where, as before, both series converge for " $y\in(\rho, \tfrac12)$ ", or equivalently, $\dfrac{27y}{4(1+y)^3}\in(-1, 1)$ .

When $x = 0$ , the above series becomes the following simpler one:

$\sum\limits_{n = 0}^{\infty} \binom{3n}{n}\frac{y^n}{(1+2n)(1+y)^{3n}} = 1+y.$

Instead, the coefficients of $x$ across (4.2) result in the general formula as below:

$\begin{align*} &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{6a \mathbf{H}_{{3n}}-(3a+c) \mathbf{H}_{{n}}-2(3a-c) \mathbf{O}_{{n}}} {1+2n}+\frac{4(3a-c)n}{(1+2n)^2}\bigg\}\\ &\; = 6a(1+y)\ln(1+y) +2c(1+y)\sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{(\frac32)_k}\Big(\frac{-y}4\Big)^k. \end{align*}$

For brevity, we introduce the notations $\mathrm{U}(y)$ and $\mathrm{V}(y)$ for the two series:

$\begin{align*} \mathrm{U}(y)& = \sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{(\frac32)_k}\Big(\frac{-y}4\Big)^k\\ \text{and} \\ \mathrm{V}(y)& = \sum\limits_{n = 0}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{n}{(1+2n)^2}. \end{align*}$

They are evaluated in closed form by the following lemma:

Lemma 11.

$\begin{align} \text{(a)}\qquad \mathrm{U}(y)& = 2+\frac{2\sqrt{4+y}}{\sqrt y} \ln\frac{\sqrt{4+y}-\sqrt{y}}{2}, &\quad&-4 < y < 4;\\ \text{(b)}\qquad \mathrm{V}(y)& = \frac{\sqrt{(1+y)^3}}{\sqrt y} \ln\big(\sqrt y+\sqrt{1+y}\big)-(1+y), &&\rho < y < 1/2. \end{align}$

Proof. The first series can be evaluated by computing the integral as follows:

$\begin{align*} \mathrm{U}(y)& = \sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{(\frac32)_k}\Big(\frac{-y}4\Big)^k = \sum\limits_{k = 1}^{\infty}B\Big(k, \frac32\Big) \Big(\frac{-y}4\Big)^k\\ & = \sum\limits_{k = 1}^{\infty} \Big(\frac{-y}4\Big)^k \int_0^1x^{k-1}\sqrt{1-x}dx = \int_0^1\frac{\sqrt{1-x}\; dx}{x} \sum\limits_{k = 1}^{\infty}\Big(\frac{-xy}4\Big)^k\\ & = \int_0^1\frac{-y\sqrt{1-x}\; dx}{4+xy} = \int_0^1\frac{-2yT^2}{4+y-T^2y}dT \qquad\boxed{\sqrt{1-x}\to T}\\ & = 2+\frac{2\sqrt{4+y}}{\sqrt y}\ln\frac{\sqrt{4+y}-\sqrt{y}}{2}. \end{align*}$

For the second series $\mathrm{V}(y)$ , by shifting forward the summation index $n\to n+1$ , we can rewrite it as

$\mathrm{V}(y) = \sum\limits_{n = 0}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{n}{(1+2n)^2} = \frac{y}{(1+y)^{3}}\sum\limits_{n = 0}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+3}{n}\frac{1}{3+2n}.$

Then, for " $\alpha = \beta = 3$ ", perform the replacement $\tau\to{xy}/{(1+y)^3}$ in Lambert's second series

$\sum\limits_{n = 0}^{\infty}\frac{x^ny^n}{(1+y)^{3n}} \binom{3n+3}{n} = \frac{(1+T)^4}{1-2T}.$

Now multiplying this equation by $x^\frac12$ and then integrating across over $x\in[0, 1]$ , we can proceed with

$\begin{align*} \sum\limits_{n = 0}^{\infty} \frac{y^n}{(1+y)^{3n}} \binom{3n+3}{n}\frac2{3+2n} & = \int_0^1x^{\frac12}\frac{(1+T)^4}{1-2T}dx \qquad\boxed{x = \frac{T(1+y)^3}{y(1+T)^3}}\\ & = \frac{\sqrt{(1+y)^9}}{y\sqrt y} \int_0^y\frac{\sqrt T}{\sqrt{(1+T)^3}}dT. \end{align*}$

By means of integration by parts, we can further compute

$\begin{align*} \int_0^y\frac{\sqrt T}{\sqrt{(1+T)^3}}dT & = \frac{-2\sqrt y}{\sqrt{1+y}} +\int_0^y\frac{1}{\sqrt{T(1+T)}}dT\\ & = 2\ln(\sqrt{y}+\sqrt{1+y})-\frac{2\sqrt y}{\sqrt{1+y}}. \end{align*}$

After substitution, the second formula in Lemma 11 follows accordingly. □

Therefore, we obtain the following reduced transformation:

$\begin{equation} \begin{aligned}[{c}]&\sum\limits_{n = 0}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{6a \mathbf{H}_{{3n}}-(3a+c) \mathbf{H}_{{n}}-2(3a-c) \mathbf{O}_{{n}}} {1+2n}\bigg\}\\ &\; = 6a(1+y)\ln(1+y)+2c(1+y) \mathrm{U}(y)-4(3a-c) \mathrm{V}(y). \end{aligned} \end{equation}$

(4.3)

By specifying two parameters, $a$ and $c$ in the above equality, we deduce four independent series:

$\begin{align} &a = 0:&\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n}\bigg\} = (1+y) \mathrm{U}(y)+2 \mathrm{V}(y), \\ &c = 0:&\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{ \mathbf{H}_{{3n}}- \mathbf{H}_{{2n}}}{1+2n}\bigg\} = (1+y)\ln(1+y)-2 \mathrm{V}(y), \\ &c = 3a:&\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{ \mathbf{H}_{{3n}}- \mathbf{H}_{{n}}}{1+2n}\bigg\} = (1+y)\ln(1+y)+(1+y) \mathrm{U}(y), \\ &c = -3a:&\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{ \mathbf{H}_{{3n}}-2 \mathbf{O}_{{n}}}{1+2n}\bigg\} = (1+y)\ln(1+y)-(1+y) \mathrm{U}(y)-4 \mathrm{V}(y). \end{align}$

For the above four equations, first replacing $\mathrm{U}(y)$ and $\mathrm{V}(y)$ by their algebraic values in Lemma 11, and then putting the resulting equations in conjunction with that in Theorem 2, we establish, after some routine simplifications, four closed formulae as in the following theorem:

Theorem 12 ( $\rho < y < 1/2$ ).

$\begin{align} &\text{(a)} &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n} && = \frac{2\sqrt{(1+y)^3}}{\sqrt y}\ln\big(\sqrt y+\sqrt{1+y}\big)\\ &&&&& \nonumber +\frac{2(1+y)\sqrt{4+y}}{\sqrt y}\ln\bigg(\frac{\sqrt{4+y}-\sqrt{y}}{2}\bigg), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\frac{\; y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{1+2n} && = \frac{2\sqrt{(1+y)^3}}{\sqrt y}\ln\big(\sqrt y+\sqrt{1+y}\big) -\frac{3+3y}{2}\ln(1-2y)\\ &&&&& \nonumber +\frac{(1+y)\sqrt{4+y}}{2\sqrt{y}} \ln\bigg(\frac{2+2y-2\sqrt{y^2+4y}} {2-y(2+y-\sqrt{y^2+4y})}\bigg), \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty}\frac{\; y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{1+2n} && = \frac{2\sqrt{(1+y)^3}}{\sqrt y}\ln\big(\sqrt y+\sqrt{1+y}\big) -\frac{3+3y}{4}\ln(1-2y)\\ &&&&& \nonumber +\frac{(1+y)\sqrt{4+y}}{2\sqrt{y}} \ln\Big(\frac{1+y-\sqrt{y^2+4y}} {\sqrt{1-2y}}\Big), \\ &\text{(d)} &\quad&\sum\limits_{n = 1}^{\infty}\frac{\; y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{1+2n} && = 2(1+y)+\frac{1+y}{2}\ln\bigg(\frac{(1+y)^2}{(1-2y)^3}\bigg)\\ &&&&& \nonumber+\frac{(1+y)\sqrt{4+y}}{2\sqrt{y}} \ln\bigg(\frac{2+2y-2\sqrt{y^2+4y}} {2-y(2+y-\sqrt{y^2+4y})}\bigg). \end{align}$

By assigning particular values for $y$ in Theorems 2 and 12, we can deduce numerous infinite series identities with different convergence rates. In order to show the variety of implications, we record five representative classes of infinite series values.

Corollary 13 ( $y\to\sqrt5-2$ in Theorems 2 and 12).

$\begin{align} &\text{(a)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n} && = 2 \sqrt2\ln \bigg(\frac{3+\sqrt{10}}{1+\sqrt2}\bigg) -(3+\sqrt5) \ln \bigg(\frac{1+\sqrt5}2\bigg), \\ &\text{(b)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{1+2n} && = 2 \sqrt2\ln \bigg(\frac{3+\sqrt{10}}{1+\sqrt2}\bigg) -(6-4\sqrt5) \ln \bigg(\frac{1+\sqrt5}2\bigg)-\sqrt5\ln5, \\ &\text{(c)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}{1+ 2n} && = (5\sqrt5-3) \ln \bigg(\frac{1+\sqrt5}2\bigg)-\sqrt5\ln5, \\ &\text{(d)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{1+2n} && = 2 \sqrt2\ln \bigg(\frac{3+\sqrt{10}}{1+\sqrt2}\bigg) -\bigg(\frac92-\frac{3\sqrt5}2\bigg) \ln \bigg(\frac{1+\sqrt5}2\bigg)-\frac{\sqrt5}2\ln5 , \\ &\text{(e)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{1+2n} && = (\sqrt5-1)(2+\ln2)-(5-3\sqrt5) \ln \bigg(\frac{1+\sqrt5}2\bigg)-\sqrt5\ln5. \end{align}$

Corollary 14 ( $y\to\tfrac{3\sqrt3-5}2$ in Theorems 2 and 12).

$\begin{align} &\text{(a)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n} && = \frac{9+3 \sqrt3}2 \ln (\sqrt{3}-1)+\frac9{\sqrt6} \ln \bigg(\frac{3+2 \sqrt2}{\sqrt3+\sqrt2}\bigg), \\ &\text{(b)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{1+2n} && = \frac92 \ln \bigg(\frac{3-\sqrt3}2\bigg) +\frac{3 \sqrt3}2 \ln \bigg(\frac{(\sqrt{3}+1)^3}{12\sqrt3}\bigg) +\frac9{\sqrt6} \ln \bigg(\frac{3+2 \sqrt2}{\sqrt3+\sqrt2}\bigg), \\ &\text{(c)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}{1+2n} && = \frac94\ln\Big(\frac34\Big) +\frac{3 \sqrt3}2 \ln \bigg(\frac{(\sqrt{3}+1)^4}{24\sqrt3}\bigg), \\ &\text{(d)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{1+2n} && = \frac34(3-\sqrt3)\ln(2\sqrt3-3)-\frac{9\ln 3 }{4\sqrt3} +\frac9{\sqrt6} \ln \bigg(\frac{3+2 \sqrt2}{\sqrt3+\sqrt2}\bigg), \\ &\text{(e)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac2{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{1+2n} && = 3\sqrt3-3+\frac32\ln\Big(\frac{2\sqrt3-3}2\Big) +\frac{3 \sqrt3}2 \ln \bigg(\frac{2+\sqrt3}{2\sqrt3}\bigg). \end{align}$

Corollary 15 ( $y\to3\sqrt2-4$ in Theorems 2 and 12).

$\begin{align} &\text{(a)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n} && = 3 \sqrt3\ln \bigg(\frac{\sqrt6-2}{\sqrt3-1}\bigg) +\frac{9\sqrt{2-\sqrt2}}{\sqrt6} \ln \Big(6\sqrt2-7+\sqrt{6 (2-\sqrt2)^3}\Big), \\ &\text{(b)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{1+2n} && = 3 \sqrt3\ln \bigg(\frac{\sqrt3-1}{\sqrt2}\bigg) -(9-9\sqrt2)\ln\bigg(\frac{1+\sqrt2}{\sqrt3}\bigg) \\ &&&+\frac{9\sqrt{2-\sqrt2}}{\sqrt6} \ln \Big(6\sqrt2-7+\sqrt{6 (2-\sqrt2)^3}\Big), \\ &\text{(c)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}{1+2n} && = 3 \sqrt3\ln \bigg(\frac{\sqrt2+\sqrt3}{2+\sqrt3}\bigg) -(9-9\sqrt2)\ln\bigg(\frac{1+\sqrt2}{\sqrt3}\bigg) , \\ &\text{(d)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{1+2n} && = \Big(\frac92-\frac9{\sqrt2}\Big)\ln\big(\sqrt6-\sqrt3\big) -\frac{3 \sqrt3}2\ln \big(\sqrt2+\sqrt3\big) \\ &&&+\frac{9\sqrt{2-\sqrt2}}{\sqrt6} \ln \Big(6\sqrt2-7+\sqrt{6 (2-\sqrt2)^3}\Big), \\ &\text{(e)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{1+2n} && = 6\sqrt2-6+3 \sqrt3\ln \bigg(\frac{\sqrt3-1}{\sqrt2}\bigg) -(3-3\sqrt2)\ln\bigg(\frac{3+2\sqrt2}{\sqrt3}\bigg). \end{align}$

Corollary 16 ( $y\to\tfrac{1}5$ in Theorems 2 and 12).

$\begin{align} &\text{(a)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{25}{216}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n} && = \frac{12\sqrt6}{5} \ln \bigg(\frac{1+ \sqrt6}{\sqrt5}\bigg) -\frac{12\sqrt{21}}{5} \ln \bigg(\frac{1+ \sqrt{21}}{2\sqrt5}\bigg), \\ &\text{(b)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{25}{216}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{1+2n} && = \frac95\ln\Big(\frac53\Big)+\frac{12\sqrt6}{5} \ln \bigg(\frac{1+ \sqrt6}{\sqrt5}\bigg) +\frac{6\sqrt{21}}{5} \ln \bigg(\frac{9- \sqrt{21}}{2\sqrt{15}}\bigg), \\ &\text{(c)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{25}{216}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}{1+2n} && = \frac95\ln\Big(\frac53\Big) +\frac{3 \sqrt{21}}5 \ln \bigg(\frac{257-13\sqrt{21}}{250}\bigg), \\ &\text{(d)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{25}{216}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{1+2n} && = \frac9{10}\ln\Big(\frac53\Big)+\frac{12\sqrt6}{5} \ln \bigg(\frac{1+ \sqrt6}{\sqrt5}\bigg) +\frac{3\sqrt{21}}{5} \ln \bigg(\frac{6- \sqrt{21}}{\sqrt{15}}\bigg), \\ &\text{(e)}\quad \sum\limits_{n = 1}^{\infty}\Big(\frac{25}{216}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{1+2n} && = \frac{12}5+\frac35\ln\Big(\frac{20}3\Big) +\frac{6\sqrt{21}}{5} \ln \bigg(\frac{9- \sqrt{21}}{2\sqrt{15}}\bigg). \end{align}$

Corollary 17 ( $y\to-\tfrac1{10}$ in Theorems 2 and 12).

$\begin{align} &\text{(a)}\quad \sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{1+2n} && = \frac{27}5 \mathrm{arccot}3-\frac{9\sqrt{39}}5 \mathrm{arccot}\sqrt{39}, \\ &\text{(b)}\quad \sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{1+2n} && = \frac{27}5 \mathrm{arccot}3 -\frac{9\sqrt{39}}{20} \mathrm{arccos}\Big(\frac{67}{80}\Big) -\frac{27}{20}\ln\Big(\frac65\Big), \\ &\text{(c)}\quad \sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}{1+2n} && = \frac{9\sqrt{39}}{20} \mathrm{arccos}\Big(\frac{7987}{8000}\Big) -\frac{27}{20}\ln\Big(\frac65\Big), \\ &\text{(d)}\quad \sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{1+2n} && = \frac{27}5 \mathrm{arccot}3-\frac{9\sqrt{39}}{20} \mathrm{arccos}\bigg(\sqrt{\frac{27}{40}}\bigg) -\frac{27}{40}\ln\Big(\frac65\Big) , \\ &\text{(e)}\quad \sum\limits_{n = 1}^{\infty}\Big(-\frac{100}{729}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{1+2n} && = \frac95-\frac{9\sqrt{39}}{20} \mathrm{arccos}\Big(\frac{67}{80}\Big) -\frac{9}{20}\ln\Big(\frac{32}{15}\Big). \end{align}$

5. Series with $\binom{3n}{n}\Big/n$ and harmonic-like numbers

Under the parameter replacements " $a\to 6ax, \; c\to2cx$ ", Bailey's cubic transformation (4.1) can be reformulated alternatively as

$\begin{align*} &\sum\limits_{n = 0}^{\infty}\Big(\frac{y}{4(1+y)^3}\Big)^n \frac{(6ax)_{3n}}{n!(1+3ax-cx)_n(\frac12+3ax+cx)_n}\\ &\; = (1+y)^{6ax}\times \Bigg\{1+12acx^2\sum\limits_{k = 1}^{\infty}\Big(\frac{-y}4\Big)^k \frac{(1+6ax)_{k-1}(1+2cx)_{k-1}(1-2cx)_k} {k!(1+3ax-cx)_k(\frac12+3ax+cx)_k}\Bigg\}. \end{align*}$

Both series in the above equation converge subject to the same condition " $y\in(\rho, \tfrac12)$ ", or equivalently, $\dfrac{27y}{4(1+y)^3}\in(-1, 1)$ (as before).

Equating the constant terms from both sides yields the algebraic identity below

$\sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{y^n}{n(1+y)^{3n}} = 3\ln(1+y).$

Instead, the coefficients of $x$ result in the following infinite series identity involving a free variable " $y$ " and two linear parameters $a$ and $c$ :

$\begin{align*} &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{6a \mathbf{H}_{{3n}}-(3a-c) \mathbf{H}_{{n}}-2(3a+c) \mathbf{O}_{{n}}}{n}-\frac{2a}{n^2}\bigg\}\\ &\; = 9a\ln^2(1+y) +6c\sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{k(\frac12)_k}\Big(\frac{-y}4\Big)^k. \end{align*}$

Let $\mathcal{{U}}(y)$ and $\mathcal{{V}}(y)$ stand for the two series

$\mathcal{{U}}(y) = \sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{k(\frac12)_k}\Big(\frac{-y}4\Big)^k \quad\text{and}\quad \mathcal{{V}}(y) = \sum\limits_{n = 1}^{\infty}\frac{y^n}{n^2(1+y)^{3n}} \binom{3n}{n}.$

They admit closed formulae as in the lemma below:

Lemma 18.

$\begin{align} &\text{(a)}\quad\mathcal{{U}}(y) = -2\ln^2\bigg(\frac{2}{\sqrt y+\sqrt{4+y}}\bigg), \quad -4 < y < 4;\\ &\text{(b)}\quad\mathcal{{V}}(y) = 3\bigg\{\frac{{\pi}^2}{6}+\ln y\ln(1+y)-2\ln^2(1+y) - \mathrm{Li}_2\Big(\frac1{1+y}\Big)\bigg\}, \quad \rho < y < 1/2. \end{align}$

Proof. The first series $\mathcal{{U}}(y)$ can be reformulated as

$\begin{align*} \mathcal{{U}}(y)& = \sum\limits_{k = 1}^{\infty} \frac{(k-1)!}{k(\frac12)_k}\Big(\frac{-y}4\Big)^k = \sum\limits_{k = 1}^{\infty}B\Big(k, \frac12\Big) \Big(\frac{-y}4\Big)^k\\ & = \sum\limits_{k = 1}^{\infty} \frac{\big(-y/4)^k}k \int_0^1\frac{x^{k-1}dx}{\sqrt{1-x}} = \int_0^1\frac{dx}{x\sqrt{1-x}} \sum\limits_{k = 1}^{\infty}\frac{\big(-xy/4)^k}k\\ & = -\int_0^1\frac{\ln\big(1+\frac{xy}4\big)dx}{x\sqrt{1-x}} = -\int_0^1\frac{dT}{T}\ln\Big(\frac{1+(2+y)T+T^2}{(1+T)^2}\Big) \qquad\boxed{x\to \frac{4T}{(1+T)^2}}\\ & = \int_0^1\frac{dT}{T}\bigg\{2\ln(1+T) -\ln\Big(1+\frac{4T}{(\sqrt y+\sqrt{4+y})^2}\Big) -\ln\Big(1+\frac{4T}{(\sqrt y-\sqrt{4+y})^2}\Big)\bigg\}\\ & = \frac{{\pi}^2}6 + \mathrm{Li}_2\bigg(\frac{-4}{(\sqrt y+\sqrt{4+y})^2}\bigg) + \mathrm{Li}_2\bigg(\frac{-4}{(\sqrt y-\sqrt{4+y})^2}\bigg). \end{align*}$

Then the closed formula for $\mathcal{{U}}(y)$ in the lemma follows by applying the dilogarithmic equation

$\mathrm{Li}_2(-x)+ \mathrm{Li}_2(-x^{-1}) = -\frac{\pi^2}{6}-\frac{\ln^2x}2, \quad\text{where}\quad x > 0.$

For the second series, we can rewrite it by reindexing $n\to n+1$ as

$\mathcal{{V}}(y) = \sum\limits_{n = 1}^{\infty} \frac{y^n}{n^2(1+y)^{3n}} \binom{3n}{n} = \frac{3y}{(1+y)^{3}}\sum\limits_{n = 0}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+2}{n}\frac{1}{(1+n)^2}.$

Now specializing Lambert's second series by " $\alpha = 2$ and $\beta = 3$ " and $\tau\to{xy}/{(1+y)^3}$

$\sum\limits_{n = 0}^{\infty}\frac{x^ny^n}{(1+y)^{3n}} \binom{3n+2}{n} = \frac{(1+T)^3}{1-2T}, \quad\text{where}\quad {x = \frac{T(1+y)^3}{y(1+T)^3}},$

then integrating twice across this equation, we can proceed with

$\begin{align*} &\sum\limits_{n = 0}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+2}{n}\frac{1}{(1+n)^2}\\ &\; = \int_0^1\frac{dt}t\int_0^t\frac{(1+T)^3}{1-2T}dx = -\int_0^1\frac{(1+T)^3\ln x}{1-2T}dx\\ &\; = -\frac{(1+y)^3}{y} \int_0^y\frac{dT}{1+T}\ln\Big(\frac{ T(1+y)^3}{y(1+T)^3}\Big) \qquad\boxed{x = \frac{T(1+y)^3}{y(1+T)^3}}\\ &\; = -\frac{(1+y)^3}{y} \bigg\{\int_0^y\frac{dT}{1+T}\ln\Big(\frac{ T(1+y)^3}{y}\Big) -3\int_0^y\frac{\ln(1+T)}{1+T}dT\bigg\}\\ &\; = \frac{(1+y)^3}{y}\bigg\{\frac{{\pi}^2}{6}+\ln y\ln(1+y) -2\ln^2(1+y)- \mathrm{Li}_2\Big(\frac1{1+y}\Big)\bigg\}. \end{align*}$

By substitution, the closed formula for $\mathcal{{V}}(y)$ in the lemma follows consequently. □

Thus, we have the following reduced transformation:

$\begin{equation} {\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \bigg\{\frac{6a \mathbf{H}_{{3n}}-(3a-c) \mathbf{H}_{{n}}-2(3a+c) \mathbf{O}_{{n}}}{n}\bigg\} = 9a\ln^2(1+y)+6c\mathcal{{U}}(y)+2a\mathcal{{V}}(y).} \end{equation}$

(5.1)

By specifying two parameters, $a$ and $c$ , we deduce four independent series

$\begin{align} &a = 0: &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{n} = -3\mathcal{{U}}(y), \\ &c = 0: &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\bigg\{\frac{ \mathbf{H}_{{3n}}- \mathbf{H}_{{2n}}}{n}\bigg\} = \frac32\ln^2(1+y)+\frac{\mathcal{{V}}(y)}3, \\ &c = 3a: &&\begin{aligned}[{t}]&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\bigg\{\frac{ \mathbf{H}_{{3n}}-2 \mathbf{O}_{{n}}}{n}\bigg\} = \frac32\ln^2(1+y)+3\mathcal{{U}}(y)+\frac{\mathcal{{V}}(y)}3, \end{aligned}\\ &c = -3a: &\quad&\begin{aligned}[{t}]&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\bigg\{\frac{ \mathbf{H}_{{3n}}- \mathbf{H}_{{n}}}{n}\bigg\} = \frac32\ln^2(1+y)-3\mathcal{{U}}(y)+\frac{\mathcal{{V}}(y)}3. \end{aligned} \end{align}$

For these four equations, replacing $\mathcal{{U}}(y)$ and $\mathcal{{V}}(y)$ first by their algebraic expressions and then relating the resulting equations to that in Theorem 3, we find, after some simplifications, four infinite series identities as below:

Theorem 19 ( $\rho < y < 1/2$ ). Letting $\Theta(y)$ be defined as in Theorem 3, the following algebraic identities hold:

$\begin{align} &\text{(a)} &&\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}{n} && = 6\ln^2\bigg(\frac{2}{\sqrt y+\sqrt{4+y}}\bigg), \\ &\text{(b)} &&\sum\limits_{n = 1}^{\infty}\frac{\; y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}{n} && = \frac{{\pi}^2}2+3\Theta(y)+3\ln y\ln(1+y)-\frac92\ln^2(1+y)+6\ln^2\bigg(\frac{2}{\sqrt y+\sqrt{4+y}}\bigg), \\ &\text{(c)} &&\sum\limits_{n = 1}^{\infty}\frac{\; y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}{n} && = \frac{{\pi}^2}4+\frac32\Theta(y)+\frac32\ln y\ln(1+y)-\frac94\ln^2(1+y) +6\ln^2\bigg(\frac{2}{\sqrt y+\sqrt{4+y}}\bigg), \\ &\text{(d)} &\; &\sum\limits_{n = 1}^{\infty}\frac{\; y^n}{(1+y)^{3n}} \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}{n} && = \frac{2{\pi}^2}3+ 3\Theta(y)+4\ln y\ln(1+y)-5\ln^2(1+y) +6\ln^2\Big(\frac{2}{\sqrt y+\sqrt{4+y}}\Big)- \mathrm{Li}_2\Big(\frac{1}{1+y}\Big) . \end{align}$

By assigning five particular values for $y$ in Theorems 3 and 19, five classes of infinite series identities are displayed in the following corollaries:

Corollary 20 ( $y\to\sqrt5-2$ in Theorems 3 and 19).

$\begin{align} &\text{(a) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}n && = \frac32 \ln ^2\bigg(\frac{1+\sqrt5}2\bigg), \\ &\text{(b) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}n && = \frac{\pi ^2}2+\frac32 \ln ^22+3\Theta(\sqrt5-2) +6 \ln(1+\sqrt5) \ln\bigg(\frac{1+\sqrt5}4\bigg) , \\ &\text{(c) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}n && = \frac{\pi ^2}2+3\Theta(\sqrt5-2) +\frac92 \ln(1+\sqrt5) \ln\bigg(\frac{1+\sqrt5}4\bigg) , \\ &\text{(d) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}n && = \frac{\pi ^2}4+\frac32 \ln ^22+\frac32\Theta(\sqrt5-2) +\frac{15}4 \ln(1+\sqrt5) \ln\bigg(\frac{1+\sqrt5}4\bigg), \\ &\text{(e)} \; \sum\limits_{n = 1}^{\infty}\Big(\frac18\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}n && = \frac{2\pi ^2}3+\frac{11}2 \ln ^22+3\Theta(\sqrt5-2) +\frac{\ln(1+\sqrt5)}2 \ln\bigg(\frac{(1+\sqrt5)^{17}}{2^{38}}\bigg) - \mathrm{Li}_2\bigg(\frac{1+\sqrt5}4\bigg). \end{align}$

Corollary 21 ( $y\to\tfrac{\sqrt5-2}{\sqrt5}$ in Theorems 3 and 19).

$\begin{align} &\text{(a) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{5}{64}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}n && = \frac32 \ln ^2\bigg(\frac{5+\sqrt5}{10}\bigg), \\ &\text{(b) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{5}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}n && = \frac{\pi ^2}2+3\Theta\bigg(\frac{\sqrt5-2}{\sqrt5}\bigg) +\frac32 \ln\bigg(\frac{5+\sqrt5}8\bigg) \ln\bigg(64+\frac{128}{\sqrt5}\bigg) +\frac32 \ln ^2\bigg(\frac{5+\sqrt5}{10}\bigg), \\ &\text{(c) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{5}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}n && = \frac{\pi ^2}2+3\Theta\bigg(\frac{\sqrt5-2}{\sqrt5}\bigg) +\frac32 \ln\bigg(\frac{5+\sqrt5}8\bigg) \ln\bigg(64+\frac{128}{\sqrt5}\bigg), \\ &\text{(d) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{5}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}n && = \frac{\pi ^2}4+\frac32\Theta\bigg(\frac{\sqrt5-2}{\sqrt5}\bigg) +\frac34 \ln\bigg(\frac{5+\sqrt5}8\bigg) \ln\bigg(64+\frac{128}{\sqrt5}\bigg) +\frac32 \ln ^2\bigg(\frac{5+\sqrt5}{10}\bigg) , \\ &\text{(e) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{5}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}n && = \frac{2\pi ^2}3+3\Theta\bigg(\frac{\sqrt5-2}{\sqrt5}\bigg) - \mathrm{Li}_2\bigg(\frac{5+\sqrt5}8\bigg)+\frac32 \ln ^2\bigg(\frac{5+\sqrt5}{10}\bigg)\\ &&&+ \ln\bigg(\frac{5+\sqrt5}8\bigg) \ln\bigg(\frac{8(5+\sqrt5)^7}{5^4}\bigg). \end{align}$

Corollary 22 ( $y\to\tfrac13$ in Theorems 3 and 19).

$\begin{align} &\text{(a)} \; \sum\limits_{n = 1}^{\infty}\Big(\frac{9}{64}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}n && = \frac32 \ln ^2\bigg(\frac{7+\sqrt{13}}6\bigg), \\ &\text{(b) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{9}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}n && = \frac{\pi ^2}2-\frac32 \ln\Big(\frac43\Big) \ln\Big(\frac{64}3\Big) +3\Theta\Big(\frac13\Big)+\frac32 \ln ^2\bigg(\frac{7+\sqrt{13}}6\bigg), \\ &\text{(c) } \;\sum\limits_{n = 1}^{\infty}\Big(\frac{9}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}n && = \frac{\pi ^2}2-\frac32 \ln\Big(\frac43\Big) \ln\Big(\frac{64}3\Big) +3\Theta\Big(\frac13\Big), \\ &\text{(d) } \;\sum\limits_{n = 1}^{\infty}\Big(\frac{9}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}n && = \frac{\pi ^2}4-\frac34\ln\Big(\frac43\Big) \ln\Big(\frac{64}3\Big) +\frac32\Theta\Big(\frac13\Big)+\frac32 \ln ^2\bigg(\frac{7+\sqrt{13}}6\bigg) , \\ &\text{(e) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{9}{64}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}n && = \frac{2\pi ^2}3- \ln\Big(\frac43\Big) \ln\Big(\frac{1024}3\Big) +3\Theta\Big(\frac13\Big)- \mathrm{Li}_2\Big(\frac34\Big) +\frac32 \ln ^2\bigg(\frac{7+\sqrt{13}}6\bigg). \end{align}$

Corollary 23 ( $y\to\tfrac{3 \sqrt{3}-5}2$ in Theorems 3 and 19).

$\begin{align} &\text{(a) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}n && = \frac32 \ln ^2(\sqrt{3}-1), \\ &\text{(b) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}n && = \frac{\pi ^2}2+\frac32 \ln (54)\ln\Big(\frac23\Big) +6 \ln \big(1+\sqrt{3}\big) \ln \bigg(\frac{1+\sqrt3}2\bigg) +3\Theta\bigg(\frac{3\sqrt3-5}3\bigg), \\ &\text{(c) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}n && = \frac{\pi ^2}2 +\frac32\ln \bigg(\frac{1+\sqrt3}3\bigg)\ln \bigg(\frac{27(1+\sqrt3)^3}4\bigg) +3\Theta\bigg(\frac{3\sqrt3-5}3\bigg) , \\ &\text{(d) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}n && = \frac{\pi^2}4 +\frac34 \ln \bigg(\frac{1+ \sqrt3}2\bigg)\ln \bigg(\frac{(1+ \sqrt3)^5}2\bigg) +\frac34\ln (54)\ln\Big(\frac23\Big) +\frac32\Theta\bigg(\frac{3\sqrt3-5}3\bigg) , \\ &\text{(e) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}n && = \frac{2\pi^2}3+\frac32 \ln^2\bigg(\frac{1+\sqrt{3}}2 \bigg) - \mathrm{Li}_2\bigg(\frac{1+\sqrt3}3\bigg)+3\Theta\bigg(\frac{3\sqrt3-5}3\bigg)\\ &&& +\ln \bigg(\frac{1+\sqrt{3}}3 \bigg) \ln\bigg(\frac{3^5(1+\sqrt3)^7}{2^4}\bigg). \end{align}$

Corollary 24 ( $y\to 3\sqrt2-4$ in Theorems 3 and 19).

$\begin{align} &\text{(a) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{\bar{ \mathbf{H}}_{{2n}}}n && = \frac32 \ln ^2\bigg(\frac{1+\sqrt3}{2+\sqrt6}\bigg), \\ &\text{(b) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{2n}}}n && = \frac{\pi ^2}2+3\Theta\Big(3\sqrt2-4\Big) +\frac32 \ln ^2\bigg(\frac{1+\sqrt3}{2+\sqrt6}\bigg)\\ &&&+\frac32 \ln\bigg(\frac{1+\sqrt2}3\bigg) \ln\bigg(\frac{27(1+\sqrt2)}2\bigg), \\ &\text{(c) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{n}}}n && = \frac{\pi ^2}2+3\Theta\Big(3\sqrt2-4\Big) +\frac32 \ln\bigg(\frac{1+\sqrt2}3\bigg) \ln\bigg(\frac{27(1+\sqrt2)}2\bigg), \\ &\text{(d) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{O}_{{n}}}n && = \frac{\pi ^2}4+\frac32\Theta\Big(3\sqrt2-4\Big) +\frac32 \ln ^2\bigg(\frac{1+\sqrt3}{2+\sqrt6}\bigg)\\ &&&+\frac34 \ln\bigg(\frac{1+\sqrt2}3\bigg) \ln\bigg(\frac{27(1+\sqrt2)}2\bigg), \\ &\text{(e) }\; \sum\limits_{n = 1}^{\infty}\Big(\frac{2+\sqrt2}{27}\Big)^n \binom{3n}{n}\frac{ \mathbf{H}_{{3n}}}n && = \frac{2\pi ^2}3+3\Theta\Big(3\sqrt2-4\Big) +\frac32 \ln ^2\bigg(\frac{1+\sqrt3}{2+\sqrt6}\bigg)\\ &&&- \mathrm{Li}_2\bigg(\frac{1+\sqrt2}3\bigg) +\ln\bigg(\frac{1+\sqrt2}3\bigg) \ln\bigg(\frac{3^5(1+\sqrt2)^3}4\bigg). \end{align}$

6. Conclusions and further comments

By integrating Lambert's series and manipulating the cubic transformations for $_3{F_2}$ -series through the "coefficient extraction method", we have shown several algebraic formulae for infinite series containing binomial coefficient $\binom{3n}{n}$ , harmonic-like numbers, and in particular, a free variable "y". As showcases, three classes of infinite series were examined in detail from Sections 3–5. More variants of these series exist and can be treated analogously. For instance, the transformation formula (3.1) under the replacements " $a\to1+6ax, \; c\to2cx$ " becomes

$\begin{aligned} & { }_3 F_2\left[\left.\begin{array}{c} 1+2 a x, \frac{2}{3}+2 a x, \frac{4}{3}+2 a x \\ 1+3 a x+c x, \frac{3}{2}+3 a x-c x \end{array} \right\rvert\, \frac{27 y}{4(1+y)^3}\right] \\ & =\frac{(1+y)^{2+6 a x}}{1-2 y} \times{ }_4 F_3\left[\left.\begin{array}{l} \frac{4}{3}+2 a x, \quad 1+6 a x, 2 c x, 1-2 c x \\ \frac{1}{3}+2 a x, 1+3 a x+c x, \frac{3}{2}+3 a x-c x \end{array} \right\rvert\, \frac{-y}{4}\right] . \\ & \end{aligned}$

Then by carrying out the same procedure as in the preceding sections, we can establish the algebraic identities for five infinite series, as in the theorem below:

Theorem 25 ( $\rho < y < 1/2$ ). Letting $\Lambda(y)$ be the function defined by

$\Lambda(y) = 3\ln(1-2y)+\frac{2-y}{\sqrt{y^2+4y}} \ln\Big(\frac{2-y(2+y+\sqrt{y^2+4y})}{2-y(2+y-\sqrt{y^2+4y})}\Big),$

we have the closed algebraic formulae for five infinite series:

$\begin{align*} &\text{(a) }\; \sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+1}{n} \bar{ \mathbf{H}}_{{2n+1}} = \frac{2(y-2)(1+y)^2}{(1-2y)\sqrt{y^2+4y}}\ln\frac{\sqrt{4+y}-\sqrt{y}}{2}, \\ &\text{(b) }\; \sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+1}{n} \mathbf{H}_{{2n+1}} = \frac{(1+y)^2}{1-2y}\Bigg\{\frac{2y-4}{\sqrt{y^2+4y}} \ln\frac{\sqrt{4+y}-\sqrt{y}}{2}-\frac{ \Lambda(y)}{2}\Bigg\}, \\ &\text{(c) }\; \sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+1}{n} \mathbf{H}_{{n}} = \frac{(1+y)^2}{4y-2} \Lambda(y), \\ &\text{(d) }\; \sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+1}{n} \mathbf{O}_{{n+1}} = \frac{(1+y)^2}{1-2y}\Bigg\{\frac{2y-4}{\sqrt{y^2+4y}}\ln\frac{\sqrt{4+y}-\sqrt{y}}{2}-\frac{ \Lambda(y)}4\Bigg\}, \\ &\text{(e) }\; \sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n+1}{n} \mathbf{H}_{{3n+1}} = \frac{(1+y)^2}{1-2y}\Bigg\{\frac{2y-4}{\sqrt{y^2+4y}}\ln\frac{\sqrt{4+y}-\sqrt{y}}{2}-\frac{ \Lambda(y)}2+\ln(1+y)\Bigg\}. \end{align*}$

From the algebraic identities exhibited for the series with harmonic-like numbers of the first order, it is natural to ask: what would happen for the corresponding series involving harmonic-like numbers of the second order? Our computations manifested that the resulting expressions are very complex and convoluted, which can be exemplified by the following attempt made by the authors. Extracting the coefficient of $x^2$ across (3.2), we can derive, after a number of reductions and simplifications, the following formulae:

$\begin{align*} \text{(a)}\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \Big\{\bar{ \mathbf{H}}_{{2n}}^{{2}}+ \mathbf{H}_{{2n}}^{ \langle{{{2}}}\rangle}\Big\} = \frac{6y+6}{2y-1}\Big\{\mathcal{{U}}(y)+\mathcal{{W}}(y)\Big\}, \\ \text{(b)}\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \Big\{\big( \mathbf{H}_{{3n}}- \mathbf{H}_{{2n}}\big)^2 + \mathbf{H}_{{2n}}^{ \langle{{{2}}}\rangle}- \mathbf{H}_{{3n}}^{ \langle{{{2}}}\rangle}\Big\} = \frac{1+y}{1-2y}\ln^2(1+y), \\ \text{(c)}\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \Big\{\big(2 \mathbf{O}_{{n}}- \mathbf{H}_{{3n}}\big)^2 +4 \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle}- \mathbf{H}_{{3n}}^{ \langle{{{2}}}\rangle}\Big\}\\ &\; = \frac{1+y}{1-2y} \Big\{\ln^2(1+y)+6\ln(1+y) \mathrm{W}(y) -10\mathcal{{U}}(y)-12\mathcal{{W}}(y)\Big\}, \\ \text{(d)}\quad &\sum\limits_{n = 1}^{\infty}\frac{y^n}{(1+y)^{3n}} \binom{3n}{n} \Big\{\big( \mathbf{H}_{{n}}- \mathbf{H}_{{3n}}\big)^2 + \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}- \mathbf{H}_{{3n}}^{ \langle{{{2}}}\rangle}\Big\}\\ &\; = \frac{1+y}{1-2y} \Big\{\ln^2(1+y)-6\ln(1+y) \mathrm{W}(y)-2\mathcal{{U}}(y)\Big\}; \end{align*}$

where $\mathrm{W}(y)\;\; and\;\; \mathcal{{U}}(y)$ are as in Lemmas 4 and 18, respectively, and $\mathcal{{W}}(y)$ is given by

$\begin{aligned} \mathscr{W}(y) & =\sum_{k=1}^{\infty} \frac{(k-1)!}{\left(\frac{1}{2}\right)_k}\left(\frac{-y}{4}\right)^k \overline{\mathbf{H}}_{2 k} \\ & =\left(1-\sqrt{\frac{y}{4+y}}\right) \ln ^2\left(\frac{\sqrt{4+y}+\sqrt{y}}{2}\right)-\sqrt{\frac{y}{4+y}} \operatorname{Li}_2\left(\frac{2 \sqrt{y}}{\sqrt{y}+\sqrt{4+y}}\right). \end{aligned}$

There are altogether nine harmonic-like numbers appearing in the above four series

$\Big\{ \mathbf{H}_{{n}}^{{2}}, \mathbf{O}_{{n}}^{{2}}, \mathbf{H}_{{3n}}^{{2}};\; \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}, \mathbf{O}_{{n}}^{ \langle{{{2}}}\rangle}, \mathbf{H}_{{3n}}^{ \langle{{{2}}}\rangle};\; \mathbf{H}_{{n}} \mathbf{O}_{{n}}, \mathbf{H}_{{n}} \mathbf{H}_{{3n}}, \mathbf{H}_{{3n}} \mathbf{O}_{{n}}\Big\}.$

To evaluate the nine corresponding independent "nuclear series", it is necessary to find five similar independent equations. It seems quite a tough problem that the authors failed to arrive at solutions, even though we did succeed in determining the following long and ugly expression involving six terms in dilogarithms (that prevents us from making further simplifications). Perhaps the only value of this formula lies in its existence.

$\begin{align*} \sum\limits_{n = 1}^{\infty} \binom{3n}{n}\frac{ \mathbf{H}_{{n}}^{ \langle{{{2}}}\rangle}\; y^n}{(1+y)^{3n}} & = \int_0^y\frac{3(1+y)^3\ln\Big(\frac{T(1+y)^3}{y(1+T)^3}\Big)\; dT} {(1-2y)(1+T)(T^2y+Ty^2+3Ty-1)}\\ & = \frac{\pi ^2 (1+y)}{2 (1-2 y)} +\frac{3 (1+y) \ln^2(1+y)}{1-2 y} +\frac{3 (1+y) \ln y \ln(1+y)}{1-2 y}\\ &-\frac{3 (1+y)}{1-2 y} \mathrm{Li}_2\Big(\frac{1}{1+y}\Big) +\frac{9 (1+y)}{1-2 y}\sqrt{\frac{y}{4+y}} \ln(1+y) \ln\Big(\frac{2+y+ \sqrt{4y+y^2}}{2}\Big)\\ &+\frac{3 (1+y)}{2 (1-2 y)} \Big(1+\sqrt{\frac{y}{4+y}}\Big) \Bigg\{3 \mathrm{Li}_2\Big(\frac{-2\sqrt{y}}{(1+y) (\sqrt{y}-\sqrt{4+y})}\Big) -3 \mathrm{Li}_2\Big(\frac{-2 \sqrt{y}}{\sqrt{y}-\sqrt{4+y}}\Big) + \mathrm{Li}_2\Big(\frac{-2 y^{3/2}}{\sqrt{y}(3+y)-(1+y) \sqrt{4+y}}\Big)\Bigg\} \\ &+\frac{3 (1+y)}{2 (1-2 y)} \Big(1-\sqrt{\frac{y}{4+y}}\Big) \Bigg\{3 \mathrm{Li}_2\Big(\frac{-2 \sqrt{y}}{(1+y) (\sqrt{y}+\sqrt{4+y})}\Big) -3 \mathrm{Li}_2\Big(\frac{-2 \sqrt{y}}{\sqrt{y}+\sqrt{4+y}}\Big) + \mathrm{Li}_2\Big(\frac{-2 y^{3/2}}{\sqrt{y}(3+y)+(1+y) \sqrt{4+y}}\Big)\Bigg\} . \end{align*}$

Therefore, to evaluate the series containing binomial coefficient $\binom{3n}{n}$ and harmonic-like numbers of the second and/or higher orders, one needs to find out different approaches. The interested readers are enthusiastically encouraged to make further explorations.

Author contributions

C. Li: Writing, computation and review; W. Chu: Methodology and supervision. Both of authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence tools in the creation of this article.

Acknowledgments

The authors express their gratitude to anonymous referees for their careful reading, critical comments and valuable suggestions that make the manuscript improved substantially during the revision.

Conflict of interest

Prof. Wenchang Chu is the Guest Editor of special issue "Combinatorial Analysis and Mathematical Constants" for AIMS Mathematics. Prof. Wenchang Chu was not involved in the editorial review and the decision to publish this article. The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

[1]	A. Melegaro, N. J. Gay, G. F. Medley, Estimating the transmission parameters of pneumococcal carriage in households, Epidemiol Infect., 132 (2004), 433–441. https://doi.org/10.1017/s0950268804001980 doi: 10.1017/s0950268804001980
[2]	E. Joseph, Mathematical analysis of prevention and control strategies of pneumonia in adults and children, University of Dar es Salaam, 2012.
[3]	D. Ssebuliba, Mathematical modelling of the effectiveness of two training interventions on infectious diseases in Uganda, PhD Thesis, Stellenbosch University, 2013.
[4]	J. Ong'ala, J. Y. T. Mugisha, P. Oleche, Mathematical model for Pneumonia dynamics with carriers, Int. J. Math. Anal., 7 (2013), 2457–2473. https://doi.org/10.12988/ijma.2013.35109 doi: 10.12988/ijma.2013.35109
[5]	H. W. Hethcote, The mathematics of infectious diseases, SIAM Rev., 42 (2000), 599–653. https://doi.org/10.1137/S0036144500371907 doi: 10.1137/S0036144500371907
[6]	G. T. Tilahun, O. D. Makinde, D. Malonza, Modelling and optimal control of pneumonia disease with cost-effective strategies, J. Biol. Dynam., 11 (2017), 400–426. https://doi.org/10.1080/17513758.2017.1337245. doi: 10.1080/17513758.2017.1337245
[7]	G. T. Tilahun, O. D. Makinde, D. Malonza, Co-dynamics of pneumonia and typhoid fever diseases with cost effective optimal control analysis, Appl. Math. Comput., 316 (2018), 438–459. https://doi.org/10.1016/j.amc.2017.07.063 doi: 10.1016/j.amc.2017.07.063
[8]	S. Saber, A. M. Alghamdi, G. A. Ahmed, K. M. Alshehri, Mathematical modelling and optimal control of pneumonia disease in sheep and goats in Al-Baha region with cost-effective strategies, AIMS Mathematics, 7 (2022), 12011–12049. https://doi.org/10.3934/math.2022669 doi: 10.3934/math.2022669
[9]	I. Podlubny, Fractional differential equations, New York: Academic Press, 1999.
[10]	P. A. Naik, M. Yavuz, S. Qureshi, J. Zu, S. Townley, Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan, Eur. Phys. J. Plus, 135 (2020), 795. https://doi.org/10.1140/epjp/s13360-020-00819-5 doi: 10.1140/epjp/s13360-020-00819-5
[11]	M. H. Alshehri, S. Saber, F. Z. Duraihem, Dynamical analysis of fractional-order of IVGTT glucose-insulin interaction, Int. J. Nonlin. Sci. Num., 24 (2023), 1123–1140. https://doi.org/10.1515/ijnsns-2020-0201 doi: 10.1515/ijnsns-2020-0201
[12]	M. H. Alshehri, F. Z. Duraihem, A. Alalyani, S. Saber, A Caputo (discretization) fractional-order model of glucose-insulin interaction: Numerical solution and comparisons with experimental data, J. Taibah Univ. Sci., 15 (2021), 26–36. https://doi.org/10.1080/16583655.2021.1872197 doi: 10.1080/16583655.2021.1872197
[13]	S. Saber, A. Alalyani, Stability analysis and numerical simulations of IVGTT glucose-insulin interaction models with two time delays, Math. Model. Anal., 27 (2022), 383–407. https://doi.org/10.3846/mma.2022.14007 doi: 10.3846/mma.2022.14007
[14]	A. Alalyani, S. Saber, Stability analysis and numerical simulations of the fractional COVID-19 pandemic model, Int. J. Nonlin. Sci. Num., 24 (2023), 989–1002. https://doi.org/10.1515/ijnsns-2021-0042 doi: 10.1515/ijnsns-2021-0042
[15]	N. Almutairi, S. Saber, Chaos control and numerical solution of time-varying fractional Newton-Leipnik system using fractional Atangana-Baleanu derivatives, AIMS Mathematics, 8 (2023), 25863–25887. https://doi.org/10.3934/math.20231319. doi: 10.3934/math.20231319
[16]	K. I. A. Ahmed, H. D. S. Adam, M. Y. Youssif, S. Saber, Different strategies for diabetes by mathematical modeling: mdified minimal model, Alex. Eng. J., 80 (2023), 74–87. https://doi.org/10.1016/j.aej.2023.07.050 doi: 10.1016/j.aej.2023.07.050
[17]	K. I. A. Ahmed, H. D. S. Adam, M. Y. Youssif, S. Saber, Different strategies for diabetes by mathematical modeling: Applications of fractal-fractional derivatives in the sense of Atangana-Baleanu, Results Phys., 2023 (2023), 106892. https://doi.org/10.1016/j.rinp.2023.106892 doi: 10.1016/j.rinp.2023.106892
[18]	S. Saber, N. Almutairi, Chaos in a nonlinear Lorentz-Lü-Chen system via the fractal fractional operator of Atangana-Baleanu, submitted for publication.
[19]	D. Baleanu, B. Shiri, Generalized fractional differential equations for past dynamic, AIMS Mathematics, 7 (2022), 14394–14418. https://doi.org/10.3934/math.2022793 doi: 10.3934/math.2022793
[20]	B. Shiri, G. C. Wu, D. Baleanu, Terminal value problems for the nonlinear systems of fractional differential equations, Appl. Numer. Math., 170 (2021), 162–178. https://doi.org/10.1016/j.apnum.2021.06.015 doi: 10.1016/j.apnum.2021.06.015
[21]	B. Shiri, D. Baleanu, All linear fractional derivatives with power functions' convolution kernel and interpolation properties, Chaos Soliton. Fract., 170 (2023), 113399. https://doi.org/10.1016/j.chaos.2023.113399. doi: 10.1016/j.chaos.2023.113399
[22]	C. Xu, D. Mu, Y. Pan, C. Aouiti, L. Yao, Exploring bifurcation in a fractional-order predator-prey system with mixed delays, J. Appl. Anal. Comput., 13 (2023), 1119–1136. https://doi.org/10.11948/20210313 doi: 10.11948/20210313
[23]	C. Xu, D. Mu, Z. Liu, Y. Pang, C. Aouitid, O. Tun, et al., Bifurcation dynamics and control mechanism of a fractional-order delayed Brusselator chemical reaction model, Match Commun. Math. Co., 89 (2023), 73–106. https://doi.org/10.46793/match.89-1.073X doi: 10.46793/match.89-1.073X
[24]	P. Li, Y. Lu, C. Xu, J. Ren, Insight into Hopf bifurcation and control methods in fractional order BAM neural networks incorporating symmetric structure and delay, Cogn. Comput., 2023 (2023), 02. https://doi.org/10.1007/s12559-023-10155-2 doi: 10.1007/s12559-023-10155-2
[25]	P. Li, R. Gao, C. Xu, S. Ahmad, Y. Li, A. Akgul, Bifurcation behavior and PD $^\gamma$ control mechanism of a fractional delayed genetic regulatory model. Chaos Soliton. Fract., 168 (2023), 113219. https://doi.org/10.1016/j.chaos.2023.113219 doi: 10.1016/j.chaos.2023.113219
[26]	P. A. Naik, Global dynamics of a fractional-order SIR epidemic model with memory, Int. J. Biomath., 13 (2020), 2050071. https://doi.org/10.1142/S1793524520500710 doi: 10.1142/S1793524520500710
[27]	M. B. Ghori, P. A. Naik, J. Zu, Z. Eskandari, M. Naik, Global dynamics and bifurcation analysis of a fractional-order SEIR epidemic model with saturation incidence rate, Math. Method. Appl. Sci., 45 (2022), 3665–3688. https://doi.org/10.1002/mma.8010 doi: 10.1002/mma.8010
[28]	A. Ahmad, M. Farman, P. A. Naik, N. Zafar, A. Akgul, M. U. Saleem, Modeling and numerical investigation of fractional-order bovine babesiosis disease, Numer. Meth. Part. D. E., 37 (2021), 1946–1964. https://doi.org/10.1002/num.22632 doi: 10.1002/num.22632
[29]	M. Farman, A. Akgül, T. Abdeljawad, P. A. Naik, N. Bukhari, A. Ahmad, Modeling and analysis of fractional order Ebola virus model with Mittag-Leffler kernel, Alex. Eng. J., 61 (2022), 2062–2073. https://doi.org/10.1016/j.aej.2021.07.040 doi: 10.1016/j.aej.2021.07.040
[30]	P. A. Naik, K. M. Owolabi, M. Yavuz, J. Zu, Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells, Chaos Soliton. Fract., 140 (2020), 110272. https://doi.org/10.1016/j.chaos.2020.110272 doi: 10.1016/j.chaos.2020.110272
[31]	H. Khan, J. Gómez-Aguilar, A. Alkhazzan, A. Khan, A fractional order HIV-TB coinfection model with nonsingular Mittag-Leffler law, Math. Method. Appl. Sci., 43 (2020), 3786–3806. https://doi.org/10.1002/mma.6155. doi: 10.1002/mma.6155
[32]	H. Khan, F. Jarad, T. Abdeljawad, A. Khan, A singular ABC-fractional differential equation with p-Laplacian operator, Chaos Soliton. Fract., 129 (2019), 56–61. https://doi.org/10.1016/j.chaos.2019.08.017 doi: 10.1016/j.chaos.2019.08.017
[33]	A. Atangana, E. Alabaraoye, Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations, Adv. Differ. Equ., 94 (2013), 94. https://doi.org/10.1186/1687-1847-2013-94 doi: 10.1186/1687-1847-2013-94
[34]	S. K. Choi, B. Kang, N. Koo, Stability for Caputo fractional differential systems, Abstr. Appl. Anal., 2014 (2014), 631419. https://doi.org/10.1155/2014/631419 doi: 10.1155/2014/631419
[35]	H. Li, L. Zhang, C. Hu, Y. Jiang, Z. Teng, Dynamical analysis of a fractional-order predator prey model incorporating a prey refuge, J. Appl. Math. Comput., 54 (2016), 435–449. https://doi.org/10.1007/s12190-016-1017-8 doi: 10.1007/s12190-016-1017-8
[36]	A. Omame, M. Abbas, A. Abdel-Aty, Assessing the impact of SARS-CoV-2 infection on the dynamics of dengue and HIV via fractional derivatives, Chaos Soliton. Fract., 162 (2022), 112427. https://doi.org/10.1016/j.chaos.2022.112427 doi: 10.1016/j.chaos.2022.112427
[37]	D. Baleanu, A. Fernandez, A. Akgül, On a fractional operator combining proportional and classical differintegrals, Mathematics, 8 (2000), 360. https://doi.org/10.3390/math8030360 doi: 10.3390/math8030360
[38]	D. Baleanu, S. Arshad, A. Jajarmi, W. Shokat, F. A. Ghassabzade, M. Wali, Dynamical behaviours and stability analysis of a generalized fractional model with a real case study, J. Adv. Res., 48 (2023), 157–173. https://doi.org/10.1016/j.jare.2022.08.010 doi: 10.1016/j.jare.2022.08.010
[39]	H. Delvari, D. Baleanu, J. Sadati, Stability analysis of Caputo fractional-order non-linear systems revisited, Nonlinear Dyn., 67 (2012), 2433–2439. https://doi.org/10.1007/s11071-011-0157-5 doi: 10.1007/s11071-011-0157-5
[40]	D. Baleanu, M. Hasanabadi, A. M. Vaziri, A. Jajarmi, A new intervention strategy for an HIV/AIDS transmission by a general fractional modeling and an optimal control approach, Chaos Soliton. Fract., 167 (2023), 113078. https://doi.org/10.1016/j.chaos.2022.113078 doi: 10.1016/j.chaos.2022.113078
[41]	A. Akgul, A novel method for a fractional derivative with non-local and nonsingular kernel, Chaos Soliton. Fract., 114 (2018), 478–482. https://doi.org/10.1016/j.chaos.2018.07.032 doi: 10.1016/j.chaos.2018.07.032
[42]	A. Akgul, M. Modanli, Crank-Nicholson difference method and reproducing kernel function for third order fractional differential equations in the sense of Atangana-Baleanu Caputo derivative, Chaos Soliton. Fract., 127 (2019), 10–16. https://doi.org/10.1016/j.chaos.2019.06.011 doi: 10.1016/j.chaos.2019.06.011
[43]	M. Caputo, M. Fabrizio, A new definition of fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 1 (2015), 73–85. https://doi.org/10.12785/pfda/010201 doi: 10.12785/pfda/010201
[44]	M. Toufik, A. Atangana, New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models, Eur. Phys. J. Plus, 132 (2017), 444. https://doi.org/10.1140/epjp/i2017-11717-0 doi: 10.1140/epjp/i2017-11717-0
[45]	S. A. Jose, R. Ramachandran, D. Baleanu, H. S. Panigoro, J. Alzabut, V. E. Balas, Computational dynamics of a fractional order substance addictions transfer model with Atangana-Baleanu-Caputo derivative, Math. Method. Appl. Sci., 46 (2023), 5060–5085. https://doi.org/10.1002/mma.8818 doi: 10.1002/mma.8818
[46]	A. Atangana, On the new fractional derivative and application to nonlinear Fisher's reaction-diffusion equation, Appl. Math. Comput., 273 (2016), 948–956. https://doi.org/10.1016/j.amc.2015.10.021 doi: 10.1016/j.amc.2015.10.021
[47]	M. Caputo, Linear model of dissipation whose Q is almost frequency independent-Ⅱ, Geophys. J. Int., 13 (1967), 529–539. https://doi.org/10.1111/j.1365-246X.1967.tb02303.x doi: 10.1111/j.1365-246X.1967.tb02303.x
[48]	S. K. Choi, B. Kang, N. Koo, Stability for Caputo fractional differential systems, Abstr. Appl. Anal., 2014 (2014), 631419. https://doi.org/10.1155/2014/631419 doi: 10.1155/2014/631419
[49]	P. van den Driessche, J. Watmough, Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6 doi: 10.1016/S0025-5564(02)00108-6
[50]	S. Baba, O. D. Makinde, Optimal control of HIV/AIDS in the workplace in the presence of careless individuals, Comput. Math. Method. M., 2014 (2014), 831506. https://doi.org/10.1155/2014/831506 doi: 10.1155/2014/831506
[51]	S. Uçar, E. Uçar, N. Özdemir, Z. Hammouch, Mathematical analysis and numerical simulation for a smoking model with Atangana-Baleanu derivative, Chaos Soliton. Fract., 118 (2019), 300–306, https://doi.org/10.1016/j.chaos.2018.12.003 doi: 10.1016/j.chaos.2018.12.003
[52]	M. Al-Refai, K. Pal, New aspects of Caputo-Fabrizio fractional derivative, Progr. Fract. Differ. Appl., 5 (2019), 157–166. https://doi.org/10.18576/pfda/050206 doi: 10.18576/pfda/050206
[53]	A. Atangana, D. Baleanu, New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model, Therm. Sci., 20 (2016), 763–769.
[54]	A. Atangana, S. Qureshi, Modeling attractors of chaotic dynamical systems with fractal-fractional operators, Chao Soliton. Fract., 123 (2019), 320–337, https://doi.org/10.1016/j.chaos.2019.04.020 doi: 10.1016/j.chaos.2019.04.020
[55]	S. Uçar, Analysis of hepatitis B disease with fractal-fractional Caputo derivative using real data from Turkey, J. Comput. Appl. Math., 419 (2023), 114692, https://doi.org/10.1016/j.cam.2022.114692 doi: 10.1016/j.cam.2022.114692
[56]	I. Koca, Modeling the heat flow equation with fractional-fractal differentiation, Chaos Soliton. Fract., 128 (2019), 83–91. https://doi.org/10.1016/j.chaos.2019.07.014 doi: 10.1016/j.chaos.2019.07.014
[57]	Z. Ali, F. Rabiei, K. Shah, T. Khodadadi, Fractal-fractional order dynamical behavior of an HIV/AIDS epidemic mathematical model, Eur. Phys. J. Plus, 136 (2021), 36. https://doi.org/10.1140/epjp/s13360-020-00994-5 doi: 10.1140/epjp/s13360-020-00994-5
[58]	L. Zhang, M. ur Rahman, H. Qu, M. Arfan, Adnan, Fractal-fractional Anthroponotic Cutaneous Leishmania model study in sense of Caputo derivative, Alex. Eng. J., 61 (2022), 4423–4433, https://doi.org/10.1016/j.aej.2021.10.001 doi: 10.1016/j.aej.2021.10.001
[59]	H. Khan, K. Alam, H. Gulzar, S. Etemad, S. Rezapour, A case study of fractal-fractional tuberculosis model in China: Existence and stability theories along with numerical simulations, Math. Comput. Simulat., 198 (2022), 455–473. https://doi.org/10.1016/j.matcom.2022.03.009 doi: 10.1016/j.matcom.2022.03.009
[60]	J. K. K. Asamoah, Fractal-fractional model and numerical scheme based on Newton polynomial for Q fever disease under Atangana Baleanu derivative, Results Phys., 34 (2022), 105189. https://doi.org/10.1016/j.rinp.2022.105189 doi: 10.1016/j.rinp.2022.105189
[61]	K. M. Saad, M. Alqhtani, J. F. Gomez-Aguilar, Fractal-fractional study of the hepatitis C virus infection model, Results Phys., 19 (2020), 103555. https://doi.org/10.1016/j.rinp.2020.103555 doi: 10.1016/j.rinp.2020.103555
[62]	S. Etemad, I. Avcı, P. Kumar, D. Baleanu, S. Rezapour, Some novel mathematical analysis on the fractal-fractional model of the AH1N1/09 virus and its generalized Caputo-type version, Chaos Soliton. Fract., 162 (2020), 112511. https://doi.org/10.1016/j.chaos.2022.112511 doi: 10.1016/j.chaos.2022.112511
[63]	H. Khan, J. Alzabut, A. Shah, S. Etemad, S. Rezapour, C. Park, A study on the fractal-fractional tobacco smoking model, AIMS Mathematics, 7 (2022), 13887–13909. https://doi.org/10.3934/math.2022767 doi: 10.3934/math.2022767
[64]	H. Najafi, S. Etemad, N. Patanarapeelert, J. K. K. Asamoah, S. Rezapour, T. Sitthiwirattham, A study on dynamics of CD4+ T-cells under the effect of HIV-1 infection based on a mathematical fractal-fractional model via the Adams-Bashforth scheme and Newton polynomials, Mathematics, 10 (2022), 1366. https://doi.org/10.3390/math10091366 doi: 10.3390/math10091366
[65]	S. Etemad, I. Avci, P. Kumar, D. Baleanu, S. Rezapour, Some novel mathematical analysis on the fractal-fractional model of the AH1N1/09 virus and its generalized Caputo-type version, Chaos Soliton. Fract., 162 (2022), 112511. https://doi.org/10.1016/j.chaos.2022.112511 doi: 10.1016/j.chaos.2022.112511
[66]	A. Atangana, Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system, Chaos Soliton. Fract., 102 (2017), 396–406. https://doi.org/10.1016/j.chaos.2017.04.027 doi: 10.1016/j.chaos.2017.04.027
[67]	H. Khan, F. Ahmad, O. Tunç, M. Idrees, On fractal-fractional Covid-19 mathematical model, Chaos Soliton. Fract., 157 (2022), 111937. https://doi.org/10.1016/j.chaos.2022.111937. doi: 10.1016/j.chaos.2022.111937
[68]	K. A. Abro, A. Atangana, Numerical and mathematical analysis of induction motor by means of AB-fractal-fractional differentiation actuated by drilling system, Numer. Methods Partial Differential Eq., 38 (2022), 293–307. https://doi.org/10.1002/num.22618 doi: 10.1002/num.22618
[69]	K. M. Owolabi, A. Atangana, A. Akgul, Modelling and analysis of fractal-fractional partial differential equations: application to reaction-diffusion model, Alex. Eng. J., 59 (2020), 2477–2490. https://doi.org/10.1016/j.aej.2020.03.022 doi: 10.1016/j.aej.2020.03.022
[70]	A. Atangana, A. Akgul, K. M. Owolabi, Analysis of fractal fractional differential equations, Alex. Eng. J., 59 (2020), 1117–1134. https://api.semanticscholar.org/CorpusID:212831086
[71]	K. M. Owolabi, A. Shikongo, A. Atangana, Fractal fractional derivative operator method on MCF-7 cell line dynamics, In: Methods of mathematical modelling and computation for complex systems, Cham: Springer, 2022,319–339. https://doi.org/10.1016/j.aej.2021.10.001
[72]	S. Qureshi, A. Atangana, Fractal-fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data, Chaos Soliton. Fract., 136 (2020), 109812. https://doi.org/10.1016/j.chaos.2020.109812 doi: 10.1016/j.chaos.2020.109812
[73]	K. Shah, M. Arfan, I. Mahariq, A. Ahmadian, S. Salahshour, M. Ferrara, Fractal-fractional mathematical model addressing the situation of Corona virus in Pakistan, Results Phys., 19 (2020), 103560. https://doi.org/10.1016/j.rinp.2020.103560 doi: 10.1016/j.rinp.2020.103560
[74]	K. I. A. Ahmed, H. D. S. Adam, M. Y. Youssif, S. Saber, Different strategies for diabetes by mathematical modeling: modified minimal model, Alex. Eng. J., 80 (2023), 74–87. https://doi.org/10.1016/j.aej.2023.07.050 doi: 10.1016/j.aej.2023.07.050
[75]	K. I. A. Ahmed, H. D. S. Adam, M. Y. Youssif, S. Saber, Different strategies for diabetes by mathematical modeling: Applications of fractal-fractional derivatives in the sense of Atangana-Baleanu, Results Phys., 2023 (2023), 106892. https://doi.org/10.1016/j.rinp.2023.106892 doi: 10.1016/j.rinp.2023.106892
[76]	A. Atangana, Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system, Chaos Soliton. Fract., 102 (2017), 396–406. https://doi.org/10.1016/j.chaos.2017.04.027 doi: 10.1016/j.chaos.2017.04.027
[77]	K. A. Abro, A. Atangana, A comparative study of convective fluid motion in rotating cavity via Atangana-Baleanu and Caputo-Fabrizio fractal-fractional differentiations, Eur. Phys. J. Plus, 135 (2020), 226. https://doi.org/10.1140/epjp/s13360-020-00136-x doi: 10.1140/epjp/s13360-020-00136-x
[78]	P. Li, L. Han, C. Xu, X. Peng, M. ur Rahman, S. Shi, Dynamical properties of a meminductor chaotic system with fractal-fractional power law operator, Chaos Soliton. Fract., 175 (2023), 114040. https://doi.org/10.1016/j.chaos.2023.114040 doi: 10.1016/j.chaos.2023.114040
[79]	A. Jamal, A. Ullah, S. Ahmad, S. Sarwar, A. Shokri, A survey of (2+1)-dimensional KdV-mKdV equation using nonlocal Caputo fractal-fractional operator, Results Phys., 46 (2023), 106294. https://doi.org/10.1016/j.rinp.2023.106294 doi: 10.1016/j.rinp.2023.106294
[80]	S. M. Ulam, A collection of mathematical problems, New York: Interscience, 1960.
[81]	S. M. Ulam, Problems in modern mathematics, London: Dover Publications, 2004.
[82]	Z. M. Odibat, N. T. Shawagfeh, Generalized Taylor's formula, Appl. Math. Comput., 186 (2007) 286–293. https://doi.org/10.1016/j.amc.2006.07.102 doi: 10.1016/j.amc.2006.07.102
[83]	Z. M. Odibat, S. M. Momani, An algorithm for the numerical solution of differential equations of fractional order, J. Appl. Math. Informatics, 26 (2008), 15–27.

This article has been cited by:

1.	Chunli Li, Wenchang Chu, Generating Functions for Binomial Series Involving Harmonic-like Numbers, 2024, 12, 2227-7390, 2685, 10.3390/math12172685
2.	Artūras Dubickas, On the Range of Arithmetic Means of the Fractional Parts of Harmonic Numbers, 2024, 12, 2227-7390, 3731, 10.3390/math12233731

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)