1.
Introduction
In [1] (see [2] for type A), the authors introduced cluster categories which were associated to finite dimensional hereditary algebras. It is well known that cluster-tilting theory gives a way to construct abelian categories from some triangulated and exact categories.
Recently, Nakaoka and Palu introduced extriangulated categories in [3], which are a simultaneous generalization of exact categories and triangulated categories, see also [4,5,6]. Subcategories of an extriangulated category which are closed under extension are also extriangulated categories. However, there exist some other examples of extriangulated categories which are neither exact nor triangulated, see [6,7,8].
When T is a cluster tilting subcategory, the authors Yang, Zhou and Zhu [9, Definition 3.1] introduced the notions of T[1]-cluster tilting subcategories (also called ghost cluster tilting subcategories) and weak T[1]-cluster tilting subcategories in a triangulated category C, which are generalizations of cluster tilting subcategories. In these works, the authors investigated the relationship between C and modT via the restricted Yoneda functor G more closely. More precisely, they gave a bijection between the class of T[1]-cluster tilting subcategories of C and the class of support τ-tilting pairs of modT, see [9, Theorems 4.3 and 4.4].
Inspired by Yang, Zhou and Zhu [9] and Liu and Zhou [10], we introduce the notion of relative cluster tilting subcategories in an extriangulated category B. More importantly, we want to investigate the relationship between relative cluster tilting subcategories and some important subcategories of modΩ(T)_ (see Theorem 3.9 and Corollary 3.10), which generalizes and improves the work by Yang, Zhou and Zhu [9] and Liu and Zhou [10].
It is worth noting that the proof idea of our main results in this manuscript is similar to that in [9, Theorems 4.3 and 4.4], however, the generalization is nontrivial and we give a new proof technique.
2.
Preliminaries
Throughout the paper, let B denote an additive category. The subcategories considered are full additive subcategories which are closed under isomorphisms. Let [X](A,B) denote the subgroup of HomB(A,B) consisting of morphisms which factor through objects in a subcategory X. The quotient category B/[X] of B by a subcategory X is the category with the same objects as B and the space of morphisms from A to B is the quotient of group of morphisms from A to B in B by the subgroup consisting of morphisms factor through objects in X. We use Ab to denote the category of abelian groups.
In the following, we recall the definition and some properties of extriangulated categories from [4], [11] and [3].
Suppose there exists a biadditive functor E:Bop×B→Ab. Let A,C∈B be two objects, an element δ∈E(C,A) is called an E-extension. Zero element in E(C,A) is called the split E-extension.
Let s be a correspondence, which associates any E-extension δ∈E(C,A) to an equivalence class s(δ)=[Ax→By→C]. Moreover, if s satisfies the conditions in [3, Definition 2.9], we call it a realization of E.
Definition 2.1. [3, Definition 2.12] A triplet (B,E,s) is called an externally triangulated category, or for short, extriangulated category if
(ET1) E:Bop×B→Ab is a biadditive functor.
(ET2) s is an additive realization of E.
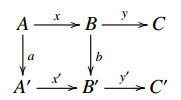
(ET3) For a pair of E-extensions δ∈E(C,A) and δ′∈E(C′,A′), realized as s(δ)=[Ax→By→C] and s(δ′)=[A′x′→B′y′→C′]. If there exists a commutative square,
then there exists a morphism c:C→C′ which makes the above diagram commutative.
(ET3)op Dual of (ET3).
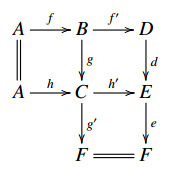
(ET4) Let δ and δ′ be two E-extensions realized by Af→Bf′→D and Bg→Cg′→F, respectively. Then there exist an object E∈B, and a commutative diagram
and an E-extension δ′′ realized by Ah→Ch′→E, which satisfy the following compatibilities:
(i). Dd→Ee→F realizes E(F,f′)(δ′),
(ii). E(d,A)(δ′′)=δ,
(iii). E(E,f)(δ′′)=E(e,B)(δ′).
(ET4op) Dual of (ET4).
Let B be an extriangulated category, we recall some notations from [3,6].
● We call a sequence Xx→Yy→Z a conflation if it realizes some E-extension δ∈E(Z,X), where the morphism x is called an inflation, the morphism y is called an deflation and Xx→Yy→Zδ⇢ is called an E-triangle.
●When Xx→Yy→Zδ⇢ is an E-triangle, X is called the CoCone of the deflation y, and denote it by CoCone(y); C is called the Cone of the inflation x, and denote it by Cone(x).
Remark 2.2. 1) Both inflations and deflations are closed under composition.
2) We call a subcategory T extension-closed if for any E-triangle Xx→Yy→Zδ⇢ with X, Z∈T, then Y∈T.
Denote I by the subcategory of all injective objects of B and P by the subcategory of all projective objects.
In an extriangulated category having enough projectives and injectives, Liu and Nakaoka [4] defined the higher extension groups as
By [3, Corollary 3.5], there exists a useful lemma.
Lemma 2.3. For a pair of E-triangles Ll→Mm→N⇢ and Dd→Ee→F⇢. If there is a commutative diagram
f factors through l if and only if h factors through e.
3.
Results
In this section, B is always an extriangulated category and T is always a cluster tilting subcategory [6, Definition 2.10].
Let A, B∈B be two objects, denote by [¯T](A,ΣB) the subset of B(A,ΣB) such that f∈[¯T](A,ΣB) if we have f: A→T→ΣB where T∈T and the following commutative diagram
where I is an injective object of B [10, Definition 3.2].
Let M and N be two subcategories of B. The notation [¯T](M,Σ(N))=[T](M,Σ(N)) will mean that [¯T](M,ΣN)=[T](M,ΣN) for every object M∈M and N∈N.
Now, we give the definition of T-cluster tilting subcategories.
Definition 3.1 Let X be a subcategory of B.
1) [11, Definition 2.14] X is called T-rigid if [¯T](X,ΣX)=[T](X,ΣX);
2) X is called T-cluster tilting if X is strongly functorially finite in B and X={M∈C∣[¯T](X,ΣM)=[T](X,ΣM) and [¯T](M,ΣX)=[T](M,ΣX)}.
Remark 3.2. 1) Rigid subcategories are always T-rigid by [6, Definition 2.10];
2) T-cluster tilting subcategories are always T-rigid;
3) T-cluster tilting subcategories always contain the class of projective objects P and injective objects I.
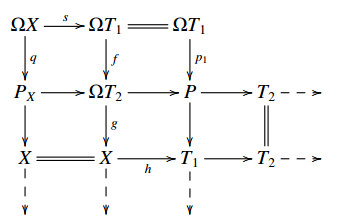
Remark 3.3. Since T is a cluster tilting subcategory, ∀X∈B, there exists a commutative diagram by [6, Remark 2.11] and Definition 2.1((ET4)op), where T1, T2∈T and h is a left T-approximation of X:
Hence ∀X∈B, there always exists an E-triangle
By Remark 3.2(3), P⊆T and B=CoCone(T,T) by [6, Remark 2.11(1),(2)]. Following from [4, Theorem 3.2], B_=B/T is an abelian category. ∀f∈B(A,C), denote by f_ the image of f under the natural quotient functor B→B_.
Let Ω(T)=CoCone(P,T), then Ω(T)_ is the subcategory consisting of projective objects of B_ by [4, Theorem 4.10]. Moreover, modΩ(T)_ denotes the category of coherent functors over the category of Ω(T)_ by [4, Fact 4.13].
Let G: B→modΩ(T)_, M↦HomB_(−,M)∣Ω(T)_ be the restricted Yoneda functor. Then G is homological, i.e., any E-triangle X→Y→Z⇢ in B yields an exact sequence G(X)→G(Y)→G(Z) in modΩ(T)_. Similar to [9, Theorem 2.8], we obtain a lemma:
Lemma 3.4. Denote proj(modΩ(T)_) the subcategory of projective objects in modΩ(T)_. Then
1) G induces an equivalence Ω(T)∼→proj(modΩ(T)_).
2) For N∈modΩ(T)_, there exists a natural isomorphism
In the following, we investigate the relationship between B and modΩ(T)_ via G more closely.
Lemma 3.5. Let X be any subcategory of B. Then
1) any object X∈X, there is a projective presentation in mod Ω(T)_
2) X is a T-rigid subcategory if and only if the class {πG(X)∣X∈X} has property ((S) [9, Definition 2.7(1)]).
Proof. 1). By Remark 3.3, there exists an E-triangle:
When we apply the functor G to it, there exists an exact sequence G(Ω(T1))→G(Ω(T0))→G(X)→0. By Lemma 3.4(1), G(Ω(Ti)) is projective in mod Ω(T)_. So the above exact sequence is the desired projective presentation.
2). For any X0∈X, using the similar proof to [9, Lemma 4.1], we get the following commutative diagram
where α=HommodΩT_(πG(X),G(X0)). By Lemma 3.4(2), both the left and right vertical maps are isomorphisms. Hence the set {πG(X)∣X∈X} has property ((S) iff α is epic iff HomB_(fX,X0) is epic iff X is a T-rigid subcategory by [10, Lemma 3.6].
Lemma 3.6. Let X be a T-rigid subcategory and T1 a subcategory of T. Then X∨T1 is a T-rigid subcategory iff E(T1,X)=0.
Proof. For any M∈X∨T1, then M=X⊕T1 for X∈X and T1∈T1. Let h: X→T be a left T-approximation of X and y: T1→Σ(X′) for X′∈X any morphism. Then there exists the following commutative diagram
with P1∈P, f=(h001) and β=(i000i1).
When X∨T1 is a T-rigid subcategory, we can get a morphism g: X⊕T1→Σ(X′)⊕Σ(T′1) such that βg=(10)y(0 1)f. i.e., ∃b: T1→I such that y=i0b. So E(T1,X′)=0 and then E(T1,X)=0.
Let γ=(r11r12r21r22): T⊕T1→Σ(X′)⊕Σ(T′1) be a morphism. As X is T-rigid, r11h: X→Σ(X′) factors through i0. Since E(T,X)=0, r12: T1→Σ(X′) factors through i0. As T is rigid, the morphism r21h: X→T→Σ(T′1) factors through i1, and the morphism r22: T1→Σ(T′1) factors through i1. So the morphism γf can factor through β=(i000i1). Therefore X∨T1 is an T-rigid subcategory.
For the definition of τ-rigid pair in an additive category, we refer the readers to see [9, Definition 2.7].
Lemma 3.7. Let U be a class of T-rigid subcategories and V a class of τ-rigid pairs of modΩ(T)_. Then there exists a bijection φ: U→V, given by : X↦(G(X),Ω(T)∩Ω(X)).
Proof. Let X be T-rigid. By Lemma 3.5, G(X) is a τ-rigid subcategory of mod Ω(T)_.
Let Y∈Ω(T)∩Ω(X), then there exists X0∈X such that Y=Ω(X0). Consider the E-triangle Ω(X0)→P→X0⇢ with P∈P. ∀X∈X, applying HomB(−,X) yields an exact sequence HomB(P,X)→HomB(Ω(X0),X)→E(X0,X)→0. Hence in B_=B/T, HomB_(Ω(X0),X)≅E(X0,X).
By Remark 3.3, for X0, there is an E-triangle Ω(T1)→Ω(T2)→X0⇢ with T1, T2∈T. Applying HomB_(−,X), we obtain an exact sequence HomB_(Ω(T2),X)→HomB_(Ω(T1),X)→E(X0,X)→E(Ω(T2),X). By [10, Lemma 3.6], HomB_(Ω(T2),X)→HomB_(Ω(T1),X) is epic. Moreover, Ω(T2)_ is projective in B_ by [4, Proposition 4.8]. So E(Ω(T2),X)=0. Thus E(X0,X)=0. Hence ∀X∈X,
So (G(X),Ω(T)∩Ω(X)) is a τ-rigid pairs of modΩ(T)_.
We will show φ is a surjective map.
Let (N,σ) be a τ-rigid pair of modΩ(T)_. ∀N∈N, consider the projective presentation
such that the class {πN|N∈N} has Property (S). By Lemma 3.4, there exists a unique morphism fN: Ω(T1)→Ω(T0) in Ω(T)_ satisfying G(fN)=πN and G(Cone(fN))≅N. Following from Lemma 3.5, X1:= {cone(fN)∣N∈N} is a T-rigid subcategory.
Let X=X1∨Y, where Y={T∈T∣Ω(T)∈σ}. For any T0∈Y, there is an E-triangle Ω(T0)→P→T0⇢ with P∈P. For any Cone(fN)∈X1, applying HomB_(−,Cone(fN)), yields an exact sequence HomB_(Ω(T0),Cone(fN))→E(T0,Cone(fN))→E(P,Cone(fN))=0. Since (N,σ) is a τ-rigid pair, HomB_(Ω(T0),Cone(fN))=G(Cone(fM))(Ω(T0))=0. So E(T0,Cone(fN))=0. Due to Lemma 3.6, X=X1∨Y is T-rigid. Since Y⊆T, we get G(Y)=HomB_(−,T)∣Ω(T)=0 by [4, Lemma 4.7]. So G(X)=G(X1)=N.
It is straightforward to check that Ω(T)∩Ω(X1)=0. Let X∈Ω(T)∩Ω(X), then X∈Ω(T) and X∈Ω(X)=Ω(X1)∨σ. So we can assume that X=Ω(X1)⊕E, where E∈σ. Then Ω(X1)⊕E∈Ω(T). Since E∈Ω(T), we get Ω(X1)∈Ω(T)∩Ω(X1)=0. So Ω(T)∩Ω(X)⊆σ. Clearly, σ⊆Ω(T). Moreover, σ⊆Ω(X). So σ⊆Ω(T)∩Ω(X). Hence Ω(T)∩Ω(X)=σ. Therefore φ is surjective.
Lastly, φ is injective by the similar proof method to [9, Proposition 4.2].
Therefore φ is bijective.
Lemma 3.8. Let T be a rigid subcategory and Aa→B→Cδ⇢ an E-triangle satisfying [¯T](C,Σ(A))=[T](C,Σ(A)). If there exist an E-extension γ∈E(T,A) and a morphism t: C→T with T∈T such that t∗γ=δ, then the E-triangle Aa→B→Cδ⇢ splits.
Proof. Applying HomB(T,−) to the E-triangle A→Ii→Σ(A)α⇢ with I∈I, yields an exact sequence HomB(T,A)→E(T,X)→E(T,I)=0. So there is a morphism d∈HomB(T,Σ(A)) such that γ=d∗α. So δ=t∗γ=t∗d∗α=(dt)∗α. So we have a diagram which is commutative:
Since [¯T](C,Σ(A))=[T](C,Σ(A)) and dt∈[T](C,Σ(A)), dt can factor through i. So 1A can factor through a and the result follows.
Now, we will show our main theorem, which explains the relation between T-cluster tilting subcategories and support τ-tilting pairs of modΩ(T)_.
The subcategory X is called a preimage of Y by G if G(X)=Y.
Theorem 3.9. There is a correspondence between the class of T-cluster tilting subcategories of B and the class of support τ-tilting pairs of modΩ(T)_ such that the class of preimages of support τ-tilting subcategories is contravariantly finite in B.
Proof. Let φ be the bijective map, such that X↦(G(X),Ω(T∩Ω(X))), where G is the restricted Yoneda functor defined in the argument above Lemma 3.4.
1). The map φ is well-defined.
If Xis T-cluster tilting, then X is T-rigid. So φ(X) is a τ-rigid pair of modΩ(T)_ by Lemma 3.7. Therefore Ω(T)∩Ω(X)⊆KerG(X). Assume Ω(T0)∈Ω(T) is an object of KerG(X). Then HomB_(Ω(T0),X)=0. Applying HomB_(−,X) with X∈X to Ω(T0)→P→T0⇢ with P∈P, yields an exact sequence
Hence we get E(T0,X)≅HomB_(Ω(T0),X)=0.
Applying HomB(T0,−) to X→I→Σ(X)⇢, we obtain
For any ba: Xa→Rb→Σ(T0) with R∈T, as T is rigid, we get a commutative diagram:
Hence we get (3.2)[¯T](X,Σ(T0))=[T](X,Σ(T0)).
By the equalities (3.1) and (3.2) and X being a T-rigid subcategory, we obtain
As X is T-cluster tilting, we get X⊕T0∈X. So T0∈X. And thus Ω(T0)∈Ω(T)∩Ω(X). Hence KerG(X)=Ω(T)∩Ω(X).
Since X is functorially finte, similar to [6, Lemma 4.1(2)], ∀Ω(T)∈Ω(T), we can find an E-triangle Ω(T)f→X1→X2⇢, where X1, X2∈X and f is a left X-approximation. Applying G, yields an exact sequence
Thus we get a diagram which is commutative, where HomB_(f,X) is surjective.
By Lemma 3.4, the morphism ∘G(f) is surjective. So G(f) is a left G(X)-approximation and (G(X),Ω(T)∩Ω(X)) is a support τ-tilting pair of modΩ(T)_ by [3, Definition 2.12].
2). φ is epic.
Assume (N,σ) is a support τ-tilting pair of modΩ(T)_. By Lemma 3.7, there is a T-rigid subcategory X satisfies G(X)=N. So ∀Ω(T)∈Ω((T)), there is an exact sequence G(Ω(T))α→G(X3)→G(X4)→0, such that X3, X4∈X and α is a left G(X)-approximation. By Yoneda's lemma, we have a unique morphism in modΩ((T))_:
Moreover, ∀X∈X, consider the following commutative diagram
By Lemma 3.4, G(−) is surjective. So the map HomB_(β,X) is surjective.
Denote Cone(β) by YR and X∨add{YR∣Ω(T)∈Ω(T)} by ˜X.
We claim ˜X is T-rigid.
(I). Assume a: YRa1→T0a2→Σ(X) with T0∈T and X∈X. Consider the following diagram:
Since X is T-rigid, ∃f: X3→I such that aγ=if. So there is a morphism g:Ω(T)→X making the upper diagram commutative. Since HomB_(β,X) is surjective, g factors through β. Hence a factors through i, i.e., [¯T](YR,Σ(X))=[T](YR,Σ(X)).
(II). For any morphism b: Xb1→T0b2→Σ(YR) with T0∈T and X∈X. Consider the following diagram:
By [3, Lemma 5.9], R→Σ(X3)→Σ(YT)⇢ is an E-triangle. Because T is rigid, b2 factors through γ1. By the fact that X is T-rigid, b=b2b1 can factor through iX. Since γ1iX=iY, we get that b factors through iY. So [¯T](X,Σ(YT))=[T](X,Σ(YT)).
By (I) and (II), we also obtain [¯T](YT,Σ(YT))=[T](YT,Σ(YT)).
Therefore ˜X=X∨add{YT∣Ω(T)∈Ω(T)} is T-rigid.
Let M∈B satisfying [¯T](M,Σ(˜X))=[T](M,Σ(˜X)) and [¯T](˜X,ΣM)=[T](˜X,ΣM). Consider the E-triangle:
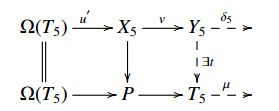
where T5, T6∈T. By the above discussion, there exist two E-triangles:
where X5, X6∈X, u and u′ are left X-approximations of Ω(T6), Ω(T5), respectively. So there exists a diagram of E-triangles which is commutative:
We claim that the morphism x=uf is a left X-approximation of Ω(T5). In fact, let X∈X and d: Ω(T5)→X, we can get a commutative diagram of E-triangles:
where P∈P. By the assumption, [¯T](M,Σ(X))=[T](M,Σ(X)). So d2h factors through iX. By Lemma 2.3, d factors through f. Thus ∃f1: Ω(T6)→X such that d=f1f. Moreover, u is a left X-approximation of Ω(T6). So ∃u1: X6→X such that f1=u1u. Thus d=f1f=u1uf=u1x. So x=uf is a left X-approximation of Ω(T5).
Hence there is a commutative diagram:
By [3, Corollary 3.16], we get an E-triangle X6(yλ)→N⊕X5→Y5x∗δ5⇢
Since u′ is a left X-approximation of Ω(T5), there is also a commutative diagram with P∈P:
such that δ5=t∗μ. So x∗δ5=x∗t∗μ=t∗x∗μ. By Lemma 3.8, the E-triangle x∗δ5 splits. So N⊕X5≃X6⊕Y5∈˜X. hence N∈˜X.
Similarly, consider the following commutative diagram with P∈P:
and the E-triangle M→N→Yg∗δ6⇢. Then ∃t: Y→T6 such that δ6=t∗δ. Then g∗δ6=g∗t∗δ=t∗(g∗δ). Since [¯T](˜X,ΣM)=[T](˜X,ΣM), the E-triangle g∗δ6 splits by Lemma 3.5 and M is a direct summands of N. Hence M∈˜X.
By the above, we get ˜X is a T-cluster tilting subcategory.
By the definition of YR, G(YR)∈G(X). So G(˜X)≃G(X)≃N. Moreover, σ=Ω(T)∩Ω(X)⊆Ω(T)∩Ω(˜X) and Ω(T)∩Ω(˜X)⊆kerG(X)=σ. So Ω(T)∩Ω(˜X)=σ. Hence φ is surjective.
3). φ is injective following from the proof of Lemma 3.7.
By [4, Proposition 4.8 and Fact 4.13], B_≃modΩ(T)_. So it is easy to get the following corollary by Theorem 3.9:
Corollary 3.10. Let X be a subcategory of B.
1) X is T-rigid iff X_ is τ-rigid subcategory of B_.
2) X is T-cluster tilting iff X_ is support τ-tilting subcategory of B_.
If let H=CoCone(T,T), then H can completely replace B and draw the corresponding conclusion by the proof Lemma 3.7 and Theorem 3.9, which is exactly [12, Theorem 3.8]. If let B is a triangulated category, then Theorem 3.9 is exactly [9, Theorem 4.3].
Acknowledgments
This research was supported by the National Natural Science Foundation of China (No. 12101344) and Shan Dong Provincial Natural Science Foundation of China (No.ZR2015PA001).
Conflict of interest
The authors declare they have no conflict of interest.









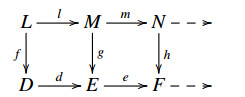
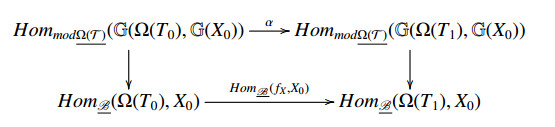
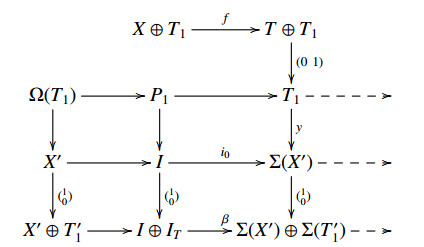
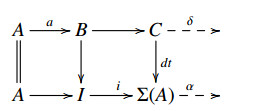
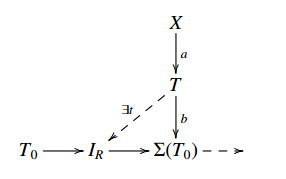
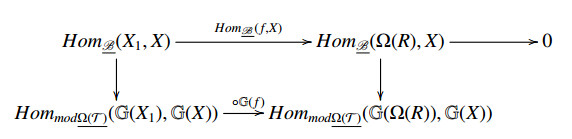
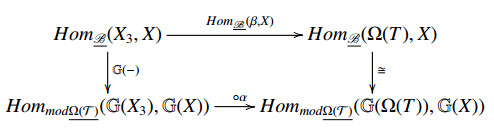
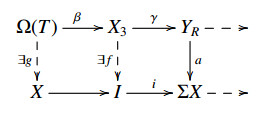
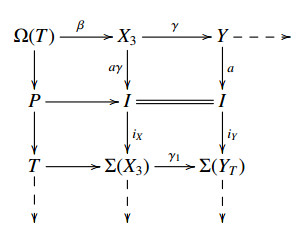
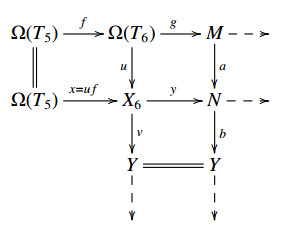
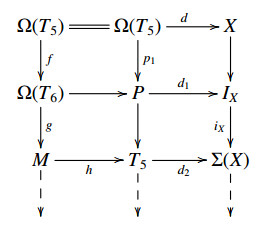
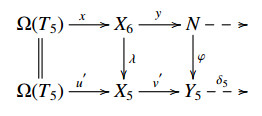
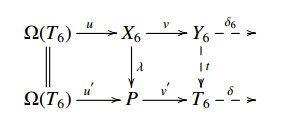








 DownLoad:
DownLoad: