Numerical simulation scheme of jointed rock masses using UAV photogrammetry and a disk-based discontinuous deformation analysis model

1.   Introduction

Habitat fragmentation is usually observed in nature related with heterogeneity in the distribution of resources. For example, food, water, shelter sites, physical factors such as temperature, light, moisture, and any feature be able to affect the growth rate of the population of a given species ^[1]. These fragments, also known as patches, are not completely isolated because they are coupled by the motion of individuals in space. Therefore, mathematicians and ecologists apply diffusion models to explain many ecological problems ^{[1,2,3,4,5,6,7]}. One of the classical population diffusion model ^[7]:

where $x_i(t)$ stands for the density of patch $i$ at time t; $r_i$ stands for the population growth rate of patch $i$; $d_{ij}$ stands for the dispersal rate of the population from the i-th patch to j-th patch, $i = 1, 2, i\neq j$.

The above diffusion processes are all based on the random movement of matter in space. However, many ecologists have found that there are many practical phenomena that cannot be explained by simple diffusion population models, such as, tripping and killing pests. In general, an important feature of many biological individuals is that they can perceive external signals and cues from a specific stimulus, especially vertebrates. Due to the attraction of some external signals, species may move in specific directions, which is called chemotaxis ^[8,9,10,11]. Colombo and Anteneodo proposed a model to consider the interplay between spatial dispersal and environment spatiotemporal fluctuations in meta-population dynamics ^[1]. Li and Guo studied a reaction-diffusion model with chemotaxis and nonlocal delay effect ^[9]. In ^[12,13], they showed that vertebrates have better sensory and differentiated nervous systems than invertebrates, which can transmit sensory information in the polluted environment to the region of brain where it can analysis and make corresponding processing, either bear the concentration of toxins in the habitat or escape from the area. Wei and Chen ^[12] proposed a single-speices population model with psychological effects in the polluted environment:

where $c_e(t)$ and $c_0(t)$ denote the concentration of toxicant in the environment and organism at time t respectively, $u_e(t)$ represents the input rate of external toxins to the habitat at time t, and, it is a continuous and bounded non-negative function. Coefficients $r, \; r_0, \; a, \; k, \; g, \; m, \; h, \; \lambda$ and $\alpha$ are positive constants, and their biological significance has been given in ^[12].

As we all know, with the influence of human economic activities, not only habitats of population are destroyed, but also the environment of habitats are polluted. The survival of those unprotected populations will be seriously threatened, even human beings, therefore, it is necessary to consider the effect of toxins in polluted patches on the population ^{[14,15,16,17]}. The "psychological effect" mentioned in ^[12,13] is also due to the response of biological individuals to the stimulation of environmental toxins in polluted environment, in other words, it is "chemotaxis". Considering the chemotaxis of biological individuals, the single-species population in heavily polluted patches will increase their diffusion to other nonpolluting or lightly polluted patches, while the populations of lightly polluted or nonpolluting patches will slow down their diffusion to heavily polluted patches under the influence of chemotaxis. In order to understand the effect of chemotaxis on population survival, we suppose that patch 1 is heavily polluted patch, and patch 2 is nonpolluting patch. On the basis of previous studies, we propose a single-species population diffusion model with chemotaxis in polluted environment:

where $\lambda_i(0\leq\lambda_i\leq 1)$ denotes the contact rate between the single-species population and the environment toxicant. The initial value satisfies $x_1(0) > 0, x_2(0) > 0, c_o(0)\geq0, c_e(0)\geq0.$

However, in nature, the population will be more or less disturbed by various random factors, which usually composed of many tiny and independent random disturbances, such as temperature, weather and climate change. May ^[18] has pointed out that even the smallest environmental randomness resulted in a qualitatively different result from the deterministic one. In recent years, stochastic population models have received a lot of attention ^{[19,20,21,22,23,24,25]}. Zou and Fan studied a single-species stochastic linear diffusion system ^[23]. Zu and Jiang focused on the extinction, stochastic persistence and stationary distribution of a single-species stochastic model with directed diffusion ^[24]. Liu and Bai considered a stochastic logistic population with biased diffusion ^[25]. Studies of single-species stochastic population models with migrations between the nature preserve and natural environment had received increasing attention in recent works ^{[26,27,28,29]}. But, few studies discuss the single-species population diffusion model with chemotaxis in population environment.

In this paper, we assume that the white noise mainly affects the intrinsic growth rate $r_i$ of system (1.3), we thus model the single-species population diffusion system by replacing the intrinsic growth rate $r_i$ of system (1.3) by a stochastic process $r_i\rightarrow r_i+\sigma_i\frac{dB(t)}{dt}$, i = 1, 2., where $\frac{dB(t)}{dt}$ denotes white noise, $\sigma_i^2$ represents the density of white noise. We therefore derive a single-species stochastic diffusion system with chemotaxis in polluted environment as follows:

Remark 1.1. ^[17]. Since $c_0(t)$ and $c_e(t)$ denote the concentration of toxicant, thus, $0\leq c_e(t)\leq 1$, $0\leq c_0(t)\leq 1$, with this end in view, we need the following constraints $f\leq g+m$, $0\leq u(t)\leq u < h$.

Because the latter two equations in model (1.4) are linear, we only need to discuss the following subsystem here:

2.   Preliminaries

In this paper, unless otherwise noted, let $(\Omega, \mathfrak{F}, P)$ is a complete probability space with a filtration $\{\mathfrak{F}\}_{t\geq 0}$ satisfying the usual conditions. (i.e., it is right continuous and contains all P-null sets)

For the convenience of later discussion, some notations, lemma and theorem are given in this section:

Definition 1. (1) population $x(t)$ is said to be extinction if $\lim\limits_{t\rightarrow+\infty}x(t) = 0, \; \; a.s.$;

(2) population $x(t)$ is said to be strongly persistent if $\liminf\limits_{t\rightarrow+\infty}x(t) > 0;$

(3) population $x(t)$ is said to be strongly persistent in the mean if $\liminf\limits_{t\rightarrow+\infty}\langle x(t)\rangle > 0$.

Lemma 2.1. (see^[22]) Suppose that $x(t)\in C(\Omega\times[0, +\infty), R_+)$.

(1) If there are $\lambda$ and positive constants $\lambda_0$, $T$, such that $\ln x(t)\leq \lambda t-\lambda_0\int_0^tx(s)ds+\sum\limits_{i = 1}^n\beta_idB_i(t), \; t\geq T,$

where $\beta_i(1\leq i\leq n)$ is constant, then

(2) If there are positive constants $\lambda$, $\lambda_0$ and $T$, such that $\ln x(t)\geq\lambda t-\lambda_0\int_0^tx(s)ds+\sum\limits_{i = 1}^n\beta_idB_i(t), \; t\geq T.$

Then $\liminf\limits_{t\rightarrow+\infty} t^{-1}\int_0^tx(s)ds\geq \frac{\lambda}{\lambda_0}, \; \; a.s.$

Theorem 2.2. (see^[19]) Let $M(t)$ be a continuous local martingale and $M(0) = 0$, then

(1) If $\lim\limits_{t\rightarrow+\infty}\langle M(t), M(t)\rangle_t = \infty, \; \; a.s.$, $\Rightarrow$ $\lim\limits_{t\rightarrow+\infty}\frac{M(t)}{\langle M(t), M(t)\rangle} = 0, \; \; a.s.$

(2) If $\lim\limits_{t\rightarrow+\infty}\langle M(t), M(t)\rangle_t < \infty, \; \; a.s.$, $\Rightarrow$ $\lim\limits_{t\rightarrow+\infty}\frac{M(t)}{t} = 0, \; \; a.s.$

Lemma 2.3. (see^[22]) Stochastic population equation $dx(t) = x(t)(r-ax(t))dt+\sigma x(t)dB(t)$, where $r$, $a$ and $\sigma$ are positive constants.

(1) If $r-0.5\sigma^2 > 0$, have $\lim\limits_{t\rightarrow+\infty}\langle x(t)\rangle = \frac{r-0.5\sigma^2}{a}, \; \; \lim\limits_{t\rightarrow+\infty}\frac{\ln x(t)}{t} = 0, \; \; a.s.$

(2) If $r-0.5\sigma^2 < 0$, have $\lim\limits_{t\rightarrow+\infty}x(t) = 0, \; \; a.s.$

Lemma 2.4. If $\lim\limits_{t\rightarrow+\infty}u_e(t) = \overline{u_e}$, then

$Proof.$ From the last two equations of model (1.4), for all $\epsilon > 0$, we can imply that

By standard comparison theorem obtains that

which implies that

Thus, it easily obtain that

3.   Survival analysis of deterministic population model (1.3)

$\mathbf{Assumption}\; H1:\; \widetilde{r_1} = r_1-r_0(c_0)_*-d_{12}(1+\frac{\lambda_1(c_e)_*}{1+\alpha(c_e^2)^*}) < 0,$ $\widetilde{{r}_2} = r_2-d_{21}(1-\frac{\lambda_2(c_e)^*}{1+\alpha(c_e^2)_*}) < 0.$

$\mathbf{Assumption}\; H2:\; \widetilde{d} = d_{21}(1-\frac{\lambda_2(c_e)_*}{1+\alpha(c_e^2)^*})d_{12}(1+\frac{\lambda_1c_e^*}{1+{\alpha}(c_e^2)_*})-\widetilde{r}_1\widetilde{r}_2 < 0.$

$\mathbf{Assumption}\; H3:\; \widehat{{r_1}} = r_1-r_0(c_0)^*-d_{12}(1+\frac{\lambda_1(c_e)^*}{1+\alpha(c_e^2)_*}) < 0,$ $\widehat{{r_2}} = r_2-d_{21}(1-\frac{\lambda_2(c_e)_*}{1+\alpha(c_e^2)^*}) < 0.$

$\mathbf{Assumption}\; H4:\; \widehat{{d}} = d_{12}(1+\frac{\lambda_1(c_e)_*}{1+\alpha(c_e^2)^*})d_{21}(1-\frac{\lambda_2c_e^*}{1+\alpha(c_e^2)_*})-\widehat{{r}_1}\widehat{{r}_2} < 0.$

Theorem 3.1. Let $x(t) = (x_1(t), x_2(t))$ be the solution of the first two equations of (3) with the initial value $x(0)\in R_+^2$,

(1) Suppose $\mathbf{Assumption}$ H1 and H2 hold simultaneously, single-species $x$ will be extinct.

(2) Suppose $\mathbf{Assumption}$ H3 or H4 are not true, single-species $x$ is strongly persistent.

$Proof.$ It follows from the first two equations of (3) that,

Comparison system

and

with $z_i(0) = y_i(0) = x_i(0) > 0, \; i = 1, \; 2.$ By comparison theorem, we have $z_i(t)\leq x_i(t)\leq y_i(t), \; i = 1, \; 2.$

(1) If $\mathbf{Assumption}$ H1 and H2 hold simultaneously, it is easy to see that the eigenvalue of system (6) at equilibrium point (0, 0) has negative real part and is quasi-monotone non-decreasing. Since $x_i(t)\geq y_i(t), \; i = 1, \; 2.$ have $\lim\limits_{t\rightarrow+\infty}x_i(t) = 0, \; i = 1, \; 2.\; a.s.$

(2) If $\mathbf{Assumption}$ H3 or H4 are not true, the proof is similar to ^[6]. we know that system (3.2) have positive equilibrium point $\underline{z}$ and zero equilibrium point. According to the conclusion and proof of Theorem 1 (see Allen^[6]), system (7) is unstable at zero equilibrium, but stable at positive equilibrium point $\underline{z}$, then $\lim\limits_{t\rightarrow+\infty}z(t) = \underline{z}$. By virtue of, $z_i(t)\leq x_i(t), i = 1, \; 2.$, we have, $\liminf\limits_{t\rightarrow+\infty}x(t)\geq\underline{z}$, that is, population x is strongly persistent.

The proof is completes.

According to the Theorem 3.1's (1), if $\mathbf{Assumption}$ H1 and H2 simultaneously true, population x will die out. By $\tilde{r}_1 < 0$ and $\tilde{r}_2 < 0$, we get

by virtue of $\tilde{d} = d_{12}d_{21}(1+\frac{\lambda_1c_e^*}{1+\alpha(c_e^2)_*})(1-\frac{\lambda_2(c_e)_*}{1+\alpha(c_e^2)^*})-\tilde{r}_1\tilde{r}_2 < 0$, we can obtain that

If $(r_1-r_0(c_0)_*)r_2\geq0$, by virtue of (3.3) and (3.4), one can imply that $(r_1-r_0(c_0)_*)r_2 < 0$, it is contradiction with $(r_1-r_0(c_0)_*)r_2\geq0$. Thus, $(r_1-r_0(c_0)_*)r_2 < 0$ is a necessary condition of $\mathbf{Assumption}$ H1 and H2 holding at the same time.

4.   Survival analysis of stochastic population model (1.4)

In order to analysis the long-time behaviors of single-species of system (1.5), first of all, we shall show that system (1.5) has unique global positive solution $x(t) = (x_1(t), x_2(t))$.

Lemma 4.1. For any given initial value $x(0)\in R_+^2$, there is a unique positive solution $x(t)$ to system (1.5), and the solution will remain $R_+^2$ with probability 1.

$Proof.$ Because the coefficients of system (1.5) is locally Lipschitz continuous for any given initial value $x(0)\in R_+^2$, there is a unique local solution $x(t)$ in $[0, \tau_e)$, where $\tau_e$ is the explosion time(see ^[23]). In order to proof the solution is global, we only need to prove $\tau_e = +\infty, \; \; a.s.$.

For each integer $n > n_0$, defining the stopping time

obviously, $\tau_n$ is increasing when $n\rightarrow\infty$. Let $\tau_\infty = \lim\limits_{n\rightarrow +\infty}\tau_n$, hence, $\tau_\infty\leq\tau_e, \; a.s.$ Next, we just need to proof $\tau_\infty = +\infty$, if the conclusion is not true, there are $T > 0$ and $\epsilon\in(0, 1)$ such that $P\{\tau_\infty\leq T\} > \epsilon$. Thus, there is a integer $n_1\geq n_0$, such that $P\{\tau_n\leq T\}\geq \epsilon, \; \; n\geq n_1.$

Defining Lyapounov function $V:R_+^2\rightarrow R_+$, have

For $x\in R_+^2$, applying It$\hat{o}$'s formula, we get

where

Obviously, there is a positive constant $K$ such that $LV(x)\leq K$.

Integrating both sides of inequality (4.1) from 0 to $\tau_n\wedge T$ and taking expectation yield

By the definition of $\tau_n$, $x_i(\tau_n\wedge T) = n$ or $\frac{1}{n}$ for some $i = 1, 2,$ hence,

It follows from (4.2) that

when $n\rightarrow\infty$, we have

which is a contradiction.

This completes the proof.

Lemma 4.2. Let $x(t)$ be the solution of system (1.5) with the initial value $x(0)\in R_+^2$, for any $\theta > 0$, have

$Proof.$ Defining function $V(x) = \ln(x_1+\theta x_2)$, applying $It\hat{o}'s$ formula to $V(x)$, we have

where $r = \max\{(r_1+\theta d_{12}(1+\frac{\lambda_1}{\sqrt{\alpha}})), (r_2+\frac{d_{21}}{\theta})\}$ and $\hat{a} = 0.5\min\{a_1, \frac{a_2}{\theta}\}$. Thus

Integrating the two sides of the above inequality in the interval $[0, t]$, we get

where $M(t) = \int_0^t e^s\frac{\sigma_1x_1(s)dB_1(s)+\sigma_2\theta x_2(s)dB_2(s)}{x_1(s)+\theta x_2(s)}ds$.

The quadratic variation of $M(t)$ is $\langle M(t), M(t)\rangle = \int_0^t\frac{\sigma_1^2x_1^2(s)+\sigma_2^2\theta^2x_2^2(s)}{(x_1(s)+\theta x_2(s))^2}ds$. According to the exponential martingale inequality, for all positive constants $\mu, \nu$ and $T_0$, we can obtain that

we choose $\mu = e^{-k}$, $\beta = \gamma e^k\ln k$, $T_0 = k$ and $\gamma > 1$,

since $\sum\limits_{k = 1}^{+\infty} k^{-\gamma} < \infty$, according to Borel-Cantalli Lemma, there exists $\Omega\in \mathfrak{F}$ and positive integer $k_1 = k_1(\omega)$ satisfy $P(\Omega) = 1$, for all $\omega\in \Omega$, and $k > k_1$, have

It follows from $\ln(x_1+\theta x_2)+{r}-\hat{a}(x_1+\theta x_2)$ that there is a positive constant $K$, such that $\ln(x_1+\theta x_2)+{r}-\hat{a}(x_1+\theta x_2)\leq K$. by (4.3) and (4.4), for all $k > k_1$, we have

for $k-1\leq t\leq k$, we get

Let $t\rightarrow+\infty$, we can observe that $\limsup\limits_{t\rightarrow+\infty}\ln\frac{\ln x_i(t)}{t}\leq\limsup\limits_{t\rightarrow+\infty}\ln\frac{\ln (x_1(t)+\theta x_2(t))}{t}\leq 0, \; \; a.s., \; \; i = 1, 2.$

This completes the proof.

4.1.   Extinction

Let $(\theta, \rho)$ be the solution of the following equations

where $b > 0$ and $d > 0$. By virtue of (4.5), it easily observe that $\theta = \frac{d}{\rho-c}$, where $\rho$ is the solution of equation

Because $a$ and $c$ are the solutions of equation $\rho^2-(a+c)\rho+ac = 0$, obviously, Eq (4.6) has two solutions, and there must be a solution

which is greater than $c$, thus $\theta > 0$.

Remark 4.3. We next come to analyze the following possible cases of the solution of Eq (4.6).

(a) If $a$ and $c$ are negative constants, when $bd-ac < 0$, all solutions of Eq (4.6) are negative. However, when $bd-ac\geq 0$, there must be a nonnegative solution of Eq (4.6).

(b) If $a$ or $c$ aren't both negative, we can imply that there must be a positive solution of Eq (4.6).

Theorem 4.4. Let $(x_1(t), x_2(t))$ be the solution of system (1.5) with initial value $(x_1(0), x_2(0))\in R_+^2$. If

the single-species population x of system (1.5) will die out, that is, $\lim\limits_{t\rightarrow+\infty}x_i(t) = 0, \; \; a.s., i = 1, 2.$

$Proof.$ Let $\theta > 0$, it follows from (1.5) that

Then for all $\epsilon > 0$, there is a positive constant $t_1$, for all $t\geq t_1$, it follows from (4.7) that

We can imply that there must be a

and $\theta = \frac{D_{21}^u+\epsilon}{\rho-R_2^u-\epsilon} > 0$, such that

Applying $It\hat{o}'s$ formula to $\ln(x_1+\theta x_2)$, we have

By (4.9), we can obtain that

where $N(t) = \int_{t_1}^t\frac{\sigma_1x_1(s)dB_1(s)+\sigma_2\theta x_2(s)dB_2(s)}{(x_1(s)+\theta x_2(s))}$.

The quadratic variation of $N(t)$, have

It follows from the Theorem 2.2, we can get that $\lim\limits_{t\rightarrow+\infty}\frac{N(t)}{t-t_1} = 0, \; \; a.s.$

If ${(R_1^u+R_2^u)+\sqrt{(R_1^u-R_2^u)^2+4D_{12}^uD_{21}^u}} < \sigma^2$, let $\epsilon$ be sufficient small such that $\rho < 0.5\sigma^2$. Because $\lim\limits_{t\rightarrow+\infty}\frac{N(t)}{t-t_1} = 0, \; \; a.s.,$ it follows from (4.10) that

which yields

This completes the proof of Theorem 4.4.

According to Theorem 4.4 and Lemma 2.4, we can obtain the following corollary.

Corollary 4.5. If $\lim\limits_{t\rightarrow+\infty}u_e(t) = \bar{u_e},$ when the coefficients $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}} < \sigma^2,$ the single-species population x will be extinct.

Remark 4.6. It follows from the proof of Theorem 4.4 and the results of Remark 4.3, if $R_1^u < 0$, $R_2^u < 0$ and $D_{12}^uD_{21}^u-R_1^uR_2^u < 0$ hold, the single-species population will be extinct.

Remark 4.7. From Theorem 4.4, if $\widetilde{r_1} < 0, \; \widetilde{r_2} < 0$ and $d_{12}d_{21}(1+\frac{\lambda_1c_e^*}{1+\alpha(c_e^2)_*})(1-\frac{\lambda_2(c_e)_*}{1+\alpha (c_e^2)^*})-\widetilde{r_1}\widetilde{r_2} < 0$, it follows from the proof of the Theorem 4.4 and the results of the Remark 4.3(a), we find that the single-species population x of stochastic model (1.4) will die out, and it is also extinction in deterministic model (1.3). When $\mathbf{Assumption}$ H3 or H4 aren't true, the single-species x of deterministic model (1.3) is strongly persistent, but Theorem 4.4 shows that the single-species x of stochastic model will die out when white noises large enough, which means that the white noises in the environment will affect the sustainable survival of the species, especially the endangered species.

4.2.   Persistence in the mean

Theorem 4.8. Let $(x_1(t), x_2(t))$ be the solution of system (1.5) with initial value $(x_1(0), x_2(0))\in R_+^2$, if

the single-species population x is strongly persistent in the mean.

$Proof.$ Let $\epsilon > 0$ be large enough that

By

and (4.7), for all $\epsilon > 0$, there exists a positive constant $t_1$, when $t\geq t_1$, we can obtain that

In view of the proof of Theorem 4.4, by virtue of (4.11), we can imply that there are positive constants $\theta$ and $\rho$ such that

where $\theta$ and $\rho$ satisfy the following equations:

Thus $\rho = \frac{({R_1^l}+{R_2^l-2\epsilon})+\sqrt{({R_1}-{R_2})^2+4(D_{12}-\epsilon)(D_{21}-\epsilon)}}{2}.$ By virtue of (4.12), we get

Integrating from $t_1$ to t and dividing by t on above inequality, have

where $N(t) = \int_{t_1}^t\frac{\sigma_1x_1(s)dB_1(s)+\sigma_2\theta x_2(s)dB_2(s)}{x_1(s)+\theta x_2(s)}.$

Taking the inferior limit on both sides of (4.13), we obtain that

Because $\lim\limits_{t\rightarrow+\infty}\frac{N_1(t)}{t} = 0, \; \lim\limits_{t\rightarrow+\infty}\frac{\ln(\phi_1(0)+\theta\phi_2(0))}{t} = 0, \; \; a.s.$ and $\rho-0.5\check{\sigma}^2 > 0$, by virtue of (4.14) and Lemma 2.3, we get $\liminf\limits_{t\rightarrow+\infty}\langle x_1(t)+\theta x_2(t)\rangle\geq\frac{\rho-0.5\check{\sigma}^2}{\max\{a_1, \frac{a_2}{\theta}\}}$.

The proof of Theorem 4.8 is completes.

It follows from Theorem 4.8 and Lemma 2.4, we can get the following corollary.

Corollary 4.9. If $\lim\limits_{t\rightarrow+\infty}u_e(t) = \overline{u_e},$ when the coefficients $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}} > \breve{\sigma}^2$, the single-species population x is strongly persistent in the mean.

We next discuss the persistence in the mean of the population of each patch.

Theorem 4.10. Let $(x_1(t), x_2(t))$ be the solution of system (1.5) with initial value $(x_1(0), x_2(0))\in R_+^2$, if

the population $x_i$ in the patch i is strongly persistent in the mean, and

$Proof.$ It follows from (1.5) that

Integrating both sides of above inequalities (4.15) and (4.16) from 0 to t,

For sufficiently small $\epsilon > 0$, such that $\langle R_i(t)\rangle^l-\epsilon > 0, \; i = 1, 2.$ It follows from (4.17) and (4.18) that

by virtue of Lemma 2.1, (4.19), (4.20) and the arbitrariness of $\epsilon$, we can obtain that

The proof of Theorem 4.10 is completes.

5.   Examples and numerical simulations

In this section, we will show the numerical simulation results to illustrate the accuracy of analytical results in above section by using the famous Milstein's method ^[30]. It is very hard to choose parameters of the model from realistic estimation, which needs to apply many methods of statistical, therefore, we will only use some hypothetical parameters to simulate the theoretical effects in this section.

$\mathbf{{Example \; 1.}}$ In deterministic system (1.3), we choose the parameters as:

$r_1 = 0.2, \; r_2 = 0.2, \; r_0 = 0.8, \; a_1 = 0.5$,$\; a_2 = 0.6, \; g = 0.3, \; m = 0.2$,$\; h = 0.5, \; f = 0.4, d_{12} = 0.5$,$d_{21} = 0.7, u_e = 0.4,$ with initial value $(x_1(0), \; x_2(0), \; c_0(0), \; c_e(0)) = (0.5, 0.5, 0.5, 0.4)$.

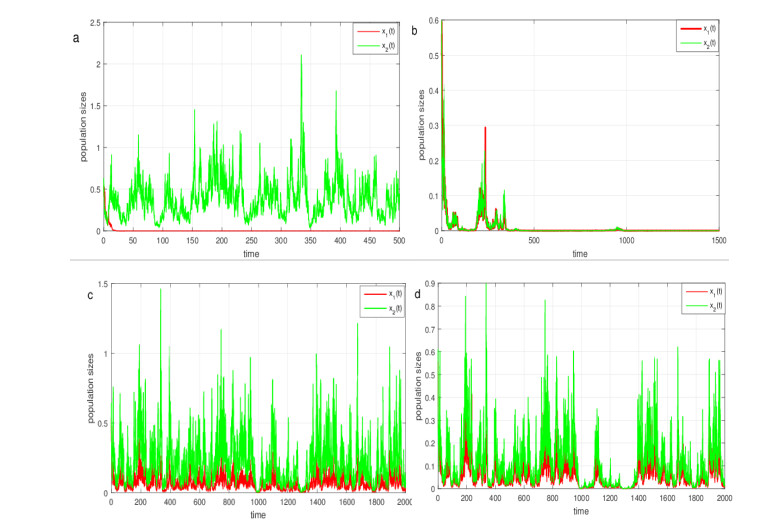
In order to simulate the influence of chemotaxis on the survival of single-species, we change the values of $\lambda_1, \lambda_2,$ and $\alpha$. We firstly adopt $\lambda_1 = 0.5,$ $\lambda_2 = 0.2, \; \alpha = 1.5$, by simple calculation, we know that it satisfy $\mathbf{Assumption}$ H1 and H2, by virtue of the Theorem 4.4, one can see that the single-species population $x$ will die out, see Figure 1(a). If $\lambda_1 = 0.5,$ $\lambda_2 = 0.5, \; \alpha = 0.1$, by computing, $\mathbf{Assumption}$ H4 is not true, by virtue of the Theorem 4.4's (2), we can observe that the single-species x is strongly persistent, see Figure 1(b).

$\mathbf{{Example\; 2.}}$ In stochastic system (1.4), Chooses the parameters as:

$r_1 = 0.2, \; r_2 = 0.3, \; r_0 = 0.8$,$\; a_1 = 0.5$,$\; a_2 = 0.6, \; g = 0.3$,$\; m = 0.12$,$\; h = 0.5$, $\; f = 0.4$,$d_{12} = 0.3$, $d_{21} = 0.4, u_e = 0.4-0.1e^{-0.2t}$, $\; \lambda_1 = 0.6, \lambda_2 = 0.4, \; \alpha = 1,$ with initial value $(x_1(0), \; x_2(0), \; c_0(0), \; c_e(0))$= $(0.5, 0.5, 0.1, 0.3)$.

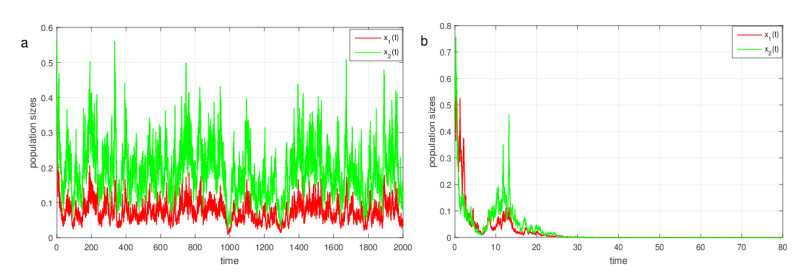
We next focus on the effect of the intensity of white noises on the survival of population $x$. we adopt $\sigma_1 = 0.2$, $\sigma_2 = 0.2$, computing shows that $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}}-\check{\sigma}^2 = 0.2298-0.04 = 0.1898 > 0,$ it follows from the Corollary 4.9 that the population $x$ is strongly persistent in the mean, see Figure 2(a). Suppose $\sigma_1 = 0.7$, $\sigma_2 = 0.8$, and other parameters are the same as Figure 2(a), by computing, one can know that $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}}-\check{\sigma}^2 = 0.2298-0.2775 = -0.0477 < 0$, according to Corollary 4.9, one can find that the population $x$ will die out (see Figure 2(b)). Therefore, from Figure 2, we can observe that the single-species x will be extinct when the densities of white noises larger enough.

$\mathbf{{Example\; 3.}}$ In stochastic system (1.4), we choose the parameters as:

$r_1 = 0.2, \; r_2 = 0.3, \; r_0 = 0.8$,$\; a_1 = 0.5, \; a_2 = 0.6$,$\; g = 0.3$, $\; m = 0.2, \; h = 0.5$,$\; f = 0.4$,$u_e = 0.4-0.1e^{-0.2t}, \sigma_1 = 0.4$, $\; \sigma_2 = 0.4,$ with initial value $(x_1(0), \; x_2(0)$, $\; c_0(0), \; c_e(0)) = (0.5, 0.5, 0.1, 0.3)$.

Case a: Suppose that $d_{12} = 0, d_{21} = 0$, the population x live in two independent patches. Simple calculation shows that $r_1-r_0\overline{\langle c_0(t)\rangle} < 0.5\sigma_1^2$ and $r_2 > 0.5\sigma_2^2$. According to the Remark 3 in ^[22] and Lemma 2.3, we can get that the population $x_1$ goes to extinction, and the population $x_2$ is strongly persistent in the mean, see Figure 3(a).

Case b: If $d_{12} = 0.3, d_{21} = 0.5, \lambda_1 = 0, \lambda_2 = 0$, thus, system (1.4) is a single-species stochastic diffusion system. By computing, $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}}-{\sigma}^2 = 0.0654-0.08 = -0.0146 < 0,$ by Theorem 4.4, population x will die out (see Figure 3(b)).

Case c: If $d_{12} = 0.3, d_{21} = 0.2, \lambda_1 = 0, \lambda_2 = 0,$ by computing, we have $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}}-{\check{\sigma}}^2 = 0.3523-0.16 = 0.1923 > 0$, by Theorem 4.8, we know that the population x is strongly persistent in the mean (see Figure 3(c)).

Case d: If $d_{12} = 0.3, d_{21} = 0.5, \lambda_1 = 0.3, \lambda_2 = 0.4, \alpha = 0.2,$ by simple computing shows that $\overline{R_1}+\overline{R_2}+\sqrt{(\overline{R_1}-\overline{R_2})^2+4\overline{D_{12}}\overline{D_{21}}}-{\check{\sigma}}^2 = 0.2161-0.16 = 0.0561 > 0$, by Theorem 4.8, the population x is strongly persistent in the mean (see Figure 3(d)).

Figure 3 shows that the properties of chemotaxis have an influence on persistence in the mean and extinction of the population.

6.   Conclusion

It is a pretty active topic to consider spatial information affects population dynamics, when the habitat of species is polluted, the species will be stimulated by the toxins in the habitat and increase diffusion to other patch. Thus, single-species population diffusion models with chemotaxis in polluted environment are proposed and studied. For the deterministic model, sufficient conditions for persistent and extinction of population are obtain. And then, considering the influence of environmental noise, a single-species population diffusion model with chemotaxis in polluted environment is proposed. Firstly, we discussed that the model (1.4) has unique global positive solution. Secondly, we investigated the persistence in the mean and extinction of system (1.4), if $R_1^u+R_2^u+\sqrt{(R_1^u-R_2^u)^2+4D_{12}^uD_{21}^u} < \sigma^2,$ the single-species population will extinction; if $R_1^l+R_2^l+\sqrt{(R_1^l-R_2^l)^2+4D_{12}^lD_{21}^l} > \check{\sigma}^2,$ the single-species population is strongly persistent in the mean. Finally, numerical simulations are used to confirm the efficiency of the main results.

Figure 2(a) and (b) show that the single-species x will die out when the densities of white noises large enough, therefore, it is significance to consider the effect of stochastic perturbation.

If we set $d_{12} = d_{21} = 0$, that is to say, the single-species population live in two independent environments, respectively. Literature ^[22] shows that, when $r_1-r_0\overline{c_e} < 0.5\sigma_1^2$, the population $x_1$ will tend to extinct, when $r_1-r_0\overline{c_e} > 0.5\sigma_1^2$, the population $x_1$ is persistent in the mean, see Figure 3(a). However, by virtue of Theorem 4.4 and Theorem 4.8, we can obtain that population diffusion would affect the survival of the population x, see Figure 3(a) and (c).

Acknowledgments

This paper is supported by the Youth Science and technology talent growth project of Guizhou Provincial Department of Education(KY[2018]341, KY[2015]456), the Project for Innovative Research Groups of Guizhou Province of China (KY[2016]051), China Postdoctoral Science Foundation funded project(2017M623074), Science and Technology Foundatiaon of Guizhou Province of China (Project No. LKT[2012]23, [2018]1162).

Conflict of interest

The authors declare that they have no competing interests.