The bifurcation of constrained optimization optimal solutions and its applications

1.   Introduction

Systems of nonlinear equations have emerged as an important modeling tool in various fields, including biology ^[1], engineering ^[2], and materials science ^[3]. The study of solution structures, such as bifurcations and multiple solutions, is essential to comprehend the behavior of these nonlinear models. Parametric nonlinear programming problems are a type of problem that seeks to determine the changes in the behavior of solutions as the parameter values change within a defined region of interest. Without loss of generality, we consider the general form of a nonlinear programming (NLP) problem:

where, the objective function $f:{\Re ^u} \to \Re$, and inequality constraints C_I = (c₁, .., c_r)^T, equality constraints C_E = (c_r+1, .., c_m)^T: ${\Re ^u} \to {\Re ^m}$ are assumed to be nonlinear and twice differentiable. Note that, by introducing slack variables, the inequality constraints are equivalently converted to equality constraints, $s.t.\ \ H(x) = 0 \in {R^m}, x \in {R^n}$. The feasible region, FR is defined by the set of solutions in which all the constraints of (1) are satisfied, $FR = \{ x \in {\Re ^n}:H(x) = 0\}$.

Under a fixed parameter $a$, a point ${x^ * } \in {\Re ^n}$ is called a LOS of (1), if ${x^ * } \in FR$ and a neighborhood U(x^∗, ε) of x^∗ exists such that $f({x^ * })\ < f(x)$ for all $x \in (U \cap FR)\backslash \{ {x^ * }\}$. for a point ${x^ * } \in {\Re ^n}$ or a pair $({x^ * }, {\lambda ^ * }), {\lambda ^ * } \in {\Re ^m}$, and ${\lambda ^ * }$ is the optimal Lagrange multiplier of the constrained optimization problem (1) at point ${x^ * }$. The Lagrangian function is $L(x, \lambda) = f(x) + H{(x)^T}\lambda$, where $L:{\Re ^{n + m}} \to \Re$. Satisfying the KKT first-order conditions, which we call ${x^ * }$ is a KKT point (also critical point).

To obtain a reasonable local structure of the feasible region for the constrained NLP problem (1), the following assumptions should be accepted.

Assumption 1:

ⅰ) (Regularity) For each $x \in FR$, $\{ \nabla {H_i}(x), i = 1, .., m\}$ are linearly independent.

ⅱ) (Non-degeneracy) At each KKT point ${x^*} \in FR$, ${d^T}\nabla _{xx}^2L({x^*}, {\lambda ^*})d \ne 0$ for all $d \ne 0$ satisfying $\nabla {H_i}{({x^*})^T}d = 0$ for all $i = 1, ..., m$.

Assumption 1(ⅰ) is known as the linear independence constraint qualification (LICQ) ^[4]. Assumption 1(ⅱ) makes the second-order sufficient condition applicable. Since the FR is compact, the non-degeneracy condition implies that it has only a finite number of KKT solutions for the (1).

The parameter change of the optimization problem will lead to the position change of the optimal solution and even lead to the emergence or disappearance of the optimal solution. To explore solution configurations, instability, and multiple solutions, analyzing the structure of the solution, studying the stability of the critical point, and developing efficient numerical algorithms for computing bifurcations of nonlinear parametric systems have been key. Past work has primarily focused on continuous parameter optimization problems ^[5] by analyzing the structure of the solution and studying the stability of critical points. Local information on variable change rates with respect to parameters can be obtained through differential analysis of Karush-Kuhn-Tucker (KKT) or Fritz John (FJ) conditions. Bifurcations may occur in the system when these parameters violate the implicit function theorem, leading to the emergence and disappearance of critical points, including minima, saddle points, and maxima. While previous work has proposed a set of conditions for Jacobian singularity of conditional parameter systems ^[5], not all conditions have been explored, and some characteristics of these conditions have been analyzed in ^[6]. These studies are referred to as the robustness problem of KKT solutions, and some local stability results of local minima have been proposed ^[7,7]. Our work takes a different approach, transforming the original optimization problem into two classes of nonlinear dynamical systems that are completely stable. This allows for more concise results to be obtained.

We find that the appearance and disappearance of optimal solutions can be explained by two kinds of bifurcation that are closely related to the change of the feasible region. By analyzing the bifurcation phenomenon of the feasible region, we can gain insights into the bifurcation of the optimal solution. One class of bifurcation is called pseudo-bifurcation, which represents the conversion of the optimal solution or connected feasible part to a class of infeasible points (DEPs). Pseudo-bifurcation manifests as the appearance and disappearance of optimal solutions and feasible parts in optimization problems. Previous work did not consider these infeasible points, which may lead to missing useful information. We propose an interesting tool for predicting optimal solutions based on the properties of pseudo-bifurcations and such infeasible points.

The optimal power flow solution, as a special feasible solution satisfying the constraint conditions, is closely related to the feasible region of the OPF problem. Relevant studies have explained the disappearance of OPF solutions from the perspective of feasible regions, such as the disappearance ^[9] and curvature change ^[10] of feasible regions of the OPF problem, and the pseudo-pitchfork bifurcation ^[11], which also leads to the disappearance of the OPF solution. In this paper, the bifurcation phenomenon of the proposed optimal solution will be verified by the OPF problem, and the appearance and disappearance of the optimal solution will be explained reasonably.

This paper develops and presents:

(1) A class of pseudo-bifurcation of optimal solutions or saddle points is presented for the general constrained optimization problems.

(2) For general constrained optimization problems, the reasons for the change in the number of optimal solutions and saddle points are explained by two types of bifurcation phenomena:

1) Pseudo-bifurcation of optimal solutions or saddle points.

2) Saddle-node bifurcations between (ⅰ) LOS and saddle point, (ⅱ) LOS and DUEP, (ⅲ) saddle point and DUEP.

(3) The relationship of the bifurcation phenomena between the feasible region and the optimal solution.

(4) The position, number, and bifurcation phenomena of the optimal solution are influenced by the feasible region (i.e., constraint set) together with the objective function of the constrained optimization problem, hence the analysis needs to clarify the prerequisites.

(5) The presented pseudo-bifurcation is applied to predict the appearance of the optimal solution and its objective function value.

The rest of this paper is organized as follows: Section 2 provides an overview of some concepts related to dynamic systems, saddle-node bifurcation, and pseudo-pitchfork bifurcation to establish a foundation for subsequent discussions. In Section 3, a simplified example is presented to illustrate the characteristics of pseudo-bifurcation and the appearance and disappearance of optimal solutions using pseudo-bifurcation and saddle-node bifurcation techniques. Section 4 discusses the application of pseudo-bifurcation. In Section 5, the bifurcation behavior of IEEE 5-bus and 9-bus systems is analyzed under varying load demands and constraint parameters. This section also examines the physical implications of saddle-node and pseudo-pitchfork bifurcations. Finally, Section 6 summarizes the key findings of the paper.

2.   Overview

2.1.   Dynamic systems formalization

Some concepts of dynamic systems will be reviewed. Consider a class of hyperbolic dynamic systems as follows,

where $H(x):{\Re }^{n}\to {\Re }^{m}$ and $L(x):{\Re }^{n}\to {\Re }^{n\times m}$, $m \leqslant n$.

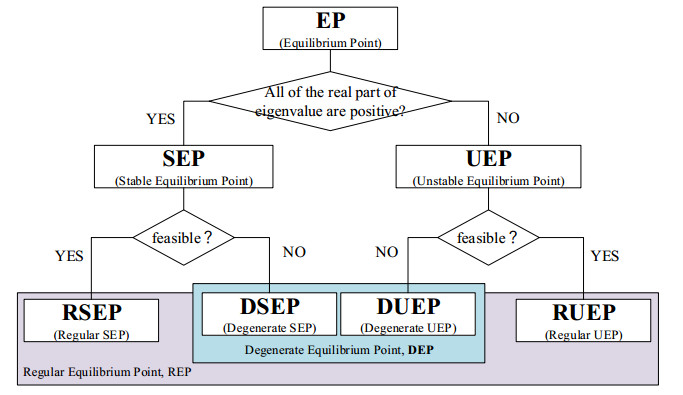
The point $\bar x \in {\Re ^n}$ is an equilibrium point (EP) of the dynamic system (2) if the corresponding Jacobian matrix $DK(\bar x) = 0$ that is, the EP is a particular type of solution that does not vary with time. A stable equilibrium point (SEP) is an EP whose corresponding Jacobian matrix $DK(\bar x)$ has all eigenvalues with negative real part. A type-k unstable equilibrium point (type-k UEP, k≥1) refers to an EP at which the Jacobian has exactly k eigenvalues with positive real part.

The present study utilizes the active set method to construct two nonlinear dynamic systems. in which, the inequality constraints are segregated into active (i.e., transboundary or critical) constraints and inactive constraints. During the computation, only the active constraints are considered, while the inactive constraints are ignored. The active set quotient gradient system (QGS) is defined as follows,

where, $BD = \{ i:C_I^i(x) \geqslant - \beta \}$ is the index set of the active inequality constraints, and $\beta \to {0^ + }$ is a sufficiently small positive scalar, $D{C_E}(x)$($DC_I^{BD}(x)$) is the Jacobian matrix of ${C_E}(x)$($C_I^{BD}(x)$).

The active set penalty-formula quotient gradient system (AQGS) is defined as follows,

where, $\nabla f(x)$ is the gradient vector of $f(x)$, and $\delta \in \Re$ is the positive constant penalty factor.

The class of dynamic system (2) includes the QGS system (3), AQGS system (4) and some other systems. Note that ${H_{{\text{QGS}}}}(x)$ is the active constraint set of the original constrained NLP problem (1), and ${L_{{\text{QGS}}}}(x)$ is the transposed Jacobian matrix of these active constraint set. The QGS system is used for characterizing the feasible region of constrained problems in ^[9]. And the proposed AQGS is inspired by the QGS system for solving local optimal solutions of constrained optimization. ${H_{{\text{AQGS}}}}(x)$ is connected with the active constraint set and the gradient of the objective function, ${L_{{\text{AQGS}}}}(x)$ is the transposed Jacobian matrix of ${H_{{\text{AQGS}}}}(x)$. After that, we specify some necessary definitions and theorems.

The QGS system (3) and AQGS system (4) are related to problem (1), they should also satisfy Assumption 1 (referred in Section 1).

Definition 1. (γ-relaxed feasible region).

The γ-relaxed feasible region of (1) is the set of solutions in which all the equality and inequality constraints relaxed by γ are satisfied, i.e.,

where ${\bf{ \pmb{\mathsf{ γ}} }}{\text{ = [}}\gamma _1^E{\text{, }}...\gamma _r^E{\text{, }}\gamma _{r + 1}^I{\text{, }}...{\text{, }}\gamma _m^I{{\text{]}}^{\bf{T}}} \in {\Re ^m}$, ${\gamma _i} \geqslant 0$.

If ${\bf{ \pmb{\mathsf{ γ}} }} = {\bf{0}}$, the relaxed feasible region is equal to the original feasible region (FR), (i.e., $RFR(0){\text{ = }}FR$). And $FR \subset RFR$. If ${{\bf{ \pmb{\mathsf{ γ}} }}_1} \geqslant 0$, ${{\bf{ \pmb{\mathsf{ γ}} }}_2} > 0$, and ${{\bf{ \pmb{\mathsf{ γ}} }}_2} - {{\bf{ \pmb{\mathsf{ γ}} }}_1} > 0$, then $RFR({{\bf{ \pmb{\mathsf{ γ}} }}_1}) \subset RFR({{\bf{ \pmb{\mathsf{ γ}} }}_2})$. It illustrates that as the constraint is relaxed, the relaxed feasible region expands, which contains both the expansion of the existing feasible component and the emergence of a new feasible component, without the disappearance of a feasible component of the relaxed feasible region.

Assumption 2 ^[12]. The objective function of a constrained optimization problem (1) is a continuous real-valued function, and the feasible region is a compact set.

According to Heine–Borel theorem ^[12], in ${\Re ^n}$, a set $S$ is compact if and only if it is closed and bounded. Continuous real-valued functions defined on compact sets are bounded and have both a maximum and a minimum value. In the majority of practical physics problems such as cost optimization ^[13], optimal power flow (OPF) ^[14] in power systems, etc., the objects under consideration are characterized by a finite region of definition, and exist within a specific space and time domain. The dynamical evolution of such objects typically manifests as a continuous process, with each of the distinct states comprising the object being ascertainable with certainty.

It is worth noting that, given that the constraint $H(x) \to \varepsilon$ is formulated in terms of per unit in numerical calculations, We add an offset a, which is guaranteed to be optimized in the positive interval, the objective function $f(x) \to f({x^*}) + a \geqslant 0$ should be normalized to per unit as well, in order to ensure consistency.

Definition 2. (Regular EP and degenerate EP).

For an equilibrium point $\bar x$ of the nonlinear dynamic system (i.e., the QGS, the AQGS), if ${C_E}(\bar x) < \varepsilon, {C_I}(\bar x) < \varepsilon$, then it is called a regular equilibrium point (REP); otherwise, it is called a degenerate equilibrium point (DEP).

Therefore, combining the definitions of SEP and UEP above, DEP contains DSEP and DUEP, and REP contains RSEP and RUEP (see Figure 1). When the penalty factor is significantly large, the DUEP of AQGS corresponds to the UEP of the QGS, and the RUEP of AQGS corresponds to the saddle point of the original constrained optimization problem.

And the next two theorems establish the relationships for the SEPs of the two dynamic systems. Then, we can establish the following two relationships.

Theorem 1. (Feasible region and regular SEMs of QGS) ^[9]. Suppose Assumption 1 holds, then, the FR of (1) equals the union of regular stable equilibrium manifolds (RSEMs) of QGS (3).

Motivated by the development of energy functions for the dynamical system, the AQGS (4) admits an energy function $E(x)$ as follows,

According to the definition of k-th power penalty function ^[15], the energy function $E(x)$ is a 2-th power penalty function.

Then, according to the theorem of optimality of the exterior penalty function method ^[15] and the formula of AQGS (4), we can establish the following relationships.

Theorem 2. (Optimal solutions and regular SEPs of AQGS). Suppose Assumption 1 and Assumption 2 hold. If the penalty factor $\delta$ is sufficiently large, then,

ⅰ) the isolated local optimal solution (LOS) of (1) is an RSEP of AQGS (4);

ⅱ) the RSEP of AQGS (4) is a local optimal solution of (1).

Proof. When Assumption 2 holds, it is easy to make

The energy function of AQGS (4), $E(x, \delta) = 1/2\delta {\left\| {H(x)} \right\|^2} + 1/2{f_{\bmod }}{(x)^2}$, is a 2-th power penalty function of constrained optimization (2).

Let $\hat x$ be a regular SEP of AQGS (4) with sufficiently large $\hat \delta$. Then, $||H(\hat x)|{|_\infty } \leqslant \varepsilon$ and $\hat x$ is a local minimum of ${\min _{x \in {\Re ^n}}}E(x, \hat \delta)$. Thus, according to the optimal theory of penalty function method ^[12], when ${\delta _k}$ is sufficiently large, the local minima of (1) are also a local optimal solution of ${\min _{x \in {\Re ^n}}}E(x, {\delta _k})$. For any $\bar \delta > {\delta _k}$, there exists an optimal solution $x(\bar \delta)$ for the corresponding unconstrained optimization problem ${\min _{x \in {\Re ^n}}}E(x, \bar \delta)$. And according to the convergence theorem ^[12] of external penalty function, for any limit point $\bar x$ of iterative sequence $\{ {x^k}\}$, which the optimal solution of ${\min _{x \in {\Re ^n}}}E(x, {\delta _k})$, is the optimal solution of the original constrained problem, $H(\bar x) < \varepsilon \to 0$ as ${\delta ^k} \to \infty$.

Let ${x^*}$ be a local minimum of original constrained optimization (1). $0 \leqslant {f_{\bmod }}({x^*}) \leqslant {f_{\bmod }}(x)$ and $H({x^*}) = 0$, so, for any $\delta$, ${f_{\bmod }}{({x^*})^2} \leqslant {f_{\bmod }}{(x)^2}$$\delta {\left\| {H({x^*})} \right\|^2} = 0$.

Hence, $1/2E({x^*}, \delta) = \delta {\left\| {H({x^*})} \right\|^2} + {f_{\bmod }}{({x^*})^2} = {f_{\bmod }}{({x^*})^2} \leqslant {f_{\bmod }}{(x)^2}$ is a local minimum of ${\min _{x \in {\Re ^n}}}E(x, \delta)$, which is a SEP of AQGS (4). And $H({x^*}) = 0$, ${x^*}$ is a regular SEP.

This completes the proof.

By choosing $\delta$ large enough, it can be made arbitrarily close to the optimal objective value of the original OPF problem (1). According to the characteristic of an exterior penalty function method ^[12], as the penalty parameter $\delta$ is made large, the generated points approach an optimal solution from outside the feasible region, i.e., it cannot strictly satisfy the constraints of the original constrained optimization problem. Hence, for a stable equilibrium point $\bar x$ of AQGS (4), if $H(\bar x) < \varepsilon, \varepsilon \to 0$, then it is called a regular stable equilibrium point (RSEP); otherwise, it is called a degenerate stable equilibrium point (DSEP). It has been proved in the paper ^[16] that the local minimum of the energy function $E(x, \delta)$ of such non-hyperbolic dynamical systems is a stable equilibrium point.

Theorem 1 establishes the relationship between the feasible region and the RSEMs of QGS. And Theorem 2 establishes the relationship between the local minima and RSEPs of AQGS. The next theorem gives the structure of the stability region of SEPs.

2.2.   Saddle-node bifurcation and pseudo-pitchfork bifurcation

Consider a nonlinear dynamic system with a parameter p:

where $x \in {\Re ^{^n}}$, depending on the parameter $p \in \Re$. For each fixed p, one defines the vector field ${f_p} = \ f(\cdot, p)$ and ${\Phi _p}\left({t, \ x} \right)$ denotes the trajectory of $\dot x = \ {f_p}\left(x \right)$ passing through $x$ at time $t$. The point $({\bar x_{{p_0}}}, {p_0}) \in {\Re ^{^n}} \times \Re$ is called a saddle-node bifurcation point of the system (6) if ${\bar x_{{p_0}}}$ is an equilibrium point and the following three conditions are satisfied.

(SN1) ${D_x}{f_{{p_0}}}({\bar x_{{p_0}}})$ has a simple eigenvalue 0 with v as an eigenvector to the right and w to the left;

(SN2) $w(D_x^2{f_{{p_0}}}({\bar x_{{p_0}}})(v, \ v)) \ne 0 ;$

(SN3) $w((\partial {f_p}/\partial p)({\bar x_{{p_0}}}, {p_0})) \ne 0 .$

If the conditions (SN2) and (SN3) are replaced by the hypotheses ${\partial ^3}{f_p}/\partial {x^3} \ne 0$ and $w(({\partial ^2}{f_p}/\partial x\partial p)(v)) \ne 0$, then one obtains the pitchfork bifurcation. Since the QGS is non-hyperbolic, it is obvious that when bifurcation between SEMs occurs in the QGS the conditions for saddle-node bifurcation and pitchfork bifurcation are not satisfied. This type of bifurcation is pseudo-pitchfork bifurcation. It still has some similar characteristics to pitchfork bifurcation. For example, there are three equilibrium manifolds before the bifurcation and only one equilibrium manifold remains after the bifurcation. More details can be found in ^[11].

3.   Bifurcation of optimal solutions

In this section, we will demonstrate a variety of bifurcation phenomena of optimal solutions as the constraint set is continuously relaxed on a small test system.

3.1.   Two-dimensional small test system

We consider the following two-dimensional nonlinear optimization problem P1. Adjusting the relaxed parameter c in (7) will affect the changes in the feasible region of the system for the optimal solution, and their properties and relationship are explored from these dynamic changes in detail.

Firstly, the corresponding QGS and AQGS are constructed, where the penalty factor in AQGS is set to be $\delta = 1 \times {10^6}$. When c = 0, there is only one feasible component and one optimal solution in Figure 2(a), which correspond to RSEM of QGS and RSEP of AQGS in Figure 2(b), respectively. This illustrates Theorems 1 and 2. Therefore, we will use the terms "feasible region" and "SEM", "optimal solution" and "SEP" interchangeably, without making a strict distinction.

Furthermore, Figure 3 depicts the stability region of the QGS and the AQGS for problem P1 when c = 0. Based on Figure 3 and Figure 4(a), we make the following observations.

● When the $\delta$ is significantly large, the stability regions of both dynamic systems exhibit the same shape and the corresponding DSEP and DUEP are located at the same position.

● The type-1 UEPs are positioned on the boundary of two adjacent SEP stability regions, and the type-2 UEP is located at the common junction of four stability regions. These findings indicate that the UEP is located at the stability region boundary with an n-1 dimensional stable manifold, as demonstrated in ^[16].

Therefore, for the sake of simplicity and for non-special cases, we will not differentiate between DSEP and DUEP of QGS and AQGS in the latter, and mark the saddle points (RUEP of AQGS) with a green '×' specifically.

The present study investigates the variation of the feasible region and the optimal solutions for a small case as the parameter c is varied from 0 to 3.3, as depicted in Figure 4. It should be noted that the value of c displayed in the figure is only an approximation of the critical change that occurs and does not represent the exact critical value at which bifurcation occurs.

Upon increasing c from 0 to 0.017, as depicted in Figure 4(b), a new feasible component and an optimal solution appear, resulting in a transition from a DSEM to an RSEM for the QGS system, and a DSEP to an RSEP for the AQGS system. This phenomenon is referred to as a pseudo-bifurcation and will be described in detail in the following section.

The feasible components continue to approach, and when c reaches approximately 0.8, as seen in Figure 4(d), a pseudo-pitchfork bifurcation ^[11] occurs, whereby two SEMs and a type-1 UEP bifurcate into one connected SEM of larger size in the QGS system. In the AQGS system, the number of equilibrium points remains unchanged, but the type-1 DUEP transforms into a type-1 RUEP, which corresponds to a saddle point of the original optimization problem. The bifurcation of the feasible region can alter the number of critical points and generate a new saddle point between the two optimal solutions. Similarly, in Figure 4(e), when c is increased to 1.1, a pseudo-bifurcation occurs, resulting in a transformation of a DSEM of QGS to an RSEM and a DSEP of AQGS to a LOS (RSEP), leading to a new feasible component and optimal solution.

As c increases to approximately 1.35, as illustrated in Figure 4(f–g), two feasible components undergo a pseudo-pitchfork bifurcation and merge into one feasible component. However, unlike the bifurcation that occurs at c = 0.8, in this case, for AQGS, a type-1 DUEP and a LOS (RSEP of AQGS) approach each other, and a saddle-node bifurcation occurs at c = 1.3434 (as seen in Figure 5), causing the optimal solution to disappear. Hence, the bifurcation of the feasible region can modify the number of optimal solutions and even cause the disappearance of an optimal solution.

At c = 2.9, the non-convexity of the feasible region boundary changes considerably, resulting in a new pair of UEPs appearing, as shown in Figure 4(h). At c = 2.91, a DSEM of QGS transforms into an RSEM, and a DSEP of AQGS transforms into a LOS (RSEP).

In Figure 4(j–k), two bifurcations occur around c = 3.03, where the two feasible components undergo a pseudo-pitchfork bifurcation. However, the optimal solution bifurcation phenomenon at this point is different. The upper type-1 DUEP is converted into a type-1 RUEP. The lower type-1 DUEP bifurcates with the optimal solution and then disappears. The change of eigenvalues for the bifurcation of type-1 DUEP and LOS are shown in Figure 6. The eigenvalues both tend to 0 where the saddle-node bifurcation occurs as c keeps increasing (for LOS, the eigenvalue 2 is suddenly tending to 0 near the pseudo-pitchfork bifurcation values).

In Figure 4(l–m), a saddle point and an optimal solution exhibit a bifurcation phenomenon and subsequently vanish as parameter c approaches approximately 3.18, thereby indicating a change in the number of optimal solutions due to nonconvexity alterations in the boundary. Additionally, Figure 7 depicts the behavior of one eigenvalue each of the type 1 RUEP and RSEP, which diminish to zero as parameter c increases, culminating in zero values at the saddle-node bifurcation.

In Figure 4(n–p), two saddle-node bifurcations transpire in the upper right quadrant of the feasible region. The first bifurcation engenders the emergence of a saddle point and an optimal solution, stemming from the shift in the boundary of the feasible region. The second bifurcation corresponds to a pseudo-pitchfork bifurcation within the feasible region, resulting in the disappearance of the optimal solution and type-1 DUEP of AQGS via a saddle-node bifurcation. Notably, at parameter values approximately 3.2 and 3.28 in Figure 4(o), two inner boundaries or ''holes'' in the feasible region contain a type-2 DUEP of AQGS and a saddle point on the boundary that approach each other and eventually bifurcate to disappear. At the saddle-node bifurcation values as depicted in Figure 8, one eigenvalue of each DUEP approaches zero and attains zero values at the bifurcation point.

3.2.   A new class of pseudo-bifurcation

Based on the findings presented in Section 3.1, it is observed that for the general constrained optimization problem, there exists interconversion between RSEM and DSEM as the constraint set is continuously relaxed or tightened. Similarly, for the AQGS system, interconversions between DSEP and RSEP, and DUEP and RUEP are observed. To describe this phenomenon, we introduce the concept of pseudo-bifurcation as follows:

Definition 3. (Pseudo-bifurcation). For a nonlinear dynamic system, QGS (3) or AQGS (4), with successive changes in system parameters, where the number of EPs remains unchanged, that all satisfy $\dot x = 0$, while the feasibility ($H(x) = 0$) of the EPs changes.

Figure 9 illustrates the variation of the two constraints of DSEP1 as parameter c is increased from 0 to 0.02, as shown in Figure 4(a, b). As the constraints are gradually relaxed, the mismatch between the two constraints approaches zero and crosses the pseudo-bifurcation value (around c = 0.0165). At this point, the original DESP1 is transformed into a newly generated optimal solution.

In summary, the pseudo-bifurcation is an observed phenomenon in nonlinear dynamic systems that correspond to constrained optimization problems. It arises when successive changes in parameters result in the feasibility of equilibrium points changing, causing the appearance or disappearance of optimal solutions, saddle points, or feasible components, while the number of equilibrium points remains constant. The pseudo-bifurcation does not alter the number of equilibrium points but leads to the interconversion of DEP and REP. The continuous approach to zero of the mismatches of each constraint as the parameters approach the pseudo-bifurcation value (i.e., DEP to REP), and vice versa after crossing the bifurcation value is a characteristic of the pseudo-bifurcation. Understanding this phenomenon's features is essential for the analysis of constrained optimization problems.

Table 1 presents a comparison between the variations in the feasible region and the variations in the optimal solutions/saddle points based on the bifurcation phenomena observed in the P1 problem. The table defines only one direction of bifurcation, and the opposite direction represents the opposite number of changes. The table highlights how the changes in the feasible region correspond to changes in the number of optimal solutions and saddle points. These observations are critical for understanding and analyzing constrained optimization problems.

Based on Tables 1 and 2, our summary is as follows.

(1) Pseudo-bifurcation occurs simultaneously in the feasible region and the optimal solution.

(2) When two feasible components merge due to pseudo-pitchfork bifurcation, the pseudo-bifurcation or saddle-node bifurcation of the optimal solution/saddle point occurs at the same time, leading to a change in the number of critical points.

(3) When disconnected localities of a global connected feasible component are connected by a pseudo-pitchfork bifurcation (e.g., Figure 4(n–o) upper right), the inner boundary is formed and the number of optimal solutions decreases due to the occurrence of saddle-node bifurcation.

(4) When the non-convexity degree of the feasible region boundary changes, it may lead to the appearance (or disappearance) of a pair of optimal solution and saddle points due to the saddle-node bifurcation.

(5) When the inner boundary of the feasible region shrinks and disappears, the saddle points on the inner boundary will disappear due to the saddle-node bifurcation.

Through the previous examples, we have explored the relationship between the bifurcation of optimal solutions and the feasible region. We have identified that the bifurcation of optimal solutions is influenced by both the constraint set, which determines the feasible region, and the objective function. Notably, when only the objective function is changed while the constraint set remains constant, it can lead to significant differences in the number of optimal solutions and their bifurcation phenomena. This suggests that the number and locations of optimal solutions are heavily influenced by the objective function, and the bifurcation behavior can be inconsistent with changes in the feasible regions. Therefore, when discussing the bifurcation of optimal solutions, it is essential to consider both the constraint set (feasible region) and the objective function as influential factors.

4.   Predicting tool of optimal solution appearance

As the relaxation parameters increase, the DSEP in a constrained optimization problem loses its significance as an optimal solution, saddle point, or even a feasible point, until a pseudo-bifurcation occurs. This conversion of the DSEP into an RSEM (feasible region) and RSEP (optimal solution) due to the pseudo-bifurcation allows us to predict the changes in the optimal solution and feasible components using the DSEP. In the case of the two-dimensional example P1, when c = 0 (as shown in Figure 4(a)), there are three DSEPs.

As c increases, three pseudo-bifurcations occur, accompanied by the appearance of three new feasible components and optimal solutions. It should be noted that these three feasible components do not appear simultaneously. Initially, at c = 0, we predict the position of the feasible component and the optimal solution, along with the objective function value of the optimal solution. Then, the changes of the three DSEPs are tracked by increasing the value of c, and the position deviation is measured using the Euclidean distance, $d = \sqrt {\sum {{({x_i} - {y_i})}^2}}$, which represents the distance deviation between the actual optimal solution appearance location and the predicted optimal solution appearance position. The function value deviation is measured using $f/\bar f \times 100\%$, where $\bar f$ is the initial predicted value of the optimal solution.

In Table 3, we present the positions of the three DSEPs and their corresponding predicted objective function values with an initial c value of 0. As c increases, the three DSEPs convert into new optimal solutions, respectively. It is evident that the predicted objective function values with the assistance of DSEP have only small errors when compared with the actual objective function values, and their positions are quite close to each other. However, we should note that due to the relaxation of the constraints, the boundary of the feasible region changes, which can cause the position of the optimal solution to shift and the prediction results to be biased. Despite this, the objective function value does not suddenly change significantly. The large deviation in the objective function value for DSEP3 is primarily due to the substantial change in c from the initial relaxation value of 0 to 2.904081. However, its position deviation remains small.

Based on the above observations, we conclude that the information derived from the DSEP calculated by the nonlinear dynamic system can be effectively used to predict the objective function value for the new emerging feasible component and to determine whether the new optimal solution is likely to be better than the current objective function. As such, the DSEP can be a useful tool for solving constrained optimization problems.

5.   The numerical study

5.1.   On the optimal power flow problems

Power system is one of the largest nonlinear dynamic systems in the world, and the optimal power flow (OPF) problem is the core of the power system operation ^[17]. According to a FERC study, a well-executed OPF solution approach has the potential to yield annual savings amounting to tens of billions of dollars ^[18]. The OPF problem is a highly complex and nonconvex NLP problem that presents significant mathematical challenges. The inclusion of AC power balance constraints introduces additional nonlinearity, while nonconvex cost functions and constraints add to the complexity of the problem ^[19,20]. Therefore, linearized DCOPF model is still used in power grid companies, instead of nonlinear ACOPF model. Recently, researchers began to pay attention to the development of ACOPF problem theory and solution methods. In particular, researcher found that the OPF solution would disappear with time change in ^[21], but did not explore its characteristics and properties. The bifurcation phenomenon and characteristics of the optimal solution proposed in this paper are illustrated in some actual OPF problems, and the results are consistent with those mentioned above. It is hoped that our research will supplement the optimality theory of OPF and other optimization fields.

A general OPF problem subject to the following equality and inequality constraint functions that conform to the standard problem form (1):

where the constant parameters are G_ij: equivalent conductance of a transmission line from bus i to bus j; B_ij: equivalent susceptance of a transmission line from bus i to bus j; and P_Li, Q_Li: the real and reactive power loads at bus i.; θ_i: voltage angle at bus i (The voltage angle of reference bus θ_ref is set as a constant); V_i: voltage magnitude at bus I; P_Gi: real power of generators at bus I; Q_Gi: reactive power of generators at bus i. Functional expressions: S_f: branch flow at the from bus of line l; S_t: branch flow at the to bus of line l.

In the context of solving the optimal power flow problem using a nonlinear solver based on optimization theory, it is often observed that the solver converges to certain KKT points that satisfy the first-order KKT condition of optimization theory but are sometimes not the optimal power flow solution. These KKT points tend to deviate from the actual optimal power flow solution as the load conditions or inequality constraints in the power system change. In the forthcoming tests, we aim to investigate how the bifurcation phenomenon manifests in the γ-relaxed feasible region and the optimal solution of the OPF problem with varying relaxation parameters γ.

5.2.   The 5-bus system

The WB5 system is taken from ^[10], the detail data and network diagram can be download from ^[22]. This system includes 2 generators and 6 buses, which have multiple feasible components and OPF solutions. In OPF problems, the active power output of the generators is the variable we are most interested in, so we concentrate on the feasible region and the variation of the optimal solution for the WB5 system in the PG plane.

Since the difference between the upper and lower limits of voltage and the rated voltage (i.e., 1 p.u.) in the optimal power flow problem is generally the same, when the lower limit of the voltage constraint is $V_i^{\min }$, the upper limit of the voltage constraint is $2 - V_i^{\min }$.

Figure 10 corresponds to the notation used in Figure 4. With the lower limit of bus-voltage amplitude set to 0.96, only one feasible component is available due to the tautness of the bus-voltage amplitude constraint. As the voltage constraint is relaxed, two DSEPs are progressively converted to RSEMs via pseudo-bifurcation. The number of OPF solutions increases with the increase of feasible components. Relaxing the lower limit of the bus voltage amplitude constraint to 0.90 results in the merging of different feasible components. Some OPF solutions vanish due to pseudo-pitchfork bifurcation. Table 4 provides detailed data on the bifurcations and parameters changes. It can be seen that the decrease of $V_i^{\min }$ from 0.96 to 0.85.

(1) A pseudo-bifurcation occurs, making the transformation of DSEP to RSEP (LOS) of AQGS, correspond to the emergence of a new feasible component as well as a new optimal solution (see Figure 10(a)→Figure 10(b)→Figure 10(c)).

(2) Three pseudo-pitchfork bifurcations occur, causing the three disconnected feasible components in Figure 10(c) to merge into a single connected feasible component (see Figure 10(c)→Figure 10(d)→Figure 10(e)→Figure 10(f)).

(3) The local optimal solution on each feasible component in Figure 10(c) disappears with a saddle-node bifurcation of type-1 DUEP (see Figure 10(c)→Figure 10(d)→Figure 10(e)→Figure 10(f)).

(4) A local optimal solution and a saddle point (type-1 RUEP) appear with a saddle-node bifurcation in Figure 10(d) enlarged part (see Figure 10(c)→Figure 10(d)).

This example provides insight into the impact of saddle-node bifurcation and pseudo-bifurcation on the emergence or disappearance of LOSs and saddle points. Specifically, the voltage amplitude at $V_i^{\min }$ bus i is chosen as the parameter for observing the changes in OPF solutions. From a practical perspective, the voltage amplitude of buses has an effect on power supply quality. When the upper and lower limits of the voltage amplitude are relaxed, the number of feasible solutions satisfying the OPF constraint increases, leading to a larger feasible region as depicted in Figure 10. However, it is worth noting that the lower limit of node voltage amplitude of less than 0.9 has little practical significance for the power system, yet it does not affect the appearance or disappearance of optimal solutions of constrained optimization problems.

5.3.   The 9-bus system

The 9-bus system, case9mod is also taken from ^[10] and can be download from ^[22], where there have three generators and nine buses. To study the bifurcation phenomenon when the system runs under different load conditions, we add the load condition parameter λ to the power flow equation:

We will use the variation of the equilibrium points to analyze the variation of the feasible region and the optimal solution for this case9mod system (see Figure 11).

Three pseudo-pitchfork bifurcations will occur in the feasible region. After the first pseudo-pitchfork bifurcation, the left two feasible components will be merged into one connected feasible component, as in Figure 11(a). After the second pseudo-pitchfork bifurcation occurs, the remaining two feasible components will be combined into a single connected feasible component, at which point only one feasible component remains, as in Figure 11(d). It should be noted that when the first two pseudo-pitchfork bifurcations are about to occur, the two disconnected feasible components will become larger and closer to each other until they finally merge into one connected feasible component. For the last pseudo-pitchfork bifurcation, since there is only one feasible component left, the final bifurcation will occur in the two disconnected parts of the feasible component and will eventually merge into a larger feasible component, as in Figure 11(f). Table 5 provides a detailed account of the data and bifurcations observed during changes in the parameters.

In this system, four local optimal solutions and one saddle point exist on three disconnected feasible components as in Figure 11(a). In the process of a relaxation parameter change, a total of three saddle-node bifurcations occurs, i.e., the LOS (RSEP of AQGS) bifurcates with the type-1 DUEP on the boundary and then vanish, and the solutions where the bifurcation disappears are all suboptimal in the optimal solution pair about the type-1 DUEP.

6.   Conclusions

This paper contributes to the advancement of research on nonlinear constrained optimization problems by utilizing feasible region theory and bifurcation theory. Specifically, the paper presents a thorough analysis of two types of bifurcation phenomena, namely, saddle-node bifurcation and pseudo-bifurcation, to explain the disappearance or appearance of optimal solutions and saddle points in general nonlinear constrained optimization problems.

The paper proposes and analyzes the characteristics and phenomena of saddle-node bifurcation and pseudo-bifurcation of optimal solutions. It explores the relationship between bifurcation phenomena of the feasible region and the optimal solution, highlighting that changes in the number of optimal solutions or saddle points may occur due to new feasible components, bifurcation of feasible regions, or changes in the boundaries of feasible regions. Detailed numerical examples show that the location, number, and bifurcation phenomenon of optimal solutions are jointly affected by the feasible region (i.e., the constraint set) and the objective function of the constrained optimization problem, so it stresses the importance of explicitly specifying preconditions for analysis. The bifurcation phenomena due to different relaxation parameters in the 5-bus system and 9-bus system OPF problems are numerically illustrated. Moreover, the paper proposes a practical predicting tool for optimal solutions based on the pseudo-bifurcation of DSEP. Suggesting future research avenues may include exploring the application of the bifurcation of the optimal solution discussed in this paper to compute the global optimal solution of general constrained optimization problems, which is very challenging.

Conflict of interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.