Figure 1.
A single-stage grid-tied PV system.
The burden of cardiovascular disease (CVD) has been on the rise in developing countries like Nigeria recently. Studies on perceived CVD risk and the risk status of adults in Ibadan are not readily available, hence this study. A mixed-method design involving a cross-sectional survey and an exploratory qualitative study was utilized. Convenience sampling was used to recruit 418 participants (209 from rural and 209 from urban) for the cross-sectional survey, while purposive sampling was used to recruit 14 participants for the qualitative aspect. The INTERHEART risk score and the Perception of Risk of Heart Disease Scale were used to investigate participants' CVD risk status and perceived risk, respectively. The data from the cross-sectional survey were summarized by using descriptive statistics, and the data were then analyzed by using the chi-square test of association and a multiple logistic regression model, while content thematic analysis was used to analyze the qualitative data. In the rural and urban areas, respectively, 39.7% and 52.2% had a positive perception of CVD risk. In the rural and urban areas, 44% and 41.6% of individuals respectively had moderate-to-high risk of CVD. Participants with at least secondary school education [2.66 (0.61–11.53)] and participants in the urban area [2.62 (0.78–7.08)] had twice higher odds of positive CVD risk perception. Males [3.91 (1.58–9.68)], adults aged 40 and above [1.59 (0.63–4.00)] and urban dwellers [1.21 (0.33–4.39)] had higher odds of a high CVD risk status. The qualitative aspect of the study corroborated the findings from the survey, as many participants did not perceive themselves as being at risk of CVD. The majority of the participants in this study were found to have a moderate-to-high risk of CVD, and many had a negative perception of their risk. Health education and CVD prevention programs are required to curb the burden of CVD.
Citation: Nse A Odunaiya, Opeyemi M Adegoke, Abiodun M Adeoye, Oluwafemi O Oguntibeju. Preliminary study of perceived cardiovascular disease risk and risk status of adults in small rural and urban locations in Ibadan, Nigeria[J]. AIMS Public Health, 2023, 10(1): 190-208. doi: 10.3934/publichealth.2023015
| [1] | Jürgen Vormann . Magnesium: Nutrition and Homoeostasis. AIMS Public Health, 2016, 3(2): 329-340. doi: 10.3934/publichealth.2016.2.329 |
| [2] | Heini Wennman, Tommi Vasankari, Katja Borodulin . Where to Sit? Type of Sitting Matters for the Framingham Cardiovascular Risk Score. AIMS Public Health, 2016, 3(3): 577-591. doi: 10.3934/publichealth.2016.3.577 |
| [3] | Md Jahoor Alam, Abdullah Ibrahim Alnafeesah, Mohd Saeed . Inter-correlation of risk factors among heart patients. AIMS Public Health, 2020, 7(2): 354-362. doi: 10.3934/publichealth.2020030 |
| [4] | W Bell Ngan, L Essama Eno Belinga, SAP Essam Nlo'o, E Abeng Mbozo'o, E Otsomoti, J Mekoulou Ndongo, EC Bika Lele, D Hupin, SH Mandengue, F Roche, B Bongue . Oral health status and cardiovascular risk profile in Cameroonian military population. AIMS Public Health, 2021, 8(1): 100-109. doi: 10.3934/publichealth.2021008 |
| [5] | Supa Pengpid, Karl Peltzer . The Prevalence of Underweight, Overweight/Obesity and Their Related Lifestyle Factors in Indonesia, 2014–15. AIMS Public Health, 2017, 4(6): 633-649. doi: 10.3934/publichealth.2017.6.633 |
| [6] | Carol L. Stone . A population-based measure of chronic disease severity for health planning and evaluation in the United States. AIMS Public Health, 2020, 7(1): 44-65. doi: 10.3934/publichealth.2020006 |
| [7] | Julia Metelka, Colin Robertson, Craig Stephen . Japanese Encephalitis: Estimating Future Trends in Asia. AIMS Public Health, 2015, 2(4): 601-615. doi: 10.3934/publichealth.2015.4.601 |
| [8] | Angelina R. Wittich, L. Aubree Shay, Belinda Flores, Elisabeth M. De La Rosa, Taylor Mackay, Melissa A. Valerio . Colorectal cancer screening: Understanding the health literacy needs of hispanic rural residents. AIMS Public Health, 2019, 6(2): 107-120. doi: 10.3934/publichealth.2019.2.107 |
| [9] | CCF Smits, JR Toelsie, MGM Eersel, ISK Krishnadath . Equity in health care: An urban and rural, and gender perspective; the Suriname Health Study. AIMS Public Health, 2018, 5(1): 1-12. doi: 10.3934/publichealth.2018.1.1 |
| [10] | Henri Olivier Tatsilong Pambou, Amandine Gagneux-Brunon, Bertrand Tatsinkou Fossi, Frederic Roche, Jessica Guyot, Elisabeth Botelho-Nevers, Caroline Dupre, Bienvenu Bongue, Celine Nguefeu Nkenfou . Assessment of cardiovascular risk factors among HIV-infected patients aged 50 years and older in Cameroon. AIMS Public Health, 2022, 9(3): 490-505. doi: 10.3934/publichealth.2022034 |
The burden of cardiovascular disease (CVD) has been on the rise in developing countries like Nigeria recently. Studies on perceived CVD risk and the risk status of adults in Ibadan are not readily available, hence this study. A mixed-method design involving a cross-sectional survey and an exploratory qualitative study was utilized. Convenience sampling was used to recruit 418 participants (209 from rural and 209 from urban) for the cross-sectional survey, while purposive sampling was used to recruit 14 participants for the qualitative aspect. The INTERHEART risk score and the Perception of Risk of Heart Disease Scale were used to investigate participants' CVD risk status and perceived risk, respectively. The data from the cross-sectional survey were summarized by using descriptive statistics, and the data were then analyzed by using the chi-square test of association and a multiple logistic regression model, while content thematic analysis was used to analyze the qualitative data. In the rural and urban areas, respectively, 39.7% and 52.2% had a positive perception of CVD risk. In the rural and urban areas, 44% and 41.6% of individuals respectively had moderate-to-high risk of CVD. Participants with at least secondary school education [2.66 (0.61–11.53)] and participants in the urban area [2.62 (0.78–7.08)] had twice higher odds of positive CVD risk perception. Males [3.91 (1.58–9.68)], adults aged 40 and above [1.59 (0.63–4.00)] and urban dwellers [1.21 (0.33–4.39)] had higher odds of a high CVD risk status. The qualitative aspect of the study corroborated the findings from the survey, as many participants did not perceive themselves as being at risk of CVD. The majority of the participants in this study were found to have a moderate-to-high risk of CVD, and many had a negative perception of their risk. Health education and CVD prevention programs are required to curb the burden of CVD.
Abbreviations: PV = Photovoltaic; Lg = Grid-side inductor; SPFBI = single-phase full-bridge inverter; S1, S2, S3, S4 = Semiconductor switches of the SPFBI; MPPT = Maximum power point tracking; P & O = Perturb and observe; SPFBI = single-phase full bridge inverter; NL = Negative large; NS = Negative small; Z = zero; PS = Positive small; PL = positive large; ΔP = crisp value of the output; K = weight factor; ΔPi = membership value corresponding to ΔP; NH = Negative high; NL = Negative low; Z = zero; PH = Positive high; PL = Positive low
The increase in electricity demand, environmental effects, limited reserves, and the price hikes of non-renewable energy sources made the entire world explore alternative energy sources. The power generated from renewables became more popular due to their omnipresence and eco-friendliness. Amidst clean energy sources, photovoltaic (PV) based electric power generation became more popular due to its availability, no environmental ramifications, less cost of operation and maintenance. PV systems' applications can be broadly categorized into two divisions: Grid-tied systems and stand-alone power generators [1]. The autonomous systems are applicable for small power applications with battery bank assistance, where grid-tied systems are suitable for high-power applications without any battery assistance [1]. The PV systems are connected to the grid using the single-stage and two-stage architectures [2]. The choice of the single- or two-stage design depends on the availability of the PV panels. The two-stage architecture consists of PV panels, dc-dc converter, dc-ac converter, and the grid with all the necessary accessories. Due to a boost/buck converter and inverter system, a system is called a two-stage approach. The conventional grid-tied two-stage system comprises the maximum power point tracking controller on the source side, the current controller that deals with power factor correction on the grid side, and the dc-link voltage regulator that balances the source and grid power.
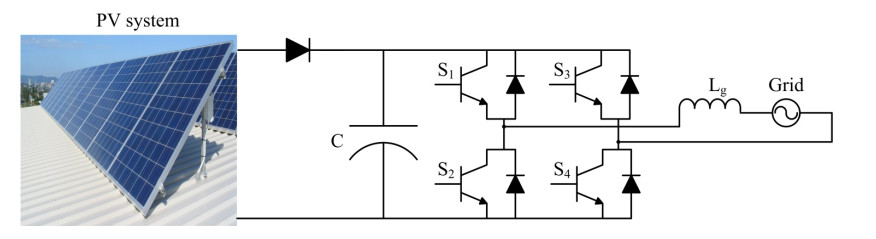
On the other hand, the single-stage converter consists of a PV system, a single-phase inverter, and the grid, as shown in Figure 1. The capacitor 'c' supports the PV voltage, and the switches S1, S2, S3, S4 are triggered by the pulses generated by an internal control scheme. The entire system is integrated into the grid using the grid-side inductor (Lg). The advantages of the single-stage system over the two-stage system are enhanced efficiency, less size, and cost. Especially in home-energy based PV systems, the primary concern is the size and the price, so a single-stage system is more beneficial than the two-stage method. In the single-stage system, the inverter itself has to tackle peak power, dc-link voltage regulation, and power factor correction.
The hill-climbing MPPT algorithm tracks the peak power by perturbing the duty ratio [4,5,6,7,8,9], while the P & O algorithm perturbs the voltage[10,11,12]. The hill-climbing MPPT algorithm and P & O can fail when the atmospheric conditions are changing rapidly. These MPPT techniques require two sensors to sense the voltage and current from the PV panel. The need for sensors also depends on the topology implemented; for instance, a voltage sensor is enough for the system prescribed in [13]. The incremental conductance states that the peak power may be obtained when the power vs. voltage curve slope is zero [14,15]. The swiftness of the peak power tracking depends on the size of the incremental parameter. But the larger size of the incremental parameter may lead the peak power point to oscillate around it. The incremental conductance concept requires a sensor to sense the voltage and another to trace PV panels' current. The fractional open circuit voltage emerged due to the linear coordination between the voltage at peak power and open-circuit voltage [16,17,18]. One of the demerits of the system is power loss for a moment. This demerit can be overpowered by the pilot cells, which have to be cautiously incorporated to safeguard the PV characteristics [16]. Since it is an approximation technique, technically speaking, it cannot steadfastly trace the peak power. It also adds complexity in control along with unnecessary loss in power. The fractional short circuit concept is based on the linear coordination between the current at the peak power and the short circuit current at variable climatic conditions[19,20]. An auxiliary switch is required to short the array to calculate the short circuit current, which increases the component number and price of the system. The flexibility and the incorporation of micro-controllers made fuzzy logic acquire a popular position over the other controllers[21,22,23,24,25,26,27,28]. The non-requirement of exact mathematical modeling, implementation with vague inputs, and capability to deal with nonlinearities made fuzzy control acquire high popularity among the controllers. It was proven to work accurately during rapidly changing climatic situations. The optimum performance of the fuzzy logic controller depends on the expertise of the user. The fuzzy logic control implemented in [22] reflects the convergence's swiftness with limited oscillations around the peak powerpoint. The neural network-based peak power controller is an adaptive technique developed along with a fuzzy logic controller [29,30,31]. It is a three-layered network that outputs a duty cycle to rigger the semiconductor switch in dc-dc converters. The performance of the neural network based-peak power control algorithm depends on the hidden layers and its training. A sliding mode observer concept [32] is proposed in the literature, and its controller state equations consist of uncertainty, which increases the system's complexity. The table of comparison between different peak power algorithms is presented in Table 1. In this paper, a fuzzy logic controller-based peak power controller and dc-link voltage controller are designed to track the PV source's peak power and to regulate the voltage across the capacitor. The traditional capacitor voltage regulator embraces a traditional proportional and integral (PI) controller and gives rise to direct-axis reference current.
| Peak power technique | Dependence on PV | A/D | Speed of convergence | Complexity | Sensors |
| Perturb and observe | × | A & D | Depends | Less | V, I |
| Incremental conducance | × | D | Depends | Moderate | V, I |
| Fractional open circuit voltage | √ | A & D | Moderate | Less | V |
| Fractional Short circuit current | √ | A & D | Moderate | Moderate | C |
| Fuzzy logic | √ | D | Speeder | More | Depends |
| Neural Network | √ | D | Speeder | More | Depends |
| Sliding mode control | × | D | Speeder | Moderate | V, I |
DownLoad:
CSV
The main contributions of the paper are:
1. A fuzzy rule-based regulator is modeled, and the rules are framed to track the peak power and control the dc-link voltage.
2. The steady-state and transient analysis is investigated to prove the robustness of the control scheme.
3. The bidirectional operation of the inverter is investigated to facilitate the usage of the dc load.
4. The effects of the load and the grid on the PV system and the effects of the PV system variations on the load and the grid are analyzed.
The work's organization is as follows: the mathematical modeling of the single-phase inverter, the modeled control design, results and discussion, conclusion, acknowledgment, nomenclature, and references.
In this paper, a full bridge hybrid inverter is implemented. It was designed by a renowned engineer, Mcmurray [33]. A single-phase full-bridge inverter (SPFBI) can be contemplated as a combination of two half bridge single phase inverters that share a common dc voltage source. This topology overcomes the demerits of a single-phase half-bridge inverter (SPHBI), which incorporates a dual dc source. The SPFBI consists of four power electronic switches (S1–S4), as shown in Figure 2. When switches S1, S2 are turned-on, SPFBI generates +Vdc, and switches S3, S4 generates -Vdc. The switches in the same leg should not operate simultaneously, which leads to a short circuit across the portion. Unipolar, bipolar, and hybrid modulation schemes are the three different kinds of schemes available for a single phase's full bridge inverter. In this paper, a unipolar modulation scheme is implemented. SPFBI comprises Vao and Vbo as pole voltages, which will be in the form of a square waveform, but consists of a phase difference. The pole voltage Vao and Vbo can be written as
| Vao=∑n=1,3,5,7…∞2Edcnπsin(nωt) | (1) |
where n = order of harmonic
| Vbo=∑n=1,3,5,7…∞2Edcnπsinn(ωt−ϕ) | (2) |
The difference between two pole voltages gives the line voltage of a single-phase full-bridge inverter (SPFBI). The circuit diagram of a conventional SPFBI has shown in Figure 2.
The merits of implementing the SPFBI when compared with single-phase half-bridge inverter (SPHBI) are:
1. Single dc source whereas the SPHBI consists of two sources
2. An enhanced output voltage with dual gain
3. An increased efficiency and quadrupled power transfer
The demerits of the SPFBI are the usage of more passive components and an increased switching loss.
The proposed structure, along with the internal control strategy, is shown in Figure 3. The proposed control strategy comprises an MPPT controller, dc voltage, and current regulator. A perturb and observe (P & O) MPPT is conventionally employed due to its independence on the PV array, the possibility of implementation on digital and analog test benches, but it suffers from many disadvantages. The main demerits of the P & O algorithm can be listed as:
1. The peak power point oscillates around the peak power [34]
2. The P & O algorithm fails to track the peak power at abrupt changes in atmospheric conditions [34]
3. P & O algorithm is inaccurate [34]
4. Decreased system efficiency [35]
A fuzzy logic-based controller is implemented to track the PV source's maximum power to overcome the demerits mentioned above. The detailed analysis of the proposed fuzzy logic peak power controller and voltage regulator across the dc-link capacitor is provided in the subsequent sections.
The proposed control scheme implements the concept of a conventional and straightforward P & O MPPT algorithm adaptively to overcome the undesired oscillations at the peak power point. The fuzzy logic control algorithm perturbs the PV voltage to acquire the preferred performance. According to the application, the main advantage of the recommended fuzzy logic-based MPPT is its adaptiveness in adjusting the reference voltage of the dc-link voltage across the dc-link capacitor or the duty cycle. The fuzzy logic controller reduces the error during the steady-state and the erroneous operation at rapid atmospheric conditions. Though the adaptive fuzzy logic controller possesses many advantages, it suffers from the demand for a considerable memory-based, very high-speed processing system, and complexity. The block diagram of the fuzzy-based controller to follow the peak power is presented in Figure 4. The fuzzy logic controller consists of the input E(n), the change in the input ΔE(n), which is obtained by the difference of the information and its delay E(n-1). The inputs E(n) and the deviation in the input ΔE(n) are considered as the inputs to the fuzzy system. The output of the fuzzy system is P(n), which is obtained from the summation of deviation in the output ΔP(n) and the delay P(n-1). The formulae governing the variations of inputs and outputs are given as below:
| ∆E(n)=E(n)−E(n−1) | (3) |
| ∆P(n)=P(n)−P(n−1) | (4) |
The fuzzy logic control works in a three-step manner. (i) Fuzzification (ii) Rule-based fuzzy control algorithm and (iii) Defuzzification. The detail analysis of the important steps included in the fuzzy logic controller is elucidated below:
(i) Fuzzification: The fuzzy logic control process requires the control algorithm to be designed by the implication of fuzzy set theory that consists of linguistic variables. The linguistic variables, along with the membership functions, are presented in Figure 5. Based on the consideration of the small steady-state error, the assigned membership function reduces the struggle to deduce the output.
(ii) Rule-based fuzzy control algorithm: A set of rules bounds the fuzzy-based algorithm to trace the required response. Table 2 provides an insight for the rule base to track the peak power for corresponding solar radiation. The variables E and ΔE represent the error and change in error for PV power and voltage. In contrast, NL variable represents a negative large, NS Represents a negative small, Z for zero, PS for a positively small, and PL represents a positive large. The linguistic variables are arranged in IF-THEN statements to form the rules. For instance,
|
NL | NS | Z | PS | PL |
| NL | Z | Z | NL | NL | NL |
| NS | Z | Z | NS | NS | NS |
| Z | NS | Z | Z | Z | PS |
| PS | PS | PS | PS | Z | Z |
| PL | PL | PL | PL | Z | Z |
DownLoad:
CSV
Rule-1: IF E is NL and ΔE is Z, THEN ΔP is NL
Rule-2: IF E is PS and ΔE is PS, THEN ΔP is Z.
(iii) Defuzzification: The final stage of the fuzzy logic system is defuzzification, which calculates a crisp value for the fuzzy logic processor's output. Traditionally, two methods are being used to trace the production's crisp value, namely the center of area method and the mean of the maximum method. In this paper, the center of area method is used to achieve high accuracy.
The center of area method can be computed as:
| ∆P=∑ni=1Ki∆Pi∑ni=1Ki | (5) |
where ΔP = crisp value of the output; K = weight factor; ΔPi = membership value corresponding to ΔP.
The working principle of the proposed fuzzy logic controller is elucidated as:
Step-1: Measure the values of PV voltage, current at all irradiations and compute the generated PV power.
Step-2: compute the change in power (∆PPV) and PV voltage (∆VPV) at the present iteration and previous iteration.
Step-3: Then calculate the change in power and voltage that serves as inputs for the fuzzy logic system to generate the reference dc-link voltage.
Step-4: Three membership-based fuzzy interface system (FIS) with triangular shape is used to formulate the rules.
Step-5: Defuzzify the system for the duty cycle and finally update the PV voltage. Continue the process until the peak power point is reached.
The entire process of operation is presented in the flow chart as Figure 6 for better understanding.
The dc-link voltage regulator's primary objective is to maintain a constant voltage across the dc-link capacitor to maintain a proper power balance between the mains and the grid [36]. The block diagram for the conventional voltage regulator to control the capacitor voltage is presented in Figure 7. The major drawback of the traditional PI regulator demands preciseness in mathematical modeling, making the system more complicated and inaccurate. In contrast, the fuzzy logic controller is an intelligent controller that doesn't require a complete system model as it is dependent on the set of rules to govern the system. The block diagram of the fuzzy-based capacitor voltage controller is demonstrated in Figure 8. The reference dc voltage generated from the MPPT controller is compared with the measured dc-link voltage, and the generated error is considered to be the input for the fuzzy system. The error is the delay for t = 1 sec. The difference between the error E(k) and the delayed error E(k-1) generates the deviation in error ΔE(k), and the same is considered an input to the fuzzy system. The rules mentioned in Table 3 are used to generate the consistent dc-link voltage even in the transients' condition. The defuzzification process developed the output's crisp value to finally provide the reference direct-axis current to control the current controller.
|
|
NH | NL | Z | PH | PL |
| NH | NH | NH | NH | NL | Z |
| NL | NH | NH | NL | Z | PL |
| Z | Z | NH | Z | PL | PH |
| PH | NS | Z | PL | PH | PH |
| PL | Z | PL | PH | PH | PH |
DownLoad:
CSV
where NH is negative high, NL is negative low, Z = zero, PH = Positive high, PL = Positive low
The results and discussion is carried in two categories: (i) simulation analysis (ii) experimental analysis
(i) Simulation analysis:
(a) Analysis of variable irradiance at the no-load condition:
The entire simulation is implemented using MATLAB/SIMULINK, and the obtained results prove the working of a robust controller. The parameters used in the simulation were tabulated in Table 4. The variable irradiance condition is presented in Figure 9. In this paper 1000 W/sq.mt, 750 W/sq.mt, 500 W/sq.mt, 250 W/sq.mt are considered.
| Parameters | Value |
| PV system (Experimental and simulation) | |
| Voc (V) (open circuit voltage) | 30.8 |
| Isc (A) (short circuit current) | 8.23 |
| Vp (V) (Peak voltage) | 24.6 |
| Ip (A) (Peak current) | 7.7 |
| Coefficient of voltage | −0.1 |
| Coefficient of current | 0.004 |
| Series modules | 6 |
| Parallel modules | 1 |
| Grid parameters | |
| Grid voltage (VRMS) (V) | 240 |
| Grid current (IRMS) (A) | 5 |
| DC voltage controller | |
| Reference DC voltage | 435 volts |
| Current controller | |
| Kp (PI) | 0.15 |
| KI (PI) | 6.6 |
| Rff | 0.002 |
| Lff | 0.20 |
| Carrier frequency | 3780 HZ |
DownLoad:
CSV
As the solar radiation changes, the generated PV current and the PV voltages vary, as seen in Figure 10. The irradiance is made to change at time t = 2 sec., 4 sec., 6 sec., and 8 sec. The voltage across the PV panels are connected directly to the SPFBI. As a result, the voltage across the capacitor needs to be regulated, and the same is the PV voltage. The PV voltage remained stable during transients, whereas the PV current underwent rigorous transitions during the irradiance change, and it is presented in Figure 10. During solar radiation change, the voltage across the capacitor experiences a voltage undershoot, decreasing irradiance and overshoot at the sudden increase in irradiance.
The transitions in the capacitor voltage s presented in Figure 11. During times t = 4 sec., 6 sec., and 8 sec., the transients are presented in the zoomed format for straightforward elucidation. The constant voltage across the capacitor is due to the fuzzy logic control's robust and adaptive nature and the created rule base. Since the voltage across the capacitor is constant, the inverter generates a voltage waveform of the same magnitude with a square shape. The filters that are used at the grid-side converts into sinusoidal quantity, as shown in Figure 12. The voltage generated by the inverter and the filtered voltage should be in the same phase. According to Figure 12, the filtered voltage and inverter voltage are in existed in the same phase. The modulation index at variable irradiance is presented in Figure 13. According to the irradiance change, the modulation index waveform remained changed and provided the inverter's necessary pulses.
The reference waveform generated out of the modulation index is presented in Figure 14. The modulation waveform is compared with the carrier waveform of frequency 3750 Hz to generate the pulses shown in Figure 15.
The internal control analysis waveforms are also presented for the beer investigation and the control scheme's robustness. The direct axis current waveform (reference) generated out of dc-link voltage regulator, and the actual direct axis current is presented in Figure 16. The fuzzy logic control regulated the voltage across the capacitor and generated the direct axis reference current, where the actual current is the direct axis component of grid current. The currents are compared and tuned perfectly by using a PI controller in the current controller. As a result, the error between the reference and the actual became zero, as shown in Figure 17. Similarly, the current reference and the actual current of the quadrature axis are compared and tuned using a PI tuner to obtain a zero error, as shown in Figure 18.
The grid voltage and the grid currents are presented in Figures 18 and 19.
The grid current underwent the transitions at time t = 2 sec., 4 sec., 6 sec., and 8 sec. At these time instants, the irradiance is varied. A constant current flow into the grid has to be maintained by the current controller and the internal control strategy waveforms presented in Figure 16, and Figure 17 is responsible for maintaining it. The dc-link voltage controller has to bear the constant dc-link voltage so that irradiance change will be reflected on the current contrtoller and the waveform in Figure 19 is due to its phenomenon. The zoomed version of the transitions are represented in Figure 19 as (a), (b), (c), (d) for better discretion.
(b) The analysis of variable irradiance along with dc load:
A dc load 500 W and 100 W are connected across the capacitor, and they turned-on at time t = 3 sec., and t = 5 sec. The voltage across the capacitor experienced transients during the load change but was controlled by the fuzzy logic controller to remain stable, as presented in Figure 20.
Since the dc-link voltage regulator's effect has to be compensated by the current regulator, it controls the grid current to maintain constant power flow. As a result, the grid's current experiences a transient during the load transient and retains to its normal position once it is removed, as shown in Figure 21.
(c) The analysis of variable irradiance along with ac load:
A variable ac load is connected across the grid terminals and are switched on at t = 3 sec. and = 5 sec.
The ac load is turned on at t = 3 sec and 5 sec. The dc-link voltage experiences transients at the instant of load turned on, and it is brought to its normal position by an adaptive fuzzy logic controller. Since the power has to be maintained constant and the grid voltage is stable, the current controller regulates the grid current, as shown in Figure 23.
(d) The analysis of variable irradiance along with grid disturbances:
The study of grid disturbances on the adaptive fuzzy logic dc-link voltage regulator is presented in this section. The voltage is decreased by 20% by its nominal value, representing the voltage sag at time t = 2.5 sec. Its nominal value is increased by 20%, representing voltage swell at time t = 5 sec. The zoomed version of the voltage sag and swelled at the time instants are presented in Figure 24.
The effect of grid disturbances on the voltage across the capacitor is presented in Figure 25. The voltage across the capacitor is perturbed at the time instants t = 2.5 sec., 5 sec., and 7.5 sec. The voltage experiences voltage overshoot at the instant of voltage sag and voltage undershoot shoot at the moment of a voltage swell, as shown in Figure 25. The adaptive fuzzy logic controller addresses the source side's issues and the grid side disturbances efficiently. Similarly, the grid frequency is increased by three times (150 Hz), as shown in Figure 26 and the voltage across the capacitor during this disturbance is analyzed in Figure 27.
The power generated by the PV panels at variable irradiance is presented in Figure 28. The adaptive fuzzy logic controller employed to track the peak power improved the system's efficiency by transferring the maximum power to the grid with reduced power loss.
(ii) Experimental analysis:
A laboratory design is fabricated to analyze the theoretical results is shown in Figure 29. The experimental prototype consists of 1KW PV panels with an SP-110 pyranometer made from the apogee instruments, as shown in Figure 29. SP-110 is a self-powered, heater less pyranometer designed to calibrate the amount of radiation available in the atmosphere. Its sensitivity is 0.2 mV/Wm-2, and its factor of calibration is 5 Wm-2/mV, which is the reciprocal of sensitivity. The range of calibrated output is 0–400 mV, and the time of response is less than a millisecond. It can view 180 degrees, and the content of the spectrum is 360–1120 nm. An industrial socket of 440 V and 10 A current is used to interconnect the SPFBI to the grid. A grid voltage of 240 V RMS is used to transfer the power generated from the PV source. A personal computer with Xilinx software is used to provide the necessary coding for Spartan-6 FPGA to trigger the semiconductor switches. The WT800 Yokogawa power analyzer and DL850E scope corder are used to extract the data or the results. The IGBTs of the model number SKM100GB12T4 are used to design the SPFBI and the necessary connectors and auxiliaries.
The PV voltage and current at the corresponding solar irradiation is demonstrated in Figure 30. As solar radiation varies, the PV cell's current varies due to the photo-electric effect; as a result, the PV voltage also varies. The fuzzy logic-based peak power controller tracks the accurate peak power at all irradiations, and it can be seen in Figure 30. Different case studies are analyzed to trace out the superior performance of the control design.
Case-1: In this section, the steady-state analysis of the system is calibrated. Constant solar irradiation of 1000 W/m2 is considered for the evaluation. As the irradiation is stable, the PV system's voltage and currents remained unchanged and can be observed from Figure 30. Due to the unvaried solar radiation, the voltage across the capacitor and corresponding load currents have also remained unvaried. The voltage and current of the distribution system also remained undisturbed due to the steady solar radiation. The practical case opposes this condition because the irradiance is intermittent.
The unfiltered voltage or the two-level voltage of the SPFBI is also presented in Figure 31. Due to the robust current controller and the perfect sine pulse width modulation analysis, the inverter's current output remains distorted less. It is an evidence of the robustly designed controller.
Case-II: In this case study, variable solar irradiation at a constant load is considered. As seen from Figure 32, as soon the PV circuit breaker is switched on, the PV current (CH2) rises immediately; thus, the voltage across the PV panel (CH1) also increases. Due to sudden transient in the solar radiation, the voltage across the capacitor (CH3) experienced the overshoot in the voltage and retained to set value. When the capacitor voltage remains the same, the SPFBI (CH5) phase voltage remained constant. Still, the current controller experiences the effect of change in irradiation, and to compensate for its impact, the magnitude of the inverter current (CH6) is enhanced, as shown in Figure 32.
Case-III: In this case, the variable solar radiation and the variable dc load and ac load on the PV system and on distribution lines are analyzed. The effect of the abrupt rise in the dc resistor bank current disturbs the PV voltage and current [(CH1) & (CH2)] as is evident from Figure 33(a). The sudden rise in the current through the dc resistor bank (CH4) introduces the transients in capacitor voltage, at that instant, the robust capacitive voltage controller regulates the voltage across the capacitor (CH3) and remains it in the constant state even after a slight disturbance. The inverter output voltage (CH5) also remained constant except at the load change condition as it underwent a voltage undershoot due to dc-link voltage (CH3). When the controller is removed, the dc-link voltage regulator loses its control; as a result, the dc-link voltage and the inverter voltage remained uncontrollable, as it is evident from the Figure 33(c). When the ac load is turned on, the ac load current (CH4) is suddenly increased in magnitude; as a result, the dc-link voltage is also increased for a moment, and it settled to its reference value due to fuzzy logic controller. Since capacitor voltage is unchanged, the converter (CH5) phase voltage has also remained constant, as shown in Figure 33. The grid current (CH6) magnitude is raised to ensure the proper power balance. Similarly, the effect of ac load off is presented in Figures 34 and 35.
Case-IV: The effect of grid disturbances on the source and on the grid is analyzed in this section. The grid voltage is reduced to 15% of the standard value by using a voltage matching transformer to create the voltage sag, as shown in Figure 36. At the instant of the voltage sag, the capacitor voltage (CH3) confronted a transient and returned to the nominal value, which is evident from Figure 36.
To compensate for voltage sag effect, the magnitude of the grid current (CH6) is increased in the magnitude due to the current controller. Similarly, the impact of voltage swell is also presented in Figure 37. The voltage of the grid is increased by 15% to create the voltage swell. The magnitude of the current is reduced to compensate for the effect of voltage swell and to ensure the power balance between the PV source and grid. The comparative analysis between the different control schemes and the proposed control scheme is presented in Table 5.
| Performance index | Fuzzy logic | Incremental conductance |
| Overshoot (%) | 0.3089 | 1.2345 |
| Damping factor (ξ) | 0.7685 | 0.5236 |
| Rise Time | 0.1254 | 0.1856 |
| Error (%) | 6.2 | 16 |
| Fluctuations in voltage | Very low | high |
| Duty cycle operation | 0.55–0.65 | 0.3–0.7 |
| Peak power point oscillations (%) | 3.2 | 1.2 |
| Handling capabi; ity of non-linearity | Comparatively low | Highly appreciable |
| In terms of cost | Comparatively high | quite low |
DownLoad:
CSV
In this paper, the PV based home based grid-tied energy is investigated using adaptive technology. The mathematical modeling of a single-phase grid-tied full bridge inverter with necessary mathematical formulae is also expounded in this paper. To overcome the disadvantages of the conventional peak power controller and PI-based dc-link voltage regulator, a fuzzy logic controller is proposed with a definite set of rules. The effect of the variable solar radiation on the distribution line parameters, the impact of the dc load and the ac load on the line and PV parameters, the effect of grid disturbances like voltage sag and swell, and third harmonics are analyzed in this work. The impact of disorders in grid parameters on the connected loads and PV source is elucidated with simulation and experimental results. This control topology's implementation can assure the drastic reduction in the financial burden to invest in dc/dc converter in a PV powered grid-tied home energy applications. It also reduces the complexity of tuning the PI parameters to achieve better peak power tracking capability and transient stability of dc-link voltage. In the future, the fuzzy-based approach can be replaced by most adaptive techniques to reduce complexity and to increase efficiency with reduced cost.
The author's want to thank DST-SERB, statutory body established through an act of parliament: SERB Act 2008, Government of India for their financial assistance for the undergoing project under project reference no. SERB-SB/S3/EECE/090/2016 and also the management of NIT, Meghalaya (An institute of National Importance) for their constant support to carry out the work.
All authors declare no conflict of interest in this paper.
| [1] |
Cappuccio FP, Miller MA (2016) Cardiovascular disease and hypertension in sub-Saharan Africa: burden, risk and interventions. Intern Emerg Med 11: 299-305. https://doi.org/10.1007/s11739-016-1423-9 
|
| [2] | World Health OrganizationCardiovascular diseases (2021). Available from: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds). |
| [3] |
Kengne AP, Ntyintyane LM, Mayosi BM (2012) A systematic overview of prospective cohort studies of cardiovascular disease in sub-Saharan Africa. Cardiovasc J Afr 23: 103-112. https://doi.org/10.5830/CVJA-2011-042
|
| [4] |
Ojji DB, Lamont K, Sliwa K, et al. (2017) Primary care in the prevention, treatment and control of cardiovascular disease in sub-Saharan Africa. Cardiovasc J Afr 28: 251-256. https://doi.org/10.5830/CVJA-2016-082
|
| [5] |
Ike SO, Onyema CT (2020) Cardiovascular diseases in Nigeria: What has happened in the past 20 years?. Nig J Cardio 17: 21-26. https://doi.org/10.4103/njc.njc_33_19
|
| [6] |
BeLue R, Okoror TA, Iwelunmor J, et al. (2009) An overview of cardiovascular risk factor burden in sub-Saharan African countries: A socio-cultural perspective. Global Health 5: 10. https://doi.org/10.1186/1744-8603-5-10
|
| [7] |
Huffman MD, Prabhakaran D, Osmond C, et al. (2011) Incidence of cardiovascular risk factors in an Indian urban cohort. Results from the New Delhi birth cohort. J Am Coll Cardiol 57: 1765-1774. https://doi.org/10.1016/j.jacc.2010.09.083
|
| [8] | World Health OrganizationNon-communicable Disease (NCD)-Country status (2018). Available from: https://www.who.int/nmh/countries/nga_en.pdf. |
| [9] |
Gersh BJ, Sliwa K, Mayosi BM, et al. (2010) Novel therapeutic concepts. The epidemic of cardiovascular disease in the developing world: Global implications. Eur Heart J 31: 642-648. https://doi.org/10.1093/eurheartj/ehq030
|
| [10] | World Health OrganizationCardiovascular diseases (2016). Available from: https://www.who.int/health-topics/cardiovascular-diseases/#tab=tab_1. |
| [11] |
Ofori SN, Odia OJ (2016) Risk assessment in the prevention of cardiovascular disease in low-resource settings. Indian Heart J 68: 391-398. https://doi.org/10.1016/j.ihj.2015.07.004
|
| [12] |
Kariuki JK, Stuart-Shor EM, Leveille SG, et al. (2013) Evaluation of the performance of existing non-laboratory based cardiovascular risk assessment algorithms. BMC Cardiovasc Disord 13: 1471-2261. https://doi.org/10.1186/1471-2261-13-123
|
| [13] |
McGorrian C, Yusuf S, Islam S, et al. (2011) Estimating modifiable coronary heart disease risk in multiple regions of the world: the INTERHEART Modifiable Risk Score. Eur Heart J 32: 581-589. https://doi.org/10.1093/eurheartj/ehq448
|
| [14] | Arnett DK, Blumenthal RS, Albert MA, et al. (2019) ACC/AHA Guideline on the primary prevention of cardiovascular disease: A report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation 140: e596-e646. https://doi.org/10.1161/CIR.0000000000000725 |
| [15] | Oladapo OO, Falase AO, Salako L, et al. (2010) Prevalence of cardiometabolic risk factors among a rural Yoruba south-western Nigerian population: A population-based survey. Cardiovasc J Afr 21: 26-31. |
| [16] |
Dahiru T, Ejembi CL (2013) Clustering of cardiovascular disease risk-factors in semi-urban population in Northern Nigeria. Niger J Clin Pract 16: 511-516. https://doi.org/10.4103/1119-3077.116903
|
| [17] |
Odunaiya NA, Grimmer K, Louw QA (2015) High prevalence and clustering of modifiable cardiovascular disease risk factors among rural adolescents in southwest Nigeria: implication for grass root prevention. BMC Public Health 15: 661. https://doi.org/10.1186/s12889-015-2028-3
|
| [18] |
Oguoma VM, Nwose EU, Ulasi II, et al. (2017) Cardiovascular disease risk factors in a Nigerian population with impaired fasting blood glucose level and diabetes mellitus. BMC Public Health 17: 36. https://doi.org/10.1186/s12889-016-3910-3
|
| [19] |
Onyemelukwe GC, Ogunfowokan O, Mbakwem A, et al. (2017) Cardiovascular risk factors in adult general out-patient clinics in Nigeria: A country analysis of the Africa and Middle East Cardiovascular Epidemiological (ACE) study. Afr Health Sci 17: 1070-1081. https://doi.org/10.4314/ahs.v17i4.15
|
| [20] |
Amadi CE, Grove TP, Mbakwem AC, et al. (2018) Prevalence of cardiometabolic risk factors among professional male long-distance bus drivers in Lagos, south-west Nigeria: a cross-sectional study. Cardiovasc J Afr 29: 106-114. https://doi.org/10.5830/CVJA-2018-006
|
| [21] |
Ammouri AA, Neuberger JL (2008) The perception of risk of heart disease scale: Development and psychometric analysis. J Nurs Meas 16: 83-97. https://doi.org/10.1891/1061-3749.16.2.83
|
| [22] | Hochbaum G, Rosenstock I, Kegels S (2016) Health belief model. Washington, DC: U.S., Public Health Service (Original work published 1952). |
| [23] |
Cainzos-Achirica M, Blaha MJ (2015) Cardiovascular risk perception in women: true unawareness or risk miscalculation?. BMC Medicine 13: 112. https://doi.org/10.1186/s12916-015-0351-2
|
| [24] |
Habib A, Johargy A, Mahmood K, et al. (2014) Design and determination of the sample size in medical research. IOSR-JDMS 13: 21-31. https://doi.org/10.9790/0853-13562131
|
| [25] | Okoro TE, Jumbo J (2021) Cardiovascular event risk estimation among residents of a rural setting in Bayelsa state, Nigeria. Am J Cardiovasc Dis 11: 300-315. |
| [26] |
Khanal MK, Mansur-Ahmed MS, Moniruzzaman M, et al. (2018) Prevalence and clustering of cardiovascular disease risk factors in rural Nepalese population aged 40–80 years. BMC Public Health 18: 677. https://doi.org/10.1186/s12889-018-5600-9
|
| [27] |
Ghorpade AG, Shrivastava SR, Kar SS, et al. (2015) Estimation of the cardiovascular risk using World Health Organization/International Society of Hypertension (WHO/ISH) risk prediction charts in a rural population of South India. Int J Health Policy Manag 4: 531-536. https://doi.org/10.15171/ijhpm.2015.88
|
| [28] |
Hajar R (2017) Risk factors for coronary artery disease: Historical perspectives. Heart Views 18: 109-114. https://doi.org/10.4103/HEARTVIEWS.HEARTVIEWS_106_17
|
| [29] | Alikor C, Emem-Chioma P (2018) Clustering of cardiovascular disease risk factors in a rural adult population in Nigeria. IJRMS 6: 765-771. https://doi.org/10.18203/2320-6012.ijrms20180593 |
| [30] | Nnabuihe SN, Lizzy E, Odunze NT (2015) Rural poor and rural health care in Nigeria: A consocial need for policy shift. Eur Sci J . |
| [31] | De Lima MM, da Silva GR, Jensem-Filho SS, Granja F (2016) Association between perceived lifetime risk of cardiovascular disease and calculated risk in a male population in Brazil. Vasc Health Manag 12: 279-286. https://doi.org/10.2147/VHRM.S107874 |
| [32] |
Nansseu JR, Assah F, Petnga S, et al. (2019) Assessing the global risk of cardiovascular disease among a group of university students: population-based cross-sectional study in Yaoundé, Cameroon. BMJ Open 9: e030594. https://doi.org/10.1136/bmjopen-2019-030594
|
| [33] |
Maharani A, Praveen D, Oceandy D, et al. (2019) Cardiovascular disease risk factor prevalence and estimated 10-year cardiovascular risk scores in Indonesia: The SMARThealth Extend study. PloS One 14: e0215219. https://doi.org/10.1371/journal.pone.0215219
|
| [34] |
Adedoyin R, Awotidebe T, Dada G, et al. (2018) Cardiovascular disease risk assessment of senior staff members of a Nigerian university. J Clin Exp Cardiol 9: 2. https://doi.org/10.4172/2155-9880.1000588
|
| [35] |
Chan F, Adamo S, Coxson P, et al. (2012) Projected impact of urbanization on cardiovascular disease in China. Int J Public Health 57: 849-854. https://doi.org/10.1007/s00038-012-0400-y
|
| [36] | World Health OrganizationTobacco fact sheet (2019). Available from: https://www.who.int/en/news-room/fact-sheets/detail/tobacco. |
| [37] |
Gong W, Wei X, Liang Y, et al. (2016) Urban and rural differences of acute cardiovascular events: A Study from the population-based real-time surveillance system in Zhejiang, China in 2012. PloS One 11: e0165647. https://doi.org/10.1371/journal.pone.0165647
|
| [38] |
Forero JP, Ferrera A, Castaño JD, et al. (2021) Bipolar Disorder and Cardiovascular Risk in Rural versus Urban Populations in Colombia: A Comparative Clinical and Epidemiological Evaluation. Ann Glob Health 87: 112. https://doi.org/10.5334/aogh.3479
|
| [39] |
Kulshreshtha A, Goyal A, Dabhadkar K, et al. (2014) Urban-rural differences in coronary heart disease mortality in the United States: 1999–2009. Public Health Rep 129: 19-29. https://doi.org/10.1177/003335491412900105
|
| [40] |
Yusuf S, Rangarajan S, Teo K, et al. (2014) Cardiovascular risk and events in 17 low-, middle-, and high-income countries. NEJM 371: 818-827. https://doi.org/10.1056/NEJMoa1311890
|
| [41] |
Dégano IR, Marrugat J, Grau M, et al. (2017) The association between education and cardiovascular disease incidence is mediated by hypertension, diabetes, and body mass index. Sci Rep 7: 12370. https://doi.org/10.1038/s41598-017-10775-3
|
| [42] | Odunaiya NA, Adesanya TB, Okoye EC, et al. (2021) Towards cardiovascular disease prevention in Nigeria: A mixed method study of how adolescents and young adults in a university setting perceive cardiovascular disease and risk factors. Afr J Prm Health Care Fam Med 13: a2200. https://doi.org/10.4102/phcfm.v13i1.2200 |
| [43] |
Mohd-Azahar NMZ, Krishnapillai A, Zaini NH, et al. (2017) Risk perception of cardiovascular diseases among individuals with hypertension in rural Malaysia. Heart Asia 9: e010864. https://doi.org/10.1136/heartasia-2016-010864
|
| [44] | Watson KE (2019) Modifiable risk factors account for a majority of cardiovascular disease and mortality. NEJM Watch . Available from: https://www.jwatch.org/na49880/2019/09/03/modifiable-risk-factors-account-majority-cardi4ovascular. |
| [45] |
Umuerri EM (2020) Public knowledge and perception of heart disease: A cross-sectional study of two communities in Delta State, Nigeria. J Trop Med 22: 65-72. https://doi.org/10.4103/jomt.jomt_3_20
|
| [46] |
Ammouri AA, Neuberger G, Mrayyan MT, et al. (2011) Perception of risk of coronary heart disease among Jordanians. J Clin Nurs 20: 197-203. https://doi.org/10.1111/j.1365-2702.2010.03192.x
|
| [47] | Poudel A, Zhou JY, Story D, et al. (2018) Diabetes and associated cardiovascular complications in American Indians/Alaskan Natives: a review of risks and prevention strategies. J Diabetes Res 13: 2742565. https://doi.org/10.1155/2018/2742565 |
| [48] |
Wekesah FM, Kyobutungi C, Grobbee DE, et al. (2019) Understanding of and perceptions towards cardiovascular diseases and their risk factors: A qualitative study among residents of urban informal settings in Nairobi. BMJ Open 9: e026852. https://doi.org/10.1136/bmjopen-2018-026852
|
| [49] |
Roos R, Myezwa H, van Aswegen H (2015) ‘If you have a problem with your heart, you have a problem with your life’: Self-perception and behaviour in relation to the risk of ischaemic heart disease in people living with HIV. Afr J Prim Health Care Fam Med 7: 772-777. https://doi.org/10.4102/phcfm.v7i1.772
|
| [50] | Abdela OA, Ayalew MB, Yesuf JS, et al. (2019) Ethiopian university students' knowledge and perception towards cardiovascular disease risk factors: a cross sectional study. Am J Cardiovasc Dis 9: 1-7. |
| [51] |
Surka S, Steyn K, Everett-Murphy K, et al. (2015) Knowledge and perceptions of risk for cardiovascular disease: Findings of a qualitative investigation from a low-income peri-urban community in the Western Cape, South Africa. Afr J Prim Health Care Fam Med 7: 891. https://doi.org/10.4102/phcfm.v7i1.891
|
| [52] | World Heart FederationRisk Factors (2017). Available from: https://www.world-heart-federation.org/resources/risk-factors/ 2017. |
| [53] | Dhingra R, Vasan RS (2016) Age as a cardiovascular risk factor. Med Clin N 96: 87-91. https://doi.org/10.1016/j.mcna.2011.11.003 |
| [54] | Stroke StatisticsState of the Nation (2016). Available from: https://www.stroke.org.uk/sites/default/files/stroke_statistics_2015.pdf 2016. |
| [55] |
Lakatta EG, Levy D (2003) Arterial and cardiac aging: major shareholders in cardiovascular disease enterprises, part I: aging arteries: a “set up” for vascular disease. Circulation 107: 139-146. https://doi.org/10.1161/01.CIR.0000048892.83521.58
|
| [56] |
Lakatta EG, Levy D (2003) Arterial and cardiac aging: major shareholders in cardiovascular disease enterprises, part II: the aging heart in health: links to heart disease. Circulation 107: 346-354. https://doi.org/10.1161/01.CIR.0000048893.62841.F7
|
| [57] |
Kubota Y, Heiss G, MacLehose RF, et al. (2017) Association of educational attainment with lifetime risk of cardiovascular disease: The atherosclerosis risk in communities study. JAMA Intern Med 177: 1165-1172. https://doi.org/10.1001/jamainternmed.2017.1877
|
| [58] |
Muhihi AJ, Anaeli A, Mpembeni RNM, et al. (2020) Public knowledge of risk factors and warning signs for cardiovascular disease among young and middle-aged adults in rural Tanzania. BMC Public Health 20: 1832. https://doi.org/10.1186/s12889-020-09956-z
|
| [59] |
Obembe AO, Olaogun MO, Bamikole AA, et al. (2014) Awareness of risk factors and warning signs of stroke in a Nigeria university. J Stroke Cerebrovasc Dis 23: 749-758. https://doi.org/10.1016/j.jstrokecerebrovasdis.2013.06.036
|
| [60] |
Aminde LN, Takah N, Ngwasiri C, et al. (2017) Population awareness of cardiovascular disease and its risk factors in Buea, Cameroon. BMC Public Health 17: 545. https://doi.org/10.1186/s12889-017-4477-3
|
| 1. | Oluwagbohunmi A. Awosoga, Olufemi O. Oyewole, Opeyemi M. Adegoke, Adesola C. Odole, Ogochukwu K. Onyeso, Chiedozie J. Alumona, Abiodun M. Adeoye, Happiness A. Aweto, Blessing S. Ige, Adetola C. Adebayo, Titilope L. Odunaiya, Grace M. Emmanuel, Nurudeen B. Sulaimon, Nse A. Odunaiya, Hilary Izuchukwu Okagbue, Cardiovascular disease risk perception among community-dwelling adults in southwest Nigeria: A mixed-method study, 2024, 19, 1932-6203, e0313578, 10.1371/journal.pone.0313578 | |
| 2. | Margaret Bukola Fatudimu, Justina Obano, Joshua Olumayowa Ojo, Knowledge of Stroke Risk Factors, Warning Signs, Emergency Response, and Prevention among Adults in an Urban Community in Nigeria, 2025, 7, 2593-8339, 94, 10.24018/ejmed.2025.7.2.2293 | |
| 3. | Md Ripon Al Mamun, Md. Rafi, Hrittik Chakraborty, Fahmida Anjum, Raiyan Gani, Mohammad Rifat Ahmmad Rashid, Raihan Ul Islam, 2024, Cardiovascular Health Analysis: Machine Learning and Explainable AI to Predict Heart Attacks, 979-8-3315-1909-4, 768, 10.1109/ICCIT64611.2024.11022132 |
Nse A Odunaiya, Opeyemi M Adegoke, Abiodun M Adeoye, Oluwafemi O Oguntibeju. Preliminary study of perceived cardiovascular disease risk and risk status of adults in small rural and urban locations in Ibadan, Nigeria[J]. AIMS Public Health, 2023, 10(1): 190-208. doi: 10.3934/publichealth.2023015
| Peak power technique | Dependence on PV | A/D | Speed of convergence | Complexity | Sensors |
| Perturb and observe | × | A & D | Depends | Less | V, I |
| Incremental conducance | × | D | Depends | Moderate | V, I |
| Fractional open circuit voltage | √ | A & D | Moderate | Less | V |
| Fractional Short circuit current | √ | A & D | Moderate | Moderate | C |
| Fuzzy logic | √ | D | Speeder | More | Depends |
| Neural Network | √ | D | Speeder | More | Depends |
| Sliding mode control | × | D | Speeder | Moderate | V, I |
DownLoad:
CSV
|
|
NL | NS | Z | PS | PL |
| NL | Z | Z | NL | NL | NL |
| NS | Z | Z | NS | NS | NS |
| Z | NS | Z | Z | Z | PS |
| PS | PS | PS | PS | Z | Z |
| PL | PL | PL | PL | Z | Z |
DownLoad:
CSV
|
|
NH | NL | Z | PH | PL |
| NH | NH | NH | NH | NL | Z |
| NL | NH | NH | NL | Z | PL |
| Z | Z | NH | Z | PL | PH |
| PH | NS | Z | PL | PH | PH |
| PL | Z | PL | PH | PH | PH |
DownLoad:
CSV
| Parameters | Value |
| PV system (Experimental and simulation) | |
| Voc (V) (open circuit voltage) | 30.8 |
| Isc (A) (short circuit current) | 8.23 |
| Vp (V) (Peak voltage) | 24.6 |
| Ip (A) (Peak current) | 7.7 |
| Coefficient of voltage | −0.1 |
| Coefficient of current | 0.004 |
| Series modules | 6 |
| Parallel modules | 1 |
| Grid parameters | |
| Grid voltage (VRMS) (V) | 240 |
| Grid current (IRMS) (A) | 5 |
| DC voltage controller | |
| Reference DC voltage | 435 volts |
| Current controller | |
| Kp (PI) | 0.15 |
| KI (PI) | 6.6 |
| Rff | 0.002 |
| Lff | 0.20 |
| Carrier frequency | 3780 HZ |
DownLoad:
CSV
| Performance index | Fuzzy logic | Incremental conductance |
| Overshoot (%) | 0.3089 | 1.2345 |
| Damping factor (ξ) | 0.7685 | 0.5236 |
| Rise Time | 0.1254 | 0.1856 |
| Error (%) | 6.2 | 16 |
| Fluctuations in voltage | Very low | high |
| Duty cycle operation | 0.55–0.65 | 0.3–0.7 |
| Peak power point oscillations (%) | 3.2 | 1.2 |
| Handling capabi; ity of non-linearity | Comparatively low | Highly appreciable |
| In terms of cost | Comparatively high | quite low |
DownLoad:
CSV
| Peak power technique | Dependence on PV | A/D | Speed of convergence | Complexity | Sensors |
| Perturb and observe | × | A & D | Depends | Less | V, I |
| Incremental conducance | × | D | Depends | Moderate | V, I |
| Fractional open circuit voltage | √ | A & D | Moderate | Less | V |
| Fractional Short circuit current | √ | A & D | Moderate | Moderate | C |
| Fuzzy logic | √ | D | Speeder | More | Depends |
| Neural Network | √ | D | Speeder | More | Depends |
| Sliding mode control | × | D | Speeder | Moderate | V, I |
|
|
NL | NS | Z | PS | PL |
| NL | Z | Z | NL | NL | NL |
| NS | Z | Z | NS | NS | NS |
| Z | NS | Z | Z | Z | PS |
| PS | PS | PS | PS | Z | Z |
| PL | PL | PL | PL | Z | Z |
|
|
NH | NL | Z | PH | PL |
| NH | NH | NH | NH | NL | Z |
| NL | NH | NH | NL | Z | PL |
| Z | Z | NH | Z | PL | PH |
| PH | NS | Z | PL | PH | PH |
| PL | Z | PL | PH | PH | PH |
| Parameters | Value |
| PV system (Experimental and simulation) | |
| Voc (V) (open circuit voltage) | 30.8 |
| Isc (A) (short circuit current) | 8.23 |
| Vp (V) (Peak voltage) | 24.6 |
| Ip (A) (Peak current) | 7.7 |
| Coefficient of voltage | −0.1 |
| Coefficient of current | 0.004 |
| Series modules | 6 |
| Parallel modules | 1 |
| Grid parameters | |
| Grid voltage (VRMS) (V) | 240 |
| Grid current (IRMS) (A) | 5 |
| DC voltage controller | |
| Reference DC voltage | 435 volts |
| Current controller | |
| Kp (PI) | 0.15 |
| KI (PI) | 6.6 |
| Rff | 0.002 |
| Lff | 0.20 |
| Carrier frequency | 3780 HZ |
| Performance index | Fuzzy logic | Incremental conductance |
| Overshoot (%) | 0.3089 | 1.2345 |
| Damping factor (ξ) | 0.7685 | 0.5236 |
| Rise Time | 0.1254 | 0.1856 |
| Error (%) | 6.2 | 16 |
| Fluctuations in voltage | Very low | high |
| Duty cycle operation | 0.55–0.65 | 0.3–0.7 |
| Peak power point oscillations (%) | 3.2 | 1.2 |
| Handling capabi; ity of non-linearity | Comparatively low | Highly appreciable |
| In terms of cost | Comparatively high | quite low |
