Potential use of <i>Bacillus paramycoides</i> for the production of the biopolymer polyhydroxybutyrate from leftover carob fruit agro-waste

Leila DJERRAB; Zohra CHEKROUD; Amer ROUABHIA; Mohamed Abdesselem DEMS; Imane ATTAILIA; Luis Isidoro Romero GARCIA; Mustapha Adnane SMADI; Leila DJERRAB; Zohra CHEKROUD; Amer ROUABHIA; Mohamed Abdesselem DEMS; Imane ATTAILIA; Luis Isidoro Romero GARCIA; Mustapha Adnane SMADI

doi:10.3934/microbiol.2022023

AIMS Microbiology

2022, Volume 8, Issue 3: 318-337. doi: 10.3934/microbiol.2022023

Previous Article Next Article

Research article

Potential use of Bacillus paramycoides for the production of the biopolymer polyhydroxybutyrate from leftover carob fruit agro-waste

1.
Laboratory of Research on the Physical Chemistry of Surfaces and Interfaces (LRPCSI), University 20 Août 1955 Skikda, Algeria
2.
Research Laboratory of Interactions, Biodiversity, Ecosystems and Biotechnology (LRIBEB) University 20 Août 1955 Skikda, Algeria
3.
Research Laboratory of Biological Treatment of Residues, Department of Chemical Engineering and Food Technology, Institute of Vitivinicultural and Agri-food Research (IVAGRO), University of Cadiz, Spain
4.
Bioinformatics and Biostatistics Unit (BIBSU), National Center for Biotechnology, Constantine, Algeria
5.
Superior School of Food Sciences and Agro Food Industries (ESSAIA), Algiers, Algeria
6.
Director Laboratory of Biological Treatment of Residues, Department of Chemical Engineering and Food Technology University of Cadiz, Spain
7.
Laboratory of Animal Biotechnologies, National Center for Biotechnology, Constantine, Algeria

Received: 10 April 2022 Revised: 15 July 2022 Accepted: 20 July 2022 Published: 08 August 2022

This study was designed to investigate, at a laboratory scale, the possibility of valorizing the leftover carob fruits to produce the eco-friendly biopolymer polyhydroxybutyrate (PHB) by using the bacterial strain Bacillus paramycoides, which has been isolated from the botanical garden of Skikda University in Algeria. The PHB production was tested under various conditions: a pH of 3–8, temperature range of 30–44 °C, carob extracted molasses concentration of 2–8% v/v, an incubation time of 24–96 h and an agitation speed of 150–300 rpm. The effects of different nitrogen sources and carob extracted molasses treatment types were also investigated. The PHB concentration was determined quantitatively as crotonic acid by measuring the absorbance at 300 nm. Cell growth was quantified by measuring the density of the culture at 600 nm. The presence of PHB was confirmed by applying high-performance liquid chromatography (HPLC) using an Aminex HPX-87H and implementing gas chromatography analysis. The best yield of PHB synthesis was obtained by using 6% v/v of 5 M H₂SO₄ treated with carob molasses as a carbon source, with peptone as a nitrogen source; incubation was conducted at 37 °C for 96 h at an agitation speed of 300 rpm (114.95 mg/L). The HPLC analysis confirmed the synthesis of PHB by B. paramycoides to have a chromatogram retention time of 22.5 min. Carob waste was successfully valorized to PHB.

Keywords:

Citation: Leila DJERRAB, Zohra CHEKROUD, Amer ROUABHIA, Mohamed Abdesselem DEMS, Imane ATTAILIA, Luis Isidoro Romero GARCIA, Mustapha Adnane SMADI. Potential use of Bacillus paramycoides for the production of the biopolymer polyhydroxybutyrate from leftover carob fruit agro-waste[J]. AIMS Microbiology, 2022, 8(3): 318-337. doi: 10.3934/microbiol.2022023

Related Papers:

[1]	Ziphozethu Ndlazi, Oualid Abboussi, Musa Mabandla, Willie Daniels . Memantine increases NMDA receptor level in the prefrontal cortex but fails to reverse apomorphine-induced conditioned place preference in rats. AIMS Neuroscience, 2018, 5(4): 211-220. doi: 10.3934/Neuroscience.2018.4.211
[2]	Chris Cadonic, Benedict C. Albensi . Oscillations and NMDA Receptors: Their Interplay Create Memories. AIMS Neuroscience, 2014, 1(1): 52-64. doi: 10.3934/Neuroscience.2014.1.52
[3]	Nao Fukuwada, Miki Kanno, Satomi Yoshida, Kenjiro Seki . Gαq protein signaling in the bed nucleus of the stria terminalis regulate the lipopolysaccharide-induced despair-like behavior in mice. AIMS Neuroscience, 2020, 7(4): 438-458. doi: 10.3934/Neuroscience.2020027
[4]	Md. Mamun Al-Amin, Robert K. P. Sullivan, Suzy Alexander, David A. Carter, DanaKai Bradford, Thomas H. J. Burne . Impaired spatial memory in adult vitamin D deficient BALB/c mice is associated with reductions in spine density, nitric oxide, and neural nitric oxide synthase in the hippocampus. AIMS Neuroscience, 2022, 9(1): 31-56. doi: 10.3934/Neuroscience.2022004
[5]	Robert A. Moss, Jarrod Moss . The Role of Dynamic Columns in Explaining Gamma-band Synchronization and NMDA Receptors in Cognitive Functions. AIMS Neuroscience, 2014, 1(1): 65-88. doi: 10.3934/Neuroscience.2014.1.65
[6]	Nisha Shantakumari, Musaab Ahmed . Whole body vibration therapy and cognitive functions: a systematic review. AIMS Neuroscience, 2023, 10(2): 130-143. doi: 10.3934/Neuroscience.2023010
[7]	Valentina Bashkatova, Athineos Philippu . Role of nitric oxide in psychostimulant-induced neurotoxicity. AIMS Neuroscience, 2019, 6(3): 191-203. doi: 10.3934/Neuroscience.2019.3.191
[8]	Tevzadze Gigi, Zhuravliova Elene, Barbakadze Tamar, Shanshiashvili Lali, Dzneladze Davit, Nanobashvili Zaqaria, Lordkipanidze Tamar, Mikeladze David . Gut neurotoxin p-cresol induces differential expression of GLUN2B and GLUN2A subunits of the NMDA receptor in the hippocampus and nucleus accumbens in healthy and audiogenic seizure-prone rats. AIMS Neuroscience, 2020, 7(1): 30-42. doi: 10.3934/Neuroscience.2020003
[9]	Toshihiko Kinjo, Shun Ebisawa, Tatsuya Nokubo, Mifu Hashimoto, Takonori Yamada, Michiko Oshio, Ruka Nakamura, Kyosuke Uno, Nobuyuki Kuramoto . Post-translational modifications of the apelin receptor regulate its functional expression. AIMS Neuroscience, 2023, 10(4): 282-299. doi: 10.3934/Neuroscience.2023022
[10]	Nicholas J. D. Wright . A review of the direct targets of the cannabinoids cannabidiol, Δ9-tetrahydrocannabinol, N-arachidonoylethanolamine and 2-arachidonoylglycerol. AIMS Neuroscience, 2024, 11(2): 144-165. doi: 10.3934/Neuroscience.2024009

Abstract

1. Introduction

A matrix $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ is called a strictly diagonally dominant (SDD) matrix if

$\begin{eqnarray} |a_{ii}| > r_i(A) \end{eqnarray}$

(1.1)

for all $i\in N: = \{1, \ldots, n\}$ , where $r_i(A) = \sum\limits_{j\in N\setminus\{i\}} |a_{ij}|$ .

The concept of SDD originated from the well-known Lévy-Desplanques Theorem ^[1], which states that if condition (1.1) holds, then $A$ is nonsingular, i.e., SDD matrices are nonsingular. It is well known that the class of SDD matrices has wide applications in many fields of scientific computing, such as the Schur complement problem ^[2,3], eigenvalue localizations ^{[4,5,6,7,8,9,10]}, convergence analysis of the parallel-in-time iterative method ^[11], estimating the infinity norm for the inverse of $H$ -matrices ^{[12,13,14,15]}, error bound for linear complementarity problems ^[16,17], structure tensors ^[18,19], etc.

Some well-known matrices have been presented and studied ^[4,7,20] by breaking the diagonal dominance condition (1.1). For instance, by allowing at most one row to be non-SDD, Ostrowski introduced the class of Ostrowski matrices ^[20] (also known as doubly strictly diagonally dominant (DSDD) matrices). Here, a matrix $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ is an Ostrowski matrix ^[20] if for all $j\neq i$ ,

$\begin{eqnarray*} |a_{ii}||a_{jj}| > r_i(A)r_j(A). \end{eqnarray*}$

In addition, based on the partition-based approach that allows more than one row to be non-SDD, a well-known class of matrices called $S$ -SDD matrices has been proposed and studied ^[7,21].

Definition 1.1. ^[7,21] Let $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ and $S$ be a nonempty proper subset of $N$ . Then, a matrix $A$ is called an $S$ -SDD matrix if

$\begin{align*} \left\{ \begin{array}{ll} |a_{ii}| > r_i^{S}(A), i\in S, \\ \big(|a_{ii}|-r_i^{S}(A)\big)\big(|a_{jj}|-r_j^{\overline{S}}(A)\big) > r_i^{\overline{S}}(A)r_j^{S}(A), i\in S, j\in\overline{S}, \end{array} \right. \end{align*}$

where $r_i^S(A) = \sum\limits_{j\in S\setminus \{i\}}|a_{ij}|$ .

Besides DSDD matrices and $S$ -SDD matrices, there are many generalizations of SDD matrices, such as Nekrasov matrices ^[22,23], $DZ$ -type matrices ^[24], CKV-type matrices ^[25] and so on.

Observe from Definition 1.1 that $S$ -SDD matrices only consider the effect of "interaction" between $i\in S$ and $j\in \overline{S}$ on the nonsingular. However, other "interaction, " such as the "constraint condition" between $i\in S$ ( $i\in \overline{S}$ ) and $j\in S$ ( $j\in \overline{S}$ ) with $i\neq j$ , might also affect the non-singularity of the matrix. Naturally, an interesting question arises: When we consider this "constraint condition, " can we get the non-singularity of the matrix? To answer this question, in this paper, we introduce a new class of nonsingular matrices arising from this "constraint condition" and show several benefits from this new class of matrices, which we will call partially doubly strictly diagonally dominant matrices.

This paper is organized as follows. In Section 2, we present a new class of matrices called PDSDD matrices and prove that it is a subclass of nonsingular $H$ -matrices, which is similar to, but different from, the class of $S$ -SDD matrices. Section 3 gives a new eigenvalue localization set for matrices and presents an infinity norm bound for the inverse of PDSDD matrices. It is proved that the obtained bound is better than the well-known Varah's bound for SDD matrices. Based on this infinity norm bound, we also obtain a new pseudospectra localization for matrices and apply it to measure the distance to instability. Finally, we give concluding remarks in Section 4.

2. Partially doubly strictly diagonally dominant matrices

We start with some preliminaries and definitions. Let $\mathbb{Z}^{n\times n}$ be the set of all matrices $A = [a_{ij}]\in \mathbb{R}^{n\times n}$ with $a_{ij}\leq 0$ and $i\neq j$ . A matrix $A\in\mathbb{Z}^{n\times n}$ is called a nonsingular $M$ -matrix if its inverse is nonnegative, i.e., $A^{-1}\geq 0$ ^[26]. A matrix $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ is called a nonsingular $H$ -matrix ^[26] if its comparison matrix $\mathcal{M}(A) = [m_{ij}]\in \mathbb{R}^{n\times n}$ defined by

$m_{ij} = \left\{ \begin{array}{cc} |a_{ij}|, &i = j, \\ -|a_{ij}|, &i\neq j, \end{array} \right.$

is a nonsingular $M$ -matrix. Let $|N|$ be the cardinality of set $N$ .

In the following, we define a new class of matrices called PDSDD matrices.

Definition 2.1. Let $S$ be a subset of $N$ and $\overline{S}$ be the complement of $S$ . Given a matrix $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ , for each subset $\Delta \in \{S, \overline{S}\}$ , denote $\Delta_{-}: = \{i\in \Delta|a_{ii}\leq r_i(A)\}$ and $\Delta_{+}: = \{i\in \Delta|a_{ii} > r_i(A)\}$ . Then, a matrix $A$ is called a partially doubly strictly diagonally dominant (PDSDD) matrix if for each $\Delta \in \{S, \overline{S}\}$ either $|\Delta_{-}| = 0$ or $|\Delta_{-}| = 1$ , and for $i\in \Delta_{-}$ ,

$\begin{align} \left\{ \begin{array}{ll} |a_{ii}| > r_i^{\overline{\Delta}}(A), \\ \big(|a_{ii}|-r_i^{\overline{\Delta}}(A)\big)\big(|a_{jj}|-r_j^{\Delta}(A)+|a_{ji}|\big) > r_i^{\Delta}(A)(r_j^{\overline{\Delta}}(A)+|a_{ji}|), &j\in \Delta_{+}, \end{array} \right. \end{align}$

(2.1)

where $r_i^\Delta(A) = \sum\limits_{j\in \Delta\setminus \{i\}}|a_{ij}|$ .

Note that the class of DSDD matrices allows at most one row to be non-SDD, whereas the class of matrices defined in Definition 2.1 allows at most one row to be non-SDD in each subset $\Delta\in \{S, \overline{S}\}$ . For this reason, we call it the class of PDSDD matrices.

The following theorem provides that the class of PDSDD matrices is a subclass of nonsingular $H$ -matrices.

Theorem 2.1. Every PDSDD matrix is a nonsingular $H$ -matrix.

Proof. According to the well-known result that SDD matrices are nonsingular $H$ -matrices, it is sufficient to consider the case that $A$ has one or two non-SDD rows. Assume, on the contrary, that $A$ is a singular matrix, and then there exists a nonzero eigenvector ${\bf x} = [x_1, x_2, \ldots, x_n]^T$ corresponding to 0 eigenvalue such that

$\begin{eqnarray} A{\bf x} = 0. \end{eqnarray}$

(2.2)

Let $|x_p|: = \max\limits_{i\in N}\{|x_i|\}$ . Then, $|x_p| > 0$ , and $p\in \Delta\cup \overline{\Delta}$ , where $\Delta\in \{S, \overline{S}\}$ . Without loss of generality, we assume that $\Delta = S$ . Next, we need only consider the case $p\in S$ , and another case $p\in \overline{S}$ can be proved similarly. For $p\in S$ , it follows from Definition 2.1 that $p\in S_{-}\cup S_{+}$ , where $S_{-}: = \{i\in S|a_{ii}\leq r_i(A)\}$ and $S_{+}: = \{i\in S|a_{ii} > r_i(A)\}$ .

If $p\in S_{-}$ , then by Definition 2.1 we have

$\begin{align} |a_{pp}| > r_p^{\overline{S}}(A), \end{align}$

(2.3)

and for all $j\in S_{+}$ ,

$\begin{align} \big(|a_{pp}|-r_p^{\overline{S}}(A)\big)\big(|a_{jj}|-r_j^{S}(A)+|a_{jp}|\big) > r_p^{S}(A)(r_j^{\overline{S}}(A)+|a_{jp}|). \end{align}$

(2.4)

Note that $|S_{-}| = 1$ . Then, $S\setminus \{p\} = S_+$ . Let $|x_q|: = \max\limits_{k\in S\setminus \{p\}}\{|x_k|\}$ . Considering the $p$ -th equality of (2.2), we have

$\begin{eqnarray*} a_{pp}x_p = -\sum\limits_{k\neq p, k\in S}a_{pk}x_k-\sum\limits_{k\neq p, k\in \overline{S}}a_{pk}x_k. \end{eqnarray*}$

Taking the modulus in the above equation and using the triangle inequality yields

$\begin{align*} |a_{pp}||x_p|&\leq\sum\limits_{k\neq p, k\in S}|a_{pk}||x_k|+\sum\limits_{k\neq p, k\in \overline{S}}|a_{pk}||x_k| \\&\leq\sum\limits_{k\neq p, k\in S}|a_{pk}||x_q|+\sum\limits_{k\neq p, k\in \overline{S}}|a_{pk}||x_p| \\& = r_p^{S}(A)|x_q|+r_p^{\overline{S}}(A)|x_{p}|, \end{align*}$

which implies that

$\begin{eqnarray} (|a_{pp}|-r_p^{\overline{S}}(A))|x_p|\leq r_p^{S}(A)|x_{q}|. \end{eqnarray}$

(2.5)

If $|x_{q}| = 0$ , then $|a_{pp}|-r_p^{\overline{S}}(A)\leq0$ as $|x_p| > 0$ , which contradicts (2.3). If $|x_{q}|\neq0$ , then from the $q$ -th equality of (2.2), we obtain

$\begin{align*} |a_{qq}||x_q|&\leq\sum\limits_{k\neq q, k\in S}|a_{qk}||x_k|+\sum\limits_{k\neq q, k\in \overline{S}}|a_{qk}||x_k| \\&\leq\bigg(\sum\limits_{k\neq q, k\in S}|a_{qk}|-|a_{qp}|\bigg)|x_q|+\bigg(\sum\limits_{k\neq q, k\in \overline{S}}|a_{qk}|+|a_{qp}|\bigg)|x_p| \\& = (r_q^{S}(A)-|a_{qp}|)|x_q|+(r_q^{\overline{S}}(A)+|a_{qp}|)|x_{p}|, \end{align*}$

i.e.,

$\begin{eqnarray} (|a_{qq}|-r_q^{S}(A)+|a_{qp}|)|x_q|\leq (r_q^{\overline{S}}(A)+|a_{qp}|)|x_{p}|. \end{eqnarray}$

(2.6)

Multiplying (2.6) with (2.5) and dividing by $|x_p||x_{q}| > 0$ , we have

$\begin{eqnarray*} (|a_{pp}|-r_p^{\overline{S}}(A))(|a_{qq}|-r_q^{S}(A)+|a_{qp}|)\leq r_p^{S}(A)(r_q^{\overline{S}}(A)+|a_{qp}|), \end{eqnarray*}$

which contradicts (2.4).

If $p\in S_{+}$ , then $|a_{pp}| > r_p(A)$ . Considering the $p$ -th equality of (2.2) and using the triangle inequality, we obtain

$\begin{align*} |a_{pp}||x_p|\leq\sum\limits_{k\neq p}|a_{pk}||x_k|\leq r_p(A)|x_p|, \end{align*}$

i.e., $|a_{pp}|\leq r_p(A)$ , which contradicts $|a_{pp}| > r_p(A)$ . Hence, we can conclude that 0 is not an eigenvalue of $A$ , that is, $A$ is a nonsingular matrix.

We next prove that $A$ is a nonsingular $H$ -matrix. For any $\varepsilon\geq 0$ , let

$B_\varepsilon = \mathcal{M}(A)+\varepsilon I = [b_{ij}].$

Note that $b_{ii} = |a_{ii}|+\varepsilon$ , $b_{ij} = -|a_{ij}|$ , and $B_\varepsilon\in \mathbb{Z}^{n\times n}$ . Then, $\Delta_{-}(B_\varepsilon)\subseteq \Delta_{-}(A)$ , and $\Delta_{+}(A)\subseteq\Delta_{+}(B_\varepsilon)$ . If $A$ is an SDD matrix, then $\Delta_{-}(A) = \emptyset$ , and thus $\Delta_{-}(B_\varepsilon) = \emptyset$ , which implies that $B_\varepsilon$ is an SDD matrix. If $A$ is not an SDD matrix, then $|\Delta_{-}(A)| = 1$ for some $\Delta\in \{S, \overline{S}\}$ . For this case, $|\Delta_{-}(B_\varepsilon)| = 0$ or $|\Delta_{-}(B_\varepsilon)| = 1$ . If $|\Delta_{-}(B_\varepsilon)| = 0$ for each $\Delta\in \{S, \overline{S}\}$ , then $B_\varepsilon$ is also an SDD matrix. If $|\Delta_{-}(B_\varepsilon)| = 1$ for some $\Delta\in \{S, \overline{S}\}$ , then $\Delta_{-}(B_\varepsilon) = \Delta_{-}(A)$ and $\Delta_{+}(B_\varepsilon) = \Delta_{+}(A)$ . Hence, for $i\in \Delta_{-}(B_\varepsilon)$ ,

$\begin{eqnarray*} |b_{ii}|-r_{i}^{\overline{\Delta}}(B_\varepsilon) = |a_{ii}|+\varepsilon-r_{i}^{\overline{\Delta}}(A) > 0, \end{eqnarray*}$

and for all $j\in \Delta_{+}(B_\varepsilon)$ ,

$\begin{equation*} \begin{aligned} (|b_{ii}|-r_{i}^{\overline{\Delta}}(B_\varepsilon))(|b_{jj}|-r_{j}^{\Delta}(B_\varepsilon)+|b_{ji}|) & = (|a_{ii}|+\varepsilon-r_{i}^{\overline{\Delta}}(A))(|a_{jj}|+\varepsilon-r_{j}^{\Delta}(A)+|a_{ji}|) \\&\geq(|a_{ii}|-r_{i}^{\overline{\Delta}}(A))(|a_{jj}|-r_{j}^{\Delta}(A)+|a_{ji}|) \\& > r_i^{\Delta}(A)(r_j^{\overline{\Delta}}(A)+|a_{ji}|) \\& = r_i^{\overline{\Delta}}(B_\varepsilon)(r_j^{\Delta}(B_\varepsilon)+|b_{ji}|). \end{aligned} \end{equation*}$

Therefore, $B_\varepsilon$ is a PDSDD matrix and thus nonsingular for each $\varepsilon\geq 0$ . This implies that $\mathcal{M}(A)$ is a nonsingular $M$ -matrix (see the condition ( $D_{15}$ ) of Theorem 2.3 in [, Chapter 6]). Therefore, $A$ is a nonsingular $H$ -matrix. The proof is complete.

Proposition 2.1. Every DSDD matrix is a PDSDD matrix.

Proof. If $A$ is an SDD matrix, then $A$ is a PDSDD matrix. If $A$ is not an SDD matrix, then by the assumptions it holds that there exists $i_0\in N$ such that $|a_{i_0i_0}|\leq r_{i_0}(A)$ and

$|a_{i_0i_0}||a_{jj}| > r_{i_0}(A)r_j(A)\; \text{for all}\; j\neq i_0.$

Taking $S = N$ , we have $r_i^{\overline{S}}(A) = 0$ and $r_i^{S}(A) = r_i(A)$ for all $i\in N$ . This implies that for all $j\in S\setminus \{i_0\}$ ,

$\begin{align*} &\big(|a_{i_0i_0}|-r_{i_0}^{\overline{S}}(A)\big)\big(|a_{jj}|-r_j^{S}(A)+|a_{ji_0}|\big)-r_{i_0}^{S}(A)(r_j^{\overline{S}}(A)+|a_{ji_0}|) \\& = |a_{i_0i_0}|(|a_{jj}|-r_j(A)+|a_{ji_0}|)-r_{i_0}(A)|a_{ji_0}| \\& = |a_{i_0i_0}||a_{jj}|-|a_{i_0i_0}|(r_j(A)-|a_{ji_0}|)-r_{i_0}(A)|a_{ji_0}| \\&\geq|a_{i_0i_0}||a_{jj}|-r_{i_0}(A)(r_j(A)-|a_{ji_0}|+|a_{ji_0}|) \\& = |a_{i_0i_0}||a_{jj}|-r_{i_0}(A)r_j(A) \\& > 0. \end{align*}$

Hence, by Definition 2.1, we conclude that $A$ is a PDSDD matrix. The proof is complete.

Next, we give an example to show that neither PDSDD matrices nor $S$ -SDD matrices are included in each other.

Example 2.1. Consider the following matrices:

$A = \left[ \begin{array}{cccc} 3 &-1 &-3 &0 \\ -1 &3 &0 &-8 \\ 0 &-1 &3 &0\\ 0 & 0 &0 & 8 \end{array} \right], \; B = \left[ \begin{array}{cccc} 3 &0 &0 &-3 \\ 0 &3 &0 &-3 \\ 0 &0 &3 &-3\\ 0 & 0 &0 & 8 \end{array} \right].$

By calculation, we know that $A$ is a PDSDD matrix for $S = \{1, 3\}$ , but it is not an $S$ -SDD matrix for any nonempty proper subset $S$ of $N$ and thus not a DSDD matrix. Meanwhile, $B$ is an $S$ -SDD matrix for $S = \{1, 2, 3\}$ , but it is not a PDSDD matrix, because $B$ has three non-SDD rows.

According to Theorem 2.1, Proposition 2.1 and Example 2.1, the relations among DSDD matrices, PDSDD matrices, $S$ -SDD matrices and $H$ -matrices can be depicted as follows:

$\{\text{PDSDD}\}\subset\{H\}, \; \{\text{PDSDD}\}\not\subset\{S\text{-SDD}\}, \; \{\text{S-SDD}\}\not\subset\{\text{PDSDD}\},$

and

$\{\text{DSDD}\}\subset\{\text{PDSDD}\}\cap\{\text{S-SDD}\}.$

3. Some possible applications

3.1. A new eigenvalue localization set for matrices

It is well known that the non-singularity of matrices can generate the equivalent eigenvalue inclusion set in the complex plane ^[4,5,7,9,24]. By the non-singularity of PDSDD matrices, we in this section give a new eigenvalue localization set for matrices. Before that, an equivalent condition for the definition of PDSDD matrices is given, which can be proved immediately from Definition 2.1.

Lemma 3.1. Let $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ and $\{S, \overline{S}\}$ be a partition of the set $N$ . A matrix $A$ is called a PDSDD matrix if and only if $S^\star$ is not empty unless $S$ is empty, and $\overline{S}^\star$ is not empty unless $\overline{S}$ is empty, where

$\begin{eqnarray*} S^{\star}: = \bigg\{i\in S:|a_{ii}| > r_i^{\overline{S}}(A), \; {{and\; for\; all}}\; j\in S\setminus\{i\}, \; |a_{jj}| > r_j(A) \; \mathit{\text{and}}\\\big(|a_{ii}|-r_i^{\overline{S}}(A)\big)\big(|a_{jj}|-r_j^{S}(A)+|a_{ji}|\big) > r_i^{S}(A)(r_j^{\overline{S}}(A)+|a_{ji}|)\bigg\}, \end{eqnarray*}$

and

$\begin{eqnarray*} \overline{S}^{\star}: = \bigg\{i\in \overline{S}:|a_{ii}| > r_i^{S}(A), \; {{and\; for\; all}}\; j\in \overline{S}\setminus\{i\}, \; |a_{jj}| > r_j(A) \; \mathit{\text{and}}\\\; \big(|a_{ii}|-r_i^{S}(A)\big)\big(|a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji}|\big) > r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|)\bigg\} \end{eqnarray*}$

with $r_i^S(A) = \sum\limits_{j\in S\setminus \{i\}}|a_{ij}|$ .

By Lemma 3.1, we can obtain the following theorem.

Theorem 3.1. Let $A = [a_{ij}] \in \mathbb{C}^{n\times n}$ and $S$ be any subset of $N$ . Then,

$\begin{eqnarray*} \sigma(A)\subseteq \Theta^{S}(A): = \theta^{S}(A)\bigcup\theta^{\overline{S}}(A), \end{eqnarray*}$

where $\sigma(A)$ is the set of all the eigenvalues of $A$ ,

$\theta^{S}(A) = \bigcap\limits_{i\in S}\left(\Gamma_i^{\overline{S}}(A)\right)\bigcup\left(\bigcup\limits_{j\in S\setminus \{i\}}\big(\widehat{V}_{ij}^{\overline{S}}(A)\cup\Gamma_j(A)\big)\right)$

and

$\theta^{\overline{S}}(A) = \bigcap\limits_{i\in \overline{S}}\left(\Gamma_i^{S}(A)\right)\bigcup\left(\bigcup\limits_{j\in \overline{S}\setminus \{i\}}\big(\widehat{V}_{ij}^{S}(A)\cup\Gamma_j(A)\big)\right)$

with

$\Gamma_i^{S}(A): = \left\{z\in \mathbb{C}:|z-a_{ii}|\leq r_i^{S}(A)\right\}, \; \Gamma_j(A): = \left\{z\in \mathbb{C}:|z-a_{jj}|\leq r_j(A)\right\},$

and

$\begin{eqnarray*} \widehat{V}_{ij}^{S}(A): = \left\{z\in \mathbb{C}:(|z-a_{ii}|-r_i^{S}(A))(|z-a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji}|)\right.\\ \left.\leq r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|)\right\}. \end{eqnarray*}$

Proof. Without loss of generality, we assume that $S$ is a nonempty subset of $N$ . For the case of $S = \emptyset$ , we have $\Theta^{S}(A) = \theta^{\overline{S}}(A)$ , and the conclusion can be proved similarly. Suppose, on the contrary, that there exists an eigenvalue $\lambda$ of $A$ such that $\lambda\notin\Theta^{S}(A)$ , that is, $\lambda\notin\theta^{S}(A)$ and $\lambda\notin\theta^{\overline{S}}(A)$ . For $\lambda\notin\theta^{S}(A)$ , there exists an index $i\in S$ such that $\lambda\notin \Gamma_i^{\overline{S}}(A)$ , and for all $j\in S\setminus \{i\}$ , $\lambda\notin \Gamma_j(A)$ and $\lambda\notin \widehat{V}_{ij}^{\overline{S}}(A)$ , that is, $|\lambda-a_{ii}| > r_i^{\overline{S}}(A)$ , $|\lambda-a_{jj}| > r_j(A)$ , and

$\begin{eqnarray*} (|\lambda-a_{ii}|-r_i^{\overline{S}}(A))(|\lambda-a_{jj}|-r_j^{S}(A)+|a_{ji}|) > r_i^{S}(A)(r_j^{\overline{S}}(A)+|a_{ji}|). \end{eqnarray*}$

Similarly, for $\lambda\notin\theta^{\overline{S}}(A)$ , there exists an index $i\in \overline{S}$ such that $\lambda\notin \Gamma_i^{S}(A)$ , and for all $j\in \overline{S}\setminus \{i\}$ , $\lambda\notin \Gamma_j(A)$ and $\lambda\notin \widehat{V}_{ij}^{S}(A)$ , that is, $|\lambda-a_{ii}| > r_i^{S}(A)$ , $|\lambda-a_{jj}| > r_j(A)$ , and

$\begin{eqnarray*} (|\lambda-a_{ii}|-r_i^{S}(A))(|\lambda-a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji}|) > r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|). \end{eqnarray*}$

These imply that $S^{\star}(\lambda I-A)$ and $\overline{S}^{\star}(\lambda I-A)$ are not empty. It follows from Lemma 3.1 that $\lambda I-A$ is a PDSDD matrix. Then, by Theorem 2.1, $\lambda I-A$ is nonsingular, which contradicts that $\lambda$ is an eigenvalue of $A$ . Hence, $\lambda\in\Theta^{S}(A)$ . This completes the proof.

Remark 3.1. Take the intersection over all possible subsets $S$ of $N$ , and we can get a satisfactory eigenvalue localization although it has more computation costs:

$\begin{eqnarray*} \sigma(A)\subseteq \Theta(A): = \bigcap \limits_{S\subseteq N}\Theta^{S}(A). \end{eqnarray*}$

To compare our set $\Theta(A)$ with the Geršgorin disks $\Gamma(A)$ in ^[8], Brauer's ovals of Cassini $\mathcal{K}(A)$ in ^[27] and the Cvetković-Kostić-Varga eigenvalue localization set $\mathcal{C}(A)$ in ^[7], }let us recall the definitions of $\Gamma(A)$ , $\mathcal{K}(A)$ and $\mathcal{C}(A)$ as follows.

Theorem 3.2. ^[8] Let $A = [a_{ij}]\in \mathbb{C}^{n \times n}$ and $\sigma(A)$ be the set of all eigenvalues of $A$ . Then,

$\begin{equation*} \sigma(A)\subseteq \Gamma(A): = \mathop \bigcup \limits_{i \in N} \Gamma_i(A), \end{equation*}$

where $\Gamma_i(A) = \{ z \in \mathbb{C}:|{a_{ii}} - z| \le {r_i}(A) \}$ .

Theorem 3.3. ^[27] Let $A = [a_{ij}]\in \mathbb{C}^{n \times n}$ and $\sigma(A)$ be the set of all eigenvalues of $A$ . Then,

$\begin{equation*} \sigma(A)\subseteq{\mathcal{K} }(A): = \mathop \bigcup \limits_{i, j\in N, i \ne j} \mathcal{K}_{ij}(A), \end{equation*}$

where $\mathcal{K}_{ij}(A) = \{ z \in \mathbb{C}:|{a_{ii}} - z||{a_{jj}} - z| \le {r_i}(A){r_j}(A)\}$ .

Theorem 3.4. ^[7] Let $S$ be any nonempty proper subset of $N$ , and $n\geq 2$ . Then, for any $A = [a_{ij}] \in \mathbb{C}^{n\times n}$ , all the eigenvalues of $A$ belong to set

$\begin{eqnarray*} \mathcal{C}^{S}(A) = \left(\bigcup\limits_{i\in S}\Gamma_i^{S}(A)\right)\bigcup\left(\bigcup\limits_{i\in S, j\in \overline{S}}V_{ij}^{S}(A)\right), \end{eqnarray*}$

and hence

$\begin{eqnarray*} \sigma(A)\subseteq \mathcal{C}(A): = \bigcap\limits_{S\subset N, S\neq\emptyset, S\neq N}\mathcal{C}^{S}(A), \end{eqnarray*}$

where $\Gamma_i^S(A)$ is given by Theorem 3.1, and

$\begin{eqnarray*} V_{ij}^{S}(A): = \left\{z\in \mathbb{C}:(|z-a_{ii}|-r_i^{S}(A))(|z-a_{jj}|-r_j^{\overline{S}}(A))\leq r_i^{\overline{S}}(A)r_j^{S}(A)\right\}. \end{eqnarray*}$

Remark 3.2. Observe that the class of SDD matrices is a subclass of DSDD matrices, which is a subclass of of PDSDD matrices. Hence, the corresponding set $\Theta(A)$ will contain Brauer's ovals of Cassini $\mathcal{K}(A)$ , which contains the Geršgorin disks $\Gamma(A)$ , that is,

$\Theta(A)\subseteq\mathcal{K}(A)\subseteq \Gamma(A).$

In addition, because PDSDD class and $S$ -SDD class do not contain each other, it follows that the relation between $\Theta(A)$ and $\mathcal{C}(A)$ is

$\Theta(A)\not\subset\mathcal{C}(A)\; \text{and}\; \mathcal{C}(A)\not\subset\Theta(A).$

3.2. An infinity norm bound for the inverse of PDSDD matrices

In this section, we consider the infinity norm bounds for the inverse of PDSDD matrices, since it might be used for the convergence analysis of matrix splitting and matrix multi-splitting iterative methods for solving large sparse systems of linear equations, linear complementarity problems and pseudospectra localizations.

Theorem 3.5. Let $A = [a_{ij}] \in \mathbb{C}^{n\times n}$ be a PDSDD matrix. Then,

$\begin{eqnarray} ||A^{-1}||_{\infty}\leq \max\left\{\min\limits_{i\in S^\star}\max\left\{\frac{1}{|a_{ii}|-r_i^{\overline{S}}(A)}, \varphi_i^{S}(A)\right\}, \min\limits_{i\in \overline{S}^\star}\max\left\{\frac{1}{|a_{ii}|-r_i^{S}(A)}, \varphi_i^{\overline{S}}(A)\right\}\right\}, \end{eqnarray}$

(3.1)

where $S^\star$ and $\overline{S}^\star$ are defined by Lemma 3.1,

$\varphi_i^{S}(A): = \max\limits_{j\in S\setminus \{i\}}\left\{\mathcal{X}_{ij}^{S}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}$

with

$\mathcal{X}_{ij}^{S}(A): = \frac{|a_{jj}|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)}{(|a_{ii}|-r_i^{\overline{S}}(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|)}.$

Proof. According to a well-known fact (see ^[10,30]),

$\begin{eqnarray*} ||A^{-1}||_{\infty}^{-1} = \inf\limits_{{\bf x}\neq 0}\frac{||A{\bf x}||_{\infty}}{||{\bf x}||_{\infty}} = \min\limits_{||{\bf x}||_{\infty} = 1}||A{\bf x}||_{\infty} = ||A{\bf x}^{*}||_{\infty} = \max\limits_{i\in N}|(A{\bf x}^{*})_i| \end{eqnarray*}$

for some ${\bf x}^{*} = [x_1^{*}, x_2^{*}, \ldots, x_n^{*}]^{T}$ such that $||{\bf x}||_{\infty} = 1$ . Denote $|x_p^{*}| = ||{\bf x}||_{\infty} = 1$ . It follows that

$\begin{eqnarray*} ||A^{-1}||_{\infty}^{-1}\geq|(A{\bf x}^{*})_p|. \end{eqnarray*}$

Consider the $p$ -th row of $Ax^*$ , and we have

$\begin{eqnarray} (A{\bf x}^{*})_p = a_{pp}x_p^{*}+\sum\limits_{j\neq p}a_{pj}x_j^{*}. \end{eqnarray}$

(3.2)

Since $A$ is a PDSDD matrix, it follows from Lemma 3.1 that $S^\star$ is not empty unless $S$ is empty, and $\overline{S}^\star$ is not empty unless $\overline{S}$ is empty. We only consider the case both $S$ and $\overline{S}$ are not empty, and the case of $S = \emptyset$ or $\overline{S} = \emptyset$ can be proved similarly.

The first case. Suppose that either $S$ or $\overline{S}$ is a singleton set. We assume that $S = \{k\}$ . Then, $\overline{S} = N\setminus\{k\}$ , and from Lemma 3.1 it holds that $S^\star$ is not empty and $\overline{S}^\star$ is not empty, that is,

$|a_{kk}| > r_k^{\overline{S}}(A) = r_k(A).$

For each $i_0\in \overline{S}^\star$ , $|a_{i_0i_0}| > r_{i_0}^{S}(A)$ , and for all $j\in \overline{S}\setminus \{i_0\}$ ,

$\begin{align} \big(|a_{i_0i_0}|-r_{i_0}^{S}(A)\big)\big(|a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji_0}|\big) > r_{i}^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji_0}|). \end{align}$

(3.3)

Note that $p\in S\cup \overline{S}$ . If $p\in S = \{k\}$ , then

$\begin{align*} |a_{pp}|&\leq|(A{\bf x}^{*})_p|+r_p(A), \end{align*}$

and

$||A^{-1}||_{\infty}^{-1}\geq|(A{\bf x}^{*})_p|\geq|a_{pp}|-r_p(A) > 0.$

Hence,

$\begin{align} ||A^{-1}||_{\infty}&\leq\frac{1}{|a_{pp}|-r_p(A)} = \frac{1}{|a_{kk}|-r_k^{\overline{S}}(A)}. \end{align}$

(3.4)

If $p\in \overline{S}$ , then $p = i_0$ or $p\neq i_0$ , where $i_0\in \overline{S}^\star$ . If $p = i_0$ , then let $|x_{q}^{*}| = \max\limits_{j\in \overline{S}\setminus\{p\}}\{|x_j^{*}|\}$ . By (3.2), it follows that

$\begin{eqnarray*} a_{pp}x_p^{*} = (A{\bf x}^{*})_p-\sum\limits_{j\neq p, j\in S}a_{pj}x_j^{*}-\sum\limits_{j\neq p, j\in \overline{S}}a_{pj}x_j^{*}, \end{eqnarray*}$

and taking absolute values on both sides and using the triangle inequality, we get

$\begin{align*} |a_{pp}||x_p^{*}|&\leq|(A{\bf x}^{*})_p|+\sum\limits_{j\neq p, j\in S}|a_{pj}||x_j^{*}|+\sum\limits_{j\neq p, j\in \overline{S}}|a_{pj}||x_j^{*}| \\&\leq|(A{\bf x}^{*})_p|+\sum\limits_{j\neq p, j\in S}|a_{pj}||x_p^{*}|+\sum\limits_{j\neq p, j\in \overline{S}}|a_{pj}||x_{q}^{*}| \\&\leq||A^{-1}||_{\infty}^{-1}+r_p^{S}(A)|x_p^{*}|+r_p^{\overline{S}}(A)|x_{q}^{*}|, \end{align*}$

which implies that

$\begin{eqnarray} |a_{pp}|-||A^{-1}||_{\infty}^{-1}-r_p^{S}(A)\leq r_p^{\overline{S}}(A)|x_{q}^{*}|. \end{eqnarray}$

(3.5)

Consider the $q$ -th row of $A{\bf x}^{*}$ , and we have

$\begin{eqnarray*} (A{\bf x}^{*})_{q} = a_{qq}x_{q}^{*}+\sum\limits_{j\neq q}a_{qj}x_j^{*}. \end{eqnarray*}$

It follows that

$\begin{align*} |a_{qq}||x_{q}^{*}|&\leq|(A{\bf x}^{*})_{q}|+\left(\sum\limits_{j\neq q, j\in \overline{S}}|a_{qj}|-|a_{qp}|\right)|x_q^{*}|+\left(\sum\limits_{j\neq q, j\in S}|a_{qj}|+|a_{qp}|\right)|x_p^{*}| \nonumber\\&\leq ||A^{-1}||_{\infty}^{-1}+\left(r_q^{\overline{S}}(A)-|a_{qp}|\right)|x_q^{*}|+\left(r_q^{S}(A)+|a_{qp}|\right), \end{align*}$

i.e.,

$\begin{eqnarray} (|a_{qq}|-r_q^{\overline{S}}(A)+|a_{qp}|)|x_{q}^{*}|\leq ||A^{-1}||_{\infty}^{-1}+(r_q^{S}(A)+|a_{qp}|). \end{eqnarray}$

(3.6)

Then, from (3.5) and (3.6), we get that

$\begin{eqnarray*} \frac{|a_{pp}|-||A^{-1}||_{\infty}^{-1}-r_p^{S}(A)}{r_p^{\overline{S}}(A)}\leq|x_{q}^{*}|\leq\frac{||A^{-1}||_{\infty}^{-1}+r_q^{S}(A)+|a_{qp}|}{|a_{qq}|-r_q^{\overline{S}}(A)+|a_{qp}|}, \end{eqnarray*}$

which implies that

$\begin{align} ||A^{-1}||_{\infty}&\leq\frac{|a_{qq}|-r_q^{\overline{S}}(A)+|a_{qp}|+r_p^{\overline{S}}(A)}{(|a_{pp}|-r_p^{S}(A))(|a_{qq}|-r_q^{\overline{S}}(A)+|a_{qp}|)-r_p^{\overline{S}}(A)(r_{q}^{S}(A)+|a_{qp}|)} \\&\leq\max\limits_{j\in \overline{S}\setminus\{i_0\}}\frac{|a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji_0}|+r_{i_0}^{\overline{S}}(A)}{(|a_{i_0i_0}|-r_{i_0}^{S}(A))(|a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji_0}|)-r_{i_0}^{\overline{S}}(A)(r_{j}^{S}(A)+|a_{ji_0}|)} \\&: = \max\limits_{j\in \overline{S}\setminus\{i_0\}}\mathcal{X}_{i_0j}^{\overline{S}}(A). \end{align}$

(3.7)

If $p\neq i_0$ , then $|a_{pp}| > r_p(A)$ . Similarly to the proof of (3.4), we obtain

$\begin{align*} ||A^{-1}||_{\infty}&\leq\frac{1}{|a_{pp}|-r_p(A)}\leq\max\limits_{j\in \overline{S}\setminus \{i_0\}}\frac{1}{|a_{jj}|-r_j(A)}. \end{align*}$

Hence,

$\begin{align*} ||A^{-1}||_{\infty}\leq\max\limits_{j\in \overline{S}\setminus \{i_0\}}\left\{\mathcal{X}_{i_0j}^{\overline{S}}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}. \end{align*}$

Since $i_0$ is arbitrary in $\overline{S}^\star$ , it follows that

$\begin{align} ||A^{-1}||_{\infty}\leq\min\limits_{i\in \overline{S}^\star}\max\limits_{j\in \overline{S}\setminus \{i\}}\left\{\mathcal{X}_{ij}^{\overline{S}}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}. \end{align}$

(3.8)

By (3.4) and (3.8), it holds that

$\begin{align*} ||A^{-1}||_{\infty}\leq\max\left\{\min\limits_{i\in S^\star}\frac{1}{|a_{ii}|-r_i^{\overline{S}}(A)}, \min\limits_{i\in \overline{S}^\star}\max\limits_{j\in \overline{S}\setminus \{i\}}\left\{\mathcal{X}_{ij}^{\overline{S}}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}\right\}. \end{align*}$

If $\overline{S}$ is a singleton set, then similar to the above case, we obtain

$\begin{align*} ||A^{-1}||_{\infty}\leq\max\left\{\min\limits_{i\in S^\star}\max\limits_{j\in S\setminus \{i\}}\left\{\mathcal{X}_{ij}^{S}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}, \min\limits_{i\in \overline{S}^\star}\frac{1}{|a_{ii}|-r_i^{S}(A)}\right\}. \end{align*}$

The second case. Suppose that both $S$ and $\overline{S}$ are singleton sets. By Lemma 3.1, it follows that $S^\star$ is not empty, and $\overline{S}^\star$ is not empty. Then, similar to the proof of the first case, we have

$\begin{align*} ||A^{-1}||_{\infty}\leq\min\limits_{i\in S^\star}\max\limits_{j\in S\setminus \{i\}}\left\{\mathcal{X}_{ij}^{S}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}, \end{align*}$

and

$\begin{align*} ||A^{-1}||_{\infty}\leq\min\limits_{i\in \overline{S}^\star}\max\limits_{j\in \overline{S}\setminus \{i\}}\left\{\mathcal{X}_{ij}^{\overline{S}}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\}. \end{align*}$

Now, the conclusion follows from the above two cases.

In ^[15], an elegant upper bound for the inverse of SDD matrices is presented.

Theorem 3.6. ^[15] Let $A = [a_{ij}] \in \mathbb{C}^{n\times n}$ be an SDD matrix. Then,

$\begin{eqnarray*} ||A^{-1}||_{\infty}\leq \max\limits_{i\in N}\frac{1}{|a_{ii}|-r_i(A)}. \end{eqnarray*}$

This bound is usually called Varah's bound and plays a critical role in numerical algebra ^{[11,16,28,29]}. As discussed before, an SDD matrix is a PDSDD matrix as well. Thus, Theorem 3.5 can be applied to SDD matrices. In the following, we show that bound (3.1) of Theorem 3.5 works better than Varah's bound of Theorem 3.6.

Theorem 3.7. Let $A = [a_{ij}] \in \mathbb{C}^{n\times n}$ be an SDD matrix and $S$ be any subset of $N$ . Then,

$\begin{eqnarray*} ||A^{-1}||_{\infty}\leq \varphi^{S}(A)\leq \max\limits_{i\in N}\frac{1}{|a_{ii}|-r_i(A)}, \end{eqnarray*}$

where

$\varphi^{S}(A): = \max\left\{\min\limits_{i\in S}\max\left\{\frac{1}{|a_{ii}|-r_i^{\overline{S}}(A)}, \varphi_i^{S}(A)\right\}, \min\limits_{i\in \overline{S}}\max\left\{\frac{1}{|a_{ii}|-r_i^{S}(A)}, \varphi_i^{\overline{S}}(A)\right\}\right\}$

and $\varphi_i^{S}(A)$ is given by Theorem 3.5.

Proof. Since $A$ is an SDD matrix, it follows from Lemma 3.1 that $S^\star = S$ for any subset $S$ of $N$ . Hence, by Theorem 3.5, it follows that

$\begin{eqnarray*} ||A^{-1}||_{\infty}\leq \varphi^{S}(A). \end{eqnarray*}$

We next prove that $\varphi^{S}(A)\leq \max\limits_{i\in N}\frac{1}{|a_{ii}|-r_i(A)}$ . Define $|a_{i_0i_0}|-r_{i_0}(A): = \min\limits_{i\in N}\{|a_{ii}|-r_{i}(A)\}$ . Obviously, for each $i\in N$ ,

$\frac{1}{|a_{ii}|-r_{i}^{S}(A)}\leq\frac{1}{|a_{i_0i_0}|-r_{i_0}(A)}\; \text{and}\; \frac{1}{|a_{ii}|-r_{i}^{\overline{S}}(A)}\leq\frac{1}{|a_{i_0i_0}|-r_{i_0}(A)}.$

Note that for each $i\in S$ ,

$\begin{align} \varphi_{i}^{S}(A): = \max\limits_{j\in S\setminus \{i\}}\left\{\mathcal{X}_{ij}^{S}(A), \frac{1}{|a_{jj}|-r_j(A)}\right\} \end{align}$

(3.9)

and

$\mathcal{X}_{ij}^{S}(A): = \frac{|a_{jj}|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)}{(|a_{ii}|-r_i^{\overline{S}}(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|)}.$

If $|a_{ii}|-r_i(A)\geq|a_{jj}|-r_j(A)$ , then

$\begin{align*} &(|a_{ii}|-r_i^{\overline{S}}(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|) \\& = (|a_{ii}|-r_i(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)+r_i^{S}(A)(|a_{jj}|-r_j(A)) \\&\geq(|a_{jj}|-r_j(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)+r_i^{S}(A)(|a_{jj}|-r_j(A)) \\& = (|a_{jj}|-r_j(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)), \end{align*}$

which implies that

$\begin{align} \mathcal{X}_{ij}^{S}(A)\leq\frac{1}{|a_{jj}|-r_{j}(A)}\leq\frac{1}{|a_{i_0i_0}|-r_{i_0}(A)}. \end{align}$

(3.10)

If $|a_{ii}|-r_i(A) < |a_{jj}|-r_j(A)$ , then

$\begin{align*} &(|a_{ii}|-r_i^{\overline{S}}(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|) \\& = (|a_{ii}|-r_i(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)+r_i^{S}(A)(|a_{jj}|-r_j(A)) \\& > (|a_{ii}|-r_i(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)+r_i^{S}(A)(|a_{ii}|-r_i(A)) \\& = (|a_{ii}|-r_i(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)), \end{align*}$

which implies that

$\begin{align} \frac{1}{|a_{jj}|-r_{j}(A)} < \mathcal{X}_{ij}^{S}(A) < \frac{1}{|a_{ii}|-r_{i}(A)}\leq\frac{1}{|a_{i_0i_0}|-r_{i_0}(A)}. \end{align}$

(3.11)

By (3.9), (3.10) and (3.11), it follows that for each $i\in S$ ,

$\varphi_i^{S}(A)\leq\frac{1}{|a_{i_0i_0}|-r_{i_0}(A)}.$

Similarly, for each $i\in \overline{S}$ , we can see that

$\varphi_i^{\overline{S}}(A)\leq\frac{1}{|a_{i_0i_0}|-r_{i_0}(A)}.$

This completes the proof.

Remark 3.3. For SDD matrices, consider the intersection over all possible subsets $S$ of $N$ , and a tighter upper bound for $||A^{-1}||_{\infty}$ can be obtained from Theorem 3.7:

$\begin{eqnarray*} ||A^{-1}||_{\infty}\leq \min\limits_{S\subseteq N}\varphi^{S}(A)\leq\varphi^{S}(A)\leq\max\limits_{i\in N}\frac{1}{|a_{ii}|-r_i(A)}. \end{eqnarray*}$

Besides SDD matrices, for other subclasses of $H$ -matrices, such as DSDD matrices, $S$ -SDD matrices and Nekrasov matrices, various infinity norm bounds for their inverse have also been derived. For details, see ^{[12,23,28,29,30,31,32,33]} and references therein. A numerical example is given to illustrate the advantage of the proposed bound in Theorem 3.6.

Example 3.1. Consider the matrix in Example 2.1:

$A = \left[ \begin{array}{cccc} 3 &-1 &-3 &0 \\ -1 &3 &0 &-8 \\ 0 &-1 &3 &0\\ 0 & 0 &0 & 8 \end{array} \right].$

By computation, we know that $A$ is a PDSDD matrix for $S = \{1, 3\}$ but neither SDD nor a Nekrasov matrix. Moreover, it is easy to verify that there is no nonempty proper subset $S$ of $N$ such that $A$ is an $S$ -SDD matrix, and so it is not a DSDD matrix. Therefore, neither of the existing bounds for SDD, DSDD, $S$ -SDD, and Nekrasov matrices can be used to estimate $||A^{-1}||_\infty$ . However, by our bound (3.1), we have

$||A^{-1}||_\infty\leq 2.$

The exact value of the infinity norm of the inverse of $A$ is $||A^{-1}||_\infty = 1.$

3.3. A new pseudospectra localization and its application

For a given $\varepsilon > 0$ , denoted by

$\Lambda_\varepsilon(A) = \{\lambda\in \mathbb{C}: \exists\; {\bf x}\in \mathbb{C}^{n}\setminus\{0\}, E\in \mathbb{C}^{n\times n}, ||E||\leq\varepsilon \; such\; that\; (A+E){\bf x} = \lambda {\bf x}\},$

the $\varepsilon$ -pseudospectrum of a matrix $A$ consists of all eigenvalues of matrices ^[30], which is equivalent to

$\begin{eqnarray} \Lambda_\varepsilon(A) = \{z\in \mathbb{C}:||(A-zI)^{-1}||^{-1}\leq\varepsilon\}, \end{eqnarray}$

(3.12)

where the convention is $||A^{-1}||^{-1} = 0$ if $A$ is singular ^[30]. This implies that the infinity norm bounds of the inverse of a given matrix could be used to generate new pseudospectra localizations. For details, see ^[13,25,30]. So, in this section, we shall give a new pseudospectra localization using the obtained bound in Section 3.2. Before that, a useful lemma is given that will be used later.

Lemma 3.2. Let $A$ be an arbitrary matrix and $S$ be any subset of $N$ . Then,

$\begin{eqnarray*} ||A^{-1}||_{\infty}^{-1}\geq \mu(A): = \min\left\{f(A), g(A)\right\}, \end{eqnarray*}$

where

$f(A): = \max\limits_{i\in S}\min\left\{|a_{ii}|-r_i^{\overline{S}}(A), \min\limits_{j\in S\setminus \{i\}}\left\{\mu_{ij}^{S}(A), |a_{jj}|-r_j(A)\right\}\right\}$

and

$g(A): = \max\limits_{i\in \overline{S}}\min\left\{|a_{ii}|-r_i^{S}(A), \min\limits_{j\in \overline{S}\setminus \{i\}}\left\{\mu_{ij}^{\overline{S}}(A), |a_{jj}|-r_j(A)\right\}\right\}$

with the convention $||A^{-1}||_{\infty}^{-1}$ if $A$ is singular, and $\mu_{ij}^{S}(A) = 0$ if $\; |a_{jj}|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A) = 0$ ; otherwise,

$\mu_{ij}^{S}(A) = \frac{(|a_{ii}|-r_i^{\overline{S}}(A))(|a_{jj}|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|)}{|a_{jj}|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)}.$

Proof. For any given subset $S$ of $N$ , if $A$ is a PDSDD matrix, then it follows from Lemma 3.1 and Theorem 3.5 that

$\begin{align*} ||A^{-1}||_{\infty}^{-1}&\geq \min\left\{\max\limits_{i\in S^{\star}}\min\left\{|a_{ii}|-r_i^{\overline{S}}(A), \min\limits_{j\in S\setminus \{i\}}\left\{\mu_{ij}^{S}(A), |a_{jj}|-r_j(A)\right\}\right\}, \right. \\ &\; \; \; \; \; \left. \max\limits_{i\in \overline{S}^{\star}}\min\left\{|a_{ii}|-r_i^{S}(A), \min\limits_{j\in \overline{S}\setminus \{i\}}\left\{\mu_{ij}^{\overline{S}}(A), |a_{jj}|-r_j(A)\right\}\right\}\right\} \\& = \mu(A). \end{align*}$

If $A$ is not a PDSDD matrix, then it follows from Lemma 3.1 that at least one of the following conditions holds: ( $i$ ) $|a_{ii}|\leq r_i^{\overline{S}}(A)$ for all $i\in S$ ; ( $ii$ ) $|a_{ii}| > r_i^{\overline{S}}(A)$ for some $i\in S$ ; but for some $j\in S\setminus \{i\}$ , $|a_{jj}|\leq r_j(A)$ or

$\big(|a_{ii}|-r_i^{\overline{S}}(A)\big)\big(|a_{jj}|-r_j^{S}(A)+|a_{ji}|\big)\leq r_i^{S}(A)(r_j^{\overline{S}}(A)+|a_{ji}|);$

( $iii$ ) $|a_{ii}|\leq r_i^{S}(A)$ for all $i\in \overline{S}$ ; ( $iv$ ) $|a_{ii}| > r_i^{S}(A)$ for some $i\in \overline{S}$ ; but for some $j\in \overline{S}\setminus \{i\}$ , $|a_{jj}|\leq r_j(A)$ or

$\big(|a_{ii}|-r_i^{S}(A)\big)\big(|a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji}|\big)\leq r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|).$

This implies that $\mu(A)\leq 0\leq ||A^{-1}||_{\infty}^{-1}$ . The proof is complete.

Now, a new pseudospectra localization for matrices is given based on Lemma 3.2.

Theorem 3.8. ( $\varepsilon$ -pseudo PDSDD set) Let $A = [a_{ij}] \in \mathbb{C}^{n\times n}$ and $S$ be any subset of $N$ . Then,

$\begin{eqnarray*} \Lambda_\varepsilon(A)\subseteq \Theta^{S}(A, \varepsilon): = \theta^{S}(A, \varepsilon)\bigcup\theta^{\overline{S}}(A, \varepsilon), \end{eqnarray*}$

where

$\theta^{S}(A, \varepsilon): = \bigcap\limits_{i\in S}\left(\Gamma_i^{\overline{S}}(A, \varepsilon)\bigcup\left(\bigcup\limits_{j\in S\setminus \{i\}}\big(\widehat{V}_{ij}^{\overline{S}}(A, \varepsilon)\cup\Gamma_j(A, \varepsilon)\big)\right)\right)$

and

$\theta^{\overline{S}}(A, \varepsilon): = \bigcap\limits_{i\in \overline{S}}\left(\Gamma_i^{S}(A, \varepsilon)\bigcup\left(\bigcup\limits_{j\in \overline{S}\setminus \{i\}}\big(\widehat{V}_{ij}^{S}(A, \varepsilon)\cup\Gamma_j(A, \varepsilon)\big)\right)\right)$

with

$\Gamma_i^{S}(A, \varepsilon): = \left\{z\in \mathbb{C}:|z-a_{ii}|\leq r_i^{S}(A)+\varepsilon\right\},$

$\Gamma_j(A, \varepsilon): = \left\{z\in \mathbb{C}:|z-a_{jj}|\leq r_j(A)+\varepsilon\right\},$

and

$\begin{eqnarray*} \widehat{V}_{ij}^{S}(A, \varepsilon): = \left\{z\in \mathbb{C}:(|z-a_{ii}|-r_i^{S}(A)-\varepsilon)(|z-a_{jj}|-r_j^{\overline{S}}(A)+|a_{ji}|)\right.\\ \left.\leq r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|+\varepsilon)\right\}. \end{eqnarray*}$

Proof. From Lemma 3.2 and (3.12), we immediately get

$\begin{align} \Lambda_\varepsilon(A) = \{z\in \mathbb{C}:||(A-zI)^{-1}||^{-1}\leq\varepsilon\}\subseteq\{z\in \mathbb{C}:\mu(A-zI)\leq\varepsilon\}, \end{align}$

(3.13)

where $\mu(A-zI)$ is defined as in Lemma 3.2. Note that $r_i^S(A-zI) = r_i^S(A)$ and $r_i^{\overline{S}}(A-zI) = r_i^{\overline{S}}(A)$ . Therefore, for any $\lambda\in \Lambda_\varepsilon(A)$ , it follows from (3.13) that

$f(A-\lambda I)\leq \varepsilon\; \text{or}\; g(A-\lambda I)\leq \varepsilon,$

where $f(A-\lambda I)$ and $g(A-\lambda I)$ are given by Lemma 3.2.

Case Ⅰ. If $f(A-\lambda I)\leq \varepsilon$ , then for all $i\in S$ , $|a_{ii}-\lambda|\leq r_i^{\overline{S}}(A)+\varepsilon$ or $|a_{ii}-\lambda| > r_i^{\overline{S}}(A)+\varepsilon$ for some $i\in S$ ; but for some $j\in S\setminus \{i\}$ , $|a_{jj}-\lambda|\leq r_j(A)+\varepsilon$ or $\mu_{ij}^{S}(A-\lambda I)\leq\varepsilon$ , i.e.,

$\begin{align} \frac{(|a_{ii}-\lambda|-r_i^{\overline{S}}(A))(|a_{jj}-\lambda|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|)}{|a_{jj}-\lambda|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)}\leq\varepsilon. \end{align}$

(3.14)

If $|a_{jj}-\lambda|-r_j^{S}(A) > 0$ , then it follows from (3.14) that

$\big(|a_{ii}-\lambda|-r_i^{\overline{S}}(A)-\varepsilon\big)\big(|a_{jj}-\lambda|-r_j^{S}(A)+|a_{ji}|\big)\leq r_i^{S}(A)(r_j^{\overline{S}}(A)+|a_{ji}|+\varepsilon).$

If $|a_{jj}-\lambda|-r_j^{S}(A)\leq0$ , then $|a_{jj}-\lambda|\leq r_j^{S}(A)+\varepsilon\leq r_j(A)+\varepsilon$ . These imply that $\lambda\in\theta^{S}(A, \varepsilon)$ .

Case Ⅱ. If $g(A-\lambda I)\leq \varepsilon$ , then for all $i\in \overline{S}$ , $|a_{ii}-\lambda|\leq r_i^S(A)+\varepsilon$ or $|a_{ii}-\lambda| > r_i^{S}(A)+\varepsilon$ for some $i\in \overline{S}$ ; but for some $j\in \overline{S}\setminus \{i\}$ , $|a_{jj}-\lambda|\leq r_j(A)+\varepsilon$ or $\mu_{ij}^{\overline{S}}(A-\lambda I)\leq\varepsilon$ , i.e.,

$\begin{align} \frac{(|a_{ii}-\lambda|-r_i^{S}(A))(|a_{jj}-\lambda|-r_j^{\overline{S}}(A)+|a_{ji}|)-r_i^{\overline{S}}(A)(r_{j}^{S}(A)+|a_{ji}|)}{|a_{jj}-\lambda|-r_j^{\overline{S}}(A)+|a_{ji}|+r_i^{\overline{S}}(A)}\leq\varepsilon. \end{align}$

(3.15)

If $|a_{jj}-\lambda|-r_j^{\overline{S}}(A) > 0$ , then it follows from (3.15) that

$\big(|a_{ii}-\lambda|-r_i^{S}(A)-\varepsilon\big)\big(|a_{jj}-\lambda|-r_j^{\overline{S}}(A)+|a_{ji}|\big)\leq r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|+\varepsilon).$

If $|a_{jj}-\lambda|-r_j^{\overline{S}}(A)\leq0$ , then $|a_{jj}-\lambda|\leq r_j^{\overline{S}}(A)+\varepsilon\leq r_j(A)+\varepsilon$ . These imply that $\lambda\in\theta^{\overline{S}}(A, \varepsilon)$ .

From Case Ⅰ and Case Ⅱ, the conclusion follows.

As an application, using Theorem 3.8, we next give a lower bound for distance to instability. Denote by $Red(A)\in \mathbb{R}^{n\times n}$ the real matrix associated with a given matrix $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ in the following way:

$(Red(A))_{ij} = \left\{ \begin{array}{cc} Re(a_{ii}), &j = i, \\ |a_{ij}|, &j\neq i. \end{array} \right.$

Theorem 3.9. Consider $A = [a_{ij}]\in \mathbb{C}^{n\times n}$ , such that $Red(A)$ is a PDSDD matrix with all diagonal elements negative. Then, $\mu(\mathit{\text{Red}}(A)) > 0$ and

$\begin{eqnarray} \Lambda_\varepsilon(A)\subseteq\Theta^{S}(A, \varepsilon) \subset \mathbb{C}^{-}\; for\; all\; 0 < \varepsilon < \mu(Red(A)), \end{eqnarray}$

(3.16)

where $\mathbb{C}^{-}$ is the open left half plane of $\mathbb{C}$ , $\mu(\mathit{\text{Red}}(A))$ is defined as in Lemma 3.2, and $\Lambda_\varepsilon(A)$ denotes the infinity norm $\varepsilon$ -pseudospectrum of $A$ .

Proof. Since $Red(A)$ is a PDSDD matrix, it follows from Lemma 3.2 that $\mu(\text{Red}(A)) > 0$ . To prove (3.16), for $0 < \varepsilon < \mu(Red(A))$ , it suffices to show that $Re(z) < 0$ for each $z\in \Theta^{S}(A, \varepsilon)$ . It follows from Theorem 3.8 that $z\in \theta^{S}(A, \varepsilon)$ or $z\in \theta^{\overline{S}}(A, \varepsilon)$ . We only consider the case of $z\in \theta^{S}(A, \varepsilon)$ , and the case of $z\in \theta^{\overline{S}}(A, \varepsilon)$ can be proved similarly. Since $z\in \theta^{S}(A, \varepsilon)$ , it follows that for all $i\in S$ , either ( $i$ ) $|a_{ii}-z|\leq r_i^{\overline{S}}(A)+\varepsilon$ or ( $ii$ ) $|a_{ii}-z| > r_i^{\overline{S}}(A)+\varepsilon$ for some $i\in S$ ; but for some $j\in S\setminus \{i\}$ , $|a_{jj}-z|\leq r_j(A)+\varepsilon$ or

$\begin{align} \big(|a_{ii}-z|-r_i^{\overline{S}}(A)-\varepsilon\big)\big(|a_{jj}-z|-r_j^{S}(A)+|a_{ji}|\big)\leq r_i^{S}(A)(r_j^{\overline{S}}(A)+|a_{ji}|+\varepsilon). \end{align}$

(3.17)

Note that

$\begin{eqnarray*} \mu(Red(A)) = \min\left\{f(Red(A)), g(Red(A)) \right\}, \end{eqnarray*}$

where

$\begin{align*} f(Red(A)): = \max\limits_{i\in S}\min\left\{|Re(a_{ii})|-r_i^{\overline{S}}(Red(A)), \min\limits_{j\in S\setminus \{i\}}\left\{\mu_{ij}^{S}(Red(A)), |Re(a_{jj})|-r_j(Red(A))\right\}\right\} \end{align*}$

and

$\begin{align*} g(Red(A)): = \max\limits_{i\in \overline{S}}\min\left\{|Re(a_{ii})|-r_i^{S}(Red(A)), \min\limits_{j\in \overline{S}\setminus \{i\}}\left\{\mu_{ij}^{\overline{S}}(Red(A)), |Re(a_{jj})|-r_j(Red(A))\right\}\right\} \end{align*}$

with $\mu_{ij}^{S}(Red(A))$ defined as in Lemma 3.2.

For case ( $i$ ), i.e., $|a_{ii}-z|\leq r_i^{\overline{S}}(A)+\varepsilon$ for all $i\in S$ , we have

$\begin{align*} Re(z)-Re(a_{ii})\leq|Re(z)-Re(a_{ii})| = |Re(z-a_{ii})| &\leq|z-a_{ii}| \\&\leq r_i^{\overline{S}}(A)+\varepsilon \\& < r_i^{\overline{S}}(A)+|Re(a_{ii})|-r_i^{\overline{S}}(A) \\& = -Re(a_{ii}), \end{align*}$

which implies that $Re(z) < 0$ .

For case ( $ii$ ), i.e., $|z-a_{ii}| > r_i^{\overline{S}}(A)+\varepsilon$ for some $i\in S$ , if $|a_{jj}-z|\leq r_j(A)+\varepsilon$ , then

$\begin{align*} Re(z)-Re(a_{jj})\leq|Re(z)-Re(a_{jj})| = |Re(z-a_{jj})| &\leq|z-a_{jj}| \\&\leq r_j(A)+\varepsilon \\& < r_j(A)+|Re(a_{jj})|-r_j(A) \\& = -Re(a_{jj}), \end{align*}$

which implies that $Re(z) < 0$ . If (3.17) holds, then

$\begin{align} Re(z)-Re(a_{jj})\leq|Re(z)-Re(a_{jj})|& = |Re(z-a_{jj})| \\&\leq|z-a_{jj}| \\&\leq \frac{r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|+\varepsilon)}{|z-a_{ii}|-r_i^{S}(A)-\varepsilon}+r_j^{S}(A)-|a_{ji}|. \end{align}$

(3.18)

{If $|z-a_{ii}| < |Re(a_{ii})|$ , then $Re(z)-Re(a_{ii})\leq|z-a_{ii}| < |Re(a_{ii})|$ , which leads to $Re(z) < 0$ . Otherwise, since}

$\begin{align*} 0 < \varepsilon& < \frac{(|Re(a_{ii})|-r_i^{\overline{S}}(A))(|Re(a_{jj})|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|)}{|Re(a_{jj})|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)} \\&\leq\frac{(|z-a_{ii}|-r_i^{\overline{S}}(A))(|Re(a_{jj})|-r_j^{S}(A)+|a_{ji}|)-r_i^{S}(A)(r_{j}^{\overline{S}}(A)+|a_{ji}|)}{|Re(a_{jj})|-r_j^{S}(A)+|a_{ji}|+r_i^{S}(A)}, \end{align*}$

it follows that

$\begin{eqnarray*} \frac{r_i^{\overline{S}}(A)(r_j^{S}(A)+|a_{ji}|+\varepsilon)}{|z-a_{ii}|-r_i^{S}(A)-\varepsilon}+r_j^{S}(A)-|a_{ji}| < |Re(a_{jj})|, \end{eqnarray*}$

which together with (3.18) yields that

$\begin{eqnarray*} Re(z)-Re(a_{jj}) < |Re(a_{jj})| = -Re(a_{jj}), \end{eqnarray*}$

and thus $Re(z) < 0$ . This completes the proof.

The following example shows that the bound $\mu(Red(A))$ in Theorem 3.9 is better than those of ^[13] and ^[30] in some cases.

Example 3.2. Consider the matrix $A\in \mathbb{R}^{10\times 10}$ in ^[13], where

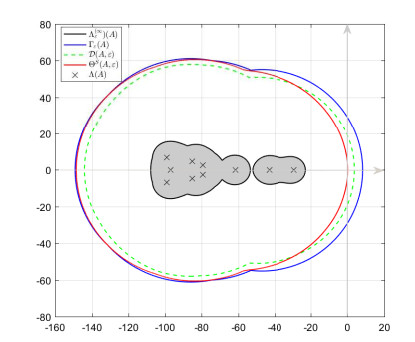
$A = \left[ \begin{array}{*{20}c} -78 &-7 &10 &5 &10 &8 &3 &5 &1 &7 \\ 4 &-95 &9 &-3 &3 &5 &3 &5 &5 &2 \\ 4 &4 &-58 &6 &8 &1 &-3 &4 &4 &6 \\ 9 &7 &8 &-87 &2 &5 &6 &-8 &8 &3 \\ 0 &2 &-4 &2 &-90 &1 &7 &2 &6 &7\\ 10 &9 &3 &6 &-3 &-80 &8 &2 &6 &9\\ -9 &6 &5 &4 &8 &7 &-86 &7 &1 &10\\ 7 &9 &1 &7 &7 &-3 &4 &-93 &11 &3\\ 10 &8 &4 &4 &3 &5 &6 &4 &-45 &-5\\ 4 &2 &2 &10 &9 &9 &2 &10 &-3 &-47 \end{array} \right].$

It follows from ^[13] that $A$ is a DZ-type matrix, and $\varepsilon = \mu(Red(A)) = 0.66$ . On the other hand, it is easy to verify that $A$ is also a PDSDD matrix for $S = \{1, 2, 3, 4, 9\}$ . Hence, from Theorem 3.9, we can get a new lower bound for distance to instability $\varepsilon = \mu(Red(A)) = 4.17$ and plot the corresponding pseudospectrum as shown in , where $\Gamma _\varepsilon(A)$ , $\mathcal{D}(A, \varepsilon)$ , $\Theta^{S}(A, \varepsilon)$ , the pseudospectrum ${\Lambda _\varepsilon }(A)$ and the eigenvalues of $A$ are represented by a blue solid boundary, a green dotted boundary, a red solid boundary, a gray area, and a black " $\times$ , " respectively.

Figure 1. Localization sets for

$\varepsilon$ -pseudospectrum for

$\varepsilon = \mu(Red(A)) = 4.17$ .

DownLoad: Full-Size Img PowerPoint

As can be seen from , the sets ${\Gamma _\varepsilon }(A)$ of ^[30] and $\mathcal{D}(A, \varepsilon)$ of ^[13] propagate far into the right half-plane of $\mathbb{C}$ , but the localization set $\Theta^{S}(A, \varepsilon)$ touches the $y$ -axis. This implies that we cannot use ${\Gamma _\varepsilon }(A)$ and $\mathcal{D}(A, \varepsilon)$ to determine the stability of $A$ . However, using the localization set $\Theta^{S}(A, \varepsilon)$ , we can determine that $A$ is a stable matrix.

4. Conclusions

This paper proposes a new class of nonsingular $H$ -matrices called PDSDD matrices, which is similar to but different from $S$ -SDD matrices. By its non-singularity, a new eigenvalue localization set for matrices is presented, which improves some existing results in ^[8] and ^[27]. Furthermore, an infinity norm bound for the inverse of PDSDD matrices is obtained, which improves the well-known Varah's bound for strictly diagonally dominant matrices. Meanwhile, utilizing the proposed infinity norm bound, a new pseudospectra localization for matrices is given, and a lower bound for distance to instability is provided as well. In addition, applying the proposed infinity norm bound to explore the error bounds for linear complementarity problems of PDSDD matrices is also an interesting problem. It is worth studying in the future.

Acknowledgments

The authors would like to thank the editor and the anonymous referees for their valuable suggestions and comments. This work was partly supported by the National Natural Science Foundations of China (61962059 and 31600299), the Young Science and Technology Nova Program of Shaanxi Province (2022KJXX-01), the Science and Technology Project of Yan'an (2022SLGYGG-007), the Scientific Research Program Funded by Yunnan Provincial Education Department (2022J0949).

Conflict of interest

The authors declare there are no conflicts of interest.

Acknowledgments

The authors gratefully thank Mr. Nasser ZAYDI, the Chief of the Hygiene Laboratory of the Wilaya of Skikda, Miss Hind ZINE EL ABIDINE and Dr. Kaoutar ABOUDI from the Faculty of Sciences at the University of Cadiz, Spain, and Miss Aroui DOUNIA from the National Center for Biotechnology, Constantine, Algeria.

Conflict of interest

The authors declare no conflict of interest.

Author contributions

All authors contributed to the study's conception and design. Material preparation, data collection and analysis were performed by Leila DJERRAB, Zohra CHEKROUD, Amer ROUABHIA, Mohamed Abdesselem DEMS, Imane ATTAILI, and Prof. Luis Isidoro Romero GARCIA and Mustapha Adnane SMADI. Leila DJERRAB and Zohra CHEKROUD wrote the first draft of the manuscript. All authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

References

[1]	Bahry H Valorisation de la mélasse de caroube par une approche bioraffinerie (2017).
[2]	(2013) FAOSTAT FAOStatistical Database (2019). FAO.
[3]	Roseiro LB, Duarte LC, Oliveira DL, et al. (2013) Supercritical, ultrasound and conventional extracts from carob (Ceratonia siliqua L.) biomass: Effect on the phenolic profile and antiproliferative activity. Ind Crops Prod 47: 132-138. https://doi.org/10.1016/j.indcrop.2013.02.026
[4]	Ercan Y, Irfan T, Mustafa K (2013) Optimization of ethanol production from carob pod extract using immobilized Saccharomyces cerevisiae cells in a stirred tank bioreactor. Bioresour Technol 135: 365-371. https://doi.org/10.1016/j.biortech.2012.09.006
[5]	Fountoulakis MS, Dokianakis SN, Daskalakis G, et al. (2014) Fermentative hydrogen production from carob pod: A typical Mediterranean forest fruit. Waste Biomass Valorization 5: 799-805. https://doi.org/10.1007/s12649-014-9295-6
[6]	Favaro L, Basaglia M, Casella S (2019) Improving polyhydroxyalkanoate production from inexpensive carbon sources by genetic approaches: a review. Biofuels Bioprod Biorefin 13: 208-227. https://doi.org/10.1002/bbb.1944
[7]	Mohapatra S, Pattnaik S, Maity S, et al. (2020) Comparative analysis of PHAs production by Bacillus megaterium OUAT 016 under submerged and solid-state fermentation. Saudi J Biol Sci 27: 1242-1250. https://doi.org/10.1016/j.sjbs.2020.02.001
[8]	Sathianachiyar S, Devaraj A (2013) Production of biopolymers by bacterial species using glycerol, a by-product of biodiesel. Int J Sci Res Publ 3: 1-5.
[9]	Boey JY, Mohamad L, Khok Y, et al. (2021) A review of the applications and biodegradation of polyhydroxyalkanoates and poly (lactic acid) and its composites. Polymers (Basel) 13: 1544. https://doi.org/10.3390/polym13101544
[10]	Lemoigne M (1926) Produits de Deshydration et de Polymerisation de L'acide β= Oxybutyrique. Bull Soc Chim Biol 8: 770-782.
[11]	Devi-Nair R, Jutemar EP, Maurer FHJ, et al. (2013) Biosynthesis of P (3HB-co-3HV-co-3HHp) terpolymer by Cupriavidus necator PHB-4 transformant harboring the highly active PHA synthase gene of Chromobacterium sp. USM2. Malays J Microbiol 9: 140-146.
[12]	Blunt W, Levin DB, Cicek N (2018) Bioreactor operating strategies for improved polyhydroxyalkanoate (PHA)productivity. Polymers (Basel) 10: 1197. https://doi.org/10.3390/polym10111197
[13]	Dhaouadi K, Belkhir M, Akinocho I, et al. (2014) Sucrose supplementation during traditional carob syrup processing affected its chemical characteristics and biological activities. LWT-Food Sci Technol 57: 1-8. https://doi.org/10.1016/j.lwt.2014.01.025
[14]	Ashraf S, Siknder Ail, Ikram-ul-haq (2015) Alternative pre-treatment of raw molasses by metal complexing agents for acid productivity by Aspergillus niger. J Adv Biol Basic Res 1: 1.
[15]	Baei MS, Najafpour GD, Younesi H, et al. (2009) Synthesis of poly(3-hydroxybutyrate) by Cupriavidus necator DSMZ 545 using various carbon sources. World Appl Sci J 7: 157-161.
[16]	Dalsasso RR, Pavan FA, Bordignon SE, et al. (2019) Polyhydroxybutyrate (PHB) production by Cupriavidus necator from sugarcane vinasse and molasses as mixed substrate. Process Biochem 85: 12-18. https://doi.org/10.1016/j.procbio.2019.07.007
[17]	Tallon P, Magajna B, Lofranco C, et al. (2005) Microbial indicators of faecal contamination in water: a current perspective. Water Air Soil Pollut 166: 139-166. https://doi.org/10.1007/s11270-005-7905-4
[18]	Başkan KS, Tütem E, Akyüz E, et al. (2016) Spectrophotometric total reducing sugars assay based on cupric reduction. Talanta 147: 162-168. https://doi.org/10.1016/j.talanta.2015.09.049
[19]	Srimachai T, Nuithitikul K, Sompong O, et al. (2015) Optimization and kinetic modeling of ethanol production from oil palm frond juice in batch fermentation. Energy Procedia 79: 111-118. https://doi.org/10.1016/j.egypro.2015.11.490
[20]	Acosta-Cárdenas A, Alcaraz-Zapata W, Cardona-Betancur M (2018) Sugarcane molasses and vinasse as a substrate for polyhydroxyalkanoates (PHA) production. Dyna 85: 220-225. https://doi.org/10.15446/dyna.v85n206.68279
[21]	Mohd Zahari MAK, Ariffin H, Mokhtar MN, et al. (2012) Factors Affecting Poly(3-hydroxybutyrate) Production from Oil Palm Frond Juice by Cupriavidus necator (CCUG 5 22 3 8 T). J Biomed Biotechnol 2012: 125865. https://doi.org/10.1155/2012/125865
[22]	Edwards U, Rogall T, Blöcker H, et al. (1989) Isolation and direct complete nucleotide determination of entire genes. Characterization of a gene coding for 16S ribosomal RNA. Nucleic Acids Res 17: 7843-78. https://doi.org/10.1093/nar/17.19.7843
[23]	Elsayed NS, Aboulwafa M, Aboshanab K, et al. (2013) PHB production in Azomonas, Acinteobacter and Bacillus species: isolation, screening and identification. Arch Clin Microbiol 4: 5025-5035. https://DOI:10.5897/AJMR2013.6060
[24]	Naheed N, Jamil N, Hasnain S, et al. (2012) Biosynthesis of polyhydroxybutyrate inEnterobacter sp. SEL2 and the bacterium Enterobacteriaceae sp. PFW1 using sugar cane molasses as a carrier. African J Biotechnol 11: 3321-3332. https://doi.org/10.5897/AJB11.1405
[25]	Karr DB, Waters JK, Emerich DW (1983) Analysis of poly-β-hydroxybutyrate in Rhizobiumjaponicum bacteroids by ion-exclusion high-pressure liquid chromatography and UV detection. Appl Environ Microbiol 46: 1339-1344. https://doi.org/10.1128/aem.46.6.1339-1344.1983
[26]	Braunegg G, Sonnleitner BY, Lafferty RM (1978) A rapid gas chromatographic method for the determination of poly-β-hydroxybutyric acid in microbial biomass. Eur J Appl Microbiol Biotechnol 6: 29-37. https://doi.org/10.1007/BF00500854
[27]	Simona C, Laura L, Francesco V, et al. (2022) Effect of the organic loading rate on the Pstoring microbiome in sequencing batch reactors operated with uncoupled carbon and nitrogen feeding. Sci Total Environ 825: 153995. https://doi.org/10.1016/j.scitotenv.2022.153995
[28]	Salgaonkar BB, Mani K, Braganca JM (2013) Characterization of polyhydroxyalkanoates accumulated by a moderately halophilic salt pan isolate B acillus megaterium strain H 16. J Appl Microbiol 114: 1347-1356. https://doi.org/10.1111/jam.12135
[29]	Narayanan M, Kumarasamy S, Ranganathan M, et al. (2020) Enzyme and metabolites attained in degradation of chemical pesticides ß Cypermethrin by Bacillus cereus. Mater Today Proc 33: 3640-3645. https://doi.org/10.1016/j.matpr.2020.05.722
[30]	Sakthiselvan P, Madhumathi R (2019) Optimization on microbial production Polyhydroxybutyrate (PHB): A review. Int J Res Anal Rev 6: 243-251.
[31]	Getachew A, Woldesenbet F (2016) Production of biodegradable plastic by polyhydroxybutyrate (PHB) accumulating bacteria using low cost agricultural waste material. BMC Res Notes 9: 509. https://doi.org/10.1186/s13104-016-2321-y
[32]	Gomaa EZ (2014) Production of polyhydroxyalkanoates (PHA) by Bacillus subtilis and Escherichia coli cultivated on cane molasses enriched in ethanol. Braz Arch Biol Technol 57: 145-154. https://doi.org/10.1590/S1516-89132014000100020
[33]	Sen KY, Hussin MH, Baidurah S (2019) Biosynthesis of poly (3-hydroxybutyrate) (PHB) by Cupriavidus necator from various pretreated molasses as carbon source. Biocatal Agric Biotechnol 17: 51-59. https://doi.org/10.1016/j.bcab.2018.11.006
[34]	Vijay R, Tarika K (2018) Banana peel as an inexpensive carbon source for microbial production from carob pod: A typical Mediterranean forest fruit. Waste Biomass Valorization 5: 799-805. https://doi.org/10.1007/s12649-014-9295-6
[35]	Aly MM, Albureikan MO, El Rabey H, et al. (2013) Effects of cultivation conditions on the growth and production of poly-beta-hydroxybutyric acid by Bacillus cereus MM7 isolated from soil samples from Saudi Arabia. Life Sci J 10: 1884-1891.
[36]	Berekaa MM, Thawadi AM Al (2012) Biosynthesis of polyhydroxybutyrate (PHB) biopolymer by Bacillus megaterium SW1-2: Application of Box- Behnken design for optimization of process parameters. Afr. J. Microbiol Res 6: 2101-2108. https://doi.org/10.5897/AJMR11.1382
[37]	Desouky SE, Abdel-rahman MA, Azab MS, et al. (2017) Batch and fed-batch production of polyhydroxyalkanoates from sugarcane molasses by Bacillus flexus Azu-A2. J Innov Pharm Biol Sci 4: 55-66.
[38]	Musa H, Bolanle BB, Kasim FH (2016) Screening and production of polyhydroxybutyrate (PHB) by bacterial strains isolated from rhizosphere soil of groundnut plants. Heal Malaysiana 45: 1469-1476.
[39]	Zhou JW, Chang YF, Xu ZH, et al. (2007) Production of thuringiensin by fed-batch culture of Bacillus thuringiensis subsp. darmstadiensis 032 with an improved pH-control glucose feeding strategy. Process Biochem 42: 52-56. https://doi.org/10.1016/j.procbio.2006.07.017
[40]	Shivakumar S (2012) Accumulation of poly(3-hydroxybutyrate) by Microbacterium barkeri DSM 20145. Turkish J Biol 36: 225-232. https://doi.org/10.3906/biy-1103-2
[41]	Lund MN, Ray CA (2017) Control of Maillard reactions in foods: Strategies and chemical mechanisms. J Agric Food Chem 65: 4537-4552. https://doi.org/10.1021/acs.jafc.7b00882
[42]	Wang X, Li Z, Li X, et al. (2016) Poly-β-hydroxybutyrate metabolism is unrelated to the sporulation and parasporal crystal protein formation in Bacillus thuringiensis. Front Microbiol 7: 836. https://doi.org/10.3389/fmicb.2016.00836
[43]	McAdam B, Fournet MB, McDonald P, et al. (2020) Production of polyhydroxybutyrate (PHB) and factors impacting its chemical and mechanical characteristics. Polymers (Basel) 12: 1-20. https://doi.org/10.3390/polym12122908
[44]	Duvigneau S, Kettner A, Carius L, et al. (2021) Fast, inexpensive, and reliable HPLC method to determine monomer fractions in poly(3-hydroxybutyrate-co-3-hydroxyvalerate). Appl Microbiol Biotechnol 105: 4743-4749. https://doi.org/10.1007/s00253-021-11265-3
[45]	Godbole S (2016) Methods for identification, quantification and characterization of polyhydroxyalkanoates-a review. Int J Bioassays 5: 4977. https://doi.org/10.21746/ijbio.2016.04.005

This article has been cited by:

Frédérique Rodieux, Flavia Storelli, François Curtin, Sergio Manzano, Alain Gervaix, Klara M. Posfay-Barbe, Jules Desmeules, Youssef Daali, Caroline F. Samer, Evaluation of Pupillometry for CYP2D6 Phenotyping in Children Treated with Tramadol, 2023, 16, 1424-8247, 1227, 10.3390/ph16091227

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)