1.
Introduction
As a result of the increase in power demand, the whole world is adapting the usage of renewable energy. With this revolution, isolated areas, or large building schemes which have Distributed Energy Resources (DER) are being converted to smart grids.
Due to the high saturation level of DER traditional inverters get stress with the system. From several studies it has found that some issues contribute to these behaviors of inverters. As a solution for these common problems the smart inverters come into play by solving most of the problems of the traditional system. With the new technology the normal inverter gets upgraded to smart inverters in order to withstand new challenges in the modern grid. Since smart inverters work autonomously, they have a positive impact on the implemented residential sector as well as the national power grid. The traditional grid requires constant maintenance due to the stress, but smart inverters could help to address these localized challenges and growth the flexibility of the system [1].
With the progress of the smart inverters in smart grids IEEE gave a standard 'IEEE 1547 Standard" for smart inverters. The main purpose is to standardize the inter-links and interoperability of DERs with the connected Electric Power Systems (EPS). Certain standards and requirements for interlinks of DERs with the EPSs, and associated interfaces were launched by this standard [2]. Certain requirements for safety, interoperability, functionality, security, testing [3,4] and maintenance are specified in the standard [5].
When updated the traditional inverters to the smart inverters, it catches some smartness with additional functions. Mainly there are two sides to consider for smartness as improvement of the user friendliness and stabilize the power system.
The objective of this paper is to review the available technologies regarding functions of smart inverters. The following sections in the paper describes the evolution of the current smart inverter in detail along with smart inverter functions.
2.
The issues with current inverters
The inverter plays a main role as a main component which is used to make the interconnection between DERs and the power system. The inverters get stuck in some abnormal conditions due to the complexity of the current power system. From those bunch of issues few several issues are discussed as below.
2.1. Overheating
Most electronic components inside the inverters are sensitive to temperatures. High temperatures will cause a considerable reduction of the power production, and if the maximum operating temperature is reached it can even stop the production. Therefore a method must be there to ensure the suitableness of the proposed thermal management system in the designing stage of the inverter.
To get the maximum efficiency, a regular checking of cooling during the operational period is highly advisable and it is better to make sure that the cooling or the ventilation system is operating correctly. Additionally, a number of steps can be taken such as installing and cleaning dust filters as well as removing soles that obstruct airflow, in order to avoid extremely high temperatures.
For the optimal cost design of an inverter, increasing the switching frequency can reduce the inductance and capacitance values. As a result of increasing the switching losses, the cost of cooling will increase [6].
2.2. Isolation fault
Inverter will report an "isolation alarm" when a short-circuit occurs between various parts of the inverter circuit. The main causes of these defects are the combination of moisture, damage to the sleeve on the cabling, installation failure, and poor connectivity to the DC cables in the panel. This is most common in areas with high humidity or near the sea. In the event of an isolation fault, the inverter will stop working completely or the inverter is not performing at its maximum capacity. In both cases, production is lost.
As a solution for this problem, preventive maintenance program can be scheduled. Sensors are used to quantify the irradiance, temperature and wind situations and to measure the fulfilment of the entire system at large PV stations [7].
2.3. Inverter does not restart after a grid fault
An inverter must be able to restart after a grid fault of an unbalance (if there are no other faults). If the inverter does not reboot, a service group will have to come to the location in order to reboot the system. This can lead to unnecessary product, loss of money and time.
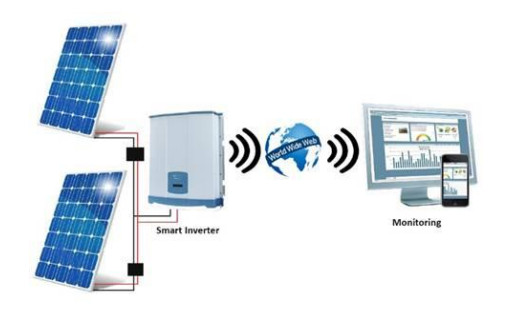
Use of a good monitoring system for 24/7 is much important for detecting the faults as quickly as possible. All PV modules linked to the inverter will be unable to send power until the fault or the error has been discovered. Therefore it is more important to have an organized system. This is especially the case in areas where grid connectivity is not always stable. Grid-connected inverters typically have software for parameter setting and system monitoring [8] which has the facilities to record the system operation and on-line visualization in a remote manner. Also some of them can contain monitoring [9] external signals such as irradiance and temperature. Different products have different capabilities in these areas and fields [10]. Figure 1 shows a sample diagram for the remote monitoring system.
2.4. The finding of MPPT
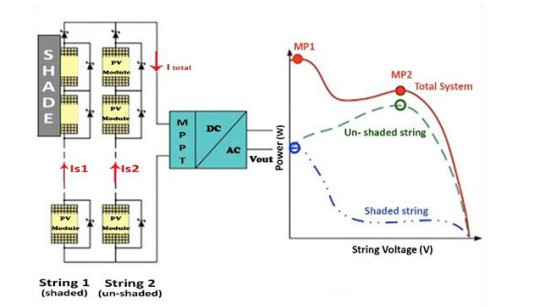
Almost all the current inverters operate on the concept of the Maximum Power Point Tracking (MPPT) operation [11]. This function has been developed with the intention of maximizing the achievements of inverters. Due to the scale of today's large PV systems, several rows of PV modules are linked together in series, called "strings". However, not all strings produce the same quantity of power as a consequence of many factors such as shading, different placing, errors in panel, etc. The strings provide dissimilar voltages, and in this respect the difference between the strings continuously changes. The MPPT algorithm is designed in such a way that the inverter is always connected to the most optimum supply voltage in spite of these variances in PV strings. The control period of MPPT has an important impression on the efficiency of power generation and the steadiness of the PV system [12]. This always maximizes the production of electricity. Therefore it is important to recognize the working order of the MPPT module in order to maximize the efficiency. A sample diagram and a graph to describe the MPPT tracking system is shown in Figure 2.
A number of algorithms has been established to track the maximum power point efficiently. Most of the current MPPT algorithms suffer from slow tracking, which in turn reduces the utility efficiency. It is difficult to estimate the efficiency of a PV inverter only by considering the translation efficiency [13]. Therefore to evaluate the overall efficiency of PV inverter, the MPPT efficiency of PV inverter should be tested [14]. The Table 1 below, shows the summary of the above issues.
3.
Development of the smart inverter
When considering the above issues, it indicates that the normal PV inverters do not have the flexibility to manage large volumes of renewable energy and manage system reliability. Most conventional inverters automatically are disconnected from the network at specific voltages or frequencies. IEEE 1547 standard gives the requirements for full disconnection of the inverter in some voltage variations. If there is a drop or spike in voltage that reaches this margin, the inverter will cut off from the system. This looks like an error to the defense [15] equipment installed on the feeder and the result is a systemic power outage. The smart inverters are flexible for these conditions which can prevent these problems. When the conventional inverters get shut off, the smart inverters can continue to allow power to flow. Smart inverters are remotely programmable components that allow to control the ramp rates, inputs and outputs of the converter, accurately. Moreover, they won't just cut out like traditional inverters since their thresholds are adjustable.
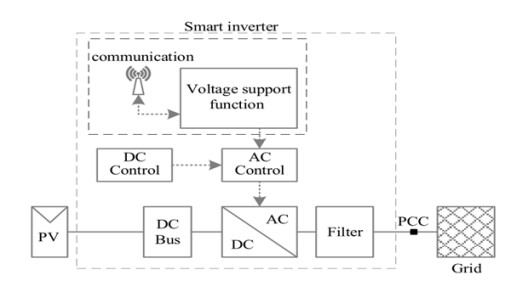
Smart inverters let two-way communication with utility control centers. In addition, advanced capabilities such as voltage and frequency sensors allow smart inverters to detect grid abnormalities and send the feedback to utility operators. The Figure 3 below, shows a general block diagram of smart PV inverter system.
4.
IEEE 1547 standard on smart inverters
IEEE Standard 1547 was cited in the U.S. Federal Energy Policy Act of 2005, under Section 1254 Interconnection Services, stating "Interconnection services shall be offered based upon the standards developed by the Institute of Electrical and Electronics Engineers Standard 1547 for Interconnecting Distributed Resources with Electric Power Systems, as they may be amended from time to time." As shown in the Figure 4, there is a series of standards IEEE 1547 which addressed the standards for Grid integration of DERs [16].
From the series of standard, IEEE Standard 1547 (2003) was the first about DER interconnection. Likewise the standard delivers requirements are applicable to the performance, procedure, testing, safety considerations, and maintenance of the interconnection. The IEEE 1547 necessities are universally needed for interconnection of DER, including synchronous and induction machines, and power inverters and converters.
Under the IEEE 1547.8 it addresses the advanced controls and communications for inverters supporting the grid and best practices focusing on the multiple inverters and micro-grids, and provides information for the behavior of DER and interactions with grid equipment (both operational and safety associated, including unintentional islanding) and interconnection system reaction to abnormal circumstances [17].
5.
Functions of smart inverters
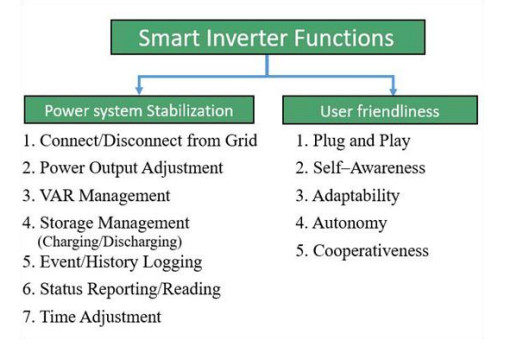
Considering the smart inverter functions and requirements to full fill common problems of the inverters, it can be defined in two sections as, functions for power system stabilization and communication based functions to improve the user friendliness. Figure 5 shows the sub functions of both categories.
5.1. Functions for power system stabilization
The smart inverters came into play with some additional smartness by adding some functions to supply a smooth service. In order to reach higher power system stability, efficiency [18] and reliability, and to improve the control [19] algorithms it is valuable to arm the inverters with "smart" features. According to several researches [20] they had identified seven high-priority inverter functions which are listed in Figure 6 that can stable the power system.
The seven functions are:
5.1.1. Connect/Disconnect from grid
This function provides two options for an inverter to cease operation and disconnect from the grid. The first is to set the power output to zero. This is also known as, a virtual disconnect. The second is the physical operation of a switch to isolate the inverter from the grid. This can be referred to as a physical disconnect.
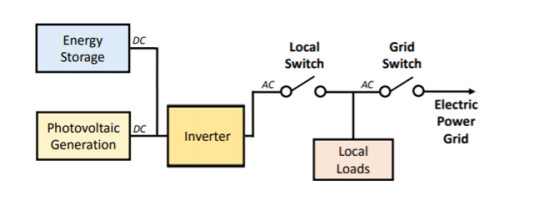
This function is not related to intentional islanding nor separating a customer from the grid. It refers to the management of a switch, or virtual switch that separates at the DER from the grid while leaving customers linking to the grid. In reference to the example diagram in Figure 7, this function relates to the operation of the "Local DER Switch, " not the "Grid Switch." The Table 2 below, further explains this relationship [21].
5.1.2. Power output adjustment
This is a main function of an inverter which includes two kinds of powers as active and reactive power. PV panel can be categorized as a DC power source. There is no reactive power connected with PV itself. Therefore, the only intention of the inverter input side will be to extract the maximum active power from the PV, and such control will be known as MPPT [22]. The inverter output side is dealing with the AC powers. That means active and reactive power components are there since active reactive power (apparent power) is only dealing with the AC side.
Grid frequency increases as a result of excessive generation and or insufficient load. Therefore, its active power output is changed relative to grid frequency. The desired response of the inverter is to reduce active power output when the frequency is high. Likewise, it is desired for the inverter to increase active power output as frequency decreases.
PV inverters typically have a maximum commanded power limit and are only able to provide an over-voltage response if the inverter is already at full active power output. Inverter should have the capability to provide voltage support to the grid via adjustment of the inverter's active power output, which changes in grid voltage [23].
Other than the pure active power, the system has a reactive power component also. When considering the inverter circuits, the inverters will remain purposeless during night hours when the renewable sources are not available. This decreases the efficient use of these inverters. One way to rise the productive operation of these inverters is to generate reactive power in each time when the renewable sources are not existing by operating them as VAR compensators. As the number of grid-tied inverters rises, their usage part as VAR compensators will support to reduce the necessity of additional capacity banks as well as in the grid voltage regulation.
There are several special designed active filter inverters in the market [24]. But they are not appropriate for grid-tie uses. It will be very supportive to allow current grid-tied inverters to operate in reactive power generation mode [25] when there is no active power input from PVs, which typically powers the control circuit, pays for the inverter internal fatalities, and keeps a regulated DC bus voltage. In the absence of activated power, the difficulty is to charge the DC bus and to keep it regulated within the certain limitations while injecting the preferred level of reactive power into the power grid [26,27]. For the inverter to operate in reactive power mode, it must compensate for its internal power losses and maintain its DC bus voltage within the appropriate range [28]. When the renewable source does not exist the inverter has to absorb little active power from the grid to pay for the inverter's internal losses, adjust the DC bus voltage to keep it within limits, as well as to keep the grid connection and operate the inverters in VAR mode. Other than the active power generation this extends the use of PV inverters and help to improve the grid stability and voltage regulation [29].
5.1.3. Var management
Under Var management, there are few Var control methods [30,31]. They are [20]
A. Unity Power Factor, Q = 0
The inverter is designed to function with a unity power factor, with partial or without re-injection of reactive power to the grid.
B.
Fixed Power Factor, Q(P)
The inverter function with a moderately leading power factor. It provides a regulation to reduce the voltage deviations attributable to active power output variations.
C.
Variable Power Factor, Q(P, R/X)
This method lets the inverter to flow the reactive power back into the grid by operating with a variable power factor.
D.
Volt/Var Control
This technique would allow the inverter to reply with a customized var reply, intended by the local utility, by monitoring its own terminal voltage [32,33].
Each of these volt/var functions can be considered as a "Mode". The following modes have been recognized as a preliminary set for large collections of inverters. With a single transmission instruction from the utility the inverters can be switched between these modes.
1) PV1 – Normal Energy preservation Mode
This mode is used as the normal state of operation for an inverter. (Inverters have one volt/var characteristic during on-peak hours and a different one during off-peak hours.)
2) PV2 – Maximum Var Sustenance Mode
Provide support for reactive power needs. This directs the distributed inverters to generate as many capacitive vars as possible.
3) PV3 – The Static Var Mode
Proposed to be used in cases where var generation does not differ with local voltage.
4) PV4 – The Passive Var Mode
This one is same as the PV3, with the exception that the percent var settings are assumed to be zero. The PV inverter volt/var control function can provide suitable voltage support for voltage deviations in primary and secondary sides due to variations in PV output [34]. Voltage deviations caused by usual load variations also can be reduced as well [20].
5.1.4. Storage management
Many number of control methods have been identified for this function. Main part of this function is charging and discharging management. Energy storage has been suggested as the solution to the power imbalance issue of power generation and load demand in view of the emergence of power grids with irregular renewable energy sources. Unlike conventional control of grid connected power inverters for injecting power in to the grid, the storage management control scheme puts the stability of the power grid as a high priority while maintaining its normal bi-directional power flow functions. The function mainly consists of the arrangement in battery's monitoring, management of charging and discharging, and output power control.
With the automatic charging and discharging approach meshed in the active power control loop, many bidirectional [35] Energy sources with limited energy storage capacities can be used with this function. With the help of this function distributed devices it can play an important role to provide active and reactive power compensation for enlightening the stability of the power grid [36].
5.1.5. Event/History logging
This function indicated a high priority on the need for a common method for event logging and reporting. For a system, it is important to monitor the behaviors or inverters and to record abnormal conditions and events.
All event log entries will contain the following 5 fields [21]:
a) Date and time stamp:
The accuracy of this function is determined by the frequency of time synchronization and the essential accuracy in keeping time of the PV system.
b) Data Reference:
The reference to the data point that activated the event log entry. For example, if the event is a voltage associated event, the Data reference will be to that data object. Same as if the event is a PV Mode event, the data reference will be the particular PV data object.
c) Value:
Value field refers for activating the event, including commands, record the changes of monitored values, quality code changes, etc.
d) Event Code:
This field is to exclusively identify event type.
e) Optional Text Field:
This contains the text of supportive information to the system. This text field can be used to offer additional specifics about the event.
The Event Code standard contains many codes for logging, with only a small fraction relevant to PV and Storage systems.
5.1.6. Status reporting/reading
This function allows the operating mode, status, and set points to be available to verify operation [37]. With increasing the penetration of DERs, it will increase the number of devices that are owned and controlled by consumers and third parties. Therefore the system can be disclosed to some cyber security issues and have to conform that the system is still authentic and safe with a high DER penetration. The control architectures with the communication [9] network implementation directly determine extent of cyber-attacks coming through the network. The smart inverter architecture must be enhanced to monitor the local system status in order to identify the attacks and hazards at the physical device layer. Therefore the cyber hazards can be sensed at an early stage. Also they can estimate the local voltage and current [38] to sense system variances. In this function, the directories of power quality, unbalanced voltages/currents, and other occasions, will be intended to detect the cyber-attacks [39].
5.1.7. Time adjustment
The ability to set the time in the DER device was considered as a main requirement, in order to support the scheduling of functions, and the time-stamping and logging of events.
Researches indicated that time-adjustment is generally supported by the specific communication protocols. Therefore as a recommended method for time-adjustment for distributed smart inverters is to apply the native time adjustment mechanism of the specific communication protocol being applied. As examples, the "DNP3" and the "ZigBee Smart Energy Profile 1.0" protocols have defined time-setting mechanisms that can be used for synchronizing smart inverter devices [21]. The Table 4 below, shows the technical possibilities and the practical issues of above functions.
5.2. Communication based functions to improve the user friendliness
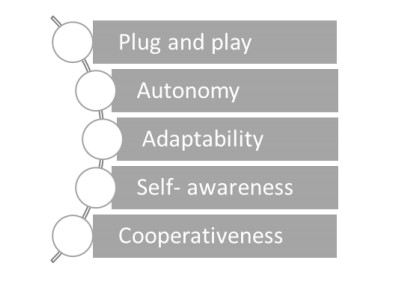
When comparing with the components in a grid system, one of the most important objectives is the control [40] of power inverters. These inverters implement interfaces between the DGs and the grid bus. In smart inverter development an explanation of "smartness" states to minimizing the requirement of communication. At the same time, being equipped with communication protocols also indicates "smartness" since the necessity of communication cannot be neglected. As well as these advantages, there is a main disadvantage regarding security that can effect the communication and monitoring improvements. Mainly, the privacy issues can spring up with these developments. A "smart inverter" should provide some features as shown in the Figure 8 below.
5.2.1. Plug and play
Plug-and-play (PnP) is the ability for a smart inverter to add for a power system and operate automatically without separate technical configuration. The PnP operation ensures in system benefits of scalability, interoperability, resilience, and reliability. PnP can be implemented at the power converters [41] with flexible hardware structures and the smart inverters for power grids in the purpose of distributing frequency/voltage regulation [42].
Plug and play means that a distributed power supply can access to the grid directly without control and defend units. Management technology will be needed when distributed power with the function of "plug and play" accesses to the grid. It consists of the control strategy of the system change, energy management, quality of power maintenance etc. Related technology of the inverter is difficult to implement in the short term because of the level of development and the limits of the current standards. The power output of the inverters can always be set aside in the rating working point. Therefore, each component can be controlled by itself according to the operational situation of the system by implementing the technology of "Plug and Play" Control [43].
5.2.2. Self-awareness
Self-awareness becomes a significant function for decentralized systems to realize advanced levels of autonomous behavior [44]. For smart inverters, self-awareness aims to improve the operative reliability and predicting the lifetime, thus enabling fail-safe or maintenance actions and effectively avoiding terrible accident in systems using power electronics. Additionally, it is expected that future smart inverters own certain degree of intelligence, as knowledge of its role or status within its environment and the likely effect of possible future actions [42].
5.2.3. Adaptability
The adaptability is another critical characteristic of a smart inverter. A smart inverter, to be able to adapt itself to the variations of the system in the operating conditions. This means the capability to evaluate the parameters, mostly the impedance of the grid, and synchronization in terms of frequency. Unintended islanding is one of the most remarkable functioning problems of grid system. This happens mainly due to grid failure, and the inverters are required to be included with islanding recognition algorithms in order to self-adapt, depending on the situation. Fault Tolerance and Islanding Detection are also categorized in this category [45].
5.2.4. Autonomy
Outline of this function is the system being smart enough to decide its own operation mode. Autonomous behavior is an elementary property for a distributed system. Furthermore, smart inverter with autonomous operation can be necessary in case of limited or no communication, or if desired for reliability [42]. One common situation is autonomous load power sharing using droop methods [46] when multiple inverters operate in parallel. For autonomous operation, smart inverters shall achieve skills such as dynamic grid feeding, dynamic grid creating, black start, seamless power transfer, and the power quality enhancement. Other autonomous functions in [47] are required by the power utility for distributed generations.
5.2.5. Cooperativeness
The meaning of this function is the ability of an inverter requires to be able to function in cooperatively and together with other inverters in a grid. All the inverters are essential to take some responsibility to regulate and rectify the unbalances and conflicts standing in the system. Their process should be in alignment with other neighboring components, when they are in operation. Therefore further disturbances will be introduced to the system. Furthermore, there are other aspects which lie in this category such as ramp rate control for renewable energy sources, reactive power and harmonic current sharing and soft start capability [45]. The Table 6 below, summarises the technical possibilities and practical issues of above functions. The Table 7 below, shows the comparing between traditional inverters and smart inverters considering the smart functions.
6.
Conclusions
As the high penetration level of the DGs the traditional inverters are being converted to the smart inverters by adding some additional functions to make the inverter smart. In order to state a device as smart, it has to represent several potentials and characteristics mostly depending on its application and operation. So that in order to standardize these smartness process, IEEE has given some series of standards called IEEE1547 which have been described above.
This paper discusses, currently available smart functions for inverters to get rid of some issues smartly. In this study, the features have been described for inverters, which are used as interfaces for DGs in power grids. As a brief summary of the concepts addressed above it can be identified that smartness of an inverter in a power grid, should have both ability to stabilize the power system by improving the power quality [33] as well as the improving the user friendliness by minimizing the communication requirements. There are some different functions to improve the power system stabilization as addressed above. Improving the user-friendliness mostly relates to minimizing communication necessities for its normal operation.
Furthermore by improving these functions further for smart inverts, it will help the world energy demand by getting the maximum usage of the renewable resources with the highest efficiency.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: