Efficient thermomechanical modelling of Laser Powder Bed Fusion additive manufacturing process with emphasis on parts residual stress fields

1.   Introduction

Laser Powder Bed Fusion (LPBF) is an Additive Manufacturing (AM) process in which metallic components with complex geometry can be fabricated ^{[1,2,3,4,5,6]}. Usually for the design of these components advanced design techniques, such as topology optimization, are utilized resulting to complex geometry parts making production with conventional manufacturing methods very difficult or impossible. LPBF process and its main variant Selective Laser Melting (SLM) process use a moving laser heat source to selectively melt a layer of powder metallic material which is placed on a substrate inside an inert chamber. After the melting and solidification of a layer, the substrate moves down at a distance equal with the layer thickness and another powder layer is placed on the top of the previous deposited layer and the process is repeated in a layer-by-layer manner until the part is completed ^[3].

LPBF process presents significant advantages over traditional manufacturing processes and has received significant interest over the last decade. However, LPBF presents some major drawbacks, which cause high unreliability in the properties and performance of LPBF parts ^{[7,8,9,10,11]}. These disadvantages prevent LPBF from the wider adoption of the process in the industry. The formation of process-induced defects and the development of residual stresses are some of the most serious drawbacks of the process. Keyhole or lack-of-fusion defects and gas porosities can be formed either by improper selection of process parameters or by process instabilities ^[8,9,10]. Residual stresses result from rapid thermal cycles that an LPBF component experiences during its build process. Residual stresses have been shown to approach material's yield strength and can lead even to premature failure of the part during its building process ^[12,13,14]. Moreover, the presence of large residual stresses and process-induced flaws can detrimentally affect the static and especially the fatigue mechanical properties of the LPBF parts. For this reason, reliable models for the prediction of residual strains and stresses of LPBF parts are needed to assist the design procedures and the optimization of the LPBF process ^[15,16]. In this study, a thermomechanical modelling method for the simulation of LPBF-AM process for the prediction of the residual strains and stresses in parts is presented.

For the modelling of part building using LPBF process a thermomechanical modelling method is required, where a thermal transient analysis is coupled with a nonlinear elastoplastic mechanical analysis in a coupled or an uncoupled way. In the thermal transient analysis, the heat transfer phenomena are modelled in order to predict the temperature fields developed in the part, which are imported as a thermal loading into the mechanical model to estimate the residual strains and stresses of part during the LPBF process. The generalized governing equations that describe the thermomechanical problem are ^[9]:

where ρ, ${C}_{p}$, k, Q, T and t in Eq 1 represent the density, specific heat, thermal heat conductivity, thermal heat input energy, temperature and time, respectively. In Eqs 2–5 [D] denotes the elastic stiffness tensor and ${\varepsilon }^{e}$, ${\varepsilon }^{pl}$, ${\varepsilon }^{th}$ are the elastic, plastic and thermal strains, respectively; $a$ is the coefficient of thermal expansion and ${T}_{0}$ is the chamber environmental temperature. Equation 1 is the heat transfer phenomena governing equation, while Eqs 2–5 describe the mechanical equilibrium of the part during the process ^[12].

Numerical finite element (FE) thermomechanical modelling of the LPBF process has huge spatial and temporal requirements ^[15,16]. Laser beam heat source, individual scan passes and laser scan strategy must be modelled for every part layer. Moreover, the size of elements and time step must be very small to capture the nonlinear phenomena in the melt pool region ^[17,18,19]. These features lead to enormous computational resource requirements, making the simulation of the LPBF process for the fabrication of a realistic part very difficult or even infeasible. For this reason, several modelling approaches have been proposed in the literature aiming to increase the method efficiency. The common ground between these approaches is the use abstractions to make the analysis simpler so that the direct modelling of each laser scan pass is no longer required ^[20,21].

Inherent strain method is a common method for the estimation of distortions in LPBF parts and is currently available in many commercial FE packages. The concept of the method was initially utilized for the numerical prediction of distortions in welded structures ^[22]. Keller and Ploshikhnin ^[23] first applied this method for the prediction of distortions in LPBF parts. In this method, the computationally expensive thermo-mechanical analysis is replaced with an elastic or an elastoplastic mechanical one, under the assumption of a uniform strain developed during the process, which is approximately the same in the different part areas. The value of the inherent strain can be either calculated by local layer analysis from a moving laser beam source or determined experimentally from small build samples, with the latter being the most usual ^[24,25]. Consequently, the inherent strain is appropriately applied on the part. Despite the computational efficiency of inherent strain method, Bugatti and Semeraro ^[26] have pointed that the assumption of a geometry independent strain is invalid and showed that the modelling of a geometry that differs from the geometry of the calibration sample can be highly inaccurate.

Other thermomechanical modelling approaches proposed in the literature for the estimation of residual stresses in LPBF parts use indirect methodologies, such as alternative heat sources, that account for heat transfer phenomena. Hodge et al. ^[27,28] utilized an approximation of lumped laser passes, in which many individual laser passes are merged into a larger single laser pass, with the phase change of metal material alloy also considered. Despite the good comparison with available results, this approach was limited on a part with small dimensions and the needed computational resources were quite high. Zaeh and Branner ^[29] and Ceidel et al. ^[30] utilized a uniform heat input as an alternative heat source on each layer of the part. For the determination of the uniform heat input, a thermal load was first calculated and then applied on the part to estimate the thermal gradients. Then, a mechanical analysis was performed to predict the mechanical response on the thermal gradients. In their model, they did not consider the laser beam interaction and laser scan strategy, which mainly influence the layer temperature gradients. Li et al. ^[31,32] developed a multiscale modelling method for the prediction of residual stresses and distortions in LPBF parts. Thermal simulation of a moving heat source was used to generate an alternative heat source of temperature profiles, which was used in a meso-scale thermomechanical analysis to calculate a residual stress tensor in hatch spacing zone. Finally, the residual stress tensor was mapped into a macro-scale mechanical analysis. Although, the predicted distortion results were successfully compared with experimental ones, an extensive validation in various build conditions was not performed to assess the main assumption of independence between the thermal and mechanical response between the individual hatch scans.

In the present work, a thermomechanical modelling method developed in ANSYS 2020R2 commercial finite element software package ^[33] for the simulation of LPBF process for the prediction of residual strains and stresses of parts is presented. In this method every layer of the fabricated part is heated to melting temperature of the considered AM alloy in order to replace the explicit modelling of laser scan strategy. To further improve the efficiency of the modelling method, a lumped layer approach was also utilized, in which many layers of the part were merged to form a super layer to minimize the computational time. A series of comparisons between modelling results with available experimental data from the open literature were performed, in order to investigate the robustness of the method under different AM part geometries, metal alloy materials and process conditions. The accuracy of results are thoroughly examined and the main limitations of the modelling procedures are discussed. The main characteristic of this work compared to literature works that use similar approaches ^{[27,28,29,30,31,32]} is the detailed validation study which showcase the pros and cons of the presented method. In addition, computational times for all the present cases are provided to assess the efficiency of the modelling approach and to provide the guidelines for the analysis of parts based on this approach.

2.   Materials and methods

2.1.   Experimental test cases

2.1.1.   Description of the experimental test cases considered

The capability of the presented modelling method to estimate the distortion, residual strains and stresses of LPBF parts was tested on a series of test cases, where the numerically predicted residual strains and stresses were compared with respective experimental data from available literature studies. Each test case involves the fabrication of a LPBF part of different geometry, fabricated of different AM metal alloy and built in different commercial LPBF-AM machines. The comparison of numerical with experimental results aims to demonstrate that the present modelling method is valid for the simulation of LPBF process for realistic parts produced by variable process conditions and material types. The process parameters and build conditions of each test case are given in a concise way in Table 1.

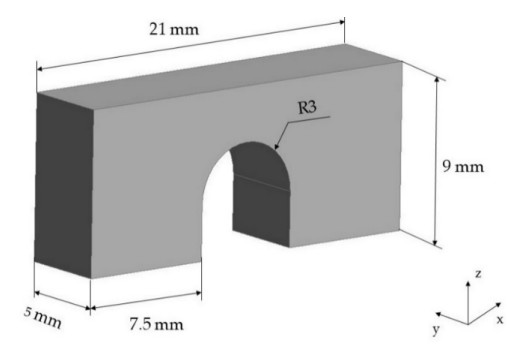
2.1.2.   Experimental test case 1: Bridge shaped Ti–6Al–4V part

Stranza et al. ^[34] designed and fabricated a bridge shaped Ti–6Al–4V specimen (Figure 1) to experimentally determine the residual strains and stresses and to compare them with their modelling results ^[34,36]. The dimensions of the part are 21 mm, 5 mm and 9 mm for its length, width and height, respectively. A circular arc with a radius of 3 mm is used to join the two legs of the specimen forming the final bridge shaped part. The part was constructed of Ti–6Al–4V AM metal alloy and fabricated in a Concept Laser M2 LPBF machine. A continuous scan strategy of 45° rotated to x-axis laser direction with 90° interlayer rotation was used with a laser power of 100 W, scanning speed of 600 mm/s, hatch spacing of 105 μm and layer thickness of 30 μm. Preheat temperature was not determined in their work and in the present model a 30 ℃ temperature (denoted in the Table 1 as Room Temperature, RT) was considered. Average layer deposition time was 17 s.

High energy X-ray diffraction method was utilized to determine the three-dimensional residual strains and stresses in the midplane cross-sectional area of the component. Contour plots of the residual strains and stresses in midplane were determined, as well as measurements of x, y and z components of strains along three-line profiles in the midplane. Measurements were collected every 0.5 mm for the x- and z- components and every 1 mm for the y-component of residual trains. These data provide a complete set that can be used for a comprehensible comparison with the predicted residual stresses and stresses of a part scale LPBF process simulation.

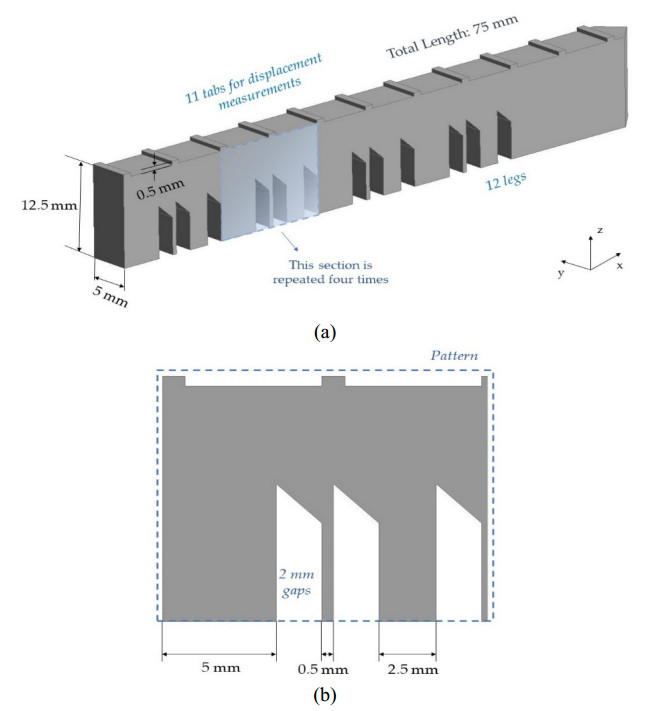
2.1.3.   Experimental test case 2: IN625 single cantilever beam part

National Institute of Standards and Technology (NIST) has developed a program of experimental test series that seeks to provide rigorous benchmark measurements for all AM materials and methods, named AM–Bench. The AMB2018-01 ^[37] test series aim to make available a robust set of data for validation and accuracy improvement of model predictions in residual stresses and other characteristics of AM parts, such as melt pools dimensions. Within the test series, a LPBF single cantilever beam of 12 legs of varying thickness was built (Figure 2) ^[35]. The 12 legs consist of 4 replications of a 3-leg section with size of 5 mm, 0.5 mm and 2.5 mm, for each leg. The resulting geometry was quite intricate stimulating the interest about the distributions of residual strains and stresses. The external dimensions of the cantilever part were 75 mm, 5 mm and 12.5 mm for length, width and height, respectively. Inconel 625 AM metal alloy was used for the fabrication of the part. Four LPBF parts were built on the middle of build plates of 100 mm² surface and 12.7 mm thickness and in the thermomechanical model only one part was considered. The part was fabricated in an EOS M270 machine. A continuous scan strategy of 45° rotated to x-axis laser direction with 90° interlayer rotation with contour scanning was applied with a laser power of 195 W, scanning speed of 600 mm/s, hatch spacing of 100 μm and layer thickness of 20 μm ^[35].

Residual strains and stresses were experimentally determined with Neutron Diffraction (ND), X-ray Diffraction (XRD) and Contour Method (CM). CM was also used to measure the displacement of the part after cutoff from the base plate. ND and XRD contour maps of residual strains and stresses were derived in the midplane cross-sectional area of the part to show their distribution and CM contour maps derived in three legs cross section. ND and XRD methods were also used to determine the distribution of residual strains along three-line profiles. Generally, all of the measuring techniques showed a high degree of agreement. In the present study, XRD measurements were preferred over ND ones because they captured the large stain data at part edges and asymmetric strain distributions from one leg to the other ^[35].

2.2.   Thermomechanical modelling approach

2.2.1.   Description of thermomechanical modelling method

The main goal of the present modelling method is the prediction of distortions, residual strains and stresses at part/component level in a computationally efficient way. For this reason, the modelling method utilizes an abstractive approach for the simulation of LPBF process of large parts to reduce the computational cost. The main assumption concerns the modelling of heat source. Rather than modelling the laser beam heat source and the scan pattern, heat input is applied on an entire layer at once. More specifically, every layer of the part is heated uniformly at the melting temperature of the considered AM metal alloy. This basic hypothesis, follows the assumption that the process parameters for the building of the part have been appropriately selected so lack of fusion and keyhole flaws resulting from insufficient and excess melt, respectively, cannot be formed ^[33].

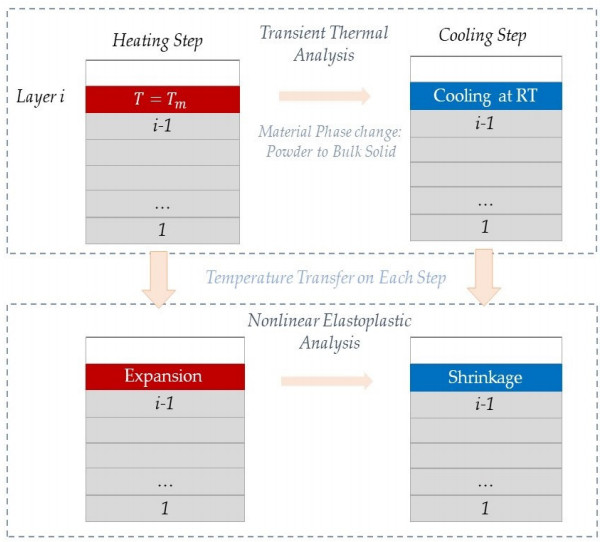
Thermomechanical analysis consists of two different analyses, a nonlinear thermal transient analysis and a quasi-static elastoplastic mechanical analysis. Thermomechanical analysis is performed in a uncoupled way. The standard element birth and death method was used to model the deposition of the processed layers of the part. Thermal transient analysis also consists of two steps. During the first step, the elements of the processed layer are activated and heated gradually at the melting temperature of the material, as mentioned previously. Then, the processed layer is cooled down at the chamber environment temperature. Cooling time is determined as the time spent by the recoater to spread the new layer of powder on the plate. The estimated temperature fields are imported as an input into the mechanical analysis to predict the material expansion during the heating step and material contraction during the cooling step for each layer. The residual stresses and distortions arise as result of subsequent new layer expansion and contraction. At the heating step, the expansion of each new layer is restricted by the cooler underlying part resulting in compressive stresses in the new layer, and tensile stresses in the underlying layers. Inversely, at the cooling step the new layer is contracted quickly but is restricted by the underlying layers resulting in tensile stresses in the new layer and compressive stresses at the underlying layers. This approach accounts for the layer expansion and contraction mechanism of residual stresses formation described by Mercelis and Kruth ^[12]. Figure 3 presents a flowchart of the present thermomechanical modelling method.

The simulation of LPBF process for the fabrication of large parts with this modelling method provide simple yet accurate means, as it is presented in the section 3, for the estimation of residuals strains and stresses in an efficient way. The basic hypothesis of the application of uniform temperature equal with melting point of AM metal alloy can be supported by the fact that with completion of the scanning of a layer the temperature fields reach approximately a uniform temperature near the melting point of the processed material. When the laser scan strategy is optimized and combined with the lumped layer approach very low computational times can be achieved. Moreover, this modelling approach is suitable for the optimization of the LPBF process for realistic parts regarding the level of residual strains and stresses, as the effect of build orientation, build conditions and the main process parameters could be effectively assessed. The main limitation of the proposed method is that, although it considers the evolution of temperature fields due to the geometric characteristics of a part, it does not account the x- and y- component of the temperature gradients. Thus, it can significantly affect the accuracy of the presented methodology especially for the thick regions of a part, where temperature fields might not present homogeneity.

2.2.2.   Part geometry and mesh strategy

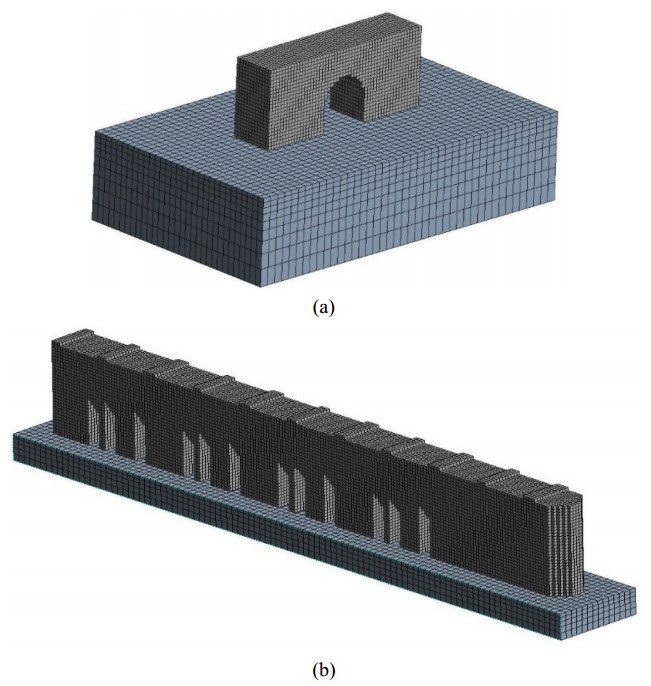
For the current modelling and simulation purposes, the ANSYS 2020R2 Additive Systems Software was used ^[33]. In the modelling of each test case, except from the part geometry a section of build plate was considered in order to account the large heat sink effect induced by the large size of the substrate compared to LPBF part. To make the computational analysis less expensive, only a comparable to part dimensions section of the build plate was considered. In any case the total size of the modelled substrate is enough to account for the heat sink effect.

A voxelated or uniform cartesian mesh scheme was chosen for the discretization of the part and build plate in each test case to achieve a structured mesh. Identical mesh was used in both thermal and structural analysis to ensure the transfer of thermal load without any need for interpolation between the temperatures of nodes. Eight-node and twenty-node thermal and structural elements were used for the part and build plate, respectively. In thermal model, three-dimensional thermal elements SOLID70 (8-node) and SOLID90 (20-node) were used for the discretization of the part and build plate, respectively. In the mechanical model, the previous combination of elements were replaced by three-dimensional structural elements SOLID185 and SOLID186 for part and build plate, respectively. In both models, the same pair of eight-node general contact elements (CONTA174-TARGE170) was utilized to ensure for the same values of temperatures and displacements on the interface between the part and the build plate in heat transfer and structural analysis.

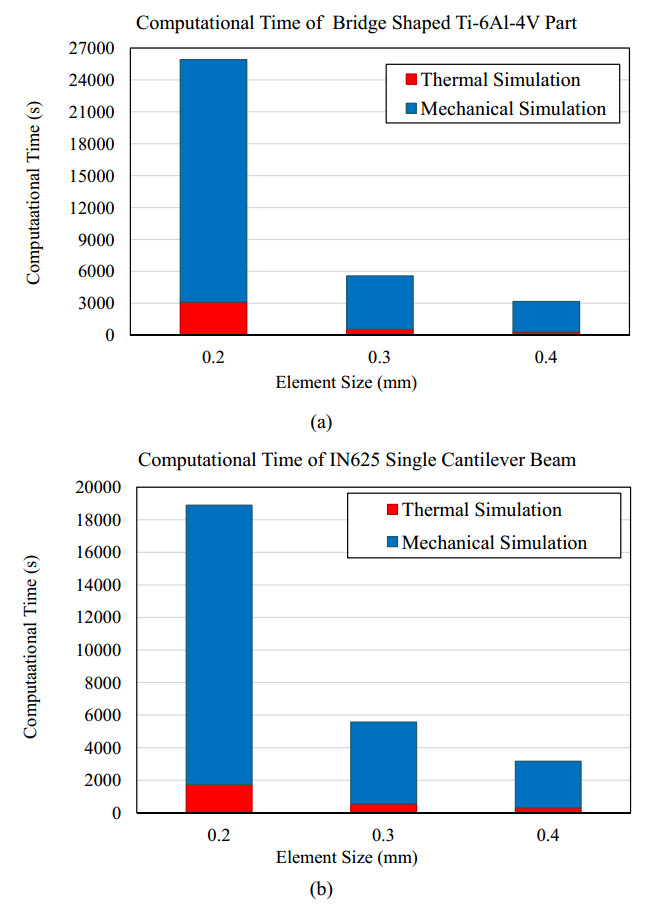
To further simplify and make the analysis more efficient a large number of layers was merged into one thick layer, as the explicit modelling of each layer would lead to enormous computational time. However, due to voxelization the size of the element is related to the number of lumped layers. A mesh convergence study was performed for each test case. Element sizes of 0.2 mm, 0.3 mm and 0.4 mm were tested which account to about 7, 10 and 13 lumped layers, respectively in the case of bridge part and 10, 15 and 20 lumped layers, respectively in the case of single cantilever. The mesh details for each test case and each element size is presented in the Table 2. Although, the results presented small differences among themselves, the computational time was exponentially increased between the models as the size of element decreased. The computational results for the 0.4 mm element size case are presented in the results. The computational times for each element size are presented in the section 3.3. Figure 4 presents the finite element model with element size of 0.4 mm for each test case. In all models the build plate is discretized with a coarser mesh to make the analysis less expensive.

2.2.3.   Temperature-dependent material properties

Ti–6Al–4V and IN625 AM metal alloys were used for the fabrication of LPBF parts of the presented test cases. A meso-scale medium approach is implemented for the modelling of material properties, where only the macroscopic properties are considered. Temperature-dependent properties of material are also considered because of the wide range of temperatures and physical states that AM materials experience during the LPBF process. Temperature-dependent data for thermal conductivity, specific heat, coefficient of thermal expansion, density and elasticity were utilized for each material. Temperature-dependent yielding behavior is also considered with a bilinear isotropic hardening model. The melting temperature of each AM metal alloy is presented in Table 3.

2.2.4.   Initial and boundary conditions

In the thermal analysis of each test case, to account for the heating of the build plate during the process, build plate was assigned an initial temperature equal with the corresponding preheating temperature and a boundary condition of the same temperature on its bottom surface to maintain this temperature during the process. In the subsequent mechanical analyses, the bottom surface of the base plate is fixed to account for the rigidity of the substrate. This way, every distortion developed during the building of the part comes a result of the development of residual stresses.

Regarding the heat loss during the cooling down step of the thermal analysis it mainly depends on the cooling temperature of the inert chamber and the convection heat transfer with the surrounding chamber environment. The sensitivity of the powder and gas convection coefficients and the cooling temperature has been investigated and it was found that slightly affected the results presented in the paragraph 3, findings which are in agreement to Yang et al. ^[40]. In the simulations at the scale of melt pool where the time increments are smaller and the heat transfer phenomena are considered more meticulously these model parameters are expected to have more influence on the model outputs.

3.   Results and discussion

3.1.   Bridge shaped Ti–6Al–4V part

In the case of the bridge shaped Ti–6Al–4V part, the experimental characterization with X-ray diffraction method provided data regarding the variation of strain components on three-line profiles placed in the midplane cross-section of the part. X-ray energy dispersive diffraction method utilized a polychromatic X-ray beam with effective spectrum from 50 to 150 keV. The incident X-ray beam was masked to a 0.2 mm × 0.2 mm cross-section by incident beam slits and penetrated the Ti–6Al–4V sample and diffracted through two sets of slits defining a fixed 2θ angle of 8° to a germanium, single element energy resolved detector. The bridge part was positioned in a four-circle goniometer with built-in translation stages that enabled the automated rotation and positioning of the sample to collect diffraction data for the three orthogonal strain components (x, y and z) over the cross-section at the midplane of the part ^[39]. The residual strains were determined from the relationships:

where $a$ and $c$ are the lattice parameters of the crystal structure of bridge part and ${a}_{0}$, ${c}_{0}$ are the stress-free lattice parameters. The strains were calculated using the averaged crystallographic strain, given by:

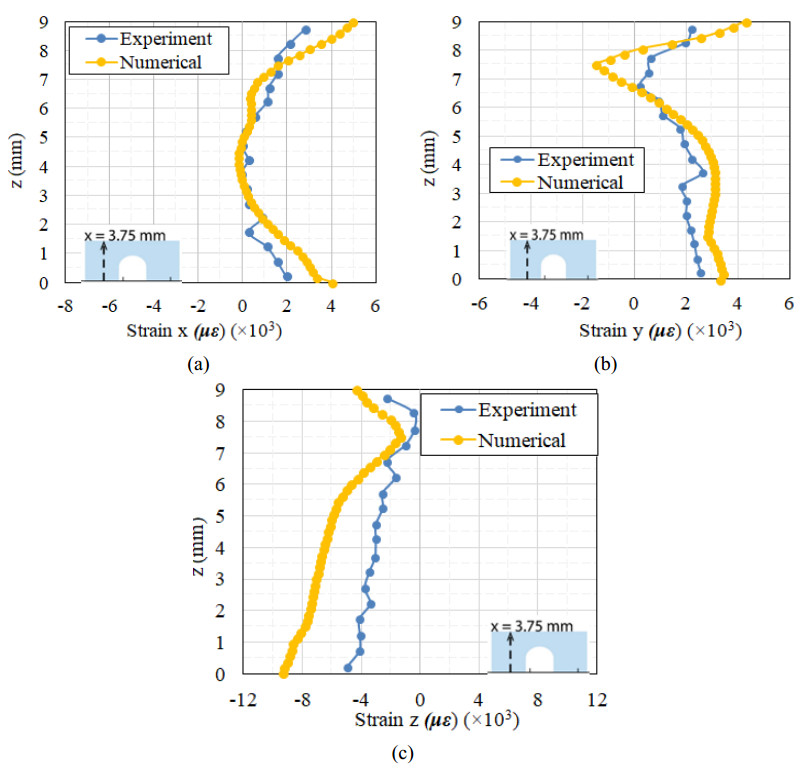
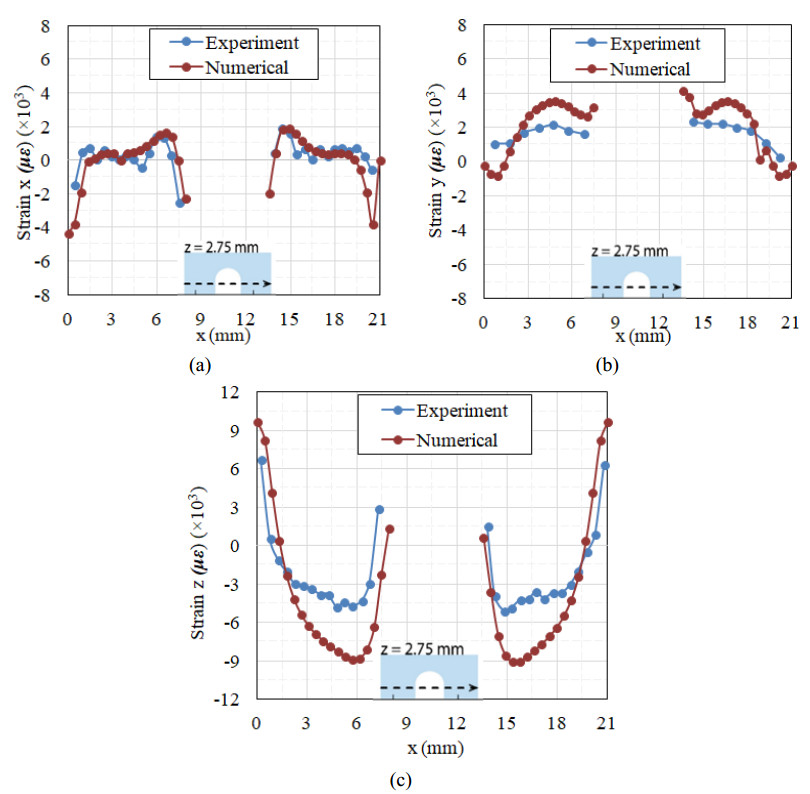
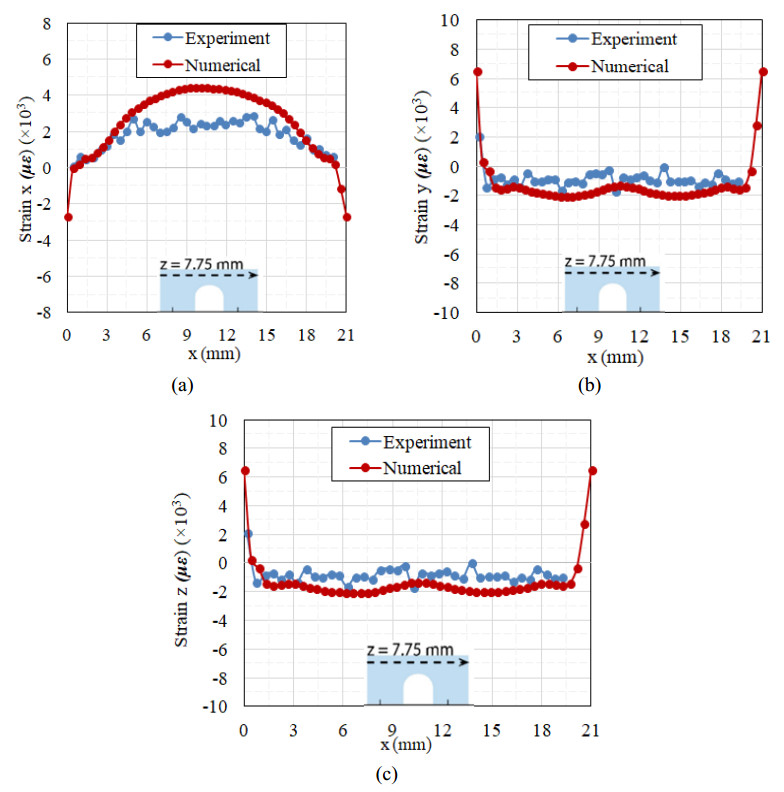
More details regarding the experimental determination of residual strains can be found in ^[39]. Similar experimental procedures were used for the measurement of residual stress and strains in IN625 single cantilever beam of the test case 2 ^[35]. The first line profile had a vertical direction to the build plate and it was placed at a distance of 3.75 mm from the left edge of the part. The second and the third line profile had a parallel direction to the build plate and they were placed at distance of 2.75 mm and 7.75 mm above the upper surface of the build plate, respectively ^[39]. Figures 5–7 present the comparison of between numerical and experimental results for the three profiles.

As it can be observed in Figures 5–7, the predicted results followed the of the experimental measurements quite well in most cases. Regarding the predicted magnitude of strain components, numerical results presented small divergence with experimental ones for most cases. The z-strain component numerical results have the higher divergence with respect to the experimental ones along the x = 3.75 mm line profile. The overestimation of y- and x- strain components in the z = 2.75 mm and z = 7.75 mm profiles, respectively, may be attributed on the assumption of uniform heat input, which did not consider the scan strategy and the subsequent variation of x- and y- temperature gradients and strains components. Τhe predicted results are comparable to the results of the work of Geniwala et al. ^[36] where a lumped laser pass method has been employed to address the effect of scan strategy. However, no considerable differences were observed indicating the capability of the presented method for precise estimation of residual strains and stresses.

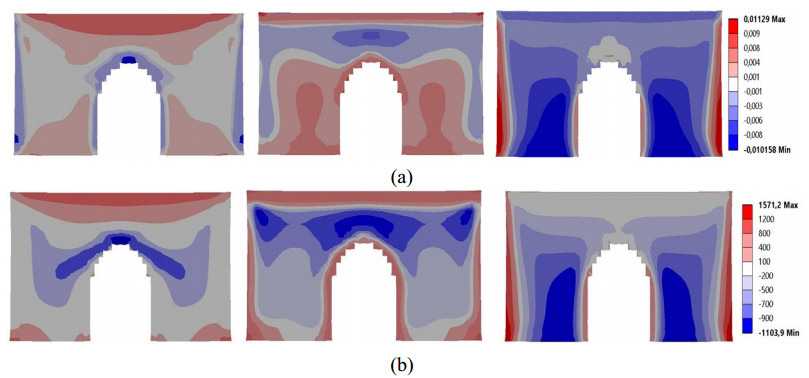
In Figure 8a, b, the numerical estimation of residual strains and stresses distribution in the midplane cross-section of the bridge part are presented. The predicted distributions agree well with experimental distribution trends presented in ^[34] for all the occasions. The magnitude of predicted residual strains and stresses present also very good correlation with the experimental ones ^[34], with the y- component of residual strains and stresses showing the higher differences compared to other ones.

3.2.   IN625 single cantilever beam

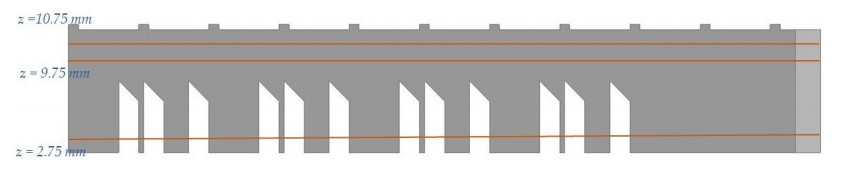
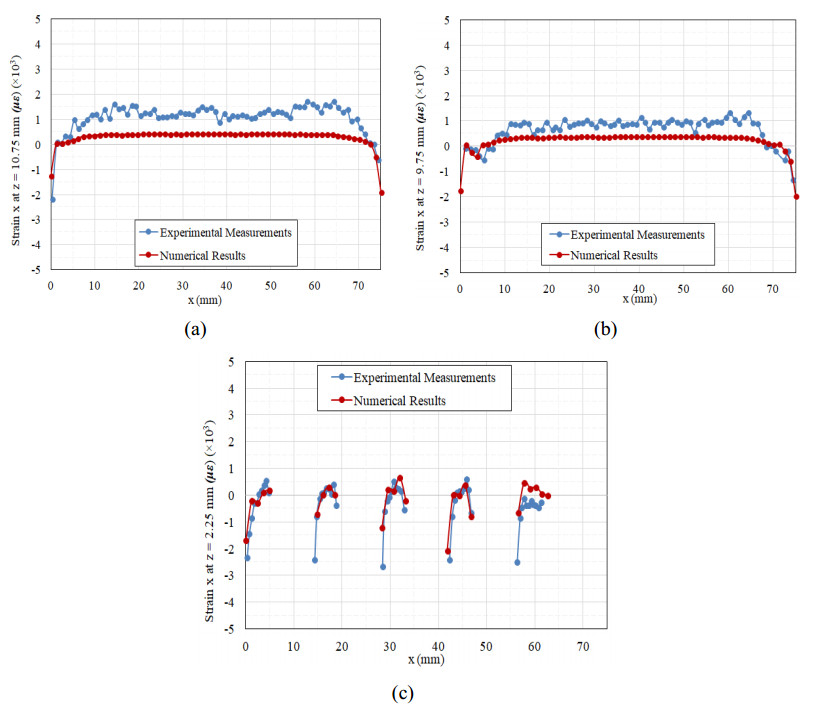
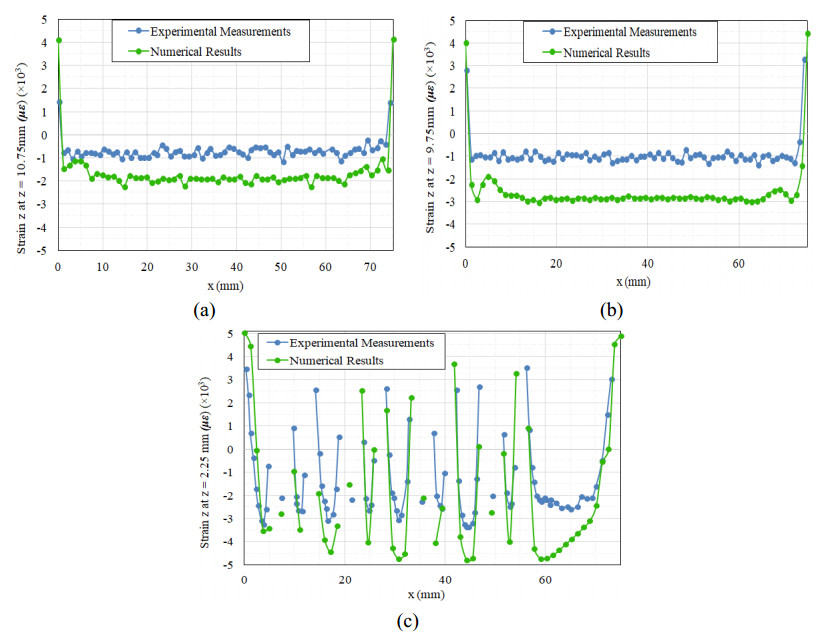
For the case of IN625 single cantilever beam, X-ray diffraction characterization provided experimental data for the variation of x- and z- components of residual strains along three-line profiles which expanded along the length of the cantilever beam ^[35]. The three-line profiles had parallel direction to the build plate and they were placed at the distance of 2.25 mm, 9.75 mm and 10.75 mm above the top surface of the substrate, as shown in Figure 9. Figures 10 and 11 present the comparison between numerical and experimental results for the x- and z- component of strains of the three-line profiles.

As can be observed in Figures 10 and 11, the numerical results follow the trending of experimental measurements very well. Regarding the prediction of the magnitude of strains, the numerical results of the strain x component present discrepancies with the respective experimental measurements especially along the line profiles, which are placed in the longest distance above the substrate (z = 9.75 mm, 10.75 mm), as it is presented in Figure 10a, b. These discrepancies can be attributed to the application of a uniform heat input on the lumped layer that neglects the effect of the laser scan strategy. The line profiles at the distance of z = 9.75 mm and 10.75 mm above the substrate are placed at the thicker areas of the part where the effect scan pattern is more profound, thus, there are larger deviations between experimentally measured and predicted residual strains. On the contrary, the predicted residual strains at the thinner legs of the part (line profile at z = 2.75 mm) where the laser raster is not so extensive present less divergence with respect to experimental results. The predicted distribution of x-, z- and xz- components of residual strains in the midplane cross-section of the cantilever beam is presented in Figure 12a–c.

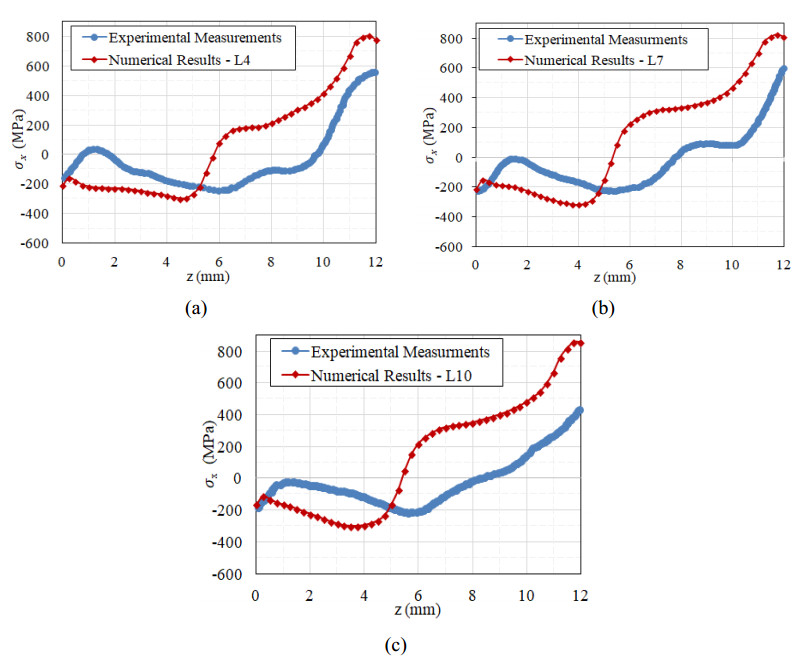
The distribution of in-plane residual stresses in the cross-sections of the part was experimentally characterized with contour method ^[35]. More specifically, the variation of σ_x component of residual stresses along the line on the midsection of the fourth, seventh and tenth leg was experimentally measured. Figure 13a–c present the comparison between experimental and numerical results for the fourth (L4), seventh (L7) and tenth (L10) leg of the cantilever beam, respectively. In the variations of all legs, it can be seen that despite the following of the trending of the experimental measurements, the predicted results present considerable divergences with experimental data, mainly, at the areas of the maximum compressive residual stresses. These characteristics are mainly attributed on the simplified prediction method of temperature fields were the in-layer temperature gradients were neglected and may serve as a primal driving mechanism for residual stresses formation ^[41]. This denotes the need of the incorporation of the laser scan strategy in the modelling techniques in an efficient way, as the laser scanning in the layer plane seems to serve as a considerable driver of residual stresses formation. In the work of Geniwala et al. ^[42], an adaptive meshing scheme was utilized in combination with lumped laser pass modelling technique in order to integrate the laser raster into the modelling scheme and the predicted strain x components of residual strains correlated better with experimental measurements.

3.3.   Computational time

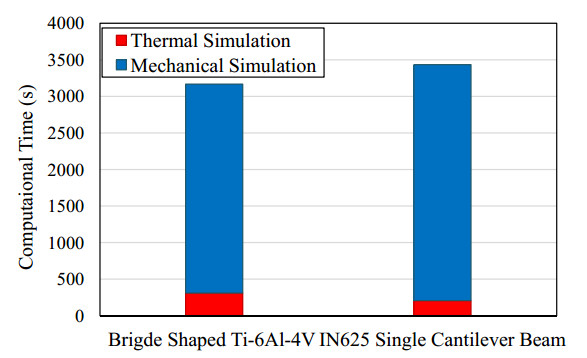
The simulations were performed on a workstation computer system of 16-Core 3.50 GHz CPU with 64 GB RAM. The total computational time for each test case with element size of 0.4 mm is presented in the Figure 14, as well as the percentage of thermal and mechanical simulation. As it can been seen, for element size of 0.4 mm the total computational time for each case was less than an hour (53 and 57 min for the bridge part and the cantilever beam, respectively). Moreover, the total amount of the thermal simulation time was significantly lesser than of the mechanical simulation. As it was expected, the part with the largest dimensions (single cantilever beam) needed a slightly larger simulation time than the part with the smaller dimensions (bridge shaped part).

In the Figure 15, the computational time of element sizes of 0.2 mm, 0.3 mm and 0.4 mm for each test case are presented. It can be seen that by decreasing the element size in linear fashion the total computational times increase exponentially without any significant difference between the predicted results. This trend shows that in cases of large parts the element size in a voxelated mesh strategy must be carefully chosen to make the analysis as efficient as it can be. An optimal choice of element size whose thickness would be equivalent with the thickness of the merged layers may lead to reasonable simulation times with accurate results. In general, the overall results point out that this thermomechanical modelling approach is suitable for a fast estimation of residual strains and stress in a LPBF part and it can be applied in realistic components for an initial analysis. Although, the comparison with previous efficient and more sophisticated modelling approaches ^[36,42,43] that use the same test cases for validation purposes cannot be directly made due to the use of different computer systems, the trend in comparison shows that the present method is more suitable for the simulation of LPBF process for large parts, though, special care has to be taken in order to examine the results carefully considering the previous limitations of the absence of scan strategy into the modelling scheme. Considering the total simulation time of the presented test cases, the simulation run time for a realistic AM part can reach a few hours even for computer systems with medium resources with a proper choice of element size.

4.   Conclusions

A thermomechanical modelling method for simulation of LPBF process for the prediction of distortions and residual stresses in parts is presented. To make feasible the simulation of LPBF process and achieve calculations of residual stresses and distortions a uniform heat input at layer level was applied during the part modelling. More specifically, on each layer of the part the melting temperature of AM metal alloy is applied simultaneously. Moreover, many thin layers were merged into a thicker one to form a lumped layer to make the analysis more efficient. Comparisons with a series of test cases of available experimental data to assess the robustness of the modelling method under different metal AM alloys, geometries and process conditions were performed.

The main concluding remarks are:

1. In all test cases, the predicted results agreed with experimental measurements regarding to the trending of residual strains and stresses. However, the magnitude of residual stresses and strains may present significant differences in some of their components and in regions of maximum and minimum distributions.

2. The differences are mainly attributed to the alternative heat source used for the estimation of temperature fields in the thermal analysis, which does not consider the scan pattern in the model.

3. The computational time required for all simulations was very short. The combination computational time reduction and accuracy makes the proposed thermomechanical modelling method suitable for the realistic calculation of residual strains and stresses distributions in realistic LPBF parts.

Therefore, this modelling approach is suitable for integration in design procedure of an AM part and it can assist in the first-time-right building of a part with the optimization of build conditions, such as build orientation angle and the selection of process parameters that lead to the minimum amount of residual stresses. Moreover, this modelling method can be combined with topology optimization methods included in the ANSYS commercial finite element package to provide topology optimized designs with high load to weight ratio. To further advance the present modelling approach, the laser beam interaction and the scan strategy for the simulation of LPBF process will be considered.

Conflict of interest

Authors declare no conflict of interest.