Topological changes of brain network during mindfulness meditation: an exploratory source level magnetoencephalographic study

1.   Introduction

The competition model is an important part in the study of population dynamics and has been discussed widely ^{[1,2,3,4,5,6,7,8]}. The classical two-dimension Lotka-Volterra competition model is constructed based on the law of mass action, that is, the competitive capacity of one species is assumed to be proportional to the number or density of its competitive species. Though the classical Lotka-Volterra competition model and its various extensions have been extensively studied in the literature ^{[9,10,11,12,13,14,15,16]}, it has a deficiency that the competitive capacity of one species may increase and go to infinity with the increase of its competitors density.

Let $u = u(t)$ and $v = v(t)$ be respectively the densities of two competitive species. The following model with saturation competitive capacity has properly overcome the above deficiency of the classical Lotka-Volterra competition model:

where $a$ and $d$ are the two species' respective intrinsic growth rates; $b$, $e$ and $c$, $f$ are their respective intra- and inter-specific interaction coefficients. The parameters here are all assumed to be positive. We refer the readers to references ^[17,18,19] for some related extension works.

Due to the ubiquitousness of spatial diffusion in the real world, the spatiotemporal dynamics of the reaction-diffusion equation have recently been increasingly discussed by many authors ^{[20,22,23,24,25,26]}. For example, one may focus on the pattern formation of biological tissues to reveal the mechanism behind the forms ^[26]. In addition, in order to better understand the interaction between prey and the predators, some diffusive population models are discussed to illustrate the influence of diffusion and the way in which different individuals interact (cooperation, competition, herd behaviors etc.) ^{[20,22,23,24,25]}. To observe how the diffusion affects the dynamical behaviour of model (1), in a recent paper ^[21], we proposed and analyzed a diffusive competition model with saturated interaction terms, and showed that cross-diffusion is of great importance in the spatial pattern formation. Besides, time delay is another important component in constructing population models. Researchers investigated the effects of both diffusion and time delay, and have observed some interesting phenomena, such as Turing pattern ^[27,28,29], stability ^[30,31] and the occurrence of Hopf bifurcation induced by time delay ^[32,33,34].

Motivated by the above mentioned biological facts and the observed nonlinear phenomena, we propose the following diffusive competition model with delay:

where $d_1$ and $d_2$ are respectively the diffusion constants for the two species, and $\Delta$ the usual Laplacian operator. The other symbols play similar roles as in model (1). The main objective of this paper is to study the effect of time delay on population dynamics of model (2). The conclusions show that delay may destabilize the stable positive equilibrium, resulting the spatially homogeneous or nonhomogeneous Hopf bifurcations.

The organization of this paper is as follows. In Section 2, by analyzing the characteristic equation, the stability of positive equilibrium and the existence of Hopf bifurcations are studied. In Section 3, we obtain the formulae that determine the direction and stability of the spatial Hopf bifurcation by applying the normal form theory and the center manifold theorem. In Section 4, some numerical simulations are given to demonstrate the theoretical results, and finally, some conclusion and discussion are presented in Section 5.

2.   Stability of the positive equilibrium and existence of Hopf bifurcations

We have shown in ^[21] that when $[(a+b)d-af][(e+d)a-cd] > 0$, model (1) has a unique positive constant equilibrium $E_* = (u_*, v_*)$, which is global asymptotically stable provided

otherwise it is unstable. Note that model (1) has the same constant equilibrium as that in model (2). Now we discuss the stability of $E_*$ and the existence of Hopf bifurcation for system (2). Under the hypothesis $(H)$, we shift the equilibrium $E_*$ to the origin by letting $\tilde{u}(x, t) = u(x, t)-u_*$, $\tilde{v}(x, t) = v(x, t)-v_*$, which yields $u(x, t) = u_*+\tilde{u}(x, t)$, $v(x, t) = v_*+\tilde{v}(x, t)$. Therefore, we obtain the following system (dropping off the tildes)

Then the linearized system corresponds to model (3) at $E_*$ is

where

Let $U = {{\left(u, v \right)}^{T}}$, ${{U}_{t}}\left(\theta \right) = U\left(t+\theta \right) = \varphi \left(\theta \right) = {{\left({{\varphi }_{1}}, {{\varphi }_{2}} \right)}^{T}}, \theta \in [-\tau, 0]$ and $D\Delta = \left(\begin{matrix} {{d}_{1}}\Delta & 0 \\ 0 & {{d}_{2}}\Delta \\ \end{matrix} \right)$. We can rewrite model (4) as an abstract functional differential equation in $C\left([-\tau, 0], X \right)$:

where $X = \{u, v\in {{W}^{2, 2}}\left(0, l\pi \right):{{u}_{x}} = {{v}_{x}} = 0 \ \mathrm{for} \ x = 0, l\pi \}$, the linear operator $L:C\left(\left[-\tau, 0 \right], X \right)\to X$ is given by

with characteristic equation being

where $dom\left(\Delta \right)\subset X$ and $(e^{\lambda\cdot}y)(\theta) = e^{\lambda\theta}y$. Notice that the linear operator $\Delta$ on $X$ has the eigenvalues $-k^2$ $(k\geq0)$. It follows from ^[35] that $\lambda$ is a characteristic value of Eq (7) provided that $\lambda$ satisfies

that is

Under condition $(H)$, we have

Let $z = \left(\lambda +{{k}^{2}} \right){{e}^{\lambda \tau }}$, Eq (8) will be transformed into the following form:

Because ${{T}^{2}}-4D = {{\left({{a}_{11}}-{{a}_{22}} \right)}^{2}}+4{{a}_{12}}{{a}_{21}} > 0$, Eq (9) has two negative real roots:

and ${{z}_{1}} < {{z}_{2}} < 0$. Eq (8) is equivalent to

When $\tau = 0$, Eq (8) has two negative real eigenvalues ${{\lambda }_{1}} = -{{k}^{2}}+{{z}_{1}}, {{\lambda }_{2}} = -{{k}^{2}}+{{z}_{2}}$ and ${{\lambda }_{1}} < {{\lambda }_{2}} < 0$ for any $k$. We can have the following lemma:

Lemma 2.1. Suppose that condition $(H)$ holds. Then all the eigenvalues of characteristic Eq (8) with $\tau = 0$ have negative real parts for all $k\geq0$.

Now we examine whether there is a positive constant $\tau^*$ such that $\operatorname{Re}\left({{\lambda }_{n}}\left(\tau^* \right) \right) = 0$. Let $\lambda = \pm \omega i$, $\omega > 0$ be a pair of roots of Eq (10), then

separating the real and imaginary parts, we obtain

which lead to

Since ${{\cos }^{2}}\omega \tau +{{\sin }^{2}}\omega \tau = 1$, the above equation is equivalent to

then

If $k = 0$, we can obtain that $\omega_n = -z_n$, cos $\omega \tau$ = 0, sin $\omega \tau = 0$, which implies that

Let

Thus, when $k = 0$ and $\tau = \tau_j^n$, Eq (8) has a pair of pure imaginary roots $\pm i \omega_n$.

If $k\neq0$, i.e. $k\geq1$. We have the following three cases.

Case 1: $-1 < z_1 < z_2 < 0.$

In this case, since ${z}_{n}^{2} < 1\le {{k}^{4}}$, no positive $\omega$ satisfies the Eq (10). That is to say that all the eigenvalues of characteristic Eq (8) have negative real parts for all $k\geq1$. Noting that $z_1 < z_2 < 0$, therefore, $\tau _{j}^{1} < \tau _{j}^{2}$ and $\tau _{j}^{n} < \tau _{j+1}^{n}$. We have

We have the following conclusion.

Lemma 2.2. Let ${{\tau }_{0}} = \tau _{0}^{1}$, Then the following conclusions hold:

(1) For $0\leq \tau < \tau_0$, all roots of Eq (8) have negative real parts;

(2) For $\tau = \tau_0$, we only have a pair of pure imaginary roots $\pm i z_1$ for Eq (8) that corresponds to $k = 0$, and all other roots have negative real parts;

(3) For $\tau = \tau_j^n$ $(n = 1, 2; j = 0, 1, 2, \cdots)$, we only have a pair of pure imaginary roots $\pm i z_n$ for each $n = 1, 2$corresponding to $k = 0$, and all other roots have negative real parts.

Next, we will examine whether the transversality condition holds. Suppose $\lambda(\tau) = \alpha(\tau)+i\omega(\tau)$ denotes the eigenvalue of Eq (10) near $\tau = \tau_j^n$ satisfying $\alpha(\tau_{j}^{n}) = 0$, $\omega(\tau _{j}^{n}) = \omega_{n}$ $(n = 1, 2; j = 0, 1, 2, \cdots)$. Differentiating Eq (10) with respect to $\tau$, we obtain

Thus, by Eq (10), we have

Thus, we have

Lemma 2.3. Suppose that condition $(H)$ is satisfied. Then

for $n = 1, 2;j = 0, 1, 2, \cdots$.

Combining Lemmas 2.2 and 2.3, we can have the following result.

Theorem 2.4. Suppose that condition $(H)$ is satisfied, then for system (2) we have

(1) if $\tau \in [0, \tau_0)$, then the equilibrium $E_*$ of model (2) is asymptotically stable;

(2) if $\tau > \tau_0$, then the equilibrium $E_*$ of model (2) is unstable;

(3) Hopf bifurcations occur at the equilibrium of (2) when $\tau = \tau_j^n(n = 1, 2;j = 0, 1, 2, \cdots)$, and these Hopf bifurcations are all spatially homogeneous.

Case 2: $z_1 < -1 < z_2 < 0$.

According to ${{\omega }_{k}} = \sqrt{{{z}_{n}}^{2}-{{k}^{4}}}$, there exists an positive integer $N_0$ such that

For any positive integer $k \in [1, N_0]$, Eq (13) exists a positive root ${{\omega }_{k1}} = \sqrt{{{z}_{1}}^{2}-{{k}^{4}}}$. Arguing similarly as in Theorem 2.1, as $\tau$ passes through the critical values

system (2) will undergo a spatially inhomogeneous Hopf bifurcation at equilibrium point $E_*$.

Case 3: $z_1 < z_2 < -1$

Define $N_n, n = 1, 2$ by

For any positive $k \in [1, N_n]$, the Eq (13) exists a positive root ${{\omega }_{kn}} = \sqrt{{{z}_{n}}^{2}-{{k}^{4}}}$. As $\tau$ passes through the critical values

model (2) will similarly undergo a spatially inhomogeneous Hopf bifurcation at equilibrium point $E_*$.

To summarize, we have the following result.

Theorem 2.5. Suppose condition $(H)$ holds, then we have for model (2) that

(1) if $-1 < z_1 < z_2 < 0$, a spatially homogeneous Hopf bifurcation occurs at equilibrium $E_*$ as $\tau$ passes though $\tau = \tau_j^n$;

(2) if $z_1 < -1 < z_2 < 0$, a spatially homogeneous Hopf bifurcation occurs at equilibrium $E_*$ as $\tau$ passes though $\tau = \tau_{0j}^1 \ \ (j = 0, 1, 2, \cdots)$ and a spatially inhomogeneous Hopf bifurcation occurs at $E_*$ as $\tau$ passes though $\tau = \tau_{kj}^1 \ \ (k = 1, 2, \cdots, N_0;j = 0, 1, 2, \cdots)$;

(3) if $z_1 < z_2 < -1$, a spatially homogeneous Hopf bifurcation occus at equilibrium point $E_*$ as $\tau$ passes though $\tau = \tau_{0j}^n \ \ (n = 1, 2;j = 0, 1, 2, \cdots)$ and a spatially inhomogeneous Hopf bifurcation occurs at $E_*$ as $\tau$ passes though $\tau = \tau_{kj}^n \ \ (n = 1, 2;k = 1, 2, \cdots, N_0;j = 0, 1, 2, \cdots)$.

3.   Direction and stability of the spatial Hopf bifurcation

In this section, using the normal form theory and center manifold theorem ^[35,36], we investigate the direction of Hopf bifurcation and the properties of the bifurcating periodic solutions at the critical value $\tau_{kj}^n$. Throughout this section, we always assume that condition $(H)$ holds, and denote $\tau_{kj}^n$ by $\tilde{\tau }$ for fixed $n \in {1, 2}$, $k \in {0, 1, 2, \cdots}$ and $j \in {0, 1, 2, \cdots}$. Then at $\tau = \tilde{\tau }$, $\pm i \omega_0$ are the corresponding purely imaginary roots of the characteristic Eq (8). Letting $t\rightarrow \frac{t}{\tau}$ and $\tau = \tilde{\tau } + \mu$, then model (3) is equivalently transformed into the following equation in the phase space $C = C\left([-1, 0], X \right)$:

where

The linear system of Eq (15) is

By the Riesz representation theorem, there exists a $2\times2$ matrix function $\eta \left(\theta, \mu \right)$, $\theta \in [-1, 0]$ with its elements being of bounded variation such that

In fact, we can choose

where $\delta(\theta)$ is the Dirac function.

For $\varphi \in {{C}^{1}}\left([\text{-1}, \text{0}], {{\mathbb{R}}^{\text{2}}} \right)$, define

and

Then system (15) is equivalent to

For $\psi \in {{C}^{1}}\left([0, 1], {{\mathbb{R}}^{\text{2}}} \right)$, define

Here, $A$ and $A^*$ are a pair of adjoint operators under the following bilinear inner product

According to the discussions in previous section, we know that $\pm i \omega$ are eigenvalues of $A$, and therefore they are also eigenvalues of $A^*$. Suppose that $q\left(\theta \right) = {{\left(1, \alpha \right)}^{T}}{{e}^{i{{\omega }_{0}}\tilde{\tau }\theta }}$ is the eigenvector of $A$ corresponding to $i{{\omega }_{0}}\tilde{\tau }$, and ${{q}^{*}}\left(s \right) = D\left(1, \beta \right){{e}^{i{{\omega }_{0}}\tilde{\tau }s}}$ is the eigenvector of $A^*$ corresponding to $-i{{\omega }_{0}}\tilde{\tau }$. From $Aq\left(\theta \right) = i{{\omega }_{0}}\tilde{\tau }q\left(\theta \right)$, ${{A}^{*}}{{q}^{*}}\left(s \right) = -i{{\omega }_{0}}\tilde{\tau }{{q}^{*}}\left(s \right)$ and $\langle {{q}^{*}}\left(s \right), q\left(\theta \right) \rangle = 1$, we can easily obtain

Next, we use the same notation as in Hassard et al. ^[36]. We first compute the coordinates to describe the center manifold $C_0$ at $\mu = 0$. Let $u_t$ be the solution of Eq (15) when $\mu = 0$. Define

On the center manifold $C_0$, we have $W\left(t, \theta \right) = W\left(z, \bar{z}, \theta \right) = \left(W^{(1)}, W^{(2)}\right)^T$ with

where $z$ and $\bar{z}$ are local coordinates for center manifold $C_0$ in the direction of $q^*$ and $\overline{q}^*$. Note that $W$ is real if $u_t$ is real, we only consider real solutions. For solution $u_t \in C_0$ of Eq (15), since $\mu = 0$, we have

where

Then, we rewrite this equation as

Notice that ${{u}_{t}}\left(\theta \right) = W\left(t, \theta \right)+z\left(t \right)q\left(\theta \right)+\bar{z}\left(t \right)\bar{q}\left(\theta \right)$, $q\left(\theta \right) = {{\left(1, \alpha \right)}^{T}}{{e}^{i{{\omega }_{0}}\tilde{\tau }\theta }}$ and ${{q}^{*}}\left(s \right) = D\left(1, \beta \right){{e}^{-i{{\omega }_{0}}\tilde{\tau }s}}$. Through simple calculations, we can compare the coefficients of like terms, $z^2, \ \ z\bar{z}, \ \ \bar{z}^2, \ \ \, z^2 \bar{z}$ in Eq (24) with that in Eq (23), and obtain

where

We have already determined $g_{20}$, $g_{11}$ and $g_{02}$. Next we compute $W_{20}(\theta)$ and $W_{11}(\theta)$ in $g_{21}$.

We can easily get from Eq (21) that

From Eqs (18), (19) and (24), notice that $Azq\left(\theta \right) = i{{\omega }_{0}}\tilde{\tau }zq\left(\theta \right)$. We have

On the other hand, in the center manifold $C_0$, $W(z, \bar{z})$ satisfies

From Eqs (22) and (24), comparing the coefficients of Eq (26) with Eq (25) about $z^2$ and $z \bar{z}$, we obtain the following two equations

and

When $\theta \in [-1, 0)$, we have from Eq (18)

Therefore,

where $E_1$ is constant vector. When $\theta = 0$, we have from Eq (18)

Substituting Eq (30) into Eq (31), we have

Therefore,

where

Similar to the discussion of solving $W_{20}$, we have

and

where

Thus, we can determine $W_{20}(\theta)$ and $W_{11}(\theta)$. Furthermore, we can determine $g_{21}$. According to the notation from ^[36], we can compute the following values:

From the conclusion ^[36], we have the main results in this section:

Theorem 3.1. Assume that model (2) undergoes a Hopf bifurcation when delay $\tau$ crosses through the $\tau_{kj}^n$, then the following statements are true:

(1) $\mu_2$ determines the direction of the Hopf bifurcation: if $\mu_2 > 0 \ \ (\mu_2 < 0)$, then the Hopf bifurcation is supercritical (subcritical),

(2) $\beta_2$ determines the stability of the bifurcating periodic solution: if $\beta_2 < 0 \ \ (\beta_2 > 0)$, then the bifurcating periodic solution is stable (unstable),

(3) $T_2$ determines the period of the bifurcating periodic solution: if $T_2 > 0 \ \ (T_0 < 0)$, then the period increases (decreases).

4.   Numerical simulations

To support the theoretical results obtained in this paper, we illustrate some numerical simulations. We choose the parameters as $a = 1.5$, $b = 1.1$, $c = 1.1$, $d = 1.1$, $e = 1.15$, $f = 0.5$, $d_{1} = d_{2} = 1$.It is easy to check that condition $(H)$ holds, which indicates that there exists a unique positive equilibrium and it is globally asymptotically stable.

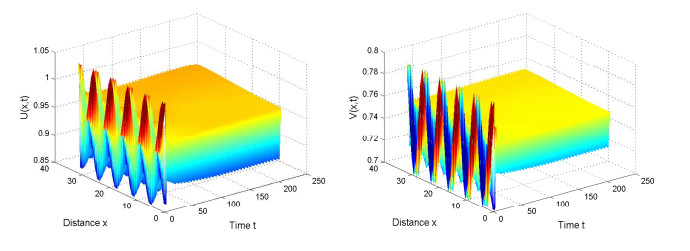
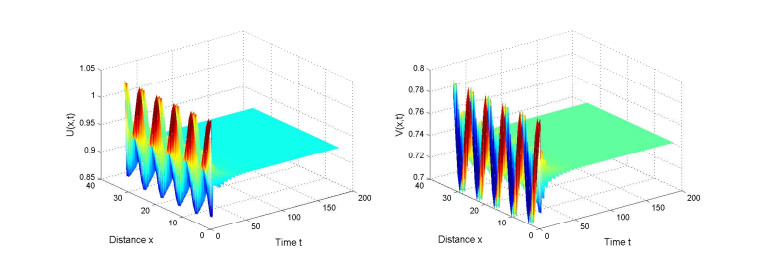
By simple calculations, we can know that the positive equilibrium is $E_* = (0.9363, 0.7463)$ and $z_1 = -1.1465 < -1 < z_2 = -0.7416$. In this case, $\omega_0 = 1.1466$ and $\tau_0 = 1.365$. Based on Theorem 2.5, we know that the positive equilibrium $E_*$ is asymptotically stable when $0\leq\tau < \tau_0$ and unstable when $\tau > \tau_0$. And a spatially homogenous periodic solution emerges from the positive equilibrium $E_*$ when delay $\tau$ is increasing across the critical value $\tau_0 = 1.365$. We can see that if $\tau = 1.2 < \tau_0$, the positive equilibrium $E_*$ is stable and an uniform distribution can be observed (see Figure 1). If $\tau = 1.37 > \tau_0$, the positive equilibrium $E_*$ lose its stability and a spatially homogeneous periodic distribution can be observed (see Figure 1). For the direction and stability of spatial Hopf bifurcation, we can obtain that $\mu_2 = 0.1691, \beta_2 = -0.4445$ and $T_2 = 0.1544$ if $\tau = \tau_0$. Due to $\mu_2 > 0, \ \beta_2 < 0$, by Theorem 3.1, it is obvious that the directions of Hopf bifurcations are supercritical and the periodic solutions are stable. In addition, the period of periodic solutions increases with the increase of delay $\tau$ since $T_2 > 0$. These phenomenon also can be observed in Figure 2.

5.   Conclusions and discussions

In this paper, we investigated the rich dynamics of a delayed diffusive competition model with saturation effect. It is known that the classical competition model does not have the Hopf bifurcation near the positive equilibrium $E_*$. However, when the delay is included, our results indicate that the delayed diffusive competition model (2) show more complex dynamics, such as the existence of the Hopf bifurcation. For example, by taking delay $\tau$ as the bifurcation parameter, stability switches phenomenon of the positive equilibrium $E_*$ can be observed. We demonstrated that if $\tau < \tau_0$, the positive equilibrium $E_*$ is asymptotically stable. It is unstable if delay $\tau > \tau_0$. And we further proved that model (2) can generate spatially homogeneous and nonhomogeneous Hopf bifurcations when the delay $\tau$ passes through some critical values. Besides, by using the normal form theory and center manifold theorems, we analysed the directions of the Hopf bifurcations and the stability of the bifurcating periodic solutions and show the Hopf bifurcation of system (2) at the equilibrium $E_*$ when delay $\tau = \tau_0$ is supercritical and the periodic solution is asymptotically stable.

In fact, time delay can be found in various biological applications, such as infectious disease modeling, population modeling and the response of vegetation coverage to climate change so on. Some rich phenomenon can be induced by time delay. For example, time delay may induce the occurrence of spatiotemporal patterns ^[37,38]. In this paper, we only consider the occurrence of Hopf bifurcation induced by time delay. The global dynamics of the diffusive competition model still needs further study.

Acknowledgments

Research is supported by the National Natural Science Foundation of China (No. 11671260; 12071293).

Conflict of interests

The authors declare there is no conflict of interest.