Recent advances in polymer structures for organic solar cells: A review

1.   Introduction

Interaction between discrete and continuous dynamics gives rise to hybrid models. This type of mathematical models mainly appear when describing technological systems, where the continuous dynamics comes from the physical process, while the discrete dynamics appears because of the technological elements of the system ^[1]. These latter elements, often based upon logical and software tools, are designed to take full control of the technological process ^[2,3].

Traditionally, continuous dynamics has been mathematically described via differential equations while automata and Petri nets have been commonly used to model the discrete dynamics. Apart from technological applications, hybrid systems have also been considered to study the dynamics of diseases in epidemiology. In this setting, hybrid systems have been applied with switching parameters, and to account different control strategies ^[4,5,6].

Although most of contributions in the theory of hybrid systems have been developed using deterministic tools, it is natural to consider a stochastic approach, since real systems are affected by uncertainties. The randomness comes from the sampled data used to conduct the corresponding study or from the partial knowledge of the phenomenon under analysis due to inherent complexity that often is present in real-world. This approach leads to stochastic/random hybrid systems where the term hybrid is also motivated because of the combination of different types of uncertainties, whose nature can be both continuous and discrete, and that may alter the dynamics of the system.

In dealing with differential equations with uncertainties, one mainly distinguishes two approaches, namely, stochastic differential equations (SDEs) and random differential equations (RDEs) [7,p. 96–98]. SDEs are those where uncertainty is forced (preselected) via stochastic processes whose trajectories or sample behaviour are very irregular, but following specific probabilistic patterns such as the Gaussian Wiener process, whose realizations are nowhere differentiable. The solution of this class of SDEs requires a special stochastic calculus, such as the Itô calculus ^[8]. RDEs are those in which random effects are directly represented in their input parameters (coefficients, forcing term, initial/boundary conditions). It is usually assumed that these inputs have regular behaviour (e.g., continuous trajectories) with respect to time and/or space ^[9]. A major advantage of RDEs is their flexibility when assigning probabilistic distributions for each input parameter. This is a key point when RDEs are used to model real-world problems, since we do not prefix the type of uncertainty that appear in the mathematical model but it is determined using inverse probabilistic techniques to assign appropriate distributions to each input parameter ^[7].

In the setting of hybrid models with uncertainties, SDEs have been widely used. In their formulation these SDEs combine both continuous and discrete stochastic processes. As mentioned before, such processes are previously chosen when formulating the SDEs, so this choice might condition the suitability of the corresponding SDE to describe the specific problem under analysis. This approach has been mainly applied by combining Wiener and Poisson processes ^[10]. The Wiener process accounts the continuous dynamics as it has continuous trajectories, while the compound Poisson process describes the discrete dynamics as its trajectories have jumps. Lévy-type processes have also been considered as continuous and discrete stochastic terms of SDEs since both the Wiener and the Poisson processes can be regarded as particular cases of the Lévy process ^[11]. In contrast, to the best of our knowledge, there is a lack of contributions dealing with RDEs whose input parameters combine hybrid uncertainties, i.e., continuous (like Gaussian, Beta, Gamma, etc.) and discrete (like Binomial, Poisson, Geometric, etc.) random variables. In this paper, we tackle this interesting scenario by studying a full randomization of an important dynamic model, namely, the linear-quadratic logistic-type differential equation. As it will be seen later, for the sake of generality, we will assume that model parameters (the coefficients and the initial condition) involve both discrete and continuous random variables. From a stochastic standpoint, this fact confers the problem hybrid nature.

It is important to stress that solving a SDE/RDE consists not only in obtaining, exactly or approximately, the solution stochastic process, say $X(t)$, but also its main probabilistic information, usually given via the first moments, such as the mean ($\mathbb{E}[X(t)]$), the variance ($\mathbb{V}[X(t)]$), etc. However, a more ambitious objective is determining the so called fidis (finite distributions) of the solution [9,Ch.3]. The first probability density function (1-PDF), $f_{X(t)}(x)$, is the simplest but the most important fidis since from it one can calculate, by integration, all the one-dimensional moments,

provided they exist. The 1-PDF also permits computing the probability that the solution lies within a specific interval of interest,

for every $t$. In the context of hybrid systems governed by SDEs, whose uncertainty is modelled by combining both continuous and discrete processes, most contributions have focussed on SDEs driven by a Wiener process (continuous uncertainty) and a Poisson process (discrete uncertainty). In such case, the 1-PDF satisfies the forward generalized Kolmogorov partial differential equation ^[12]. The exact solution of this partial differential equation can be obtained only under exceptional conditions and, in general, numerical methods are required ^[13]. In the setting of RDEs, the following result, called Random Variable Transformation (RVT) method, allows us to calculate the 1-PDF of RDEs in the case the solution admits an explicit closed-form or when it can be represented via an analytic expression. The RVT technique avoids solving the corresponding partial differential equation satisfied by the 1-PDF of the solution stochastic process, which might be unaffordable. Moreover, the RVT technique has demonstrated to be very useful to solve both ordinary RDEs ^[14,15] and partial RDEs ^[16,17]. The RVT method is stated in the following theorem.

Theorem 1 (Random Variable Transformation method). [9,page 25]. Let us consider ${\bf{U}} = (U_1, \ldots, U_n)$ and ${\bf{V}} = (V_1, \ldots, V_n)$ two $n$-dimensional absolutely continuous random vectors defined on a complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$. Let ${\bf{r}}: \mathbb{R}^n \rightarrow \mathbb{R}^n$ be a one-to-one deterministic transformation of ${\bf{U}}$ into ${\bf{V}}$, i.e., ${\bf{V}} = {\bf{r}}({\bf{U}})$. Assume that ${\bf{r}}$ is continuous in ${\bf{U}}$ and has continuous partial derivatives with respect to each $U_i$, $1\leq i \leq n$. Then, if $f_{{\bf{U}}}({\bf{u}})$ denotes the joint probability density function of random vector ${\bf{U}}$, and ${\bf{s}} = {\bf{r}}^{-1} = (s_1(v_1, \ldots, v_n), \ldots, s_n(v_1, \ldots, v_n))$ represents the inverse mapping of ${\bf{r}} = (r_1(u_1, \ldots, u_n), \ldots, r_n(u_1, \ldots, u_n))$, the joint probability density function of random vector ${\bf{V}}$ is given by

where $\left| J \right|$, which is assumed to be different from zero, is the absolute value of the Jacobian defined by the determinant

It is important to re¡mark that, in order to apply this results, the random vector ${\bf{U}} = (U_1, \ldots, U_n)$ must be absolutely continuous, so having a PDF. To the best of our knowledge, in the contributions where the RVT technique has been applied to determine the 1-PDF of the solution stochastic process of ordinary/partial RDEs, all the inputs parameters are assumed to be absolutely continuous random variables. However, the interesting case where both discrete and continuous random variables are involved in the RDE, has not been already analysed. As we shall explain right-down, in this paper we tackle this situation by studying the following random initial value problem (IVP), based on a general linear-quadratic logistic equation,

Here, $X(t)$ is the unknown stochastic process, and $C$, $D$, $X_0$ and $N$ are random variables defined in a common complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$. This IVP can be applied to describe the dynamics of many phenomena. For example, in Biology, $X(t)$ represents the total population at the time instant $t$, $X_0 > 0$ is the initial condition, $N > 0$ is the carrying capacity, $C > 0$ is the logistic-growth rate and $D > 0$ is the autonomous-growth rate. The above IVP generalizes the classical Verlhust model, also termed logistic model, by including the linear term, $D(N - X(t))$, that represents the autonomous growth of the population, $X(t)$, at time instant $t$. Apart from Biology, the IVP (1.2) can also be used to model the diffusion of a new technology in a market with $N$ potential customers taking into account the diffusion can be due both to contacts (encounters) between individuals who already use the new technology and the non-users, and the effect of advertising among those who do not use the new technology ^[18,19]. Assuming that at the initial time instant, $t = 0$, there are $X_0$ users of the new technology, the instantaneous change of the number of new users at time $t$, given by $X'(t)$, is calculated as the sum of $CX(t) (N-X(t))$ and $D(N-X(t)$. The first addend, $CX(t) (N-X(t))$, can be interpreted as the part of instantaneous rate due to successful encounters (contagion) between those non-users, $N-X(t)$, and users, $X(t)$, of the new technology, being $C > 0$, the contagion rate parameter. The second addend, $D(N-X(t))$, models the part of instantaneous rate of new technology's users because of their autonomous decision (not being influenced by individuals that already use the new technology). For instance, they might adopt the new technology because advertising campaigns. So, coefficient $D > 0$ can be interpreted as an autonomous-growth rate. In this illustrative example, is clear that parameters $C$ and $D$ embed the factors that account for the transition rates from subpopulation $N-X(t)$ to $X(t)$ due to contagion and to autonomous behaviour, respectively. These factors are not deterministically known because of the difficulty to determine them. This motivates rates are treated as random variables rather than deterministic quantities. Similarly, in real-world problems the number of users of a new technology is usually estimated by sampling, so containing errors and uncertainties. This suggests to consider the initial condition $X_0$ as a random variable too. We will illustrate these issues in the last example, where the IVP (1.2) will be applied to modelling the dynamics of Spotify users.

The quadratic logistic equation with uncertainties has been studied in recent contributions using the RVT technique, but only in the case that its inputs are absolutely continuous random variables ^[15,20]. In this paper, we go further, and we first perform a full probabilistic study of the aforementioned generalized version of the logistic model, and secondly, we consider hybrid randomness in its formulation. To the best of our knowledge, this latter feature has not been dealt in the extant literature. Henceforth, in order to conduct our probabilistic study, we will assume that $X_0$ is an absolutely continuous random variable with PDF, $f_{X_0}(x_0)$; $(C, D)$ is an absolutely continuous random vector with joint PDF, $f_{C, D}(c, d)$; and $N$ is a discrete random variable such that $\mathbb{P}[\{\omega\in \Omega: N(\omega) = n_i\}] = p_i$, $i\in I$, where $\sum_{i\in I}p_i = 1$ and $I$ is a discrete set that will be specified later. We will further assume that $X_0$, $(C, D)$ and $N$ are independent. This latter hypothesis is intuitive taking into account the interpretation of model parameters and initial condition. In particular, observe that random rates $C$ and $D$ are probabilistically related since both determine the transitions from subpopulation $N-X(t)$ to $X(t)$. Anyway, the case where all random variables $X_0$, $C$, $D$ and $N$ are independent, which is a more standard assumption, can be easily inferred from our analysis too. In such scenario the PDFs of $C$ and $D$ are denoted by $f_C(c)$ and $f_D(d)$, respectively.

The paper is organized as follows. In Section 2 we revise how to express the probability mass function of a discrete random variable via a PDF using the Dirac delta function. This permits unifying the treatment of discrete and continuous random variables. In Section 3, we determine a closed-form expression, in terms of an expectation, of the 1-PDF of the solution stochastic process of the random IVP (1.2). Section 4 is devoted to determine the PDF of a quantity of great interest in applications, namely, time until a given population size is reached. To illustrate these theoretical findings, two examples are included in Section 3 and 4. In these examples, the distributions of model inputs are chosen just to carry out some illustrative simulations. In Section 5, we apply all the results established in Sections 3 and 4 to describe the dynamics of the number of users of Spotify music streaming service using real data. To this end, we use an inverse probabilistic technique, based on the Principle of Maximum Entropy, to assign appropriate probability distributions to model parameters. Conclusions are drawn in Section 6.

Finally, we point out that in order to facilitate the reading of the paper, a list of all mathematical symbols and abbreviations appearing throughout the paper has been added at the end of the document.

2.   Obtaining a PDF of a discrete random variable

For the sake of completeness, this section is addressed to explain how a probability mass function associated to a discrete random variable can be represented as a PDF. This is convenient to jointly handle both discrete and continuous random variables when computing the 1-PDF of the solution stochastic process, $X(t)$, of the IVP (1.2) via the RVT method. To apply this technique, the random vector ${\bf{U}}$, which will be defined as ${\bf{U}} = (X_0, C, D, N)$, must have a PDF. As mentioned in Section 1, $X_0$ and $(C, D)$ are absolutely continuous random variables, being $f_{X_0}(x_0)$ and $f_{C, D}(c, d)$ their respective PDFs. Therefore, a PDF must be associated to the random variable $N$ to legitimate the application of Theorem 1. To do that, we will take advantage of Dirac delta distribution to express the probability mass function of $N$ in a generalized form that permits identifying it as a PDF.

The Dirac delta distribution (or generalized function) is defined by ^[21],

This function has the following two properties that will be used in our subsequent development,

Let $N$ be a discrete random variable taking a countable number of values, say $n_i$, with associated probability $p_i$, i.e. having the following probability mass function

being $I$ a countable set, and $p_i$ such that $\sum_{i \in I} p_i = 1$.

Then, its probability mass function can be formally represented as

since, using the first property of the Dirac delta function listed in (2.1),

Moreover, notice that $f_{N}(n)\geq 0$. Thereof, the probability mass function $f_N(n)$ can be regarded as a PDF. Furthermore, using the second property of the Dirac delta function stated in (2.1) and the representation of $f_{N}(n)$ given in (2.2), we can obtain the probability that $N$ lies in a closed interval, say $[n_l, n_u]$,

We shall use the above result to associate a PDF to random variable $N$, then we will can apply the RVT method, stated in Theorem 1, to determine the PDF of the solution stochastic process of the random IVP (1.2).

3.   Computing the first probability density function of the solution stochastic process of the random linear-quadratic logistic model

This section is addressed to compute the 1-PDF, $f_{X(t)}(x)$, of the solution stochastic process to random IVP (1.2) taking advantage of RVT method.

First, using classical integration methods, it is easy to check that the solution of equation (1.2) is given by

Next, we fix $t > 0$. Then, we apply Theorem 1 taking ${\bf{U}} = (X_0, C, D, N)$ to obtain the PDF of the random vector ${\bf{V}} = (V_1, V_2, V_3, V_4),$ defined by the mapping ${\bf{r}}: \mathbb{R}^4 \rightarrow \mathbb{R}^4$, whose components $r_1$, $r_2$, $r_3$ and $r_4$ are defined by

To keep the same notation as in Theorem 1, the inverse mapping of ${\bf{r}},$ ${\bf{s}}: \mathbb{R}^4 \rightarrow \mathbb{R}^4$, ${\bf{s}} = {\bf{r}}^{-1} = (s_1, s_2, s_3, s_4)$, is given by

To construct the PDF of the random vector ${\bf{V}}$, via the RVT method, it is also required to obtain the absolute value of the Jacobian of ${\bf{s}}$,

Observe that $|\mathcal{J}|\neq 0$ with probability one (w.p. 1), since $v_2$, $v_3$ and $v_4$ represent arbitrary realizations of random variables, $C = C(\omega)$, $D = D(\omega)$ and $N = N(\omega)$, which are positive for every $\omega \in \Omega$. Furthermore the denominator defining the value of $|\mathcal{J}|$ is different from zero, w.p. 1, since it is defined by absolutely continuous random variables.

Applying Theorem 1, the PDF of ${\bf{V}}$ is given by

As it has been indicated in Section 1, $X_0$, $(C, D)$ and $N$ are assumed to be independent, thereof the PDF of the random vector ${\bf{U}} = (X_0, C, D, N)$ can be expressed as $f_{{\bf{U}}}({\bf{u}}) = f_{X_0, C, D, N}(x_0, c, d, n) = f_{X_0}(x_0)f_{C, D}(c, d)f_{N}(n).$ As a consequence,

So far, the PDF of the random vector ${\bf{V}}$ has been computed. To determine the 1-PDF of the solution to random IVP (3.1), which is given by $V_1$, we now marginalize with respect to $V_2 = C$, $V_3 = D$ and $V_4 = N$,

Applying the second property in (2.1) with $a = -\infty$ and $b = \infty$, the above expression can be simplified as

It is interesting to observe that the last double integral can be expressed in terms of the expectation, $\mathbb{E}_{C, D}[\cdot]$, of random vector $(C, D)$,

This expression is also useful to compute the 1-PDF of $X(t)$ via simulations.

Remark 1. In the particular case that $(C, D)$ are independent random variables, the factor $f_{C, D}\left(c, d\right)$ appearing in formulas (3.2) and (3.3) writes $f_{C}(c)f_D(d)$.

Now, we show a numerical example where the previous theoretical findings are illustrated.

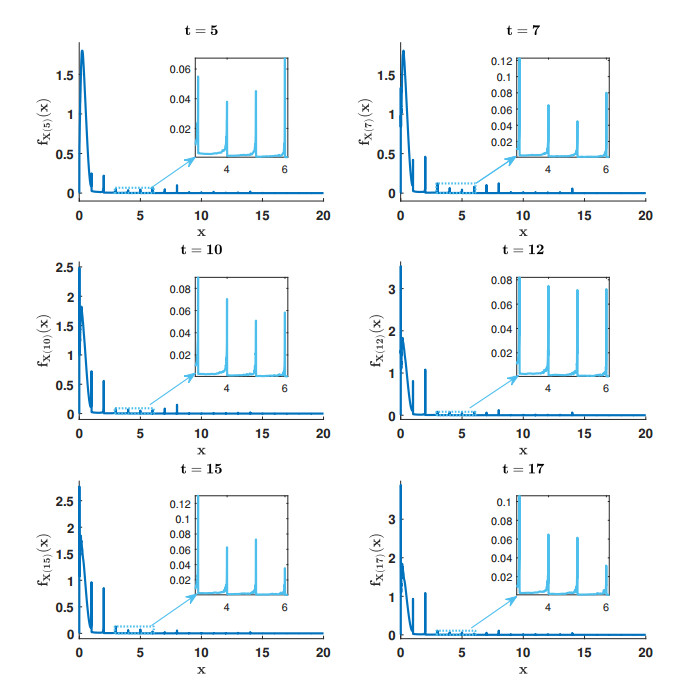
Example 1. Let us consider that $X_0$ is a Beta distribution with parameters $2$ and $3$, i.e. $X_0 \sim Be(2, 3)$. Let $N$ be a Beta Binomial distribution with parameters $20$, $0.1$ and $3$, i.e. $N \sim Bi(20, p)$, being $p \sim Be(0.1, 3)$. The random vector $(C, D)$ has been chosen as a Gaussian copula of dependent Gamma distributions with parameters $0.2, 0.4$ and $0.1, 0.3$, respectively, and with correlation factor $\rho = 0.5$, i.e. $(C, D)\sim \left(Ga(0.2, 0.4), \, Ga(0.1, 0.3), \, \rho = 0.5\right)$ ^[22].

Figure 1 shows the 1-PDF given in (3.3) at different time instants $t\in\{ 5, 7, 10, 12, 15, 17\}$. As a consequence of considering hybrid uncertainty ($N$ is a discrete random variable), from these plots we can observe the peaks of the curves when $x$ takes non-negative entire values.

4.   Computing the PDF of time until a given population size is reached

Once the 1-PDF of the solution stochastic process of IVP (3.1) has been determined, an important additional information is the PDF of the time, $T$, until a given population size, say $x$, has been reached. To this end, we fix $x$ and we consider the expression of the solution while $T$ is regarded as a random variable,

Solving for $T$ yields

We will determine the PDF of $T$ applying the RVT method. Let ${\bf{r}}$ be the transformation of ${\bf{U}} = (X_0, C, D, N)$ into a random vector ${\bf{V}}$, defined as follows

The inverse mappings ${\bf{s}}$ of ${\bf{r}}$, ${\bf{s}} = {\bf{r}}^{-1}$, ${\bf{s}}:\mathbb{R}^4 \rightarrow \mathbb{R}^4$ has the following components, $s_i$, $1 \leq i \leq 4$,

Now, we calculate the absolute value of the Jacobian of transformation ${\bf{s}}$,

Applying Theorem 1, we obtain the PDF of random vector ${\bf{V}}$,

where in the last step we have used that $X_0$, $(C, D)$ and $N$ are independent.

Since $T$ is the first component, $V_1$, of random vector ${\bf{V}}$, in order to compute the PDF of $T$, we marginalize with respect to $V_2 = C$, $V_3 = D$ and $V_4 = N$ and we also use the representation (2.2) of the discrete random variable $N$ via a PDF,

Now, we apply the second property in (2.1) with $a = -\infty$ and $b = \infty$,

Again, the Remark 1 applies to express (4.2) and (4.3) in terms of the marginal distributions $f_C(c)$ and $f_D(d)$ of $C$ and $D$, respectively, when $(C, D)$ are independent random variables.

Now, we shall illustrate the results by means of an example.

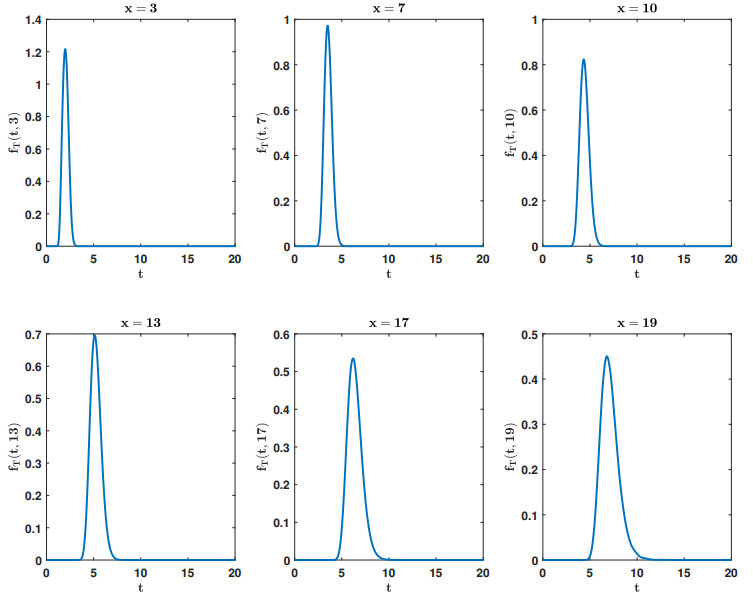
Example 2. Let us consider the random IVP (1.2), where the initial condition has a Beta distribution of parameters, $(2, 3)$, i.e. $X_0 \sim Be(2, 3)$. Let $C$ and $D$ be independent random variables with Uniform distributions in the interval $[0.2, 0.25]$, i.e. $C, D\sim U ([0.2, 0.25])$, and $N$ has a shifted binomial distribution with shift $20$ and binomial parameters, $(10, 0.5)$, i.e $N\sim 20+Bi(10, 0.5)$. In Figure 2, we have plotted the PDF of $T$ for different values of $x$. From these graphical representations, we can observe that the mean and the variance of $T$ increase as $x$ does.

5.   Modelling Spotify users with uncertainty in the data

So far, we have illustrated the theoretical results by choosing arbitrary distributions to model parameters, however when dealing with real-world problems such distributions must be carefully determined so that the model properly captures data uncertainty. This is a critical point which requires inverse estimation techniques [23,Chapter 2]. In this section, we tackle this very interesting problem to studying the dynamics of Spotify's users from the random IVP (1.2), assuming that $X_0$, $C$, $D$ and $N$ are independent random variables. We will use the yearly data about Spotify's users (measured in million of individuals) during the period 2015–2019.

At this point, it is important to stress the meaning of the above sentence: "properly captures output uncertainty". Indeed, most of the contributions focus on computing the model parameters by fitting the expectation of solution stochastic process to sampled data. To this end, some specific goodness-of-fit measure is minimized (typically, the mean square error). Then, confidence intervals are built to capture data uncertainty. Therefore, this approach is based on the punctual information contained in the the expectation to perform the fitting, and then one calculates the standard deviation to build confidence intervals. In our example, we will perform the model fitting using a more complete information that the one based only on the two first moments, since we will determine the distribution of each model parameter. This will be done by minimizing a goodness-of-fit measure, that will be specified later, based on the 1-PDF of the solution stochastic process, $f_{X(t)}(x)$, given by (3.3) (or, equivalently, (3.4)). In this manner, as we directly work with the 1-PDF of the solution stochastic process, our model fitting is more complete since it takes into account more information of the solution than only the expectation.

To perform the aforementioned fitting via the 1-PDF, $f_{X(t)}(x)$, we will apply the methodology recently developed in ^[24]. This approach takes extensively advantage of the Principle of Maximum Entropy (PME) to assign reasonable distributions to sample data and model inputs.

Given a real random variable, say $Y$, the PME is an efficient method to assign it a probabilistic distribution using all the available statistical information of $Y$, such as its support, moments, etc. For instance, if $Y$ is an absolutely continuous random variable with support, $\mathcal{D}(Y)$, and its two first moments, $m_{1} = \mathbb{E}[Y]$ and $m_{2} = \mathbb{E}[Y^2]$, are known, then the PME looks for an approximation, $f_Y$, of the true PDF of $Y$ that maximizes the Shanonn's entropy

subject to the following constraints

As $f_Y$ must represent a PDF, the first restriction indicates the normalization condition that guarantees it integrates the unit over the whole real line. Using the variational formulation of method of Lagrange multipliers, it can be seen that the PDF of $Y$ has the following form ^[25]

where $\mathbb{1}_{\mathcal{D}(Y)}$ denotes the characteristic function on the domain $\mathcal{D}(Y)$, and parameters, $\lambda_i$, $i\in\{ 0, 1, 2\}$, are calculated by solving the constraints given in (5.1).

Roughly speaking and using the interpretation of entropy, the PME method seeks for the PDF, $f_Y$, that corresponds to the maximal uncertainty (based on the Shannon's entropy measure) and the minimal quantity of information (based on the available statistical moments).

Now, we explain how the PME is applied to assign a PDF to sampled data for the number of Spotify's users. These data are collected in third column of Table 1 and considered as the mean of sampled distribution, ^[26]. For convenience, hereinafter, we will denote by $X_{t}$ the random variable that represents the number of Spotify's users at the time instant $t$. In our setting, $t$ is measured in months. Since the number of Spotify's users is known yearly during the period 2015–2019, the data is determined at $t\in \mathcal{T} = \{0, 12, 24, 36, 48\}$ (see second column of Table 1). To construct the constraints required to apply the PME, we proceed as follows. On the one hand, we will assume that sampled data represent the mean or expectation, $m_{1, t}$, of random variable $X_{t}$. On the other hand, since sampled data are rounded-off to million units, we will assume they contain an intrinsic sampling error depending on the number of users in every time instant. Thereof, we will take as standard deviation $1\%$ of each sampled data, i.e. ${\sigma_{t}} = 0.01 m_{1, t}$. This allows us to compute the second-order moment, $m_{2, t} = m_{1, t}^2+\sigma^2_{t}$ (see last column in Table 1). Notice that, by means of this reasoning, we are implicitly considering that, at every time instant $t \in \mathcal{T}$, each sampled data comes from a random variable, $X_{t}$, whose mean ($m_{1, t}$) and second moment ($m_{2, t}$) are listed in Table 1.

With this information, we apply the PME to assign a PDF, $f_{X_{t}}$, of each random variable $X_{t}$ of the form

where $\mathcal{D}(X_{t})$ denotes its domain and, the parameters $\lambda_0^{t}$, $\lambda_1^{t}$ and $\lambda_2^{t}$, are calculated by numerically solving the following system of nonlinear equations

where $m_{1, t}$ and $m_{2, t}$ are given in Table 1. The results are shown in Table 2.

Once reliable PDFs have been assigned to sampled data, we proceed to assign suitable distributions for every model parameters so that the 1-PDF of the logistic model, given by (3.2), fits the PDFs of data detailed above at $t \in \{0, 12, 24, 36, 48\}$. To do that for, $X_0$, $C$ and $D$, we will apply the PME method again. First observe that, for consistency, the PDF of $X_0$ is given by (see values of $\lambda_0^{t = 0}$, $\lambda_1^{t = 0}$ and $\lambda_2^{t = 0}$ in Table 2)

To determine the endpoints, $x_{0, 1}$ and $x_{0, 2}$, we have used the $\sigma$-rule [27,page 122]. Specifically, we have taken $x_{0, 1} = \max\{0, m_{1, t = 0}-k \sigma_{t = 0}\}$ (as $X_0$ must be positive) and $x_{0, 2} = m_{1, t = 0}+k \sigma_{t = 0}$ with $k = 30$. This guarantees the interval $[x_{0, 1}, x_{0, 2}]$ embraces more than $99.9\%$ of the probability regardless the distribution of $X_0$. As $m_{1, t = 0}-30 \sigma_{t = 0} < 0$ and $m_{1, t = 0}+30 \sigma_{t = 0} = 119.6182$, this results $[x_{0, 1}, x_{0, 2}] = [0,119.6182]$.

The PDFs, $f_{C}(c)$ and $f_{D}(d)$, of random variables $C$ and $D$, respectively, are constructed via PME method taking into account that their corresponding domains are non-negative, since they represent growth-rates. Then, they have the following form

and

Finally, the probability mass function of discrete random variable, $N$, is modelled by a shifted Binomial distribution, with parameters $n_1$, $n_2$ and $\nu_N$, i.e., $N \sim n_1 + \mathrm{Bi}(n_2, \nu_N)$, where

At this point, the parameters $\lambda_0^{C}$, $\lambda_1^{C}$, $\lambda_2^{C}$, $c_2$ $\lambda_0^{D}$, $\lambda_1^{D}$, $\lambda_2^{D}$, $d_2$, $n_1$, $n_2$ and $\nu_N$ need to be calculated. This will be done by fitting the 1-PDF, $f_{X(t)}(x)$, calculated in (3.3) (or equivalently (3.4)), to the PDF, $f_{X_{t}}(x)$, given by (5.2), at the time instants $t\in \mathcal{T} = \{0, 12, 24, 36, 48\}$. Notice that $f_{X(t)}(x)$ depends on $f_{X_0}(x_0)$, $f_C(c)$, $f_D(d)$ and $p_i$, where $f_{X_0}(x_0)$ is completed determined in (5.4); $f_C(c)$ depends on $\lambda_0^{C}$, $\lambda_1^{C}$, $\lambda_2^{C}$ and $c_2$ (see (5.5)); $f_D(d)$ depends on $\lambda_0^{D}$, $\lambda_1^{D}$, $\lambda_2^{D}$ and $d_2$ (see (5.6)), and $p_i$ depends on $n_1$, $n_2$ and $\nu_N$ (see (5.7)). Similarly as in the algorithm recently described in Steps 7 and 8 in [24,Sec. 5], we take as goodness-of-fit function

where $x_i$ is a mesh on a domain determined by the PDF, $f_{X_{t}}(x)$, of sampled data (see further details in Step 3 in [24,Sec. 5]). Notice that $E_0 = 0$ since by construction $f_{X(0)} = f_{X_0}$.

We have used Particle Swarm Optimization ^[28], to find the values of $\lambda_0^{C}$, $\lambda_1^{C}$, $\lambda_2^{C}$, $c_2$ $\lambda_0^{D}$, $\lambda_1^{D}$, $\lambda_2^{D}$, $d_2$, $n_1$, $n_2$ and $\nu_N$ that minimize the function $E$ functional defined in (5.8). In Table 3, we show the obtained values. To carry out these computations, the 1-PDF $f_{X(t)}(x)$ has been evaluated via the expectation given in (3.4). To this end, we firstly fix $t\in \mathcal{T}$. Secondly, we obtain a simulation of each random variable $C$ and $D$ (recall that, according to (5.5) and (5.6)), we know their respective PDF. Thirdly, we evaluate the argument of the expectation. This process is repeated many times and the results are averaged. This permits approximating $f_{X(t)}(x)$. More details of this computational procedure can be seen in [24,Sec. 5].

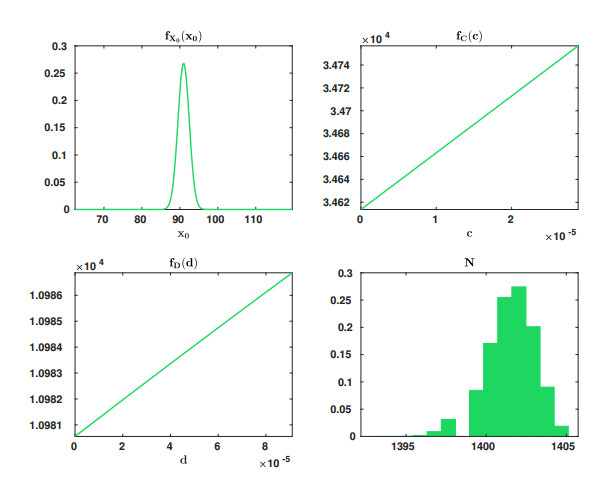
From figures listed in Table 3, and using expressions (5.5), (5.6) and (5.7), we have calculated the distributions $f_C(c)$, $f_D(d)$ and $f_N(n)$, respectively. In Figure 3, we show the graphical representations of these distributions and of $f_{X_0}$ from expression (5.4).

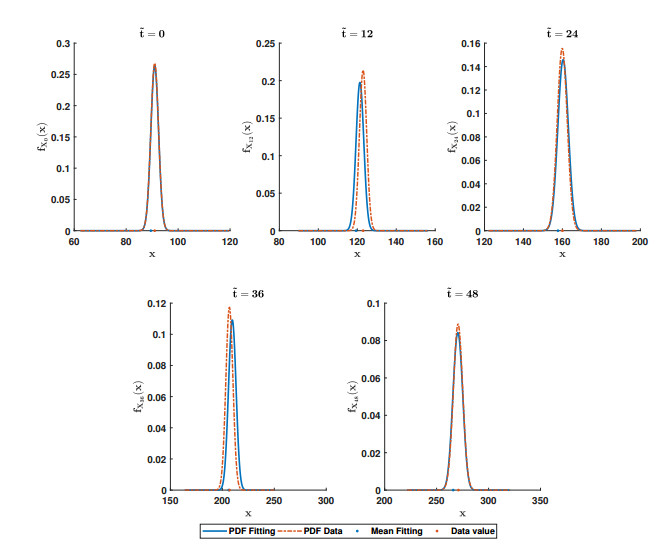
To better compare the obtained results, in Figure 4 we plot the PDFs associated to sampled data (red lines) and the PDFs of the solution stochastic process, given by (3.3), at the time instants $t\in \mathcal{T} = \{0, 12, 24, 3, 6, 48\}$. Red and blue points, plotted on the horizontal axis represent, respectively, the sampled data of Spotify's users listed in the second column ($m_{1, t}$) of Table 1 and the expectation of the solution stochastic process calculated by means of expression (1.1) with $m = 1$ where $f_{X(t)}(x)$ is given by (3.3). From these plots we can see the fitting via the PDFs is very good.

6.   Conclusions

In this paper we have performed a probabilistic study of a generalized version of the random logistic differential equation which has a linear term in its formulation. This additional term describes the autonomous behaviour that affects the model dynamics. For the sake of generality, in our analysis we have assumed that all model parameters and the initial condition are random variables having arbitrary distributions. The randomness is treated from a hybrid standpoint in the sense we consider a combination of discrete and continuous random variables for model inputs. The key tools to conduct our study are, on the one hand, the Dirac delta function to unify the treatment of discrete and continuous random variables with their respective probability density functions and, on the other hand, the Random Variable Transformation method that permits computing the density of certain differentiable mappings that act onto absolutely continuous random vectors. We have included a number of examples that illustrate different cases where our theoretical findings can be applied including the application of a model using real-world data. Nevertheless, we must point out that our approach relies on two critical points, first the availability of a closed-form expression of the solution stochastic process of the general linear-quadratic differential equation and, secondly, the exact computation of the inverse of the mapping defined when applying the Random Variable Transformation method. In other models, where some of the above exact expressions are not available, the method can still be applied using numerical approximations, which certainly will increase the computational burden. Finally, we think that approach proposed in this paper may open new avenues in the analysis of problems formulated by means of differential equations with hybrid (discrete-continuous) randomness.

Acknowledgments

This work has been supported by the Spanish Ministerio de Economía, Industria y Competitividad (MINECO), the Agencia Estatal de Investigación (AEI) and Fondo Europeo de Desarrollo Regional (FEDER UE) grant MTM2017-89664-P. Computations have been carried thanks to the collaboration of Raúl San Julián Garcés and Elena López Navarro granted by European Union through the Operational Program of the European Regional Development Fund (ERDF)/European Social Fund (ESF) of the Valencian Community 2014–2020, grants GJIDI/2018/A/009 and GJIDI/2018/A/010, respectively.

Conflict of interest

The authors declare that there are not conflict of interest.

Nomenclature

$(\Omega, \mathcal{F}, \mathbb{P})$     complete probability space.

$\mathbb{E}[X]$     mean of the random variable $X$.

$\mathbb{V}[X]$     variance of the random variable $X$.

$f_{X}(x)$     probability density function of the random variable $X$.

$\delta_{x_0}(x)$     Dirac delta function at value $x_0$.

$\mathbb{1}_{[a, b]}$     characteristic function on the interval $[a, b]$.

fidis     finite distributions.

IVP     initial value problem.

PDF     probability density function.

1-PDF     first probability density function.

PME     Principle of Maximum Entropy.

RDE     random differential equation.

RVT     Random Variable Transformation.

SDE     stochastic differential equation.

w.p. 1     with probability one.