Figure 1.
Carotid bifurcation geometry.
After the rare earth element (REE) crisis in 2011, companies invested in new supply routes of REEs, such as the recycling from end-of-life fluorescent lamps. Although recycling is in the current market situation not economically profitable anymore, it does fit in a strategy towards a low-carbon and a circular economy, for example to mitigate the supply risk of REEs. However, is recycling of REEs indeed environmentally beneficial? Should their recycling therefore be subsidized? This is assessed with a Consequential Life Cycle Assessment (CLCA). The results show that the answer to this question strongly depends on the market situation of the REEs, and the applications in which they are used. At the time that the recycling process was operating—where fluorescent lamps could still displace halogen lamps and there was sufficient demand for the REE europium and yttrium—environmental benefits could be achieved by increasing the recovery of REEs from end-of-life fluorescent lamps. The results of this study can be used to increase the understanding on the type of market interactions that could be considered in the decision-making processes regarding the supply and recycling of raw materials—especially materials that are often produced as by-products, such as many critical raw materials.
Citation: Dieuwertje L. Schrijvers, Philippe Loubet, Guido W. Sonnemann. The influence of market factors on the potential environmental benefits of the recycling of rare earth elements[J]. Clean Technologies and Recycling, 2022, 2(1): 64-79. doi: 10.3934/ctr.2022004
| [1] | Ayman Elsharkawy, Ahmer Ali, Muhammad Hanif, Fatimah Alghamdi . Exploring quaternionic Bertrand curves: involutes and evolutes in E4. AIMS Mathematics, 2025, 10(3): 4598-4619. doi: 10.3934/math.2025213 |
| [2] | Samah Gaber, Abeer Al Elaiw . Evolution of null Cartan and pseudo null curves via the Bishop frame in Minkowski space R2,1. AIMS Mathematics, 2025, 10(2): 3691-3709. doi: 10.3934/math.2025171 |
| [3] | Esra Damar . Adjoint curves of special Smarandache curves with respect to Bishop frame. AIMS Mathematics, 2024, 9(12): 35355-35376. doi: 10.3934/math.20241680 |
| [4] | Yasin Ünlütürk, Talat Körpınar, Muradiye Çimdiker . On k-type pseudo null slant helices due to the Bishop frame in Minkowski 3-space E13. AIMS Mathematics, 2020, 5(1): 286-299. doi: 10.3934/math.2020019 |
| [5] | Emad Solouma, Mohamed Abdelkawy . Family of ruled surfaces generated by equiform Bishop spherical image in Minkowski 3-space. AIMS Mathematics, 2023, 8(2): 4372-4389. doi: 10.3934/math.2023218 |
| [6] | Wei Zhang, Pengcheng Li, Donghe Pei . Circular evolutes and involutes of spacelike framed curves and their duality relations in Minkowski 3-space. AIMS Mathematics, 2024, 9(3): 5688-5707. doi: 10.3934/math.2024276 |
| [7] | Bahar UYAR DÜLDÜL . On some new frames along a space curve and integral curves with Darboux q-vector fields in E3. AIMS Mathematics, 2024, 9(7): 17871-17885. doi: 10.3934/math.2024869 |
| [8] | Ibrahim AL-Dayel, Emad Solouma, Meraj Khan . On geometry of focal surfaces due to B-Darboux and type-2 Bishop frames in Euclidean 3-space. AIMS Mathematics, 2022, 7(7): 13454-13468. doi: 10.3934/math.2022744 |
| [9] | Fatemah Mofarreh, Rashad A. Abdel-Baky . Singularities of swept surfaces in Euclidean 3-space. AIMS Mathematics, 2024, 9(9): 26049-26064. doi: 10.3934/math.20241272 |
| [10] | Areej A. Almoneef, Rashad A. Abdel-Baky . Surface family pair with Bertrand pair as mutual geodesic curves in Euclidean 3-space E3. AIMS Mathematics, 2023, 8(9): 20546-20560. doi: 10.3934/math.20231047 |
After the rare earth element (REE) crisis in 2011, companies invested in new supply routes of REEs, such as the recycling from end-of-life fluorescent lamps. Although recycling is in the current market situation not economically profitable anymore, it does fit in a strategy towards a low-carbon and a circular economy, for example to mitigate the supply risk of REEs. However, is recycling of REEs indeed environmentally beneficial? Should their recycling therefore be subsidized? This is assessed with a Consequential Life Cycle Assessment (CLCA). The results show that the answer to this question strongly depends on the market situation of the REEs, and the applications in which they are used. At the time that the recycling process was operating—where fluorescent lamps could still displace halogen lamps and there was sufficient demand for the REE europium and yttrium—environmental benefits could be achieved by increasing the recovery of REEs from end-of-life fluorescent lamps. The results of this study can be used to increase the understanding on the type of market interactions that could be considered in the decision-making processes regarding the supply and recycling of raw materials—especially materials that are often produced as by-products, such as many critical raw materials.
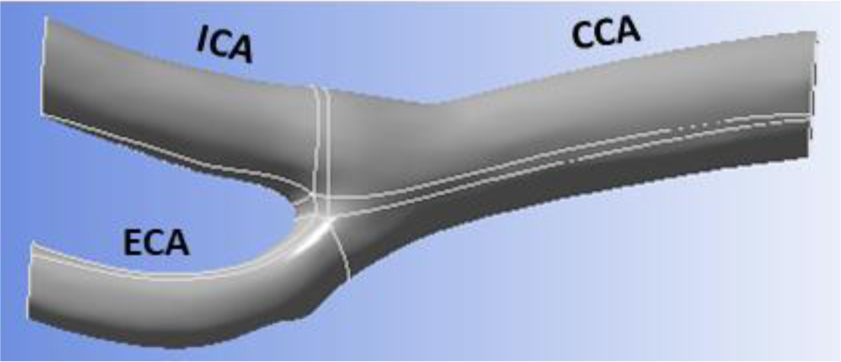
The carotid artery is one of the most important arteries in the human body [1]; its primary function is to supply blood to the brain through the basilar trunk. Its complex structure has many curved areas, particularly the carotid sinus. Furthermore, at the carotid branches, there is a siphon that forms a highly curved spiral. Under real physiological conditions, hemodynamic factors (blood pressure, blood flow, flow velocity, etc.) in this complex anatomy contribute to the appearance of atherosclerosis [2]–[4]. The latter is strongly linked to stenotic obstruction (reduction of the section of the blood vessel). In addition to differential pressure, bifurcation geometry, and arterial wall properties, several studies confirm that hemodynamic factors such as flow distribution, recirculation, low and oscillatory wall shear stress play a significant role in the development and progression of atherosclerotic plaques and other arterial lesions [5]–[7]. Therefore, thoroughly understanding the carotid artery's blood flow seems crucial.
Accessing biological flows poses a significant challenge in the study of hemodynamic phenomena. In recent years, computational fluid dynamics (CFD) has proven to be an effective solution to study similar problems and understand hemodynamics using mathematical tools [8],[9]. Numerical simulation of constitutive models can accurately describe the rheological blood response under physiological flow conditions [10]. It is recognized as an invaluable tool for interpretation and analysis of the functionality of the circulatory system in physiological and pathological situations [11],[12].
In this context, the present work studies blood flow in a specific carotid bifurcation. The flow is considered incompressible, laminar in the first case, and turbulent modeled with the k-ϵ model in the second case. The carotid wall is assumed to be rigid. Two different forms of physiological pulses from the literature were applied as boundary conditions to generate blood movement. These pulses are summarized in two pressure-velocity states: P1-V1 (theoretical) and P2-V2 (actual). Three viscosity models were used to model the non-Newtonian blood flow: Cross, Carreau, and Quemada. The resolution of the governing equations system is carried out using the Fluent solver based on the finite volume method. The calculations are performed over a total time of 2.4 s with a period of 0.8 s.
The study investigates the blood flow characteristics in a specific rigid carotid bifurcation. (Figure 1, Table 1). It consists of two main parts, separately examining laminar and turbulent flow regimes. The laminar flow case considers incompressible blood with a 1050 kg/m3 density. In the turbulent flow case, the k-ϵ model is employed.
The rheological behavior of blood is analyzed by comparing the Newtonian case, where the blood viscosity is constant at 0.0035 Pa.s, with the non-Newtonian instances described by the Cross (1), Carreau (2) and Quemada (3) models [13]. These models capture the non-Newtonian characteristics of blood flow.
Physiological pulsatile flow is modeled using two pairs of periodic boundary conditions: P1-V1 (theoretical) and P2-V2 (real). The velocity conditions are imposed at the inlet, while the pressure conditions are imposed at the outlets of the carotid artery. The Reynolds number at the inlet ranges from 431.15 to 605.81, indicating the flow regime.
The calculations are performed for a period of 0.8 s and a total time of 2.4 s, which covers three complete periods of the physiological flow.
µ∞ = 0.00345 Pa.s, µ0 = 0.0364 Pa.s, λ = 0.380, n = 1.45 for the Cross model (1);
µ∞ = 0.00345 Pa.s, µ0 = 0.056 Pa.s, λ = 3.313, n = 0.3568 for the Carreau model (2);
µc = 0.002982 Pa.s, τy = 0.02876 Pa.s et λ = 4.020 s for the Quemada model (3).
| CCA diameter | ICA diameter | ECA diameter | Bifurcation total length |
| 7.37 mm | 5.22 mm | 4 mm | m |
DownLoad:
CSV
The mathematical system for transient, incompressible and laminar blood flow in a rigid artery includes the continuity (4) and the Navier-Stokes equations (5):
For turbulent flows, the use of turbulent models is needed, and some modifications are included to the momentum equation (6):
The turbulent blood flow is modeled using the k-ϵ model. The turbulent kinetic energy k, as well as its dissipation rate ϵ, are obtained from the following transport equations:
µt is the turbulent viscosity and it is given as follow:
Gk is the generation of turbulence kinetic energy due to mean velocity gradients; σk = 1 and σϵ = 1.3 are the turbulent Prandtl numbers for k and ϵ, respectively; C1ϵ = 1.44 and C2ϵ = 1.92 are constants.
In our study, several pressure and velocity profiles have been considered to solve the above system. Taking into account the Womersley approximation [14], the pulsating velocity profile V1 (Figure 2a) [15], given by equation (9), will be used as the first condition at the inlet of the carotid bifurcation.
Where: A = 2/3 and
The second velocity condition, V2, is fitted using a Gaussian function (10) as described by Kleinstreuer [16]:
The coefficients values ai bi and ci are given in the Table 2 below:
| a1 | -0.0214 | b1 | 0.5458 | c1 | 0.008372 |
| a2 | 0.04842 | b2 | 0.3374 | c2 | 0.1284 |
| a3 | 0.0407 | b3 | 0.4749 | c3 | 0.1268 |
| a4 | 0.08353 | b4 | 0.6215 | c4 | 0.234 |
| a5 | 0.09432 | b5 | 0.002087 | c5 | 0.3171 |
| a6 | 0.08364 | b6 | 1.006 | c6 | 0.314 |
DownLoad:
CSV
The pressure conditions have been used to model the pulsating pressure at the carotid outlets. The first condition P1 (11) is the one used by P. Kumar Mandal et al [17],[18]. The pressure gradient was taken according to Burton [19] as follows [20],[21]:
Where A0 is the constant amplitude of the pressure gradient, A1 is the amplitude of the pulsatile component giving rise to the systolic and diastolic pressures.
The second condition, P2, is the one used by Vasava et al. [22], it is given as an eighth-degree polynomial correlation (12) developed from data provided by Conlon et al. [23].
The Ci coefficients are summarized in Table 3:
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| 0.5601 | 0.1882 | -1.4424 | 1.2239 | -0.426 | 0.0664 | -0.00492 | 0.000432 |
DownLoad:
CSV
The discussed conditions (V1, V2, P1 and P2) are shown in Figure 2:
Our study employed the finite volume method [24] implemented in the Fluent solver to solve the governing equations. The pressure-velocity coupling was achieved using the SIMPLE algorithm. Spatial discretization involved using a second-order scheme for pressure and a second-order upwind scheme for momentum.
The boundary conditions mentioned earlier, specifically the P1-V1 and P2-V2 pairs, were applied as boundary conditions in the solver using User-Defined Function (UDF) files. These files defined the prescribed velocity and pressure conditions at the respective boundaries.
Since the phenomenon being investigated is transient, we adopted an implicit first-order scheme for time discretization. The calculations were conducted for a total duration of 2.4 seconds, equivalent to three periods of the pulsatile flow. A time step size of 0.004 seconds was employed during the simulations.
Convergence of the solution was determined based on the criterion that the velocity components fall below a threshold value of 10−6.
As presented below, we utilized an undisclosed formula (13) to evaluate the wall shear stress at the carotid walls.
The discretization of the physical domain directly impacts the computational process and the accuracy of the results. Thus, the analysis of the mesh effect is a precious step in any simulation procedure, aiming to ensure the independence of the obtained results from the chosen mesh. With this objective in mind, a thorough investigation of the mesh effect on the phenomena under study was conducted. Due to the intricate nature of the carotid structure, an unstructured mesh composed of tetrahedral elements proves to be more suitable for addressing our specific problem. By Figure 3, a mesh of 145068 elements was carefully chosen to accurately solve the blood flow within the designated domain, as indicated in Table 4.
| Nombre d'éléments | u (m/s) |
| 105438 | 0,00372 |
| 110007 | 0,00383 |
| 119054 | 0,00402 |
| 133468 | 0,00426 |
| 145068 | 0,00432 |
| 209791 | 0,00432 |
| 466421 | 0,00459 |
DownLoad:
CSV
To establish our solver's reliability, we compared our results with those obtained by K. Mamuna and K. Funazakia [25], who investigated blood flow in a rigid and elastic stenotic artery. Their study considered the flow incompressible, non-Newtonian using the Cross model, and turbulent utilizing the k-omega model. We specifically focused on comparing the diastole wall shear stress (at t = 0.5945 s) for the 55% stenotic artery. The results comparison, as depicted in Figure 4, reveals a slight disparity between the two curves, indicating a significant level of agreement between our findings and those of K. Mamuna and K. Funazakia [25].
The subsequent section presents the results obtained from simulating pulsed blood flow through a rigid carotid bifurcation, considering two sets of pressure-velocity boundary conditions (P1-V1 and P2-V2) and three viscosity models (Cross, Carreau, and Quemada). Three radial sections were created to visualize the evolution of velocity profiles within the studied geometry (Figure 5). To ensure a fully developed flow, the results are presented for the second heart cycle, specifically within the interval of [0.8 s, 1.6 s]. For each set of boundary conditions, pressure, velocity, and wall shear stress variations are presented at the systolic peak and early diastole moments. The corresponding timing for each of these moments is summarized in Table 5.
| Systolic peak | Early diastole | ||||||
| P1 | V1 | P2 | V2 | P1 | V1 | P2 | V2 |
| 1 s | 1.04 s | 0.967 s | 1.056 s | 1.42 s | 1.23 s | 1.072 s | |
DownLoad:
CSV
Figures 6, 7, 8, and 9 illustrate the temporal evolution of pressure and velocity in the CCA (common carotid artery) for all viscosity models and boundary conditions mentioned in section 2.1. From Figures 6a, 7a, 8a, and 9a, it can be observed that the pressure in the carotid bifurcation remains unaffected by the various parameters investigated, including the flow regime, viscosity model, and type of boundary conditions. However, when examining velocity variations, it becomes evident that the impact of the viscosity model is more pronounced in laminar flow than turbulent flow.
Despite the slight differences observed in the curves (Figures 6a and 7a), it is apparent that the Carreau model yields the highest velocity value (37 m/s). The Cross model exhibits a lower weight (36.5 m/s). In turbulent flow, the simulation results using the P1-V1 boundary condition (Figure 8b) demonstrate that the velocity differences between the Newtonian, Cross, and Carreau cases are negligible, with all curves reaching a maximum velocity of 38 m/s. However, the Quemada model predicts the highest velocity value (38.5 m/s). When considering the second boundary condition pair, P2-V2 (Figure 9b), it is noteworthy that the Cross model yields the highest velocity value, while the Carreau model corresponds to the lowest velocity value.
Figures 10 to 17 depict the variations in flow field pressure during the systolic peak and early diastole under different conditions, including flow regime (laminar and turbulent), viscosity models (Newtonian, Cross, Carreau, and Quemada), and boundary conditions (P1-V1, P2-V2). Across all the figures, a common observation is that the pressure rapidly decreases in the CCA (Common Carotid Artery), regardless of these parameters. The unique anatomy of the carotid bifurcation, particularly the branching of the CCA and the curvature of the ECA (External Carotid Artery), introduces a radial pressure gradient and gives rise to significant secondary flows (Figures 24, 25, 26, and 27), unlike typical internal flows characterized by axial pressure gradients.
Furthermore, the pressure in the ICA (Internal Carotid Artery) is higher than in the ECA. However, the branch point of the bifurcation exhibits the highest-pressure values due to the abrupt change in velocity. The pressure distribution in this region varies depending on the viscosity model and the pair of boundary conditions. Figures 11 and 13 show that the P2-V2 boundary condition yields the highest-pressure values.
The transition from laminar to turbulent blood flow modeling in the carotid bifurcation is essential. The intricate anatomy of this artery theoretically promotes the development of chaotic movements, particularly in the ICA. Figures 24, 25, 26, and 27 vividly demonstrate the presence of secondary solid flows in the carotid sinus.
By examining Figures 14, 15, 16, and 17, it is evident that the pressure difference between the laminar and turbulent regimes is minimal during the systolic peak. However, during early diastole, the turbulent flow exhibits higher pressure, potentially damaging endothelial cells [26],[27].
The Figures presented in this section depict the velocity profiles in different areas of the geometry (S1, S2, and S3) for each case studied. In section S1, the velocity profile exhibits a quasi-parabolic shape (Figures 18 and 19). Notably, the asymmetry of the carotid artery alters the position of the velocity maxima, which is shifted towards the ICA (internal carotid artery).
In the branching zone, as shown in contours (Figures 20, 21, 22, and 23), it is observed that a significant amount of fluid is dragged towards the inner wall of the ICA [10],[28]. This region is of great physiological importance and exhibits more complex physical phenomena than those observed in the CCA (common carotid artery).
Typically, in circular pipes, decreasing the flow section results in an increase in velocity values. However, in the case of carotid bifurcation, this relationship no longer holds. The velocity values in the ICA (more extensive section) are higher than those in the ECA (smaller section). This is attributed to the increase in the CCA section for a constant flow rate and the curvature of the ECA, which introduces an opposite pressure gradient and relatively lower flow in the ECA compared to the ICA. A compensatory increase in the ICA velocity occurs to maintain flow conservation, explaining the apparent differences in velocity values between the two branches.
The shape of the branching zone plays a significant role in the deformation of flow and the interference of streamlines, leading to complex blood movement in the carotid sinus. Examining the contours in Figures 24, 25, 26, and 27, as well as the curves presented in Figures 28 and 31, it is evident that the velocity profiles are aligned towards the internal wall of the ICA (internal carotid artery). This profile shape is closely associated with a secondary flow near the outer wall of the carotid sinus and the formation of a strong vortex in the positive direction within this acceleration region.
However, despite the vortex motion, it is essential to note that this region cannot be regarded as a recirculation zone since the fluid is not trapped within it. The contours also demonstrate that velocity variations along this branch are not dependent on the flow cross-section. It can be observed that the velocity increases from the carotid sinus towards the exit of the ICA, with values higher than those surveyed in the ECA (external carotid artery). This acceleration near the wall results from locally large pressure gradients induced by the effects of curvature.
Considering the ECA (external carotid artery), the curvature of the vessel contributes to generating a radial pressure gradient, as observed in Figures 10–17. This gradient leads to a secondary flow and the emergence of two counter-rotating vortices directed toward the center of the artery, as depicted in Figures 35, 36, 38, and 39.
Pathologically, these phenomena observed in the carotid sinus are closely associated with developing atheromatous plaques, particularly in atherosclerosis's early and moderate stages. It is worth noting that the ECA is typically affected by lipid deposits, primarily in the advanced stages of the disease.
The dimensions of the physical domain highly influence the rheological behavior of blood in the carotid artery. In the CCA (common carotid artery), the distinction between Newtonian and non-Newtonian behavior of blood is minimal. As depicted in Figures 18 and 19, the curves for the Newtonian case and the non-Newtonian instances described by the Cross, Carreau, and Quemada models overlap, and the velocity values are nearly identical at the selected presentation times of systolic peak and early diastole.
However, in the ECA (external carotid artery) (Figures 34 and 37), a noticeable difference is observed compared to the ICA (internal carotid artery) (Figures 28 and 31). The diameter of the vessel directly impacts the rheological behavior of blood. Moreover, the figures indicate that the non-Newtonian behavior of blood becomes more prominent at the P2-V2 systolic peak. Among the non-Newtonian models, the Carreau model exhibits the highest velocity values, followed by the Quemada and Cross models. The Newtonian case demonstrates the lowest velocity values.
The following figures depict the velocity variations obtained from turbulent blood flow modeling using the k-epsilon (k-ϵ) model. In the CCA and ICA (Figures 40, 41, 50, and 53), the viscosity model and type of boundary conditions have a negligible effect on the velocity curves. However, a slight difference can be observed in the velocity curves of the ECA for the P2-V2 boundary condition pair (Figure 59). The velocity obtained using the Carreau model is slightly higher than that of the Quemada model, followed by the Cross model. The Cross model yields the same velocity as the Newtonian approach. This difference in velocity is more noticeable in laminar flow than in turbulent flow.
Regarding axial velocity, the contours presented in Figures (42, 43, 44, and 45) appear to have similar distributions, with only the velocity values changing with the presentation moments and the pairs of boundary conditions (P1-V1 and P2-V2).
The figures presented in this section depict the distribution of wall shear stress along the carotid artery during the systolic peak and early diastole for all conducted simulations. In general, the wall shear stress exhibits variations, reaching a maximum value of approximately 10 Pa during the systolic peak and 8 Pa during early diastole.
Due to the Poiseuille-like flow in the CCA, it is evident that the wall shear stress decreases rapidly along this branch. However, in the branching zone, an important observation can be made. A blue C-shaped band represents a stagnation zone, indicating a significantly low wall shear stress value. Moving downstream from this band, the wall shear stress increases again, and the maximum values are found in the inner wall of the carotid sinus near the apex, creating a region of high shear stress. Wall shear stress values are higher towards the height of the bifurcation and lower towards the outer wall.
In the external carotid artery, the wall shear stress exhibits relatively high values near the apex and lower values at the outer corner.
According to studies, variations in wall shear stress within the carotid bifurcation significantly impact the development of lipid plaques and the occurrence of atherosclerosis [29]. Several experimental studies [30]–[32] have demonstrated that areas affected by atherosclerosis correspond to regions of low wall shear stress. It is commonly observed that lipid particles tend to accumulate in the C-shaped part rather than at the apex of the bifurcation. The presence of low velocity and wall shear stress in this region of the carotid artery promotes the accumulation of lipid particles [33],[34]. Moreover, some researchers have identified flow separation and carotid sinus vortices as additional factors contributing to the formation of lipid particles [35],[36].
Comparing the figures also reveals that the impact of changing between the proposed boundary conditions (P1-V1 and P2-V2) on the wall shear stress is relatively small, with comparable values observed between the two states.
When transitioning to turbulent modeling, it becomes apparent that the CCA's wall shear stress is higher than that observed in laminar flow (Figures 66, 67, 68, and 69). Regarding the viscosity model effect, the results obtained in laminar flow are consistent with turbulent flow simulations. The Newtonian behavior aligns with the Cross model (66.a, 66.b, 67.a, 67.b, 68.a, 68.b, 69.a, and 69.b), while the Carreau model exhibits similarities to the Quemada model (66.c, 66.d, 67.c, 67.d, 68.c, 68.d, 69.c, and 69.d). Moreover, slightly higher wall shear stress values are observed when using turbulent flow and the P2-V2 boundary conditions than those obtained using the P1-V1 pair.
This study looked at the dynamics of blood flow in a rigid carotid bifurcation, taking into account things like the flow regime, the viscosity model, and the boundary conditions. Utilizing the Fluent solver, we observed intriguing phenomena within the carotid bifurcation and presented the results through diverse visualization methods, including curves, contours, and vectors. The findings obtained can be summarized as follows:
In the common carotid artery (CCA), the flow exhibits a Poiseuille-like profile, independent of the flow regime, viscosity model, and boundary conditions form.
The branching zone creates a depression area, where the enlargement of the CCA cross-section and the curvature of the internal carotid artery (ICA) and external carotid artery (ECA) significantly impact velocity and wall shear stress. This leads to the formation of a C-shaped stagnation zone with low velocity and wall shear stress values, accompanied by secondary flow development in the carotid sinus. These currents are most prominent during early diastole under P2-V2 boundary conditions.
In the ICA, the flow is directed towards the inner wall with a higher velocity than in the ECA. The differences between the viscosity models are more noticeable in laminar flow than in turbulent flow, particularly when considering the actual boundary conditions of P2-V2.
The non-Newtonian behavior of blood in the ECA is more apparent during laminar flow when utilizing the P2-V2 boundary conditions.
It's imperative to acknowledge an inherent limitation in our analysis. We admit that we didn't factor in the variations in distal vascular resistance between the internal and external carotid arteries, which could significantly impact the formation of observed flow patterns and fluid behavior at the bifurcation point. These fluctuations in vascular resistance might introduce complexities that haven't been examined in this study. While we've considered this limitation when interpreting our findings, the fact that we haven't explicitly analyzed this variable is a limited aspect of our investigation. Subsequent research could benefit from a more comprehensive exploration of this factor to fully understand the mechanisms influencing flow patterns at the bifurcation.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
| [1] |
Guyonnet D, Planchon M, Rollat A, et al. (2015) Material flow analysis applied to rare earth elements in Europe. J Clean Prod 107: 215-228. https://doi.org/10.1016/j.jclepro.2015.04.123 doi: 10.1016/j.jclepro.2015.04.123
|
| [2] | Salla Ahonen, Arvanitidis N, Auer A, et al. (2015) Strengthening the European Rare Earths Supply-Chain: Challenges and policy options-A report by the European Rare Earths Competency Network (ERECON). Available from: https://hal-cea.archives-ouvertes.fr/cea-01550114/document. |
| [3] |
Schlinkert D, van den Boogaart KG (2015) The development of the market for rare earth elements: Insights from economic theory. Resour Policy 46: 272-280. https://doi.org/10.1016/j.resourpol.2015.10.010 doi: 10.1016/j.resourpol.2015.10.010
|
| [4] | European Commission (2015) Report on critical raw materials for the EU-Critical raw materials profiles. Available from: https://ec.europa.eu/docsroom/documents/11911/attachments/1/translations. |
| [5] | Solvay (2012) Solvay launches its rare earth recycling activity in France. Available from: http://www.solvay.com/nl/media/press_releases/20120927-coleopterre.html. |
| [6] | GlobeNewswire (2015) Molycorp to move its mountain pass rare earth facility to 'care and maintenance' mode. Available from: http://globenewswire.com/news-release/2015/08/26/763530/0/en/Molycorp-to-Move-Its-Mountain-Pass-Rare-Earth-Facility-to-Care-and-Maintenance-Mode.html. |
| [7] | Lynas Corporation LTD (2016) FY16 Financial Report. Available from: https://www.lynascorp.com/Shared Documents/Investors and media/Reporting Centre/Annual reports/2016/160929 FY16 Financial Report 1548914.pdf. |
| [8] | Sud Ouest (2016) La Rochelle: closure of Solvay's rare earth recycling plant by the end of 2016 (in French). Available from: https://www.sudouest.fr/economie/la-rochelle-fermeture-de-l-atelier-de-recyclage-des-terres-rares-de-solvay-d-ici-fin-2016-4728900.php#:~:text=ArchivesL%C3%A9galesCarnet-,La%20Rochelle%20%3A%20fermeture%20de%20l'atelier%20de%20recyclage%20des%20terres, Solvay%20d'ici%20fin%202016&text=Le%20groupe%20Solvay%20(ex%2DRhodia, personnes%2C%20les%20deux%20sites%20confondus. |
| [9] |
Tukker A (2014) Rare earth elements supply restrictions: Market failures, not scarcity, hamper their current use in high-tech applications. Environ Sci Technol 48: 9973-9974. https://doi.org/10.1021/es503548f doi: 10.1021/es503548f
|
| [10] | European Commission (2017) Study on the review of the list of critical raw materials-Critical raw materials factsheets. Available from: https://op.europa.eu/en/publication-detail/-/publication/7345e3e8-98fc-11e7-b92d-01aa75ed71a1/language-en. |
| [11] |
Binnemans K, Jones PT, Van Acker K, et al. (2013) Rare-earth economics: the balance problem. JOM 65: 10-12. https://doi.org/10.1007/s11837-013-0639-7 doi: 10.1007/s11837-013-0639-7
|
| [12] |
Schrijvers D, Hool A, Blengini GA, et al. (2020) A review of methods and data to determine raw material criticality. Resour Conserv Recy 155: 104617. https://doi.org/10.1016/j.resconrec.2019.104617 doi: 10.1016/j.resconrec.2019.104617
|
| [13] |
Rollat A, Guyonnet D, Planchon M, et al. (2015) Prospective analysis of the flows of certain rare earths in Europe at the 2020 horizon. Waste Manage 49: 427-436. https://doi.org/10.1016/j.wasman.2016.01.011 doi: 10.1016/j.wasman.2016.01.011
|
| [14] | European Commission (2018) Circular economy-Implementation of the circular economy action plan. Available from: http://ec.europa.eu/environment/circular-economy/index_en.htm. |
| [15] |
Tan Q, Song Q, Li J (2015) The environmental performance of fluorescent lamps in China, assessed with the LCA method. Int J Life Cycle Assess 20: 807-818. https://doi.org/10.1007/s11367-015-0870-2 doi: 10.1007/s11367-015-0870-2
|
| [16] |
Schrijvers DL, Loubet P, Sonnemann G (2021) "Allocation at the point of substitution" applied to recycled rare earth elements: what can we learn? Int J Life Cycle Assess 26: 1403-1416. https://doi.org/10.1007/s11367-021-01884-3 doi: 10.1007/s11367-021-01884-3
|
| [17] | Sonnemann GW, Vigon BW (2011) Global guidance principles for life cycle assessment databases-A basis for greener processes and products. Available from: https://www.lifecycleinitiative.org/wp-content/uploads/2012/12/2011%20-%20Global%20Guidance%20Principles.pdf. |
| [18] | ISO 14040: Environmental management-Life cycle assessment-Principles and framework. The International Organization for Standardization, 2006. Available from: https://www.iso.org/standard/37456.html. |
| [19] | ISO 14044: Environmental management-Life cycle assessment-Requirements and guidelines. The International Organization for Standardization, 2006. Available from: https://www.iso.org/obp/ui/#iso:std:iso:14044:en. |
| [20] |
Ekvall T, Weidema BP (2004) System boundaries and input data in consequential life cycle inventory analysis. Int J Life Cycle Assess 9: 161-171. https://doi.org/10.1007/BF02994190 doi: 10.1007/BF02994190
|
| [21] | Weidema BP, Ekvall T, Heijungs R (2009) Guidelines for application of deepened and broadened LCA-Deliverable D18 of work package 5 of the CALCAS project. Available from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.628.948&rep=rep1&type=pdf. |
| [22] | Weidema BP, Bauer C, Hischier R, et al. (2013) Overview and Methodology: Data Quality Guideline for the Ecoinvent Database Version 3. St. Gallen: The Ecoinvent Centre. |
| [23] |
Schrijvers DL, Loubet P, Weidema BP (2021) To what extent is the Circular Footprint Formula of the Product Environmental Footprint Guide consequential? J Clean Prod 320: 128800. https://doi.org/10.1016/j.jclepro.2021.128800 doi: 10.1016/j.jclepro.2021.128800
|
| [24] | Consequential-LCA (2015) Further theory on normalising market trends. Available from: https://consequential-lca.org/. |
| [25] | Consequential-LCA (2015) Further theory on marginal production costs. Available from: https://consequential-lca.org/. |
| [26] | Consequential-LCA (2015) When all co-products have alternatives. Available from: https://consequential-lca.org/. |
| [27] |
Kätelhön A, von der Assen N, Suh S, et al. (2015) Industry-cost-curve approach for modeling the environmental impact of introducing new technologies in life cycle assessment. Environ Sci Technol 49: 7543-7551. https://doi.org/10.1021/es5056512 doi: 10.1021/es5056512
|
| [28] | PRé (2022) About SimaPro. Available from: https://simapro.com/about/. |
| [29] |
Kara P, Korjakins A, Kovalenko K (2012) The usage of fluorescent waste glass powder in concrete. Constr Sci 13: 26-32. https://doi.org/10.2478/v10311-012-0004-z doi: 10.2478/v10311-012-0004-z
|
| [30] | Krishnamurthy N, Gupta CK (2016) Extractive Metallurgy of Rare Earths, 2 Ed., Boca Raton: CRC Press. https://doi.org/10.1201/b19055 |
| [31] | Long KR, Van Gosen BS, Foley NK, et al. (2012) The principal rare earth elements deposits of the United States-A summary of domestic deposits and a global perspective. In: Sinding-Larsen R, Wellmer FW, Non-Renewable Resource Issues. International Year of Planet Earth, 1 Ed., Dordrecht: Springer. https://doi.org/10.1007/978-90-481-8679-2_7 |
| [32] |
Schulze R, Lartigue-Peyrou F, Ding J, et al. (2017) Developing a life cycle inventory for rare earth oxides from ion-adsorption deposits: key impacts and further research needs. J Sustain Metall 3: 753-771. https://doi.org/10.1007/s40831-017-0139-z doi: 10.1007/s40831-017-0139-z
|
| [33] | USGS (2015) 2012 Minerals Yearbook-Rare Earths. Available from: https://s3-us-west-2.amazonaws.com/prd-wret/assets/palladium/production/mineral-pubs/rare-earth/myb1-2012-raree.pdf. |
| [34] | Holland C, Energy N, Alliance E (2014) Are LEDs the next CFL: a diffusion of innovation analysis. ACEEE Summer Study Energy Effic Build 2014: 184-196. |
| [35] | Habib K (2015) Critical resources in clean energy technologies and waste flows[PhD's thesis]. University of Southern Denmark, Denmark. |
| [36] | National Research Council (2008) Minerals, Critical Minerals, and the U.S. Econom, Washington DC: National Academies Press. |
| [37] |
Eggert RG (2011) Minerals go critical. Nat Chem 3: 688-691. https://doi.org/10.1038/nchem.1116 doi: 10.1038/nchem.1116
|
| [38] | Guyonnet D, Planchon M, Rollat A, et al. (2014) Primary and secondary sources of rare earths in the EU-28: results of the ASTER project. ERES 2014-1st Conference on European Rare Earth Resources, 66-72. |
| [39] | Binnemans K (2014) Economics of rare earths: the balance problem. Proceedings of the 1st European Rare Earth Resources Conference (ERES 2014), 37-46. |
| [40] | Chu S (2011) Critical Materials Strategy, Collingdale: DIANE Publishing. |
| [41] | Scholand M, Dillon H (2013) Life-Cycle Assessment of Energy and Environmental Impacts of LED Lighting Products-Part 2: LED Manufacturing and Performance, Richland: U.S. Department of Energy. https://doi.org/10.2172/1044508 |
| [42] |
Binnemans K, Jones PT, Müller T, et al. (2018) Rare earths and the balance problem: how to deal with changing markets? J Sustain Metall 4: 126-146. https://doi.org/10.1007/s40831-018-0162-8 doi: 10.1007/s40831-018-0162-8
|
| [43] | Weidema BP (2003) Market Information in Life Cycle Assessment, Copenhagen: Denmark. |
 ctr-01-01-004-S1.pdf |
 |
Figures(5) / Tables(2)
Dieuwertje L. Schrijvers, Philippe Loubet, Guido W. Sonnemann. The influence of market factors on the potential environmental benefits of the recycling of rare earth elements[J]. Clean Technologies and Recycling, 2022, 2(1): 64-79. doi: 10.3934/ctr.2022004
| CCA diameter | ICA diameter | ECA diameter | Bifurcation total length |
| 7.37 mm | 5.22 mm | 4 mm | m |
DownLoad:
CSV
| a1 | -0.0214 | b1 | 0.5458 | c1 | 0.008372 |
| a2 | 0.04842 | b2 | 0.3374 | c2 | 0.1284 |
| a3 | 0.0407 | b3 | 0.4749 | c3 | 0.1268 |
| a4 | 0.08353 | b4 | 0.6215 | c4 | 0.234 |
| a5 | 0.09432 | b5 | 0.002087 | c5 | 0.3171 |
| a6 | 0.08364 | b6 | 1.006 | c6 | 0.314 |
DownLoad:
CSV
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| 0.5601 | 0.1882 | -1.4424 | 1.2239 | -0.426 | 0.0664 | -0.00492 | 0.000432 |
DownLoad:
CSV
| Nombre d'éléments | u (m/s) |
| 105438 | 0,00372 |
| 110007 | 0,00383 |
| 119054 | 0,00402 |
| 133468 | 0,00426 |
| 145068 | 0,00432 |
| 209791 | 0,00432 |
| 466421 | 0,00459 |
DownLoad:
CSV
| Systolic peak | Early diastole | ||||||
| P1 | V1 | P2 | V2 | P1 | V1 | P2 | V2 |
| 1 s | 1.04 s | 0.967 s | 1.056 s | 1.42 s | 1.23 s | 1.072 s | |
DownLoad:
CSV
| CCA diameter | ICA diameter | ECA diameter | Bifurcation total length |
| 7.37 mm | 5.22 mm | 4 mm | m |
| a1 | -0.0214 | b1 | 0.5458 | c1 | 0.008372 |
| a2 | 0.04842 | b2 | 0.3374 | c2 | 0.1284 |
| a3 | 0.0407 | b3 | 0.4749 | c3 | 0.1268 |
| a4 | 0.08353 | b4 | 0.6215 | c4 | 0.234 |
| a5 | 0.09432 | b5 | 0.002087 | c5 | 0.3171 |
| a6 | 0.08364 | b6 | 1.006 | c6 | 0.314 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| 0.5601 | 0.1882 | -1.4424 | 1.2239 | -0.426 | 0.0664 | -0.00492 | 0.000432 |
| Nombre d'éléments | u (m/s) |
| 105438 | 0,00372 |
| 110007 | 0,00383 |
| 119054 | 0,00402 |
| 133468 | 0,00426 |
| 145068 | 0,00432 |
| 209791 | 0,00432 |
| 466421 | 0,00459 |
| Systolic peak | Early diastole | ||||||
| P1 | V1 | P2 | V2 | P1 | V1 | P2 | V2 |
| 1 s | 1.04 s | 0.967 s | 1.056 s | 1.42 s | 1.23 s | 1.072 s | |
