Self-adaptive algorithms for the split problem of the quasi-pseudocontractive operators in Hilbert spaces

1.   Introduction

Inverse problems in various disciplines can be expressed as split feasibility problems and their generalizations, such as multiple-sets split feasibility problems and split common fixed point problems, and many iterative algorithms have been presented to solve these problems (see ^{[1,2,3,4,5,6]} for multiple-sets split feasibility problems, ^[7,8,9,10] for split feasibility problems, ^{[11,12,13,14,15,16,17,18]} for split common fixed point problems, or ^{[19,20,21,22,23,24]} for a self-adaptive method).

The present article is focusing on the split common fixed point problem by virtue of self-adaptive algorithms such that involved methods are simpler. The split common fixed point problem is a generalization of the split feasibility problem which is a general way to characterize various inverse problems arising in many real-world application problems, such as medical image reconstruction and intensity-modulated radiation therapy.

Recall that the split common fixed point problem is to find a point $u\in H_{1}$ such that

The split feasibility problem is to find a point satisfying

where $C$ and $Q$ are two nonempty closed convex subsets of real Hilbert spaces $H_{1}$ and $H_{2}$, respectively and $A:H_{1}\rightarrow H_{2}$ is a bounded linear operator. Problem (1.2) was firstly introduced by Censor and Elfving ^[25] in finite-dimensional Hilbert spaces. In ^[26], note that solving (1.1) can be translated to solve the fixed point equation

Whereafter, Censor and Segal proposed an algorithm for directed operators. Since then, there has been growing interest in the split common fixed point problem. In ^[27], based on the work ^[26], Moudafi investigated an algorithm for solving the split common fixed-point problem for the class of demicontractive operators in a Hilbert space. In ^[28], Kraikaew et al. modified the iterative scheme studied by Moudafi for quasi-nonexpansive operators to obtain strong convergence to a solution of the split common fixed point problem. In ^[29], based on Halpern's type method, Boikanyo constructed an algorithm for demicontractive operators that produces sequences that always converge strongly to a specific solution of the split common fixed point problem. In ^[30], Ansari introduced an implicit algorithm and an explicit algorithm for solving the split common fixed point problems. In ^[31], using the hybrid method and the shrinking projection method in mathematical programming, Takahashi proved strong convergence theorems for finding a solution of the split common fixed point problem in two Banach spaces. In ^[32], Wang proposed a new algorithm for the split common fixed-point problem that does not need any priori information of the operator norm.

In the case where $C$ and $Q$ in (1.2) are the intersections of finitely many fixed point sets of nonlinear operators, problem (1.2) is called by Censor and Segal (^[26]) the split common fixed point problem. More precisely, the split common fixed point problem requires one to seek an element $u\in H_{1}$ such that

where $\text{Fix}(S_{i})$ and $\text{Fix}(T_{i})$ denote the fixed point sets of two classes of nonlinear operators $S_{i}: H_{1}\rightarrow H_{1}$ and $T_{i} : H_{2}\rightarrow H_{2}$, respectively.

In particular, Yao et al. ^[21] introduced the following new iterative algorithms for the split common fixed point problem of demicontractive operators.

Algorithm 1.1. Choose an arbitrary initial guess $x_{0}\in H_{1}$. Assume $x_{n}$ has been constructed. If

then stop; otherwise, continue and construct via the manner

where $\gamma\in(0, \min\{1-\beta, 1-\mu\})$ is a positive constant and $\tau_{n}$ is chosen self-adaptively as

Algorithm 1.2. Let $u\in H_{1}$ and choose an arbitrary initial value $x_{0}\in H_{1}$. Assume $x_{n}$ has been constructed. If

then stop; otherwise, continue and construct via the manner

where $\gamma\in(0, \min\{1-\beta, 1-\mu\})$ is a positive constant and $\tau_{n}$ is chosen self-adaptively as

Yao et al. obtained the weak and strong convergence of Algorithms 1.1 and 1.2, respectively. It should be pointed out that Algorithm 1.1 and 1.2 do not need any prior information of the operator norm. Inspired by the work in the literature, the main purpose of this paper is to present two new self-adaptive algorithms for approximating a solution of the split common fixed point problem (1.3) for the class of quasi-pseudocontractive operators which is more general than the classes of quasi-nonexpansive operators, directed operators and demicontractive operators. Weak and strong convergence theorems are given under some mild assumptions.

2.   preliminaries

In this section, we collect some tools including some definitions, some useful inequalities and lemmas which will be used to derive our main results in the next section.

Let $H$ be a real Hilbert space with inner product $\langle\cdot, \cdot\rangle$ and norm $\|\cdot\|$, respectively. Let $C$ be a nonempty closed convex subset of $H$. Let $T:C\longrightarrow C$ be an operator. We use $\text{Fix}(T)$ to denote the set of fixed points of $T$, that is, $\text{Fix}(T) = \{u | u = Tu, u \in C\}.$

First, we give some definitions related to the involved operators.

Definition 2.1. An operator $T:C\longrightarrow C$ is said to be

(i) nonexpansive if $\|Tu - Tv\|\leq\|u - v\|$ for all $u, v \in C$.

(ii) quasi-nonexpansive if $\|Tu - u^{\ast}\|\leq\|u - u^{\ast}\|$ for all $u\in C$ and $u^{\ast}\in \text{Fix}$$(T)$.

(iii) firmly nonexpansive if $\|Tu - Tv\|^{2}\leq \|u - v\|^{2}-\|(I - T)u-(I - T)v\|^{2}$ for all $u, v \in C$.

(iv) directed(or firmly quasi-nonexpansive) if $\|Tu-u^{\ast}\|^{2}\leq\|u-u^{\ast}\|^{2}-\|Tu-u\|^{2}$for all $u\in C$ and $u^{\ast}\in \text{Fix}$$(T)$.

Definition 2.2. An operator $T:C\longrightarrow C$ is said to be pseudo-contractive if $\langle Tu-Tv, u-v\rangle \leq\|u-v\|^{2}$ for all $u, v \in C$.

The interest of pseudocontractive operators lies in their connection with monotone operators; namely, $T$ is a pseudocontraction if and only if the complement $I-T$ is a monotone operator. It is well known that T is pseudocontractive if and only if

for all $u, v \in C$.

Definition 2.3. An operator T is said to be strictly pseudocontractive if

for all $u, v \in C$, where $k \in [0, 1)$.

Definition 2.4. An operator T is said to be demicontractive if there exists a constant $k \in [0, 1)$ such that

or equivalently,

for all $u\in C$ and $u^{\ast}\in \text{Fix}$$(T)$.

Remark 2.1. From the above definitions, we note that the class of demicontractive operators contains important operators such as the directed operators, the quasi-nonexpansive operators and the strictly pseudocontractive operators with fixed points. Such a class of operators is fundamental because it includes many types of nonlinear operators arising in applied mathematics and optimization.

Definition 2.5. An operator $T:C\longrightarrow C$ is said to be quasi-pseudocontractive if $\|Tu - u^{\ast}\|^{2}\leq \|u - u^{\ast}\|^{2}+\|Tu - u\|^{2}$ for all $u\in C$ and $u^{\ast}\in \text{Fix}(T)$.

Definition 2.6. An operator $T:C\longrightarrow C$ is said to be L-Lipschitzian if there exists $L > 0$ such that $\|Tu - Tv\|\leq L\|u - v\|$ for all $u, v \in C$.

Usually, the convergence of fixed point algorithms requires some additional smoothness properties of the mapping $T$ such as demi-closedness.

Definition 2.7. An operator $T$ is said to be demiclosed if, for any sequence $\{u_{n}\}$ which weakly converges to $u^{*}$, and if $Tu_{n}\longrightarrow w$, then $Tu^{*} = w$.

Definition 2.8. A sequence $\{u_{n}\}$ is called Fej$\acute{e}$r-monotone with respect to a given nonempty set $\Omega$ if for every $u\in\Omega$,

for all $n\geq0$.

Recall that the (nearest point or metric) projection from $H$ onto $C$, denoted by $P_{C}$, assigns to each $u\in H$, the unique point $P_{C}u\in C$ with the property

The metric projection $P_{C}$ of $H$ onto $C$ is characterized by

for all $u\in H, v\in C$. It is well known that the metric projection $P_{C}:H\rightarrow C$ is firmly nonexpansive, that is,

for all $u, v\in H$.

Next we adopt the following notations:

$\bullet$ $u_{n}\rightharpoonup u$ means that $\{u_{n}\}$ converges weakly to $u$;

$\bullet$ $u_{n}\rightarrow u$ means that $\{u_{n}\}$ converges strongly to $u$;

$\bullet$ $\omega_{w}(u_{n})$ stands for the set of cluster points in the weak topology, that is,

Lemma 2.1. (^[33]) Let $C$ be a nonempty closed convex subset in $H$. If the sequence $\{u_{n}\}$ is Fej$\acute{e}$r monotonewith respect to $\Omega$, then we have the following conclusions:

(i) $u_{n}\rightharpoonup u\in\Omega$ iff $\omega_{w}(u_{n})\subset\Omega$;

(ii) the sequence $\{P_{\Omega}u_{n}\}$ converges strongly;

(iii) if $u_{n}\rightharpoonup u\in\Omega$, then $u = \lim_{n\rightarrow \infty}P_{\Omega}u_{n}$.

For all $u, v \in H$, the following conclusions hold:

and

Lemma 2.2. (^[34]) Let $H$ be a Hilbert space and $\emptyset\neq C\subset H$ be a closed convex set. If $T:C\rightarrow C$ is an L-Lipschitzian operator with $L\geq1$. Then

where $\delta\in(0, \frac{1}{L})$.

Lemma 2.3. (^[34]) Let $H$ be a Hilbert space and $\emptyset\neq C\subset H$ be a closed convex set. If $T:C\rightarrow C$ is an L-Lipschitzian operator with $L\geq1$ and $I-T$ is demiclosed at $0$, then the composition operator

is also demiclosed at $0$ provided $\delta\in(0, \frac{1}{L})$.

Lemma 2.4. (^[34]) Let $H$ be a Hilbert space and $\emptyset\neq C\subset H$ be a closed convex set. If $T:C\rightarrow C$ is an L-Lipschitzian quasi-pseudocontractive operator. Then we have

for all $u\in C$ and $u^{\ast}\in Fix(T)$ when $0 < \zeta < \frac{1}{\sqrt{1+L^{2}}+1}$.

Lemma 2.5. (^[35])Assume that $\{\alpha_{n}\}$ is a sequence of nonnegative real numbers such that

where $\{\gamma_{n}\}$ is a sequence in $(0, 1)$ and $\{\delta_{n}\}$ is a sequence such that

(1) $\sum^{\infty}_{n = 1}\gamma_{n} = \infty$;

(2) $\limsup_{n\rightarrow \infty}\frac{\delta_{n}}{\gamma_{n}}\leq0$ or $\sum^{\infty}_{n = 1}|\delta_{n}| < \infty.$

Then $\lim_{n\rightarrow \infty}\alpha_{n} = 0.$

3.   Results

Throughout the present article, let $H_{1}$ and $H_{2}$ be two real Hilbert spaces. We use $\langle\cdot, \cdot\rangle$ to denote the inner product, and $\|\cdot\|$ stands for the corresponding norm. Let $s$ and $t$ be positive integers, and let $T_{i}:H_{1}\longrightarrow H_{1}$ be an $L_{1i}$-Lipschitzian quasi-pseudocontractive operator with $1 < L_{1i}\leq L_{1}$ and $S_{j}:H_{2}\longrightarrow H_{2}$ be an $L_{2j}$-Lipschitzian quasi-pseudocontractive operator with $1 < L_{2j}\leq L_{2}$, where $L_{1}, L_{2} > 1$. Denote the fixed point sets of $T_{i}$ and $S_{j}$ by $\text{Fix}(T_{i})$ and $\text{Fix}(S_{j})$, respectively. Let $A:H_{1}\longrightarrow H_{2}$ be a bounded linear operator with its adjoint $A^{\ast}$. Throughout, assume

Next we present the following iterative algorithm to solve (1.3).

Algorithm 3.1. Choose an arbitrary initial value $x_{1}\in H_{1}$. Assume $x_{n}$ has been constructed. Compute

where $0 < \zeta_{n} < \frac{1}{\sqrt{1+L_{1}^{2}}+1}$, $0 < \eta_{n} < \frac{1}{\sqrt{1+L_{2}^{2}}+1}$,

and

If

then stop (in this case by Remark 3.2 below); otherwise, continue and construct via the manner

where

in which $\lambda_{n} > 0$.

Remark 3.1. The equality (3.2) holds if and only if $x_{n}$ is a solution of (1.3). First, assume that $x_{n}$ is a solution of (1.3), that is,

According to Lemma 2.2, we get that

and

From (3.1), it turns out that $z_{n} = 0$ and $x_{n} = y_{n}$. Therefore, $u_{n} = x_{n}-y_{n}+A^{\ast}z_{n} = 0$.

In the sequel, we assume that the equality (3.2) holds. For any $u\in\Omega$, we have

By Lemma 2.4, $T_{i_{n}}((1-\zeta_{n})I+\zeta_{n} T_{i_{n}})$ and $S_{j_{n}}((1-\eta_{n})I+\eta_{n} S_{j_{n}})$ are demicontractive, from (2.1), we deduce

and

By(3.5)–(3.7), we get

Since $\zeta_{n}, \eta_{n}\in(0, 1)$, we deduce

and

According to the definitions of $i_{n}$ and $j_{n}$, it follows from (3.9) and (3.10) that

for all $i\in I_{1}$ and

for all $j\in I_{2}$. Hence, by Lemma 2.2, we have

and

Therefore, $x_{n}\in \Omega$.

Assume that the sequence $\{x_{n}\}$ generated by Algorithm 3.1 is infinite. In other words, Algorithm 3.1 does not terminate in a finite number of iterations. Next, we demonstrate the convergence analysis of the sequence $\{x_{n}\}$ generated by Algorithm 3.1.

Theorem 3.1. Suppose that $I-T_{i}$ (for all $i\in I_{1}$) and $I-S_{j}$ (for all $j\in I_{2}$) are demiclosed at zero. If $\Omega\neq\emptyset$ and the followingconditions are satisfied:

($C_{1}$) $0 < \zeta\leq\zeta_{n} < \frac{1}{\sqrt{1+L_{1}^{2}}+1}$;

($C_{2}$) $0 < \eta\leq\eta_{n} < \frac{1}{\sqrt{1+L_{2}^{2}}+1}$;

($C_{3}$) $0 < \liminf_{n\rightarrow \infty}\lambda_{n}\leq \limsup_{n\rightarrow \infty}\lambda_{n} < \min\{\zeta, \eta\}$.

Then the sequence $\{x_{n}\}$generated by Algorithm 3.1 converges weakly to a solution $z^{\ast}( = \lim_{n\rightarrow \infty}P_{\Omega}(x_{n}))$ of problem (1.3).

Proof. Firstly, we prove that the sequence $\{x_{n}\}$ is Fej$\acute{ \text{e}}$r-monotone with respect to $\Omega$. Picking up $z\in\Omega$, from (3.8), we have

According to (3.1), (3.3), (3.4) and (3.13), we derive

where

By virtue of (3.14), we deduce that the sequence $\{x_{n}\}$ is Fej$\acute{ \text{e}}$r-monotone with respect to $\Omega$. Next, we show that every weak cluster point of the sequence $\{x_{n}\}$ belongs to the solution set of problem (1.3), i.e. $\omega_{w}(x_{n})\subset\Omega$.

From the Fej$\acute{ \text{e}}$r-monotonicity of $\{x_{n}\}$ it follows that the sequence $\{x_{n}\}$ is bounded, and so are the sequences $\{Ax_{n}\}$, $\{T_{i}x_{n}\}(i\in I_{1})$ and $\{S_{j}Ax_{n}\}(j\in I_{2})$. Further, from (3.14), we obtain

which implies that

This together with the boundedness of the sequence $\{u_{n}\}$ implies that

and

Hence,

for all $i\in I_{1}$ and

for all $j\in I_{2}$. It follows that

for all $i\in I_{1}$ and

for all $j\in I_{2}$. By $(C_{1})$, we have $\zeta_{n}(\sqrt{1+L_{1}^{2}}+1) < 1$ and so $\zeta_{n}L_{1} < 1-\zeta_{n}\leq1-\zeta.$ This together with (3.17) implies that

for all $i\in I_{1}$. Employing a similar way, we obtain

for all $j\in I_{2}$. Therefore,

for all $i\in I_{1}$, and

for all $j\in I_{2}$. By the demiclosedness (at zero) of $I-T_{i}$ (for all $i\in I_{1}$) and $I-S_{j}$ (for all $j\in I_{2}$), we deduce immediately $\omega_{w}(x_{n})\subset\Omega$. To this end, the conditions of Lemma 2.1 are all satisfied. Consequently, $x_{n}\rightharpoonup z^{\ast}( = \lim_{n\rightarrow \infty}P_{\Omega}x_{n})$. The proof is completed.

Algorithm 3.1 has only weak convergence. Now, we present a new algorithm with strong convergence.

Algorithm 3.2. Let $u\in H_{1}$ and choose an arbitrary initial value $x_{1}\in H_{1}$. Assume $x_{n}$ has been constructed. Compute

where $0 < \zeta_{n} < \frac{1}{\sqrt{1+L_{1}^{2}}+1}$, $0 < \eta_{n} < \frac{1}{\sqrt{1+L_{2}^{2}}+1}$,

and

If

then stop; otherwise, continue and construct via the manner

where $\alpha_{n}\in(0, 1)$ and

in which $\lambda_{n} > 0$.

Assume that the sequence $\{x_{n}\}$ generated by Algorithm 3.2 is infinite. In other words, Algorithm 3.2 does not terminate in a finite number of iterations.

Theorem 3.2. Suppose that $I-T_{i}$ (for all $i\in I_{1}$) and $I-S_{j}$ (for all $j\in I_{2}$) are demiclosed at zero. If $\Omega\neq\emptyset$ and the followingconditions are satisfied:

($C_{1}$) $0 < \zeta\leq\zeta_{n} < \frac{1}{\sqrt{1+L_{1}^{2}}+1}$;

($C_{2}$) $0 < \eta\leq\eta_{n} < \frac{1}{\sqrt{1+L_{2}^{2}}+1}$;

($C_{3}$) $\lim_{n\rightarrow \infty}\alpha_{n} = 0$ $\sum^{\infty}_{n = 1}\alpha_{n} = +\infty$;

($C_{4}$) $0 < \liminf_{n\rightarrow \infty}\lambda_{n}\leq \limsup_{n\rightarrow \infty}\lambda_{n} < \min\{\zeta, \eta\}$.

Then the sequence $\{x_{n}\}$generated by Algorithm 3.2 converges strongly to a solution $z( = P_{\Omega}(u))$ of problem (1.3).

Proof. Set $v_{n} = x_{n}-\tau_{n}u_{n}$ for all $n\geq0$. By (3.14), we have

In particular, we have $\|v_{n}-z\|\leq\|x_{n}-z\|$. Thus, from (3.23), we obtain

By induction, we derive

Hence, $\{x_{n}\}$ is bounded and so are the sequences $\{Ax_{n}\}$, $\{T_{i}x_{n}\}(i\in I_{1})$ and $\{S_{j}Ax_{n}\}(j\in I_{2})$.

From (3.23), we have

By virtue of (3.25) and (3.27), we deduce

Set $\varpi_{n} = \|x_{n}-z\|^{2}$ and

for all $n\geq1$. Then, from (3.28), we have

It is obvious that

So, $\limsup_{n\rightarrow \infty}\delta_{n} < \infty$. Next, we show that $\limsup_{n\rightarrow \infty}\delta_{n}\geq-1$ by contradiction. Assume that $\limsup_{n\rightarrow \infty}\delta_{n} < -1$. Then there exists $m$ such that $\delta_{n}\leq-1$ for all $n\geq m$. It follows from (3.29) that

for all $n\geq m$. Thus,

Hence, by taking $\limsup$ as $n\rightarrow \infty$ in the last inequality, we obtain

which is a contradiction. Therefore, $\limsup_{n\rightarrow \infty}\delta_{n} > -1$ and it is finite. Consequently, we can take a subsequence $\{n_{i}\}$ such that

Since $\langle u-z, x_{n_{i}+1}-z\rangle$ is a bounded real sequence, without loss of generality, we may assume the limit $\lim_{i\rightarrow \infty}\langle u-z, x_{n_{i}+1}-z\rangle$ exists. Consequently, from (3.31), the following limit also exists

This together with conditions $(C_{3})$ and $(C_{4})$ implies that

which yields $\lim_{i\rightarrow \infty}\|x_{n_{i}}-y_{n_{i}}\| = 0$ and $\lim_{i\rightarrow \infty}\|z_{n_{i}}\| = 0$. By a similar proof as in Theorem 3.3, we conclude that any weak cluster point of $\{x_{n_{i}}\}$ belongs to $\Omega$. Note that

This indicates that $\omega_{w}(x_{n_{i}+1})\subset\Omega$. Without loss of generality, we assume that $x_{n_{i}+1}$ converges weakly to $x^{\dagger}\in\Omega$. Now by (3.31), we infer that

due to the fact that $z = P_{\Omega}u$ and (2.2). Finally, applying Lemma 2.5 to (3.29), we conclude that $x_{n}\rightarrow z$. This completes the proof.

4.   Numerical illustrations

In this section, some numerical results are presented. The MATLAB codes run in MATLAB version 9.5 (R2018b) on a PC Intel(R) Core(TM)i5-6200 CPU @ 2.30 GHz 2.40 GHz, RAM 8.00 GB. In all examples $y$-axes shows the value of $x_{n}$ while the $x$-axis indicates to the number of iterations.

Example 4.1. Let $T_{1}:R\rightarrow R$ be odd function and defined by

Let $S_{1}:R\rightarrow R$ be odd function and defined by

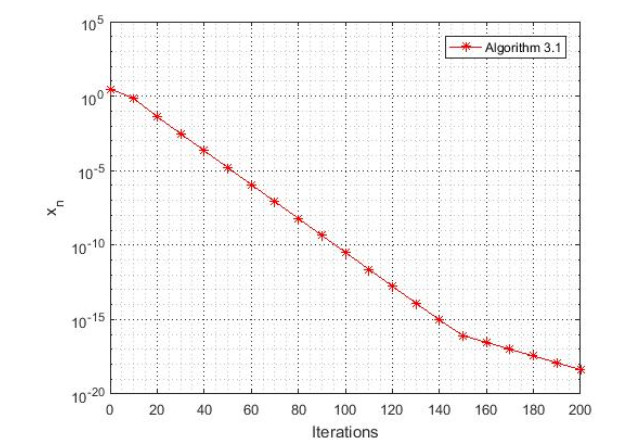
Let $T_{2}:R\rightarrow R$ and $S_{2}:R\rightarrow R$ be defined by $T_{2}(x) = T_{1}(x+1)-1$ and $S_{2}(x) = S_{1}(x+1)-1$, respectively. It is obvious that $\text{Fix}(T_{1}) = [-1, 1]$, $\text{Fix}(S_{1}) = [-1, 1]$, $\text{Fix}(T_{2}) = [-2, 0]$ and $\text{Fix}(S_{2}) = [-2, 0]$. We can easily see that $T_{1}, \ T_{2}, \ S_{1}$ and $S_{2}$ are quasi-pseudocontractive operators but neither pseudocontractive nor quasi-nonexpansive operators. We also observe that $T_{1}, \ T_{2}, \ S_{1}$ and $S_{2}$ are Lipschitzian operators. The values of control parameters for Algorithm 3.1 and Algorithm 3.2 are $\eta_{n} = \zeta_{n} = 0.125$, $\lambda_{n} = 0.1$, $\alpha_{n} = \frac{1}{n}$, $x_{1} = 3$ and $u = 3$.

The numerical results regarding Example 4.1 is reported in Figures 1 and 2.

Remark 4.1. In finite dimensional Hilbert spaces, weak convergence and strong convergence are equivalent. As can be seen from Figures 1 and 2, Algorithm 3.1 is more efficient than Algorithm 3.2 for finite dimensional Hilbert spaces. However, for infinite dimensional Hilbert spaces, in order to ensure strong convergence, generally speaking, we have to use Algorithm 3.2.

5.   Conclusions

In this paper, we considered a class of the split common fixed point problem. we present two new self-adaptive algorithms for approximating a solution of the split common fixed point problem (1.3) for the class of quasi-pseudocontractive operators. Besides, weak and strong convergence theorems are established under some mild assumptions. Numerical findings have been documented to compare the numerical efficiency of Algorithms 3.1 and 3.2.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant (No. 62103289), National Natural Science Foundation of China (No. 11761074), Project of Jilin Science and Technology Development for Leading Talent of Science and Technology Innovation in Middle and Young and Team Project (No. 20200301053RQ), and Natural Science Foundation of Jilin Province (No. 2020122336JC).

Conflict of interest

The authors declare that they have no competing interests.