Diversity and bioprospecting for industrial hydrolytic enzymes of microbial communities isolated from deserted areas of south-east Morocco

1.   Introduction

Sweeping surface is the surface swept out by the movement of a plane curve (the profile curve or generatrix) whilst the plane is moved through space in such away that the movement of the plane is always in the direction of the normal to the plane. Sweeping is a very substantial, strongly, and spread method in geometric modelling. The fundamental idea is to select various geometrical object (generators), which is then swept over a spine curve (trajectory) in the space. The result of such evolution, depend on movement through space and intrinsic shape deformation, is a sweep object. The sweep object type is given by the choice of the generator and the trajectory. Additional specifics on the sweeping surfaces can be found in ^[1,2,3,4]. In recent years, the ownerships of sweeping surfaces and their offset surfaces have been examined in Euclidean and non-Euclidean spaces (see e.g., ^[5,6,7,8,9]). There are several different names for the sweeping surface in previous written works, namely, tubular surface, pipe surface, string, and canal surface ^[10,11]. However, to the best of the authors knowledge, we can not find any literature on the study for regarding curves lying in surfaces as the original objects and considering the singularities and convexity of sweeping surfaces generated by these curves. Serve such a need and as the extension of the study^[7], the current study focuses our attention on the geometrical properties of sweeping surfaces whose center curves in surfaces in Euclidean 3-space $\mathbb{E}^{3}$.

In this work, in analogous with the well known Bishop and Frenet-Serret frames, we define a new version of Darboux frame using a common tangent vector field to a surface along a curve and call this frame the rotation minimizing Darboux frame (RMDF). By using this frame, we give the parametric representation for a sweeping surface. We also show that the parametric curves on this surface are curvature lines. Then, we study the local singularities and convexity of a sweeping surface. Consequently, the necessary and sufficient condition for the sweeping surface to be a developable ruled surface is derived. In addition, some examples of application are introduced and explained in detail.

2.   Preliminaries

The ambient space is the Euclidean 3-space $\mathbb{E}^{3}$, and for our work we have used ^[10,11] as general references. Let

represent a regular surface $M$. The ${\bf R}^{\prime }s$ tangent vectors are

The unit normal vector to the surface $M$ is

where $\times$ denotes the cross product in $\mathbb{E}^{3}$. The metric (first fundamental form) $I$ is defined by

where $g_{11} = < {\bf R}_{s}, {\bf R}_{s} >$, $g_{12} = < {\bf R}_{s}, {\bf R}_{u} > , \ g_{22} = < {\bf R}_{u}, {\bf R}_{u} >$. We define the second fundamental form $II$ of $M$ by

where $h_{11} = < {\bf R}_{ss}, {\bf u} >$, $h_{12} = < {\bf R}_{su}, {\bf u} > , \ h_{22} = < {\bf R}_{uu}, {\bf u} >$. The Gaussian $K(s, u)$ and mean $H(s, u)$ curvature are defined by

Let ${\bf \gamma }:I\subseteq \mathbb{R} \rightarrow M$ is a unit speed curve on $M$. Since ${\bf \gamma }(s)$ is a space curve, there exists the Serret-Frenet frame $\{{\bf t}(s),$ ${\bf n}(s)$, ${\bf b}(s)\}$. The derivative formulas for Serret-Frenet frame are given by

where $\kappa (s)$ is the curvature and $\tau (s)$ is the torsion of ${\bf \gamma }(s)$. Due to ${\bf \gamma }(s)$ on the surface $M$, we have the moving Darboux frame $\{{\bf \gamma }(s); \; {\bf e}_{1}, \; {\bf e}_{2}, \; {\bf e}_{3}\}$; ${\bf t = e}_{1}(s)$, ${\bf e}_{3} = {\bf e}_{3}{\bf (}s)$ is the surface unit normal restricted to ${\bf \gamma }$, and ${\bf e}_{2}{\bf = e}_{3}{\bf \times e}_{1}$ be the unit tangent to the surface $M$. The the relationships between these frames is expressed as:

Then we have the following Frenet-Serret type formulae:

where $\widetilde{\boldsymbol{\omega }}{\bf (}s){\bf = }\tau _{g}{\bf e} _{1}-\kappa _{n}{\bf e}_{2}+\kappa _{g}{\bf e}_{3}$ is referred to as the Darboux vector. Here,

We call $\kappa _{g}(s)$ a geodesic curvature, $\kappa _{n}(s)$ a normal curvature, and $\tau _{g}(s)$ a geodesic torsion of ${\bf \gamma }(s)$, respectively. In terms of these quantities, the geodesics, curvatures lines, and asymptotic lines on a smooth surface may be characterized, as loci along which $\kappa _{g} = 0$, $\tau _{g} = 0$, and $\kappa _{n} = 0$, respectively.

3.   New rotation minimizing Darboux frame

Now, we introduce a new rotation minimizing frame using a common tangent vector field to a surface along a curve and call this frame the rotation minimizing Darboux frame.

Definition 3.1. A moving orthogonal frame $\{\boldsymbol{\xi }_{1},$ $\boldsymbol{\xi }_{3}$, $\boldsymbol{\xi }_{3}\}$, along a space curve ${\bf r} (s)$, is called rotation minimizing frame (RMF) with respect to a certain reference direction if its angular velocity $\boldsymbol{\omega }$ has no component along that direction.

Although the Darboux frame is not RMF with respect to ${\bf e}_{i}(i = 1$, 2, 3), one can easily derive such a RMF from it. New plane vectors ($\boldsymbol{ \xi }_{1}$, $\boldsymbol{\zeta }_{2}$) are specified through a rotation of (${\bf e}_{2}$, ${\bf e}_{3}$) according to

with a certain angle $\vartheta (s)$. Here, we will call the set $\{\boldsymbol{ \zeta },$ $\boldsymbol{\zeta }_{1}$, $\boldsymbol{\zeta }_{2}\}\}$ as rotation minimizing Darboux frame (RMDF). Therefore, we have the alternative frame equations:

where ${\bf \omega }(s) = -\kappa _{2}{\bf \zeta }_{1}+\kappa _{1} {\bf \zeta }_{2}$ is the Darboux vector. One can show that:

From Eqs (2.2) and (3.2) we observe that the relative velocity is

This shows that, the Darboux frame involves an additional rotation about the tangent, whose speed equals the geodesic torsion $\tau _{g}(s)$. This examination explains the integral formula of Eq (3.3) for computing the RMDF by rectifying the unwanted rotation of the Darboux frame. Hence, the Darboux frame is conformable with the RMDF for curvature lines, that is, $\tau _{g} = 0$. This is in analogous with Klok's result^[1].

Proposition 3.1. Under the above notations we state the following:

(1) If ${\bf \gamma }(s)$ is a geodesic curve on $M$, then the curvatures $\kappa _{1}(s)$, and $\kappa _{2}(s)$ satisfy the following:

(2) If ${\bf \gamma }(s)$ is an asymptotic curve on $M$, then the curvatures $\kappa _{1}(s)$, and $\kappa _{2}(s)$ satisfy the following:

3.1.   Sweeping surfaces due to RMDF

In this subsection, we give the parametric representations of sweeping surface through the spine curve ${\bf \gamma }(s)$ on the surface $M$ in the following: The sweeping surface associated to ${\bf \gamma }(s)$, is the envelope of the family of unit spheres, with the center on the curve ${\bf \gamma }(s)\in M$.

Remark 3.1. Clearly, if ${\bf \gamma }(s)$ is a straight line, thus the sweeping surface is just a circular cylinder, having ${\bf \gamma }(s)$ as symmetry axis. If, on the other hand, ${\bf \gamma }(s)$ is a circle, then the corresponding sweeping surface is a torus.

Now, it is easy to see that the connect between the spheres from the family and the sweeping surface is a great circle of the unit sphere, lying in the subspace $Sp\{\boldsymbol{\zeta }_{1}(s), \boldsymbol{\zeta }_{2}(s)\}$, of the spine curve ${\bf \gamma }(s)$. Let us indicate by ${\bf q}$ the position vector attaching the point from the curve ${\bf \gamma }(s)$ with the point from the sweeping surface. Then, clearly, we have

where the unit vector ${\bf r}$ itself lies in the same subspace $Sp\{ \boldsymbol{\zeta }_{1}(s), \boldsymbol{\zeta }_{2}(s)\}$. Let us indicate by the angle $u$ between the vectors ${\bf r}$ and $\boldsymbol{\zeta }_{1}$. Then, as one can see immediately, we have

which is the characteristic circles of sweeping surface. Combining Eqs (3.4) and (3.5), we see that we obtained a representation of the sweeping surface,

This representation of $\Upsilon$ excludes sweeping surfaces with stationary vector $\boldsymbol{\zeta }$, because its geometrical properties that is not very important and very easy to be studied.

The ${\bf q}^{\prime }s$ tangent vectors are

Then,

which shows that surface normal is included in the subspace $Sp\{\boldsymbol{ \zeta }_{1}(s), \boldsymbol{\zeta }_{2}(s)\}$, since it is orthogonal to $\boldsymbol{ \zeta }$. The coefficients of the first fundamental form $g_{11}$, $g_{12}$ and $g_{22}$ are

For the second fundamental form, we have

Hence, the elements of the second fundamental form $h_{11}$, $h_{12}$, and $h_{22}$ are

Then, the $u$-and $s$ curves are curvature lines, that is, $g_{12}$ and $h_{12 \; }$ vanish identically ($g_{12} = h_{12\; } = 0)$. Thus, the Gaussian and mean curvature are calculated as

and

Corollary 3.1. The sweeping surface defined by Eq (3.6) has a constant Gaussian curvature iff

for some real constant c.

Corollary 3.2. The sweeping surface defined by Eq (3.6) has a constant mean curvature iff

for some real constant c.

Corollary 3.3. The sweeping surface defined by Eq (3.6) is a ($K(s, u), H(s, u))$-Weingarten surface.

Corollary 3.4. The sweeping surface defined by Eq (3.6) is a ($K(s, u), H(s, u))$-linear Weingarten surface iff

where c, c$_{1}$ and c$_{2}$ are not all zero real numbers.

On the other hand, the isoparametric curve

is a planar unit speed curvature line. Equation (3.10) define a set of one-parameter set of planes in $\mathbb{E}^{3}$. The unit tangent vector to ${\bf \beta }(u)$ is

and thus the unit principal normal vector of $\boldsymbol{\beta }(u)$ is given by

Thus, the surface normal ${\bf u(}s_{0}, u)$ is parallel to the principal normal ${\bf n}_{\beta }$, that is, the curve $\boldsymbol{\beta }(u)$ is a geodesic planar curvature line, and cannot be asymptotic curve.

Surfaces whose parametric curves are curvature lines have several implementations in geometric design^[1,2,3,4]. In the situation of sweeping surfaces, one has to figure the offset surfaces ${\bf q}_{f}(s, u) = {\bf q}(s, u)+f$ ${\bf u(}s, u)$ of a given surface ${\bf q}(s, u)$ at a certain distance $f$. In consequence of this equation, the offsetting process for sweeping surface can be reduced to the offsetting of planar profile curve, which is considerably easier to deal with. Hence, we can state the following proposition:

Proposition 3.2. Consider a sweeping surface $\Upsilon$ defined by Eq (3.6). Let ${\bf x}_{f}(u)$ be the planar offset of the profile ${\bf r}(u)$ at constant distance $f$. Then the offset surface ${\bf q} _{f}(s, u)$ is still a sweeping surface, generated by the spine curve ${\bf \gamma }(s)$ and profile curve ${\bf r}_{f}(u)$.

3.1.1.   Singularity and convexity of sweeping surfaces

Singularities and convexity are useful for grasping the ownerships of sweeping surfaces and are investigated in the following:

The sweeping surface $\Upsilon$ has singular points iff the first derivatives are linearly dependent, that is,

Since ${\bf u}$ is a nonzero unit vector, then $1-\kappa _{1}\cos u-\kappa _{2}\sin u = 0$, that is,

and

Hence, there are two singular points on every generating circle. Connecting these two sets of singular points gives two curves that contain all the singular points of a sweeping surface. From Eqs (3.6) and (3.12) it follows that the expression of the two curves is

From the above analysis it can easily be seen that:

Corollary 3.5. The sweeping surface $\Upsilon$ represented by Eq (3.6), has no singular points if the condition

is satisfied.

In Computer Aided Geometric Design, conditions that guarantee the convexity of a surface are required in various applications (such as manufacturing of sculptured surfaces, or layered manufacturing). In the case of the sweeping surface $\Upsilon$, however, the convexity can be controlled with the help of the differential geometric properties. Therefore, we discuss the Gaussian curvature $K(s, u) = \chi _{1}\chi _{2}$; $\chi _{i}(s, u)$ ($i = 1, 2$) are the principal curvatures, as follows:

Since $g_{12} = h_{12\; } = 0$, the value of one principal curvature is

The other principal curvature is easy to get

On the other hand, the curvature for the s-curves (u-constant) can be obtained as:

In view of Meusnier's theorem, the expression of $\chi _{2}(s, u)$ in Eq (3.16) is

Here $\psi = \cos ^{-1} < {\bf n, u > }$. Thus, the the Gaussian curvature $K(s, u)$ can be obtained as:

We now concentrate on the curves on $\Upsilon$ that are created by parabolic points, that is, points with vanishing Gaussian curvature. These curves separate elliptic ($K > 0$, locally convex) and hyperbolic ($K < 0$, hence non-convex) parts of the surface. From Eq (3.18), it follows that

It can be seen that there are two main cases that cause parabolic points:

Case 3.1. When $\chi (s, u) = 0$, that is $\kappa = 0$. Thus, a planar point of the spine curve ${\bf \gamma }$ generates a parabolic curve u = const. on $\Upsilon$. In other words, the spine curve ${\bf \gamma }$ is degenerate to a straight line. Therefore, an inflection or flat point of the spine curve gives a parabolic curve u = const.

Case 3.2. When $\psi = \frac{\pi }{2}$($< {\bf n, u > = }0$), that is, the osculating plane of ${\bf \gamma }$ at each point coincides with the tangent plane to the surface $\Upsilon$ at that point. Then, the spine curve ${\bf \gamma }$ is not only a curvature line but also an asymptotic curve on $\Upsilon$.

In fact we have the following:

Corollary 3.6. Consider a sweeping surface represented by Eq (3.6) with spine and profile curves have non-vanishing curvatures anywhere. If the spine curve ${\bf \gamma }$ is a curvature line and also asymptotic curve, then $\Upsilon$ has parabolic points.

3.2.   Developable surfaces

This part exmaine in what conditions the sweeping surfaces are developable surfaces. Therefore, we analyze the case that the profile curve ${\bf r} (u)$ degenerates into a line. Then, we have the following developable surface

We also have that

It is easy to show ${\bf P}(s, 0) = \boldsymbol{\alpha }(s)$ (resp. ${\bf P} ^{\bot }(s, 0) = \boldsymbol{\alpha }(s)$), $0\leq s\leq L$, that is, the surface $S$ (resp. $S^{\bot }$) interpolate the curve ${\bf \gamma }(s)$. Furthermore, since

then $S^{\bot }$ is the normal developable surface of $S$ along ${\bf \gamma }(s)$. Hence, the curve ${\bf \gamma }(s)$ is a curvature line on $S$ (resp. $S^{\bot }$).

Theorem 3.1. Let $\Upsilon$ be the sweeping surface expressed by Eq (3.6). Then we have the following:

(1) the developable surfaces $S$ and $S^{\bot }$ intersect along ${\bf \gamma }(s)$ at a right angle,

(2) the curve ${\bf \gamma }(s)$ is a curvature line on $S$ and $S^{\bot }$.

Theorem 3.2. (Existence and uniqueness). Under the above notations there exists a unique developable surface represented by Eq (3.19).

Proof. For the existence, we have the developable represented by Eq (3.19). Furthermore, since $S$ is a ruled surface, we may write that

It can be immediately seen that $S$ is developable iff

On the other hand, in view of Eq (3.21), we have

where $\theta = \theta \left(s, u\right)$ is a differentiable function. Furthermore, the normal vector ${\bf P}_{s}\times {\bf P}_{v}$ at the point $(s, 0)$ is

Thus, from Eqs (3.24), and (3.25), one finds that:

which follows from Eq (3.23) that $\eta _{2}\eta _{3}\kappa _{1} = 0$, which leads to $\eta _{2}\eta _{3} = 0$, with $\kappa _{1}\neq 0$. If $(s, 0)$ is a regular point (i.e., $\theta \left(s, 0\right) \neq 0$), then $\eta _{2}(s)\neq 0$, and $\eta _{3} = 0$. Therefore, we obtain ${\bf \eta }(s) = {\bf \zeta }_{2}$. This means that uniqueness holds.

As an application (such as flank milling or cylindrical milling), during the movement of the RMDF along ${\bf \gamma }$, let a cylindrical cutter be rigidly linked to this frame. Then the equation of a set of cylindrical cutters, which is defined by the movement of cylindrical cutter along ${\bf \gamma }(s)$, can be gotten as follows:

where $\rho$ denotes cylindrical cutter radius. This surface is a developable surface offset of the surface ${\bf P}(s, u)$. The equation of $S_{f}$, can therefore be written as:

The normal vector of cylindrical cutter can be represented as

Also, from Eq (3.27), we have

The derivative of Eq (3.30) with respect to $s$ can be derived as follows

Equation (3.22) shows that the vector $\overline{{\bf P}}_{s}(s, u)$ is orthogonal to the normal vector $\boldsymbol{\zeta }_{1}$. And, the vector $\boldsymbol{\zeta }_{1}$ is orthogonal to the tool axis vector $\boldsymbol{\zeta } (s)$. Subsequently, the envelope surface of the cylindrical cutter and the developable surface ${\bf P}(s, u)$ have the common normal vector and the distance between the two surfaces is cylindrical cutter radius $\rho$. Hence, we can draw a conclusion as follows:

Proposition 3.3. Consider a developable surface $S$ defined by Eq (3.19). Let $S_{f}$ be the envelope surface of cylindrical cutter at distance $\rho$. Then the two surfaces $S$ and $S_{f}$ are offset developable surfaces.

As it is will known, there are three types of developable surfaces, the given curve can be distributed into three kinds correspondingly^{[12,13,14,15]}. In what follows, we will discuss the relationship between the given curve ${\bf \gamma }(s)\in M$ and its isoparametric developable surface. The first case is when,

In this situation, $S$ is referred to as a cylindrical surface. Since ${\bf \zeta }_{1}$ is a nonzero unit vector, then $\Upsilon$ is a cylindrical surface iff

Similarly, we can also have $\boldsymbol{\zeta }_{2}\times \boldsymbol{\zeta } _{2}^{^{\prime }}\neq {\bf 0}$. In this situation, $S$ is referred to as a non-cylindrical surface. Therefore, the first derivative of the directrix is

where ${\bf c}^{^{\prime }}$ is the first derivative of the striction curve, $\sigma (s)$ is a smooth function. By an immediate calculation, we can show that

Then the next two situations hold:

The first situation is when the first derivative of the striction curve is ${\bf c}^{^{\prime }} = 0$. Geometrically this position implies that the striction curve degenerates to a point, and $S$ becomes a cone; the striction point of a cone is generally referred to as the vertex. By using Eqs (3.2) and (3.34) we have that $S$ is a cone iff there exists a fixed point ${\bf c}$ and a function $\sigma (s)$ such that $\sigma \kappa _{2} = -1, \ \sigma ^{^{\prime }} = 0$, which imply that

The second situation is when ${\bf c}^{^{\prime }}\neq 0$, that is,

From Eq (3.35), we have $< {\bf c}^{^{\prime }}, \boldsymbol{\zeta }_{2}\times \boldsymbol{\zeta }_{2}^{^{\prime }} > = 0$, that is, ${\bf c}^{^{\prime }}\in Sp\{\boldsymbol{\zeta }_{2}$, $\boldsymbol{\zeta }_{2}^{^{\prime }}\}$. The condition for ${\bf c}$ to be striction curve is therefore equivalent to ${\bf c} ^{^{\prime }}$ and $\boldsymbol{\zeta }_{2}^{^{\prime }}$ are perpendicular to each other. Therefore, we may conclude that the ruling is parallel to the first derivative of the striction curve, which is also the tangent of the striction curve. This ruled surface is referred too as a tangent ruled surface. So, the surface $S$ is a tangent surface iff there exists a curve ${\bf c}(s)$ so that $\sigma (s) = const.\neq \frac{1}{\kappa _{2}}$.

3.3.   Application

In this subsection, as an application of our main results, we give the following examples.

Example 1. Let $M$ be a hyperboloid of one sheet defined by

It is easy to see that ${\bf \gamma }(s) = \left(\cos s, \sin s, 0\right)$ lies on $M$. Then, we have the Darboux frame as follows:

The normal curvature, the geodesic curvature, and the geodesic torsion of ${\bf \gamma }(s)$ on $M$, respectively, are

Then $\vartheta (s) = \vartheta _{0}$ is a constant, moreover,

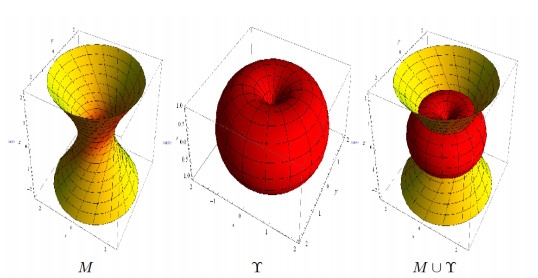
1) If we take $\vartheta _{0} = \frac{\pi }{2}$($\kappa _{2}(s) = 0$), then we immediately obtain a sweeping surface given by

The graphs of the surfaces $M$, $\Upsilon$, and $M\cup \Upsilon$ are shown in Figure 1; $0\leq u, s\leq 2\pi$. Obviously, $\kappa _{2}(s) = 0$ satisfies Eq (3.33), and the developable surface

is a cylinder with ${\bf \gamma }(s)$ as a curvature line; $0\leq s\leq 2\pi$, and $-1\leq u\leq 1$ (Figure 2).

2) In the case of $\vartheta _{0} = \frac{\pi }{4}(\kappa _{2}(s) = const.$), we obtain a sweeping surface given by

The graphs of the surfaces $\boldsymbol{M}$, $\boldsymbol{\Upsilon}$, and $\boldsymbol{M\cup \Upsilon }$ are shown in Figure 3; $0\leq u, s\leq 2\pi$. Also, the developable surface

is a cone with ${\bf \gamma }(s)$ as a curvature line; $0\leq s\leq 2\pi$, and $-5\leq u\leq 2$ (Figure 4).

Example 2. Consider the tubular surface parameterized by

where $0\leq u, s\leq 2\sqrt{2}\pi$. It is clear that ${\bf \gamma } (s) = \left(\cos \frac{s}{\sqrt{2}}, \sin \frac{s}{\sqrt{2}}, \frac{s}{\sqrt{2}} \right)$ lies on $M$. By a similar procedure as in Example 1, we have

Then $\vartheta (s) = -\frac{s}{2}+\vartheta _{0}$. If we choose $\vartheta _{0} = 0$, for example, we have

Therefore, the sweeping surface is

The graphs of the surfaces $M$, $\Upsilon$, and $M\cup \Upsilon$ are shown in Figure 5; $0\leq u, s\leq 2\sqrt{2}\pi$. In view of $\kappa _{2}(s)\neq \kappa _{2}(s_{0})$ and Eq (3.37), the developable surface

is a tangent surface with ${\bf \gamma }(s)$ as a curvature line; $0\leq s\leq 2\sqrt{2}\pi$, and $-1\leq u\leq 1$ (Figure 6).

4.   Conclusions

This paper introduce and study sweeping surface with a new RMDF associated with a curve on the surface. The paper further investigated the problem of requiring the sweeping surface is a developable surface. There are several opportunities for further work. An analogue of the problem addressed in this paper may be consider for surfaces in Minkowski 3-space. We will study this problem in the future.

Conflict of interest

All of the data are available within the paper. The authors have no conflicts of interest.