New error bound for linear complementarity problem of $S$-$SDDS$-$B$ matrices

1.   Introduction

Many fundamental problems in optimization and mathematical programming can be described as a linear complementarity problem (LCP). Such as quadratic programming, nonlinear obstacle problem, invariant capital stock, the Nash eqilibrium point of a bimatrix game, optimal stopping, free boundary problem for journal bearing and so on, see ^[1,2,3]. The error bound on the distance between an arbitrary point in $\mathbb{R}^{n}$ and the solution set of the LCP plays an important role in the convergence analysis of algorithm, for details, see ^[4,5,6,7].

It is well known that LCP has a unique solution for any vector $q\in\mathbb{R}^{n}$ if and only if $M$ is a $P$-matrix. Some basic definitions for the special matrix are given below: A matrix $M = (m_{ij})\in\mathbb{R}^{n\times n}$ is called a $Z$-matrix, if $m_{ij}\leq 0$ for any $i\neq j$; a $P$-matrix, if all its principal minors are positive; an $M$-matrix, if $M^{-1}\geq 0$ and $M$ is a $Z$-matrix; an $H$-matrix, if its comparison matrix $\langle M\rangle$ is an $M$-matrix, where the comparison matrix is given by

Linear complementarity problem is to find a vector $x\in \mathbb{R}^{n}$ such that

or to prove that no such vector $x$ exists, where $M = (m_{ij})\in\mathbb{R}^{n\times n}$ and $q\in\mathbb{R}^{n}$. One of the essencial problems in the LCP($M$, $q$) is to estimate

which is used to bound the error $\|x-x^{*}\|_{\infty}$, that is

where $x^{*}$ is the solution of the LCP($M, q$), $r(x) = min\{x, Mx+q\}$, $D = diag(d_{i})$ with $0\leq d_{i}\leq\; 1$, and the min operator $r(x)$ denote the componentwise of the two vectors. When real $H$-matrices with positive diagonal entries form a subclass of $P$-matrices, the error bound becomes simpler (see formula (2.4) in ^[8]). Nowadays, many scholars interest in the research on special $H$-matrices, such as $QN$-matrices ^[9], $S$-$SDD$ matrices ^[10], Nekrasov matrices ^[11] and Ostrowski matrices ^[12]. The corresponding error bounds for LCPs of $QN$-matrices are achieved by Dai et al. in ^[13] and Gao et al. in ^[14]. A new error bound for the LCP of $\Sigma$-$SDD$ matrices was given in ^[15], which only depended on the entries of the involved matrices.

When the matrix $A$ is not an $H$ matrix we can not use formula (2.4) in ^[8]. However, for some subclasses of $P$-matrices that are not $H$-matrices, error bounds for LCPs have also been needed. For example, for $SB$-matrices ^[16], for $B^{S}$-matrices ^[17], for weakly chained diagonally dominant $B$-matrices ^[18], for $DB$-matrices ^[19] and for $MB$-matrices ^[20]. $B$-matrices as an important subclass of $P$-matrices has been researched for years and has achieved fruitful results, see ^{[18,21,22,23,24,25]}.

In this paper, we focus on the error bound for the LCP($M, q$) when $M$ is an $S$-$SDDS$-$B$-matrix, that is a $P$-matrix. In Section 2, we introduce some notations, definitions and lemmas, which will be used in the subsequence analysis. In Section 3, a new error bound is presented, then the new error bound is compared with the bound in ^[1]. In Section 4, we give some numerical examples and graphs to show the efficiency of the method in our paper.

2.   Preliminaries

In this section, some notations, definitions and lemmas are recalled.

Give a matrix $A = (a_{ij})\in \mathbb{R}^{n\times n}$ and a subset $S\subset\langle n\rangle$, $n\geq 2$, we denote

and also

$\bar{S}\cup S = \langle n\rangle$, $\bar{S}$ is the complement of $S$ in $\langle n\rangle$.

In according with ^[26], a matrix $A = (a_{ij})$, $n\geq 2$ is said to be $S$-$SDD$ if the following conditions are fulfilled:

and

We extend the $S$-$SDD$ matrices by introducing the following definitions.

Definition 2.1. ^[26] A matrix $A = (a_{ij})\in\mathbb{R}^{n\times n}$ is said to be $S$-$SDDS$ ($S$-$SDD$ Sparse) if the following conditions are satisfied:

(i) $|a_{ii}| > r_{i}^{S}(A)$ for all $i\in S$,

(ii) $|a_{jj}| > r_{j}^{\bar{S}}(A)$ for all $j\in \bar{S}$,

(iii) For all $i\in S$ and all $j\in\bar{S}$ such that $a_{ij}\neq 0$ or $a_{ji}\neq 0$

If $A = (a_{ij})\in\mathbb{R}^{n\times n}$ for each $i = 1, \cdots, n$ and $r_{i}^{+}: = \max\{0, a_{ij}|j\neq i\}$, then we write $A = B^{+}+C$, where

Definition 2.2. Suppose that $A = (a_{ij})\in\mathbb{R}^{n\times n}$, $n\geq 2$ is matrix with the form of $A = B^{+}+C$, we say $A$ is an $S$-$SDDS$-$B$ matrix if and only if $B^{+}$ is an $S$-$SDDS$ matrix with positive diagonal entries.

There is an equivalence definition in ^[27], which is closely related to strictly diagonally dominant matrices.

Definition 2.3. ^[27] Let $A = (a_{ij})\in\mathbb{R}^{n\times n}$ and $A = B^{+}+C$, where $B^{+}$ is defined as $(2.2)$, then $A$ is an $B$-matrix if and only if $B^{+}$ is a strictly diagonally dominant matrix.

Immediately, we know $S$-$SDDS$-$B$ matrices contain $B$-matrices from Definition 2.3. That is

Now, we will introduce some useful lemmas.

Lemma 2.1. ^[26] Let $A = (a_{ij})\in\mathbb{R}^{n\times n}, n\geq 2$ is an $S$-$SDDS$ matrix, then $A$ is a nonsingular $H$-matrix.

Lemma 2.2. ^[26] Let $A = (a_{ij})\in\mathbb{R}^{n\times n}, n\geq 2$ is an $S$-$SDDS$ matrix, then

where

Lemma 2.3. ^[1] Let $A\in\mathbb{R}^{n\times n}$ is a $B$-matrix, $B^{+}$ is the matrix in $(2.2)$, then

where $\beta = \min_{i\in N}\{\beta_{i}\}$, $\beta_{i} = b_{ii}-\sum_{j\neq i}^{n}|b_{ij}|$.

Lemma 2.4. ^[21] Let $\gamma > 0$ and $\eta > 0$, for any $x\in[0, 1]$,

Lemma 2.5. ^[27] Let $A\in \mathbb{R}^{n\times n}$ is a nonsingular $M$-matrix, $P$ is a nonnegative matrix with rank $1$, then $A+P$ is a $P$-matrix.

3.   Main results

In this section, a new error bound of LCP($M, q$) is presented when $M$ is an $S$-$SDDS$-$B$ matrix. Firstly, we prove that an $S$-$SDDS$-$B$ matrix is a $P$-matrix.

Lemma 3.1. Let $A\in\mathbb{R}^{n\times n}$ ($n\geq 2$) be an $S$-$SDDS$-$B$ matrix, then $A$ is a $P$-matrix.

Proof. By Definition 2.2, we have that $C$ in (2.2) is a nonnegative matrix with rank 1. By the fact that $S$-$SDDS$ matrix is a nonnegative $H$-matrix, we have $B^{+}$ is a nonnegative $M$-matrix. We can conclude $A$ is a $P$-matrix from Lemma 2.5.

Lemma 3.2. Suppose that $M = (m_{ij})\in\mathbb{R}^{n\times n}$ ($n\geq 2$) is an $S$-$SDDS$ matrix with positive diagonal entries, let

then $\tilde{M}$ is an $S$-$SDDS$ matrix with positive diagonal entries.

Proof. From $\tilde{M} = I-D+DM = (\tilde{m}_{ij})$, we have

Because $M$ is an $S$-$SDDS$ matrix with positive diagonal entries and $D = diag(d_{i}), 0\leq d_{i}\leq 1$, for any $i\in S$, we get

Similarly, for some $j\in \bar{S}$, we have

For any $i\in S$, $j\in\bar{S}$, we obtain

From Definition 2.1, $\tilde{M}$ is an $S$-$SDDS$ matrix with positive diagonal entries.

Theorem 3.1. Let $A = [a_{ij}]\in\mathbb{R}^{n\times n}$ is an $S$-$SDDS$-$B$ matrix, denote $A = B^{+}+C$, where $B^{+} = (b_{ij})$ is defined as $(2.2)$, then

where

Proof. We denote $A_{D} = I-D+DA$, then

where $B_{D}^{+} = I-D+DB^{+}$, $C_{D} = DC$. Since $B^{+}$ is an $S$-$SDDS$ matrix with positive diagonal entries, it's easy to know $B_{D}^{+}$ is an $S$-$SDDS$ matrix from Lemma 3.2.

Note that

the estimation of the $\|(B_{D}^{+})^{-1}\|_{\infty}$ will be given below. Since $B_{D}^{+} = I-D+DB^{+} = :(\tilde{b}_{ij})$, from Lemma 2.2, we have

When $r_{i}^{S}(B_{D}^{+}) = 0$, it is easy to get $r_{i}^{S}(B^{+}) = 0$, or $d_{i} = 0$ for any $i\in N$.

(1) If $d_{i} = 0$, for any $i\in N$, we get

(2) If $r_{i}^{\bar{S}}(B^{+}) = 0$, for any $i\in S$, we have

(3) If $r_{i}^{\bar{S}}(B^{+}) = 0$, for any $i\in S$, $j\in\bar{S}$, we obtain

(4) If $r_{i}^{\bar{S}}(B_{D}^{+})\neq0$, there exist $\tilde{b}_{ij}\neq 0$ for some $j\in \bar{S}$, we derive $\|(B_{D}^{+})^{-1}\|_{\infty}$ as follow:

(5) If $r_{j}^{S}(B_{D}^{+})\neq0$, there exist $\tilde{b}_{ji}\neq 0$ for some $i\in S$, we arrive at the inequality

Consequently, (3.1) holds. The proof is completed.

The bound in (3.1) also holds for $B$-matrix, because $B$-matrix is a subclass of $S$-$SDDS$-$B$-matrix. Next, we will indicate that the bound in Theorem 3.1 is better than that in Lemma 2.3 in some conditions.

Theorem 3.2. If $A = (a_{ij})\in \mathbb{R}^{n\times n}$ is an S-SDDS-B matrix which can be written as $A = B^{+}+C$, where $B^{+} = (b_{ij})$ and $C$ are as $(2.2)$. For all $i\in S$, $j\in\bar{S}$, if $b_{ii}-r_{i}^{S}(B^{+}) < 1$, $b_{jj}-r_{j}^{\bar{S}}(B^{+}) < 1$, then

Proof. From Lemma 2.3, $\beta = \min_{i\in N}\{\beta_{i}\}$ and $\beta_{i} = b_{ii}-\sum_{j\in N, j\neq i}b_{ij}$, when $b_{ii}-r_{i}^{S}(B^{+}) < 1$ and $b_{jj}-r_{j}^{\bar{S}}(B^{+}) < 1$, it is obvious that

In the same way, we get

When $b_{ii}-r_{i}^{S}(B^{+}) < 1$ and $b_{jj}-r_{j}^{\bar{S}}(B^{+}) < 1$, it holds that

When $b_{jj}-r_{j}(B^{+}) > b_{ii}-r_{i}(B^{+}) = b_{ii}-r_{i}^{S}(B^{+})-r_{i}^{\bar{S}}(B^{+})$, for any $i\in S$, $j\in\bar{S}$, we can multiply $r_{i}^{\bar{S}}(B^{+})$ on two sides and plus $(b_{ii}-r_{i}^{S}(B^{+}))(b_{jj}-r_{j}^{\bar{S}}(B^{+}))$, then

we have

When $b_{jj}-r_{j}(B^{+}) = b_{jj}-r_{j}^{S}(B^{+})-r_{j}^{\bar{S}}(B^{+})\leq b_{ii}-r_{i}(B^{+})$, $r_{j}^{S}(B^{+})$, the following inequality can obtain in the same way

So the conclusion in $(3.8)$ holds.

4.   An application

In this section, an example is given to show the advantage of the bound in Theorem 3.1.

Example 1. Consider the $S$-$SDDS$-$B$ matrix

Matrix $A$ can be split into $A = B^{+}+C$, where

Since $A$ is a $B$-matrix, by Lemma 2.3, then

Because $A$ is a $B$-matrix, so it is an $S$-$SDDS$-$B$ matrix. When $S = (1, 2, 3), \bar{S} = (4)$, we also can compute the complementarity error bound by Theorem $3.1$ as follow:

The results in $(4.1)$ and $(4.2)$ indicate that Theorem $3.1$ is better than Lemma $2.3$.

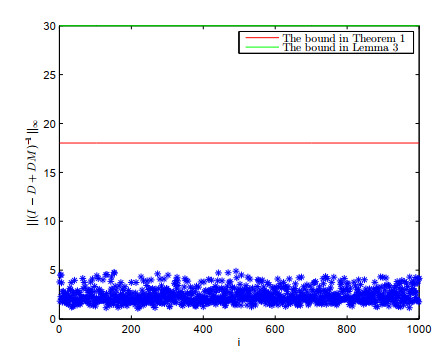
It is shown by Figure 1, in which the first 1000 matrices are given by the following MATLAB codes, that 18 is better than 30 for $\max\|(I-D+DA)^{-1}\|_{\infty}$. Blue stars in Figure 1 represent the $\|(I-D+DA)^{-1}\|_{\infty}$ when matrices $D$ come from 1000 different random matrices in [0, 1].

MATLAB codes: For i = 1:1000; D=diag(rand(5,1)); end.

Example 2.

$A$ can be split into $A = B^{+}+C$, where

Taking in account that $B^{+}$ is not a a strictly diagonally dominant matrix and so $A$ is not a $B$-matrix. It is easy to check that when $S = \{1, 2, 3, 4\}$ and $\bar{S} = \{5, 6, 7\}$, it fulfills Definition $2.2$. Therefore, by Theorem $1$, we obtain

5.   Conclusions

In this paper, we first give a new error bound for the LCP($M$, $q$) with $S$-$SDDS$-$B$ matrices, which depends only on the matrix of $M$. Then, based on the new result, we compare it with the error bound in ^[1]. From Figure 1, we can find that our result improves that in ^[1].

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11861077), the Foundation of Science and Technology Department of Guizhou Province (20191161, 20181079), the Research Foundation of Guizhou Minzu University (2019YB08) and the Foundation of Education Department of Guizhou Province (2018143).

Conflict of interest

The authors declare that they have no competing interests.